2. 安徽理工大学 机械工程博士后科研流动站, 安徽 淮南 232001;
3. 江南大学 机械工程学院, 江苏 无锡 214122;
4. 上海交通大学 机械系统与振动国家重点实验室, 上海 200240
2. Postdoctoral Research Station of Mechanical Engineering, Anhui University of Science and Technology, Huainan 232001, China ;
3. School of Mechanical Engineering, Jiangnan University, Wuxi 214122, China ;
4. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University, Shanghai 200240, China
六自由度Gough-Stewart并联机器人机构已被应用于并联机床、微操作机器人、空间对接机构模拟器等多个高精技术领域[1].其空间多环并联运动链属性,决定了该类型机构存在复杂的奇异位形.并联机器人机构若处于奇异状态,机构将严重失稳、失控甚至被损坏,因此,有必要在探索得到并联机器人奇异位形分布规律的基础上进一步研究如何规避奇异.对于并联机器人来说,规避机构奇异位形的一个重要方法是增加冗余驱动[2-5].但对于六自由度的Gough-Stewart并联机器人机构,一般采用添加相同的冗余分支,由于被动关节转角及分支杆之间的干涉限制,会带来机构控制的复杂性,并且会进一步限制机构的工作空间.另一个规避奇异的有效方法便是利用路径规划来避免奇异位形,即基于任务空间计算出预期的运动轨迹,对其整个工作过程实施无奇异的路径规划,以保证机器人在整个任务操作过程中,机构不会出现奇异位形.文献[6]将并联机构的一系列奇异点看成是工作空间内的障碍物,提出利用一种局部避障算法来避开机构奇异点.任意给定起始点和目标点,文献[7]给出了一种能够有效地规避并联机构奇异位形的轨迹规划算法,但没有给出并联机构奇异轨迹分布性质以及无奇异路径存在与否的具体判别方法.白志富和陈五一[8]研究了不同位置正解之间的无奇异连接路径问题,指出如果机构的2个正解位形对应的雅可比矩阵行列式的值符号相反,则一定不存在无奇异路径能将这2个位形连接,如果2个雅可比矩阵行列式值同时为正或同时为负,则需要依赖于机构奇异轨迹分布情况进行判定.目前已产生多种奇异位形的判别方法,主要有代数法[9-14]、线几何及螺旋理论法[15-19]以及其他各种方法[20-23]等.其中,代数法能够掌握机构奇异轨迹在机构位形空间内的分布情况,从而为进一步研究基于轨迹规划方法的奇异规避研究提供必要的依据.Bandyopadhyay等[12]和Huang等[13]通过建立机构的雅可比矩阵,分别研究了Gough-Stewart并联机构位于Z截面和θ截面上的奇异轨迹几何性质及其分布情况.
本文在利用代数法得到Gough-Stewart并联机器人机构位于给定姿态时的奇异轨迹方程以及奇异轨迹几何性质基础上,得到机构位于给定姿态时的动平面上无奇异路径规划方法.
1 奇异轨迹及其几何性质机构动、定平台分别为2个半规则正六边形B1B2…B6,C1C2…C6,6个支链BiCi均通过SPS或SPU支链相连.点Bi和点Ci分别为动平台和定平台与各支链连接的铰接点,点P和点O分别为六角动平台和六角定平台的几何中心点,Aj (j=1,3,5)为六角定平台长边延长线的交点,βm和βb分别为动平台和定平台对应边的中心角,Rm和Rb分别为动平台和定平台的外接圆半径.Gough-Stewart并联机构的结构简图如图 1所示.
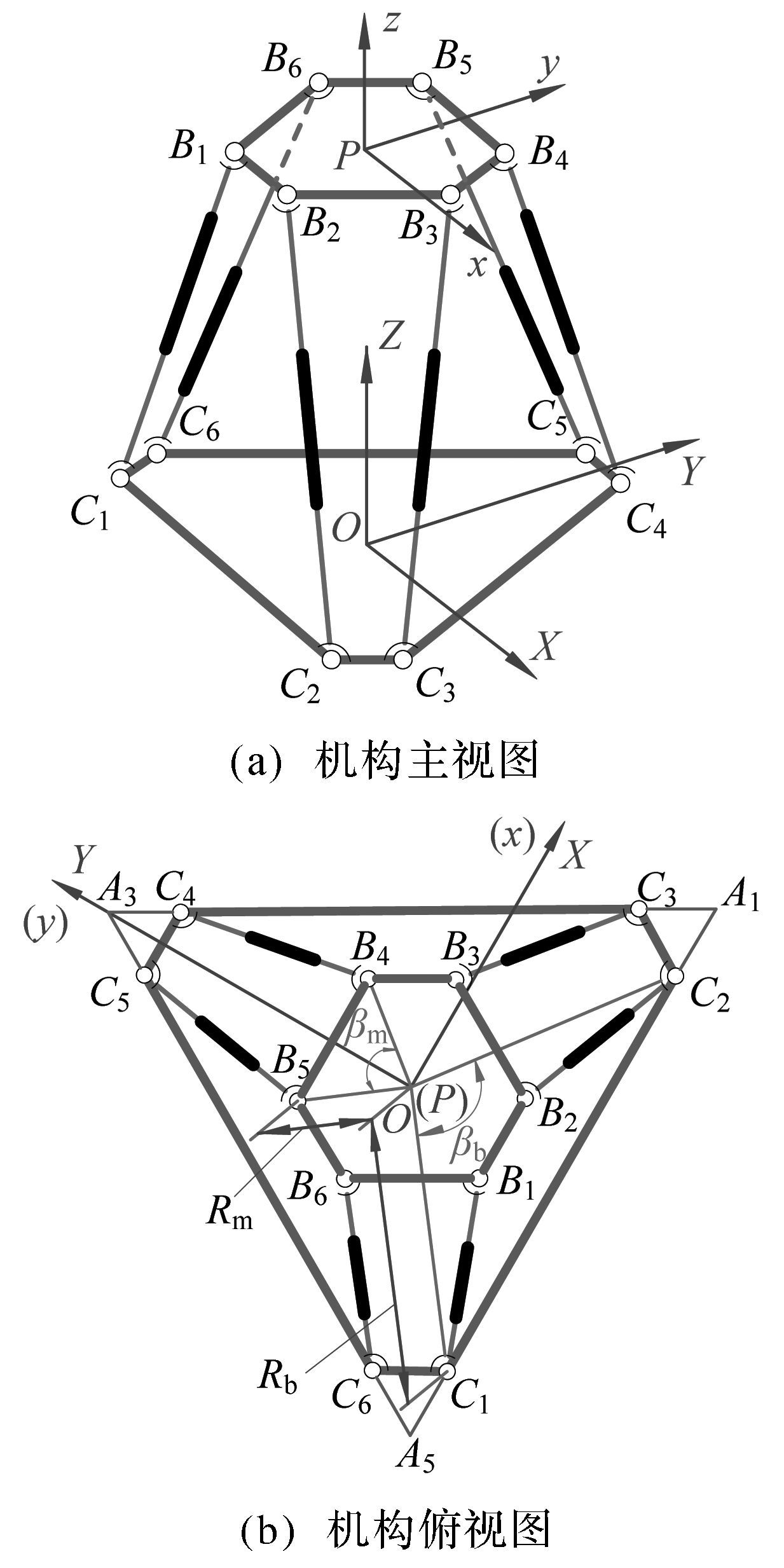
|
| 图 1 Gough-Stewart并联机构的结构简图 Fig.1 Schematic of the Gough-Stewart parallel mechanism |
在动、定平台上分别建立动坐标系P-xyz和固定坐标系O-XYZ.根据坐标变换法则,不难得到Bi在固定坐标系中的位置矢量Bi(i=1,2,…,6), Ci在固定坐标系中的位置矢量Ci(i=1,2,…,6).将它们代入机构的雅可比矩阵[1]
| ${{J}^{T}}={{\left[ \begin{matrix} {{S}_{1}} & {{S}_{2}} & {{S}_{3}} & {{S}_{4}} & {{S}_{5}} & {{S}_{6}} \\ {{S}_{01}} & {{S}_{02}} & {{S}_{03}} & {{S}_{04}} & {{S}_{05}} & {{S}_{06}} \\ \end{matrix} \right]}_{6\times 6}},$ | (1) |
式中:
| ${{S}_{i}}=\frac{{{B}_{i}}-{{C}_{i}}}{\left\| {{B}_{i}}-{{C}_{i}} \right\|},{{S}_{0i}}={{B}_{i}}\times {{S}_{i}}=\frac{{{C}_{i}}\times {{B}_{i}}}{\left\| {{B}_{i}}-{{C}_{i}}\text{ } \right\|}(i=1,2,\ldots ,6).$ |
雅可比矩阵行列式为零或矩阵条件数为无穷大,机构处于奇异位形状态[1].
假定机构的姿态参数给定,令上述雅可比矩阵(1)行列式为零[14],便可得到机构姿态给定时位置位于定坐标系O-XYZ中的奇异轨迹一般符号表达式:
| $\begin{align} & {{f}_{1}}{{Z}^{3}}+{{f}_{2}}X{{Z}^{2}}+{{f}_{3}}Y{{Z}^{2}}+{{f}_{4}}{{X}^{2}}Z+{{f}_{5}}{{Y}^{2}}Z+{{f}_{6}}XYZ+{{f}_{7}}{{Z}^{2}}+{{f}_{8}}XZ+ \\ & {{f}_{9}}YZ+{{f}_{10}}{{X}^{2}}+{{f}_{11}}XY+{{f}_{12}}{{Y}^{2}}+{{f}_{13}}Z+{{f}_{14}}X+{{f}_{15}}Y+{{f}_{16}}=0, \\ \end{align}$ | (2) |
式中: fi (i=1,2,…,16)是姿态参数以及机构构型参数βm,βb,Rm,Rb的显式表示.从式(2)可以看出,式(2)是关于机构3个位置参数X,Y,Z的三次多项式,位置参数X,Y的最高次数均为2,位置参数Z的最高次数为3.
ZYZ-欧拉角(ø,θ,ψ)可以直观地描述动平面和基平面的交线(脊线)位置,故为方便得到机构的位置奇异轨迹性质,在此利用ZYZ-欧拉角(ø,θ,ψ)描述动平台的姿态.
若θ≠0时,机构在给定姿态参数(ø,θ,ψ)时的位姿如图 2所示.将定平台所在平面O-XY定义为“基平面”,将动平台所在平面P-xy定义为“动平面”,动平面P-xy和基平面O-XY之间的夹角为θ.称基平面O-XY与动平面(动平面P-xy)的交线UV为“脊线”,W,V,U三个点分别为脊UV与直线C1C2、直线C3C4、直线C5C6的交点.V-xy为建立在动平面上的随动坐标系,其原点V在定坐标系O-XYZ中的坐标记为(Xv,Yv).记点P在随动坐标系V-xy中的坐标为(x,y),则其与定坐标系中坐标(X,Y,Z)关系为:
| $\left. \begin{matrix} X=xcos~\phi cos~\theta -ysin~\phi +{{X}_{v}}, \\ Y=xsin~\phi cos~\theta +ycos~\phi +{{Y}_{v}}, \\ Z=-xsin~\theta . \\ \end{matrix} \right\}$ | (3) |
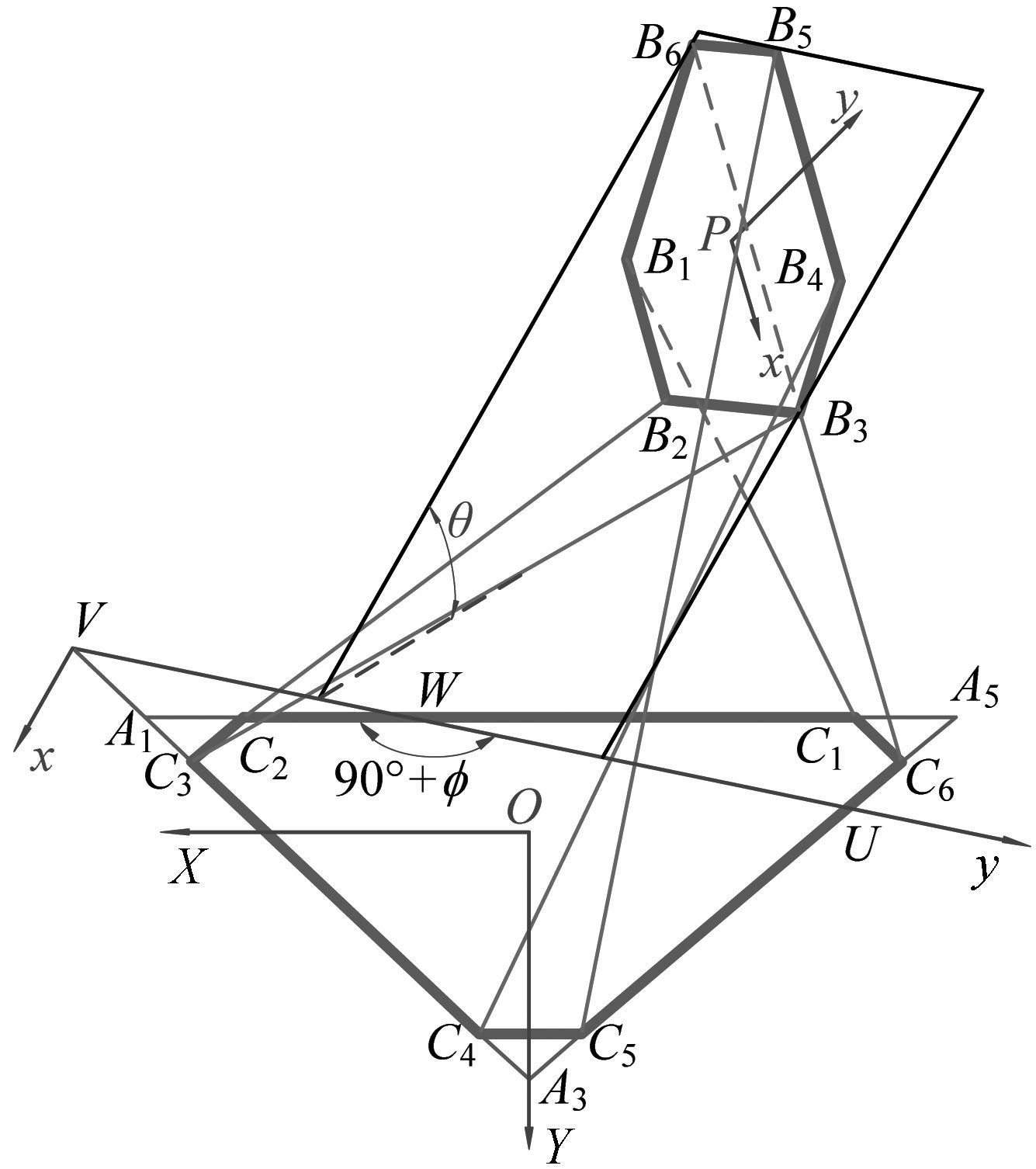
|
| 图 2 机构处于给定姿态时的位形 Fig.2 Pose of the mechanism for a constant-orientation |
将式(3)代入式(2)并考虑到θ ≠0便可得到动平面上的奇异轨迹在随动坐标系V-xy中的方程:
| $a{{x}^{2}}+2bxy+2dx+2ey+f=0.$ | (4) |
式(4)便是机构在随动坐标系V-xy中描述的、位于特征平面上的二维位置奇异轨迹方程.关于动平面上位置奇异轨迹详细推导过程以及动平面上的位置奇异几何性质具体分析,请参阅作者前期研究成果文献[24],限于篇幅,这里直接给出2个重要的推论.
推论1 对于六自由度Gough-Stewart并联机器人机构,若机构在某个动平面上的位置奇异轨迹形式是一对双曲线,那么,其中一条渐近线一定与V-xy坐标系的y轴(脊线)相平行,并且这2条渐近线的方程均可以由形如式(5)与式(6)所示的方程描述:
| $x\text{ }=-e/b,$ | (5) |
| $abx+2{{b}^{2~}}y+2bd-ae=0.$ | (6) |
推论2 对于六自由度Gough-Stewart并联机器人机构,若机构在某个动平面上的位置奇异轨迹形式为一对相交直线,那么,该对相交直线的其中一条直线一定与V-xy坐标系中的y轴(脊线)相平行,另外,这2条相交直线在V-xy坐标系中的方程表示形式与上述双曲线的2条渐近线在V-xy坐标系中的方程表示形式一定相同.
通常情况下,式(2)所示的三次多项式表示的三维奇异轨迹曲面与一般倾斜平面的交线也是一个以三次多项式表示的曲线.然而,机构位于动平面上的奇异轨迹是如式(4)所示的一条具有明显几何性质的二次曲线.如文献[8]所述,机构无奇异路径存在与否的判定需要依赖于机构奇异轨迹分布性质的判别,上述奇异轨迹几何性质极大地方便了对机构实施位于动平面上的无奇异运动路径规划.
2 无奇异路径规划 2.1 无奇异路径存在的条件众所周知,机构在三维空间进行连续的位姿变换时,机构位姿参数一定是连续变化的,这样机构的雅可比矩阵行列式值也必将是连续变化的.记起始点Pi与目标点Pf对应的雅可比矩阵分别为Ji,Jf,若det(Ji)×det(Jf)≤0,由函数的中值定理可知,欲使机构从Pi运动到Pf,机构必然会通过奇异点;若起始位置Pi和目标位置Pf所对应的机构雅可比矩阵行列式值同号,即det(Ji)×det(Jf)>0,则Pi与Pf之间无奇异路径的存在与否,需由起始点Pi、目标点Pf以及奇异轨迹曲线三者之间的相对位置关系确定.机构在任意截面上的奇异轨迹将该截面内的工作区间分成若干不连通的区域,如图 3所示.若Pi与Pf分别位于不同区域内,则Pi与Pf之间不存在无奇异路径;反之,若Pi与Pf位于同一区域内,则Pi与Pf之间存在无奇异路径.
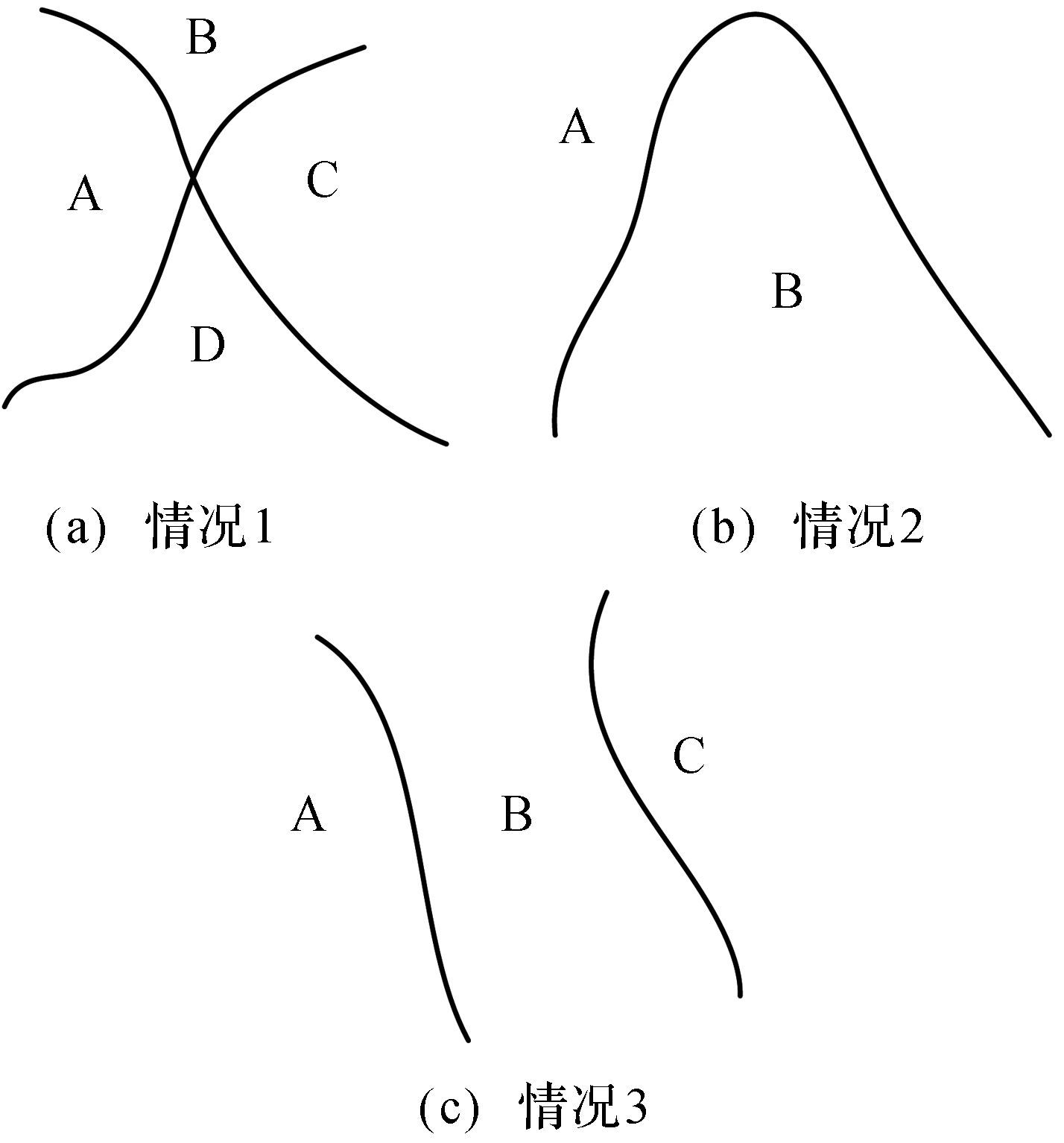
|
| 图 3 动平面上的若干区域 Fig.3 Several zones in the moving plane |
在机构动平面上建立如图 2所示动坐标系V-xy,在该坐标系下建立直线PiPf方程,并与动平面上的位置奇异轨迹曲线方程式(3)联立得方程组:
| $y=\frac{{{y}_{f}}-{{y}_{i}}}{{{x}_{f}}-{{x}_{i}}}(x-{{x}_{i}})+{{y}_{i}},$ | (7a) |
| $a{{x}^{2}}+2bxy+2dx+2ey+f=0.$ | (7b) |
设以上方程组的实数解分别为P1(x1,y1),P2 (x2,y2)(只有1个实数解时可以看成具有2个相等的实数解).这2个实数解也即直线PiPf与动平面上位置奇异二次曲线的交点坐标.如式(7b)所示的动平面上位置奇异轨迹曲线包括:1对双曲线、1对相交直线、1条抛物线、1对平行直线或1条直线[24].
由动平面上的位置奇异轨迹几何性质可以看出,在det(Ji)×det(Jf)>0的情况下,令
δ=-b2≤0,Δ=-ae2-b2f+2bde.
是否存在无奇异路径,根据以下情况进行判别:
1) 当δ=0且Δ≠0时,动平面上的位置奇异轨迹曲线为抛物线,此时,Pi与Pf一定位于奇异轨迹分隔的同一区域内,如图 4所示,Pi与Pf之间一定存在无奇异路径.
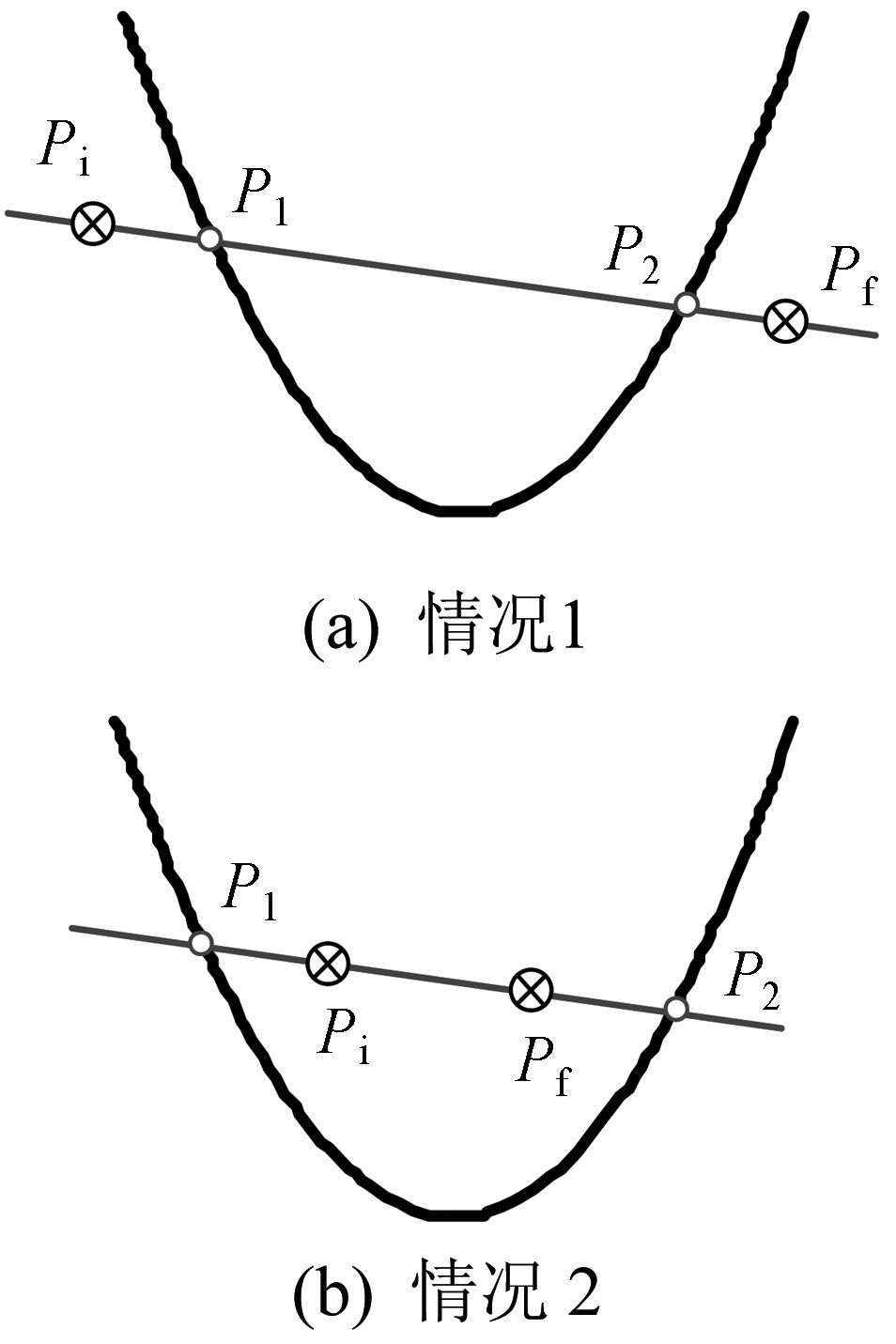
|
| 图 4 抛物线情况 Fig.4 Case of parabola |
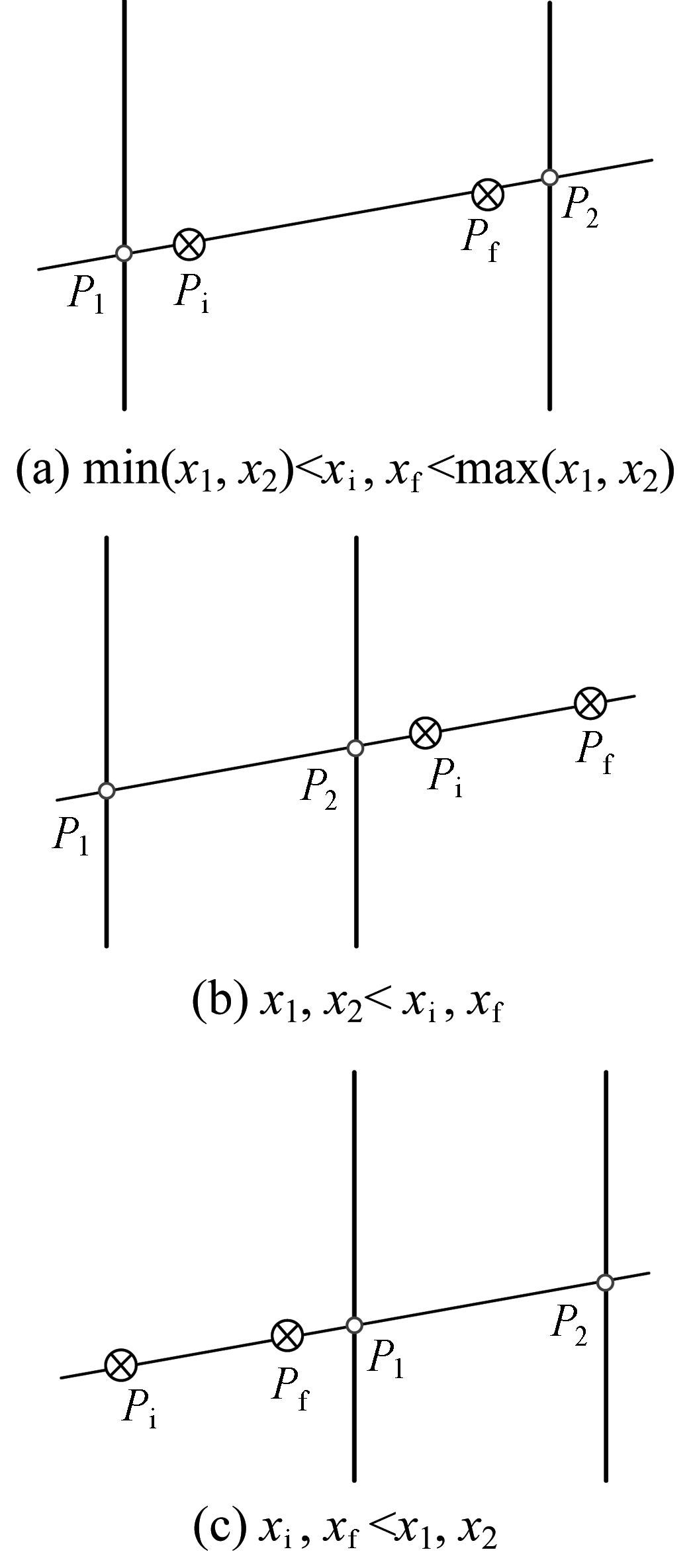
2)当且仅当(ø,ψ)=(±90°,=±90°)时,δ=0且Δ=0,此时,动平面上的位置奇异轨迹曲线为一对平行直线或一条直线,并且上述的一系列直线均与V-xy坐标系中的y轴相平行,此时只要
min(x1,x2)<xi ,xf<max(x1,x2),
或x1,x2<xi,xf,
或xi ,xf<x1,x2,
如图 5所示,Pi与Pf之间一定存在无奇异路径.
|
| 图 5 平行直线情况 Fig.5 Case of parallel lines |
3) 当δ <0时,动平面上的位置奇异轨迹曲线为一对双曲线或一对相交直线.
① 若min(xi ,xf)<x1,x2<max(xi,xf),此时Pi与Pf位于奇异轨迹分隔的同一区域内,如图 6所示,Pi与Pf之间存在无奇异路径.
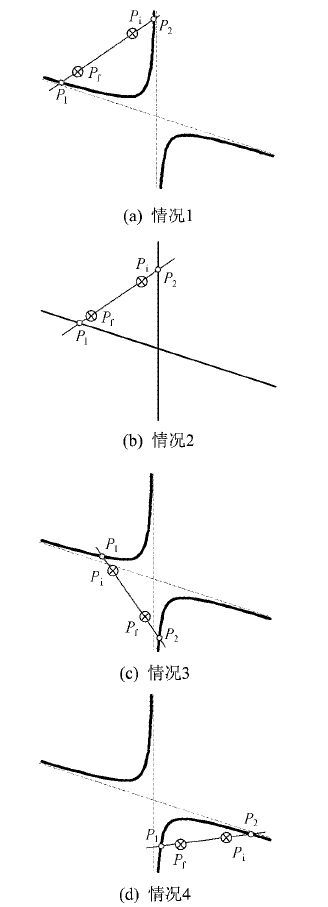
|
| 图 6 min(xi,xf)<x1,x2<max(xi,xf)情况 Fig.6 Case of min(xi,xf)<x1,x2<max(xi,xf) |
②若x1,x2∉R,也即直线PiPf与奇异轨迹无交点,如图 7所示,此时一定存在无奇异路径.
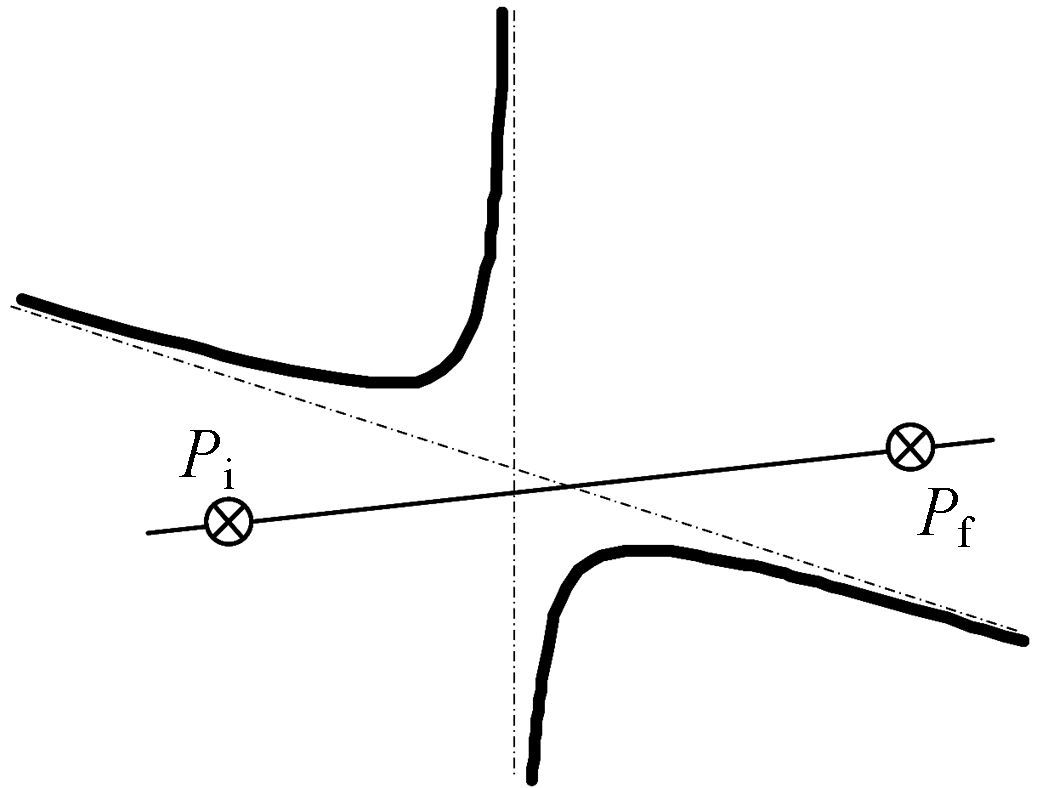
|
| 图 7 x1,x2∉R情况 Fig.7 Case of x1,x2∉R |
③ 若min(xi,xf<x1,x2 <max(xi ,xf)且(x1+e/b))(x2+e/b)>0(直线Pi Pf与奇异轨迹的交点P1,P2位于直线x=e/b同侧),如图 8所示,则Pi与Pf之间存在无奇异路径.
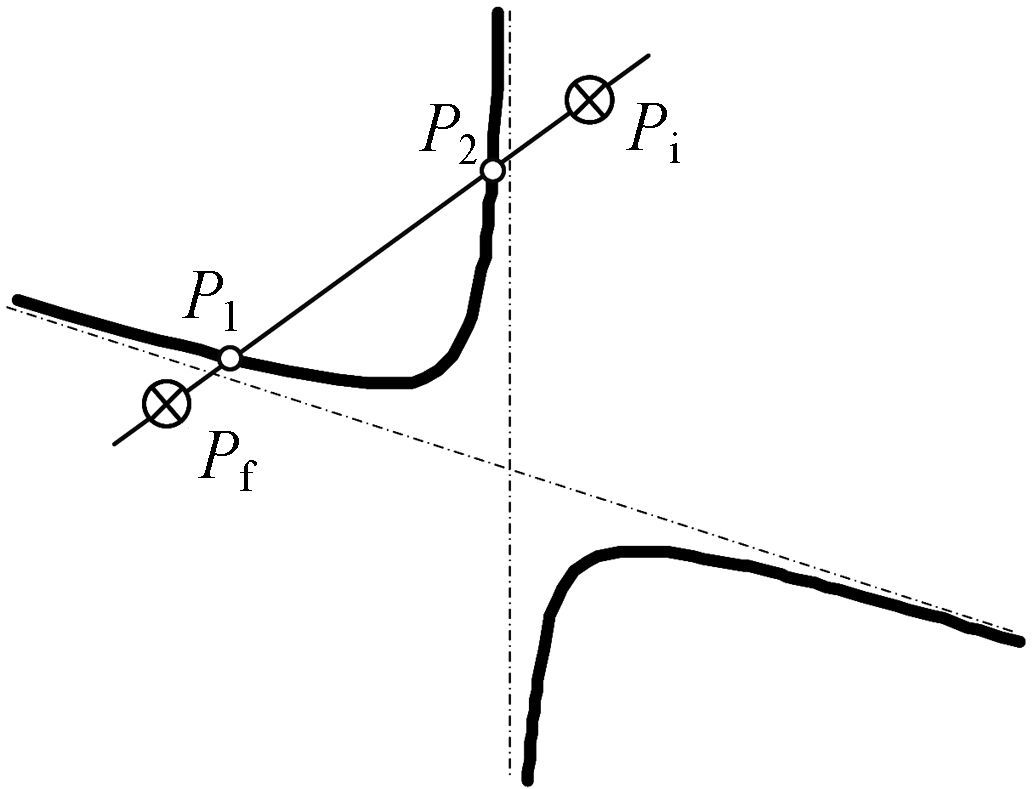
|
| 图 8 min(xi,xf)<x1,x2<max(xi,xf)且(x1+e/b)×(x2+e/b)>0 情况 Fig.8 Case of min(xi,xf)< x1,x2 >max(xi,xf) and (x1+e/b)×(x2+e/b)>0 |
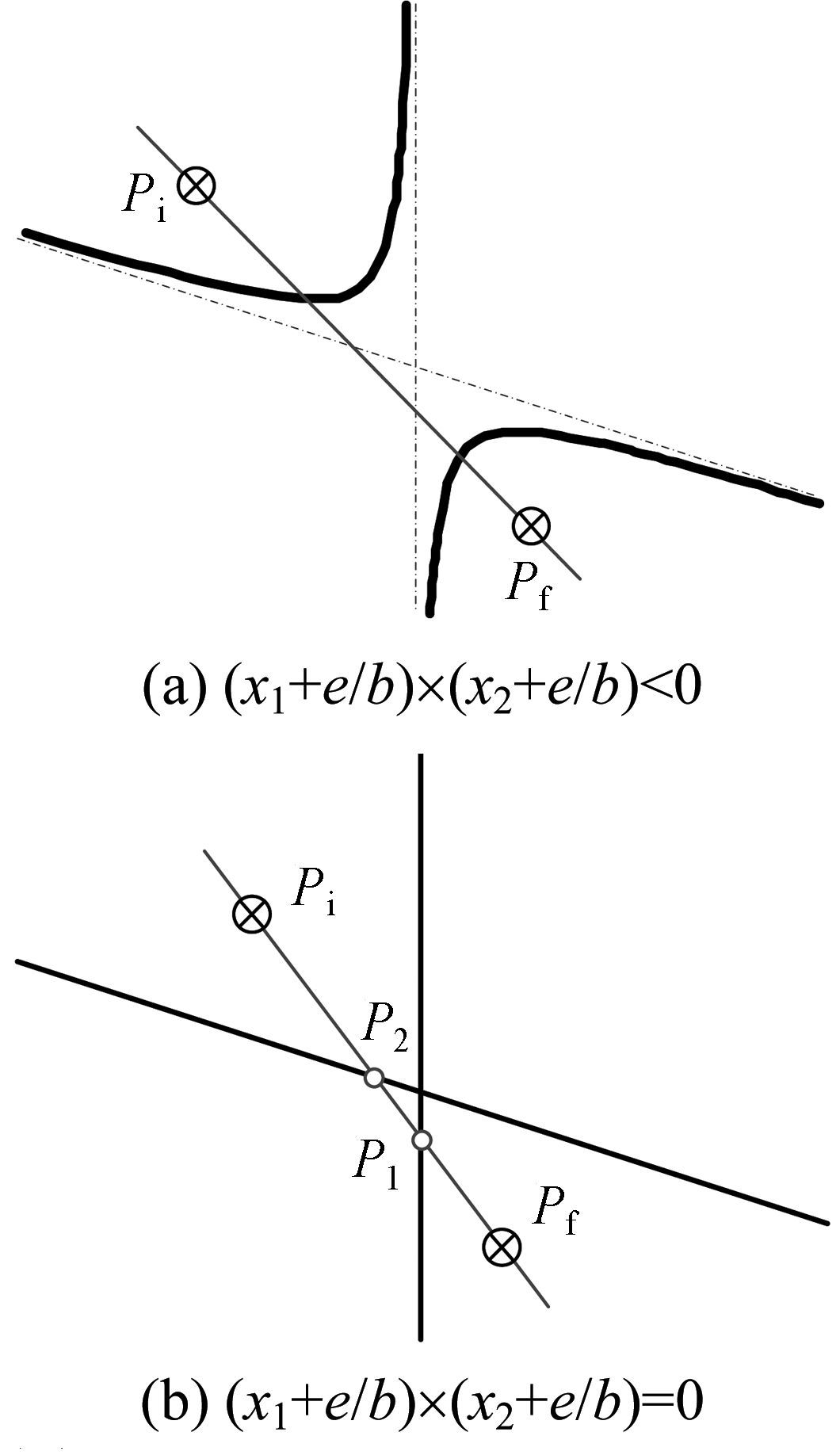
④ 若min(xi,xf)<x1,x2 <max(xi,xf)但(x1+e/b)×(x2+e/b)≤0,此时不存在无奇异路径.其中:“<”时,直线Pi Pf与奇异轨迹双曲线的交点P1,P2位于渐近线x=-e/b两侧,如图 9(a)所示;“=”时,P1,P2其中一点位于奇异轨迹相交直线x=-e/b上,如图 9(b)所示.
|
| 图 9 min(xi,xf)<x1,x2<max(xi,xf)情况 Fig.9 Case of min(xi,xf)<x1,x2<max(xi,xf) |
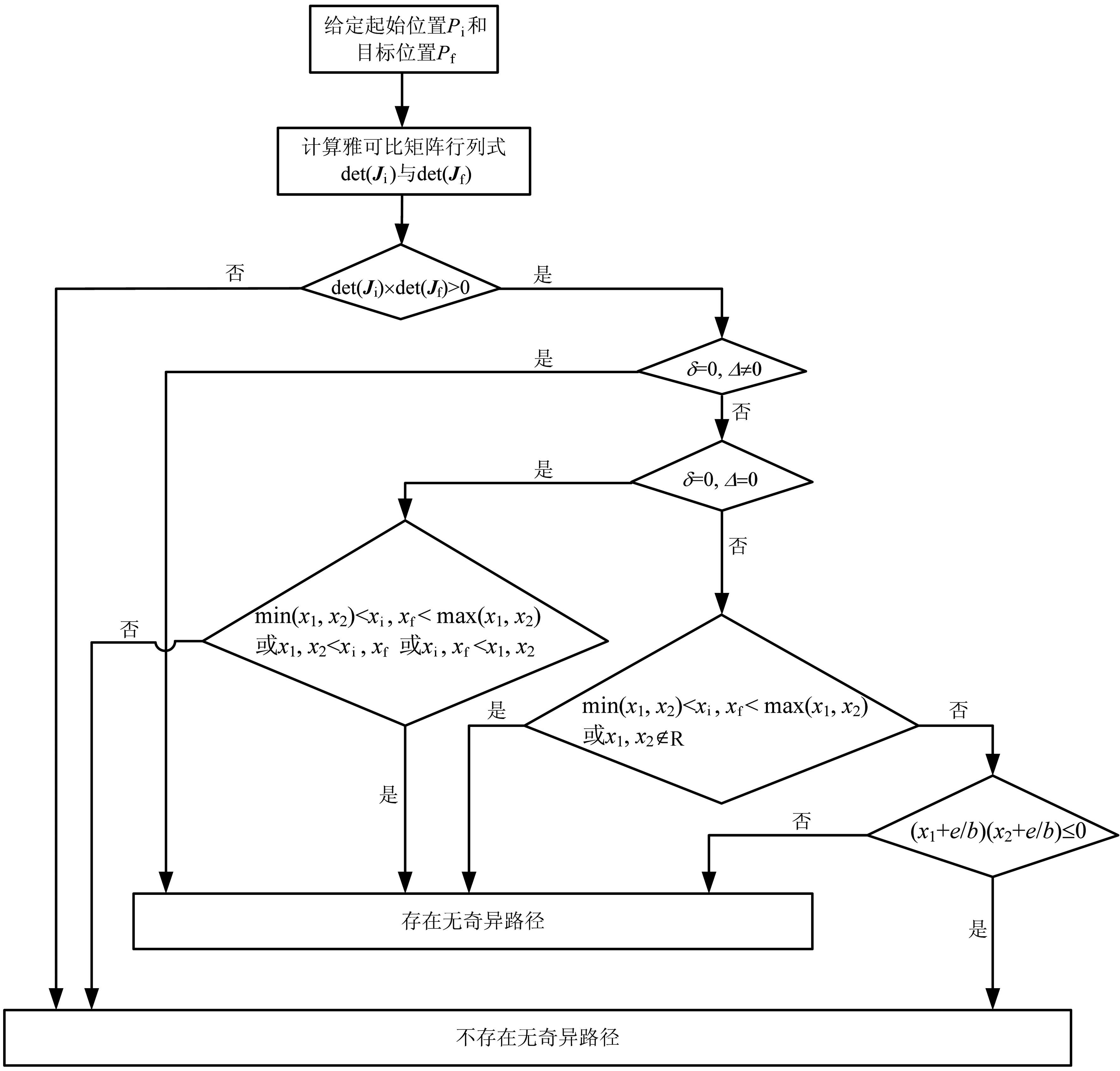
根据以上所述,动平面上任意两位置点之间无奇异路径的存在与否的具体判别方法如图 10所示.
|
| 图 10 无奇异路径存在与否的判别 Fig.10 Existence discrimination of singularity-free path |
在动坐标系V-xy中,当满足存在无奇异路径的前提时,若有
| $\left. \begin{matrix} {{x}_{1}},{{x}_{2}}<{{x}_{i}},{{x}_{f}}或~{{x}_{i}},{{x}_{f}}<{{x}_{1}},{{x}_{2}}, \\ 或min({{x}_{1}},{{x}_{2}})<{{x}_{i}},{{x}_{f}}{{x}_{1}},{{x}_{2}}), \\ 或\left( {{x}_{1}},{{x}_{2}} \right)\notin {{R}^{2}}, \\ \end{matrix} \right\}$ | (8) |
此时直线段PiPf便可作为无奇异路径;若不满足式(8),则需要以曲线路径形式绕过奇异点,如图 5所示.直线段PiPf与奇异轨迹曲线交点分别为P1,P2,将直线段P1P2分成若干离散点,并将离散点记为(x0i,y0i).过任一等分点(x0i,y0i)作平行于y轴的直线交奇异轨迹曲线于点(xsi,ysi),根据动平面上的位置奇异轨迹几何性质可知,若将动平面上的位置奇异表达式看成是y关于自变量x的函数方程,则该函数一定为凸函数或是凹函数,故令
| $\left. \begin{matrix} {{x}_{pi}}={{x}_{si}}+sign(\frac{dy}{dx})\Delta x, \\ {{y}_{pi}}={{y}_{si}}-sign(\frac{{{d}^{2}}y}{d{{x}^{2}}})\Delta y, \\ \end{matrix} \right\}$ | (9) |
式中:sign——将数值取符号值,若结果为正值,取数值“1”,结果为负数,取数值“-1”,结果为0,取数值“0”;Δx,Δy的具体数值一般根据机构的结构尺寸和轨迹精度要求设定.
由动平面上奇异轨迹方程式(4)得
| $y=-\frac{1}{2}\frac{a{{x}^{2}}+2dx+f}{bx+e},$ | (10) |
故有
| $\begin{align} & \frac{dy}{dx}=-\frac{1}{2}\frac{2ax+2d}{bx+e}+\frac{1}{2}\frac{(a{{x}^{2}}+2dx+f)b}{{{\left( bx+e \right)}^{2}}}, \\ & \frac{{{d}^{2}}y}{d{{x}^{2}}}=-\frac{a}{bx+e}+\frac{\left( 2ax+2d \right)b}{{{\left( bx+e \right)}^{2}}}-\frac{(a{{x}^{2}}+2dx+f){{b}^{2}}}{{{\left( bx+e \right)}^{3}}}. \\ \end{align}$ |
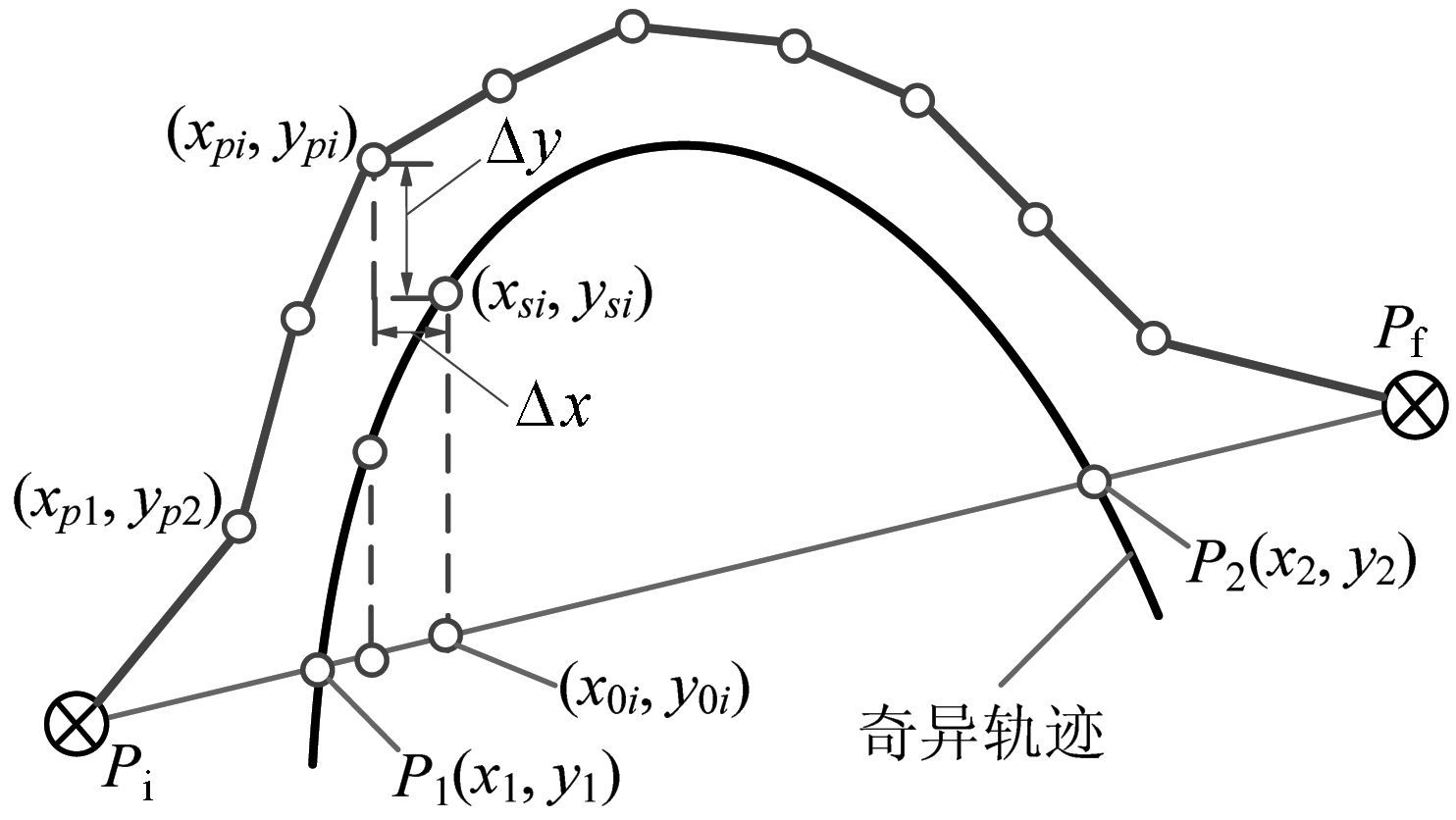
将Pi,(xpi,ypi)及Pf依次连接,即可得到动坐标系V-xy下Pi到Pf之间的无奇异运动路径,如图 11所示.
|
| 图 11 曲线无奇异路径 Fig.11 Singularity-free curve path |
以上讨论的是θ≠0时相互平行的动平面上的无奇异路径规划问题.若θ=0,此时主要分为3种情况:1)Z=0时,机构动、定平台相互重合,此时位置参数(X,Y)无论取何值,机构一定处于奇异位形;2)Z≠0时,当且仅当(+ψ)=±90°,机构发生奇异位形.当机构位于给定姿态时,上述2种情况下,机构均处于奇异位形,起始点和目标点均处于奇异位形状态,且这样的两位置点之间不存在任何无奇异路径连接;3)Z≠0时,且(+ψ)≠±90°,任意给定目标点和位置点,连接两位置点之间的任意路径均为无奇异路径.
3 数值实例机构构型参数给定为Rb=2 m,Rm=1 m,βb=105°,βm=75°,不考虑机构结构约束限制,给定姿态参数(∉,θ,ψ )=(60°,30°,-45°),机构在动平面上的起始点Pi和目标点Pf在坐标系V-xy中的位置参数如表 1所示.要求判断Pi与Pf之间是否存在无奇异连接路径,若存在,要求规划两点之间的无奇异运动路径.
| 实例 | Xv | 起始点Pi (xi,yi) | 目标点Pf (xf,yf) |
| 1 | 1 m | (-4 m,-4 m) | (-2 m,4 m) |
| 2 | 1 m | (-4 m,0 m) | (2 m,6 m) |
路径规划是机器人机构设计及应用过程中值得关注的问题,优良的运动路径能够使机构满足任务要求的同时,也可以优化机构的某些性能指标,例如时间最优[25]、能耗最优[26-27]、驱动力/力矩最优[5]等.当机构位于奇异位形附近时,机构的雅可比矩阵为病态矩阵,其逆矩阵的精度降低,此时,机构输入-输出运动关系严重失真[1].雅可比矩阵的条件数可以定量描述矩阵求逆的精确度和稳定性,并衡量机构运动的失真程度以及无奇异路径规划的有效性.
具体方法如下所述.
计算起始点和目标点分别对应的雅可比矩阵行列式值,如表 2所示.
| 实例 | Xv | 起始点(xi,yi)雅可比矩阵行列式det(Ji) | 目标点(xf,yf)雅可比矩阵行列式det(Jf) |
| 1 | 1 m | 149.643 290 188 519 | -66.271 339 642 730 8 |
| 2 | 1 m | 27.912 443 480 646 | 55.141 211 011 291 2 |
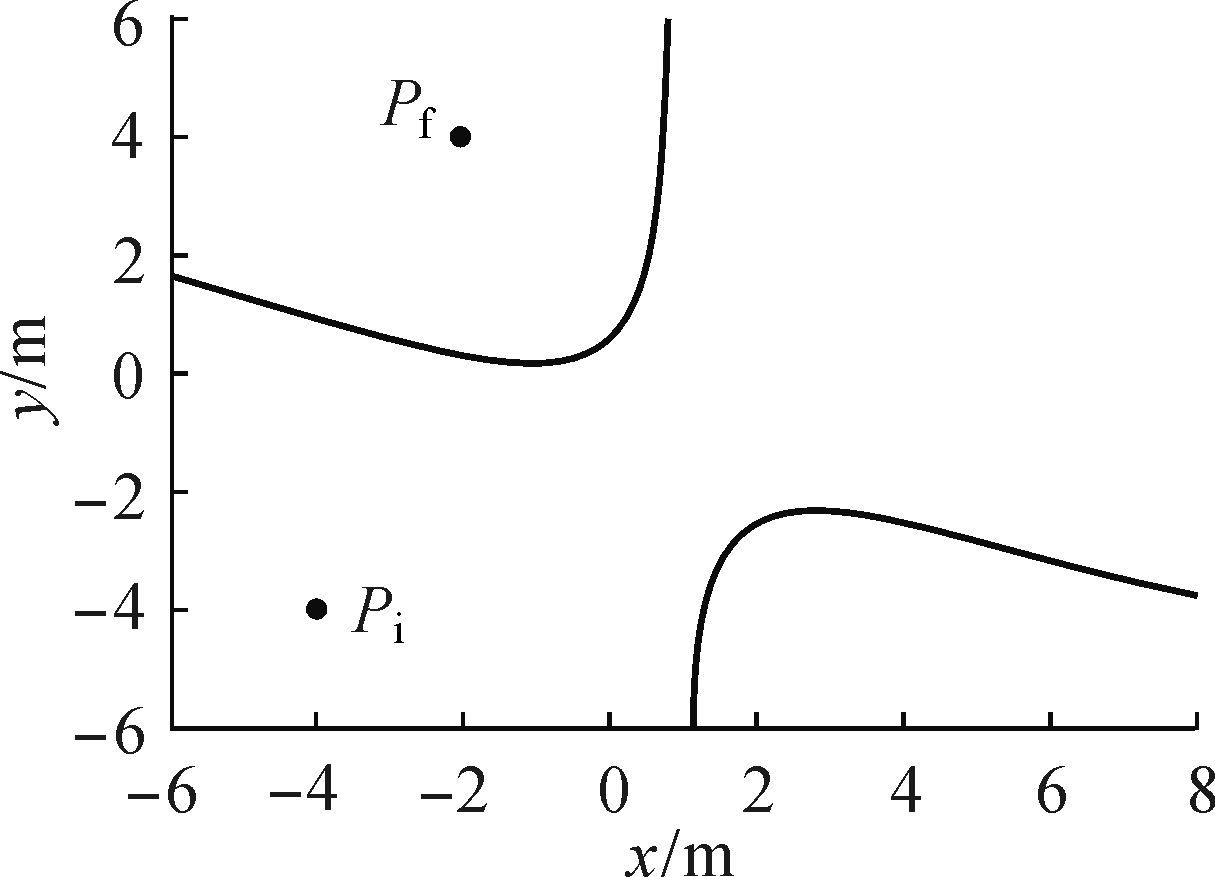
根据图 10所示是否存在无奇异路径判断方法,显然,实例1中,由于起始位置点和目标位置点行列式值异号,因此,不存在无奇异位置运动路径连接这2点.图 12所示为起始位置点与目标位置点在动平面上的位置,可以看到,起始位置和目标位置确实被奇异轨迹“隔断”,这2点之间的确不存在无奇异路径.
|
| 图 12 实例1的起始点和目标点位置 Fig.12 Initial position and final position of example 1 |
对于实例2,起始位置点和目标位置点行列式值均同号,故应根据图 10流程图继续判别是否存在无奇异路径.δ=-603.434 48,Δ=-34 165.755 97;解方程组(6)可得到动坐标系V-xy下,
(x1,y1)=(0.756 73 m,4.756 73 m),
(x2,y2)=(-3.298 92 m,0.701 08 m),
(x1,y1)≠(x2,y2),不满足
min(x1,x2)<xi,xf<max(x1,x2),
又-e/b=-0.955 478,得(x1+e/b)×(x2+e/b)>0,故存在无奇异运动路径.根据以上所述,应利用图 5所示以曲线路径形式规划并利用式(9)计算无奇异路径点.否则,若将起始点(-4 m,0 m)和目标点(2 m,6 m)以直线段形式连接,如图 13所示,将该位置路径离散化,对应的雅可比矩阵条件数随离散点变化如图 14所示,可以看到,以直线路径连接起始点和目标点时会存在奇异点,故应基于式(8)并如图 15所示对机构实施无奇异路径规划.
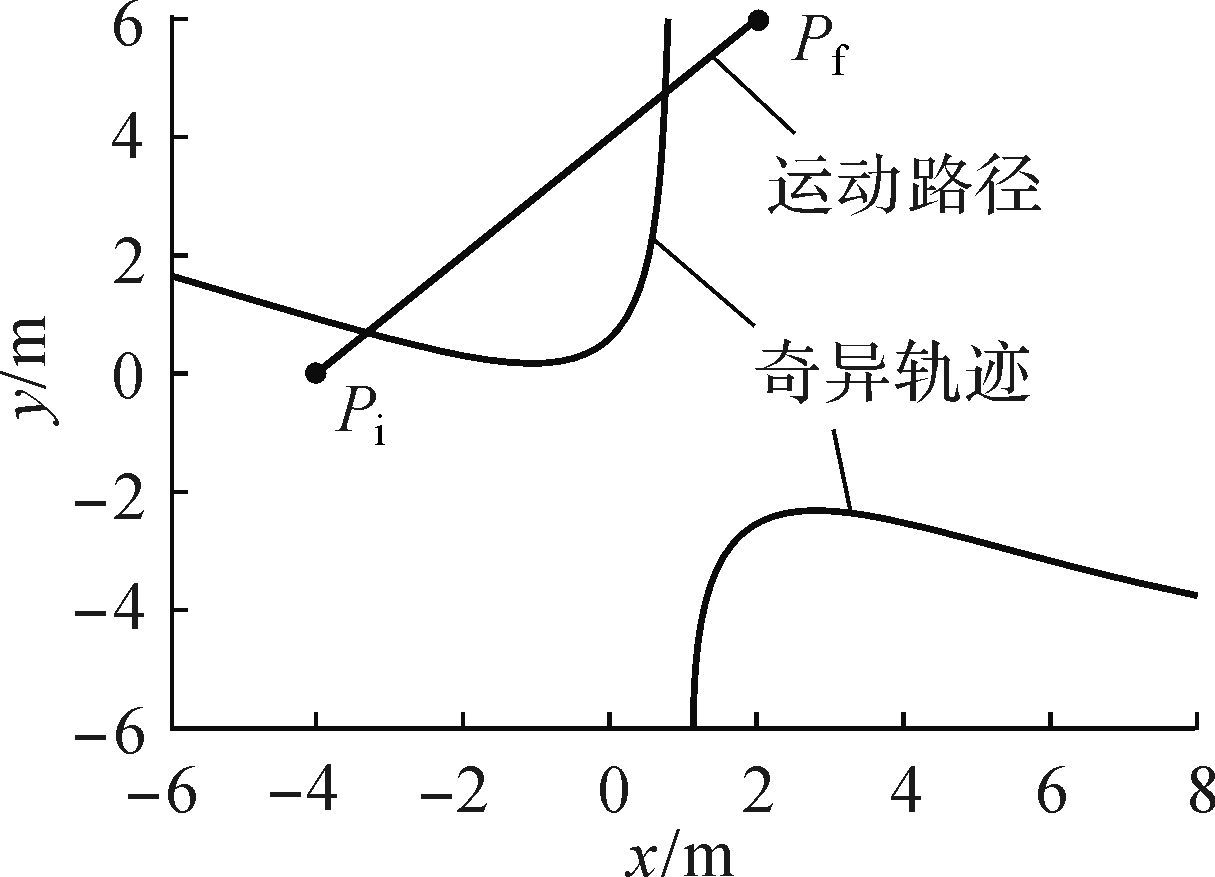
|
| 图 13 实例2的直线路径规划 Fig.13 Line path of example 2 |
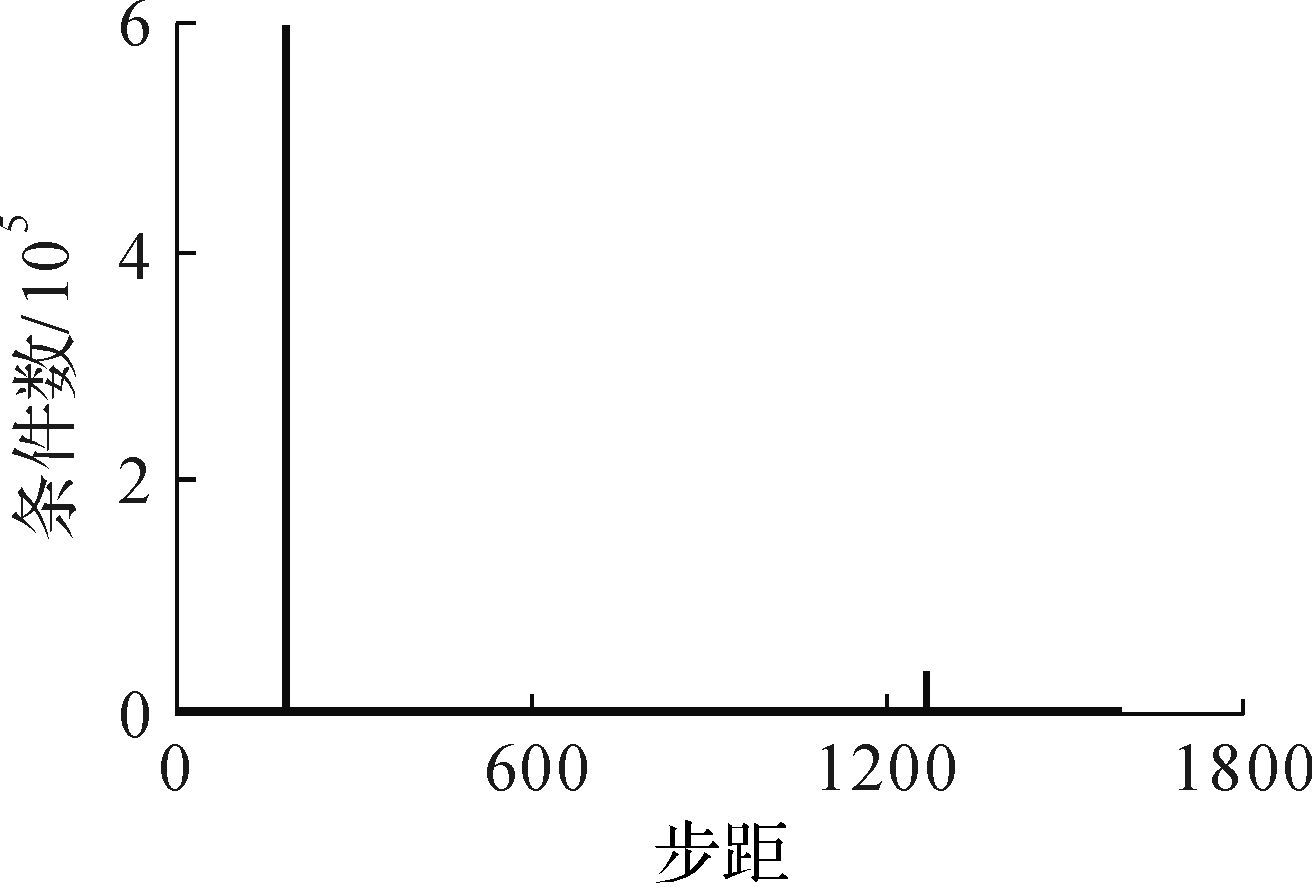
|
| 图 14 离散点的条件数 Fig.14 Condition number for discrete positions |
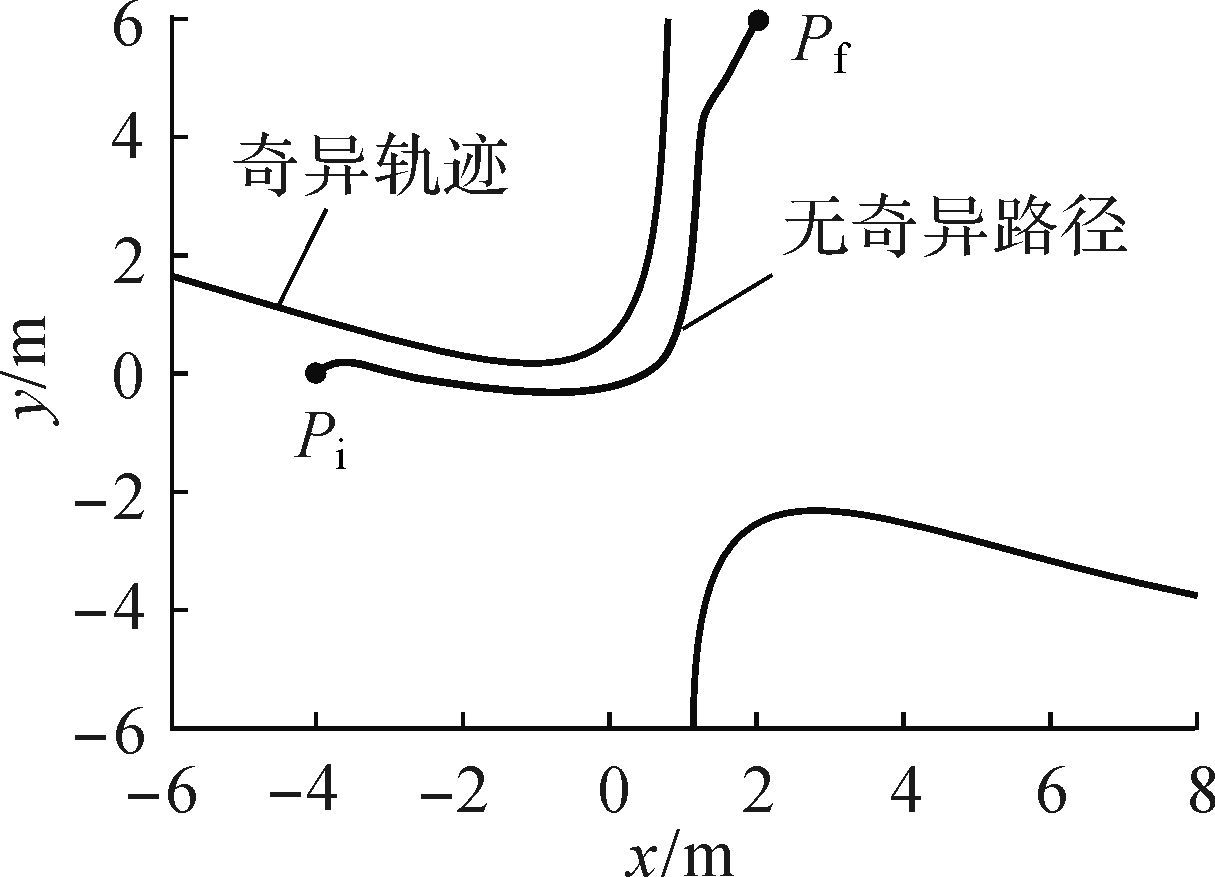
|
| 图 15 实例2的无奇异路径规划 Fig.15 Singularity-free path of example 2 |
图 15为利用如图 11所示的曲线路径规划得到的无奇异运动路径,此处,Δx=Δy=0.5 m,机构雅可比矩阵条件数变化如图 16所示.可以看到,重新规划的运动路径顺利避开了奇异点.
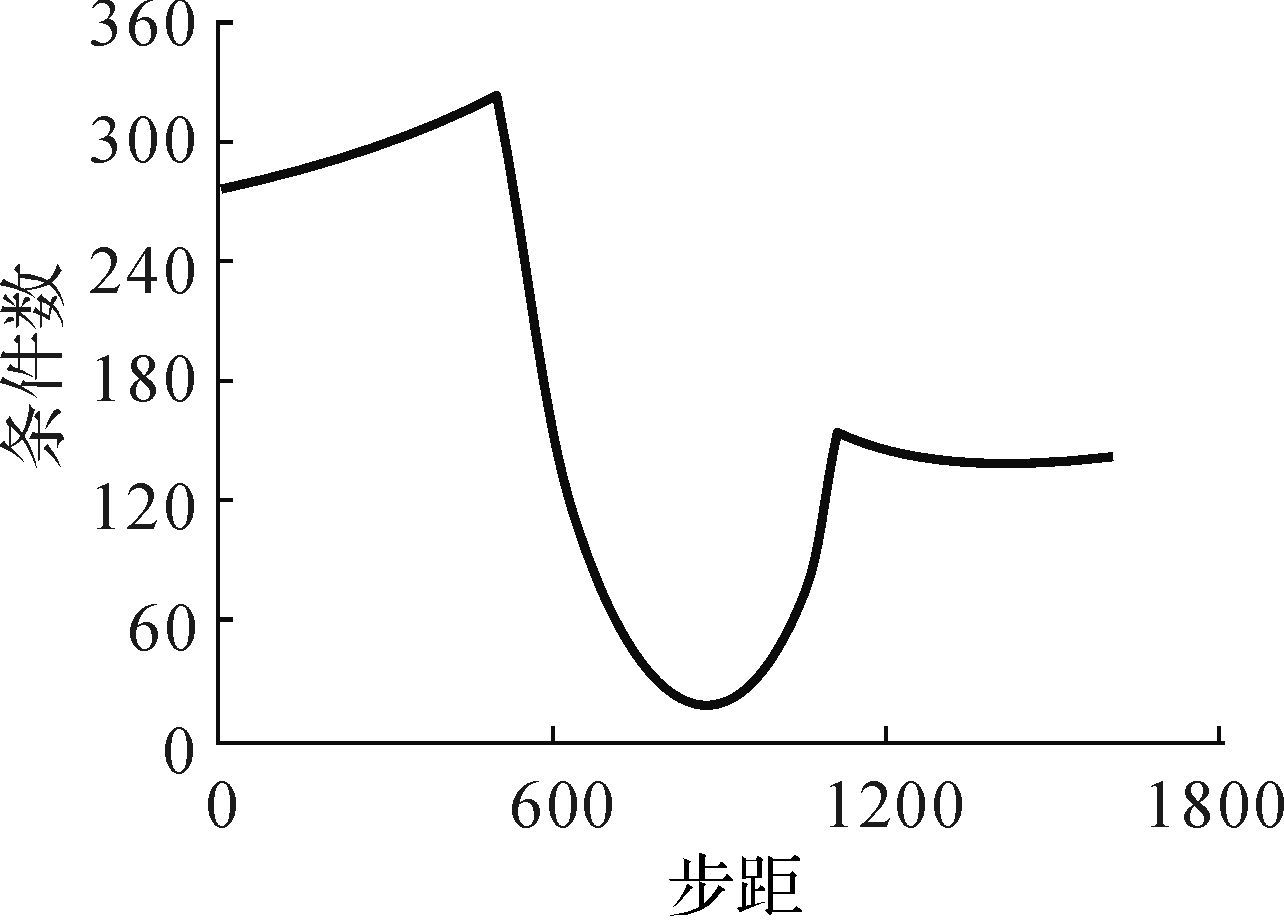
|
| 图 16 无奇异路径的条件数 Fig.16 Condition number for singularity-free path |
需要指出的是,论文中对图 16和图 14进行的比较,是为了阐明上述无奇异路径规划的有效性.但由于论文选取的路径起始点和目标点距离机构奇异位形较为接近,故图 15所示的无奇异路径轨迹对应的条件数(如图 16所示)仍然很大,但重新规划后的条件数相比未规划之前有了极大改善,说明了上述无奇异路径规划算法是有效的.
4 结 论1) 基于Gough-Stewart并联机器人机构奇异轨迹几何性质,给出机构的无奇异路径存在与否的识别以及无奇异路径具体规划方法.该方法不依赖于动平面上奇异轨迹分布情况的观察,任意给定两位置点,利用相关解析公式并编制相应的计算机程序即可自动判别无奇异运动路径的存在性,并得到具体运动路径,为进一步扩展至三维空间内的无奇异运动路径规划奠定了良好的前期基础.研究成果对其他类型并联机器人机构基于轨迹规划的奇异规避问题研究亦具有重要的参考价值.
2) 论文探讨的动平面上无奇异路径的具体规划方法具有一定的实际应用价值,例如在将机构应用于倾斜平面上的多孔钻、铣削、装配等顺序动作时,就需要对机构位于动平面上的位置变换实施无奇异路径规划.
3) 机器人机构的路径规划与其作业任务要求、机械结构等相关,针对不同的轨迹运动要求,路径规划也有不同的优化指标.论文仅以改善机构的雅可比矩阵条件数为目标对机构实施路径规划以规避奇异位形,暂未考虑机构的实际结构约束条件影响.作者下一步的研究目标将在考虑机构结构条件约束条件下,以时间最优、能耗最优以及驱动力/力矩最优等为目标,对机构实施无奇异路径规划.
| [1] |
黄真, 赵永生, 赵铁石.
高等空间机构学[M]. 北京: 高等教育出版社 ,2006 : 238 -268.
HUANG Zhen, ZHAO Yong-sheng, ZHAO Tie-shi. Advanced spatial mechanism[M]. Beijing: Higher Education Press , 2006 : 238 -268. |
| [2] | LIU G F, WU Y L, WU X Z, et al. Analysis and control of redundant parallel manipulators[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Seoul, Korea, May 21-26, 2001:3748-3754. |
| [3] |
杨建新, 余跃庆.
平面三自由度冗余并联机构的驱动奇异性分析[J]. 中国机械工程 , 2006, 17 (6) : 629–632.
YANG Jian-xin, YU Yue-qing. Actuator singularity analysis of planar 3-DOF redundant parallel mechanisms[J]. China Mechanical Engineering , 2006, 17 (6) : 629–632. |
| [4] |
张彦斐, 宫金良, 高峰.
冗余驱动消除并联机构位形奇异原理[J]. 中国机械工程 , 2006, 17 (5) : 445–448.
ZHANG Yan-fei, GONG Jin-liang, GAO Feng. Theory of singularity elimination by redundant actuation for parallel mechanism[J]. China Mechanical Engineering , 2006, 17 (5) : 445–448. |
| [5] | BOUDREAU R, NOKLEBY S. Force optimization of kinematically-redundant planar parallel manipulators following a desired trajectory[J]. Mechanism and Machine Theory , 2012, 56 (10) : 138–155. |
| [6] | DASH A K, CHEN I, YEO S H, et al. Workspace generation and planning singularity-free path for parallel manipulators[J]. Mechanism and Machine Theory , 2004, 40 (7) : 776–805. |
| [7] | BHASKAR D, MRUTHYUNJAYA T S. Singularity-free path planning for the Stewart platform manipulator[J]. Mechanism and Machine Theory , 1998, 33 (6) : 711–725. DOI:10.1016/S0094-114X(97)00095-5 |
| [8] |
白志富, 陈五一.
并联机构不同正解间无奇异转换问题探讨[J]. 机器人 , 2006, 28 (5) : 463–469.
BAI Zhi-fu, CHEN Wu-yi. On the non-singular path between different forward kinematic configurations of parallel mechanism[J]. Robot/Jiqiren , 2006, 28 (5) : 463–469. |
| [9] | GOSSELIN C M, ANGELES J. Singularity analysis of closed-loop kinematic chains[J]. IEEE Transactions on Robotics and Automation , 1990, 6 (3) : 281–290. DOI:10.1109/70.56660 |
| [10] | CHENG Shi-li, WU Hong-tao, WANG Chao-qun, et al. A novel method for singularity analysis of the 6-SPS parallel mechanisms[J]. Science China:Technological Sciences , 2011, 54 (5) : 1220–1227. DOI:10.1007/s11431-011-4323-2 |
| [11] | DOYON K, GOSSELIN C M, CARDOU P. A vector expression of the constant-orientation singularity locus of the Gough-Stewart platform[J]. ASME Journal of Mechanisms and Robotics , 2013, 5 (3) : 034502-1–034502-4. |
| [12] | BANDYOPADHYAY S, GHOSAL A. Geometric characterization and parametric representation of the singularity manifold of a 6-6 Stewart platform manipulator[J]. Mechanism and Machine Theory , 2006, 41 (11) : 1377–1400. DOI:10.1016/j.mechmachtheory.2005.12.006 |
| [13] | HUANG Zhen, CAO Yi. Property identification of the singularity loci of a class of the Gough-Stewart manipulators[J]. The International Journal of Robotics Research , 2005, 24 (8) : 675–685. DOI:10.1177/0278364905054655 |
| [14] | LI Hai-dong, GOSSELIN C M, RICHARD M J, et al. Analytic form of the six-dimensional singularity locus of the general Gough-Stewart platform[J]. ASME Journal of Mechanical Design , 2006, 128 (1) : 279–287. DOI:10.1115/1.2118733 |
| [15] | MERLET J P. Singular configurations of parallel manipulators and Grassmann geometry[J]. The International Journal of Robotics Research , 1989, 8 (5) : 45–56. DOI:10.1177/027836498900800504 |
| [16] | ZHU Si J, HUANG Zhen, ZHAO M Y. Singularity analysis for six practicable 5-DOF fully-symmetrical parallel manipulators[J]. Mechanism and Machine Theory , 2009, 44 (4) : 710–725. DOI:10.1016/j.mechmachtheory.2008.05.012 |
| [17] |
张耀军, 张玉茹.
基于Grassmann线几何的平面柔索驱动并联机构奇异分析[J]. 机械工程学报 , 2011, 47 (19) : 1–7.
ZHANG Yao-jun, ZHANG Yu-ru. Singularity analysis of planar cable-driven parallel mechanisms with Grassmann geometry[J]. Journal of Mechanical Engineering , 2011, 47 (19) : 1–7. DOI:10.3901/JME.2011.19.001 |
| [18] | FANG Hai-rong, FANG Yue-fa, ZHANG Ke-tao. Reciprocal screw theory based singularity analysis of a novel 3-DOF parallel manipulator[J]. Chinese Journal of Mechanical Engineering , 2012, 25 (4) : 647–653. DOI:10.3901/CJME.2012.04.647 |
| [19] | LIU Xin-jun, WU Chao, WANG Jin-song. A new approach for singularity analysis and closeness measurement to singularities of parallel manipulators[J]. ASME Journal of Mechanisms and Robotics , 2012, 4 (4) : 041001-1–041001-10. |
| [20] |
沈辉, 吴学忠, 刘冠峰.
并联机构中奇异位形的分类与判定[J]. 机械工程学报 , 2004, 40 (4) : 26–31.
SHEN Hui, WU Xue-zhong, LIU Guan-feng. Classification and identification of singularities of parallel mechanism[J]. Journal of Mechanical Engineering , 2004, 40 (4) : 26–31. DOI:10.3901/JME.2004.04.026 |
| [21] | BEN-HORIN P, SHOHAM M. Singularity analysis of a class of parallel robots based on Grassmann-Cayley algebra[J]. Mechanism and Machine Theory , 2006, 41 (8) : 958–970. DOI:10.1016/j.mechmachtheory.2006.03.008 |
| [22] | SEMAAN A, MEHDI T M, Stéphane C, et al. Singularity analysis of 3T2R parallel mechanisms using Grassmann-Cayley algebra and Grassmann geometry[J]. Mechanism and Machine Theory , 2012, 52 (7) : 326–340. |
| [23] | PARK F C, KIM J W. Singularity analysis of closed kinematic chains[J]. ASME Journal of Mechanical Design , 1999, 121 (1) : 32–38. DOI:10.1115/1.2829426 |
| [24] |
李保坤, 曹毅, 张秋菊, 等.
Stewart并联机构位置奇异研究[J]. 机械工程学报 , 2012, 48 (9) : 33–42.
LI Bao-kun, CAO Yi, ZHANG Qiu-ju, et al. Position-singularity analysis of the Stewart parallel mechanism[J]. Journal of Mechanical Engineering , 2012, 48 (9) : 33–42. DOI:10.3901/JME.2012.09.033 |
| [25] | HUANG T, WANG P F, MEI J P, et al. Time minimum trajectory planning of a 2-DOF translational parallel robot for pick-and-place operations[J]. CIRP Annals-Manufacturing Technology , 2007, 56 (1) : 365–368. DOI:10.1016/j.cirp.2007.05.085 |
| [26] |
张连东, 王德伦.
一种基于测地线的机器人轨迹规划方法[J]. 机器人 , 2004, 26 (1) : 83–86.
ZHANG Lian-dong, WANG De-lun. Robot trajectory planning based on geodesics[J]. Robot/Jiqiren , 2004, 26 (1) : 83–86. |
| [27] | UR-REHMAN R, CARO S, CHABLAT D, et al. Multi objective path placement optimization of parallel kinematics machine based energy consumption, shaking forces and maximum actuator torques[J]. Mechanism and Machine Theory , 2010, 45 (8) : 1125–1141. DOI:10.1016/j.mechmachtheory.2010.03.008 |



