2. 杭州娃哈哈集团有限公司 机电研究院, 浙江 杭州 310020
2. Mechanical and Electrical Institute, Hangzhou Wahaha Group Co., Ltd., Hangzhou 310020, China
工业机器人轨迹规划算法是保证工业机器人实现稳定运动的核心技术.对于弧焊等机器人来说,通常要求末端执行器尽量以给定速度沿着指定示教路径前进,并保证在相邻路径之间能够自动平滑过渡.为解决路径平滑过渡这一难题,最早采用的是基于样条曲线插补等方式的关节空间轨迹规划算法[1-3],此类算法具有约束条件少和计算速度快等优势,但同时存在空间轨迹不直观和轨迹形状会随速度不同而改变等缺点,因此逐渐被机器人厂商弃用.近年来,国内外学者大多转向了操作空间轨迹规划算法的研究.常见的工作空间轨迹规划算法主要有3类:第1类是卷积类算法,该方法通常是给定混叠时间参数,对路径进行均匀离散化后采用卷积计算来实现加减速规划,但此类算法存在着很多与关节空间轨迹规划算法类似的缺点[4].第2类则是混叠类算法,包括速度混叠算法[5]和位置混叠算法[6-7],此类算法一般需要给定加减速时间,然后通过线性、多项式或者摆线等函数形式的同伦变形获得速度曲线或者位置曲线,缺点是加速度约束涉及时间变量,需要复杂的处理流程,其中文献[7]是对ABB公司TrueMove技术的一次不完全尝试.最后一类算法是规划类算法,包括速度规划算法[8]和位置规划算法[9-10],这一类算法通过设计过渡曲线的数学表达式来实现.其中速度规划算法计算流程复杂,且难以保证轨迹不随速度参数的更改而变化.而位置规划算法的研究中,Siciliano等将关节空间的位置规划算法扩展到笛卡尔空间,获得了抛物线形状的过渡轨迹,使得加速度约束不再取决于时间常数,但是仍存在加速度矢量方向突变的问题[9].林仕高等提出五次多项式位置规划过渡算法,但是因加速度约束是涉及时间变量的非线性函数而未能找到加速度约束处理方案[10].此外,还有一些研究通过先选取过渡路径,然后将其细分为微小路径段,最后采用前瞻算法实现速度平滑和轨迹修形,然而此类算法计算复杂,难以保证在高速运动条件下的实时性[4, 11].
为此,提出一种计算效率高的基于有限项正弦级数的新型位置规划算法来解决上述问题.
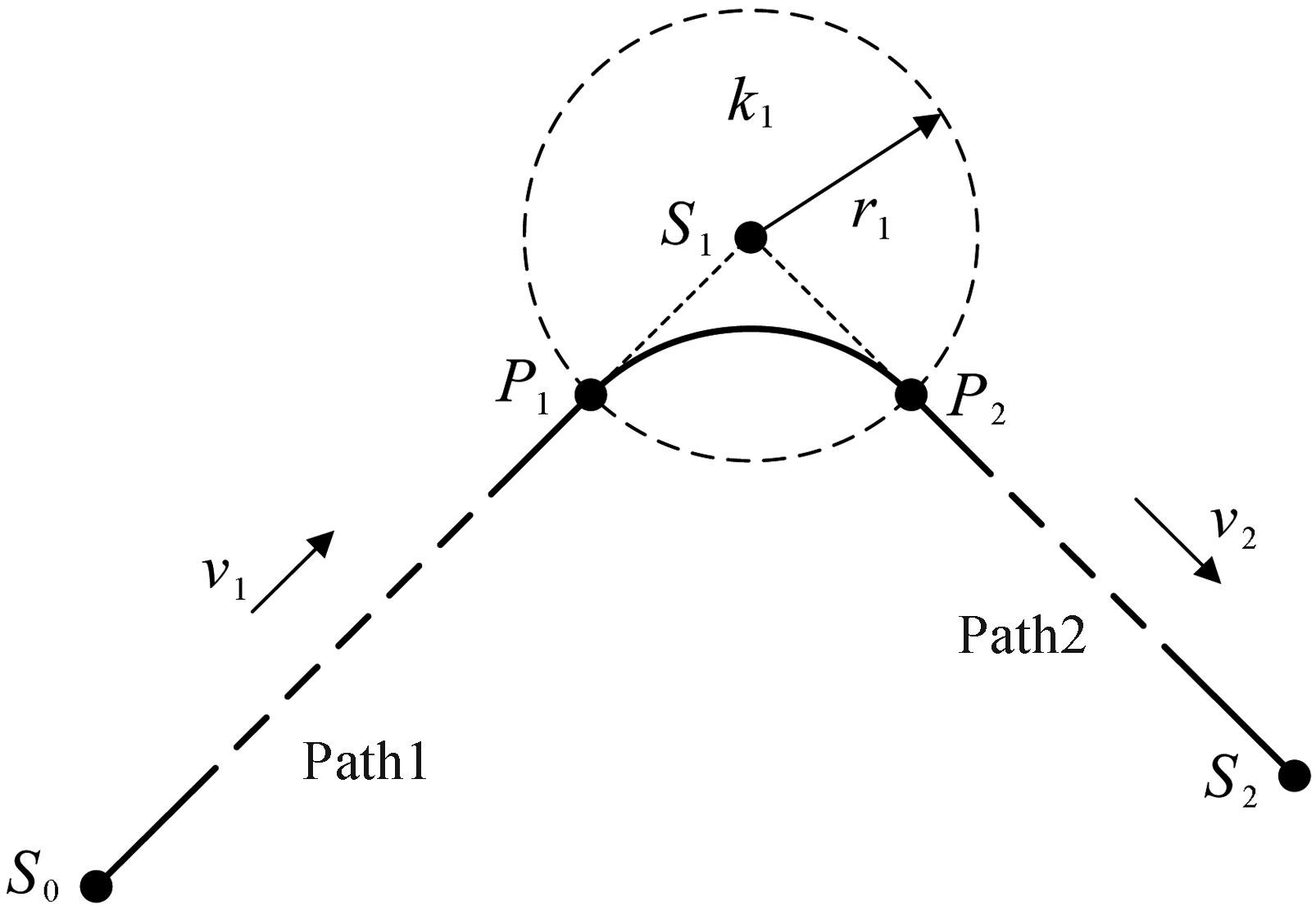
1 节点配置操作空间中典型的连续轨迹包括直线段与直线段、直线段与圆弧段以及圆弧段与圆弧段间的衔接.如图 1所示,为简化论述,取平面直线段Path1与直线段Path2间的衔接为代表进行本文算法的论述,而空间连续轨迹可以很轻松地从平面算法中导出.
|
| 图 1 带过渡的典型轨迹 Fig.1 Typical trajectory with transition |
其中:S0为Path1的起始点,S1为Path1和Path2的衔接点,S2为Path2的结束点;r1为S1处的过渡半径;P1和P
首先设t为完成过渡所需要的时间,点P1和P2的位置矢量分别用p0和pT表示.
为保证在平移坐标系中轨迹不变,将位置矢量p0和pT以相对位置矢量$\tilde{p}$0和$\tilde{p}$T来表示.其中,
$\tilde{p}$0=p0-p0=0,$\tilde{p}$T=pT-p0.
采用各轴分别进行平滑过渡的算法,故将相对位置、速度和加速度矢量分别向坐标轴投影以获得分量.该算法假设所有过渡节点的切向加速度均为0,从而使后续推导大为简化.过渡节点P1处的相对位置、速度和加速度的坐标轴分量配置如下:
p0j=$\tilde{p}$0·ej,$\tilde{v}$0j=k10j,a0j=k12$\tilde{a}$0j,
其中,${\tilde{v}}$0j=v1·e0τ·ej,${\tilde{a}}$0j=a1·e0n·ej,a1=v12R1-1,e0τ和e0n分别为P1处的切向单位向量和法向单位向量,ej为坐标轴j的单位向量,R1为P1处的曲率半径(若为直线,R1→∞,a1=0),j=x,y.
同理,可得过渡节点P2处的相对位置、速度和加速度的坐标轴分量配置为
pTj=${\tilde{p}}$T·ej,${\tilde{p}}$Tj=k1Tj,aTj=k12${\tilde{a}}$Tj.
由上述可知,在确定k1之后,过渡节点的实际配置将随之确定.对于非过渡区域的轨迹只需采用经典的起止点的速度和加速度为给定值的直线段或圆弧段的轨迹规划算法[9-10, 12-17]即可.由此可见本文过渡算法的关键在于确定k1.以下将具体阐述算法的原理和计算步骤.
2 算法原理对于每一个坐标轴方向,引入基于有限项正弦级数的位置规划函数:
| ${{p}_{j}}\left( t \right)=\sum\limits_{i={{n}_{s}}}^{{{n}_{e}}}{{{A}_{ij}}}sin(\frac{\pi }{{{2}^{i-1}}}\frac{t}{T}+{{\varphi }_{ij}}),0\le t\le T.$ | (1) |
则过渡节点的运动学约束方程组如下:
| $\begin{matrix} {{p}_{0j}}={{p}_{j}}\left( 0 \right),{{p}_{Tj}}={{p}_{j}}\left( T \right), \\ {{v}_{0j}}{{=}_{j}}\left( 0 \right),{{v}_{Tj}}{{=}_{j}}\left( T \right), \\ {{a}_{0j}}{{=}_{j}}\left( 0 \right),{{a}_{Tj}}{{=}_{j}}\left( T \right). \\ \end{matrix}$ | (2) |
为保证上述方程组解的确定性,方程数量与待定系数数量需相同,选取ns=3,ne=5.
考察待优化的速度比例系数k1,易知其与过渡总时间T成反相关,定义为
| $T={{k}^{-1}}_{1}s,$ | (3) |
式中s=4r1(v1+v2)-1.将式(3)代入式(2)的约束方程组,借助正弦函数的特点可消去k1,得到
| $Z=CV,$ | (4) |
式中:
Z=p0j,[pTj,${\tilde{v}}$0j,${\tilde{v}}$Tj,${\tilde{v}}$0j,${\tilde{v}}$Tj]T,
C=[α3,α4,α5,β3,β4,β5,]
αi=[oi,0,qi,0,0,-pi,1,-oi,2,-qi,2]T,
βi=[0,pi,0,oi,1,qi,1,0,-pi,2]T,
oi,n=2-n(i-1)un,u=πs-1,
pi,n=oi,nsin 2-(i-1)π,qi,n=oi,ncos 2-(i-1)π,
V=[v3j,v4j,v5j,w3j,w4j,w5j]T,
vij=Aijsin φij,wij=Aijcos φij.
故由V=C-1Z可解得向量V.而由向量V可得
| $\begin{matrix} {{\varphi }_{ij}}=arctan~({{v}_{ij}}/{{w}_{ij}}), \\ {{A}_{ij}}={{v}_{ij}}/sin~{{\varphi }_{ij}}, \\ i=3,4,5. \\ \end{matrix}$ | (5) |
下面进一步考虑加速度性能约束.
将式(1)进行二次求导可得加速度表达式为
| ${{a}_{j}}\left( t \right)=-\sum\limits_{i=3}^{5}{{{(\frac{{{k}_{1}}u}{{{2}^{i-1}}})}^{2}}}{{A}_{ij}}sin~(\frac{{{k}_{1}}u}{{{2}^{i-1}}}t+{{\varphi }_{ij}}).$ |
取ø=k1ut/16,有ø∈[0,π/16],可得
| $|{{a}_{j}}\left( \phi \right){{|}_{max}}={{(\frac{1}{16}{{k}_{1}}u)}^{2}}\centerdot |{{\rho }_{j}}\left( \phi \right){{|}_{max}},$ | (6) |
其中:
| $\begin{align} & {{\rho }_{j}}\left( \phi \right)=\sum\limits_{i=3}^{5}{({{E}_{ij}}s}in~{{\phi }_{i}}+{{F}_{ij}}cos~{{\phi }_{i}}){{\phi }_{i}}={{2}^{-(i-5)}}\phi ,{{E}_{ij}}={{2}^{-2(i-5)}}{{A}_{ij}}cos~{{\varphi }_{ij}}, \\ & {{F}_{ij}}={{2}^{-2(i-5)}}{{A}_{ij}}sin~{{\varphi }_{ij}}. \\ \end{align}$ |
可以看出,在给定|aj(ø)|max的允许值ajmax后,对于每一个坐标轴j,分别存在一个k1满足式(6),将其记为k1j,则对应有
| ${{k}_{1j}}=\frac{16\sqrt{{{a}_{jmax}}}}{u\sqrt{|{{\rho }_{j}}\left( \phi \right){{|}_{max}}}}.$ | (7) |
为获得k1j,并避免繁杂的数值判断,可采用近似计算方法计算|ρj(ø)|max.将ρj(ø)表达式中的正弦和余弦函数用下面的幂级数前3项近似:
| $sin~{{\phi }_{i}}={{\phi }_{i}}-\frac{{{\phi }^{3}}_{i}}{3!}+\frac{{{\phi }^{5}}_{i}}{5!},cos~{{\phi }_{i}}=1-\frac{{{\phi }^{2}}_{i}}{2!}+\frac{{{\phi }^{4}}_{i}}{4!},$ |
可得近似表达式为
| ${{\rho }_{j}}\left( \phi \right)=\sum\limits_{l=0}^{5}{{{b}_{jl}}{{\phi }^{l}}},\phi \in \left[ 0,\pi /16 \right].$ | (8) |
上式为五次多项式,其系数bjl为常量,求导可得四次多项式.可以通过解析法得到式(8)的极值,考虑边界情况,进而可获得ρj(ø)的近似最大值和近似最小值,分别记为ρjmax和ρjmin.为确认上述近似方法的有效性,需评估幂级数截断所产生的近似误差,定义为
| $\begin{matrix} {{e}_{sin~}}({{\phi }_{i}})=|1-{{(sin~{{\phi }_{i}})}^{-1}}({{\phi }_{i}}-\frac{{{\phi }^{3}}_{i}}{3!}+\frac{{{\phi }^{5}}_{i}}{5!})|, \\ {{e}_{cos~}}({{\phi }_{i}})=|1-{{(cos~{{\phi }_{i}})}^{-1}}(1-\frac{{{\phi }^{2}}_{i}}{2!}+\frac{{{\phi }^{4}}_{i}}{4!})|. \\ \end{matrix}$ | (9) |
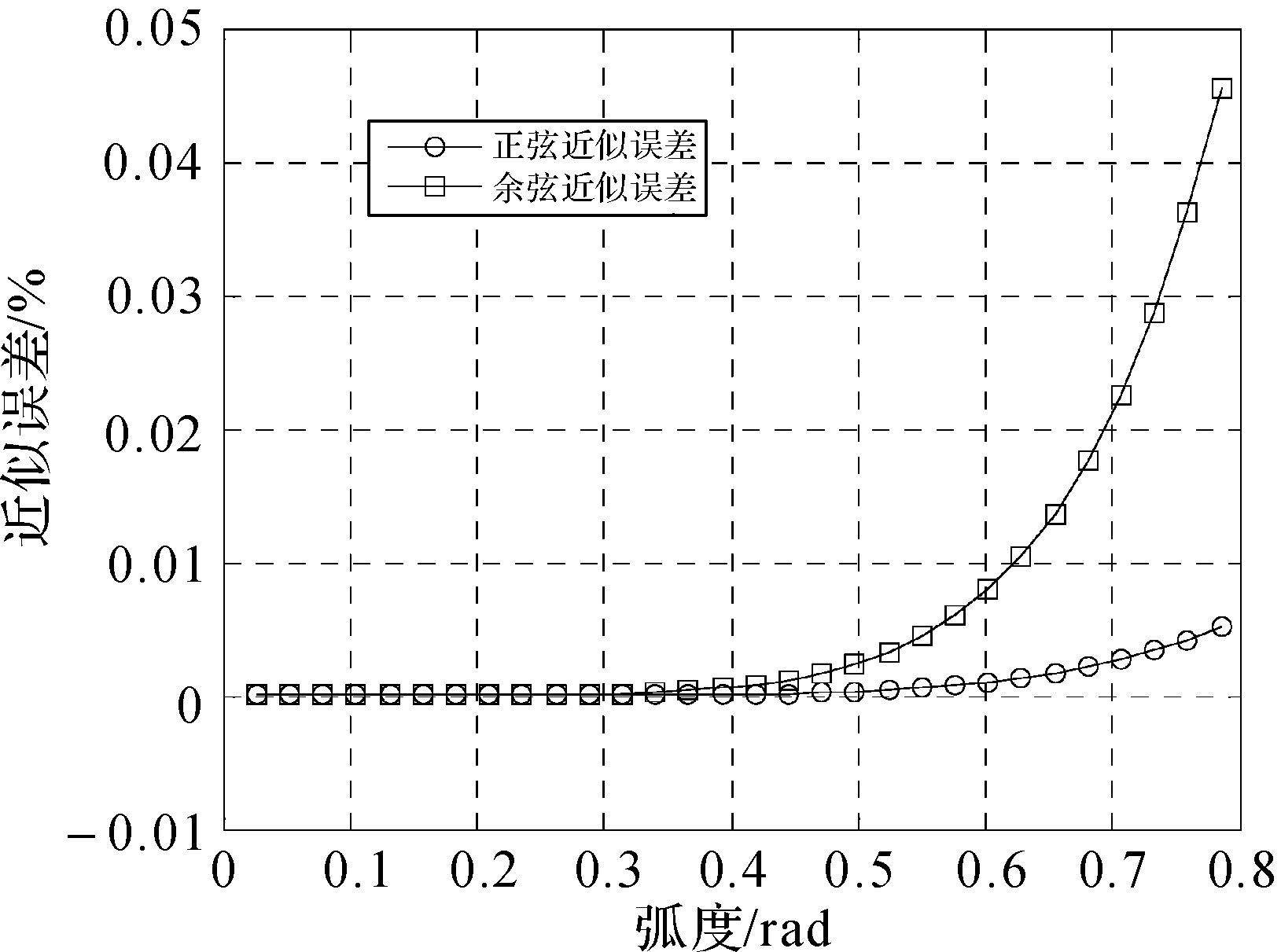
可得近似误差如图 2所示.
|
| 图 2 幂级数近似公式的误差 Fig.2 Errors of approximate power series |
由图 2可知,在øi∈0,π/4时,近似方法所得的|ρj(ø)|max误差不超过0.05%,而在此基础上可采用全局优化方法计算获得精确解.此处为简化表述,取
| $|{{\rho }_{j}}\left( \phi \right){{|}_{max}}\approx \frac{max\left\{ |{{\rho }_{jmax}}\left| , \right|{{\rho }_{jmin}}| \right\}}{1-0.05%},$ | (10) |
由此解得
| ${{k}_{1j}}\approx \frac{64{{r}_{1}}\sqrt{{{a}_{jmax}}}}{\pi ({{v}_{1}}+{{v}_{2}})\sqrt{\frac{max\{|{{\rho }_{jmax}}\left| , \right|{{\rho }_{jmin}}|\}}{1-0.05%}}},$ | (11) |
则k1值由下式取得:
| ${{k}_{1}}=min\left\{ {{k}_{1j}} \right\}.$ | (12) |
基于上述理论可以建立过渡区域的过渡算法,步骤如下:
1) 根据式(4)和式(5)求解φij和Aij.
2) 根据式(8)求解ρjmax和ρjmin.
3) 根据式(11)和式(12)分别求解k1j和k1.
4) 计算基本过渡曲线为
| ${{p}_{j}}\left( t \right)=\sum\limits_{i=3}^{5}{{{A}_{ij}}}sin~(\frac{{{k}_{1}}u}{{{2}^{i-1}}}t+{{\varphi }_{ij}}),0\le t\le T.$ | (13) |
由式(11)可知,若对v1和v2进行同比变化,则k1与速度成反比,使得过渡节点配置不变,进而可知幅值系数与相位系数均不变,因此过渡轨迹的路径和速度剖面形状等均不改变.
5) 如果(v1+v2)过小或者r1过大,可能造成k1>1.若k1>1,则可对式(13)进行时间缩放处理:
| ${{p}_{j}}\left( t \right)=\sum\limits_{i=3}^{5}{{{A}_{ij}}sin}~(\frac{u}{{{2}^{i-1}}}t+{{\varphi }_{ij}}),0\le t\le {{k}_{1}}T.$ | (14) |
即:将过渡时间扩大k1倍,使速度缩小k1倍,而过渡轨迹的路径形状不发生改变.
6) 将所得相对位置矢量变换成绝对位置矢量即可得到最终过渡曲线.
但需注意,如果k1>>1,则上述方法会使得过渡速度最小值过小,不利于保持运动过程中速度的相对稳定.因此在实际机器人控制器中仍需提供类似于文献[4, 8, 11]的分段细化和速度前瞻算法以处理(v1+v2)过小的情况.而对于r1过大的情况,通常意味着示教程序质量不高,需要进行一些局部调整,例如插入圆弧或增加示教点等.
4 仿真与实验采用辰星(天津)自动化设备有限公司的D2-350两自由度高速并联机械手[18-19]为工业机器人模型,并以门式轨迹(bw=305 mm,hw=25 mm)[19]为典型轨迹在MATLAB软件上进行算法的仿真测试.
D2-350两自由度高速并联机械手如图 3所示[19],其操作空间为水平和铅锤方向所形成的平面,具体参数见表 1[19].

|
| 图 3 D2-350机械手 Fig.3 The D2-350 manipulator |
| 长度/mm | 高度/mm | 最大速度/(mm/s) | 最大加速度/(mm/s2) |
| 350 | 150 | 200 | 4 000 |
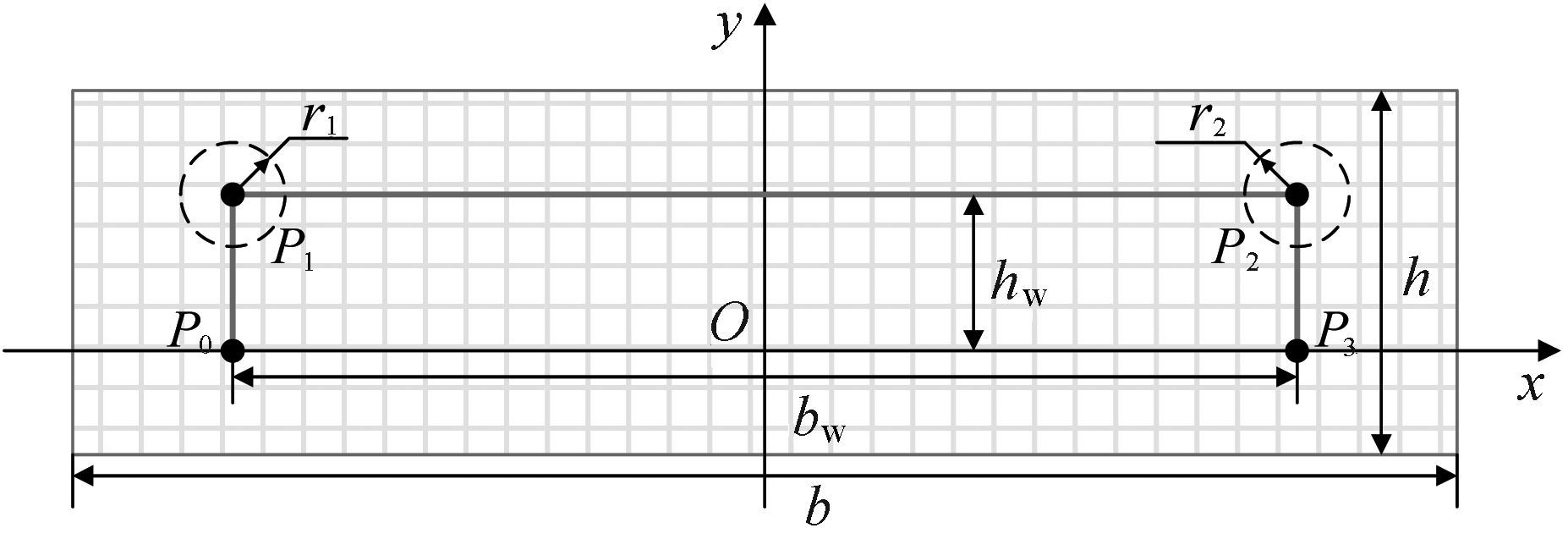
给定门式轨迹如图 4所示,其基本参数见表 2,参考D2-350机械手设定过渡参数,见表 3.
|
| 图 4 给定门式轨迹 Fig.4 The given gantry trajectory |
| b/mm | bw/mm | h/mm | hw/mm |
| 350 | 305 | 150 | 25 |
| 过渡点 | 过渡半径/mm | 速度/(mm/s) | 最大加速度/(mm/s2) |
| P1 | 1 | 200 | ax=4 000 |
| ay=4 000 | |||
| P2 | 1 | 200 | ax=4 000 |
| ay=4 000 |
由于该算法主要用于过渡节点的选取以及过渡曲线的生成,为更直观地分析该算法的特性,以下主要对P1点处过渡区域进行详细分析.
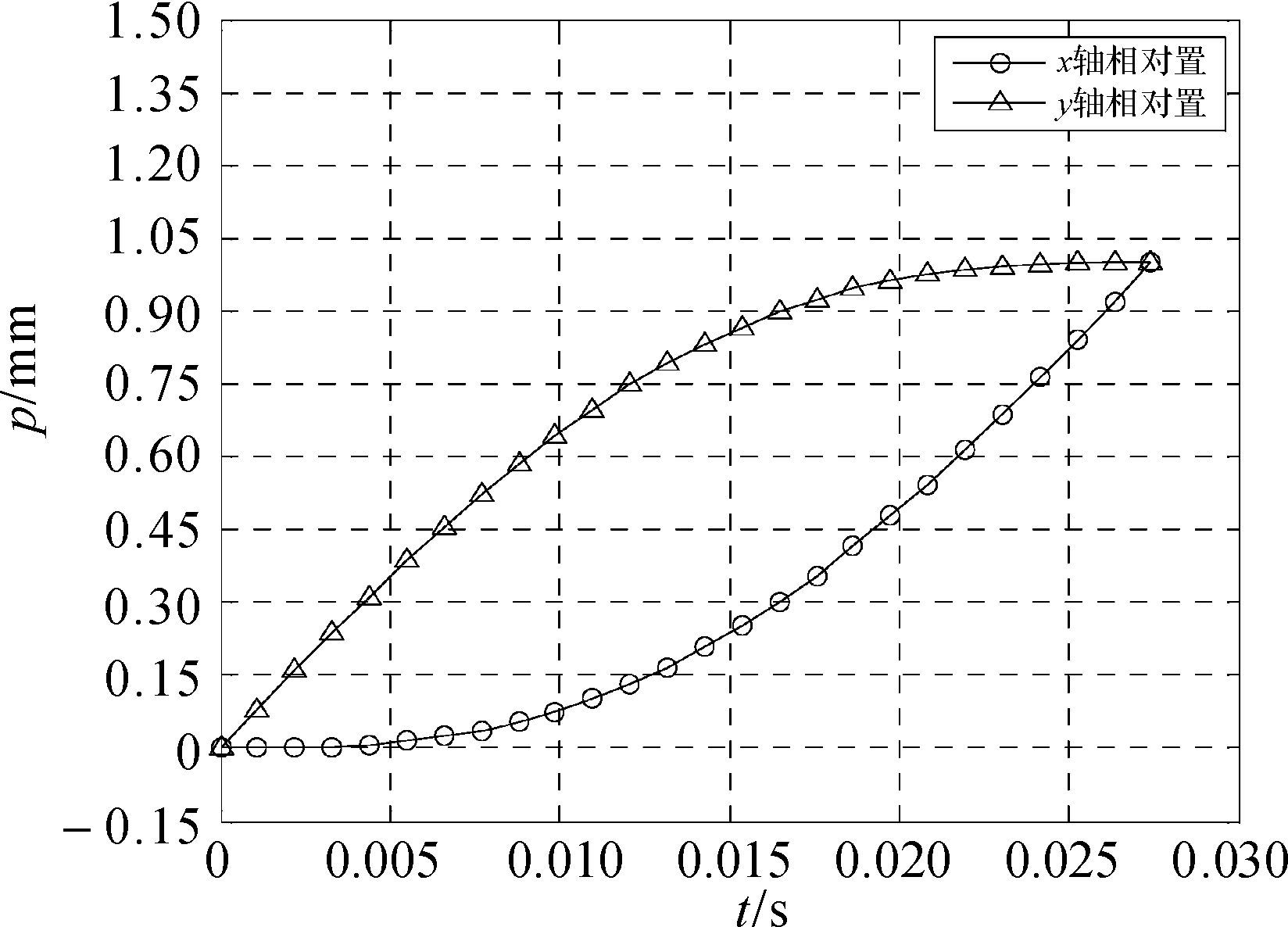
经过计算可得k1=0.36,则P1点处过渡区域的相对位置、速度、加速度和过渡轨迹的曲线分别如图 5、图 6、图 7和图 8所示.
|
| 图 5 P1点处过渡区域相对位置-时间曲线 Fig.5 Relative position-time curve in P1 transition section |
|
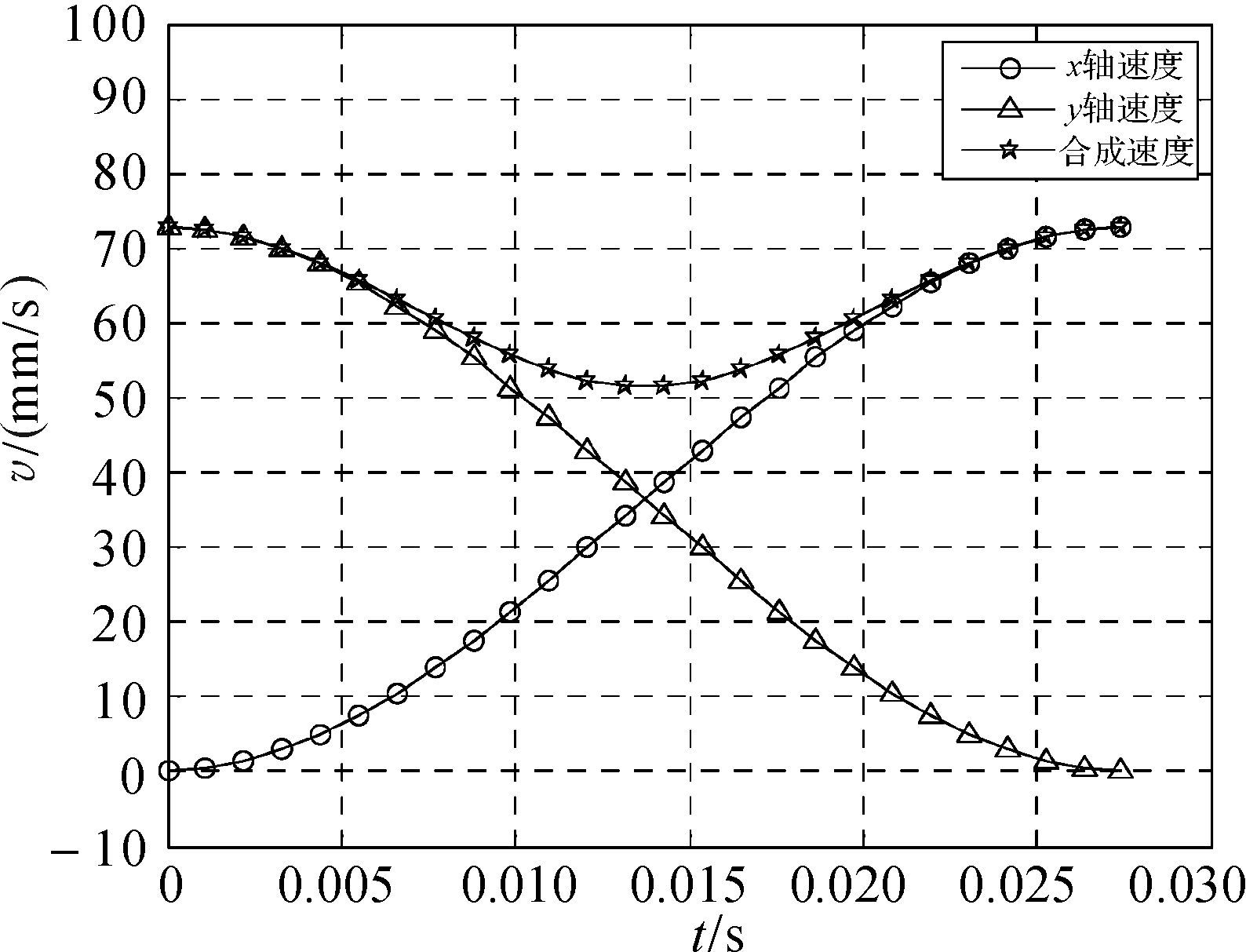
| 图 6 P1点处过渡区域速度-时间曲线 Fig.6 Velocity-time curve in P1 transition section |
|
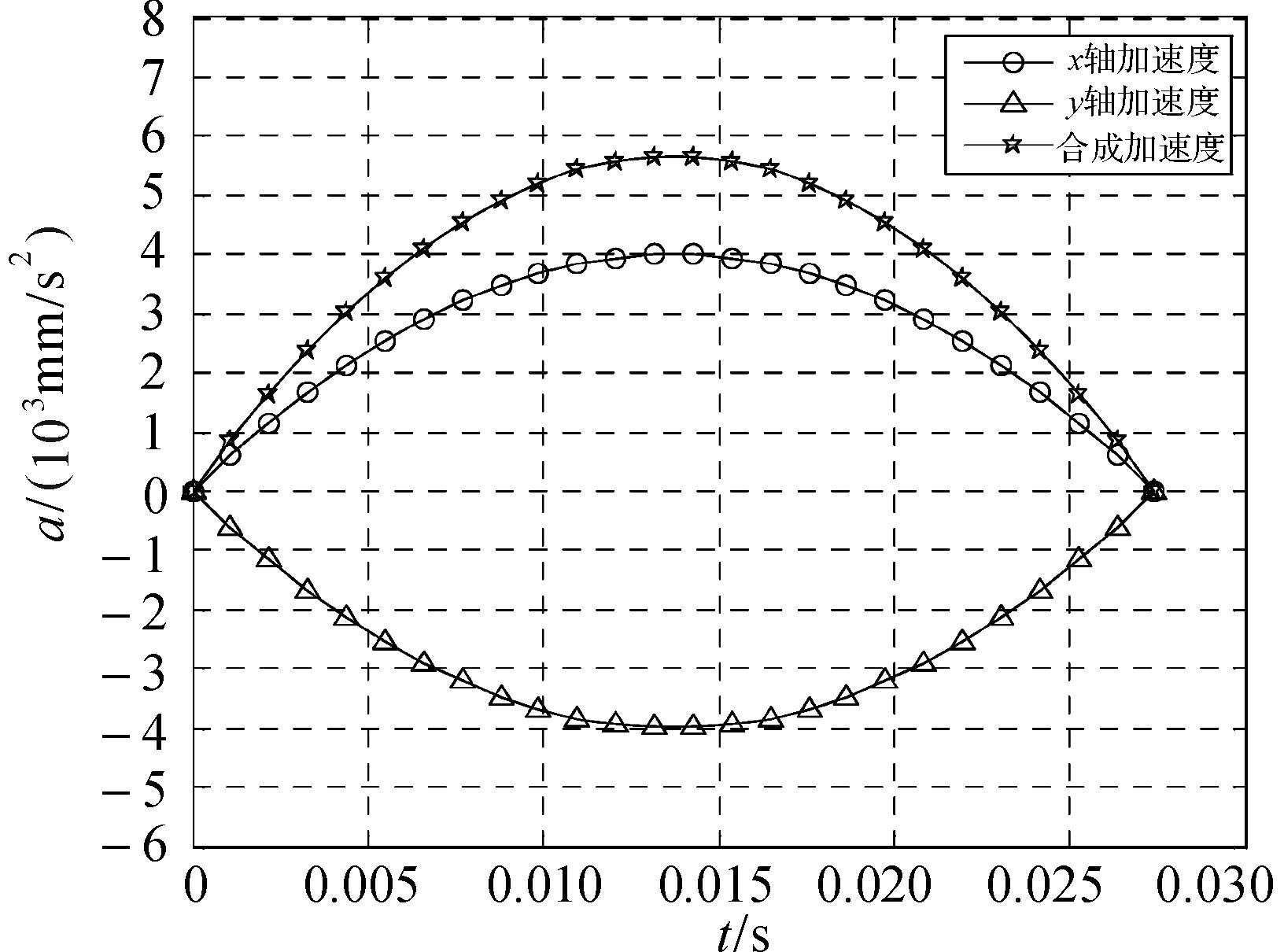
| 图 7 P1点处过渡区域加速度-时间曲线 Fig.7 Acceleration-time curve in P1 transition section |
|
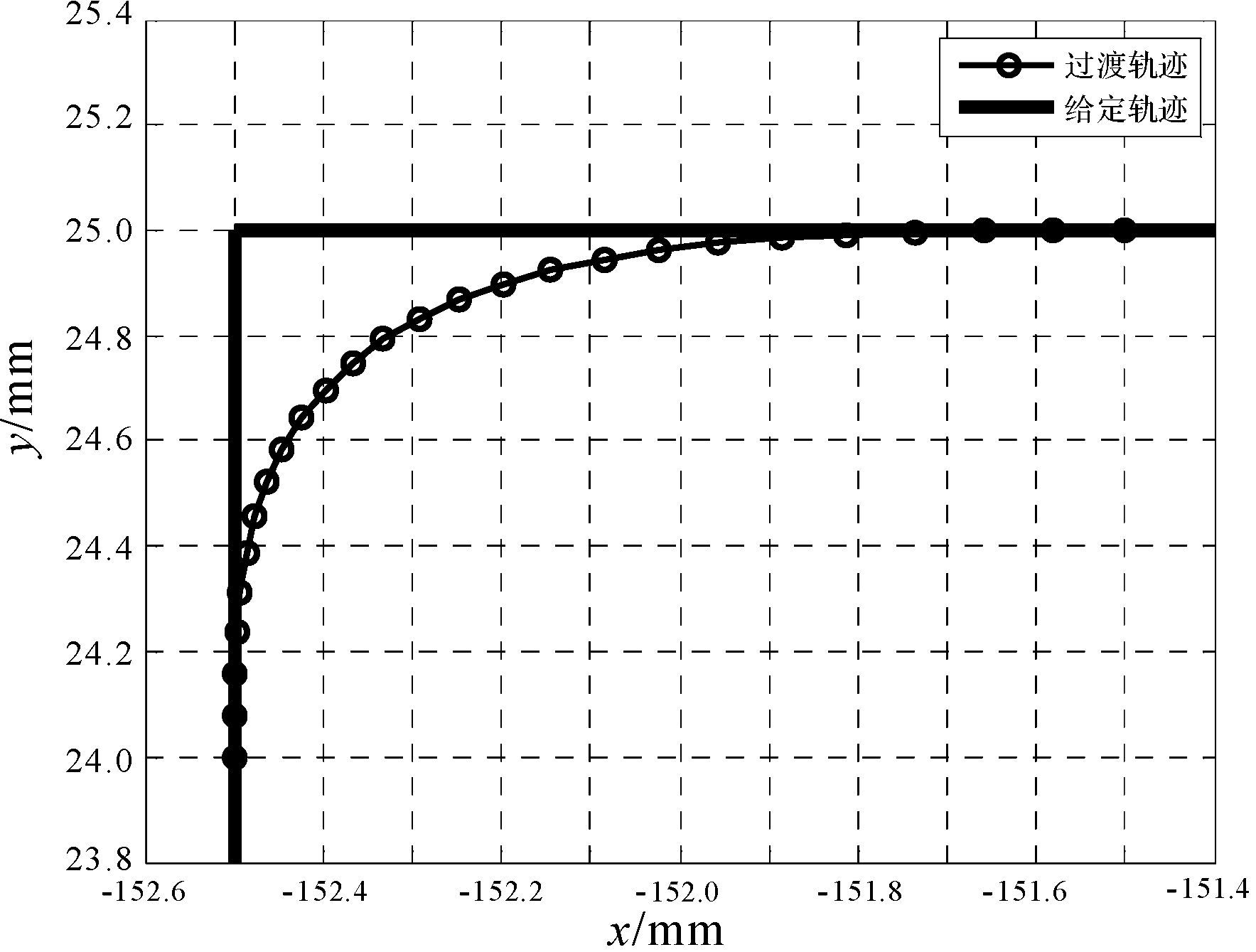
| 图 8 P1点处过渡轨迹 Fig.8 The P1 transition trajectory |
从P1过渡区域加速度曲线可以看出,用该算法求取的过渡曲线的加速度完全满足所施加的物理约束,说明该算法可以达到预期效果.
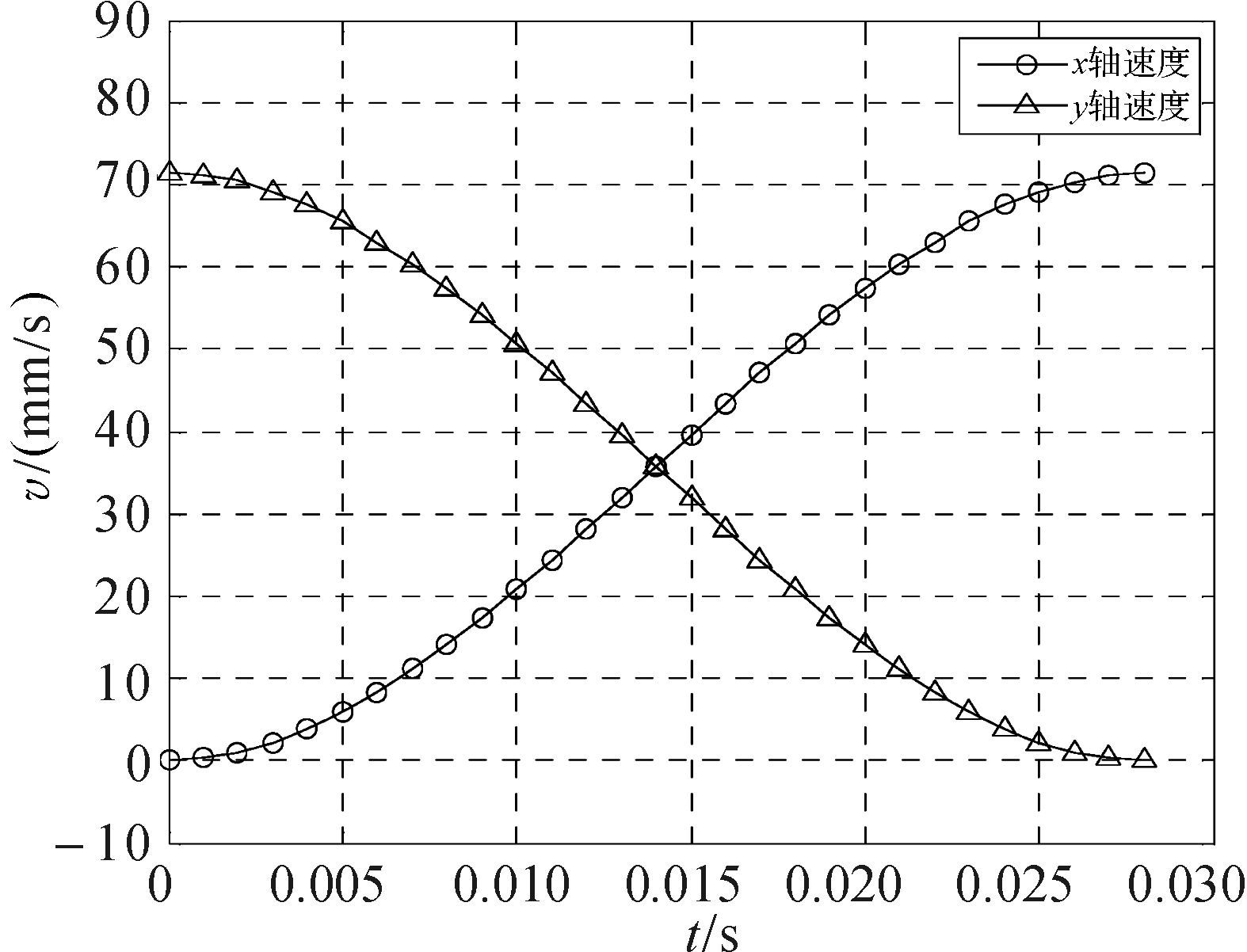
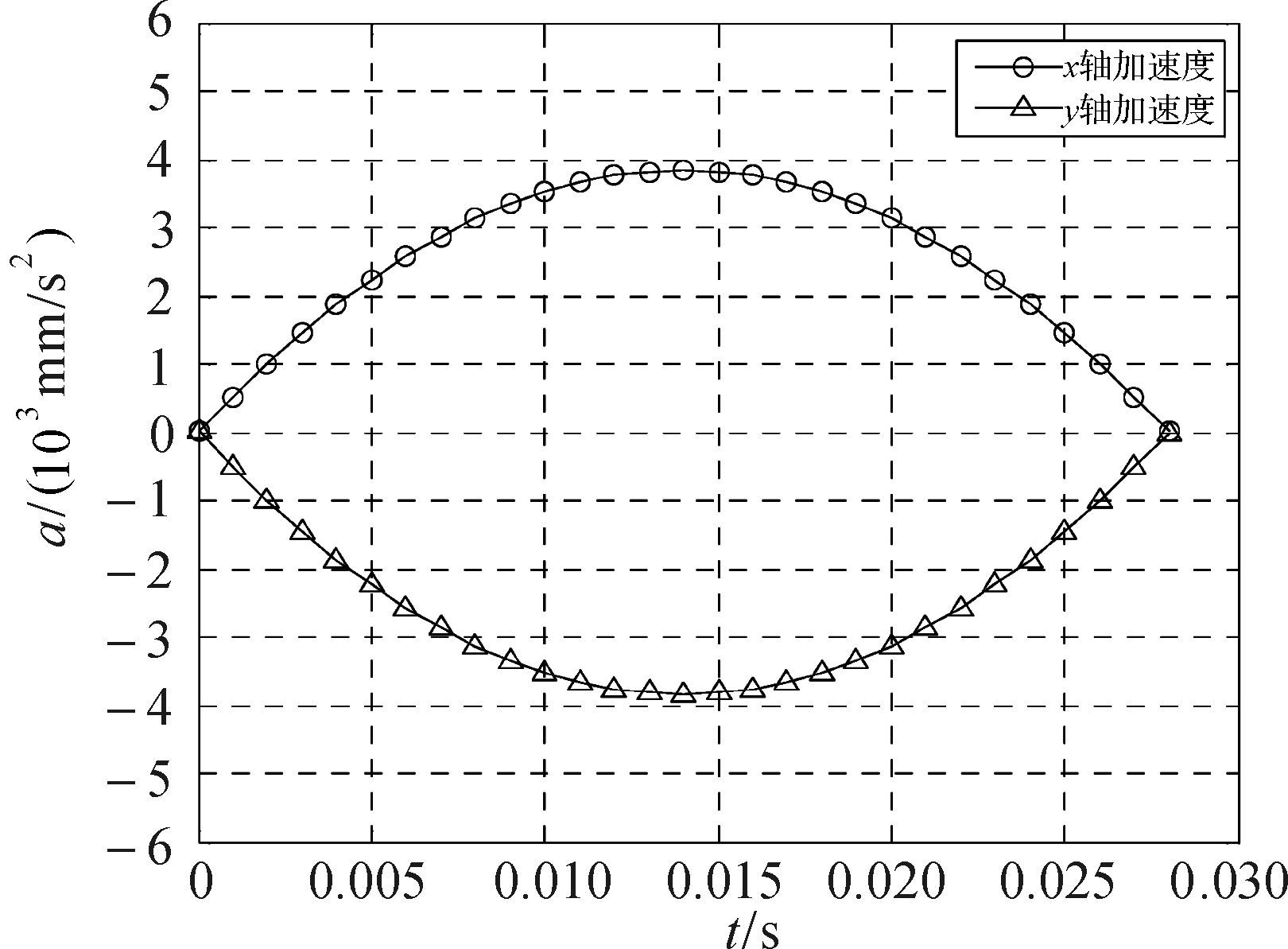
为验证仿真结果,进行实验测试.本测试采用摆线加减速方式实现非过渡区域轨迹规划,同时,由于高速运动需要很高的采样频率,故采用编码器反馈的关节转角进行运动学正解计算得到实际过渡轨迹.实际过渡轨迹、速度和加速度曲线分别如图 9、图 10和图 11所示,采样时间为1 ms.
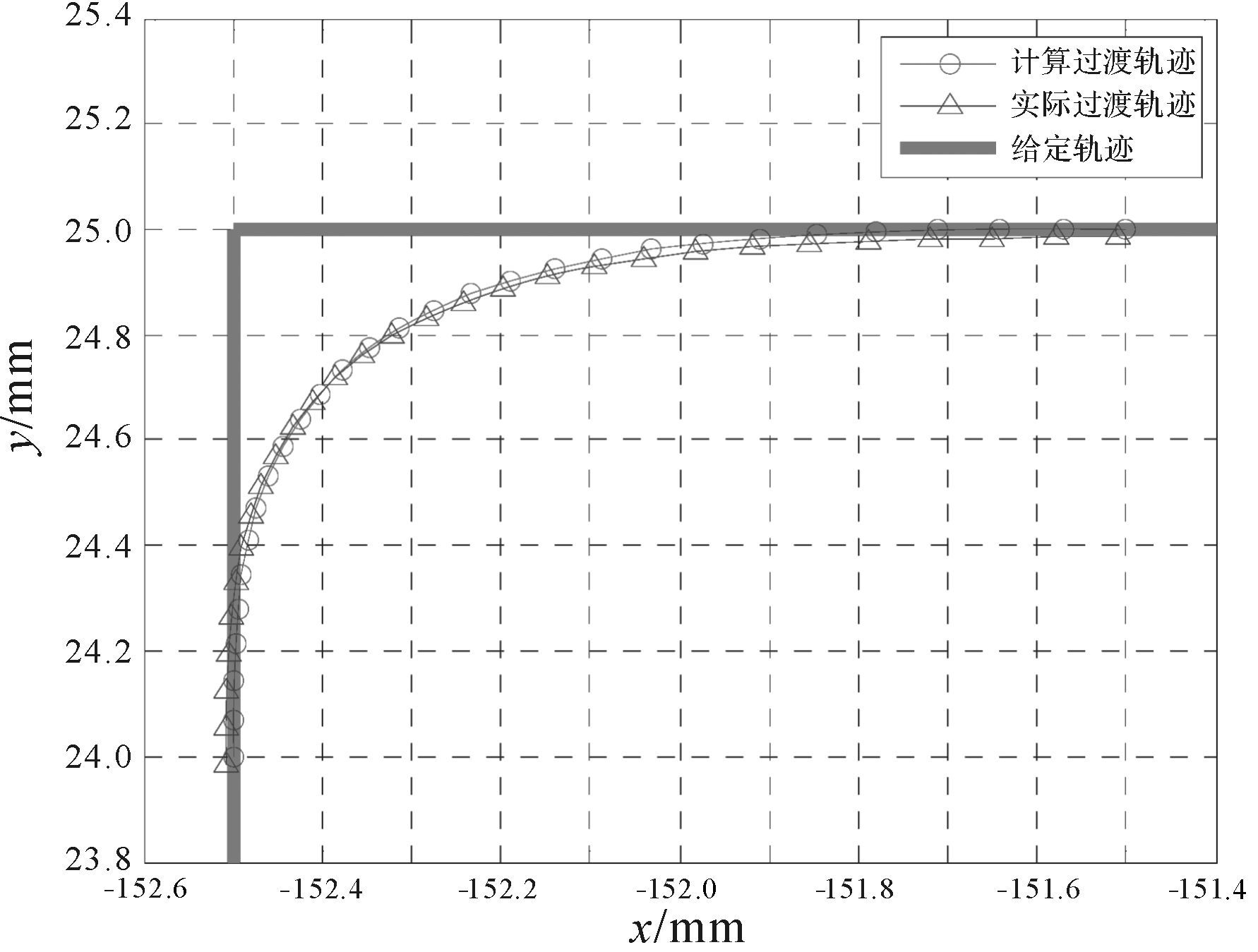
|
| 图 9 实际过渡轨迹与计算过渡轨迹对比 Fig.9 The contrast of actual transition trajectory and computed transition trajectory |
|
| 图 10 过渡区域实际速度-时间曲线 Fig.10 The actual velocity-time curve in transition section |
|
| 图 11 过渡区域实际加速度-时间曲线 Fig.11 The actual acceleration-time curve in transition section |
由图 9可知实际过渡轨迹与计算过渡轨迹基本吻合,而由图 11可知其加速度满足机械手物理约束条件,故该算法得到验证.
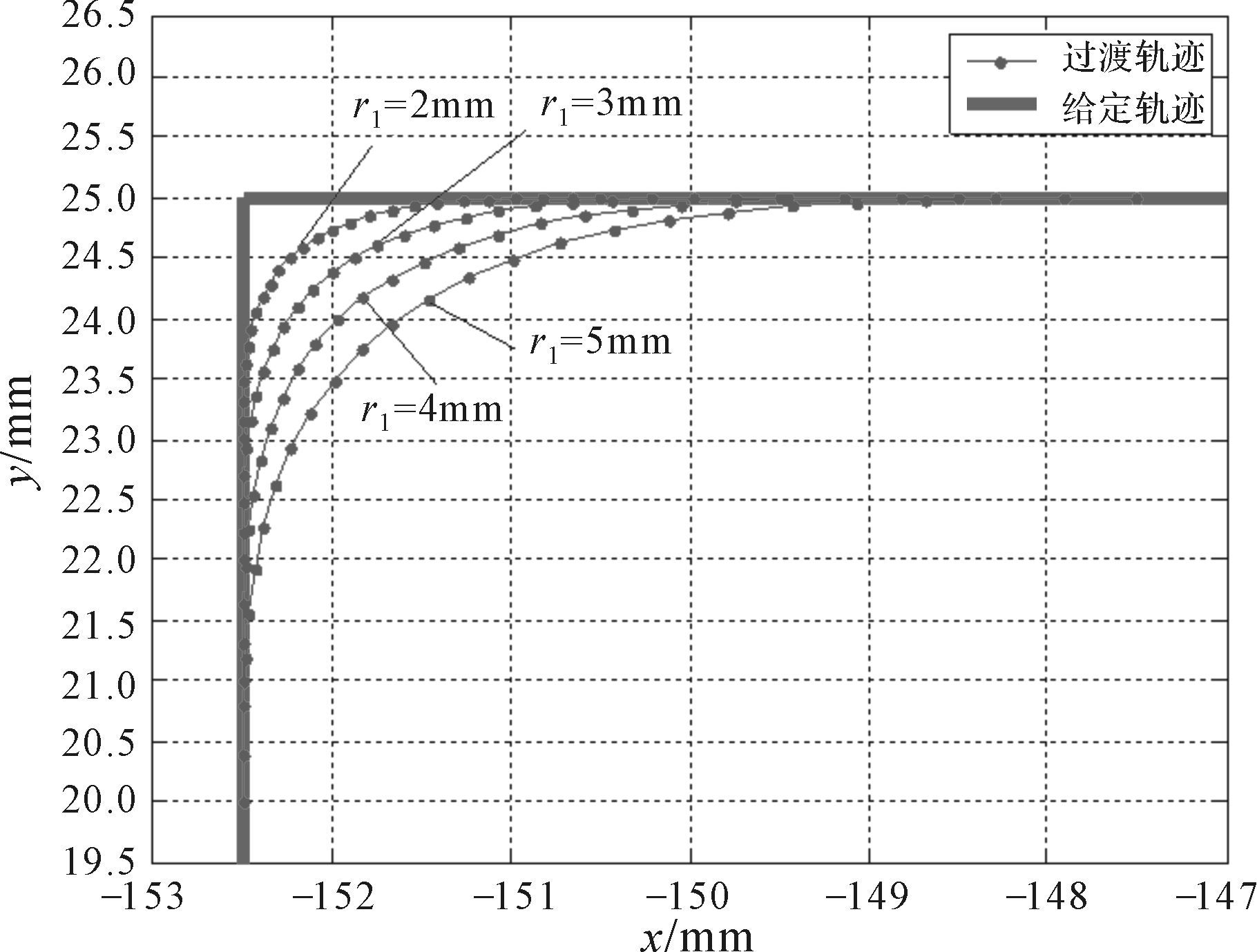
同时,用户可以通过调整过渡半径r1,得到不同的过渡轨迹,图 12所示过渡轨迹簇中的过渡轨迹分别为r1=2,3,4,5 mm时所生成的过渡轨迹.
|
| 图 12 过渡轨迹簇 Fig.12 The transition trajectory cluster |
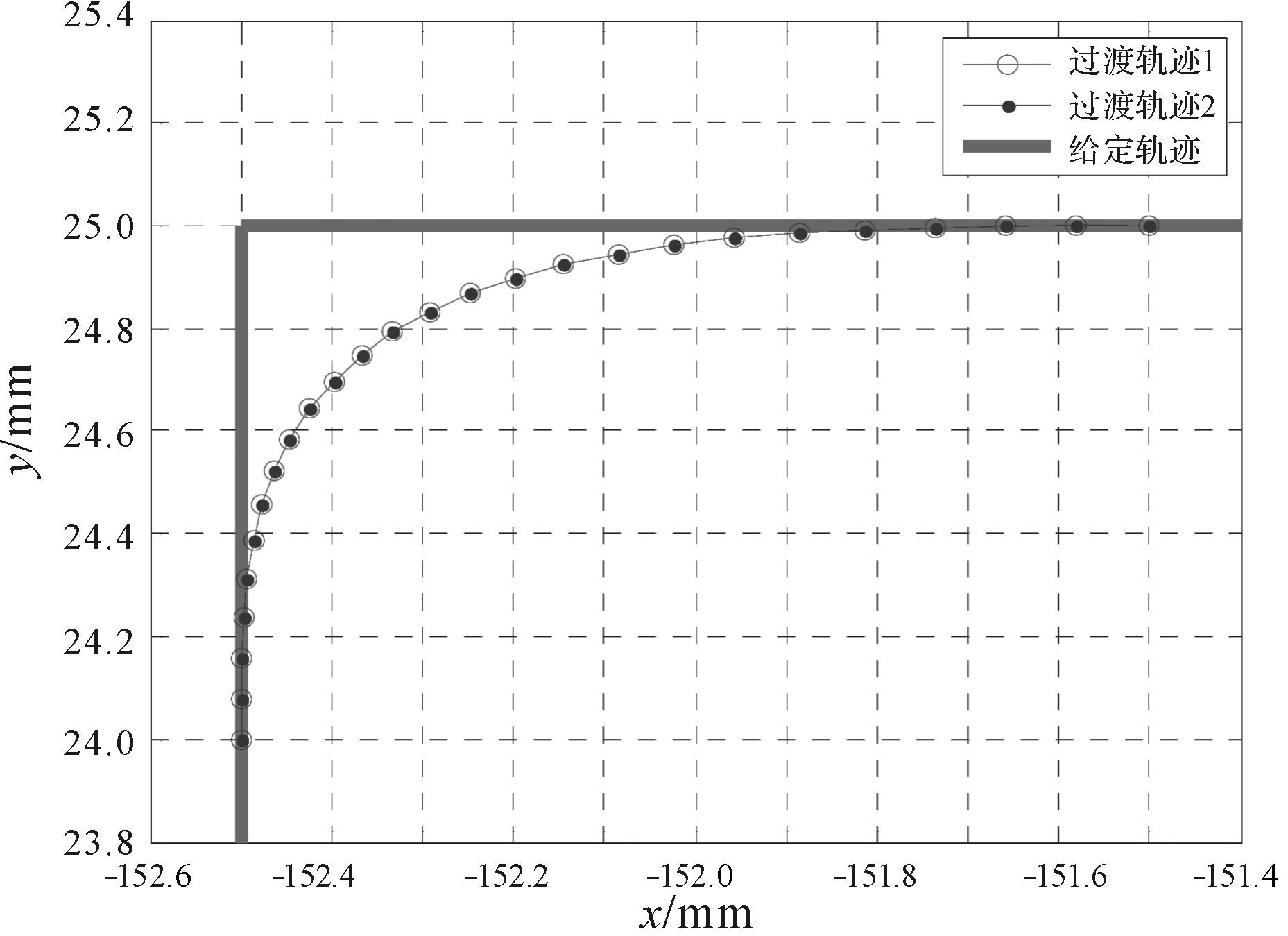
如图 13所示:过渡轨迹1为v1=v2=200 mm/s时的过渡轨迹,而过渡轨迹2为v1=v2=100 mm/s时的过渡轨迹,两者完全重合,证明在速度等比例变化时,所得过渡轨迹不变.
|
| 图 13 速度等比例变化过渡轨迹对比 Fig.13 Comparison of transition trajectories with proportion change of velocities |
本文给出了一种工业机器人操作空间连续轨迹规划的过渡算法,该算法的主要目的是在保证连续轨迹过渡精度和工业机器人物理约束的条件下充分发挥工业机器人的能力,尽量提高过渡区域的速度,减少过渡所需时间,同时尽可能地使计算过程简便,以便用于在线规划,提高算法的通用性.通过MATLAB仿真和两自由度高速并联机械手的实验验证,证实了该算法能够在保证连续轨迹平滑过渡的同时,保证其物理约束条件.此外,该算法具备在速度等比例变化的条件下过渡轨迹不变的特性,这种特性使其能够更广泛地应用于机器人应用领域.此外,该算法是位置规划方法,容易计入位置约束条件,因此其可扩展性良好.后续研究将对姿态配置进行类似处理,进而实现包含空间姿态的轨迹过渡,推动位置规划类连续轨迹规划方法的创新和发展.
| [1] | FU K S, GONZALEZ R C, LEE C S G. Robotics:control, sensing, vision, and intelligence[M]. Blacklick, Ohio: McGraw-Hill Book Company , 1987 : 149 -200. |
| [2] |
刘承立, 栾楠.
关节空间样条的连续点位运动规划算法[J]. 机械与电子 , 2014 (8) : 74–78.
LIU Cheng-li, LUAN Nan. Continuous point to point motion planning algorithm based on splines in joint space[J]. Machinery & Electronics , 2014 (8) : 74–78. |
| [3] |
张斌.
基于多约束的机器人关节空间轨迹规划[J]. 机械工程学报 , 2011, 47 (21) : 1–6.
ZHANG Bin. Joint-space trajectory planning for robots under multiple constraint[J]. Journal of Mechanical Engineering , 2011, 47 (21) : 1–6. DOI:10.3901/JME.2011.21.001 |
| [4] | SUH S-H, KANG S-K. Theory and design of CNC systems[M]. London: Springer-Verlag , 2008 : 107 -156. |
| [5] | VOLPE R. Task space angular velocity blending for real-time trajectory generation:US 5602968[P]. 1997-02-11. |
| [6] | LLOYD J, HAYWARD V. Real-time trajectory generation using blend functions[C]//Proceedings of IEEE International Conference on Robotics and Automation. Sacramento, CA, Apr.9-11, 1991:784-789. |
| [7] | USTYAN T, JÖNSSON V. Implementation of a generic virtual robot controller[D]. Sweden:Chalmers University of Technology, Department of Signals and Systems, Division of Automatic Control, Automation and Mechatronics, 2011:8-31. |
| [8] | KOICHI Funaya. Method of and apparatus for robot tip trajectory control:US 5740327A[P]. 1998-04-14. |
| [9] | SICILIANO B, SCIAVICCO L, VILLANI L. Robotics:modelling, planning and control[M]. London: Springer-Verlag , 2009 : 167 -190. |
| [10] |
林仕高, 刘晓麟, 欧元贤.
机械手笛卡尔空间轨迹规划研究[J]. 机械设计与制造 , 2013 (3) : 49–52.
LIN Shi-gao, LIU Xiao-lin, OU Yuan-xian. The study of trajectory planning of manipulators in Cartesian space[J]. Machinery Design & Manufacture , 2013 (3) : 49–52. |
| [11] |
王允航. 连续轨迹的S型速度规划的研究[D].深圳:哈尔滨工业大学深圳研究生院,2010:5-46.
WANG Yun-hang. Research on S-shaped continuous trajectory planning[D]. Shenzhen:Harbin Institute of Technology, Graduate School at Shenzhen, 2010:5-46. |
| [12] | SONJA Macfarlane, ELIZABETH A Croft. Jerk-bounded manipulator trajectory planning:design for real-time applications[J]. IEEE Transactions on Robotics and Automation , 2003, 19 (1) : 42–52. DOI:10.1109/TRA.2002.807548 |
| [13] | LUIGI Biagiotti, CLAUDIO Melchiorri. Trajectory planning for automatic machines and robots[M]. Berlin: Springer-Verlag , 2008 : 341 -414. |
| [14] | JEON J W, HA Y Y. A generalized approach for the acceleration and deceleration of industrial robotics and CNC machine tools[J]. IEEE Transaction on Industrial Electronics , 2000, 47 (1) : 133–139. DOI:10.1109/41.824135 |
| [15] | CUI J, CHU Z Y. An improved approach for the acceleration and deceleration of industrial robots and CNC machine tools[C]//Proceedings of the 2005 IEEE International Conference on Industrial Technology. Hong Kong, Dec. 14-17, 2005:1269-1273. |
| [16] | JEON J W. Efficient acceleration and deceleration technique for short distance movement in industrial robots and CNC machine tools[J]. Electronics Letters , 2000, 36 (8) : 766–768. DOI:10.1049/el:20000559 |
| [17] | NG Y K, XIE Y, WANG C, et al. Development of a new velocity profile generation for improvement of CNC Machining Efficiency[C]//Proceedings of the 2008 IEEE International Conference on Mechatronics and Automation. Takamatsu, Aug. 5-8, 2008:313-318. |
| [18] | HUANG Tian, LI Zhan-xian, LI Meng, et al. Conceptual design and dimensional synthesis of a novel 2-DOF translational parallel robot for pick-and-place operations[J]. Journal of Mechanical Design , 2004, 126 (3) : 449–455. DOI:10.1115/1.1711822 |
| [19] |
辰星(天津)自动化设备有限公司. D2-350技术参数[EB/OL]. (2015-09-03)[2016-03-27]. http://www.cxrobot.com/gsby/1203_30.html.
Chenxing (Tianjin) Automation Equipment Co., Ltd.. The technical parameters of D2-350[EB/OL]. (2015-09-03)[2016-03-27]. http://www.cxrobot.com/gsby/1203_30.html. |



