2. 新泽西州立大学 机械宇航学院, 新泽西 Piscataway, 08854;
3. 西北工业大学 航空学院, 陕西 西安 710072
2. Department of Mechanical and Aerospace Engineering, Rutgers, The State University of New Jersey, Piscataway NJ 08854 ;
3. School of Aeronautics, Northwestern Polytechnical University of China, Xi'an 710072, China
在科学研究和工程技术中,几乎所有的变量和参数都是非精确、非完全的,几乎所有问题中都包含着不确定性,例如大气状态的扰动、机械的制造误差、主观判断的经验偏差等都是不确定性的表现.近年来,随着计算机科学的飞速发展,为了使设计结果更具可靠性和稳健性,基于数值模拟的不确定性研究越来越多地引起各界关注[1-5].然而,在很多数值模拟的研究中,即使对控制方程单状态的解算都需要消耗较多的计算资源,毫无疑问,对于需要大量重复采样的不确定性研究而言,计算量更是难以承受.
由于代理模型可以通过有限次采样得到整个空间可靠的响应信息,因此其在计算量较大的数值模拟研究中已被广泛应用.目前应用较多的是确定性(deterministic)代理模型[6],其可以通过已知的确定性样本为输入输出建立映射关系,进而取代传统的数值模拟,这类模型包括多项式响应面、支持向量机、Kriging和RBF等.而随机(stochastic)代理模型是专门针对不确定性问题进行建模的.对于不确定性问题而言,由于随机代理模型具有对问题针对性强、响应可靠等优势[7],在不确定性研究中受到了广泛关注,其通过不确定性统计矩信息作为输入建立不确定性输入输出间的映射关系,可直接对不确定性问题进行分析处理.由于不确定性研究仍属于新兴领域,因此现有随机代理模型理论相对于确定性代理模型而言还不多,其中包括多项式混沌方法[8]、Stochastic Kriging[9]和Stochastic RBF[10].Kriging理论具有数学背景强、插值非线性程度高的特点,其作为确定性代理模型理论是非常具有吸引力的,而Stochastic Kriging是Kriging理论在随机空间的拓展.因此,本文将基于Stochastic Kriging对不确定性的试验设计方法展开研究.
试验设计可以有效地减少不确定性研究中的计算量,其目的是通过合理采样,充分地运用有限的计算资源.传统的试验设计方法[11],比如拉丁超立方法[12]、均匀分布法等,由于在资源配置过程中具有不依赖现有的样本信息、充满设计空间等优势,已被较多地用于不确定性初始采样过程中.目前考虑不确定性的试验设计方法研究大多仍专注于这类传统的试验设计方法,但对不确定性问题而言,理论上通过传统试验设计准则基本不可能得到最优的试验分布[13-14].序贯试验设计已被证明是比传统试验设计更行之有效的方法[15-16],相比传统试验设计而言,序贯试验设计在采样过程中很大程度上利用了已有信息的价值,其不仅需要较少的计算资源,而且与真实试验分阶段、阶次产生样本过程比较接近.因此,对不确定性问题开展序贯设计的研究具有重要意义.同时值得注意的是,要进行序贯试验设计,就需要基于已知信息额外建立序贯采样的判断标准[17-18].
在基于代理模型进行试验设计的研究中,即使是很多确定性问题,其初始采样都较为耗时,毫无疑问对于需要在各设计位置处进行重复取样的不确定性问题更是如此.因此,基于针对不确定性问题的随机代理模型开发高效的试验设计方法,以对有限的计算资源进行合理分配,对不确定性问题的研究具有重要意义.在基于确定性Kriging模型的序贯试验设计研究中,就判断标准而言,大部分工作都是根据Kriging估计的均方差来开展的.其中具有代表性的包括最大均方差法(MMSE)和均方差积分法(IMSE)[17].IMSE是理论上直接表示整个预测模型精度的概念,因而在试验设计中得到广泛应用.
目前在基于随机代理模型开展的试验设计研究方面,大部分研究仍采用传统的试验设计方法,对于序贯试验设计方法的研究还不多,其中有代表性的工作包括:Van等通过Bootstrapping对估计方差进行处理[14],Ankenman等通过对IMSE优化问题的求解得到了采样处重复样本个数的估计[19].然而,这些方法还未能同时对不确定性问题的取样位置和重复样本个数进行处理.因此,本文在借鉴前人工作的基础上,将基于作者前期建立的针对不确定性问题的有限样本Stochastic Kriging模型[9]来开发序贯试验设计方法,构建序贯试验设计准则,通过模型初始化、预选样本选取和单轮最终选点准则的构建,对取样位置和各位置上的重复样本点的个数进行选取.
本文将分为如下4个部分进行阐述:第1部分首先对Stochastic Kriging模型进行简要叙述;第2部分将基于Stochastic Kriging模型提出分为3个阶段的序贯试验设计标准与方法;第3部分将通过基础算例验证所提出试验设计方法的有效性;最后,对全文进行总结和展望.
1 Stochastic Kriging简述本小节将首先对Stochastic Kriging理论进行简要阐述,详细的推导可参见参考文献[18].空间中的随机样本将通过如下形式表示:
| $\left. \begin{matrix} {{Y}_{j}}\left( x \right)=\beta +M\left( x \right)+{{\varepsilon }_{j}}\left( x \right), \\ \eta \left( x \right)=Var\left( \varepsilon \left( x \right) \right). \\ \end{matrix} \right\}$ | (1) |
式中:ε(x)被定义为固有不确定性,用来表示扰动项,并被假设为正态分布;εj(x)是固有不确定性的一个实现,表示的是在x处重复样本的扰动,并且假设它与其他重复样本的固有和非固有不确定性Mx之间相互独立;ηx代表的是固有不确定性的方差.这里的输入变量为若干组(xi,Yj(xi),Ni; i=1,2,…,n),其中Ni表示在位置xi处的重复样本的个数,j为第j个重复样本.
各个位置处样本的均值表示为
| $\bar{Y}({{x}_{i}})={{\frac{1}{N}}_{i}}\sum\limits_{j=1}^{{{N}_{i}}}{{{Y}_{j}}}({{x}_{j}}).$ | (2) |
此处,$\bar{Y}$={$\bar{Y}$x1,$\bar{Y}$x2,…,$\bar{Y}$xn}T,用来表示各已知位置均值的向量.
Stochastic Kriging方法采用最优线性估计的形式进行预测,以得到未知位置的均值:
| ${{\bar{Y}}^{*}}\left( x \right)={{w}_{0}}x+\sum\limits_{i=1}^{n}{{{w}_{i}}}\left( x \right)\bar{Y}\left( x \right)={{w}_{0}}+{{w}^{T}}\bar{Y},$ | (3) |
式中wix表示的是赋予已知各位置均值的权值量,也就是通过已知均值的权重来估计未知采样位置处的均值.对于不确定性的Stochastic Kriging模型,均方差表示为
| $MSE=E\left[ \left( {{Y}_{j}}\left( x \right)-\overline{{{Y}^{*}}}{{x}^{2}} \right) \right].$ | (4) |
而后通过一系列统计学推导,均方差MSE变为如下的形式:
| $\begin{align} & MSE={{\left( \beta -{{w}_{0}}-{{w}^{T}}{{l}_{n}}\beta \right)}^{2}}+{{C}_{M}}\left( x,x \right)+ \\ & {{w}^{T}}\left( {{C}_{M}}+{{C}_{\varepsilon }} \right)w-2{{w}^{T}}{{C}_{M}}\left( x,\centerdot \right)+{{\eta }^{*}}\left( x \right), \\ \end{align}$ | (5) |
式中:CM为非固有不确定性的相关性函数,CM为n×n的关于非固有不确定性的相关性矩阵,Cε表示的是关于固有不确定性的相关性矩阵,η*(x)表示在未知采样位置处关于固有不确定性的方差.
随后,Stochastic Kriging模型优化问题的形式可表示为
| $\left. \begin{matrix} find~{{w}_{0}},w, \\ min\text{ }MSE=\beta -{{w}_{0}}-{{w}^{T}}{{l}_{n}}{{\beta }^{2}}{{C}_{M}}\left( x,x \right)+ \\ {{w}^{T}}{{C}_{M}}+{{C}_{\varepsilon }}w- \\ 2{{w}^{T}}{{C}_{M}}\left( x,\centerdot \right)+{{\eta }^{*}}\left( x \right). \\ \end{matrix} \right\}$ | (6) |
通过对这一优化问题的求解可得:
| $w={{({{C}_{M}}+{{C}_{\varepsilon }})}^{-1}}{{C}_{M}}\left( x,\centerdot \right),$ | (7) |
| ${{w}_{0}}=\beta -{{C}_{M}}{{\left( x,\centerdot \right)}^{T}}{{({{C}_{M}}+{{C}_{\varepsilon }})}^{-1}}{{l}_{n}}\beta .$ | (8) |
因此,均值和均方差也即:
| $\overline{{{Y}^{*}}}\left( x \right)=\beta +{{C}_{M}}\left( x,\centerdot \right){{({{C}_{M}}+{{C}_{\varepsilon }})}^{-1}}(\bar{Y}-\beta {{l}_{n}}),$ | (9) |
| $\begin{align} & MSE=\text{ }{{C}_{M}}\left( x,x \right)-{{C}_{M}}{{\left( x,\centerdot \right)}^{T}}{{({{C}_{M}}+{{C}_{\eta }})}^{-1}} \\ & {{C}_{M}}\left( x,\centerdot \right)+\bar{\eta }+{{C}_{\eta }}\left( x,\centerdot \right){{C}^{-1}}_{\eta }({{\eta }_{vector}}-{{l}_{n}}). \\ \end{align}$ | (10) |
选取试验设计标准是为了提高预测模型在整个设计域H内的估计精度,所以本节将基于Stochastic Kriging模型构建IMSE.该方法大致流程如下:
阶段1:
1) 通过拉丁超立方采样(LHS)对设计变量的初始样本{x1,x2,…,xn}进行选择,获得充满设计域的样本位置;
2) 考虑随机因素的影响,在初始样本处进行n0次数值模拟,得到各初始位置n0个重复样本;
3) 基于所得采样得到Stochastic Kriging模型不确定性相关性矩阵中的初始参数.
阶段2:
1) 对每次序贯试验设计确定模型精度的目标水平r;
2) 基于LHS获取额外采样位置;
3) 通过额外样本构建基于IMSE的试验设计准则,以获得增量样本个数ΔN和采样分布信息.
阶段3:
1) 建立基于IMSE的试验设计标准,以同时对取样位置和分布信息进行考虑;
2) 运用粒子群优化算法进行寻优.
根据所得结果对Stochastic Kriging模型参数进行更新,并循环返回到第2阶段的试验设计中,直至达到所需精度.
2.1 样本增量的选取本部分将针对试验设计阶段2中获取样本增量个数的问题进行研究.如阶段1所述,通过初始样本选取,已经得到Stochastic Kriging模型中的参数.假设要在额外k个位置进行取样,通过LHS选取X0={xn+1,xn+2,…,xn+k}.这时需要得到的是样本增量数ΔN和样本分布n={Nn+1,Nn+2,…,Nn+k}.为了通过对样本分布n的选取获得最高的模型精度,对优化问题的构建可以表示为
| $\left. \begin{matrix} min\text{ }IMSE\left( n \right)={{\int }_{{{x}_{0}}\in H}}^{MSE{{x}_{0}};nd{{x}_{0}},} \\ S.T.\text{ }SUM\left( n \right)\text{ }\le \Delta N. \\ \end{matrix} \right\}$ | (11) |
式中:Ni≥0(n+1≤i≤n+k),
| $\begin{align} & MSE\left( {{x}_{0}};n \right)={{C}_{M}}\left( {{x}_{0}},{{x}_{0}} \right)-{{C}_{M}}{{\left( {{x}_{0}},\centerdot \right)}^{T}} \\ & {{\left[ {{C}_{M}}+{{C}_{\varepsilon }}n \right]}^{-1}}{{C}_{M}}\left( {{x}_{0}},\centerdot \right)+\bar{\eta }+{{C}_{\eta }}\left( {{x}_{0}},\centerdot \right){{C}^{-1}}_{\eta }({{\eta }_{vector}}-{{l}_{n}}), \\ \end{align}$ |
并且,
| ${{C}_{\varepsilon }}\left( n \right)=Diag\left\{ \frac{\eta \left( {{x}_{1}} \right)}{{{N}_{1}}},\frac{\eta \left( {{x}_{2}} \right)}{{{N}_{2}}},\ldots ,\frac{\eta \left( {{x}_{n}} \right)}{{{N}_{n}}},\ldots ,\frac{\eta \left( {{x}_{n+k}} \right)}{{{N}_{n+k}}} \right\}.$ |
为了简化推导过程,CM+Cε(n)将被写为C(n)的形式,未知位置MSE(x0;n)中的后两项将表示为η(x0),从而如上公式可以表示为
| $\begin{align} & MSE\left( {{x}_{0}};n \right)={{C}_{M}}\left( {{x}_{0}},{{x}_{0}} \right)-{{C}_{M}}{{\left( {{x}_{0}},\centerdot \right)}^{T}}C{{\left( n \right)}^{-1}}{{C}_{M}}\left( {{x}_{0}}, \right)+ \\ & \eta ({{x}_{0}})={{\tau }^{2}}-{{\tau }^{4}}\sum\limits_{i,j=1}^{n+k}{{{\left[ C{{n}^{-1}} \right]}_{i,j}}}{{r}_{i}}({{x}_{0}}){{r}_{j}}({{x}_{0}})+\eta ({{x}_{0}}). \\ \end{align}$ | (12) |
此后
| $\begin{matrix} IMSEn={{\int }_{{{x}_{0}}\in H}}\{{{\tau }^{2}}-{{\tau }^{4}}\sum\limits_{i,j=1}^{n+k}{\left[ C{{\left( n \right)}^{-1}}_{i,j} \right]} \\ {{r}_{i}}\left( {{x}_{0}} \right){{r}_{j}}\left( {{x}_{0}} \right)+\eta ({{x}_{0}})\}d{{x}_{0}}= \\ {{\int }_{{{x}_{0}}\in H}}[{{\tau }^{2}}+\eta ({{x}_{0}})]d{{x}_{0}}- \\ {{\tau }^{4}}\sum\limits_{i,j=1}^{n+k}{\left[ C{{n}^{-1}}_{i,j} \right]}{{\int }_{{{x}_{0}}\in H}}~{{r}_{i}}\left( {{x}_{0}} \right){{r}_{j}}\left( {{x}_{0}} \right)~d{{x}_{0}}= \\ {{\int }_{{{x}_{0}}\in H}}[{{\tau }^{2}}+\eta ({{x}_{0}})]d{{x}_{0}}- \\ {{\tau }^{4}}{{l}^{T}}\left[ W\bigcirc C\left( n \right) \right]l, \\ \end{matrix}$ | (13) |
式中:W是含有Wij(1≤i,j≤n+k)的矩阵,Wij=${{\int }_{\underset{{{x}_{0}}\in H}{\mathop{{{r}_{i}}\left( {{x}_{0}} \right)}}\,}}~{{r}_{i}}\left( {{x}_{0}} \right){{r}_{j}}\left( {{x}_{0}} \right)~d{{x}_{0}}$,“○”为Hadamard乘子.
为了对样本增量的分配进行估计,同时因为相对于非固有不确定性而言,固有不确定性是较小量,而随着采样数量的增多及重复样本个数的增加,固有不确定将趋于零,所以这里近似取C(n)≈CM.随后,运用拉格朗日法对优化问题进行求解,ΔN的点数分布为
| ${{N}^{a}}_{i}=\Delta N\frac{\sqrt{\eta ({{x}_{i}}){{\left[ {{C}^{-1}}MW{{C}^{-1}}_{M} \right]}_{ii}}}}{\sum\limits_{j=n+1}^{n+k}{\sqrt{\eta \left( {{x}_{j}} \right){{\left[ {{C}^{-1}}_{M}W{{C}^{-1}}_{M} \right]}_{jj}}}}},n+1\le i\le n+{{k}_{.}}$ | (14) |
至此已得到相对于样本增量总数在固定位置最佳重复样本分配近似值,每个样本增量都会有相应的最佳分布与其对应.所以为了得到目标的预测模型精度r,样本增量的总个数可以通过公式IMSE≤r得到.
2.2 阶段3的试验设计本部分将基于阶段2的预选信息提出同时考虑采样位置和重复采样分布的试验设计标准,将此标准转化为优化问题可表示为
| $\left. \begin{matrix} min\text{ }IMSE({{X}_{0}};n)=\int \underset{{{x}_{0}}\in H}{\mathop{MSE}}\,\left( {{x}_{0}};{{X}_{0}};n \right)d{{x}_{0}}, \\ S.T.SUM\left( n \right)=\Delta N, \\ \end{matrix} \right\}$ | (15) |
式中:Ni≥0( n+1≤i≤n+k),
MSE(x0;X0;n)=CM(x0,x0;X0)-
CMx0,·;X0TCMX0+CεX0;n-1
CMx0,·;X0++Cη(x0,·)ηC-1(ηvector-ηln).
随后,通过推导IMSE的计算公式可以转化为下面的形式:
| $IMSE=\int \underset{{{x}_{0}}\in H}{\mathop{[{{\tau }^{2}}+\eta ({{x}_{0}})]d{{x}_{0}}-}}\,{{\tau }^{4}}{{l}^{T}}[W({{X}_{0}})\cdot C{{({{X}_{0}};n)}^{-1}}]l.$ | (16) |
从中可见,目标函数变量为待取样位置X0和各位置上的取样个数向量n
| $\begin{align} & {{v}_{id}}=w\times {{v}_{id}}+{{c}_{1}}\times {{r}_{1}}\times \left( pbes{{t}_{id}}-{{X}_{0}}_{id} \right)+ \\ & {{c}_{2}}\times {{r}_{2}}\times (gbes{{t}_{d}}-{{X}_{0}}_{id}),{{X}_{0}}_{id}={{X}_{0}}_{id}+{{v}_{id}}, \\ \end{align}$ | (17) |
式中:d=1,2,…,k;m为粒子个数,1≤i≤m;惯性因子是从0.8到0.2的递减函数;加速因子c1=c2=2;pbestid为d维i粒子的最优值;gbestd为当前全局最优值.
3 算例分析本部分将分别通过方差各处非均等和各处均等的排队论问题来研究所建立的序贯试验设计方法.所建立方法在预选步进信息时,需要对具体问题计算资源、代理模型的目标精度与步进信息权衡处理.例如,为了更精确地描述问题,对某实际问题设置了代理模型的目标精度,该问题随即转变为选定序贯设计多少次进行采样较为合适.对于这一问题,可根据模型目标精度和现有精度之间的差值得到,同时依据步进信息由公式(14)得到所需步进的样本数量.因此,本部分将重点对预选准则的有效性进行验证,并对比分析试验设计方法的最终结果.此外,为便于分析不确定性问题,所得结果精度将被近似到同一个数量级.
1) 不确定性各处非均等的排队论.
在稳定状态下排队论的等待时间Y的均值具有解析解,对于负荷x(0 <x<1),平均等待时间可表示为
| $Y\left( x \right)=\frac{x}{1-x}.$ | (18) |
此处,各位置取样点是有限的,采样位置为[0.1 0.3 0.5 0.7 0.9].在各位置处,响应值为一系列重复样本,表 1是基于排队论的样本信息,其中Y是真实响应值,Ymean是各位置根据20个重复样本获得的均值,由公式(2)计算得到,Variance是采样位置的方差.
| 输入变量x | 输出变量Y | 方差Variance | 输出变量均值Ymean |
| 0.1 | 0.111 1 | 0.1 | 0.093 1 |
| 0.3 | 0.428 6 | 0.2 | 0.435 0 |
| 0.5 | 1.000 0 | 0.3 | 1.023 5 |
| 0.7 | 2.333 3 | 0.4 | 2.276 8 |
| 0.9 | 9.000 0 | 0.5 | 9.011 6 |
基于表 1中的数据,可得到Stochastic Kriging模型的初始参数,同时可得Stochastic Kriging的初始IMSE=0.468 78.为了得到样本增量的总个数ΔN,并对方法的有效性进行验证,这里假定步进的目标精度r=0.33,即需要IMSE≤0.33.此时结合公式(13)和(14),可得样本增量数为20.其间,首先通过拉丁超立方选取额外的采样位置X0={0.2,0.4,0.6,0.8},进而由公式(14)可知,最佳分布比例是353∶471∶565∶611.当增量数是20时,根据公式(13)可知,IMSE=0.322 76.这是约束条件下的最佳分布结果,即20个样本将被用来作为增量数进行阶段3的分析.
在阶段3中,根据对公式(16)的优化,所得结果如表 2中“最优”部分所示.一般来说,为了使模型更精确,对不确定性问题常采用均匀分布,等分样本空间,或者根据直觉在不确定性大的位置多取样本.所以表 2同时给出了均匀分布和直觉分布的IMSE结果.通过分析可知,所建立方法得到的样本分布为非均匀分布,并且在不确定性相对较小的0.19和不确定性相对较大的0.81位置上重复取样个数较多.也即:要使模型更精确,不仅需要在不确定性较大处采样,同时也要在已较精确处添加样本.
| 类型 | 变量名 | 处理所得数据 | IMSE | |||
| 均匀 | x0 | 0.2 | 0.4 | 0.6 | 0.8 | 0.325 19 |
| n | 5 | 5 | 5 | 5 | ||
| 直觉 | x0 | 0.2 | 0.4 | 0.6 | 0.8 | 0.325 14 |
| n | 3 | 5 | 5 | 7 | ||
| 最优 | x0 | 0.19 | 0.4 | 0.6 | 0.81 | 0.324 14 |
| n | 5 | 4 | 4 | 7 | ||
对基于Stochastic Kriging进行的这一不确定性问题研究而言,IMSE数值结果主要来源于固有不确定性η(x0),因为η(x0)本身是个较大的量.然而,随着样本个数的增加,在IMSE数值中这一部分将渐趋恒定,其不会对优化结果产生过多影响.
此外,在阶段2预估样本增量时,所得IMSE的结果为0.322 76,稍低于所建立方法优化所得结果.这是由于在预估步中,为得到更合理的样本增量值,代入公式(13)的是样本分配的小数值,分别为3.53,4.71,5.65,6.11,但阶段3的优化中所采用的试验设计准则与阶段2不同,所得到的是整数化的结果.
2) 不确定性各处均等的排队论.
为了便于与不确定性各处非均等的问题对比研究,本算例采用各处不确定性均等的设置中,对表 1中的数据只改变方差列,将其都设为0.1.
与算例1相似,首先可通过已知信息建立Stochastic Kriging模型,得到初始参数,这时初始IMSE=0.262 57.为对比算例1,同时保证阶段2预估点的有效性,此处将增量样本的个数设置为20.通过公式(13)和(14)可知,点数在X0={0.2,0.4,0.6,0.8}处的分布n={4.90,5.10,5.10,4.90}.将n代入(13),可得IMSE=0.115 79.随后,根据20个样本增量个数开展阶段3的分析,对公式(16)进行优化,所得结果如表 3所示.
| 类型 | 变量名 | 处理所得数据 | IMSE | |||
| 最优 | x0 | 0.19 | 0.4 | 0.6 | 0.81 | 0.109 63 |
| n | 6 | 4 | 4 | 6 | ||
通过分析可知,与算例1类似,采样都分布在偏离均匀分布的位置,且重复样本分布也趋于在0.19和0.81位置上多取.与算例1不同的是,此问题的结果在0.19和0.81处拥有相同的分布.相对于原始模型的精度而言,两者之间具有极大的可比性,显示了预估步的实效性.
3) 飞行器机翼气动扰动的不确定性问题.
通常情况下对飞行器气动问题的考量都是在给定设计状态下进行的,属于确定性问题.然而实际上,飞行器气动问题常常由于各种不确定因素的扰动,确定性的考量结果偏离真实响应,这极可能使飞行器性能急剧变差.因此,目前在飞行器气动问题的研究中,越来越多的研究工作开始考虑气动扰动下的不确定性问题.
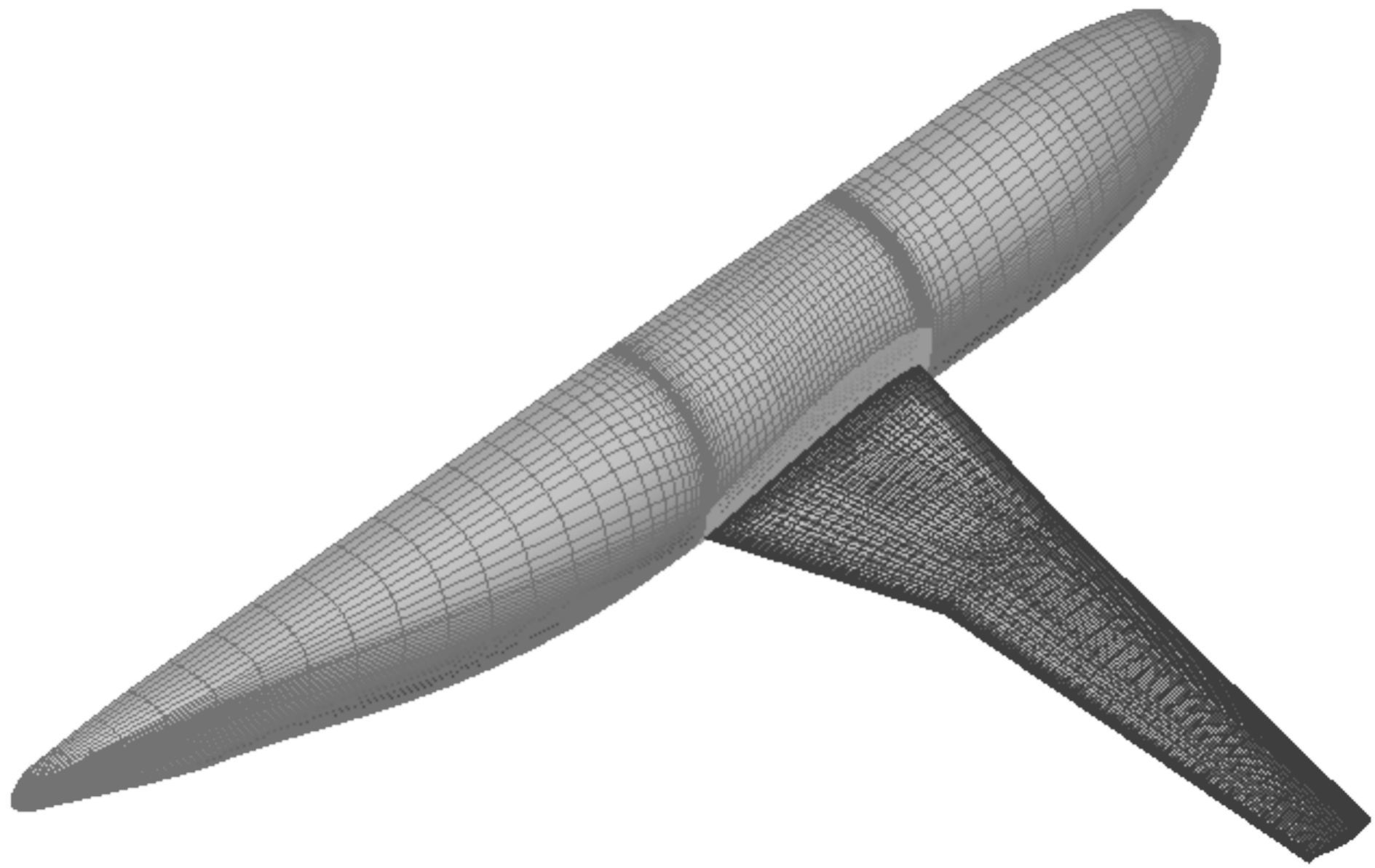
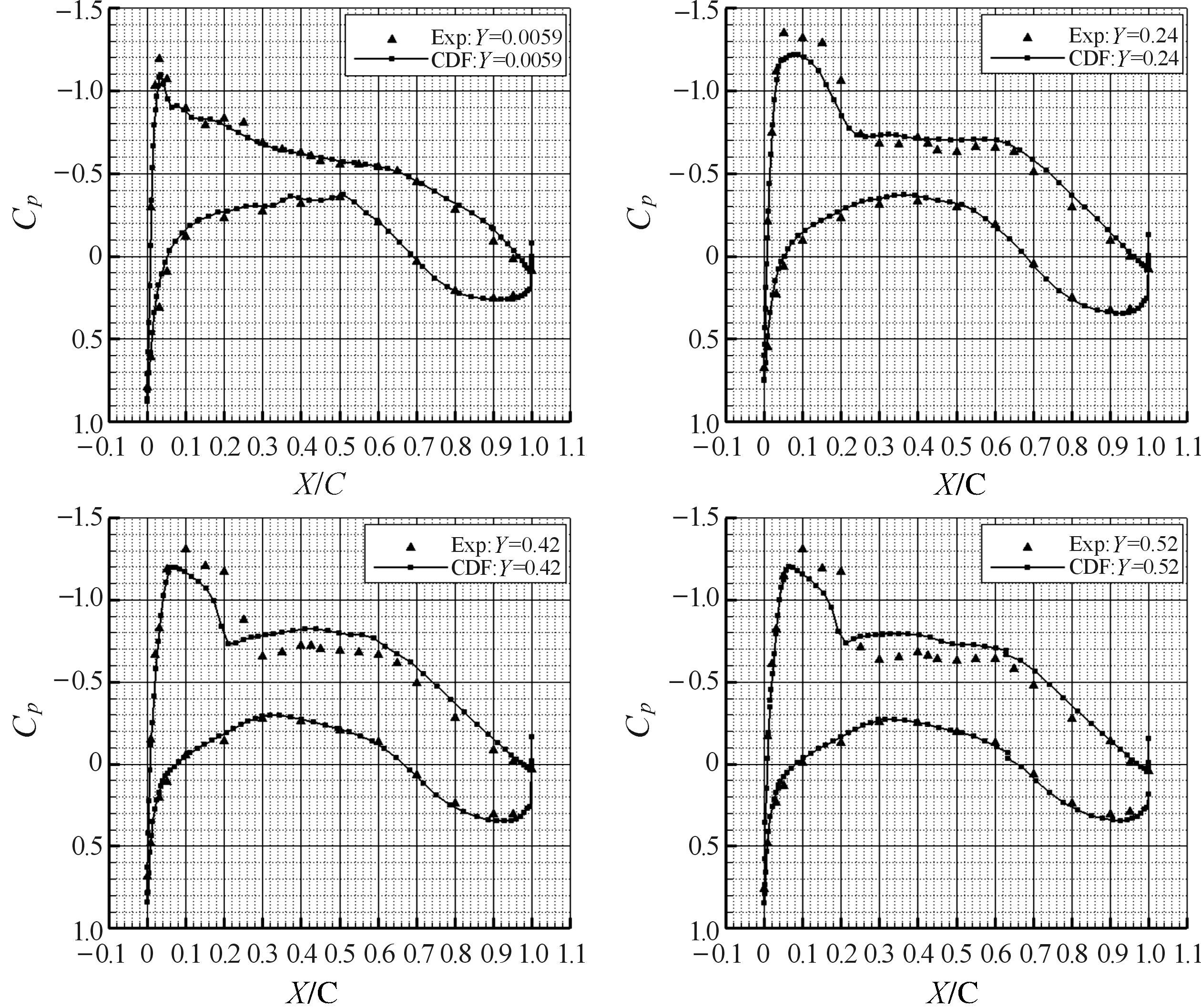
为了对所构建方法开展应用研究,选用DLR-F4的翼身组合体,采用结构网格,划分的网格量为1.2×106个,DLR-F4翼身组合体表面网格如图 1所示.采用RANS方程、S-A湍流模型进行流场计算,单状态计算时间为15 min.通过对Ma=0.75,Cl=0.50,Re=3×106的实验结果进行对比检验,结果表明所采用流场计算方法结果较好地反映了实验结果的变化趋势,各典型剖面处的压力分布对比如图 2所示,其中X/C为采用归一化处理的相对弦长,Cp为压力系数.
|
| 图 1 DLR-F4翼身组合体表面网格 Fig.1 The surface grid of DLR-F4 wing-body configuration |
|
| 图 2 DLR-F4翼身组合体计算和实验结果对比 Fig.2 The comparison between computation and experiment of DLR-F4 wing-body configuration |
此处对机翼在马赫数扰动情况下的不确定性问题进行研究,马赫数的扰动服从正态分布N(0,0.1).与验证算例类似,马赫数各位置处采样点个数是有限的,不确定性初始采样个数为20个,采样位置为{0.69 0.71 0.73 0.75 0.77}.据此可得模型的初始参数,同时可得模型初始IMSE=0.128 3×10-5.而后,通过设定步进的目标精度0.10×10-5,并结合公式(13)和(14),得到样本增量的总个数ΔN=16.在阶段3中,将ΔN作为增量数进行分析,根据对公式(16)的优化,所得结果如表 4所示.
| 类型 | 变量名 | 处理所得数据 | IMSE | |||
| 最优 | x0 | 0.702 | 0.721 | 0.743 | 0.76 | 0.907 3×10-6 |
| n | 4 | 3 | 3 | 6 | ||
本文基于Stochastic Kriging模型构建了适用于不确定性研究的序贯试验设计方法,建立了预选点步进信息的选取策略和基于步进信息的单轮选点准则.通过算例分析验证了所建立试验设计方法的有效性和可行性.未来可对高维不确定性问题开展进一步的工作.
| [1] | ZANG T A, HEMSCH M J, HILBURGER M W. et al. Needs and opportunities for uncertainty-based multidisciplinary design methods for aerospace vehicles[R/OL].[2016-11-02]. http://www.cs.odu.edu/~mln/ltrs-pdfs/NASA-2002-tm211462.pdf. |
| [2] | SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study:a path to revolutionary computational aerosciences[R/OL].[2016-11-02]. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20140003093.pdf. |
| [3] | BLATTNIG S R, LUCKRING J M, JOSEPH H M, et al. NASA standard for models and simulations:philosophy and requirements overview[J]. Journal of Aircraft , 2012, 50 (1) : 20–28. |
| [4] | Editorial policy statement on numerical and experimental accuracy[J/OL].[2015-07-06]. http://servidor.demec.ufpr.br/CFD/bibliografia/erros_numericos/AIAA_Journals_NumericalAccuracy.pdf. |
| [5] | MURTHY J Y, MATHUR S R. Computational heat transfer in complex systems:a review of needs and opportunities[J]. Journal of Heat Transfer , 2012, 134 (3) : 031016. DOI:10.1115/1.4005153 |
| [6] | RAZAVI S, TOLSON B A, BURN D H. Review of surrogate modeling in water resources[J]. Water Resources Research , 2012, 48 (7) : 107–116. |
| [7] | XUE Z, MARCHI M, PARASHAR S, et al. Comparing uncertainty quantification with polynomial chaos and metamodels-based strategies for computationally expensive CAE simulations and optimization applications[R/OL].[2016-11-02]. http://papers.sae.org/2015-01-0437/. |
| [8] | GHANEM R, SPANOS P. Stochastic finite elements:a spectral approach[M]. New York: Courier Dover Publications , 2003 . |
| [9] | WANG Bo, BAI Jun-qiang. GEA Haechang. Stochastic kriging for random simulation metamodeling with finite sampling[C]. 39th ASME Design Automation Conference, Portland, Oregon, Aug. 5-8, 2013. |
| [10] | VOLPI S, DIEZ M, GAUL N J, et al. Development and validation of a dynamic metamodel based on stochastic radial basis functions and uncertainty quantification[J]. Structural Multidisciplinary Optimization , 2015, 51 (2) : 347–368. DOI:10.1007/s00158-014-1128-5 |
| [11] | SANCHEZ S M. Work smarter, not harder:guidelines for designing simulation experiments[C]//Proceedings of the 2005 Winter Simulation Conference. Orlando, FLorida, Dec. 4-7, 2005:69-82. |
| [12] | KOEHLER J R, OWEN A B. Computer experiments[M]. Pennsylvania: Handbook of Statistics , 1996 : 261 -308. |
| [13] | RIDGE E. KUDENKO D. Sequential experiment designs for screening and tuning parameters of stochastic heuristics[R/OL].[2016-11-02]. http://www.imada.sdu.dk/~marco/EMAA/Papers/EMAA06-ridge.pdf. |
| [14] | VAN Beers, KLEIJNEN JACK PC. Customized sequential designs for random simulation experiments:Kriging metamodeling and bootstrapping[J]. European Journal of Operation Research , 2008, 186 (3) : 1099–1113. DOI:10.1016/j.ejor.2007.02.035 |
| [15] | PARK S, FOWLER J W, MACKULAK G T, et al. D-optimal sequential experiments for generating a simulation-based cycle time-throughput curve[J]. Operations Research , 2002, 50 (6) : 981–990. DOI:10.1287/opre.50.6.981.347 |
| [16] | GHOSH B K, SEN P K. Handbook of sequential analysis[M]. New York:Marcel Dekker Inc., 1991. |
| [17] | SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments[J]. Statistical Science , 1989, 4 (4) : 409–423. DOI:10.1214/ss/1177012413 |
| [18] | WELCH W J, BUCK ITJ, Sacks J. Predicting and computer experiments[J]. Technometrics , 1992, 34 (1) : 15–25. DOI:10.2307/1269548 |
| [19] | ANKENMAN B E, NELSON B L, STAUM J. Stochastic kriging for simulation metamodeling[J]. Operations Research , 2010, 58 (2) : 371–382. DOI:10.1287/opre.1090.0754 |


