液压凿岩机工作时, 活塞冲击静止的钎杆, 并通过钎杆将动能以应变能的形式作用介质而完成破碎[1-2].由于波阻和应力波反射的存在, 如果介质没有完全吸收这部分应变能, 钎杆和活塞都可能发生回弹.回弹现象降低了液压凿岩机的工作效率, 同时使得钎具和机体发生刚性冲击, 严重影响其工作可靠性和使用寿命[3].因此, 液压凿岩机回弹对其结构设计和工作效率有着重要的影响[3].目前, 对回弹缓冲的研究主要集中在波动力学理论[3-7]和力学模型[8-9]方面, 对回弹缓冲装置进行非线性建模、动力学仿真的研究很少, 而对不同工况下缓冲装置的动态特性的研究则更少.为了研究和改善液压凿岩机回弹缓冲的性能, 本文基于应力波的传播机理, 提出回弹速度计算方法, 设计了一种回弹缓冲装置, 并建立相关运动状态的非线性方程, 对回弹缓冲装置进行动力学分析及仿真和实验研究, 最后分析了预充压力和工况对液压凿岩机回弹缓冲的影响.
1 回弹缓冲装置数学模型的建立 1.1 回弹速度的计算方法在液压凿岩机冲击中, 活塞比钎杆短很多, 所以可以近似看作是有限长杆与半无限长杆的共轴碰撞[5].在冲击过程中, 动能以应变能的形式完成介质的破碎.由于介质、钎杆和活塞的波阻不同, 必然存在一部分未被利用的应力波从冲击面反射重新回到打击端面而引起钎杆和活塞的回弹.为了便于分析, 这里将钎杆和介质的冲击面、活塞和钎杆的打击端面看成是固定的, 并作如下假设:
1) 活塞和钎杆的波阻和截面相等, 且长度能满足入射波波形不变, 忽略入射波透射损失;
2) 只研究一次反射应力波的影响, 考虑到碰撞时间可以不计, 忽略透射波叠加的影响;
3) 考虑到冲击所产生的作用力远大于重力, 忽略各部件重力的影响.
大量实验和工况表明[3-4]:在实际钻凿作业中, 钻头的作用力与钻进量可以简化成线性关系.所以, 以钎杆和介质的冲击面为研究对象, 其负载边界条件为
| $ {{F}_{\text{R}}}=K\cdot x+{{F}_{\text{ku}}}+{{F}_{\text{Ru}}}, $ | (1) |
式中:K为介质系数;x为钻进量, 规定与活塞冲击速度方向一致为正;Fku为介质的黏性阻力, Fku=Jsdx/dt, Js为黏弹性系数;FRu介质黏性阻力.
在式(1)所示的负载边界条件下, 以活塞和钎尾的打击端面为研究对象, 根据波动叠加方程, 则有
| $ \left. \begin{matrix} P+Q={{F}_{\text{R}}}, \\ P-Q=\lambda \frac{\text{d}x}{\text{d}t}. \\ \end{matrix} \right\} $ | (2) |
式中:P,Q分别为入射波和反射波的形式, 规定压缩波为正;λ为活塞、钎杆的波阻.联立式(1)和式(2), 可得钻进量微分方程为
| $ K\cdot x+\left( \lambda +{{J}_{\text{s}}} \right)\cdot \frac{\text{d}x}{\text{d}t}=2P-{{F}_{\text{Ru}}}. $ | (3) |
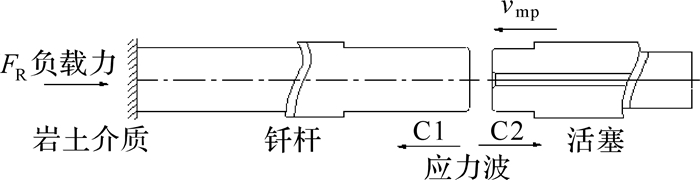
活塞和钎杆完成冲击时, 所产生的入射波将从打击端面分别向活塞和钎杆发生透射, 如图 1所示, 该入射波以压缩波的形式(C1, C2)传播, 其中, 压缩波C2右行, 并在活塞的尾部以拉伸波的形式发生反射, 并开始向左传播, 此时压缩波的传播时间tp=lp /c(其中:lp为活塞的长度,c为应力波传播速度).在t=2tp=2lp /c时, 反射回来的拉伸波到达活塞的打击端面, 所以该入射波的表达式[6]为
| $ P=\left\{ \begin{matrix} \begin{matrix} \frac{{{\lambda }_{\text{p}}}\cdot {{\lambda }_{\text{g}}}}{{{\lambda }_{\text{p}}}+{{\lambda }_{\text{g}}}}{{v}_{\text{mp}}}, & 0<t\le {{t}_{p}}, \\ \end{matrix} \\ \begin{matrix} \frac{{{\lambda }_{\text{p}}}\cdot {{\lambda }_{\text{g}}}}{{{\lambda }_{\text{p}}}+{{\lambda }_{\text{g}}}}\left( \frac{{{\lambda }_{\text{p}}}-{{\lambda }_{\text{g}}}}{{{\lambda }_{\text{p}}}+{{\lambda }_{\text{g}}}} \right){{v}_{\text{mp}}}, & {{t}_{p}}<t\le 2{{t}_{p}}. \\ \end{matrix} \\ \end{matrix} \right. $ | (4) |
式中:λp, λg分别为活塞和钎杆的波阻;vmp为活塞冲击钎杆时的最大速度.
|
| 图 1 液压凿岩机活塞和钎杆冲击示意图 Fig.1 The stroke sketch between piston and buffer of hydraulic rock drill |
可见, 活塞和钎杆的波阻比对其波形有很大的影响.结合工况和假设1), 取入射波P近似为矩形波, 即λp=λg=λ, 这里只分析第1个应力波, 所以P可表示为
| $ P=\left\{ \begin{matrix} \begin{matrix} \frac{1}{2}\lambda \cdot {{v}_{\text{mp}}}, & 0\le t<{{t}_{p}}, \\ \end{matrix} \\ \begin{matrix} 0, & {{t}_{p}}<t\le 2{{t}_{p}}. \\ \end{matrix} \\ \end{matrix} \right. $ | (5) |
将式(5)代入式(3), 不计介质的塑性阻力, 整理可得钻进量x的函数为
| $ x=-\frac{\lambda {{v}_{\text{mp}}}}{K}{{\text{e}}^{-\frac{K}{\lambda +{{J}_{\text{S}}}}\cdot t}}+\frac{\lambda {{v}_{\text{mp}}}}{K}. $ | (6) |
将式(6)代入式(2), 可得反射波Q的表达式为
| $ Q=P-\lambda \frac{\text{d}x}{\text{d}t}=\frac{1}{2}\lambda {{v}_{\text{mp}}}-\frac{{{\lambda }^{2}}{{v}_{\text{mp}}}}{\lambda +{{J}_{\text{S}}}}{{\text{e}}^{-\frac{K}{\lambda +{{J}_{\text{S}}}}\cdot t}}. $ | (7) |
反射波透射到活塞, 在经时间tp后, 使得活塞和钎杆再次分离, 此时, 根据动量守恒, 可得活塞回弹速度vph为
| $ {{v}_{\text{ph}}}=\frac{1}{{{m}_{\text{p}}}}\int{Q\text{d}t, } $ | (8) |
式中mp为活塞的质量.
将式(7)代入式(8)中, 积分整理可得
| $ {{v}_{\text{ph}}}=\frac{1}{{{m}_{\text{p}}}}\left( \frac{1}{2}\lambda {{v}_{\text{mp}}}{{t}_{p}}+\frac{{{\lambda }^{2}}{{v}_{\text{mp}}}}{K}{{\text{e}}^{-\frac{K}{\lambda +{{J}_{\text{S}}}}{{t}_{p}}}}-\frac{{{\lambda }^{2}}{{v}_{\text{mp}}}}{K} \right). $ | (9) |
此后, 活塞的动能将以应变能的形式通过钎杆作用介质实现介质破碎, 如果介质没有完全吸收这部分应变能, 则钎杆会发生回弹, 忽略反射波在油液和机体中的透射以及介质的热损失, 可得钎杆的回弹速度vgh为
| $ {{v}_{\text{gh}}}=\sqrt{\frac{{{m}_{\text{g}}}v_{\text{mp}}^{2}-{{m}_{\text{p}}}v_{\text{ph}}^{2}-Kx_{\text{max}}^{2}}{{{m}_{\text{g}}}}}, $ | (10) |
式中:mg为钎杆的质量;xmax为最大钻进量, 其计算式为
| $ {{x}_{\max }}={{x}_{\left| t={{t}_{\text{p}}} \right.}}=\frac{\lambda {{v}_{\text{mp}}}}{K}\left( 1-{{\text{e}}^{-\frac{K}{\lambda +{{J}_{\text{S}}}}\cdot {{t}_{p}}}} \right). $ |
钎杆回弹带动活塞回弹, 降低了液压凿岩机的工作效率[10], 且容易造成钎具和机体间刚性冲击.所以, 对于液压凿岩机来说, 回弹缓冲设计是必要的.
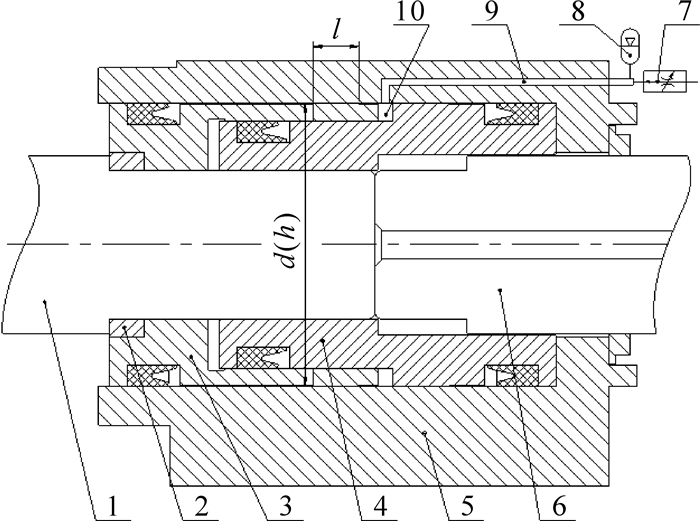
1.2 回弹缓冲装置的动力学分析液压凿岩机回弹缓冲装置工作原理如图 2所示.缓冲腔10通过内设进油油路9与活塞前腔、缓冲蓄能器8相通, 常通压力油, 腔内压力为phc, 其可调.在破碎作业中, 活塞6冲击钎杆1时, 在压力油的作用下, 缓冲活塞3压紧钎杆1, 随着钎杆1一起运动, 使得钎杆1能够压紧介质.当介质没有完全被破碎时, 钎杆1回弹, 缓冲活塞3向右运动, 使缓冲腔10的体积减小, 腔内压力phc迅速升高, 这样, 钎杆1在压力油的作用下迅速减速直至为零, 避免和机体发生刚性冲击.在回弹复位过程中, 由于缓冲活塞运动, 其缓冲腔油液体积和压力随时间动态变化, 缓冲蓄能器进行充油和排油, 考虑油液压缩量[12]和蓄能器充排油体积变化量的等效关系, 即以蓄能器工作压力作为参考点, 可得相应腔室压力.
|
| 1—钎杆; 2—缓冲挡圈; 3—缓冲活塞; 4—衬套; 5—中间缸体; 6—活塞; 7—调速阀; 8—缓冲蓄能器; 9—进油油路; 10—缓冲腔. 图 2 液压凿岩机回弹缓冲装置工作原理 Fig.2 The working principle of anti-rebound buffer device of hydraulic rock drill |
下面结合具体工作状态, 对其进行动力学分析.
1) 回弹过程.
当钻杆回弹时, 缓冲活塞和钎杆的回弹速度相等, 初始速度uhp|t=0=vgh, 在缓冲活塞回弹的过程中, 缓冲腔的压力phc升高, 其内的压力油通过内设油路进入缓冲蓄能器吸油储能, 所以, 进入蓄能器的油液体积Vh为
| $ {{V}_{\text{h}}}=\int{{{u}_{\text{hp}}}{{A}_{\text{hc}}}\text{d}t, } $ | (11) |
式中Ahc为缓冲腔的通流面积.
根据气体绝热方程, 可得此状态下蓄能器的工作压力ph为
| $ {{p}_{\text{h}}}={{p}_{\text{ah}}}{{\left( \frac{{{V}_{\text{ah}}}}{{{V}_{\text{ah}}}-{{V}_{\text{h}}}} \right)}^{k}}, $ | (12) |
式中:pah为缓冲蓄能器的预充压力;Vah为缓冲蓄能器预充体积;k为气体绝热状态参数.
从局部阻力损失的角度, 建立缓冲蓄能器和缓冲腔的压差模型, 因此, 可得到在这一过程中缓冲腔的压力phc1为
| $ {{p}_{\text{hc1}}}={{p}_{\text{h}}}+\frac{{{\xi }_{10}}\rho }{2}{{\left( \frac{{{u}_{\text{p}}}{{A}_{\text{hc}}}}{{{A}_{10}}} \right)}^{2}}, $ | (13) |
式中:ξ10为局部阻力系数;ρ为液压油的密度;A10为连通缓冲腔和缓冲蓄能器的油道通流面积.
由此, 可得此状态下缓冲活塞运动学方程为
| $ -{{m}_{\text{hp}}}\frac{{{\text{d}}^{2}}{{S}_{hp}}}{\text{d}{{t}^{2}}}={{p}_{\text{hc1}}}\cdot {{A}_{\text{hc}}}-{{F}_{\text{sh}}}-{{F}_{\text{lh}}}, $ | (14) |
式中:Shp为缓冲活塞的运动位移;Fsh为黏性摩擦力, 其计算式为
| $ {{F}_{\text{sh}}}=\frac{\text{ }\!\!\pi\!\!\text{ }\mu \cdot l\cdot d}{\sqrt{1-{{\varepsilon }^{2}}}h}{{u}_{\text{hp}}}\pm \frac{\text{ }\!\!\pi\!\!\text{ }\cdot d\cdot h}{2}\vartriangle p, $ |
当相对运动方向与压差方向一致时, “±”取“-”, 反之取“+”,如图 2所示, l为缓冲活塞和缸体配合面的长度,d为缓冲活塞的直径,h为缓冲套和中间缸体的配合间隙,uhp为缓冲活塞的速度,Δp为缓冲活塞和中间缸体配合面两端压差,ε为缓冲活塞和中间缸体的偏心率;Flh为液压卡紧力, Flh=τldΔp, 其中τ为液压卡紧力系数;mhp为缓冲套的质量, 所以有
| $ {{F}_{\text{sh}}}=\frac{\text{ }\!\!\pi\!\!\text{ }\mu ld}{\sqrt{1-{{\varepsilon }^{2}}}h}{{u}_{\text{hp}}}\pm \frac{\text{ }\!\!\pi\!\!\text{ }dh}{2}{{p}_{\text{hc1}}}, $ | (15) |
| $ {{F}_{\text{lh}}}=\tau \cdot l\cdot d\cdot {{p}_{\text{hc1}}}. $ | (16) |
2) 复位过程.
活塞向左冲击钎杆时, 缓冲活塞在缓冲腔压力油的作用下, 随着钎杆一起运动, 其运动位移和钎杆几乎相同, 这样就能够保证钎杆重新压紧介质, 为下一次冲击作好准备, 缩短了回弹复位时间, 提高了工作效率[10].此状态下, 缓冲腔的压力phc为回弹阶段末缓冲腔的压力, 系统供油, 认为在复位过程中, 缓冲腔压力恒定, 所以可得此状态中缓冲活塞的运动学方程为
| $ {{m}_{\text{hp}}}\frac{{{\text{d}}^{2}}{{S}_{\text{hp}}}}{\text{d}{{t}^{2}}}={{p}_{\text{hc}}}\cdot {{A}_{\text{hc}}}-{{F}_{\text{sh}}}-{{F}_{\text{lh}}}, $ | (17) |
其中, 结合式(15), 可得:
| $ {{F}_{\text{sh}}}=\frac{\text{ }\!\!\pi\!\!\text{ }\mu ld}{\sqrt{1-{{\varepsilon }^{2}}}h}{{u}_{\text{hp}}}\pm \frac{\text{ }\!\!\pi\!\!\text{ }dh}{2}{{p}_{\text{hc}}}, $ | (18) |
| $ {{F}_{\text{lh}}}=\tau \cdot l\cdot d\cdot {{p}_{\text{hc}}}. $ | (19) |
活塞冲程方向为正方向, 由上述的缓冲活塞运动分析, 可得如下边界条件:
缓冲活塞处于回弹阶段时的约束条件为
| $ {{S}_{\text{hp}}}=\{{{S}_{\text{hp}}}\left| {{S}_{\text{hp}}}<0 \right.\}\cap \frac{\text{d}{{S}_{\text{hp}}}}{\text{d}t}=\{\frac{\text{d}{{S}_{\text{hp}}}}{\text{d}t}\left| \frac{\text{d}{{S}_{\text{hp}}}}{\text{d}t}\le 0 \right.\}; $ |
缓冲活塞处于复位阶段时的约束条件为
| $ {{S}_{\text{hp}}}=\{{{S}_{\text{hp}}}\left| 0\le {{S}_{\text{hp}}}\le {{x}_{\max }}, {{S}_{\text{hp}}}\left( 0 \right)=0, \frac{\text{d}{{S}_{\text{hp}}}}{\text{d}t}\left( 0 \right)=0 \right.\}. $ |
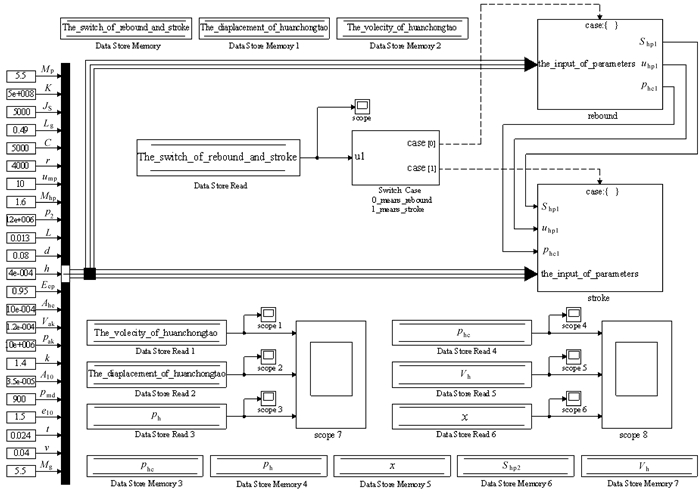
前面通过对回弹的波动研究获得2个描述活塞、钎杆、介质入射波和反射波的方程, 并通过积分, 得到2个钎杆钻进量和回弹速度计算方程, 结合蓄能器气体状态方程和压差模型方程, 分析并获得各状态下缓冲套动力学方程, 共计9个方程.这9个方程构成了一组非线性代数方程组, 用来描述回弹缓冲装置的运动学特性.考虑到使用Simulink建立动态仿真后, 每一帧仿真都需要对回弹速度uhp、钻进量x等边界约束条件进行1次求解[11], 所以采用MATLAB编写uhp和x的求解和判定函数嵌入模块的方式实现状态切换.在Simulink平台建立的基于MATLAB函数的回弹缓冲装置动力学仿真模型如图 3所示, 其参数包括外部输入参数(共23项)和各个MATLAB函数输出, 这些参数构成各运动状态的输入.MATLAB函数的输出包括运动状态参数以及压力、流量等参数.
|
| 图 3 基于Simulink的回弹缓冲装置仿真模型 Fig.3 The simulation model of anti-rebound buffer device based on Simulink |
通过以上仿真模型, 可以对液压凿岩机回弹机理和回弹缓冲的运动特性进行研究, 结合具体工况, 对预充压力的影响和回弹缓冲的工况响应等方面进行研究.
3 仿真和实验验证在正常情况下, 液压凿岩机回弹现象和工况、预充压力有关, 即在钎杆回弹时, 会出现2种情况:一是当缓冲腔压力降到预充压力时, 其速度还没有降为零, 这样就仍存在机体冲击的现象;二是当缓冲腔压力仍大于预充压力时, 其速度已经降为零, 这个时候系统卸荷, 产生瞬时压力突变.因此, 预充压力和回弹速度的匹配对回弹缓冲装置特性的影响是很重要的.
以湖南山河智能装备股份有限公司研制的某型液压凿岩机为研究对象, 主要的结构参数和介质系数设定如表 1所示.
| ℃ | |
| 参数 | 量数 |
| mhp | 1.6 kg |
| mp | 5.5 kg |
| Ahc | 9.5 mm2 |
| pah | 5.5 MPa |
| Vah | 120 mL |
| p2 | 6/8/10 MPa |
| d | 80 mm |
| l | 13 mm |
| h | 0.04 mm |
| Lg | 490 mm |
| Js | 5 000 |
| K | 0.15(软岩) 0.30(硬岩) 0.45(钢板) |
为了增强仿真和实验的可比性, 保证结构参数不变, 对MATLAB函数和Simulink仿真模型的输入进行相应修改, 即可得到预充压力分别为6,8和10 MPa的3种仿真模型以及介质系数分别为0.15,0.3和0.45的3种工况的仿真模型.实测中, 调定相应预充压力并分别在软岩、硬岩和钢板中进行实验, 同时, 将仿真结果与实测结果进行对比分析,以进行验证.
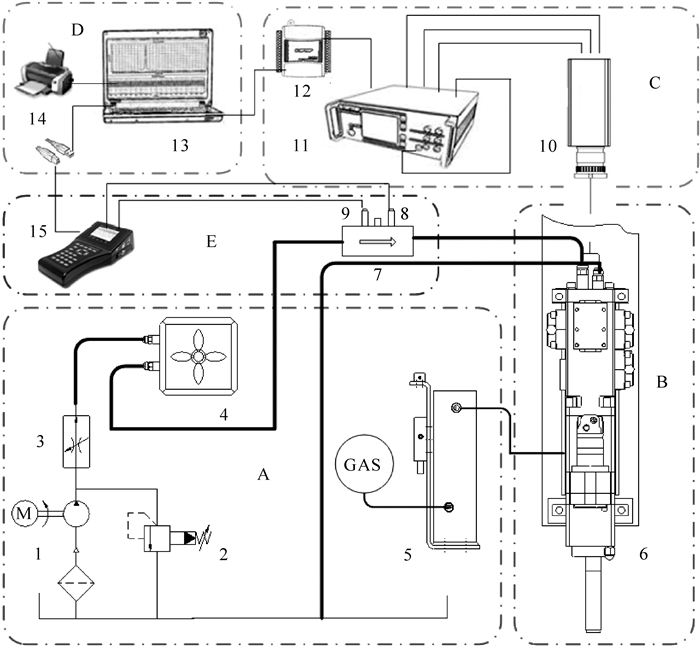
3.1 现场实验方案根据仿真输出, 实测对象主要包括液压凿岩机缓冲腔和缓冲蓄能器的压力、流量以及缓冲活塞速度、位移.实验测试方案如图 4所示.方案中, 以钻机为平台, 系统预充压力由调速阀控制, 主要包括2个测试模块, 分别是以5060测试仪为主的流量压力测试模块和以多普勒激光测试仪为主的速度测试模块.2个模块共用PC机数据采集系统.其中在测试速度时, 中间缸体观察孔贴有聚光防油的膜片, 以保证测试的准确性.
|
| A—泵站; B—冲击试验系统; C—激光测速系统; D—数据采集分析系统; E—流量监测系统.1—电机泵组; 2—溢流阀; 3—调速阀; 4—油冷却散热器; 5—供气润滑装置; 6—液压凿岩机; 7—流量计; 8—压力传感器; 9—流量传感器; 10—激光测速仪; 11—控制箱; 12—信号采集卡; 13—计算机(内含数据采集处理分析程序); 14—打印机; 15—Multi-system 5060. 图 4 液压凿岩机冲击试验原理 Fig.4 The principle of impact test of hydraulic rock drill |
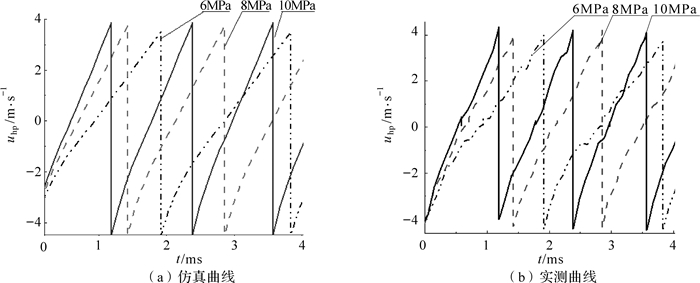
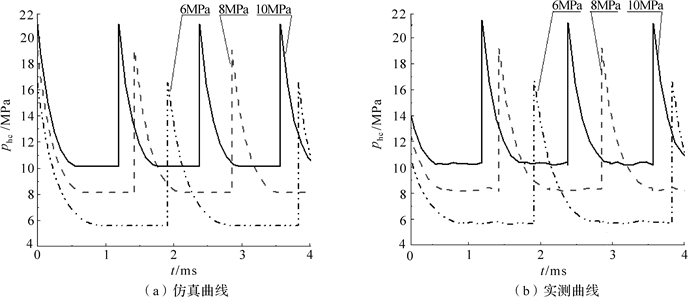
预充压力直接作用在缓冲腔, 其和回弹缓冲装置的运动特性有着直接的关系, 因此保证系统输入流量不变, 在被冲击体为钢板的工况下, 缓冲腔的预充压力分别调定为6,8和10 MPa, 对其动力学特性以及缓冲腔压力变化进行仿真和实验, 可得不同预充压力下缓冲活塞速度曲线和缓冲腔压力曲线, 并与实测结果进行对比分析, 其结果如图 5、图 6所示, 对其仿真结果和实测结果进行整理, 可得表 2.
|
| 图 5 不同预充压力下缓冲活塞的速度曲线 Fig.5 Velocity curve of buffer piston under different precharge pressures |
|
| 图 6 不同预充压力下缓冲腔的压力曲线 Fig.6 Pressure curve in buffer cavity under different precharge pressures |
| 预充压力/MPa | 回弹时间/ms | 复位时间/ms | 峰值压力/MPa | 最大回弹速度/m·s-1 | ||||
| 仿真 | 实测 | 仿真 | 实测 | 仿真 | 实测 | 仿真 | 实测 | |
| 6 | 0.92 | 0.96 | 0.98 | 1.10 | 16.54 | 17.10 | 4.47 | 4.40 |
| 8 | 0.70 | 0.76 | 0.72 | 0.81 | 19.03 | 19.42 | 4.51 | 4.45 |
| 10 | 0.59 | 0.67 | 0.62 | 0.74 | 21.04 | 21.24 | 4.54 | 4.51 |
如图 5、图 6所示, 预充压力越大, 缓冲活塞作用时间越短, 缓冲腔峰值压力越大.结合表 2所示的仿真和实测结果, 通过比较分析发现, 在预充压力一定时, 缓冲活塞运动时间和峰值压力的实测结果都比仿真结果大, 回弹速度的实测结果则较小, 这是由于在实际工况中存在泄漏[12-13]和蓄能损失, 但其误差能控制在5.3%以内, 故该模型是合理的.当预充压力增加, 作用在缓冲活塞的力增大, 回弹和复位所用的时间就减小, 峰值压力也增大, 这对凿岩机本身的可靠性要求也提高, 所以在选择预充压力时, 应以保护机体为主要原则.同时, 在开始回弹时, 其回弹速度uhp都约为4.5 m/s, 实测结果稍偏小.因此, 可以认为在确定的工况下, 缓冲活塞回弹速度是相同的, 与预充压力无关.
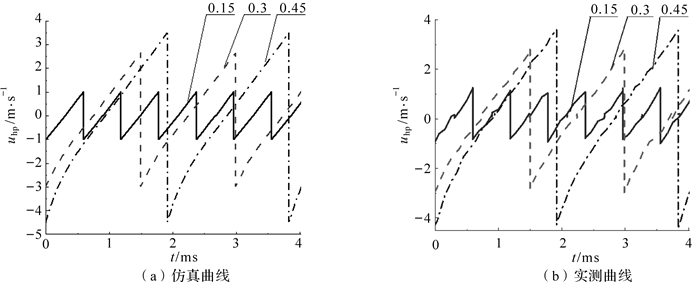
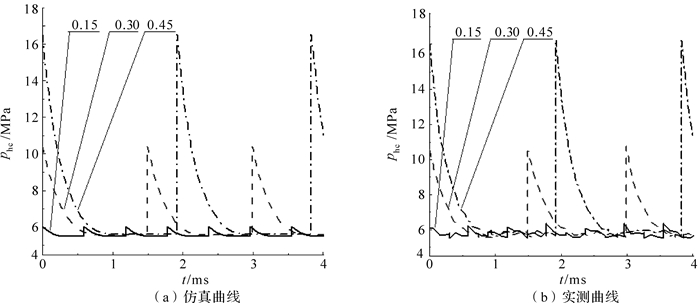
3.3 工况对回弹缓冲装置动特性的影响在介质没有完全吸收所作用的应变能时, 钎杆可能发生回弹, 所以工况直接决定回弹缓冲装置的动特性.由上述分析可知, 回弹速度与预充压力无关, 因此, 有必要研究工况对其的影响.所以, 保证输入流量不变, 预充压力为6 MPa, 分别调定工况系数为0.15,0.30和0.45三种工况进行仿真和实验, 可得不同工况下缓冲活塞速度曲线和缓冲腔压力曲线, 并与实测结果进行对比分析, 其结果如图 7、图 8所示, 对其结果进行整理, 如表 3所示.
|
| 图 7 不同介质下缓冲活塞的速度曲线 Fig.7 Velocity curve of buffer piston under different mediums |
|
| 图 8 不同介质下缓冲腔的压力曲线 Fig.8 Pressure curve in buffer cavity under different mediums |
| 介质系数 | 回弹时间/ms | 峰值压力/MPa | 最大回弹速度/m·s-1 | |||
| 仿真 | 实测 | 仿真 | 实测 | 仿真 | 实测 | |
| 0.15(软岩) | 0.34 | 0.42 | 6.22 | 6.43 | 1.02 | 0.89 |
| 0.30(硬岩) | 0.70 | 0.76 | 10.41 | 10.76 | 2.98 | 2.57 |
| 0.45(钢板) | 0.92 | 0.96 | 16.54 | 17.10 | 4.48 | 4.27 |
由图 7、图 8可知, 随着工况系数的增大, 回弹速度增大, 缓冲腔峰值压力也随之增大, 这说明了回弹速度由工况直接决定.结合表 3进行比较分析, 实测回弹速度较小, 回弹时间和缓冲腔压力峰值实测结果较大.这是由于存在泄漏[12-13]和胶管蓄能效应, 其误差约为4.7%.而由图 8可知, 尽管缓冲腔压力会增大, 但始终在系统允许的最大压力范围内, 这说明回弹缓冲装置能匹配工况, 有很好的工况响应能力, 且在工况系数为0.15时, 其缓冲腔压力峰值和预充压力相差不大, 反弹速度也没超过1 m/s, 由此可知, 在软岩工况下, 凿岩机可以不配备回弹缓冲装置.在系数为0.45的工况下, 对于频率为35 Hz的凿岩机, 采用回弹缓冲设计, 由于没有回弹的影响, 缩短了回弹复位时间, 冲击频率可达到37.5 Hz左右, 工作效率约可以提高7.23%.
4 结论1) 回弹缓冲装置的回弹速度和预充压力无关, 与工况有关, 随着工况系数的增大, 回弹速度增大.
2) 考虑预充压力不影响回弹缓冲速度, 在调定回弹缓冲装置预充压力时, 应以保护机体为主要原则, 可参考工况系数为0.15时的预充压力进行选择.
3) 回弹缓冲装置能够匹配工况, 采用回弹缓冲设计的液压凿岩机有更好的工况响应能力, 且由于没有回弹的影响, 在同等输入的情况下, 输出频率增大, 其工作效率约提高7.23%.
| [1] | AENDT F K. Power recovery in hydraulic impact mechanisms[J]. Technische Mitteilungen Krupp , 1986, 1 (5) : 158–165. |
| [2] |
丁问司, 黄晓东.
自配流型液压冲击器建模与仿真[J]. 振动与冲击 , 2010, 29 (2) : 103–106.
DING Wen-si, HUANG Xiao-dong. Modeling and simulation for a self-distributing flow hydraulic impactor[J]. Journal of Vibration and Shock , 2010, 29 (2) : 103–106. |
| [3] |
杨襄璧, 刘德顺, 胡均平.
撞击回弹问题的理论研究[J]. 中国有色金属学报 , 1996, 6 (4) : 171–175.
YANG Xiang-bi, LIU De-shun, HU Jun-ping. Study on the theory of the anti-rebound[J]. The Chinese Journal of Nonferrous Metals , 1996, 6 (4) : 171–175. |
| [4] | KARLSSON L G. Experimental study of a percussive process for rock fragmentation[J]. Int J Rock Mech Min Sci & Geomech Abstr , 1989, 26 (1) : 45–50. |
| [5] |
张新, 陈子辰, 孙国辉.
液压冲击器镐钎冲击反弹缓冲机构研究[J]. 中国机械工程 , 2002, 17 (8) : 7–9.
ZHANG Xin, CHEN Zi-chen, SUN Guo-hui. Research on the anti-rebound buffer device of the drill rod of hydraulic impact machine[J]. China Mechanical Engineering , 2002, 17 (8) : 7–9. |
| [6] |
朱萍玉.冲击机械动态反演设计方法研究[D]:长沙:中南大学机电工程学院, 2003:30-31.
ZHU Ping-yu.Study of dynamic inverse design method on impact machines[D].Changsha:Central South University, College of Mechanical and Electrical Engineering, 2003:30-31. http://cdmd.cnki.com.cn/article/cdmd-10533-2004116109.htm |
| [7] | DANIEL G.Simulation of hydraulic dampers in drill percussion[D].Sweden:Linkoping University, College of Mechanical and Electrical Engineering, 2008:47-54. |
| [8] |
赵宏强.
冲击器防反弹冲击缓冲装置的设计[J]. 凿岩机械气动工具 , 2004 (4) : 12–16.
ZHAO Hong-qiang. Design of the anti-rebound buffer device of the impactor[J]. Rock Drilling Machinery & Pneumatic Tools , 2004 (4) : 12–16. |
| [9] | JOO Young Oh, GEN Ho Lee, HANK Soon Kang, et al. Modeling and performance analysis of rock drill drifter for rock stiffness[J]. International Journal of Precision Engineering and Manufacturing , 2012, 12 (13) : 2187–2193. |
| [10] |
伍先明, 刘德顺.
水压凿岩机冲击部件结构形状、轴向推力、转钎角度与凿岩效率的实验研究[J]. 振动与冲击 , 2007, 26 (8) : 154–157.
WU Xian-ming, LIU De-shun. Experimental study on impact part structural form axial thrust, rotation angle and rock drilling efficiency of water-power rock drill[J]. Journal of Vibration and Shock , 2007, 26 (8) : 154–157. |
| [11] |
GARDNER J F.机构动态仿真:使用MATLAB和Simulink[M].周进雄, 张陵, 译.西安:西安交通大学出版社, 2002.
GARDNER J F.Simulations of machines:using MATLAB and Simulink[M].Translated by ZHOU Jin-xiong, ZHANG Ling.Xi'an:Xi'an Jiaotong University Press, 2002. |
| [12] |
方晓瑜, 赵宏强, 文国臣.
基于AMESim恒功率变量泵的仿真研究[J]. 工程设计学报 , 2011, 18 (6) : 437–443.
FANG Xiao-yu, ZHAO Hong-qiang, WEN Guo-chen. Simulation research on constant power variable pump based on AMESim[J]. Chinese Journal of Engineering Design , 2011, 18 (6) : 437–443. |
| [13] |
赵宏强, 傅斯龙, 周茂贤, 等.
液压凿岩机配流阀零位开口设计与实验研究[J]. 工程设计学报 , 2016, 23 (3) : 288–294.
ZHAO Hong-qiang, FU Si-long, ZHOU Mao-xian, et al. Design and experiment on the opening at zero position of distribute valve of hydraulic rock drill[J]. Chinese Journal of Engineering Design , 2016, 23 (3) : 288–294. |



