2. 四川大学 制造科学与工程学院, 四川 成都 610065
2. School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China
圆弧齿轮是一种较新型的机械传动副, 由日本学者长谷川吉三郎等人于20世纪80年代提出, 它具有接触线长、重合度大、传动平稳、无退刀槽、无轴向力等特点, 能够取代传统的渐开线直齿轮、斜齿轮及人字齿轮[1-2].
由于圆弧齿轮的齿面是一种曲面, 传统的渐开线直齿、斜齿、人字齿的加工方法不能用于加工此种新型齿轮.国内外学者对圆弧齿轮的加工方式进行了深入的研究, 比较有代表性的加工方式有:旋转刀盘法、大刀盘分度切齿法、三刀头旋转切制法、数控滚切法、挤齿法、圆拉法和平行连杆加工法等[3-6].
虚拟轴机床是一种具有运动精度高、刚度大、负载能力强、结构紧凑、抗振性强、运动惯性小、切削稳定性好等特点的机床[7].考虑到圆弧齿轮的齿面精度会影响其性能, 本文利用虚拟轴机床来实现圆弧齿轮的齿面加工;利用虚拟轴机床加工圆弧齿轮可以提高其曲面的精度, 从而提高圆弧齿轮的性能.而虚拟轴机床加工曲面的精度与机床杆的位置精度息息相关, 目前国内外学者对于直线伺服电机的位置控制算法研究较多, 主要包括PID控制[8-9]、迭代控制[10-11]和滑模控制[12-13]等.
本文以虚拟轴机床的直线伺服电机为研究对象, 提出了一种基于干扰观测器的滑模控制算法来控制虚拟轴机床各杆的位置;同时为了进一步抑制滑模控制中存在的抖动现象, 减小抖动现象对控制的精度和稳定性的影响, 对提出的基于干扰观测器的滑模控制算法进行了改进;为了验证所提算法的有效性, 在MATLAB中进行了仿真, 仿真结果表明:所设计的控制算法能够有效地对虚拟轴机床各杆的干扰进行观测, 改善了虚拟轴机床的轨迹跟踪性能, 同时滑模控制中的抖动现象也得到了改善.
1 基于改进干扰观测器的滑模控制器设计 1.1 系统描述考虑干扰后, 虚拟轴机床伺服电机的状态方程可以表示为
| $ x\left( k+1 \right)=[\boldsymbol{A}+\vartriangle A]x\left( k \right)+\boldsymbol{b}u\left( k \right)+f\left( k \right). $ | (1) |
定义1:系统(1)中的参数必须满足
假设1:系统是可控的;
假设2:系统满足定义中的匹配条件.
根据定义1、假设1和假设2, 系统(1)的离散形式可以改写为
| $ x\left( k+1 \right)=\boldsymbol{A}x\left( k \right)+\boldsymbol{b}\left[u\left( k \right)+d\left( k \right) \right], $ | (2) |
式中:d(k)为系统中存在的不确定因素ΔA和f(k)的函数,
以虚拟轴机床各轴的轨迹跟踪问题为研究对象, 各轴的理想轨迹可用向量xr表示, xr=[xr1 xr2 xr3 xr4 xr5 xr6]T, 各轴的实际轨迹用向量xa表示, xa=[xa1 xa2 xa3 xa4 xa5 xa6]T, 则系统各轴的跟踪误差为
| $ e\left( k \right)={{x}_{\text{a}}}\left( k \right)-{{x}_{\text{r}}}\left( k \right). $ | (3) |
则滑模面函数可定义为
| $ s\left( k \right)={{\boldsymbol{C}}^{\text{T}}}e\left( k \right). $ | (4) |
为了分析在滑模面函数值等于零时的动态情况, 结合式(2)、式(3)和式(4), 则
| $ \begin{matrix} s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}e\left( k+1 \right)= \\ {{\boldsymbol{C}}^{\text{T}}}\left[\boldsymbol{A}x\left( k \right)+\boldsymbol{b}u\left( k \right)+\boldsymbol{b}d\left( k \right)-{{x}_{\text{r}}}\left( k+1 \right) \right]. \\ \end{matrix} $ | (5) |
根据上式可以得到系统的控制律为
| $ u\left( k \right)=-d\left( k \right)-{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}{{\boldsymbol{C}}^{\text{T}}}\left[\boldsymbol{A}x\left( k \right)-{{x}_{\text{r}}}\left( k+1 \right) \right]. $ | (6) |
根据式(4)和式(6), 可得:
| $ \begin{matrix} e\left( k+1 \right)=\left[I-\boldsymbol{b}{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}{{\boldsymbol{C}}^{\text{T}}} \right]Ae\left( k \right)- \\ \left[I-\boldsymbol{b}{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}{{\boldsymbol{C}}^{\text{T}}} \right]\left[{{x}_{\text{r}}}\left( k+1 \right)-\boldsymbol{A}x\left( k \right) \right]. \\ \end{matrix} $ | (7) |
为了保证所设计的滑模控制器能够使得系统的跟踪误差收敛于零, 根据假设1, 式(7)可以简化为(证明略)
| $ e\left( k+1 \right)=\left[I-\boldsymbol{b}{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}{{\boldsymbol{C}}^{\text{T}}} \right]Ae\left( k \right). $ | (8) |
对于如式(2)所示的虚拟轴机床电机伺服系统而言, 引入干扰观测后, 本文设计的控制律和干扰观测律分别为:
| $ \begin{matrix} u\left( k \right)=-\widehat{d}\left( k \right)+{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}[{{\boldsymbol{C}}^{\text{T}}}{{x}_{\text{r}}}\left( k+1 \right)-\\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{A}x\left( k \right)+qs\left( k \right)-\eta sgn \left( s\left( k \right) \right)], \\ \end{matrix} $ | (9) |
| $ \begin{matrix} \widehat{d}\left( k \right)=\widehat{d}\left( k-1 \right)+{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}g[s\left( k \right)-\\ qs\left( k-1 \right)-\eta sgn \left( s\left( k-1 \right) \right)], \\ \end{matrix} $ | (10) |
式中
为了进一步提高系统的抗抖动能力, 本文采用饱和函数来代替式(9)和式(10)中的符号函数, 则式(9)和式(10)改写为:
| $ \begin{matrix} u\left( k \right)=-\widehat{d}\left( k \right)+{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}[{{\boldsymbol{C}}^{\text{T}}}{{x}_{\text{r}}}\left( k+1 \right)-\\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{A}x\left( k \right)+qs\left( k \right)-\eta \operatorname{sat}\left( \frac{s\left( k \right)}{\phi } \right)], \\ \end{matrix} $ | (11) |
| $ \begin{matrix} \widehat{d}\left( k \right)=\widehat{d}\left( k-1 \right)+{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}g[s\left( k \right)-\\ qs\left( k-1 \right)-\eta \operatorname{sat}\left( \frac{s\left( k-1 \right)}{\phi } \right)]. \\ \end{matrix} $ | (12) |
推论1:滑模及干扰估计误差的动态必须满足以下特性:
1)
证明:由式(2)至(4)和式(11),有
| $ \begin{matrix} s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}e\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}x\left( k+1 \right)-{{\boldsymbol{C}}^{\text{T}}}{{x}_{\text{r}}}\left( k+1 \right)= \\ \begin{matrix} {{\boldsymbol{C}}^{\text{T}}}\left\{ \boldsymbol{A}x\left( k \right)+\boldsymbol{b}\left[u\left( k \right)+d\left( k \right) \right] \right\}-{{\boldsymbol{C}}^{\text{T}}}{{x}_{\text{r}}}\left( k+1 \right)= \\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{A}x\left( k \right)+{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}u\left( k \right)+{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}d\left( k \right)-{{\boldsymbol{C}}^{\text{T}}}{{x}_{\text{r}}}\left( k+1 \right)= \\ \end{matrix} \\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{A}x\left( k \right)+{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\{-\widehat{d}\left( k \right)+{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}[{{\boldsymbol{C}}^{\text{T}}}{{x}_{\text{r}}}\left( k+1 \right)-\\ \begin{matrix} {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{A}x\left( k \right)+qs\left( k \right)-\eta \operatorname{sat}\left( \frac{s\left( k \right)}{\phi } \right)]\}+{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}d\left( k \right)-\\ {{\boldsymbol{C}}^{\text{T}}}{{x}_{\text{r}}}\left( k+1 \right). \\ \end{matrix} \\ \end{matrix} $ |
定义:
| $ \widetilde{d}\left( k \right)=d\left( k \right)-\widehat{d}\left( k \right), $ |
| $ s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)-\eta \operatorname{sat}\left( \frac{s\left( k \right)}{\phi } \right). $ |
2)
证明:
| $ \widetilde{d}\left( k+1 \right)=d\left( k+1 \right)-\widehat{d}\left( k+1 \right), $ |
| $ \begin{matrix} \widetilde{d}\left( k+1 \right)=d\left( k+1 \right)-\widehat{d}\left( k+1 \right)-{{\left( {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b} \right)}^{-1}}g[s\left( k+1 \right)-\\ qs\left( k \right)+\eta \operatorname{sat}\left( \frac{s\left( k \right)}{\phi } \right)]. \\ \end{matrix} $ |
因为
| $ s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)-\eta \operatorname{sat}\left( \frac{s\left( k \right)}{\phi } \right). $ |
所以
| $ \begin{matrix} \widetilde{d}\left( k+1 \right)=d\left( k+1 \right)+\widehat{d}\left( k \right)-d\left( k \right)-g\widetilde{d}\left( k \right)= \\ d\left( k+1 \right)-d\left( k \right)+\left( 1-g \right)\widetilde{d}\left( k \right). \\ \end{matrix} $ |
推论2:当
| $ \eta >{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\frac{m}{g}, \eta >\left| {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right) \right|, 0<q<1, \frac{\eta }{\phi }<q, $ |
则
| $ \left| s\left( k \right) \right|<\phi, 0<\phi <1. $ |
证明:
①当s(k)≥ϕ, 因为
| $ s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)-\eta <qs\left( k \right)<s\left( k \right). $ |
| $ \begin{matrix} s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)-\eta \ge \\ q\phi-\eta +{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)>{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)>-\phi . \\ \end{matrix} $ |
结论:当s(k)≥ϕ时, s(k+1)逐渐减小, 直到进入边界层.
②当s(k)≤-ϕ, 则
| $ \begin{matrix} s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)+\eta > \\ qs\left( k \right)>s\left( k \right), \\ \end{matrix} $ |
| $ \begin{matrix} s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)+\eta \le-q\phi +\eta + \\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right). \\ \end{matrix} $ |
又
| $ \begin{matrix} s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)+\eta \le-q\phi +\eta + \\ \phi <\phi . \\ \end{matrix} $ |
结论:当s(k)≤-ϕ时, s(k+1)逐渐减小, 直到进入边界层.
③当|s(k)| < ϕ, 则
| $ s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)-\eta \frac{s\left( k \right)}{\phi }. $ |
当ϕ>s(k)≥0, 则
| $ \begin{matrix} s\left( k+1 \right)<{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+\left( q-\frac{\eta }{\phi } \right)\phi =q\phi-\eta + \\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)<\phi . \\ \end{matrix} $ |
当-ϕ < s(k) < 0,则
| $ \begin{matrix} s\left( k+1 \right)>{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+\left( q-\frac{\eta }{\phi } \right)\left(-\phi \right)=-q\phi + \\ \eta +{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)>-\phi . \\ \end{matrix} $ |
结论:当|s(k)| < ϕ时, s(k+1)将保持在边界层之内.因此, 推论2成立.
1.3 稳定性分析根据推论2可知, 当|s(k)| < ϕ时, s(k+1)将保持在边界层之内;那么只需要讨论当|s(k)|≥ϕ时控制器的稳定情况.分2种情况讨论.
1) 当s(k)≥ϕ时:
因为
| $ s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)-\eta <qs\left( k \right)<s\left( k \right), $ |
所以
| $ s\left( k+1 \right)-s\left( k \right)<0. $ |
又
| $ \begin{matrix} s\left( k+1 \right)+s\left( k \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+\left( 1+q \right)s\left( k \right)-\eta > \\ \left( 1+q \right)\phi-\eta +{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)> \\ \eta +{{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)>0, \\ \end{matrix} $ |
所以
| $ \left[s\left( k+1 \right)-s\left( k \right) \right]\left[s\left( k+1 \right)+s\left( k \right) \right]<0. $ |
因此控制器是稳定的.
2) 当s(k)≤-ϕ时:
因为
| $ s\left( k+1 \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+qs\left( k \right)+\eta >qs\left( k \right)>s\left( k \right), $ |
所以
| $ s\left( k+1 \right)-s\left( k \right)>0. $ |
又
| $ \begin{matrix} s\left( k+1 \right)+s\left( k \right)={{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)+\left( 1+q \right)s\left( k \right)+ \\ \eta \le-\left( 1+q \right)\phi +\eta + \\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)<-\eta + \\ {{\boldsymbol{C}}^{\text{T}}}\boldsymbol{b}\widetilde{d}\left( k \right)<0, \\ \end{matrix} $ |
所以
| $ \left[s\left( k+1 \right)-s\left( k \right) \right]\left[s\left( k+1 \right)+s\left( k \right) \right]<0. $ |
因此控制器是稳定的.
根据上述分析和推论2可知, 当|s(k)| < ϕ时, s(k+1)将保持在边界层之内;当|s(k)|≥ϕ时, 控制器是稳定的, 因此系统也是稳定的.
2 数字仿真为了验证本文所提出算法的有效性, 在MATLAB中采用该算法控制虚拟轴机床的伺服电机, 电机离散后的方程为
| $ x\left( k+1 \right)=\boldsymbol{A}x\left( k \right)+\boldsymbol{b}\left[u\left( k \right)+f\left( k \right) \right]. $ |
式中,
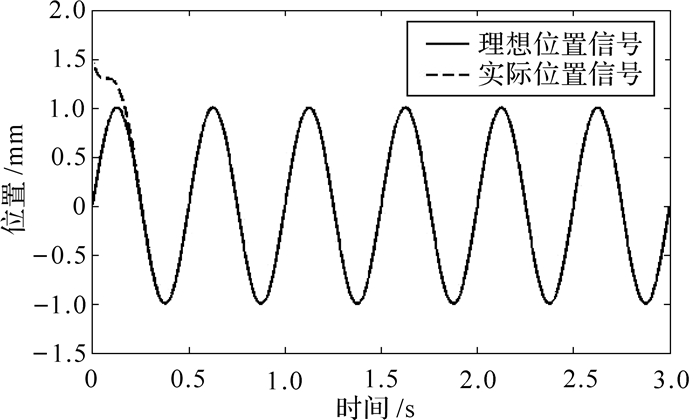
仿真过程中主要仿真参数为:d(k)=2sin(4πt), xr(k)=sin(4πt), 控制器参数CT=[15 1], 仿真结果如图 1至图 4所示, 图 1,2分别为改进前、后的位置跟踪效果, 图 3,4为改进前、后的滑模面相轨迹.
|
| 图 1 基于干扰观测器的位置跟踪效果 Fig.1 Location tracking effect based on the disturbance observer |
|
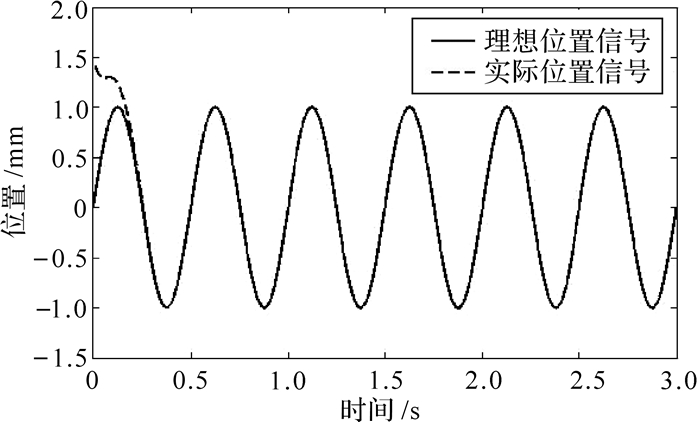
| 图 2 基于改进干扰观测器的位置跟踪效果 Fig.2 Location tracking effect based on the improved disturbance observer |
|
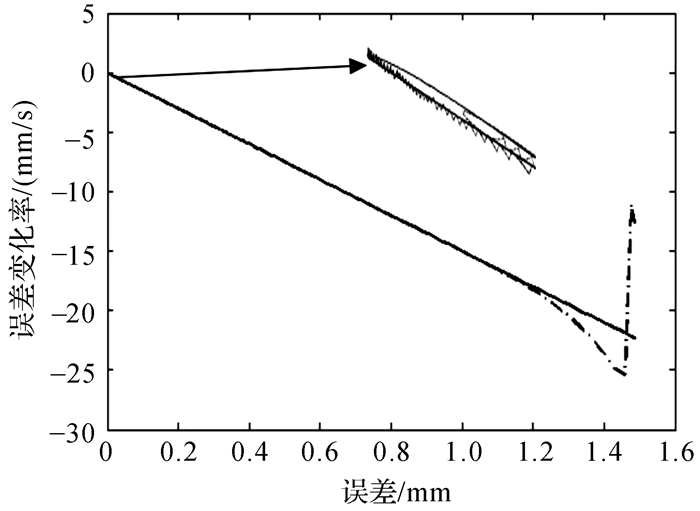
| 图 3 基于干扰观测器的相轨迹 Fig.3 The phase trajectory based on the disturbance observer |
|
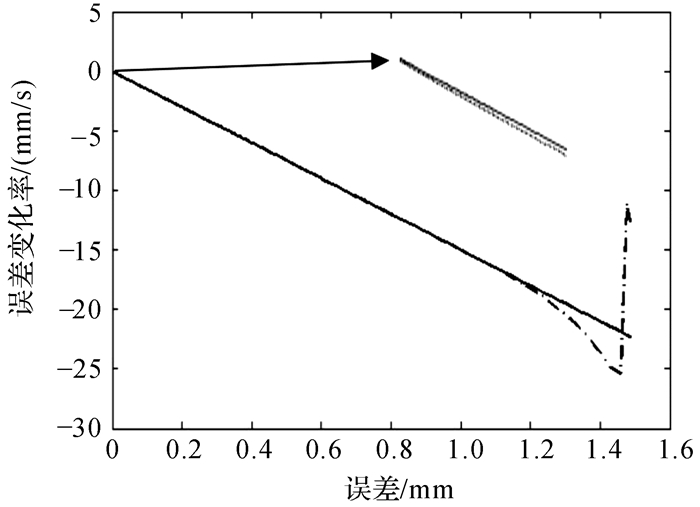
| 图 4 基于改进干扰观测器的相轨迹 Fig.4 The phase trajectory based on the improved disturbance observer |
从图 1,2可知, 引入改进干扰观测器后, 控制器能够有效地对系统中存在的不确定性因素进行观测, 从而抑制了不确定性因素对位置跟踪性能的影响, 系统具有良好的抗干扰能力;从图 3,4可以看出, 利用饱和函数替代原控制律中的符号函数后, 从其放大部分可以看出系统的抖动现象得到了明显的抑制.
3 结论本文以一种圆弧齿轮加工用虚拟轴机床为研究对象, 为提高虚拟轴机床的加工精度和抑制滑模控制中的抖动现象, 提出了基于改进干扰观测器的滑模变结构控制算法来控制虚拟轴机床的伺服电机.仿真结果表明:提出的基于改进观测器的滑模变结构控制算法能够有效地观测系统中存在的不确定性因素, 从而抑制了不确定性因素对位置跟踪性能的影响, 系统具有良好的抗干扰能力;同时滑模控制中的抖动现象也得到了明显改善.
| [1] |
邹旻, 祝海林.
新型圆弧齿线圆柱齿轮[J]. 制造技术与机床 , 1995 (5) : 43–47.
ZHOU Min, ZHU Hai-lin. New type arc tooth cylindrical gear[J]. Manufacturing Technology & Machine Tool , 1995 (5) : 43–47. |
| [2] |
宋爱平, 易红, 汤文成, 等.
渐开线弧齿圆柱齿轮及其啮合特性[J]. 中国机械工程 , 2006, 17 (18) : 1888–1892.
SONG Ai-ping, YI Hong, TANG Wen-cheng, et al. Involute arc cylindrical gear and its mesh characteristics[J]. China Mechanical Engineering , 2006, 17 (18) : 1888–1892. |
| [3] |
宋爱平, 吴伟伟, 高尚, 等.
弧齿圆柱齿轮理想几何参数及其加工方法[J]. 上海交通大学学报 , 2010, 44 (12) : 1735–1740.
SONG Ai-ping, WU Wei-wei, GAO Shang, et al. The ideal geometry parameters of arch cylindrical gear and its process method[J]. Journal of Shanghai Jiaotong University , 2010, 44 (12) : 1735–1740. |
| [4] |
宋爱平.弧齿圆柱齿轮及其加工方法和加工装置.ZL200410041297.2[P].2005-02-23.
SONG Ai-ping.Arc tooth cylindrical gears and its machining method and devices[J].ZL200410041297.2[P].2005-02-23. |
| [5] |
王少江, 侯力, 董璐, 等.
面向制造的弧齿圆柱齿轮建模及强度分析[J]. 四川大学学报(工程科学版) , 2012, 44 (2) : 210–215.
WANG Shao-jiang, HOU Li, DONG Lu, et al. Modeling and strength analysis of cylindrical gears with curvilinear shape teeth for manufacture[J]. Journal of Sichuan University (Engineering Science Edition) , 2012, 44 (2) : 210–215. |
| [6] |
肖华军, 侯力, 董璐, 等.
旋转刀盘母面成形的弧齿线圆柱齿轮数学建模[J]. 四川大学学报(工程科学版) , 2013, 45 (3) : 171–175.
XIAO Hua-jun, HOU Li, DONG Lu, et al. Mathematical modeling of rotary cutter arc tooth line of cylindrical gear shaped by origin face of rotary cutter[J]. Journal of Sichuan University (Engineering Science Edition) , 2013, 45 (3) : 171–175. |
| [7] |
张立杰, 李永泉, 黄真.
一种新型运动副及其在并联机床上的应用[J]. 机械工程学报 , 2005, 41 (12) : 216–221.
ZHANG Li-jie, LI Yong-quan, HUANG Zhen. Novel compound-sphere-joint and its application in parallel machine tool[J]. Journal of Mechanical Engineering , 2005, 41 (12) : 216–221. DOI:10.3901/JME.2005.12.216 |
| [8] |
韩庆涛, 郭庆鼎, 谢冬梅.
直线伺服6杆虚拟轴机床轨迹跟踪控制的研究[J]. 沈阳工业大学学报 , 2002, 24 (6) : 485–489.
HAN Qing-tao, GUO Qing-ding, XIE Dong-mei. Trajectory tracking control for 6-DOF virtual axis machine tool driven by permanent magnetic synchronous linear motor[J]. Journal of Shenyang University of Technology , 2002, 24 (6) : 485–489. |
| [9] |
陆华才, 徐月同, 杨伟民, 等.
永磁直线同步电机进给系统模糊PID控制[J]. 电工技术学报 , 2007, 22 (4) : 59–63.
LU Hua-cai, XU Yue-tong, YANG Wei-min, et al. Fuzzy pid controller design for a permanent magnet linear synchronous motor feeding system[J]. Transactions of China Electrotechnical Society , 2007, 22 (4) : 59–63. |
| [10] |
张宏伟, 余发山, 卜旭辉, 等.
基于鲁棒迭代学习的永磁直线电机控制[J]. 电机与控制学报 , 2012, 16 (6) : 81–86.
ZHANG Hong-wei, YU Fa-shan, BU Xu-hui, et al. Robust iterative learning control for permanent magnet linear motor[J]. Electric Machines and Control , 2012, 16 (6) : 81–86. |
| [11] |
蔡满军, 赵成圆.
永磁直线同步电机的自适应迭代学习控制[J]. 微特电机 , 2014, 42 (6) : 48–51.
CAI Man-jun, ZHAO Cheng-yuan. Adaptive and iterative learning control of pmlsm[J]. Small & Special Electrical Machines , 2014, 42 (6) : 48–51. |
| [12] |
刘军, 韩明文, 俞金寿.
基于滑模变结构的永磁同步直线电机控制系统研究[J]. 控制工程 , 2012, 19 (6) : 1093–1096.
LIU Jun, HAN Ming-wen, YU Jin-shou. Research on permanent magnet linear synchronous motor based on sliding mode control[J]. Control Engineering of China , 2012, 19 (6) : 1093–1096. |
| [13] |
王辉, 万里瑞, 王才东.
基于智能滑模控制的永磁直线同步电机调速系统[J]. 电机与控制应用 , 2014, 41 (2) : 6–10, 38.
WANG Hui, WAN Li-rui, WANG Cai-dong. Research of speed regulating system based on intelligent SMC for permanent magnet linear synchronous motor[J]. Electric Machines & Control Application , 2014, 41 (2) : 6–10, 38. |


