许多轻工行业使用的机器,常需要实现多个平行轴间传递转矩不大的同步转动,比如食品和药品自动包装机械、烟草机械、多轴专用钻床等,若采用带传动、齿轮传动或链条等传动,通常会使传动链结构变得复杂,机构尺寸也变得异常庞大[1-2].为解决这一难题,提出了一种新型传动机构——曲柄群驱动机构.
曲柄群驱动机构是一种包含多个定轴转动的曲柄和一个作平动的连杆桁架,且具有冗余约束的平面连杆机构[3-4].其具有结构简单紧凑、传动链较短、可实现较大中心距等速传动、加工制造容易等优点,机构中虚约束的存在对提高强度、刚度和传动平稳性也有重要作用,因此曲柄群机构因工作效率高及成本低廉等优越性广泛应用于自动化流水线、组合机床和专用工艺设备中.但由于曲柄群机构工作时总质心的偏心会使其产生较大的振动和噪音,因此为提高机构性能、减小振动,需解决曲柄群驱动机构的动平衡问题.
机构动平衡一直是机构学研究中的重要课题,连杆机构的动平衡问题由来已久,此类机构不能自行消除自身的惯性作用,需附加惯性元件加以抵消.20世纪70年代以来国内外学者对连杆机构动平衡提出了各种有效的理论模型和实验方法,尤其是刚性平面连杆机构,按机构被平衡程度分为部分平衡、完全平衡和综合优化平衡.1968年,Berkof和Lowen[5]对惯性力、惯性力矩和输入力矩平衡方法进行了全面的总结,以输入转矩、摆动力和摆动力矩为优化目标函数进行优化计算.2007年,Hinanshu和Subir[6]提出运用递归动力学算法的最大值对四杆机构进行最优平衡,这种方法是基于转动副轴承的动力学方程的递归最大值进行分析,该方法也适用于多环平面机构.2008年,Hinanshu和Subir[7]利用等动量系统的点质量代替平面机构的惯性性质进行动平衡研究,每根杆件用3个等力矩点质量替代,进一步发展了平面机构综合优化平衡方法.近年来国内许多学者对平面机构动平衡创新方法也做了大量的研究工作.1986年,黄真等[8]提出一种完全平衡平面连杆机构摆动力矩的非圆齿轮——变速转子法,这种方法的优点是平衡构件数目少,适用于多杆机构同时还可以平衡惯性输入扭矩的波动.2009年,沈惠平、张慧芳等[9-10]提出机构摆动力和摆动力矩完全平衡有限位置法,该方法不需进行连杆的附加配重计算,只需知道机构在运动过程中的(ν+f+1)个位置的角位置和角加速度,易于自动生成平衡条件方程.另外,在曲拐传动多轴钻以及框架传动机构等曲柄群驱动机构的实际应用中[11-12],各曲柄所在平面和连杆桁架平面在2个平行平面中,2个平面的质量必然会使机构产生一个惯性力偶矩[13],使机架产生反力偶,为了验证由平面机构动平衡理论推导出的曲柄群机构动平衡条件的合理性,建立虚拟样机模型时应尽量减小2个平面的距离以降低或消除惯性力偶的影响,机构动平衡仿真如果完全按照柔性体特性来进行,仿真分析的工作量和结果处理难度将大大增加,所以建模时针对刚度大、变形小的曲柄构件可将其视为刚性体,对于连杆桁架中受载情况复杂、刚性小的独立连杆可部分视为柔性体,建立的这种刚柔耦合模型既能反映机构的动力特性又可以为物理样机动平衡实验提供参考.
1 曲柄群驱动机构的动平衡条件曲柄群驱动机构中任取2个曲柄和连杆桁架均可组成平行四边形机构,连杆桁架中每根独立连杆为连枝构件,机构中所有曲柄为树枝构件,根据质量矩和动量矩替代法分别建立连枝构件的质量矩和动量矩公式[14-15],推导出任意独立连杆作用在相邻2个曲柄上的附加质量矩和附加动量矩公式.
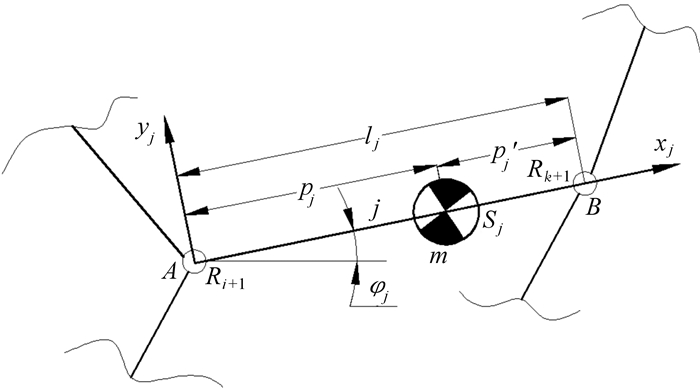
图 1中连枝构件j与树枝构件i, k以转动副Ri+1, Rk+1相联接,φj为连枝构件j与水平方向的夹角,pj, pj′, qj是以连杆轴线为xj轴建立直角坐标系中的位置参数,mj0为连枝构件j未施加配重时的质量,lj, rj分别为连枝构件j的杆长和矢径.得到连枝构件j的动量矩为

|
| 图 1 相邻树枝构件上连枝构件动量矩等效替代 Fig.1 The equivalent substitution of momentum moment for linkage component in the adjacent tree component |
| $\begin{gathered} {H_{0j}} = m_j^0\frac{{p{'_j}}}{{{l_j}}}\left( {{x_{i + 1}},{{\dot y}_{i + 1}} - {{\dot x}_i}_{ + 1}{y_{i + 1}}} \right) + \hfill \\ m_j^0\frac{{{p_j}}}{{{l_j}}}\left( {{x_{k + 1}},{{\dot y}_{k + 1}} - {{\dot x}_{k + 1}}{y_{k + 1}}} \right) - \hfill \\ m_j^0{q_j}({x_{i + 1}}\sin {\varphi _j}{{\dot \varphi }_j} + {{\dot x}_i}_{ + 1}\cos {\varphi _j} + \hfill \\ {{\dot y}_{i + 1}}\sin {\varphi _j} - {y_{i + 1}}\cos {\varphi _j}{{\dot \varphi }_j}) + \hfill \\ m_j^0\left( {r_j^2 + K_j^2 - {p_j}{l_j}} \right){{\dot \varphi }_j}. \hfill \\ \end{gathered} $ | (1) |
连枝构件j施加配重后成为直形连枝构件(如图 2所示),质量为mj(mj=mj0+mj*)且质心落在运动副Ri+1和Rk+1的中心线上.
|
| 图 2 直形连枝构件 Fig.2 Straight branch component |
任意直形连枝构件(独立连杆)j的质量矩可转化为等效在相邻曲柄构件i, k上的附加质量矩,
| $\begin{gathered} \left( \begin{gathered} {m_j}{x_{sj}} \hfill \\ {m_j}{y_{sj}} \hfill \\ \end{gathered} \right) = \frac{{{m_j}{p_j}'}}{{{l_j}}}\left( {\frac{{{x_i}}}{{{y_i}}}} \right) + \frac{{{m_j}{p_j}'{l_1}}}{{{l_j}}}\left( \begin{gathered} \cos {\varphi _1} \hfill \\ \sin {\varphi _1} \hfill \\ \end{gathered} \right) + \hfill \\ \frac{{{m_j}{p_j}}}{{{l_j}}}\left( \begin{gathered} {x_k} \hfill \\ {y_k} \hfill \\ \end{gathered} \right) + \frac{{{m_j}{p_j}{l_1}}}{{{l_j}}}\left( \begin{gathered} \cos {\varphi _1} \hfill \\ \sin {\varphi _1} \hfill \\ \end{gathered} \right). \hfill \\ \end{gathered} $ | (2) |
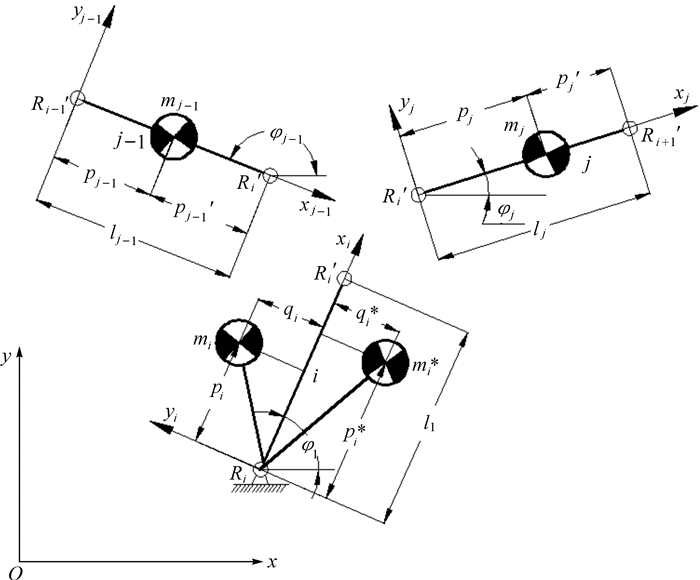
考虑连杆桁架中每根直形连枝构件的质量矩完全等效在与其相邻的曲柄(树枝构件)上,机构中由所有曲柄组成的二副杆树系统满足摆动力完全平衡条件,即曲柄群驱动机构摆动力完全平衡,其动平衡分析如图 3所示.
|
| 图 3 任意曲柄构件的动平衡分析 Fig.3 Dynamic balancing analysis of arbitrary crank member |
所有曲柄摆动力平衡条件联立组成曲柄群驱动机构摆动力完全平衡条件:
| $\left. \begin{gathered} \frac{{{m_j}{p_j}'{l_1}}}{{{l_j}}} + \frac{{{m_{j - 1}}{p_{j - 1}}{l_1}}}{{{l_{j - 1}}}} + {m_i}{p_i} + m_i^ * p_i^ * = 0, \hfill \\ {m_i}{q_i} + m_i^ * p_i^ * = 0, \hfill \\ i = 1,2, \cdots . \hfill \\ \end{gathered} \right\}$ | (3) |
故任意曲柄构件i的总动量矩H0i为
| $\begin{gathered} {H_{0i}} = {H_{{\text{LF}}}} + {m_i}\left( {{x_{Si}}{{\dot y}_{Si}} - {{\dot x}_{Si}}{y_{Si}}} \right) + \hfill \\ m_i^ * \left( {x_{Si}^ * \dot y_{Si}^ * - \dot x_{Si}^ * y_{Si}^ * } \right) + {J_i}{{\dot \varphi }_1} = \hfill \\ \left( {{m_j}\frac{{{p_j}'}}{{{l_j}}} + {m_{j - 1}}\frac{{{p_{j - 1}}}}{{{l_{j - 1}}}} + {m_i} + m_i^ * } \right)\left( {{x_i}{{\dot y}_i} - {{\dot x}_i}{y_i}} \right) + \hfill \\ \left[ {\left( {{m_j}\frac{{{p_j}'}}{{{l_j}}} + {m_{j - 1}}\frac{{{p_{j - 1}}}}{{{l_{j - 1}}}}} \right)l_1^2 + r_i^2 + r{{_i^ * }^2} + {J_i}} \right]{{\dot \varphi }_1} + \hfill \\ \left( {{x_i}\cos {\varphi _1}{{\dot \varphi }_1} + y\sin {\varphi _1}{{\dot \varphi }_1} + {{\dot y}_i}\cos {\varphi _1} - {{\dot x}_i}\sin {\varphi _1}} \right) \times \hfill \\ \left( {{m_j}\frac{{{p_j}'{l_1}}}{{{l_j}}} + {m_{j - 1}}\frac{{{p_{j - 1}}{l_1}}}{{{l_{j - 1}}}} + {m_i}{p_i} + m_i^ * p_i^ * } \right) + \hfill \\ \left( {{y_i}\cos {\varphi _1}{{\dot \varphi }_1} - {x_i}\sin {\varphi _1}{{\dot \varphi }_1} - {{\dot x}_i}\cos {\varphi _1} - {{\dot y}_i}\sin t{\varphi _1}} \right) \times \hfill \\ \left( {{m_i}{q_i} + m_i^ * p_i^ * } \right). \hfill \\ \end{gathered} $ | (4) |
上述机构中每个曲柄已实现摆动力完全平衡,将任意曲柄摆动力完全平衡条件代入式(4)得
| $\begin{gathered} {H_{0i}} = \left( {{m_j}\frac{{{p_j}'}}{{{l_j}}} + {m_{j - 1}}\frac{{{p_{j - 1}}}}{{{l_{j - 1}}}} + {m_i} + m_i^ * } \right)\left( {{x_i}{{\dot y}_i} - {{\dot x}_i}{y_i}} \right) + \hfill \\ \left[ {\left( {{m_j}\frac{{{p_j}'}}{{{l_j}}} + {m_{j - 1}}\frac{{{p_{j - 1}}}}{{{l_{j - 1}}}}} \right)l_1^2 + r_i^2 + r{{_i^ * }^2} + {J_i}} \right]{{\dot \varphi }_1}. \hfill \\ \end{gathered} $ | (5) |
从运动学可知主动曲柄以角速度
综上所述,曲柄群驱动机构动平衡条件为
| $\left\{ \begin{gathered} \frac{{{m_j}{p_j}'{l_1}}}{{{l_j}}} + \frac{{{m_{j - 1}}{p_{j - 1}}{l_1}}}{{{l_{j - 1}}}} + {m_i}{p_i} + m_i^ * p_i^ * = 0, \hfill \\ {m_i}{q_i} + m_i^ * q_i^ * = 0, \hfill \\ {{\dot \varphi }_i} = 常数 \hfill \\ i = 1,2, \cdots . \hfill \\ \end{gathered} \right.$ | (6) |
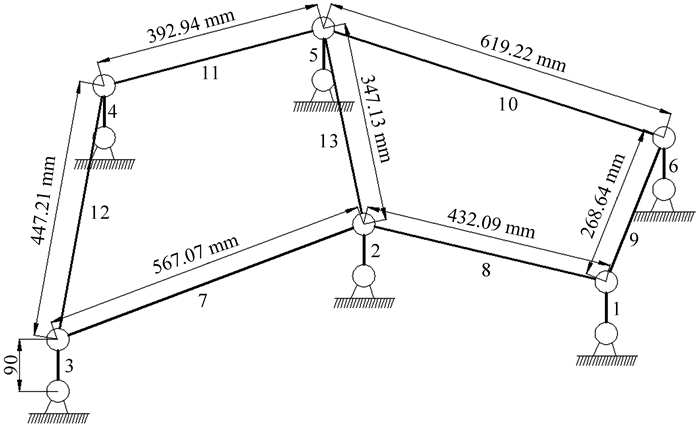
图 4为未施加配重的六曲柄群驱动机构简图,杆3为驱动曲柄,杆1,2,4,5,6为输出曲柄,杆7至13组成连杆桁架,各杆件均为均质杆,密度ρ=7.801×103 kg/m3.
|
| 图 4 未施加配重的六曲柄群驱动机构简图 Fig.4 The diagram of six crank-group driving mechanism without counterweight |
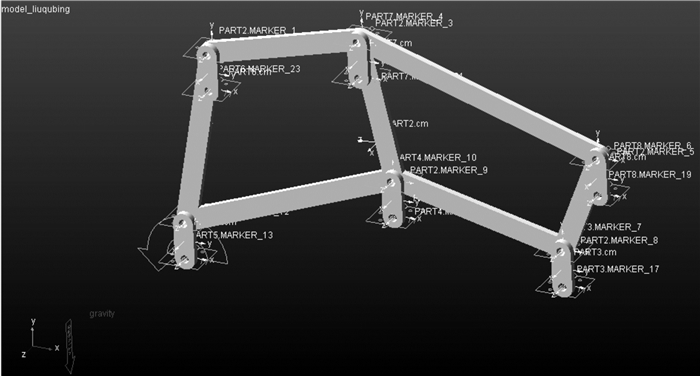
应用Pro/E三维建模软件,忽略轴承、曲柄轴、螺栓等对仿真结果影响不大的零件,建立六曲柄机构的三维实体模型[16-17],将其保存为.x_t格式文件,通过产品交换库的标准文件格式将三维实体模型导入机械系统动力学分析软件ADAMS环境中,在ADAMS界面中定义各构件的材料属性为刚性(在Material Type栏依次选择Material→Guesses→steel),再按机构的约束关系定义各曲柄与连杆桁架之间的转动副,得到如图 5所示的未配重六曲柄群驱动机构虚拟样机模型.
|
| 图 5 未施加配重的六曲柄群驱动机构虚拟样机模型 Fig.5 The virtual prototype model of six crank-group driving mechanism without counterweight |
进行动力学仿真时,在曲柄3上添加1 200 °/s的转动驱动,设定仿真时间为3 s,仿真步长为0.01,仿真完成后以各固定转动副的载荷情况来表征六曲柄群机构作平面运动时的动态特性.仿真结果通过ADAMS/PostProcessor中的Ploting输出[18-19],图 6至图 11为未配重六曲柄群驱动机构中各曲柄固定转动副处的反作用力矩.
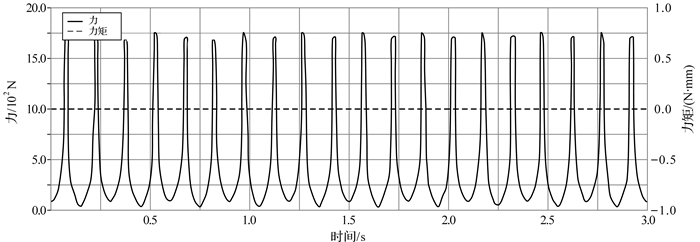
|
| 图 6 六曲柄群驱动机构配重前曲柄1转动副处的反作用力与反作用力矩曲线 Fig.6 The reaction force and torque curve of rotation pair of crank 1 of six crank-group driving mechanism before adding the counterweight |
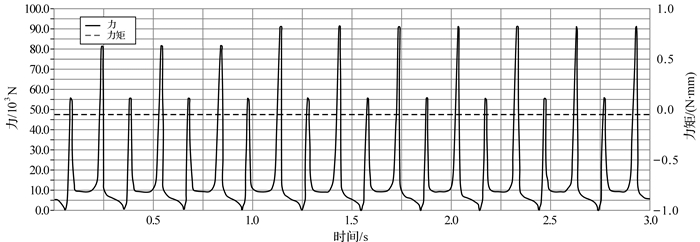
|
| 图 7 六曲柄群驱动机构配重前曲柄2转动副处的反作用力与反作用力矩曲线 Fig.7 The reaction force and torque curve of rotation pair of crank 2 of six crank-group driving mechanism before adding the counterweight |
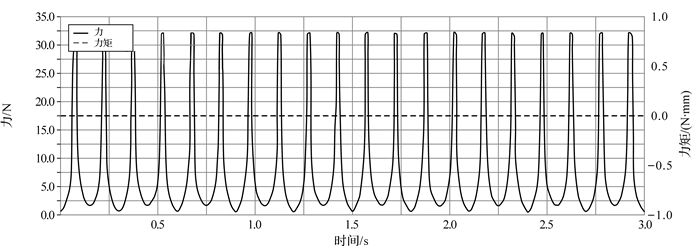
|
| 图 8 六曲柄群驱动机构配重前曲柄3转动副处的反作用力与反作用力矩曲线 Fig.8 The reaction force and torque curve of rotation pair of crank 3 of six crank-group driving mechanism before adding the counterweight |
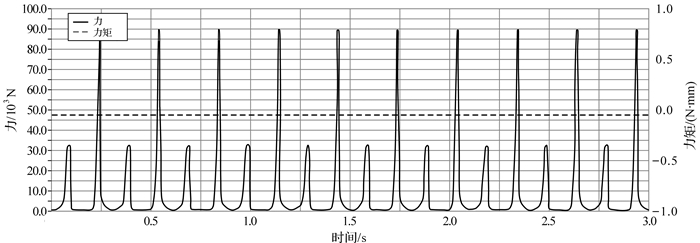
|
| 图 9 六曲柄群驱动机构配重前曲柄4转动副处的反作用力与反作用力矩曲线 Fig.9 The reaction force and torque curve of rotation pair of crank 4 of six crank-group driving mechanism before adding the counterweight |
|
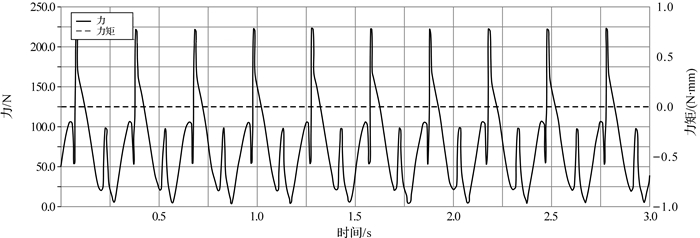
| 图 10 六曲柄群驱动机构配重前曲柄5转动副处的反作用力与反作用力矩曲线 Fig.10 The reaction force and torque curve of rotation pair of crank 5 of six crank-group driving mechanism before adding the counterweight |
|
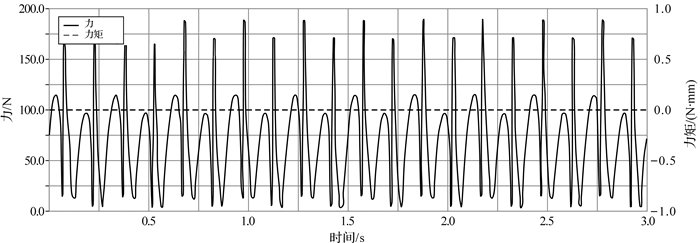
| 图 11 六曲柄群驱动机构配重前曲柄6转动副处的反作用力与反作用力矩曲线 Fig.11 The reaction force and torque curve of rotation pair of crank 6 of six crank-group driving mechanism before adding the counterweight |
从各曲柄转动副处的反作用力和反作用力矩曲线图(见图 6至图 11)可以看出,机构运转时各曲柄固定转动副处作用反力的大小随时间呈周期性变化,这种变化是加剧转动副中轴承与轴之间磨损,降低机构传动效率,造成机座产生振动、噪音的原因.曲柄1,2,4的总反作用力峰值最大,分别为1 750,9 000,9 000 N,相比其他曲柄,这3个曲柄对六曲柄群机构的运动平稳性影响更为显著.而每个曲柄固定转动副处的反作用力矩始终为零,说明此类曲柄群机构在匀速运转时机构的摆动力矩恒为零,与上述曲柄群驱动机构摆动力矩完全平衡条件符合,说明了该动力学模型的正确性.
3 基于动平衡条件的六曲柄群机构质量配重模型将六曲柄群机构中的6个曲柄均设计为相同扇角、不同扇形半径的扇形曲柄,如表 1所示,通过改变扇形半径调整配重曲柄质量矩的中心位置,如图 12所示.
| 扇形曲柄的扇角 | 量值/(°) |
| α1 | 150 |
| α2 | 150 |
| α3 | 150 |
| α4 | 150 |
| α5 | 150 |
| α6 | 150 |
| 扇形曲柄的扇形半径 | 量值/mm |
| R1 | 151.141 |
| R2 | 183.365 |
| R3 | 168.342 |
| R4 | 121.531 |
| R5 | 183.909 |
| R6 | 161.848 |
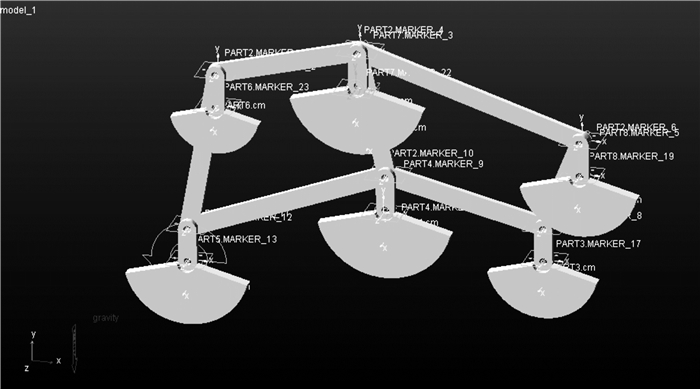
|
| 图 12 利用扇形曲柄配重后的六曲柄群驱动机构模型 Fig.12 The virtual prototype model of six crank-group driving mechanism by using fan shaped crank |
| $m_i^ * p_i^ * = \frac{{{\alpha _i}R_i^2}}{2} \times t \times \rho \times \frac{{4{R_i}\sin \frac{{{\alpha _i}}}{2}}}{{3{\alpha _i}}},$ | (7) |
式中:α为扇形曲柄的扇角大小,ρ为曲柄的材料密度,Ri为扇形曲柄的扇形半径,t为曲柄厚度,每个扇形曲柄均取t=30 mm.
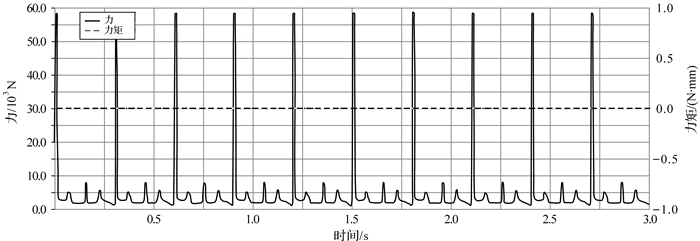
在ADAMS中添加与未配重六曲柄机构相同的约束以及驱动,图 13至图 18为扇形曲柄配重后各曲柄固定转动副处的反作用力和反作用力矩曲线图.
|
| 图 13 六曲柄群驱动机构配重后扇形曲柄1固定转动副处的反作用力与反作用力矩曲线 Fig.13 The reaction force and torque curve of rotation pair of fan shaped crank 1 of six crank-group driving mechanism after adding the counterweight |
|
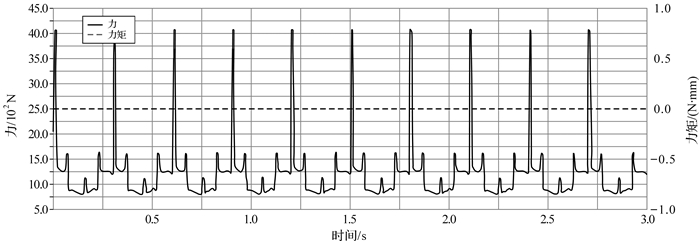
| 图 14 六曲柄群驱动机构配重后扇形曲柄2固定转动副处的反作用力与反作用力矩曲线 Fig.14 The reaction force and torque curve of rotation pair of fan shaped crank 2 of six crank-group driving mechanism after adding the counterweight |
|
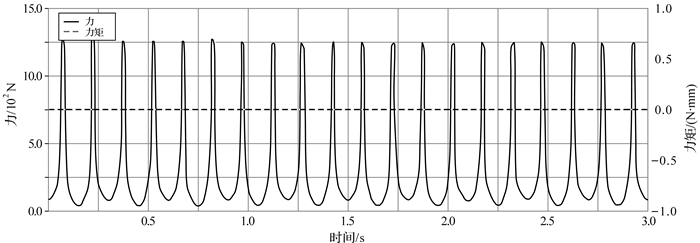
| 图 15 六曲柄群驱动机构配重后扇形曲柄3固定转动副处的反作用力与反作用力矩曲线 Fig.15 The reaction force and torque curve of rotation pair of fan shaped crank 3 of six crank-group driving mechanism after adding the counterweight |
|
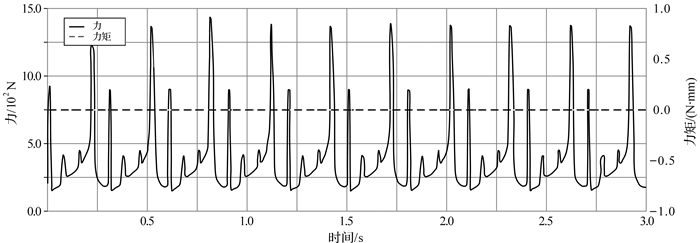
| 图 16 六曲柄群驱动机构配重后扇形曲柄4固定转动副处的反作用力与反作用力矩曲线 Fig.16 The reaction force and torque curve of rotation pair of fan shaped crank 4 of six crank-group driving mechanism after adding the counterweight |
|
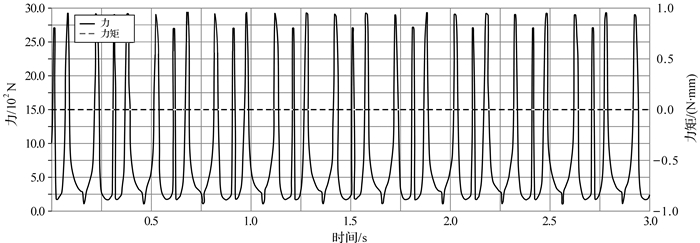
| 图 17 六曲柄群驱动机构配重后扇形曲柄5固定转动副处的反作用力与反作用力矩曲线 Fig.17 The reaction force and torque curve of rotation pair of fan shaped crank 5 of six crank-group driving mechanism after adding the counterweight |
|
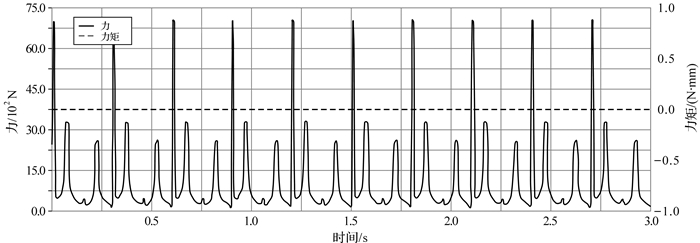
| 图 18 六曲柄群驱动机构配重后扇形曲柄6固定转动副处的反作用力与反作用力矩曲线 Fig.18 The reaction force and torque curve of rotation pair of fan shaped crank 6 of six crank-group driving mechanism after adding the counterweight |
通过对比施加配重前后六曲柄群驱动机构各曲柄固定转动副处的受力与力矩发现,机构配重前后曲柄受载曲线图中出现较大的周期瞬时载荷,产生这种情况的原因可能是机构运动到死点时受力不明确及构件之间存在的尺寸误差引起构件在转动副处发生碰撞,引起冲击载荷使运动副反作用力出现高频振荡影响机构的动态特性.在同样的转速下,各曲柄固定转动副处反作用力矩仍为零,曲柄1,2,4的总反作用力分别下降了85.71%,91.67%,93.33%;相反,曲柄3,5,6固定转动副处总反力上升了95.9%,90%和93.15%.从机构整体反作用力变化幅值来看,添加扇形曲柄平衡六曲柄群驱动机构后,机构对机座的摆动力大大降低,但不平衡惯性力未能如动平衡条件推导的那样完全消失,所以单纯利用质量配重的动平衡效果并不能达到完全平衡状态.
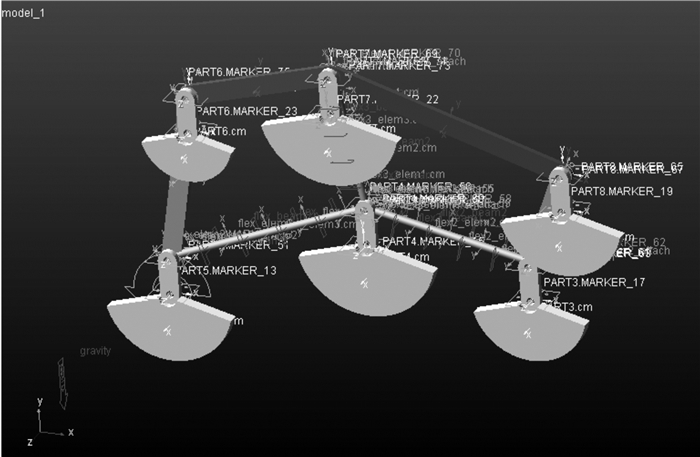
4 六曲柄群驱动机构引入部分柔性连杆桁架的动平衡模型根据上述刚性体扇形配重后的六曲柄群驱动机构的仿真结果,曲柄2固定转动副处所受的反作用载荷最大,为协调机构各杆件受载时发生的变形以及降低曲柄2处的受力幅值,考虑到连杆桁架作为联接各输入输出曲柄的传动部件时,所受载荷最复杂,而连杆桁架刚度过大可能会加剧转动副间的摩擦与磨损,降低传动效率,甚至使机构发生“卡死”现象.因此把连杆桁架进行部分柔性处理,用离散柔性连接件替换连杆桁架中独立刚性连杆7,8,13,使整个机构的误差和间隙在曲柄2与连杆桁架的连接处得到补偿[20-21].其中ADAMS动力学软件中的离散柔性连接件是直接利用柔性梁把被离散的刚性构件中的多个小刚性体联接起来,离散柔性连接件产生的变形即柔性连接梁的变形,小刚性体上任意两点不能相对移动,严格来说离散柔性连接件仍属于刚性构件的范畴,因而该方法只适合用于结构简单的零件.图 19为对六曲柄群驱动机构施加配重的基础上,连杆桁架中加入柔性连杆的曲柄群驱动机构虚拟样机模型.
|
| 图 19 引入部分柔性连杆桁架的六曲柄群驱动机构虚拟样机模型 Fig.19 The virtual prototype model of six crank-group driving mechanism with partial flexible connecting rod truss |
在曲柄与机架、曲柄与连杆桁架之间添加相同的转动副约束,仍在曲柄3固定转动副处添加1 200 °/s的旋转驱动,设置仿真时间为1.5 s,即各曲柄旋转3周的时间,仿真步长为0.01,各曲柄运动副处的反作用力和反作用力矩仿真结果如图 20至图 25所示.
|
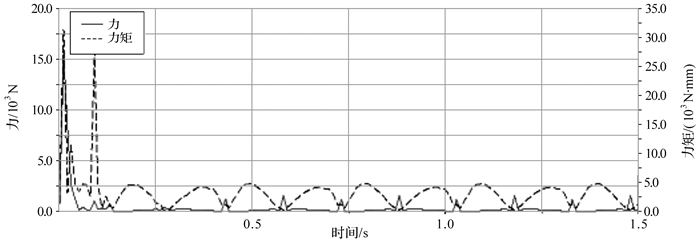
| 图 20 六曲柄群驱动机构引入部分柔性连杆桁架后扇形曲柄1转动副处的反作用力与反作用力矩曲线 Fig.20 The reaction force and torque curve of rotation pair of fan shaped crank 1 of six crank-group driving mechanism with partial flexible connecting rod truss |
|
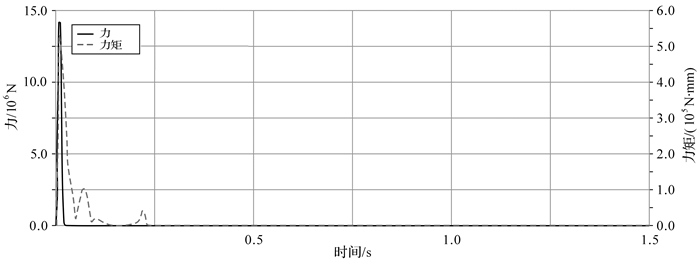
| 图 21 六曲柄群驱动机构引入部分柔性连杆桁架后扇形曲柄2转动副处的反作用力与反作用力矩曲线 Fig.21 The reaction force and torque curve of rotation pair of fan shaped crank 2 of six crank-group driving mechanism with partial flexible connecting rod truss |
|
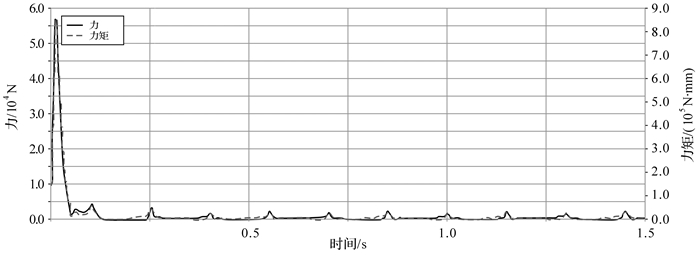
| 图 22 六曲柄群驱动机构引入部分柔性连杆桁架后扇形曲柄3转动副处的反作用力与反作用力矩曲线 Fig.22 The reaction force and torque curve of rotation pair of fan shaped crank 3 of six crank-group driving mechanism with partial flexible connecting rod truss |
|
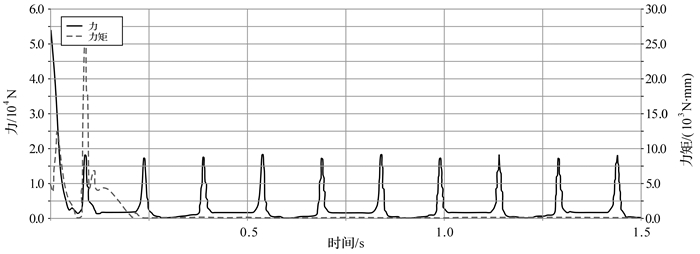
| 图 23 六曲柄群驱动机构引入部分柔性连杆桁架后扇形曲柄4转动副处的反作用力与反作用力矩曲线 Fig.23 The reaction force and torque curve of rotation pair of fan shaped crank 4 of six crank-group driving mechanism with partial flexible connecting rod truss |
|
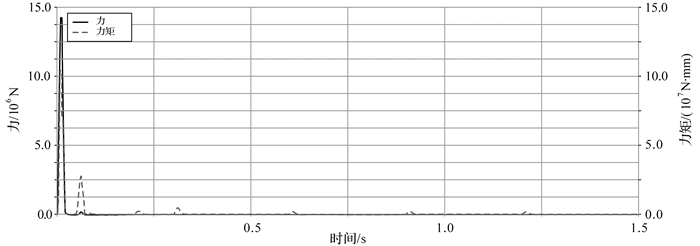
| 图 24 六曲柄群驱动机构引入部分柔性连杆桁架后扇形曲柄5转动副处的反作用力与反作用力矩曲线 Fig.24 The reaction force and torque curve of rotation pair of fan shaped crank 5 of six crank-group driving mechanism with partial flexible connecting rod truss |
|
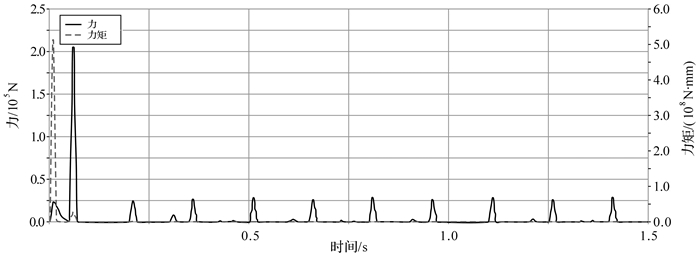
| 图 25 六曲柄群驱动机构引入部分柔性连杆桁架后扇形曲柄6转动副处的反作用力与反作用力矩曲线 Fig.25 The reaction force and torque curve of rotation pair of fan shaped crank 6 of six crank-group driving mechanism with partial flexible connecting rod truss |
从上述仿真曲线图中可以看出,机构在启动阶段有较大的动载荷,初始振动因连杆桁架部分柔性连杆的弹性变形在短时间振荡后迅速降低,各固定转动副处的反作用力和反作用力矩立刻变小,其幅值在零值附近作小范围周期性变化.尤其是曲柄2固定转动副处的反作用力得到完全平衡,整个过程中各曲柄固定转动副处受力平稳,机构动平衡效果明显.这种结构会大幅降低构件之间的冲击载荷,防止连杆桁架中各独立连杆发生断裂破坏和减少机构工作过程中的噪音,使机构的使用寿命和传递效率明显提高.
5 结论本文结合质量矩和动量矩替代法得出的曲柄群驱动机构动平衡条件和ADAMS/Flex柔性体理论,建立了多组六曲柄群驱动机构的动平衡模型并进行了仿真分析,比较模型间各曲柄固定转动副处反作用载荷的变化曲线图,发现只利用质量配重的方法并不能实现机构的完全平衡.将连杆桁架中与受载情况最恶劣曲柄相连的独立连杆替换为柔性体后,对曲柄群驱动机构刚柔耦合动平衡方法模型进行仿真分析,结果表明后者动平衡效果明显优于前者,说明柔性构件的引入对机构动平衡效果的提高存在较大影响,该刚柔耦合动平衡方法能较好地平衡机构传给机架的摆动力和摆动力矩.因此在动平衡物理样机设计时一定要考虑连杆桁架中相关连杆弹性变形对各曲柄固定转动副受载的影响,合理地对结构进行优化以满足机构工作的平稳性能要求,为曲柄群驱动机构实验物理样机的研制提供可靠保证.
| [1] |
汪玉琪, 曹巨江.
曲柄群驱动机构的运动特点研究[J]. 机械传动 , 2013, 37 (10) : 79–81.
WANG Yu-qi, CAO Ju-jiang. Study on the motion feature of crank-group driving mechanism[J]. Journal of Mechanical Transmission , 2013, 37 (10) : 79–81. |
| [2] |
焦楠.曲柄群驱动装置虚拟样机研究[D].西安:陕西科技大学机电工程学院, 2014: 1-4.
JIAO Nan.Virtual prototyping of crank-group driving device[D].Xi'an: Shanxi University of Science and Technology, College of Mechanical and Electrical Engineering, 2014: 1-4. http://cdmd.cnki.com.cn/article/cdmd-10708-1014339634.htm |
| [3] |
任升, 曹巨江, 刘言松, 等.
曲柄群驱动机构单元化平衡[J]. 轻工机械 , 2015, 33 (1) : 8–10.
REN Sheng, CAO Ju-jiang, LIU Yan-song, et al. Inertia force balance of crank-group driving mechanism based on crank unit[J]. Journal of Light Industrial Machinery , 2015, 33 (1) : 8–10. |
| [4] |
洪光辉.框架传动机构集成优化动力平衡研究[D].长沙:湖南大学机械与汽车工程学院, 2006: 1-3.
HONG Guang-hui.The research of integrated optimization dynamical balancing in framework transmission mechanism[D].Changsha: Hunan University, College of Mechanical and Automobile Engineering, 2006: 1-3. |
| [5] | BERKOF R S, LOWEN G G. A new method for completely force balancing simple linkages[J]. Journal of Engineering for Industry , 1969, 91 (1) : 21–26. DOI:10.1115/1.3591524 |
| [6] | HINANSHU Chaudhary, SUBIR Kumar Saha. Balancing of four-bar linkages using maximum recursive dynamic algorithm[J]. Mechanism and Machine Theory , 2007, 42 (2) : 216–232. DOI:10.1016/j.mechmachtheory.2006.02.008 |
| [7] | HIMANSHU Chaudhary, SUBIR Kumar Saha. Balancing of shaking forces and shaking moments for planar mechanisms using the equimomental systems[J]. Mechanism and Machine Theory , 2008, 43 (3) : 310–334. DOI:10.1016/j.mechmachtheory.2007.04.003 |
| [8] |
黄真, 石镇德.
平衡机构摆动力矩的非园齿轮法[J]. 东北重型机械学院学报 , 1986 (4) : 40–45.
HUANG Zhen, SHI Zhen-de. Non-circular gear method for balancing shaking moment of mechanism[J]. Journal of Northeast Heavy Machinery College , 1986 (4) : 40–45. |
| [9] |
张会芳, 沈惠平, 杨廷力.
机构摆动力完全平衡有限位置法及其应用[J]. 机械科学与技术 , 2009, 28 (3) : 360–366.
ZHANG Hui-fang, SHEN Hui-ping, YANG Ting-li. A finite place method for balancing the shaking force of mechanism and its application[J]. Mechanical Science and Technology for Aerospace Engineering , 2009, 28 (3) : 360–366. |
| [10] |
沈惠平, 张会芳, 丁少华, 等.
机构摆动力矩完全平衡的有限位置法[J]. 机械科学与技术 , 2011, 30 (6) : 861–864.
SHEN Hui-ping, ZHANG Hui-fang, DING Shao-hua, et al. A finite place method for solving the shaking moment of a mechanism[J]. Mechanical Science and Technology for Aerospace Engineering , 2011, 30 (6) : 861–864. |
| [11] |
朱波儿, 黎东升.
曲拐传动及其在机加工中的应用[J]. 机电工程技术 , 2002, 31 (1) : 44–45.
ZHU Bo-er, LI Dong-sheng. Crankshaft transmission and its application in machining[J]. Journal of Electromechanical Technology , 2002, 31 (1) : 44–45. |
| [12] |
谢明金, 刘子建, 汪祥, 等.
卸载方式在高速框架传动机构中的应用研究[J]. 现代制造工程 , 2008 (5) : 99–102.
XIE Ming-jin, LIU Zi-jian, WANG Xiang, et al. The application research of unloading methods in high-speed framework transmission mechanism[J]. Journal of Modern Manufacturing Engineering , 2008 (5) : 99–102. |
| [13] |
杨敬涵, 黄季灵.
平面连杆机构震动力矩平衡的行星转子法[J]. 机械工程师 , 1998 (4) : 2–4.
YANG Jing-han, HUANG Ji-ling. Planetary rotor method for balancing shaking moment of planar linkage mechanisms[J]. Journal of Mechanical Engineer , 1998 (4) : 2–4. |
| [14] |
郭瑞琴, 孔宪文.
平面连杆机构摆动力完全平衡的质量矩替代法[J]. 机械传动 , 2000, 24 (1) : 9–12.
GUO Rui-qin, KONG Xian-wen. Mass moment substitution method for balancing shaking force of planar linkage mechanism[J]. Journal of Mechanical Transmission , 2000, 24 (1) : 9–12. |
| [15] |
孔宪文, 杨廷力.
全R副空间连杆机构摆动力和摆动力矩的完全平衡[J]. 机械科学与技术 , 1997 (3) : 442–447.
KONG Xian-wen, YANG Ting-li. Complete balance of the swing force and the swing moment of spatial linkage mechanism with only R pairs[J]. Mechanical Science and Technology for Aerospace Engineering , 1997 (3) : 442–447. |
| [16] |
童宝宏, 桂长林, 陈华, 等.
内燃机曲柄连杆机构的建模与仿真研究[J]. 计算机仿真 , 2007, 24 (12) : 229–234.
TONG Bao-hong, GUI Chang-lin, CHEN Hua, et al. Modeling and simulation of the crank-connecting rod mechanism in internal combustion engine[J]. Journal of Computer Simulation , 2007, 24 (12) : 229–234. |
| [17] |
姜峣, 李铁民, 王立平.
过约束并联机构动力学建模方法[J]. 机械工程学报 , 2013, 49 (17) : 123–129.
JIANG Yao, LI Tie-min, WANG Li-ping. Research on the dynamic model of an over-constrained parallel mechanism[J]. Journal of Mechanical Engineering , 2013, 49 (17) : 123–129. DOI:10.3901/JME.2013.17.123 |
| [18] |
刘剑钊, 党建军, 张进军.
基于ADAMS的摆盘机构动力学仿真分析[J]. 机械设计与制造 , 2012 (4) : 76–78.
LIU Jian-zhao, DANG Jian-jun, ZHANG Jin-jun. ADAMS-based dynamic simulation analysis for wobble-plate mechanism[J]. Journal of Mechanical Design and Manufacturing , 2012 (4) : 76–78. |
| [19] |
吴艳荣, 金国光, 李东福.
基于ADAMS的变胞机构动力学仿真[J]. 机械设计与制造 , 2007 (5) : 87–88.
WU Yan-rong, JIN Guo-guang, LI Dong-fu. Dynamic simulation of metamorphic mechanism with ADAMS software[J]. Machinery Design & Manufacture , 2007 (5) : 87–88. |
| [20] |
孙建锐.基于刚柔耦合模型的门座起重机动力学仿真研究[D].武汉:武汉理工大学物流工程学院, 2010: 61-67.
SUN Jian-rui.Crane based on rigid-flexible multiply model[D].Wuhan: Wuhan University of Technology, College of Logistics Engineering, 2010: 61-67. http://cdmd.cnki.com.cn/article/cdmd-10497-2010164038.htm |
| [21] | DYER S S, SHI Jian-jun. Robust optimal influence-coefficient control of multiple-plane active rotor balancing systems[J]. Journal of Dynamic Systems (Measurement and Control) , 2002, 124 (1) : 41–46. DOI:10.1115/1.1435622 |



