2. 杭州乾知科技服务有限公司, 浙江 杭州 311112
2. M-Tech Science and Technology Service Co., Ltd., Hangzhou 311112, China
碳纤维增强复合材料储氢气瓶因其有诸多优点而备受重视和青睐,但是在复合材料储氢气瓶的设计及力学性能分析方面仍然存在一些难点,原因在于复合材料是一种力学性能复杂的新型材料.因此如何有效地预测复合材料气瓶的极限强度,对于储氢气瓶的安全应用显得尤为重要[1-3].
自20世纪50年代开始,国内外开展了许多关于复合材料层合板结构损伤、失效和破坏力学性能方面的研究工作.对于碳纤维/环氧复合材料层合板结构,在连续或循环载荷等作用下,其损伤失效后宏观表现为各向异性刚度退化,这是层合板结构在破坏失效过程中的一个重要物理现象.对于如何解释复合材料层合板刚度退化后的失效特性,国内外专家通过在原有连续损伤力学(continuum damage mechanics, CDM)的基础上引入内部损伤变量、建立损伤演化规律等方法对损伤力学理论进行了更为详尽的描述,并将该理论创造性地应用于不同材料的破坏损伤机理研究中,包括金属材料、黏弹性高分子材料以及复合材料等,加大损伤力学研究深度的同时,拓宽了连续损伤力学的适用范围,将连续损伤力学理论推向了一个新高度[4-9].但是,这些研究多局限于宏观(整个层合板结构)尺度范围,而失效准则通常包括最大应力或应变、Hashin、Hoffman、Tsai-Wu和Tsai-Hill等失效理论,没有涉及纤维/基体的细观尺度,因此很难揭示复合材料破坏损伤的真实特性[10-13].
对于复合材料储氢气瓶,由于碳纤维的强度支撑着气瓶的承载能力,再加上纤维强度分布具有统计特性以及碳纤维和环氧基体中潜在的各种缺陷,复合材料层合板刚度退化特性被视为复合材料中微裂纹和微孔洞增长的宏观体现,这表明单纯运用连续损伤力学和复合材料均一化理论来研究复合材料层合板结构的宏观破坏失效力学性能是不够的,而必须进一步联合复合材料的细观力学性能,开展细观-宏观多尺度破坏力学性能的研究[14-16].
韩国汉阳大学Sung Kyu Ha教授提出一种基于微观力学失效(MMF)的复合材料分析理论[17],通过建立周期的代表性体积单元(representative volume element,RVE)模型来研究纤维/基体失效以及界面分离对复合材料力学性能的影响,提出了从细观力学性能提取数据分析而反映宏观材料属性的方法,并通过有限元计算建立了复合材料多尺度失效分析方法.本文基于微观力学失效(MMF)理论推断组分的初始损伤、失效情况,进而应用连续损伤力学(CDM)分析方法模拟组分材料的刚度退化和损伤,从而最终确定复合材料容器结构的极限强度并预测其爆破压力.
1 微观力学失效理论(MMF) 1.1 失效准则根据微观力学失效理论[17],纤维的模量远大于基体的模量,纤维承担了复合材料层板纵向的绝大部分拉伸和压缩载荷.因此,对于纤维失效准则,可以忽略横向应力和剪切应力的影响,这样可以得到纤维失效准则为
| $\left. \begin{gathered} \frac{{{\sigma _{{\text{f1}}}}}}{{{T_{\text{f}}}}} = 1,{\sigma _{{\text{f1}}}} > 0, \hfill \\ \frac{{ - {\sigma _{{\text{f1}}}}}}{{{C_{\text{f}}}}} = 1,{\sigma _{{\text{f1}}}} < 0, \hfill \\ \end{gathered} \right\}$ | (1) |
式中:σf1为纤维纵向微观应力,Tf为纤维纵向拉伸强度,Cf为纤维纵向压缩强度.
树脂基体可以认为是各向同性材料,但是其拉压强度并不相同.理论与实验表明,基体强度与Mises等效应力和第一应力不变量I1有关,因此基体失效准则可以表示为
| $\frac{{\sigma _{{\text{vm}}}^2}}{{{C_{\text{m}}}{T_{\text{m}}}}} + \left( {\frac{1}{{{T_{\text{m}}}}} - \frac{1}{{{C_{\text{m}}}}}} \right){I_1} = 1,$ | (2) |
式中:Tm为基体拉伸强度,Cm为基体压缩强度,σvm为Mises等效应力,可表示为
| $\left. \begin{gathered} {I_1} = {\sigma _1} + {\sigma _2} + {\sigma _3}, \hfill \\ {I_2} = {\sigma _1}{\sigma _2} + {\sigma _2}{\sigma _3} - {\sigma _3}{\sigma _1} - \left( {\sigma _4^2 + \sigma _5^2 + \sigma _6^2} \right), \hfill \\ {\sigma _{{\text{vm}}}} = \sqrt {I_1^2 - 3{I_2}} . \hfill \\ \end{gathered} \right\}$ | (3) |
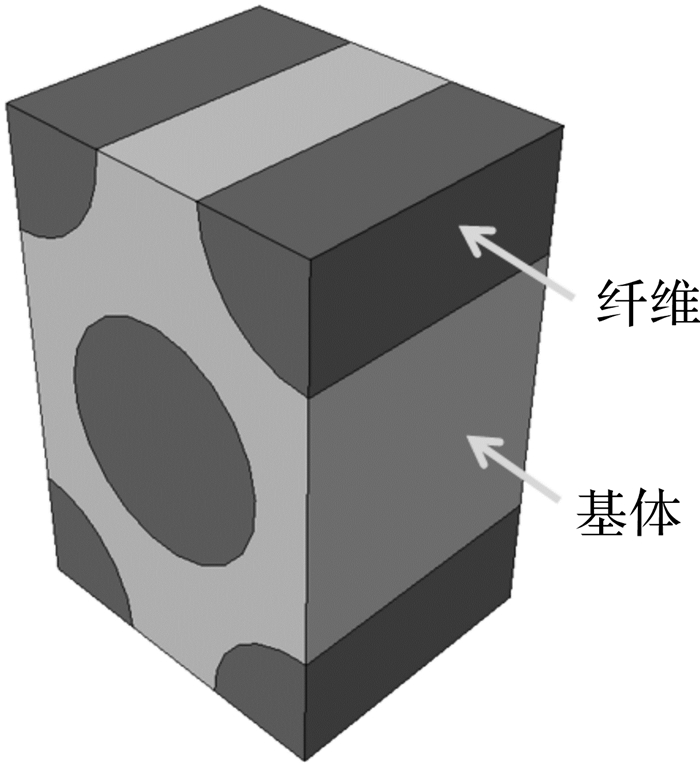
上述失效准则中的组分微观应力,可以通过建立代表性体积单元(RVE)获得,从而提取细观力学性能数据,建立细观组分与宏观材料的性能联系.图 1为六边形体积元,包含基体和纤维两个组分,其中基体是各向同性材料,纤维是正交各向异性材料,纤维体积分数为0.62.通过对RVE模型施加合理的对称边界条件和周期性边界条件,使其能够代表真实的复合材料内部组分的应力和位移分布.这样组分微观应力可以通过宏观应力和应力放大因子M和A求得:
|
| 图 1 RVE几何模型 Fig.1 The geometric model of RVE |
| $\sigma = {M_\sigma }\bar \sigma + {A_\sigma }\Delta T,$ | (4) |
式中,
| ${M_\sigma } = \left[ {\begin{array}{*{20}{c}} {{M_{11}}}&{{M_{12}}}&{{M_{13}}}&{{M_{14}}}&{{M_{15}}}&{{M_{16}}} \\ {{M_{21}}}&{{M_{22}}}&{{M_{23}}}&{{M_{24}}}&{{M_{25}}}&{{M_{26}}} \\ {{M_{31}}}&{{M_{32}}}&{{M_{33}}}&{{M_{34}}}&{{M_{35}}}&{{M_{36}}} \\ {{M_{41}}}&{{M_{42}}}&{{M_{43}}}&{{M_{44}}}&{{M_{45}}}&{{M_{46}}} \\ {{M_{51}}}&{{M_{52}}}&{{M_{53}}}&{{M_{54}}}&{{M_{55}}}&{{M_{56}}} \\ {{M_{61}}}&{{M_{62}}}&{{M_{63}}}&{{M_{64}}}&{{M_{65}}}&{{M_{66}}} \end{array}} \right],$ | (5) |
| ${A_\sigma }{\text{ = }}\left[ {{A_1}\;\;\;{A_2}\;\;\;{A_3}\;\;\;{A_4}\;\;\;{A_5}\;\;\;{A_6}} \right]_\sigma ^T,$ | (6) |
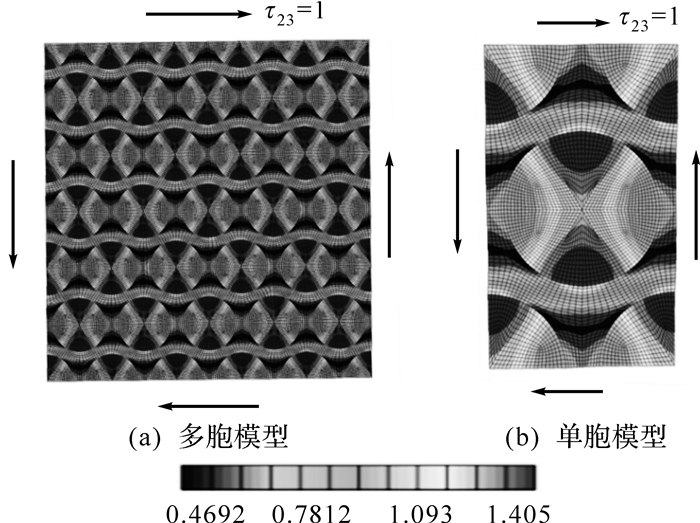
σ为宏观应力,ΔT为温度差.对于给定的复合材料,其基体与纤维的材料属性与几何分布是确定的,因此应力放大因子是固定值.通过对RVE施加不同的单位应力载荷(即3个正应力、3个切应力和温度载荷),即可以得到相应的组分微观力学响应,从而提取纤维和基体的应力放大因子.例如:为了得到横向剪切载荷作用下的应力放大因子,可以在横向对称侧面施加单位应力载荷τ23=1,如图 2所示,同时耦合各个面上的节点使其保持为平面变形,这样可以得到纤维和基体的应力分布;在纤维和基体组分处各取若干关键点,提取相应应力放大因子,将其值存储在ABAQUS子程序UMAT中,在后续有限元分析中,用于计算组分微观应力.
|
| 图 2 单位横向剪切载荷作用下RVE应力分布 Fig.2 Micro stress distribution of RVE under the unit transverse shear stress |
复合材料损伤分析是复合材料层板结构性能分析的重要部分.Kachanov教授提出,材料损伤对复合材料结构整体性能的影响可以通过材料刚度矩阵退化的方法来确定[18].根据McCarthy等提出的损伤强度计算模型[19]并结合微观力学失效理论,当单元满足失效准则以后,可以根据组分失效定义不同的损伤因子(df,dm)和退化材料的刚度性能.
当纤维失效,相应损伤因子定义为
| ${d_{\text{f}}} = 0.99,$ | (7) |
当基体失效,相应损伤因子定义为
| ${d_{\text{m}}} = 0.99,$ | (8) |
这样,材料损伤后的刚度矩阵可以表示为
| ${C_{ijkl}} = \left[ {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}&{{C_{13}}}&0&0&0 \\ {}&{{C_{22}}}&{{C_{23}}}&0&0&0 \\ {}&{}&{{C_{33}}}&0&0&0 \\ {}&{{\text{symm}}}&{}&{{C_{44}}}&0&0 \\ {}&{}&{}&{}&{{C_{55}}}&0 \\ {}&{}&{}&{}&{}&{{C_{66}}} \end{array}} \right],$ | (9) |
其中各项可以通过复合材料弹性常数求得:
| $ \begin{gathered} {C_{11}} = {E_1}\left( {1 - {d_{\text{f}}}} \right)\left[ {1 - {{\left( {1 - {d_{\text{m}}}} \right)}^2}v_{23}^2} \right]/A, \hfill \\ {C_{22}} = {C_{33}}{\text{ = }}{E_{\text{2}}}\left( {1 - {d_{\text{m}}}} \right)\left[ {1 - \left( {1 - {d_{\text{m}}}} \right)\left( {1 - {d_{\text{f}}}} \right){v_{12}}{v_{21}}} \right]/A, \hfill \\ {C_{12}} = {C_{13}}{\text{ = }}{E_{\text{2}}}\left( {1 - {d_{\text{m}}}} \right)\left( {1 - {d_{\text{f}}}} \right)\left[ {\left( {1 - {d_{\text{m}}}} \right){v_{12}}{v_{23}} + {v_{12}}} \right]/A, \hfill \\ {C_{23}} = {E_2}{\left( {1 - {d_{\text{m}}}} \right)^2}\left[ {v_{23}^2 + \left( {1 - {d_{\text{f}}}} \right){v_{12}}{v_{21}}} \right]/A, \hfill \\ {C_{44}} = {C_{55}} = {C_{12}}\left( {1 - {d_{\text{m}}}} \right)\left( {1 - {d_{\text{f}}}} \right), \hfill \\ {C_{66}} = {C_{23}}\left( {1 - {d_{\text{m}}}} \right)\left( {1 - {d_{\text{f}}}} \right), \hfill \\ A = 1 - 2\left( {1 - {d_{\text{m}}}} \right)\left( {1 - {d_{\text{f}}}} \right){v_{12}}{v_{21}} - {\left( {1 - {d_{\text{m}}}} \right)^2}{v_{23}}{v_{32}}{\text{ - }} \hfill \\ 2{\left( {1 - {d_{\text{m}}}} \right)^2}\left( {1 - {d_{\text{f}}}} \right){v_{12}}{v_{21}}{v_{23}} \hfill \\ \end{gathered} $ |
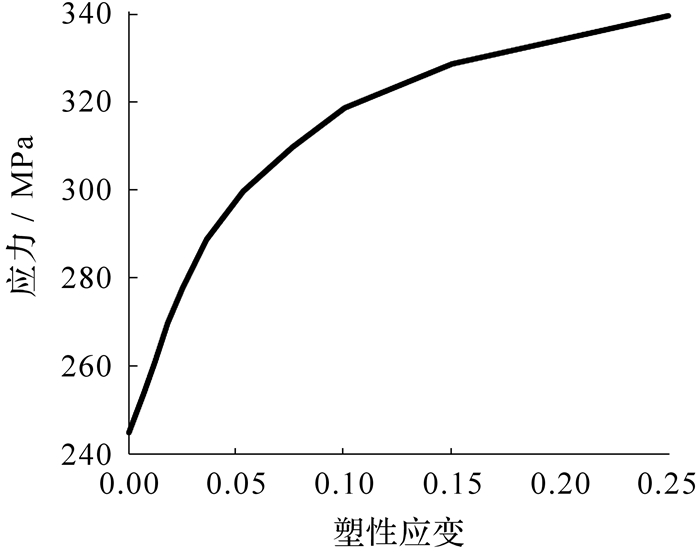
图 3为碳纤维复合材料储氢气瓶,由Al6061-T6铝合金内衬和T700复合材料缠绕层构成[20].气瓶的内直径为237 mm,内衬壁厚为2 mm,缠绕后的直径为275 mm.复合材料铺层沿壁厚方向由内向外依次为: 90°层铺设28层,15°层铺设6层,18°层铺设6层,20°层铺设6层,28°层铺设4层,33°层铺设4层,42°层铺设2层,48°层铺设2层.气瓶材料参数见表 1,其中复合材料为线弹性正交各向异性,铝合金内衬为弹塑性材料,其塑性部分应力应变曲线如图 4所示.本文失效分析采用的纤维和基体组分强度参数,可根据单层板强度参数并利用1.2节所述的微观力学分析方法计算求得.例如:对RVE施加轴向(纤维方向)的拉伸载荷,其值取单层板轴向拉伸强度XT,可以得到RVE内部纤维的微观应力分布,其轴向应力最大值即为纤维拉伸强度Tf,同理可以求得其他组分强度参数,其值列于表 2.

|
| 图 3 碳纤维复合材料储氢气瓶 Fig.3 Carbon fiber/epoxy composite hydrogen storage vessel |
| 材料 | E 1 /MPa | E 2/MPa | v 12 | v 23 | G 12/MPa | G 23/MPa |
| 复合材料 | 142 | 8.5 | 0.25 | 0.42 | 3.7 | 2.6 |
| 铝合金 | 70 | - | 0.35 | - | - | - |
| 碳纤维 | 232 | 18 | 0.2 | 0.49 | 8.7 | 5.8 |
| 环氧树脂 | 3.5 | 3.5 | 0.33 | 0.33 | 1.25 | 1.25 |
|
| 图 4 铝内衬塑性部分应力—应变曲线 Fig.4 Stress-strain curve of the aluminum liner at plastic stage |
| 强度 | 量值 |
| 纤维拉伸强度Tf | 4 150 MPa |
| 纤维压缩强度Cf | 2 075 MPa |
| 基体拉伸强度Tm | 105 MPa |
| 基体压缩强度Cm | 241 MPa |
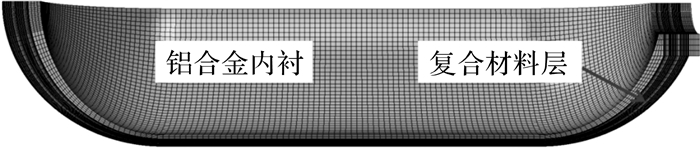
为了简化计算,本文建立了复合材料气瓶1/4有限元模型,有限元网格模型如图 5所示.采用ABAQUS三维实体单元C3D8R划分86 120个网格,且进一步加密网格使结果不再发生变化,表明网格适用于当前计算.对气瓶模型施加对称边界条件,内壁面施加压力载荷p,同时对气瓶整体结构施加操作温度载荷ΔT.
|
| 图 5 复合材料气瓶有限元网格模型 Fig.5 Finite element mesh model of the composite vessel |
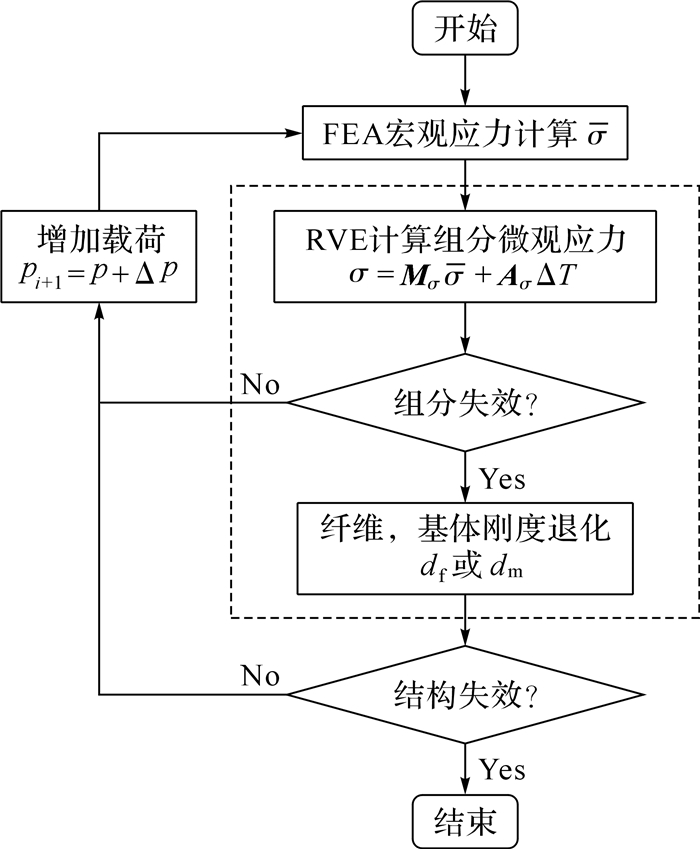
整个分析过程由ABAQUS有限元分析软件完成,计算流程如图 6所示.计算采用Newton-Raphson迭代算法,在每一分析步计算结构宏观应力;通过UMAT读取由应力放大因子计算得到的组分微观应力;依据微观力学失效准则判断组分是否失效,若单元有组分发生失效,则退化相应的材料刚度,更新材料刚度矩阵重新计算结构宏观应力,直到没有其他单元发生失效为止;增加载荷开始下一分析步.最终,当复合材料层因大范围失效而出现应变软化现象,且载荷不再增加,则停止计算,得到气瓶结构最终爆破压力.
|
| 图 6 基于微观力学的复合材料气瓶爆破失效有限元分析流程 Fig.6 Finite element analysis flow chart for implementing the micromechanics-based burst failure analysis of composite vessel |
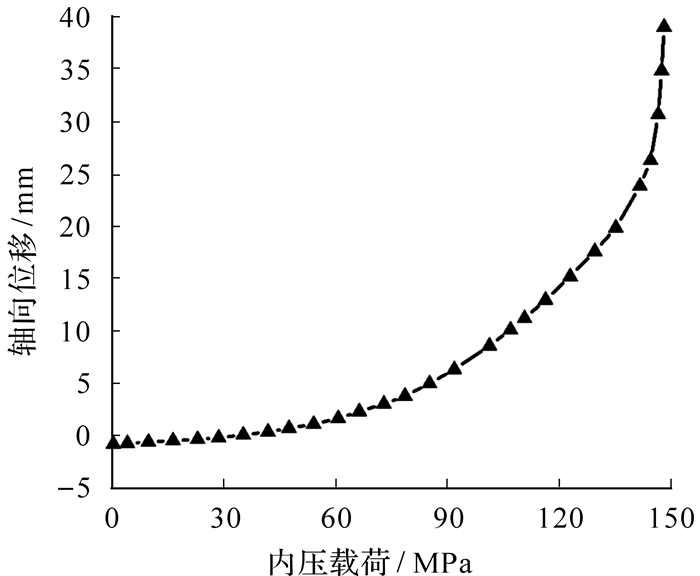
有限元计算得到气瓶结构的轴向位移—载荷曲线如图 7所示.当内压载荷为30 MPa左右时,位移曲线开始出现拐点,表明此时气瓶内衬层发生塑性屈服现象,气瓶结构承载能力降低;当内压继续增加达到60 MPa左右时,位移曲线斜率明显增大,表明此时复合材料层出现大面积基体失效引起材料刚度退化,复合材料层承载能力降低;当内压超过90 MPa以后,位移曲线斜率进一步增大,以致最后逐渐趋于垂直,表明此时复合材料层开始出现纤维失效,复合材料承载能力大幅度降低.最终气瓶轴向位移迅速增加但是内压几乎不再变化,说明气瓶在此处发生爆破,爆破压力为135.2 MPa.由此可见,复合材料纤维组分承担着结构的主要载荷,一旦纤维开始出现大面积失效时,复合材料结构便进入整体失效阶段而丧失承载能力,而基体组分失效会引起复合材料整体刚度降低,对结构承载能力的影响要小很多.
|
| 图 7 气瓶轴向位移曲线 Fig.7 Axial displacement curve of the vessel |
图 8是气瓶在不同内压下的Mises应力分布云图,由图分析可得气瓶筒体部分应力比封头部分大得多,且每层的最大应力都出现在筒体两侧.这是由于封头部分结构的特殊性,设计时将封头部分从与筒体相接处到顶部逐渐加厚,因此封头较筒体部分应力水平低;此外,筒体与封头相接存在应力集中,导致在筒体靠近封头部位出现最大应力,即爆破位置所在.此外,随着内压不断增大,气瓶应力变化呈现明显的非线性,这是由于铝内衬的塑性行为以及复合材料发生损伤以后刚度不断退化,导致应力重新分布.

|
| 图 8 气瓶Mises应力分布 Fig.8 Mises stress distribution of the vessel |
图 9为在不同内压下复合材料层纤维和基体组分失效情况.从图分析可以得到,当内压达到60 MPa时,基体开始发生失效;当内压进一步升高至90 MPa时,复合材料层已经出现大面积基体失效,并且开始出现纤维失效;内压超过120 MPa以后纤维失效加速,纤维失效单元由封头和筒体连接处迅速扩展至整个筒身,此时,失效单元使得结构应力重新分布,并导致局部应力集中,引起复合材料层大范围失效,复合材料进入应变软化阶段,运算最终不收敛,表明气瓶在此点发生爆破失效.

|
| 图 9 复合材料层纤维和基体失效 Fig.9 Failure patterns of fiber and matrix in composite layer |
为了进一步证明有限元分析的准确性,将模拟预测结果与气瓶爆破试验进行对比.气瓶爆破试验在多功能承压设备试验台上完成,试验介质采用洁净水,试验温度为常温.实验压力呈线性增加,直至气瓶出现破裂导致压力突然下降,实验结束.实验得到气瓶的爆破压力为138 MPa,与有限元预测值135.2 MPa吻合较好.气瓶爆破后外观如图 10所示[21],爆破发生在筒体靠封头处,断口处有大量纤维拉断和纤维拔出现象.试验中气瓶发生爆破的位置与有限元失效分析所预测结果一致,这进一步说明本文所提出的复合材料气瓶爆破压力预测方法是有效的,且准确度较高.

|
| 图 10 气瓶爆破试验后外观图 Fig.10 Vessel specimen after burst failure experiment |
复合材料储氢气瓶是高压储氢技术的重要实现方式,以其独特的优势而倍受青睐.然而,高压储氢的安全性能一直是人们关注的重中之重.复合材料气瓶的极限强度以及爆破压力研究一直是一项重要而有意义的课题.不同于传统复合材料分析方法,本文提出一种基于微观力学失效理论的复合材料气瓶强度和爆破压力预测方法:基于微观力学分析,采用基于组分微观应力的失效判断准则;同时引入损伤变量,根据不同组分失效情况退化材料刚度,进而模拟复合材料失效后的力学行为.分析过程由ABAQUS用户子程序(UMAT)实现,有限元预测结果与实验值吻合良好.本文研究内容可为复合材料高压气瓶的设计、制造提供理论指导,同时也可以为复合材料储氢气瓶在氢能储运的实际应用中提供有意义的参考.
| [1] |
冯雪, 沈俊, 田桂, 等.
复合材料压力容器在航天领域的应用研究[J]. 火箭推进 , 2014, 40 (4) : 35–42.
FENG Xue, SHEN Jun, TIAN Gui, et al. Research of composite over-wrapped pressure vessels for space application[J]. Journal of Rocket Propulsion , 2014, 40 (4) : 35–42. |
| [2] |
张雷枫, 朱斌, 郑传祥, 等.
轻质复合材料高压容器的研究和结构设计[J]. 化工装备技术 , 2007, 28 (1) : 9–13.
ZHANG Lei-feng, ZHU Bin, ZHENG Chuan-xiang, et al. Research and structural design of lightweight carbon fiber filament composite high pressure vessel[J]. Chemical Equipment Technology , 2007, 28 (1) : 9–13. |
| [3] | WANG L, ZHENG C, WEI S, et al. Thermo-mechanical investigation of composite high-pressure hydrogen storage cylinder during fast filling[J]. International Journal of Hydrogen Energy , 2015, 40 (21) : 6853–6859. DOI:10.1016/j.ijhydene.2015.04.018 |
| [4] |
习年生, 于志成, 陶春虎.
纤维增强复合材料的损伤特征及失效分析方法[J]. 航空材料学报 , 2000, 20 (2) : 55–63.
XI Nian-sheng, YU Zhi-cheng, TAO Chun-hu. Damage characterization and failure analysis in fiber reinforced composites[J]. Journal of Aeronautical Materials , 2000, 20 (2) : 55–63. |
| [5] | WANG L, ZHENG C, LUO H, et al. Continuum damage modeling and progressive failure analysis of carbon fiber/epoxy composite pressure vessel[J]. Composite Structures , 2015, 134 (15) : 475–482. |
| [6] | KURAISHI A, TSAI S W, LIU K K S. A progressive quadratic failure criterion, part B[J]. Composites Science and Technology , 2002, 62 (12) : 1683–1695. |
| [7] | BASU S, WAAS A M, AMBUR D R. Prediction of progressive failure in multidirectional composite laminated panels[J]. International Journal of Solids and Structures , 2007, 44 (9) : 2648–2676. DOI:10.1016/j.ijsolstr.2006.08.010 |
| [8] | APALAK Z G, APALAK M K, GENC M S. Progressive damage modeling of an adhesively bonded unidirectional composite single-lap joint in tension at the mesoscale level[J]. Journal of Thermoplastic Composite Materials , 2006, 19 (6) : 671–702. DOI:10.1177/0892705706067487 |
| [9] | PAL P, RAY C. Progressive failure analysis of laminated composite plates by finite element method[J]. Journal of Reinforced Plastics and Composites , 2002, 21 (16) : 1505–1513. DOI:10.1177/0731684402021016488 |
| [10] | TSAI S W, WU E M. A general theory of strength for anisotropic materials[J]. Journal of Composite Materials , 1971, 5 (1) : 58–80. DOI:10.1177/002199837100500106 |
| [11] | HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics , 1980, 47 (2) : 329–334. DOI:10.1115/1.3153664 |
| [12] | ORIFICI A C, HERSZBERG I, THOMSON R S. Review of methodologies for composite material modelling incorporating failure[J]. Composite Structures , 2008, 86 (1) : 194–210. |
| [13] | SODEN P D, HINTON M J, KADDOUR A S. A comparison of the predictive capabilities of current failure theories for composite laminates[J]. Composites Science and Technology , 1998, 58 (7) : 1225–1254. DOI:10.1016/S0266-3538(98)00077-3 |
| [14] |
郑晓霞, 郑锡涛, 缑林虎.
多尺度方法在复合材料力学分析中的研究进展[J]. 力学进展 , 2010, 40 (1) : 41–56.
ZHENG Xiao-xia, ZHENG Xi-tao, GOU Lin-hu. The research process on multiscale method for the mechanical analysis of composites[J]. Advances in Mechanics , 2010, 40 (1) : 41–56. |
| [15] | SUN X S, TAN V B C, TAY T E. Micromechanics-based progressive failure analysis of fibre-reinforced composites with non-iterative element-failure method[J]. Computers & Structures , 2011, 89 (11) : 1103–1116. |
| [16] | SPAHN J, ANDRA H, KABEL M, et al. A multiscale approach for modeling progressive damage of composite materials using fast Fourier transforms[J]. Computer Methods in Applied Mechanics and Engineering , 2014, 268 : 871–883. DOI:10.1016/j.cma.2013.10.017 |
| [17] | HA S K, JIN K K, HUANG Y. Micro-mechanics of failure (MMF) for continuous fiber reinforced composites[J]. Journal of Composite Materials , 2008, 42 (18) : 1873–1895. DOI:10.1177/0021998308093911 |
| [18] | KACHANOV L M. Rupture time under creep conditions[J]. International Journal of Fracture , 1999, 97 (1/4) : 11–8. DOI:10.1023/A:1018671022008 |
| [19] | MCCARTHY C T, O'HIGGINS R M, FRIZZELL R M. A cubic spline implementation of non-linear shear behaviour in three-dimensional progressive damage models for composite laminates[J]. Composite Structures , 2010, 92 (1) : 173–181. DOI:10.1016/j.compstruct.2009.07.025 |
| [20] | ZHENG C, LEI S. Mechanical analysis and optimal design for carbon fiber resin composite wound hydrogen storage vessel with aluminum alloy liner[J]. Journal of Pressure Vessel Technology , 2009, 131 (2) : 021204. DOI:10.1115/1.3027459 |
| [21] | ZHENG C, WANG L, LI R, et al. Fatigue test of carbon epoxy composite high pressure hydrogen storage vessel under hydrogen environment[J]. Journal of Zhejiang University SCIENCE A , 2013, 14 (6) : 393–400. DOI:10.1631/jzus.A1200297 |



