2. 智能物流装备山西省重点实验室, 山西 太原 030024
2. Shanxi Key Laboratory of Intelligent Logistics Equipment, Taiyuan 030024, China
磁流变制动器是一种新型的线控制动器,与传统液压制动器相比,具有能耗低、制动时间短、制动力矩可调可控、便于集成新型控制技术等优点,在健身器材、医疗器械、汽车制动系统等方面具有广泛的应用前景[1-3].
磁流变制动器主要由磁流变液、壳体以及浸在磁流变液中的制动盘构成.目前,磁流变制动器主要分为圆盘式[4]、圆筒式[5]和单线圈混合式[6].圆盘式磁流变制动器以制动盘的2个端面作为工作面,此种结构的制动器径向尺寸偏大,制动力矩较小,不适合在较高的转速下使用.圆筒式磁流变制动器以制动盘的圆柱面为工作面,虽然增加制动盘的轴向和径向尺寸均可增大制动器的制动力矩,但该种结构未能充分利用制动盘的端面.单线圈混合式磁流变制动器虽然同时以制动盘的端面和圆柱面为工作面,但是由于励磁线圈位于工作间隙正上方,制动盘圆柱面并不全是有效工作面,未能充分利用材料性能.为了获得更大的制动力矩,出现了多盘式磁流变制动器[7-8]、多线圈磁流变制动器[9-10].多盘式磁流变制动器也是利用制动盘的端面作为工作面,制动时多个制动盘的端面分别与定子相互作用,以此增大制动力矩.多线圈磁流变制动器通过增加线圈的数量来增加工作间隙磁感应强度,从而获得更大的制动力矩.但这2种制动器均存在结构复杂、加工装配困难、能量消耗大等问题.
针对上述问题,本文在单线圈混合式磁流变制动器的基础上进行改进,设计了一种将制动盘端面和圆柱面均作为有效工作面的双线圈旁置式磁流变制动器,在提高制动力矩的同时,使其具有较简单的结构.首先建立了双线圈旁置式磁流变制动器的力矩模型,提出了其磁路设计方法,并将其与单线圈混合式磁流变制动器进行有限元对比分析,然后在制动器外壳和端盖厚度相等的情况下,分析制动器长宽比变化对材料利用率、输出制动力矩的影响,最后在特定条件下,对制动器进行了多目标优化.
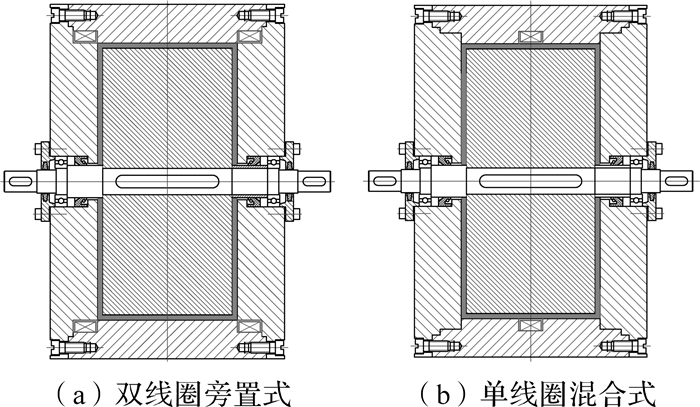
1 磁流变制动器结构双线圈旁置式与单线圈混合式磁流变制动器结构分别如图 1中(a),(b)所示.制动器由转轴、制动盘、外壳、端盖、励磁线圈、密封圈、隔磁圈几部分组成.转轴一端与液力耦合器相连,另一端与减速器相连,端盖位于制动盘两侧,并与外壳固连构成定子.制动盘与定子之间充满磁流变液,并通过密封圈进行密封,当线圈中无励磁电流通过时,即无外加磁场作用,磁流变液表现出牛顿流体特性,此时磁流变液在黏性作用下将产生很小的摩擦阻力,而当在线圈中通入励磁电流时,在定子与制动盘的工作间隙间会产生外加磁场,磁流变液瞬间由液态变为类固体状态,产生阻碍制动盘转动的阻力矩,从而达到制动目的.
|
| 图 1 磁流变制动器结构简图 Fig.1 Configuration of MR brakes |
与单线圈混合式磁流变制动器相比,所设计的双线圈旁置式磁流变制动器采用双线圈结构,励磁线圈线槽位于制动盘外的两个角上,制动时2个线圈中通异向电流,一方面使得制动盘的2个端面及圆柱面均为有效的工作面,减小磁路总磁阻,显著增加周面间隙内的磁感应强度;另一方面使得工作间隙内的磁场分布更加均匀.
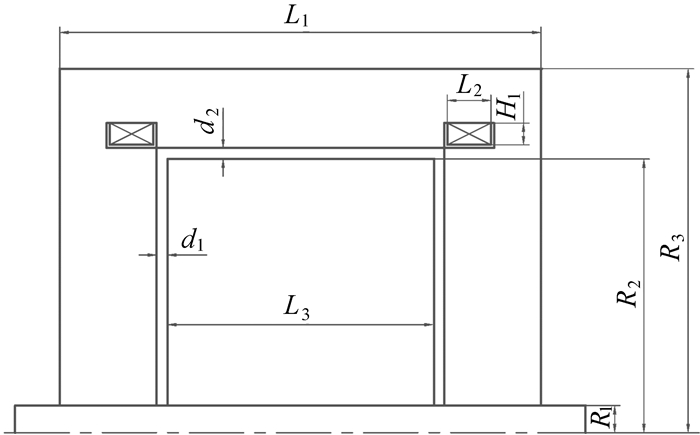
2 磁流变制动器磁路设计磁流变制动器设计的关键在于建立制动力矩与制动器基本结构参数、磁感应强度之间的关系.考虑到轴肩的高度较小,将制动器的结构进行简化,如图 2所示.其中,R1,R2分别为制动盘的最小和最大工作半径,R3为制动器半径,L1,L2,L3分别为制动器、线圈线槽、制动盘宽度,H1为线圈线槽厚度,d1,d2分别为端面工作间隙与周向工作间隙厚度.
|
| 图 2 双线圈旁置式几何结构参数示意图 Fig.2 Geometric structure dimensions sketch of MRB with double coils placed on the side housing |
磁流变液本构关系表征了磁流变液在不同磁场强度和剪应变率下剪切应力的变化.在稳态剪切的情况下,磁流变液的流变特性可由BingHam黏塑性模型和Herscher-Bulkley模型来描述.由于BingHam黏塑性模型不能解释磁流变液的剪切稀化现象和屈服应力对磁场强度的依赖性,当磁流变液工作于高剪切应变率时,会使得制动力矩计算值偏大[11],因此,选用Herscher-Bulkley模型来描述磁流变液的流变特性.其本构方程为[11]
| $\tau ={{\tau }_{\text{y}}}\left( H \right)+K\left( H \right){{\left( {\dot{\gamma }} \right)}^{n\left( H \right)}},$ | (1) |
式中:τ为磁流变液的剪切应力,τy为磁流变液的磁致屈服应力,H为磁场强度,K为磁流变液黏度,
在满足理想状态情况下,剪应变率可表示为[12]
| $\dot{\gamma }=\frac{\omega r}{d},$ | (2) |
式中:ω为制动盘角速度,r为磁流变液工作半径,d为工作间隙厚度.
2.2 制动力矩计算忽略由于密封所产生的摩擦阻力矩,双线圈旁置式磁流变制动器的制动力矩由两部分组成:制动盘端面与磁流变液之间的剪切力矩TD;制动盘圆柱面与磁流变液之间的剪切力矩TC.
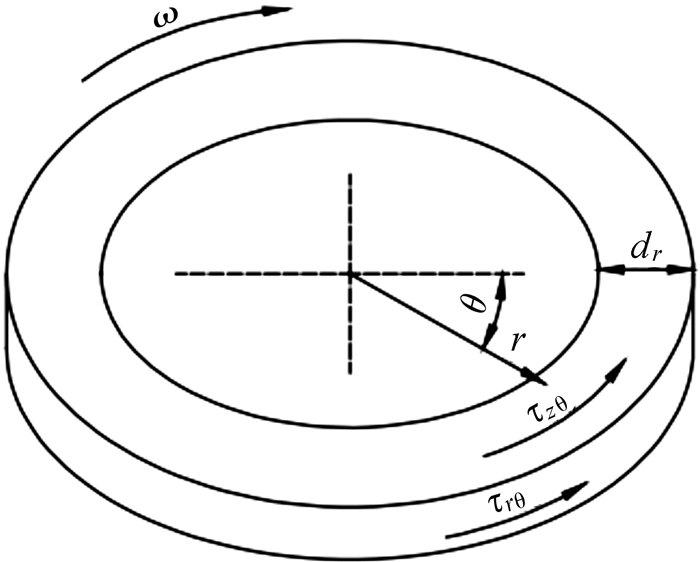
若在半径为r,宽为dr,高为dz的微圆环区域内工作,如图 3所示,则制动盘端面与磁流变液之间的剪切力矩为
| ${{T}_{\text{D}}}=2\text{ }\!\!\pi\!\!\text{ }\int_{{{R}_{1}}}^{{{R}_{2}}}{{{r}^{2}}{{\tau }_{z\theta }}\text{d}r}+2\text{ }\!\!\pi\!\!\text{ }\int_{0}^{d}{{{r}^{2}}{{\tau }_{r\theta }}\text{d}z}.$ | (3) |
|
| 图 3 磁流变液工作间隙微圆环单元 Fig.3 Annular ring element of MR fluid in the gap |
由于磁流变液的工作间隙d相对于制动盘的径向尺寸R1,R2及剪切应力τrθ相对剪切应力τzθ均很小,可以忽略不计,故(3)式可以简化为
| ${{T}_{\text{D}}}=2\text{ }\!\!\pi\!\!\text{ }\int_{{{R}_{1}}}^{{{R}_{2}}}{{{r}^{2}}{{\tau }_{z\theta }}\text{d}r}.$ | (4) |
联立(1)至(4)式可得制动盘单个端面与磁流变液之间的剪切力矩为
| $\begin{align} & {{T}_{\text{D}}}=\frac{2\text{ }\!\!\pi\!\!\text{ }}{3}\int_{{{R}_{1}}}^{{{R}_{2}}}{{{\tau }_{\text{yD}}}}\left( R_{2}^{3}-R_{1}^{3} \right)+ \\ & \ \ \ \ \ \ \ \ \frac{2K\text{ }\!\!\pi\!\!\text{ }\omega R_{2}^{4}}{\left( n+3 \right)d}{{\left( \frac{{{R}_{2}}\omega }{d} \right)}^{n-1}}\left[ 1-{{\left( \frac{{{R}_{1}}}{{{R}_{2}}} \right)}^{n+3}} \right], \\ \end{align}$ | (5) |
式中τyD为制动盘端面间隙平均磁致屈服应力.
制动盘圆柱面与磁流变液之间的剪切力矩为
| ${{T}_{\text{C}}}=\tau \cdot 2\text{ }\!\!\pi\!\!\text{ }R_{2}^{2}L.$ | (6) |
将式(1)代入式(6),可得
| ${{T}_{\text{C}}}=2\text{ }\!\!\pi\!\!\text{ }R_{2}^{2}L\left( {{\tau }_{\text{yc}}}+{{K}_{\text{C}}}{{\left( \frac{\omega {{R}_{2}}}{{{d}_{2}}} \right)}^{n}} \right),$ | (7) |
式中:τyC为制动盘周向有效工作间隙平均磁致屈服应力;L为制动盘圆柱面有效工作长度,对于双线圈旁置式,L=L3,对于单线圈混合式,L=L3-L2.
参考文献[13],磁流变液的流变特性可由下式描述:
| $Y={{Y}_{\infty }}+\left( {{Y}_{0}}-{{Y}_{\infty }} \right)\left( 2{{\text{e}}^{-{{B}_{\alpha }}_{_{\text{SY}}}}}-{{\text{e}}^{-2{{B}_{\alpha }}_{_{\text{SY}}}}} \right),$ | (8) |
式中:Y为磁流变液的流变参数,如动态屈服应力、黏度、流动系数等;Y0为磁流变液在零磁场条件下的流变参数;Y∞为磁流变液在磁饱和条件下的流变参数;αSY为流变参数的磁饱和指数;B为磁感应强度.
由于制动盘的2个端面均为工作面,故总的制动力矩为
| $T=2{{T}_{\text{D}}}+{{T}_{\text{C}}}.$ | (9) |
磁路设计优劣直接影响磁流变制动器的制动性能.磁流变制动器的结构决定着制动器内磁力线的走向,合理的磁路结构应尽可能提高工作间隙内磁感应强度,避免各材料磁饱和的发生,保证结构紧凑,充分发挥磁流变液的流变特性.本结构中制动盘和制动器外壳均采用磁导率高、矫顽力低、退磁性能好的DT4E型电磁纯铁,磁流变液采用MRF-132DG,磁流变液的流变参数参见文献[13].
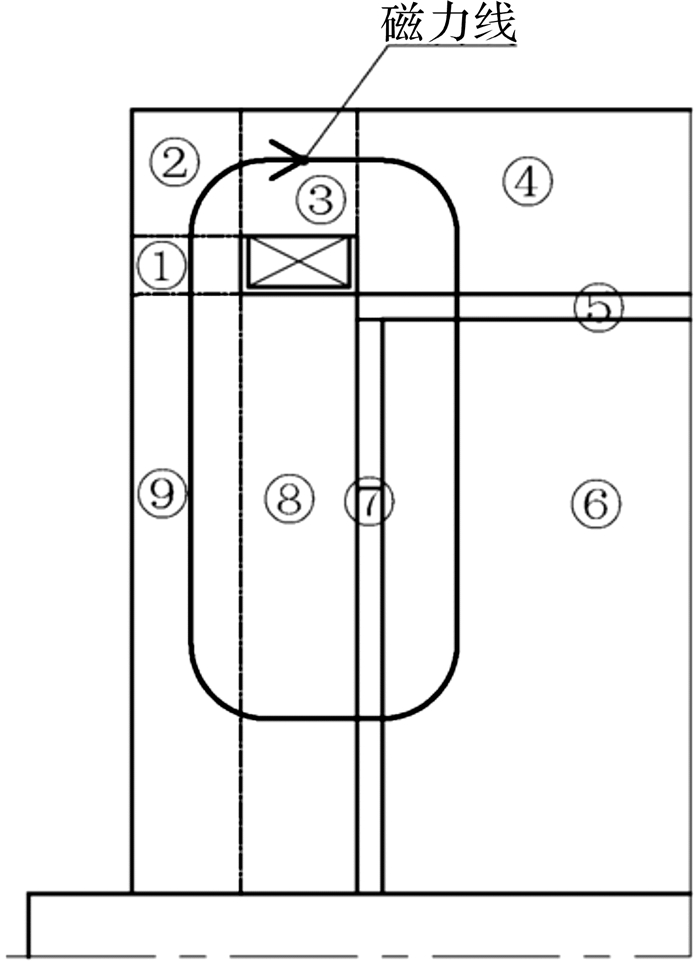
双线圈旁置式磁流变制动器的1/4磁路结构如图 4所示,将磁路划分为9个区域,其中区域5和区域7分别为制动盘周向和端面间隙处的磁流变液,其它区域为磁性材料区域,磁力线同时穿过制动盘端面和圆柱面区域形成闭合回路.
|
| 图 4 双线圈旁置式磁路模型示意图 Fig.4 Magnetic circuit model sketch of MRB with double coils placed on the side housing |
由于磁路中各处磁通量相等,根据磁路安培环路定律,有
| ${{B}_{1}}{{A}_{1}}={{B}_{2}}{{A}_{2}}=\cdots ={{B}_{9}}{{A}_{9}}=\mathit{\Phi} ,$ | (10) |
式中:Φ为穿过闭合截面A1,A2,…,A9的磁通量,B1,B2,…,B9为各区域平均磁感应强度.由于DT4E型电磁纯铁和磁流变液的磁导率呈高度非线性,通过多项式拟合,可得磁感应强度与磁场强度之间的关系.
对于DT4E型电磁纯铁:
| $H={{f}_{\text{D}}}\left( B \right).$ | (11) |
对于磁流变液:
| $H={{f}_{\text{MR}}}\left( B \right).$ | (12) |
根据图 4中闭合磁力线的走向,由基尔霍夫第二定律可得
| $\sum\limits_{k=1}^{9}{{{H}_{k}}{{l}_{k}}}=NI,$ | (13) |
式中:Hk为区域k的平均磁场强度;lk为区域k的平均磁路长度;N为励磁线圈匝数;I为励磁电流.
将式(10)至(12)代入式(13),有
| $\sum\limits_{k=1,k\ne 5,7}^{9}{{{f}_{\text{D}}}}\left( \frac{{{A}_{7}}}{{{A}_{k}}}{{B}_{7}} \right){{l}_{k}}+\sum\limits_{k=5,7}{{{f}_{\text{MR}}}}\left( \frac{{{A}_{7}}}{{{A}_{k}}}{{B}_{7}} \right){{l}_{k}}=NI.$ | (14) |
由于函数fD与fMR均为单调函数,式(14)可由数值方法进行求解.
基于磁路欧姆定律,工作间隙d越小,工作间隙内的磁感应强度越大且越均匀,但d过小会使得残留力矩过大且安装制造困难,故求解时,工作间隙取1.0 mm,根据所需制动力矩,确定端面和周面间隙内的平均磁感应强度.结合式(9)至式(14)反复试算,初步确定各参数的初始设计值如表 1所示.
| mm | |||||||||
| 参数 | R1 | R2 | R3 | L1 | L2 | L3 | H1 | d1 | d2 |
| 量值 | 10 | 96 | 112 | 92 | 12 | 41 | 6 | 1 | 1 |
通过对双线圈旁置式磁流变制动器进行磁路设计,获得了制动器的主要结构参数,为制动器制动性能有限元分析和优化提供了基础数据.
3 磁流变制动器制动力矩分析 3.1 初始参数有限元分析为进一步验证初始设计方案的正确性,深入了解双线圈旁置式与单线圈混合式磁流变制动器的制动性能差异,在主要结构参数和磁动势相同的情况下,按表 1中的尺寸建立双线圈旁置式与单线圈混合式磁流变制动器的有限元分析模型.由于结构的对称性,将结构简化为二维轴对称模型,对2种结构形式的磁流变制动器进行对比分析,结果如图 5和图 6所示.
|
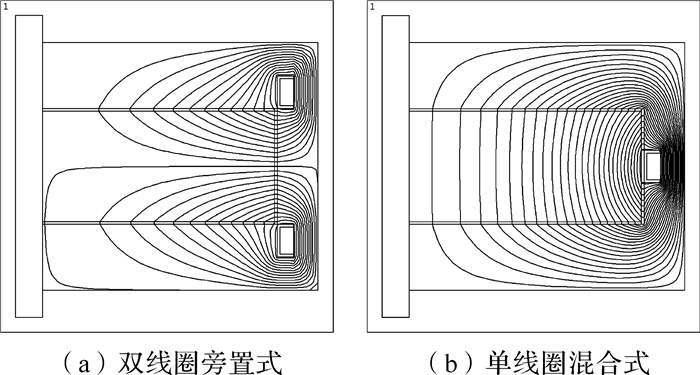
| 图 5 磁力线分布图 Fig.5 Distribution of magnetic lines |

|
| 图 6 磁感应强度分布云图 Fig.6 Nephogram of magnetic flux density distribution |
图 5、图 6分别为双线圈旁置式与单线圈混合式磁流变制动器的磁力线与磁感应强度分布情况.由图可知,双线圈旁置式的磁力线分布与初始预先设计要求相一致,先后垂直穿过制动盘的端面间隙与周向间隙,只是与传统单线圈混合式相比,其磁力线相对较疏.2种结构形式的最大磁感应强度均出现在励磁线圈线槽底部,其最大磁感应值近乎相等,约2.1 T,小于DT4E型电磁纯铁的饱和磁感应强度,满足设计要求.为进一步分析2种结构形式的磁流变制动器工作间隙内磁感应强度分布情况,分别绘制出端面与周向工作间隙内的磁感应强度沿路径的分布情况,如图 7所示.
|
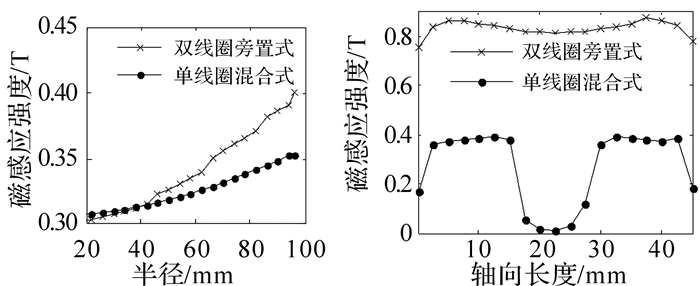
| 图 7 磁感应强度沿路径分布 Fig.7 Distribution of magnetic flux density along path |
由图 7可知,双线圈旁置式磁流变制动器的端面和圆柱面均为有效工作面,端面间隙内磁感应强度沿径向逐渐增加,周向间隙磁感应强度近似均匀分布,工作间隙内最大磁感应强度值为0.82 T,接近但小于磁流变液的饱和磁感应强度0.85 T,符合磁路设计要求.单线圈混合式磁流变制动器在周向间隙线圈线槽处磁感应强度近乎为零,周向圆柱面并不全是有效工作面,端面间隙磁感应强度沿径向也逐渐增加,但增加速度要明显小于双线圈旁置式.
有限元数值分析结果如表 2所示,从表 2可知,双线圈旁置式在端面间隙内的平均磁感应强度与单线圈混合式大致相等,在周向间隙内平均磁感应强度要远大于单线圈混合式.在体积和磁动势相同的条件下,双线圈旁置式磁流变制动器的总制动力矩为241.1 N·m,远高于单线圈混合式的161 N·m,这是因为双线圈旁置的结构布置形式使得制动盘的圆柱面均为有效工作面,中间不存在磁感应强度为零的区域,在端面间隙内磁感应强度略有增加的同时,显著增加了周面间隙内的磁感应强度,从而极大地提高了磁流变制动器的输出制动力矩.但是,双线圈旁置式在端面间隙内的平均磁感应强度仍然较低,未能充分发挥磁流变液的流变性能,还有待进一步的优化改进.
| 比较项 | 双线圈 旁置式 |
单线圈 混合式 |
| 端面间隙平均磁感应强度B1/T | 0.342 | 0.324 |
| 周面间隙平均磁感应强度B2/T | 0.821 | 0.355 |
| 端面间隙磁致力矩TD/(N·m) | 111 | 105.7 |
| 周面间隙磁致力矩TC/(N·m) | 130.1 | 55.3 |
| 总制动力矩T/(N·m) | 241.1 | 161.0 |
从上述分析可知,在主要结构参数和磁动势相同的情况下,双线圈旁置式磁流变制动器较单线圈混合式磁流变制动器具有较大的有效工作面积,能输出更大的制动力矩,充分利用了材料的效能.但是,要让双线圈旁置式磁流变制动器处于最佳工作状态,还需合理分配制动器的轴向和径向尺寸.
保持制动器外壳厚度、端盖厚度以及励磁电流为定值,得到不同制动器宽度条件下,制动器端面工作间隙和周向工作间隙内的平均磁感应强度、制动器输出制动力矩随制动器长宽比R3/L1的变化情况,分别如图 8和图 9所示.
|
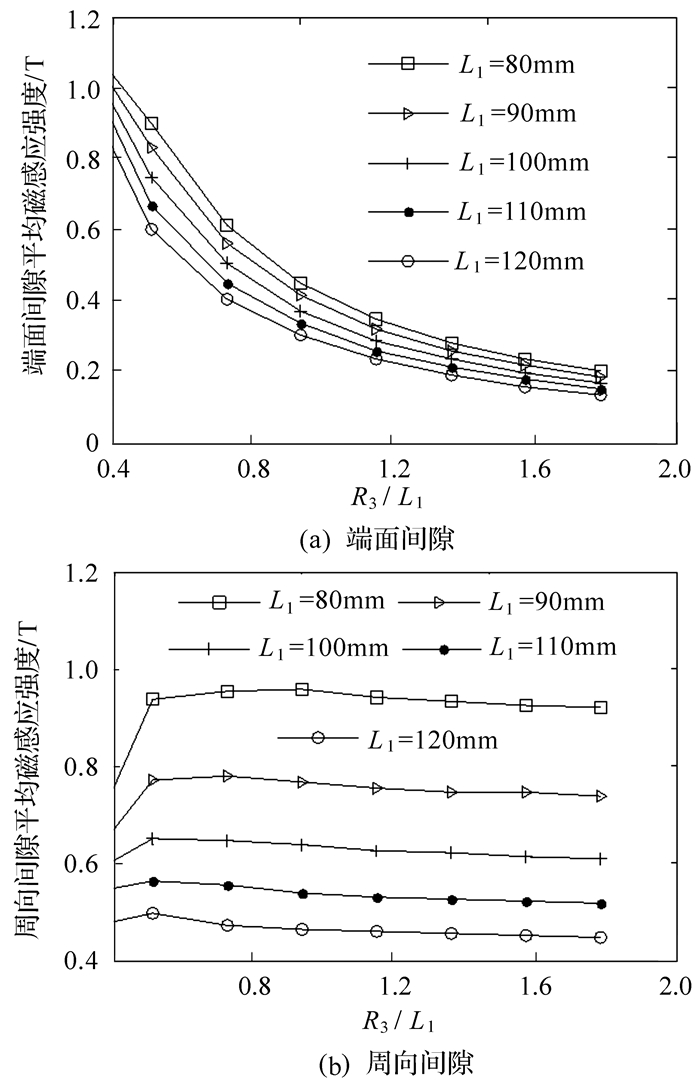
| 图 8 平均磁感应强度与长宽比R3/L1的关系 Fig.8 Relationship between average magnetic flux density and length-width ratio R3/L1 |
|
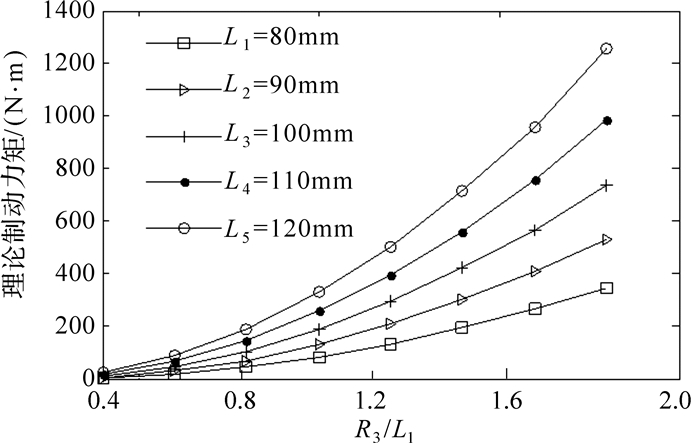
| 图 9 输出制动力矩与长宽比R3/L1的关系 Fig.9 Relationship between output brake torque and length-width ratio R3/L1 |
从图 8可以看出,在L1固定不变的情况下,随着长宽比R3/L1的增加,图 4区域7中的磁阻增加,导致了端面间隙内的平均磁感应强度逐渐减小;当0.4 < R3/L1 < 0.6时,周向间隙内平均磁感应强度随R3/L1的增大而增加,当R3/L1>0.6后,周向间隙内平均磁感应强度基本保持不变.
从图 9可以看出,当L1保持不变时,随着R3/L1的增大,虽然端面间隙平均磁感应强度有所降低,但是由于有效工作面积和制动力矩的力臂增加,理论输出制动力矩仍然快速增加;当R3/L1为定值时,随着L1的增大,端面间隙和周向间隙内的平均磁感应强度均逐渐减小,但是由于轴向有效工作面积的增大,理论输出制动力矩仍缓慢增加.
综合图 8、图 9可以得出,虽然理论输出制动力矩随轴向和径向尺寸的增加而增大,但是当L1>100 mm时,周向间隙内平均磁感应强度低于0.6 T,当R3/L1>1.2时,无论L1取何值,端面间隙平均磁感应强度均小于0.35 T,这样严重降低了磁流变液材料的利用率,使得磁流变制动器的结构笨重,因此合理的轴向和径向尺寸以及长宽比范围分别为80 mm < L1 < 100 mm,0.6 < R3/L1 < 1.2.
4 磁流变制动器多目标优化为进一步提高磁流变制动器的输出制动力矩,实现磁流变制动器的轻量化,以磁流变制动器质量最小、输出制动力矩最大为优化目标,选取关键结构尺寸参数为设计变量,建立其参数化优化模型.结合双线圈旁置式磁流变制动器轴向和径向尺寸范围,经过反复试算得到设计变量的取值范围如表 3所示.
| 设计变量 | Xmin | Xmax |
| 制动半半径R2/mm | 35 | 130 |
| 制动器半径R3/mm | 50 | 160 |
| 制动器宽度L1/mm | 80 | 100 |
| 线圈槽宽度L2/mm | 8 | 18 |
| 制动盘宽度L3/mm | 25 | 80 |
| 线圈线槽厚度H1/mm | 5 | 10 |
根据实际加工及安装制造要求,多目标优化问题的约束条件为
| $\left\{ \begin{align} & {{B}_{1\max }}<0.85\text{T}, \\ & {{B}_{2\max }}<2.1\text{T}, \\ & 0.6<{{R}_{3}}/{{L}_{1}}<1.2, \\ & \frac{{{L}_{1}}-{{L}_{3}}}{2}>{{d}_{1}}+{{L}_{2}}+5, \\ & {{R}_{3}}-{{R}_{2}}>{{d}_{2}}+{{H}_{1}}+5, \\ \end{align} \right.$ |
式中:B1max和B2max分别为工作间隙磁流变液和DT4E单元上的最大磁感应强度.
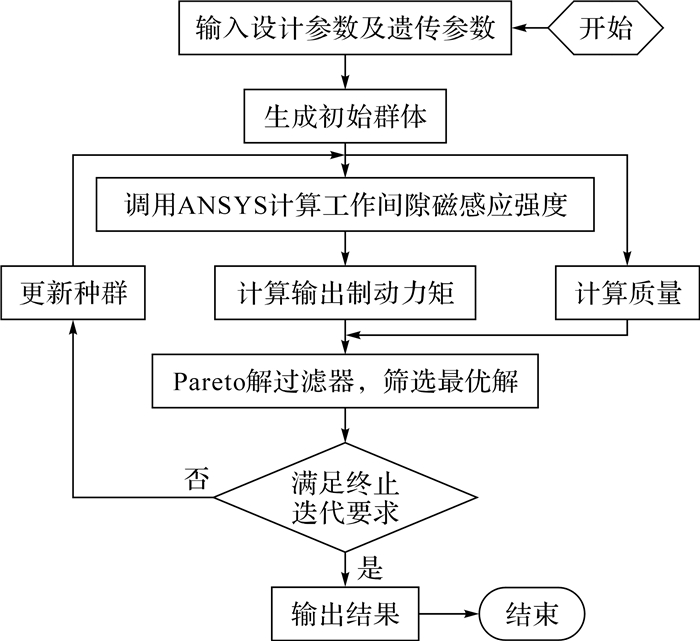
运用基于有限元分析和多目标遗传算法的联合优化仿真方法对建立的优化模型进行优化.其中,遗传控制参数:种群规模为90,交叉概率为0.8,变异概率为0.2,最大进化代数为200.具体优化流程如图 10所示.
|
| 图 10 双线圈旁置式磁流变制动器多目标优化流程图 Fig.10 Multi-objective optimization flow chart of MRB with double coils placed on the side housing |
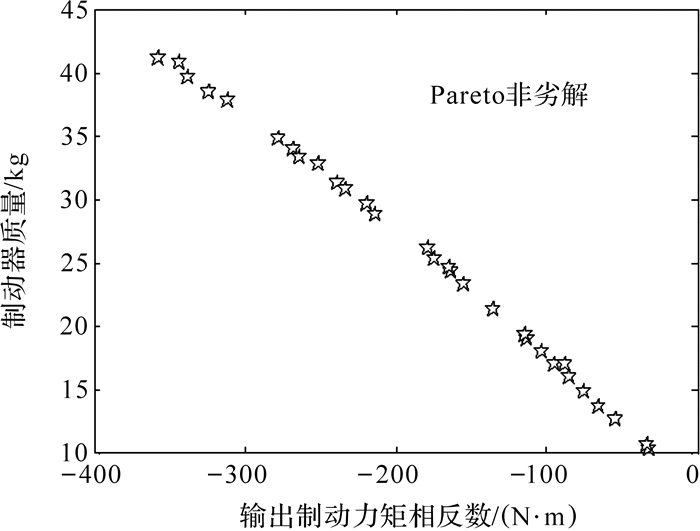
经过190代运算,得到了磁路结构的Pareto最优解集,如图 11所示.
|
| 图 11 磁路结构的Pareto最优解集 Fig.11 The Pareto optimal solution set of magnetic circuit structure |
由图 11可知,制动力矩的增加是以制动器质量的增加为代价.运用组合赋权法[14],以Pareto解集为决策矩阵,以制动器质量和输出制动力矩为决策属性,得到制动器质量和输出制动力矩的权重,利用TOPSIS法[15]对Pareto解集对应方案的加权属性进行排序,并从中挑选出最优的磁路结构参数方案,优化前后各主要参数对比情况如表 4所示.
| 变量含义 | 优化前 | 优化后 |
| 制动盘半径R2/mm | 96 | 93 |
| 制动器半径R3/mm | 112 | 109 |
| 制动器宽度L1/mm | 92 | 99.3 |
| 线圈槽宽度L2/mm | 12 | 8.3 |
| 制动盘宽度L3/mm | 41 | 59.3 |
| 线圈线槽厚度H1/mm | 6 | 5.3 |
| 端面间隙平均磁感应强度B1/T | 0.342 | 0.387 6 |
| 周向间隙平均磁感应强度B2/T | 0.821 | 0.620 |
| 端面磁致力矩TD/(N·m) | 111 | 111.8 |
| 周面磁致力矩TC/(N·m) | 130.1 | 155.21 |
| 制动器长宽比R3/L1 | 1.22 | 1.1 |
| 总制动力矩T/(N·m) | 241.1 | 267.1 |
| 制动器质量m/kg | 34.5 | 34.0 |
从表 4可以看出,优化后制动器端面间隙平均磁感应强度提高了13%,而周向间隙平均磁感应强度降低了约24%.但是由于优化后,制动器长宽比略有下降,制动器的径向尺寸减小,轴向尺寸增加,使得制动器在质量基本保持不变的情况下,总制动力矩增加了约11%,材料利用率得到了显著提高.
5 结论1)与单线圈混合式磁流变制动器相比,提出的双线圈旁置式磁流变制动器能产生更大的制动力矩,更能充分利用材料的性能,且结构简单,易加工制造.
2)提出了适用于双线圈旁置式磁流变制动器的力矩模型及磁路设计方法,并通过有限元分析进行了验证.
3)双线圈旁置式磁流变制动器的宽度及长宽比的合理取值范围分别为80~100 mm,0.6~1.2.
4)由多目标优化结果可知,优化后在制动器质量基本不变的情况下,制动力矩提高了约11%,进一步提高了材料的利用率.
| [1] | GUDMUNDSSON K H, JONSDOTTIR F, THORSTEINSSON F. A geometrical optimization of a magneto-rheological rotary brake in a prosthetic knee[J]. Smart Materials and Structures , 2010, 19 (19) : 335–341. |
| [2] | SENKAL D, GUROCAK H, KONUKSEVEN E I. Passive haptic interface with mr-brakes for dental implant surgery[J]. Presence: Teleoperators and Virtual Environments , 2011, 20 (3) : 207–222. DOI:10.1162/PRES_a_00045 |
| [3] | MA L, YU L, SONG J, et al. Design, testing and analysis of a novel multiple-disc magnetorheological braking applied in vehicles[R]. SAE Paper No.2014-01-2534, SAE International Congress, Brake Colloquium & Exhibition-32nd Annual Burlingame, 2014. |
| [4] |
李志华, 喻军, 曾宁, 等.
圆盘式磁流变制动器仿真优化设计[J]. 农业机械学报 , 2015, 10 (46) : 364–369.
LI Zhi-hua, YU Jun, ZENG Ning, et al. Simulation and optimization design of disc-type magnetorheological brake[J]. Transactions of the Chinese Society for Agricultural Machinery , 2015, 10 (46) : 364–369. |
| [5] |
李志华, 林阳, 朱丰友, 等.
圆筒式磁流变制动器结构与磁路耦合的优化设计[J]. 工程设计学报 , 2009, 16 (4) : 261–265.
LI Zhi-hua, LIN Yang, ZHU Feng-you, et al. Optimization design of structure and magnetic circuit for drum-type magnetorheological brake[J]. Chinese Journal of Engineering Design , 2009, 16 (4) : 261–265. |
| [6] | SONG B K, NGUYEN Q H, CHOI S B, et al. The impact of material and design on magnetorheological brake performance[J]. Smart Materials and Structures , 2013, 22 (10) : 426–437. |
| [7] | WANG D M, HOU Y F, TIAN Z Z. A novel high-torque magnetorheological brake with a water cooling method for heat dissipation[J]. Smart Materials and Structures , 2013, 22 (22) : 25019–25029. |
| [8] | NGUYEN Q H, CHOI S B. Optimal design of an automotive magnetorheological brake considering geometric dimensions and zero-field friction heat[J]. Smart Materials and Structures , 2010, 19 (11) : 161–167. |
| [9] | KIKUCHI T, KOBAYASHI K. Design and development of cylindrical MR fluid brake with multi-coil structure[J]. Journal of System Design and Dynamics , 2011, 5 (7) : 1471–1484. DOI:10.1299/jsdd.5.1471 |
| [10] | SHIAO Y, NGUYEN Q A, ZHANG Z. Design and experiment of a new magnetorheological brake[J]. International Journal of Applied Electromagnetics and Mechanics , 2015, 48 (4) : 1–18. |
| [11] | FARJOUD A, YAHDATI N, FAH Y F. Mathematical model of drum-type MR brakes using herschel-bulkley shear model[J]. Journal of Intelligent Material Systems and Structures , 2008, 19 (5) : 565–572. |
| [12] |
沙树静, 张贺, 张和权.
双盘式磁流变制动器的结构设计和性能研究[J]. 机械设计与制造 , 2015 (11) : 100–102.
SHA Shu-jing, ZHANG He, ZHANG He-quan. Structure design and performance research of dual disk magnetorheological brake[J]. Machinery Design & Manufacture , 2015 (11) : 100–102. |
| [13] | SOHN J W, JEON J, NGUYEN Q H, et al. Optimal design of disc-type magneto-rheological brake for mid-sized motorcycle: experimental evaluation[J]. Smart Materials and Structures , 2015, 24 (8) : 209–223. |
| [14] |
李楠, 王明辉, 马书根, 等.
基于多目标遗传算法的水陆两栖可变形机器人结构参数设计方法[J]. 机械工程学报 , 2012 (17) : 10–20.
LI Nan, WANG Ming-hui, MA Shu-gen, et al. Mechanism-parameters design method of an a mphibious transformable robot based on multi-objective genetic algorithm[J]. Journal of Mechanical Engineering , 2012 (17) : 10–20. |
| [15] | HUANG J. Combining entropy weight and TOPSIS method for information system selection[C]//Cybernetics and Intelligent Systems, 2008 IEEE Conference on. IEEE, 2008: 1281-1284. |



