赛车车架是整车的承载基体,车架的性能直接影响着赛车的性能,车架的轻量化设计不仅能大幅减轻整车质量,而且能很好地改善赛车的操纵性[1].结构的拓扑优化是轻量化设计方法中最重要的方法之一,被广泛地应用到结构设计的初期阶段,在整车的轻量化设计中发挥了重要的作用[2].然而,在实际行驶过程中车架会受到各种工况的考验,因此车架结构的拓扑优化设计是一个多工况下的拓扑优化问题.
对于多工况下的拓扑优化设计,一般的处理方法是采用线性加权方法将多工况这个多目标问题转化为单目标问题求解,扶原放等[3-4]采用线性加权方法将各个工况下车架刚度最大转化为各工况的加权柔度最小的单一目标问题.但是如果目标函数中至少有2个目标存在不一致性,线性加权方法就不能确保得到所有的Pareto最优解[5].而折衷规划法就能够很好地解决上述问题,其思想是将多目标的折衷解视为距每一个目标函数的理想解距离最小的矢量,因而实现了单一目标的转化.兰凤崇等[5-7]运用折衷规划法定义了整车各个工况下车身结构静态刚度和动态振动频率最大化的综合目标函数,并在此基础上完成了车身结构的优化设计,验证了折衷规划法的有效性.但是,无论采用哪种方法进行多目标转化,都会遇到如何分配各个工况权重比值的问题,这个问题的解决与否直接影响着最终优化结果的质量.
代理模型结合遗传算法寻找最优解的方法,是一种通过构造数学模型来代替原有有限元模型并能充分利用遗传算法全局搜索的优越性的方法,在结构的多目标优化中被广泛应用.该方法一方面可以大大提高优化效率,另一方面,相当精度的代理模型能够很好地保证优化结果有较高的精度.陈国栋等[8]采用代理模型结合遗传算法的方法对车身结构进行优化,验证了该方法在多目标优化中的高效性;洪煌杰等[9-10]将该方法应用到空投气囊和飞机飞翼这种更复杂的结构的多目标优化设计中,结果显示,该方法能够很好地解决多目标优化寻优问题,结果满足设计要求.
基于此,通过借助折衷规划法构建多个工况下的车架拓扑优化综合目标函数模型,以各个工况的权重比为变量,以综合目标函数最优为优化目标,并引入代理模型和遗传算法(NSGA-Ⅱ)对目标函数模型中的各个工况的权重比进行最优搜索.将多目标优化方法中的代理模型结合遗传算法的方法巧妙地应用于多工况拓扑优化中各个工况权重比寻优的问题中,不仅验证了所采用方法的有效性,同时很好地解决了多目标转化过程中各个工况权重比的分配这一优化难题.
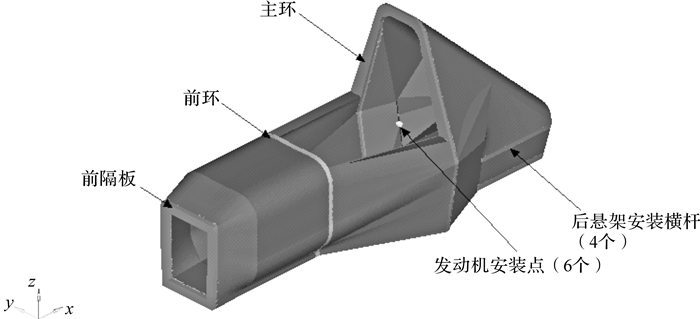
1 车架多工况下拓扑优化设计 1.1 设计问题描述在进行结构优化设计之前,需参考赛车车身结构模型进行设计区域的填充.构建拓扑空间,并在考虑方程式赛车车架设计规范的基础上[11],在拓扑优化中的模型设定了不可设计区域,如图 1所示.
|
| 图 1 赛车车架拓扑空间模型(标记部分为不可设计区域) Fig.1 Topological space model of racing car frame (marked parts are not devisable) |
车架的前后悬架采用双横臂悬架,车架材料弹性模量为210 GPa,泊松比为0.3,密度为7.85 g/cm3.为了提高计算精度,有限元模型网格采用退化的四面体单元即十节点四面体单元.为保证车身结构设计的对称性,在Hypermesh中对模型进行了纵向对称设置.同时,为了避免最终拓扑结构中出现细小的传力路径,保证结构最小尺度不至于太小,设置最小拓扑结构为20 mm,最大拓扑结构为60 mm.
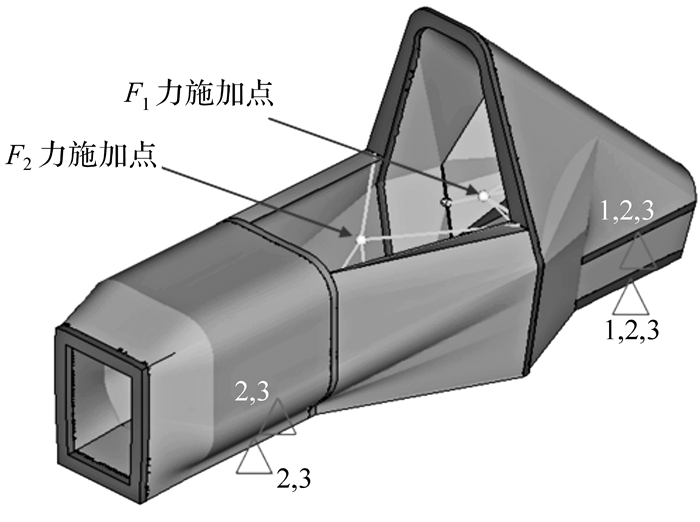
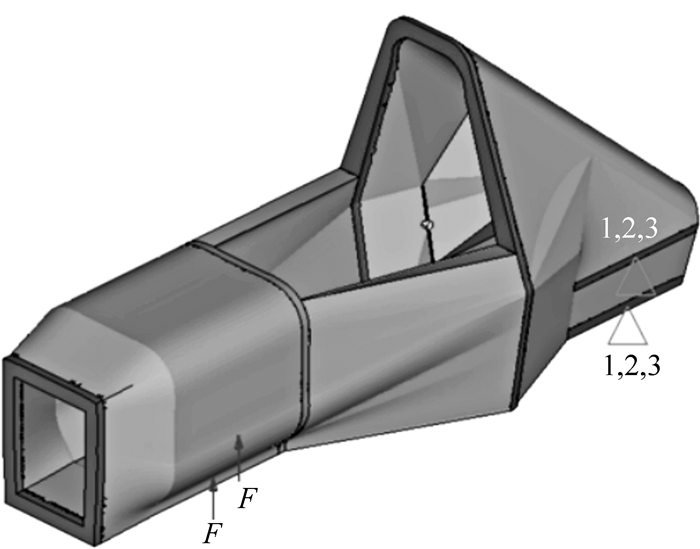
1.2 多工况分析选取赛车在实际使用过程中常遇到的工况进行分析, 即:弯曲工况、扭转工况、加速工况、制动工况、转弯工况.为了简化计算,取悬架上下安装点的中点为简化点,前后悬架安装点简化为4个,分别在简化点施加约束与载荷[11-12].成员和发动机的重量通过RBE3单元分别加载在座椅安装处和6个发动机安装点处,各个工况下约束和加载情况如表 1所示,边界条件设置如图 2和图 3所示.同时,赛车设计规则明确规定:车架主环最高位置处最大位移不得超过25 mm,车架重要安装硬点的变形范围要控制在合理的范围内.在此,限制赛车手质量加载点处总位移上限为5 mm,发动机安装点处总位移上限为3 mm,车架顶端总位移约束为25 mm[13].约束设置中1,2,3分别代表x,y,z方向的平动自由度.
| 序号 | 拓扑工况 | 约束设置 | 载荷设置/N |
| 1 | 弯曲工况 | 后悬约束1,2,3,前悬约束2,3 | F1,z=975,F2,-z=900 |
| 2 | 扭转工况 | 后悬约束1, 2, 3,前悬无约束 | F左,z=456,F右,-z=456 |
| 3 | 加速工况 | 后悬约束1, 2, 3,前悬约束2, 3 | F1,x=1 194,F2, x=1 103 |
| 4 | 制动工况 | 后悬约束1, 2, 3,前悬约束2, 3 | F1, -x=1365,F2, -x=1260 |
| 5 | 转弯工况 | 后悬约束1, 2, 3,前悬约束2, 3 | F1, y=1463,F2, y=13 500 |
|
| 图 2 弯曲、加速、制动和转弯工况边界条件设置 Fig.2 Boundary conditions of bending, accelerating, braking and turning conditions |
|
| 图 3 扭转工况边界条件设置 Fig.3 Boundary conditions of twist conditions |
在静态问题中,结构的拓扑优化问题是通过最小化结构的平均柔度l(u)来实现的,由总应变能通过下式定义[14]:
| ${{F}_{s}}\left( \upsilon \right)=\frac{1}{2}a\left( \upsilon ,\upsilon \right)-l\left( \upsilon \right),\ \ \ \ \forall \upsilon \in K.$ | (1) |
式(1)等同于以下表达式:
| ${{F}_{s}}\left( u \right)=\frac{1}{2}a\left( u,u \right)-l\left( u \right)=-\frac{1}{2}l\left( u \right),$ | (2) |
式中:K为可行解组成的空间,l(v)为负载的线性形式,a(v, v)表示单元由虚位移v在v方向产生的能量,a(u, u)表示单元由虚位移u在u方向产生的能量.通过式(1)和式(2)可得,结构的平均柔度最小的问题等价于结构的应变能最大的问题.
在实现过程中,将车架的结构刚度问题转化为结构的平均柔度(compliance)问题,即单元的总应变能问题.借助折衷规划法及功效函数法建立以结构体积分数上限为0.3为约束、以柔度最小为目标的多刚度拓扑优化综合目标函数模型[5]:
| $\left. \begin{align} & \underset{\mathit{\pmb{\rho}} ={{\left( {{\mathit{\pmb{\rho}} }_{1}},\cdots ,{{\rho }_{n}} \right)}^{\text{T}}}}{\mathop{\min C\left( \rho \right)}}\,={{\left[ \sum\limits_{i=1}^{l}{\omega _{i}^{p}}{{\left( \frac{{{C}_{i}}\left( \mathit{\pmb{\rho}} \right)-C_{i}^{\min }}{C_{i}^{\max }-C_{i}^{\min }} \right)}^{p}} \right]}^{\frac{1}{p}}}, \\ & \text{s}\text{.t}\text{.}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{0<}{{\rho }_{j}}<1, \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ V\left( \mathit{\pmb{\rho}} \right)-\bar{V}\le 0, \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=1,2,\cdots ,l;j=1,2,\cdots ,n. \\ \end{align} \right\}$ | (3) |
式中:ρ1, ρ2, …, ρn为设计变量;n为单元总数;l为载荷工况总数;ωi为第i个工况的权重比;p为惩罚因子,p≥2;Ci(ρ)为第i个工况的柔度目标函数;V为结构的体积分数要求;Cimax及Cimin为第i个工况柔度目标函数的最大值和最小值,分别通过对填充拓扑空间的结构和对优化前原始结构进行分析得到.
1.4 各个工况权重比分配优化方法从式(3)可以看到各个工况下的柔度权重比ωi(第i个工况的柔度权重比)直接影响着综合目标函数值,不同的方法会得到不同的分配结果,这就导致优化具有很大的自由度.因此,如何恰当地选取各个工况的权重比是获得更优综合目标函数值中急需解决的问题.
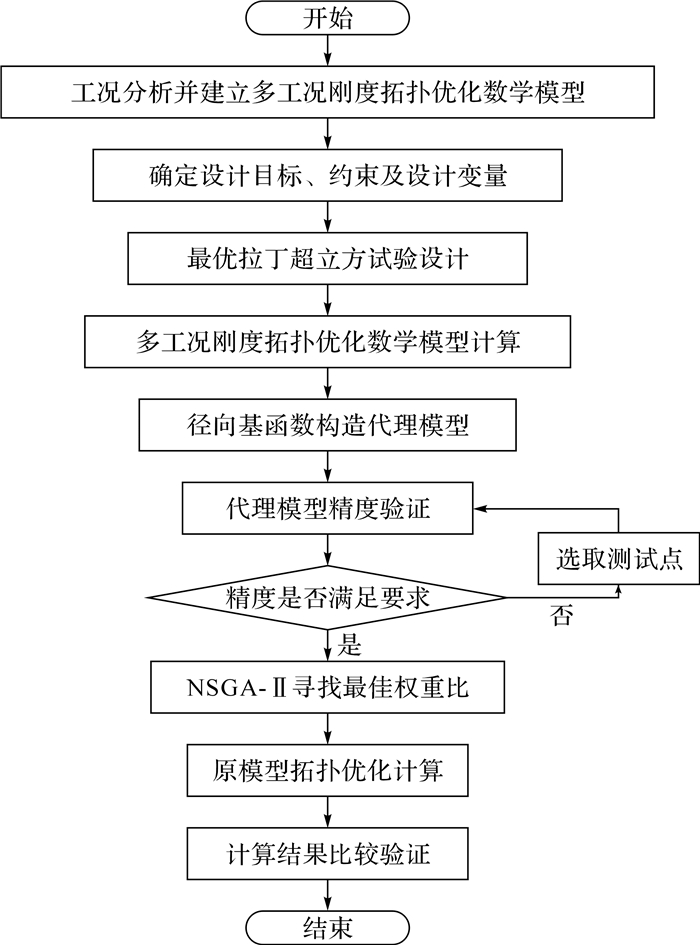
针对此问题,通过结合径向基代理模型和遗传算法对多工况下拓扑优化中各个工况权重比的分配问题进行研究.首先,对多目标问题进行合理转化,采用折衷规划法建立同时考虑多个工况下车架刚度的拓扑优化综合目标函数模型;然后,考虑到实际有限元模型的复杂性及计算的低效性,构造径向基函数代理模型代替复杂的有限元模型,并结合遗传算法(NSGA-Ⅱ)进行最佳工况权重比组合的寻找,获得各个工况的最佳权重比;最后,将获得的各个工况的最佳权重比代入有限元模型中进行拓扑优化计算.在上述流程计算结果的基础上,将各个工况下车架柔度计算结果与参考方法进行比较验证.主要过程流程图如图 4所示.
|
| 图 4 各工况权重比分配优化方法的主要过程流程图 Fig.4 The main process flow chart of the weight ratio distribution optimization method for respective condition |
最优拉丁超立方试验设计(optimal latin hypercube design,OLHD)是在LHD的基础上增加了优化准则,能较好地满足样本采集的投影均匀性和空间均布性[8].因此,采用最优拉丁超立方试验设计方法,将5个工况的权重比作为取样对象,样本数为25,并将采样结果进行归一化处理.最后将5个工况的权重比代入拓扑模型中进行计算,获得各个取值样本点的综合目标函数值,样本点及输出目标值如表 2所示.
| 序号 | 弯曲工况A | 扭转工况B | 加速工况C | 制动工况D | 转弯工况E | 目标函数值 |
| 1 | 0.12 | 0.26 | 0.14 | 0.30 | 0.18 | 7.852 7×10-2 |
| 2 | 0.15 | 0.16 | 0.22 | 0.36 | 0.11 | 6.943 1×10-2 |
| 3 | 0.32 | 0.11 | 0.17 | 0.22 | 0.17 | 7.541 6×10-2 |
| 4 | 0.27 | 0.18 | 0.08 | 0.30 | 0.17 | 7.843 3×10-2 |
| 5 | 0.24 | 0.06 | 0.18 | 0.27 | 0.24 | 6.705 9×10-2 |
| 6 | 0.09 | 0.26 | 0.20 | 0.18 | 0.27 | 7.902 3×10-2 |
| 7 | 0.24 | 0.12 | 0.15 | 0.13 | 0.36 | 8.122 2×10-2 |
| 8 | 0.10 | 0.30 | 0.29 | 0.20 | 0.11 | 7.305 8×10-2 |
| 9 | 0.20 | 0.20 | 0.21 | 0.20 | 0.21 | 8.216 1×10-2 |
| 10 | 0.08 | 0.11 | 0.26 | 0.27 | 0.28 | 6.797 7×10-2 |
| 11 | 0.15 | 0.19 | 0.27 | 0.26 | 0.13 | 7.232 1×10-2 |
| 12 | 0.22 | 0.22 | 0.09 | 0.19 | 0.29 | 8.474 6×10-2 |
| 14 | 0.24 | 0.28 | 0.16 | 0.20 | 0.12 | 7.962 7×10-2 |
| 15 | 0.34 | 0.22 | 0.12 | 0.13 | 0.20 | 8.404 2×10-2 |
| 16 | 0.29 | 0.14 | 0.24 | 0.25 | 0.08 | 7.142 7×10-2 |
| 17 | 0.15 | 0.18 | 0.30 | 0.08 | 0.29 | 7.989 3×10-2 |
| 18 | 0.10 | 0.24 | 0.25 | 0.15 | 0.25 | 7.742 1×10-2 |
| 19 | 0.21 | 0.33 | 0.10 | 0.22 | 0.14 | 8.362 0×10-2 |
| 20 | 0.19 | 0.26 | 0.26 | 0.12 | 0.18 | 8.264 4×10-2 |
| 21 | 0.28 | 0.27 | 0.27 | 0.11 | 0.08 | 7.811 2×10-2 |
| 22 | 0.12 | 0.20 | 0.08 | 0.28 | 0.31 | 7.882 1×10-2 |
| 23 | 0.29 | 0.11 | 0.26 | 0.12 | 0.21 | 7.442 3×10-2 |
| 24 | 0.19 | 0.32 | 0.15 | 0.07 | 0.26 | 8.524 5×10-2 |
| 25 | 0.22 | 0.17 | 0.20 | 0.20 | 0.21 | 7.948 5×10-2 |
采用径向基函数根据相应样本点所构建的代理模型是一种能够很好地平衡精度和计算效率的代理模型[8],因此采用径向基函数构建代理模型,其中近似模型如下:
| $\hat{y}\left( x \right)=\sum\limits_{j=1}^{N}{{{\lambda }_{j}}\varphi }\left( {{\left\| x-{{x}_{j}} \right\|}^{2}} \right),$ | (4) |
式中:N为差值样本点的个数;λj为通过差值确定的系数;φ是径向距离r=‖x-xj‖2的函数,取常用的Multi-quadric函数:
| $\varphi \left( r \right)=\sqrt{{{r}^{2}}+{{c}^{2}}},$ | (5) |
其中c为光滑参数,且0 < c < 5,通过寻找最佳的光滑参数c值来建立精确的代理模型,最终得到c′=2.265 678 055.
代理模型构建完后必须验证模型的精度,RBF是一种插值模型,样本点处误差为零,不能像多项式拟合那样通过样本点误差来评价整个代理模型的误差,必须通过额外的测试点来评价,所以本文采用平均相对误差RAAE(即样本点处相对误差的平均值)来评价模型的精度.
| $\text{RAAE=}\frac{\sum\limits_{i=1}^{{{n}_{\downarrow }}}{\left| {{f}_{i}}-{{{\tilde{f}}}_{j}} \right|}}{{{n}_{i}}\times \text{STD}},$ | (6) |
| $\text{STD=}\sqrt{\frac{1}{{{n}_{i}}-1}\sum\limits_{i=1}^{{{n}_{i}}}{\left( {{f}_{i}}-{{{\tilde{f}}}_{i}} \right)}},$ | (7) |
式中:ni是测试点的个数;fi,
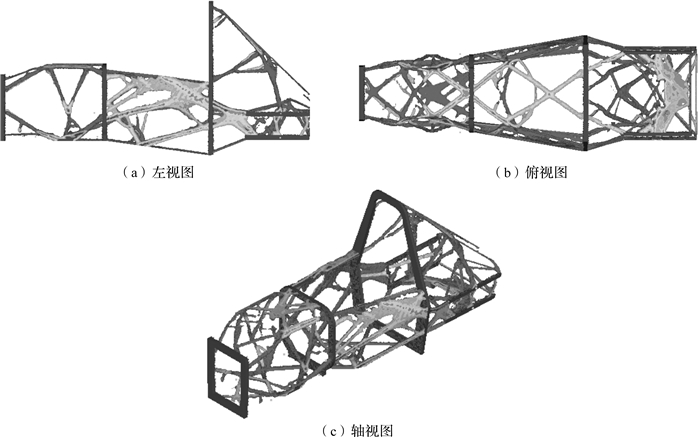
采用NSGA-Ⅱ方法计算得到各个工况的最佳权重比分别为0.13,0.07,0.30,0.32,0.18,将各个工况最佳权重比代入有限元模型中进行计算.借助高效并被广泛使用的SIMP法即密度法进行拓扑优化计算,经过64次迭代后结束,车架最终的拓扑结构清晰、合理,如图 5所示.拓扑结构显示,车架结构整体上呈左右对称分布,车架的底部及侧部出现了较多的三角形结构,车架发动机安装处的结构比较合理,这些结构对车架的刚度提高有很好的参考价值.
|
| 图 5 车架拓扑优化结果 Fig.5 Topology optimization results of the frame |
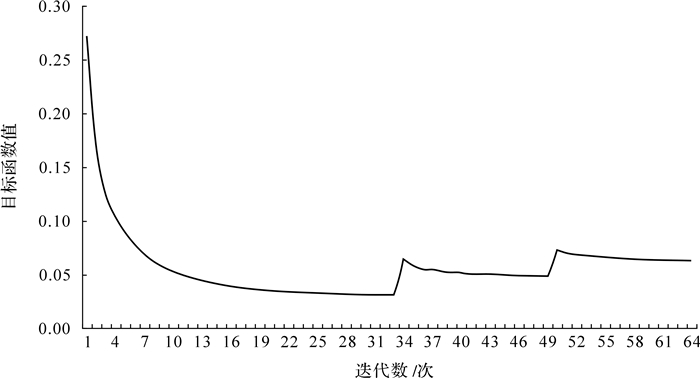
综合目标函数的迭代过程如图 6所示.由图可知综合目标函数值逐渐减小并最终达到稳定值,迭代过程经历了3个阶段,这是由于在计算过程中,为避免结构中出现半密度单元而引入惩罚系数,因此出现了模型再次计算的过程[5],直至满足精度要求,迭代过程停止.
|
| 图 6 综合目标函数迭代过程 Fig.6 Iterative process of the comprehensive objective function |
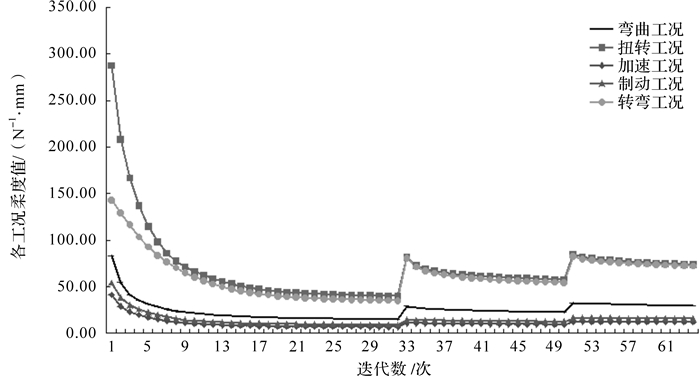
柔度目标的迭代过程如图 7所示.由图可得:在整个拓扑优化迭代过程中,5个工况下车架结构的柔度随着迭代的进行不断减小,其中扭转工况下的车架柔度优化后较优化前变化最大,表明车架扭转工况下的刚度有了很大程度的提高;各个工况的柔度曲线波动趋势相近,并最终达到稳定状态.
|
| 图 7 车架柔度迭代过程 Fig.7 Iterative process of frame compliance |
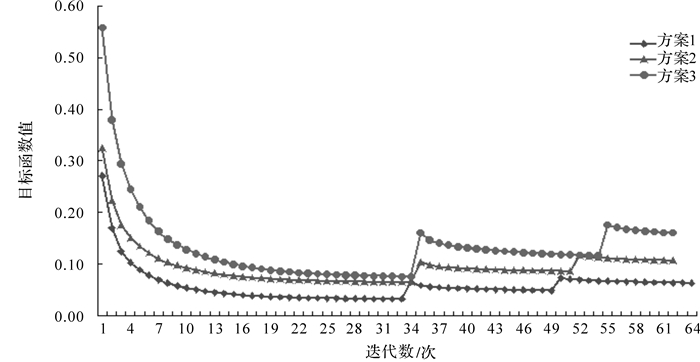
为了验证本文采用方法的有效性及优越性,将本文确定各个工况权重比的方法设为方案1,按照正交试验和层次分析法拟定了2组不同的权重比组合,分别为表 2中的方案2、方案3.基于正交试验确定权重比的方法参考文献[15],基于层次分析法确定权重比的方法参考文献[16-18].对3种方案分别进行相同的拓扑优化计算,各个方案的目标函数迭代过程如图 8所示,权重比组合方案及各个方案各工况柔度最终优化值如表 3和表 4所示.
| 方案 | 弯曲工况 | 扭转工况 | 加速工况 | 制动工况 | 转弯工况 |
| 1 | 0.130 | 0.070 | 0.300 | 0.320 | 0.180 |
| 2 | 0.090 | 0.090 | 0.360 | 0.360 | 0.090 |
| 3 | 0.408 | 0.850 | 0.109 | 0.125 | 0.290 |
|
| 图 8 各个方案的综合目标函数迭代过程 Fig.8 Iterative process of the comprehensive objective function of each method |
| 方案 | 迭代数/次 | 弯曲工况柔度/ (N-1·mm) |
扭转工况柔度/ (N-1·mm) |
加速工况柔度/ (N-1·mm) |
制动工况柔度/ (N-1·mm) |
转弯工况柔度/ (N-1·mm) |
| 1 | 64 | 14.81 | 89.72 | 5.35 | 6.94 | 94.55 |
| 2 | 63 | 16.83 | 171.5 | 5.37 | 7.15 | 91.47 |
| 3 | 61 | 15.22 | 93.15 | 14.02 | 18.33 | 82.24 |
根据图 8可发现:3种方案的目标函数的迭代过程都经历了3个过程,目标函数值不断减小并最终收敛;方案1中目标函数的收敛曲线始终是最低的,也就是说方案1中车架的综合柔度值是最小的;虽然方案1迭代次数最多,但是方案1中目标函数在开始迭代时是下降最快的.此外,方案1中目标函数的最终迭代值为0.062 765 7,通过代理模型计算得到的目标函数值为0.063 957 4,计算误差为1.86%,可以认为代理模型精度可靠.
通过表 4比较3个方案的加权柔度数值
针对多工况下结构拓扑优化过程中遇到的各个工况权重比分配的问题进行了研究,采用代理模型与遗传算法相结合的方法很好地解决了该问题,并通过方程式赛车车架多工况下拓扑优化这一实例进行了验证.对结果分析比较发现,与参考方法相比,本文采用的方法具有明显的优越性.同时,本文采用的方法在解决各个工况权重比分配问题的过程中,借助遗传算法NSGA-Ⅱ求解最佳权重比过程是连续的,可以在优化总目标的同时针对性地寻找重点工况下车架的最优柔度值,因此更具有灵活性.此外,研究不仅解决了多工况下车架拓扑优化各工况权重比分配的问题,而且对其他同类型的权重比分配问题也具有很好的参考价值.
| [1] |
柴天. FSAE赛车整车性能分析与研究[D].长沙:湖南大学机械与运载工程学院, 2009:11-12.
CHAI Tian. Analysis and research on performance of FSAE racing car[D]. Changsha: Hunan University, College of Mechanical and Vehicle Engineering, 2009: 11-12. |
| [2] | CHEN T Y, WU S C. Multi-objective optimal topology design of structures[J]. Computational Mechanics , 1998, 21 (6) : 483–492. DOI:10.1007/s004660050327 |
| [3] |
扶原放, 金达锋, 乔蔚炜.
多工况下微型电动车车身结构拓扑优化设计[J]. 机械设计 , 2010, 27 (2) : 77–80.
FU Yuan-fang, JIN Da-feng, QIAO Wei-wei. Topological optimization design on the body structure of mini electric cars under multi-working conditions[J]. Journal of Machine Design , 2010, 27 (2) : 77–80. |
| [4] |
崔伟.某重型汽车车架多目标拓扑优化设计及其有限元分析[D].长沙:湖南大学机械与运载工程学院, 2012:40-45.
CUI Wei. Multi-objective topology optimization and finite element analysis to a heavy automobile frame[D]. Changsha: Hunan University, College of Mechanical and Vehicle Engineering, 2012:40-45. |
| [5] |
兰凤崇, 赖番结, 陈吉清, 等.
考虑动态特性的多工况车身结构拓扑优化研究[J]. 机械工程学报 , 2014, 50 (20) : 122–128.
LAN Feng-chong, LAI Fan-jie, CHEN Ji-qing, et al. Multi-case topology optimization of body structure considering dynamic characteristic[J]. Journal of Mechanical Engineering , 2014, 50 (20) : 122–128. DOI:10.3901/JME.2014.20.122 |
| [6] |
范文杰, 范子杰, 桂良进, 等.
多工况下客车车架结构多刚度拓扑优化设计研究[J]. 汽车工程 , 2008, 30 (6) : 531–533.
FAN Wen-jie, FAN Zi-jie, GUI Liang-jin, et al. Multi-stiffness topology optimization of bus frame with multiple conditions[J]. Automotive Engineering , 2008, 30 (6) : 531–533. |
| [7] |
兰凤崇, 张浩锴, 王家豪, 等.
汽车转向节拓扑优化方法研究及应用[J]. 汽车工程 , 2014, 36 (4) : 464–468.
LAN Feng-chong, ZHANG Hao-kai, WANG Jia-hao, et al. Study and application of topology optimization technique for vehicle steering knuckles[J]. Automotive Engineering , 2014, 36 (4) : 464–468. |
| [8] |
陈国栋, 韩旭.
基于代理模型的多目标优化方法及其在车身设计中的应用[J]. 机械工程学报 , 2014, 50 (9) : 70.
CHEN Guo-dong, HAN Xu. Multi-objective optimization method based on metamodel and its applications in vehicle body design[J]. Journal of Mechanical Engineering , 2014, 50 (9) : 70. |
| [9] |
洪煌杰, 王红岩, 李建阳, 等.
基于代理模型的空投装备气囊缓冲系统多目标优化[J]. 振动与冲击 , 2015, 34 (3) : 215–220.
HONG Huang-jie, WANG Hong-yan, LI Jian-yang, et al. Multi-objective optimization of an airbag cushion system for airdropping equipment based on surrogate model[J]. Journal of Vibration and Shock , 2015, 34 (3) : 215–220. |
| [10] |
刘俊, 宋文萍, 韩忠华.
基于代理模型的飞翼多目标气动优化设计[J]. 航空计算技术 , 2015, 45 (2) : 1–5.
LIU Jun, SONG Wen-ping, HAN Zhong-hua. Multi-objective aerodynamic design optimization of a flying wing using surrogate model[J]. Aeronautical Computing Technique , 2015, 45 (2) : 1–5. |
| [11] |
居小凡. Formula SAE赛车的设计制造及测试[D].上海:上海交通大学汽车工程学院, 2009:15-19.
JU Xiao-fan. Design-bulid-test of a formula SAE racing car[D]. Shanghai: Shanghai Jiaotong University, Institute of Automotive Engineering, 2009:15-19. |
| [12] | JIANG Li-man, WANG Guo-quan, GONG Guo-qing, et al. Lightweight design for a FSC car based on modal and stiffness analysis[C]//Proceedings of the FISITA 2012 World. Berlin, Heidelberg: Springer-Verlag, 2013: 1009-1022. |
| [13] |
阳文君, 郭振辉.
FSC车架静态性能的有限元分析与试验验证[J]. 湖北汽车工业学院学报 , 2012, 26 (4) : 68–71.
YANG Wen-jun, GUO Zhen-hui. Finite element analysis and test validation on static performance of FSC frame[J]. Journal of Hubei University of Automotive Technology , 2012, 26 (4) : 68–71. |
| [14] | MIN S, NISHIWAKI S, KIKUCHI N. Unified topology design of static and vibrating structures using multiobjective optimization[J]. Computers & Structures , 2000, 75 (1) : 93–116. |
| [15] |
高云凯, 王婧人, 汪翼.
基于正交试验的大型客车车身结构多工况拓扑优化研究[J]. 汽车技术 , 2011 (11) : 16–19.
GAO Yun-kai, WANG Jing-ren, WANG Yi. Multi-case topology optimization of bus body structure based on orthogonal test[J]. Automobile Technology , 2011 (11) : 16–19. |
| [16] |
代丽, 朱爱华, 赵匀.
应用层次分析法计算分插机构优化目标的权重[J]. 农业工程学报 , 2013, 29 (2) : 60–65.
DAI Li, ZHU Ai-hua, ZHAO Yun. Using AHP to calculate optimization objective weights of transplanting mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering , 2013, 29 (2) : 60–65. |
| [17] |
田启华, 王进学, 杜义贤, 等.
基于密度-敏度层次更新策略的三维连续体结构拓扑优化[J]. 工程设计学报 , 2015, 22 (2) : 155–160.
TIAN Qi-hua, WANG Jin-xue, DU Yi-xian, et al. Three-dimensional continuum topology optimization based on density-sensitivity level update policy[J]. Chinese Journal of Engineering Design , 2015, 22 (2) : 155–160. |
| [18] |
骆正清, 杨善林.
层次分析法中几种标度的比较[J]. 系统工程理论与实践 , 2004, 24 (9) : 51–60.
LUO Zheng-qing, YANG Shan-lin. Comparative study on several scales in AHP[J]. Systems Engineering-theory and Practice , 2004, 24 (9) : 51–60. |



