2. 湖北省油气钻完井工具工程技术研究中心, 湖北 荆州 434023;
3. 中国石油化工集团石油工程机械有限公司第四机械厂, 湖北 荆州 434000
2. Oil and Gas Drilling and Well Completion Tools Research Center of Hubei Province, Jingzhou 434023, China ;
3. SJ Petroleum Machinery Co., Sinopec Group, Jingzhou 434000, China
随着自动化技术的发展,井场作业的自动化程度不断提高,而提高管柱输送装置的自动化程度能有效提高钻井作业效率[1-2].钢丝绳拉升式自动猫道具有设计简单、运输方便等优点,因此该自动猫道逐渐被重视并得到较快的发展.自动猫道技术在国外已经发展得较为成熟,加拿大CANRIG公司生产的Power CAT自动猫道与美国NOV公司生产的Pipe Cat[3-4]钢丝绳牵引式自动猫道结构简单,传递动力大,提升效率高,安装灵活,可以进行无级调节,易于操作与维护.钢丝绳拉升式自动猫道在国内同样得到较快发展,但是仍然存在一定缺陷,如:宝鸡石油机械有限责任公司研发的自动猫道[5]设计简单,运输方便,缺点在于不能用于超深井石油的开采;四川宏华设备有限公司生产的自动猫道[6]采用钢丝绳起升,自动化程度高,但是整机晃动严重,循环时间长,控制元件故障频发,设计不成熟,需要进一步优化.
为了给自动猫道的优化[7-10]提供理论支持,李娇艳等[11]采用动力学的方法对某一链传动式动力猫道进行了受力分析,分析的结果与仿真软件模拟结果相吻合.任德勇等[12]对自动猫道的起升钢丝受力作了一定研究,为钢丝绳的设计选型提供了理论基础,但是所采用的是静力学分析方法,并且运动过程分析不完整,不能完全反映自动猫道在工作过程中的力学特性.因此,本文根据钢丝绳拉升式自动猫道的工作原理,将运送钻柱的过程划分为4个阶段,考虑运动过程中惯性力的影响,利用达朗贝尔原理建立4个阶段的动力学模型,分析自动猫道的结构尺寸对起升力的影响,为钢丝绳拉升式自动猫道的设计提供指导.
1 钢丝绳拉升式自动猫道主要结构钢丝绳拉升式自动猫道整体结构如图 1所示,其结构主要包括基座、支撑臂、移送臂、滑车、坡道、液压绞车和钢丝绳.支撑臂的一端与移送臂通过铰链连接,该铰接位置与移送臂端点有一定距离,另一端可在基座的轨道上滑动.移送臂上制作有V形槽,用于放置管柱,滑车可在该V形槽内移动将管柱推出移送臂.移送臂的一端装有滑轮,可在基座的轨道内滑动,另一端安装在斜坡的轨道内并装有缠绕钢丝绳的定滑轮,可在钢丝绳的牵引下沿坡道向上滑动,当该端点移动至坡道顶端时,移送臂可以将坡道顶端作为支撑点继续移动一段距离,该距离可根据实际作业情况进行控制.坡道上靠近顶端的位置装有缠绕钢丝绳的定滑轮,底端与基座通过铰链连接,方便调节斜坡倾角以适应不同高度的钻台.
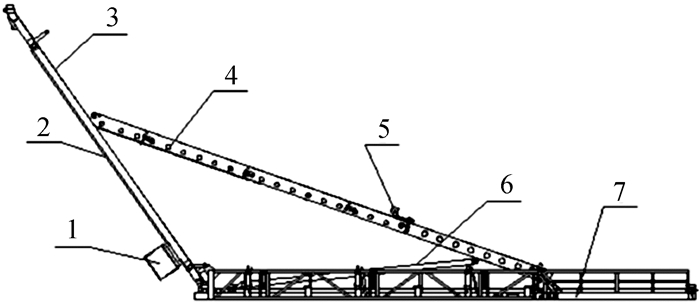
|
| 1—液压绞车;2—钢丝绳;3—坡道;4—移送臂;5—滑车;6—支撑臂;7—基座. 图 1 钢丝绳拉升式自动猫道结构 Fig.1 Structure of rope pulled automatic catwalk |
根据动力学特性,将自动猫道的工作过程分为4个阶段.第1阶段:移送臂靠在坡道的那一端受钢丝绳的拉动作用沿着坡道向上滑动,另一端在基座的轨道上向坡道底端滑动;支撑臂一端与移送臂铰接,另一端也在基座上滑动.第2阶段:支撑臂滑动一定距离后与基座上的挡块接触,随后,支撑臂开始转动,移送臂被举升.第3阶段:移送臂沿坡道向上滑动时,移送臂的端点经过坡上缠绕钢丝绳的滑轮后,钢丝绳脱离移送臂的滑轮,移送臂继续沿着坡道向上滑动.第4阶段:移送臂运动到达坡道顶部后以坡道顶部作为支点继续作平面运动,直至到达指定位置.自动猫道的动力学分析过程如图 2所示.
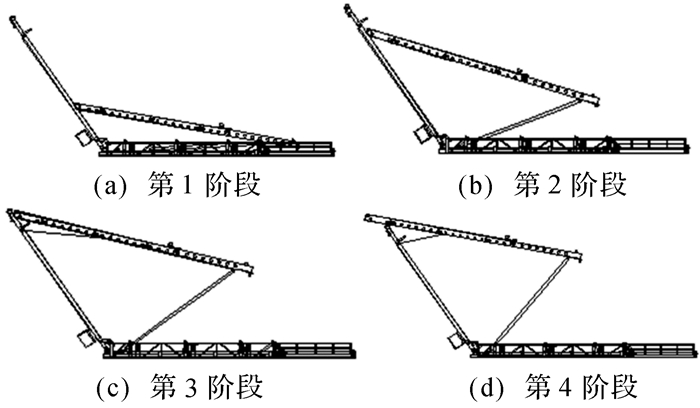
|
| 图 2 钢丝绳拉升式自动猫道运动状态图 Fig.2 The motion state diagram of rope pulled automatic catwalk |
根据自动猫道的工作原理与钢丝绳的受力情况,对自动猫道运动过程的4个阶段分别进行动力学分析.对于第3阶段而言,移送臂和支撑臂的运动形式与第2阶段相似,但是钢丝绳对移送臂的拉力作用形式发生了改变,所以,需将该过程独立出来进行力学分析.自动猫道的整体结构相对简单,为便于力学分析[13],作如下假设:
1)对于所分析的自动猫道,其各运动过程皆处于动态平衡;
2)铰接位置充分润滑,无摩擦力;
3)各结构件的重心都位于几何中心;
4)结合实际工况,对运动过程中钢丝绳的收绳速度采用连续函数s(t)进行约束,其中s(t)=0.5t,即收绳速度为0.5 m/s;
5)运动速度较低,无需考虑振动载荷作用.
自动猫道的结构示意图如图 3所示,计算参数及符号说明如表 1所示.
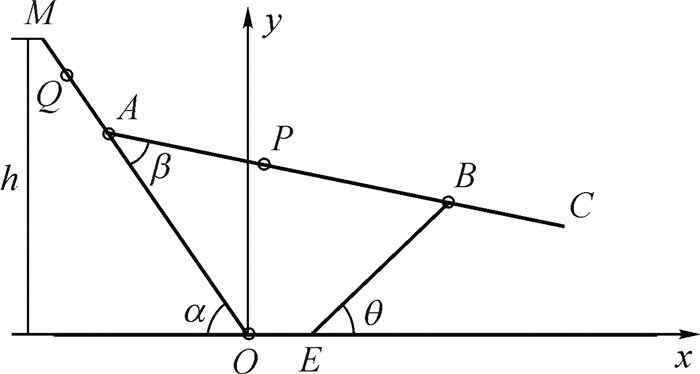
|
| 图 3 自动猫道结构示意图 Fig.3 Structure diagram of automatic catwalk |
| 符号 | 量值 | 备注 |
| m1 | 1 200 kg | 支撑臂质量 |
| m3 | 1 200 kg | 输送的管柱质量 |
| m4 | 4 500 kg | 移送臂质量 |
| BE | 8.78 m | 支撑臂长度 |
| BC | 2.7 m | 移送臂尾端长度 |
| AC | 17.65 m | 移送臂长度 |
| AP | 6 m | 钢丝绳节点位置 |
| h | 10.445 m | 钻台高度 |
| α | 55° | 坡道与水平面之间的夹角 |
| β | 待求 | 移送臂与坡道之间的夹角 |
| θ | 待求 | 支撑臂与水平面之间的夹角 |
| e | 0.5 m | 坡道底端与基座上挡块之间的距离 |
| Ft | 待求 | 钢丝绳拉力 |
| Fn | 待求 | 坡道对移送臂的支持力 |
| ft | 待求 | 摩擦力 |
| μ | 0.1 | 摩擦因子 |
①第1阶段动力学分析.
第1阶段的动力学分析简图如图 4所示.在该运动过程中,移送臂与所输送的管柱的质心为Z点,支撑臂的质心为F点.AC以A点为基点作平面运动,A点的加速度为aA1,Z点的牵引加速度所产生的惯性力为FZ3,向心加速度所产生的离心力为FZ2,切向加速度所产生的惯性力为FZ1;BE杆以E点为基点作平面运动,E点的加速度为aE,F点的牵引加速度所产生的惯性力为FF3,向心加速度所产生的离心力为FF2,切向加速度所产生的惯性力为FF1.C点的支持力和摩擦力分别为FCy和FCx,E点的支持力和摩擦力分别为FEy和FEx.
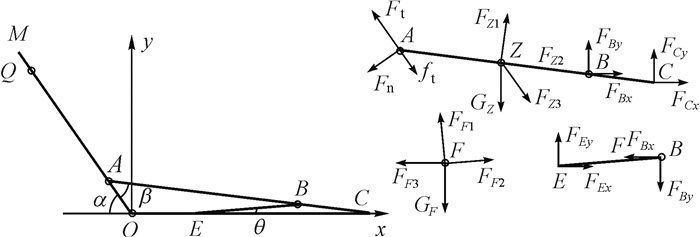
|
| 图 4 第1阶段动力学分析简图 Fig.4 Dynamics analysis diagram of first stage |
| 质心Z点 | 质心F点 |
| FZ1=(m3+m4) |
FF1=m1 |
| FZ2=(m3+m4) |
FF2=m1 |
| FZ3=(m3+m4)aA | FF2=m1aErEF |
| GZ=(m3+m4)g | GF=m1g |
将BE杆隔离作受力分析,根据力矩平衡,将BE杆所受外力对B点取矩,如下式所示:
| $\begin{align} & \sum{{{M}_{B1}}}={{M}_{B}}\left( {{F}_{1}} \right)+{{M}_{B}}\left( {{F}_{2}} \right)+{{M}_{B}}\left( {{F}_{3}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{B}}\left( {{F}_{\text{F}}} \right)+{{M}_{B}}\left( {{F}_{Ey}} \right)+{{M}_{B}}\left( {{F}_{Ex}} \right)=0. \\ \end{align}$ | (1) |
将BE杆和AC杆整体作受力分析,根据力矩平衡,依次将所有外力对A点、C点、E点取矩,可得方程如式(2)、(3)、(4)所示.
| $\begin{align} & \sum{{{M}_{A1}}}={{M}_{A}}\left( {{F}_{1}} \right)+{{M}_{A}}\left( {{F}_{2}} \right)+{{M}_{A}}\left( {{F}_{3}} \right)+{{M}_{A}}\left( {{G}_{\text{F}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{A}}\left( {{F}_{Ey}} \right)+{{M}_{A}}\left( {{F}_{Ex}} \right)+{{M}_{A}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{A}}\left( {{F}_{Z2}} \right)+{{M}_{A}}\left( {{F}_{Z3}} \right)+{{M}_{A}}\left( {{G}_{Z}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{A}}\left( {{F}_{Cy}} \right)+{{M}_{A}}\left( {{F}_{Cx}} \right)=0, \\ \end{align}$ | (2) |
| $\begin{align} & \sum{{{M}_{C1}}}={{M}_{C}}\left( {{F}_{1}} \right)+{{M}_{C}}\left( {{F}_{2}} \right)+{{M}_{C}}\left( {{F}_{3}} \right)+{{M}_{C}}\left( {{G}_{\text{F}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{C}}\left( {{F}_{Ey}} \right)+{{M}_{C}}\left( {{F}_{Ex}} \right)+{{M}_{C}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{C}}\left( {{F}_{Z2}} \right)+{{M}_{C}}\left( {{F}_{Z3}} \right)+{{M}_{C}}\left( {{G}_{Z}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{C}}\left( {{F}_{\text{t}}} \right)+{{M}_{C}}\left( {{F}_{\text{n}}} \right)+{{M}_{C}}\left( {{f}_{\text{t}}} \right)=0, \\ \end{align}$ | (3) |
| $\begin{align} & \sum{{{M}_{E1}}}={{M}_{E}}\left( {{F}_{1}} \right)+{{M}_{E}}\left( {{F}_{2}} \right)+{{M}_{E}}\left( {{F}_{3}} \right)+{{M}_{E}}\left( {{G}_{\text{F}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{F}_{\text{t}}} \right)+{{M}_{E}}\left( {{F}_{\text{n}}} \right)+{{M}_{E}}\left( {{f}_{\text{t}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{F}_{Z1}} \right)+{{M}_{E}}\left( {{F}_{Z2}} \right)+{{M}_{E}}\left( {{F}_{Z3}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{G}_{Z}} \right)=0. \\ \end{align}$ | (4) |
②第2阶段动力学分析.
第2阶段的动力学分析简图如图 5所示.在该运动过程中,E点处为固定铰接,BE杆绕E点转动,A点在钢丝绳的牵引下沿坡道向上滑动,AC杆在BE杆的作用下被举升,此时仍假设AC杆以A点为基点作平面运动,A点的加速度为aA2.
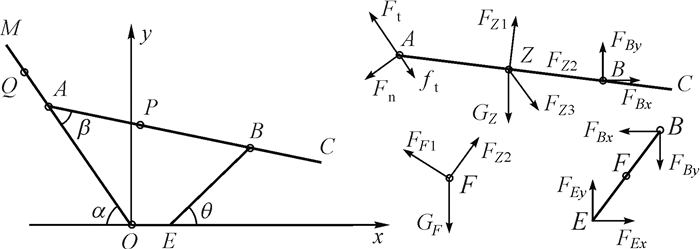
|
| 图 5 第2阶段动力学分析简图 Fig.5 Dynamics analysis diagram of second stage |
质心Z和F点处力的表达式参考表 2.根据AC杆力矩平衡,将AC杆所受外力对B点取矩,可列力矩平衡方程(5),然后对BE杆和AC杆整体作受力分析,根据E点力矩平衡,可得方程(6).
| $\begin{align} & \sum{{{M}_{B2}}}={{M}_{B}}\left( {{F}_{\text{t}}} \right)+{{M}_{B}}\left( {{F}_{\text{n}}} \right)+{{M}_{B}}\left( {{f}_{\text{t}}} \right)+{{M}_{B}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{B}}\left( {{F}_{\text{Z2}}} \right)+{{M}_{B}}\left( {{F}_{Z3}} \right)+{{M}_{B}}\left( {{G}_{\text{Z}}} \right)=0, \\ \end{align}$ | (5) |
| $\begin{align} & \sum{{{M}_{E2}}}={{M}_{E}}\left( {{F}_{\text{1}}} \right)+{{M}_{E}}\left( {{F}_{\text{2}}} \right)+{{M}_{E}}\left( {{G}_{F}} \right)+{{M}_{E}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{F}_{\text{Z2}}} \right)+{{M}_{E}}\left( {{F}_{Z3}} \right)+{{M}_{E}}\left( {{G}_{Z}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{F}_{\text{t}}} \right)+{{M}_{E}}\left( {{F}_{\text{n}}} \right)+{{M}_{E}}\left( {{f}_{\text{t}}} \right)=0. \\ \end{align}$ | (6) |
③第3阶段动力学分析.
第3阶段的动力学分析简图如图 6所示.在该运动过程中,E点处为固定铰接,BE杆绕E点作旋转运动,A点在钢丝绳的牵引下继续沿坡道向上滑动,当A点经过滑轮Q点时,钢丝绳从AC杆端点的滑轮脱离,牵引力开始作用于P点,并且力的方向随时间变化.
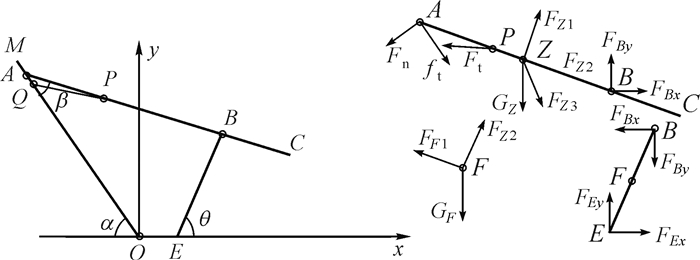
|
| 图 6 第3阶段动力学分析简图 Fig.6 Dynamics analysis diagram of third stage |
质心Z和F点处力的表达式参考表 2.对BE杆和AC杆整体作受力分析,可列出关于E点力矩平衡方程(7),对AC杆作受力分析,可列出关于B点的力矩平衡方程(8).
| $\begin{align} & \sum{{{M}_{E3}}}={{M}_{E}}\left( {{F}_{\text{1}}} \right)+{{M}_{E}}\left( {{F}_{\text{2}}} \right)+{{M}_{E}}\left( {{G}_{F}} \right)+{{M}_{E}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{F}_{\text{Z2}}} \right)+{{M}_{E}}\left( {{F}_{Z3}} \right)+{{M}_{E}}\left( {{G}_{Z}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{F}_{\text{t}}} \right)+{{M}_{E}}\left( {{F}_{\text{n}}} \right)+{{M}_{E}}\left( {{f}_{\text{t}}} \right)=0, \\ \end{align}$ | (7) |
| $\begin{align} & \sum{{{M}_{B3}}}={{M}_{B}}\left( {{F}_{\text{t}}} \right)+{{M}_{B}}\left( {{F}_{\text{n}}} \right)+{{M}_{B}}\left( {{f}_{\text{t}}} \right)+{{M}_{B}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{B}}\left( {{F}_{\text{Z2}}} \right)+{{M}_{B}}\left( {{F}_{Z3}} \right)+{{M}_{B}}\left( {{G}_{Z}} \right)=0. \\ \end{align}$ | (8) |
④第4阶段动力学分析.
第4阶段的动力学分析简图如图 7所示.在该运动过程中,AC杆越过M点继续作平面运动,此时,坡道对AC杆支持力的方向随时间变化,假设AC杆以B点为中心作平面运动,BE杆以E点为中心作旋转运动.
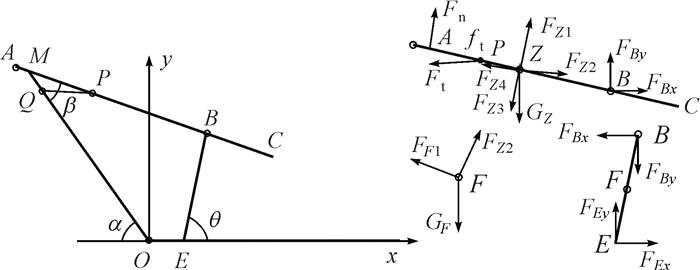
|
| 图 7 第4阶段动力学分析简图 Fig.7 Dynamics analysis diagram of fourth stage |
质心F点处力的表达式参考表 2,质心Z点处的力FZ3和FZ4分别为由B点的向心加速度和切向加速度引起的惯性力.将BE杆和AC杆整体作受力分析,可列出关于E点力矩平衡方程(9),对AC杆作受力分析,可列出关于B点的力矩平衡方程(10).
| $\begin{align} & \sum{{{M}_{E4}}}={{M}_{E}}\left( {{F}_{\text{1}}} \right)+{{M}_{E}}\left( {{F}_{\text{2}}} \right)+{{M}_{E}}\left( {{G}_{F}} \right)+{{M}_{E}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{F}_{\text{Z2}}} \right)+{{M}_{E}}\left( {{F}_{Z3}} \right)+{{M}_{E}}\left( {{F}_{Z4}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{G}_{Z}} \right)+{{M}_{E}}\left( {{F}_{\text{t}}} \right)+{{M}_{E}}\left( {{F}_{\text{n}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{E}}\left( {{f}_{\text{t}}} \right)=0, \\ \end{align}$ | (9) |
| $\begin{align} & \sum{{{M}_{B4}}}={{M}_{B}}\left( {{F}_{\text{t}}} \right)+{{M}_{B}}\left( {{F}_{\text{n}}} \right)+{{M}_{B}}\left( {{f}_{\text{t}}} \right)+{{M}_{B}}\left( {{F}_{Z1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{B}}\left( {{F}_{\text{Z2}}} \right)+{{M}_{B}}\left( {{F}_{Z3}} \right)+{{M}_{B}}\left( {{F}_{Z4}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{B}}\left( {{G}_{Z}} \right)=0. \\ \end{align}$ | (10) |
通过以上力学分析分别建立了关于Ft和Fn的数学模型,如公式(1)至(10)所示.由于表达式参数过多,故关于Ft和Fn的数学模型仅以隐函数表示.
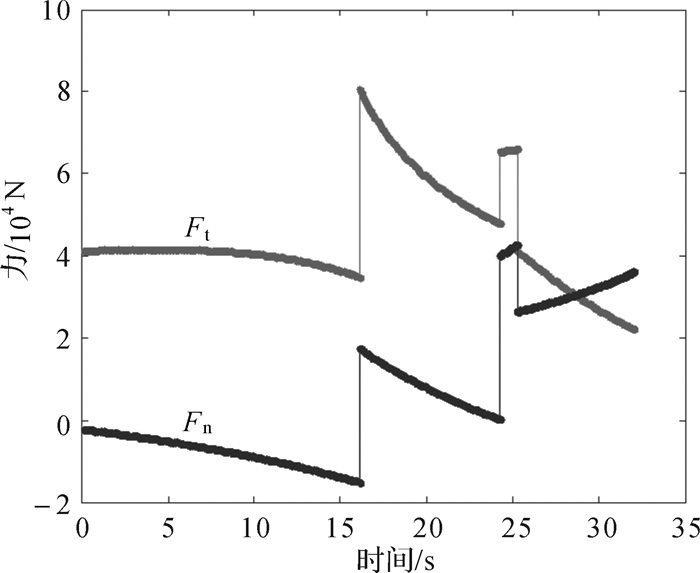
4 数学模型求解与力学特性分析 4.1 数学模型求解采用关于时间的连续函数s(t)对实际工况中钢丝绳的收绳速度进行模拟,对于第1、第2和第3阶段模型的求解,可先根据机构的几何关系求得θ(t),β(t)以及各关键点与时间t的函数.对于第4阶段模型的求解,由于几何关系较复杂,需采用差分[14-15]的方法进行求解.利用MATLAB软件[16-17]高效的计算能力对模型求解.求解得到自动猫道的运动状态模型,以及运动全过程中钢丝绳的拉力Ft和坡道对移送臂的支持力Fn随时间的变化,如图 8和图 9所示.
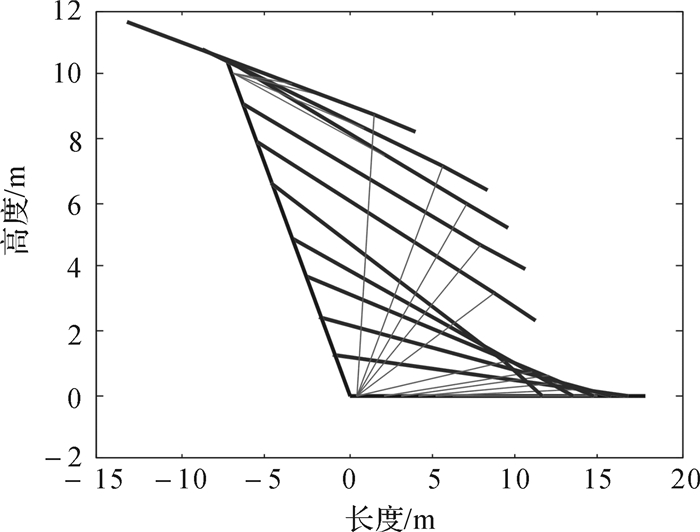
|
| 图 8 自动猫道的运动状态模拟 Fig.8 Motion simulation of automatic catwalk |
|
| 图 9 拉力Ft和支持力Fn随时间的变化 Fig.9 The change of tension Ft and support force Fn with time |
通过模拟自动猫道的运动状态可以得到各结构件的位置随时间变化关系,并可检测钢丝绳的节点在移送臂的位置、支撑臂的最大偏转角、移送臂与水平面的夹角和移送臂进入钻台的长度,以及整体结构的尺寸是否合理,为自动猫道的结构设计提供指导.
根据图 9所示的计算结果可以得到,在自动猫道工作过程中,随着液压绞车启动,钢丝绳牵引移送臂和支撑臂沿轨道滑动.当支撑臂与挡块接触后开始转动时,钢丝绳拉力的力臂变小导致拉力突然增加,随着移送臂沿坡道继续上升,钢丝绳的拉力逐渐减小.当移送臂与坡道的接触点经过滑轮后,钢丝绳作用力方向的改变导致拉力又突然增加,直到移送臂到达坡道顶端,所需钢丝绳的拉力减小,但是支持力在第3和第4阶段相对较高.第2阶段钢丝绳起升拉力的突然增加极大地增加了液压绞车的起升载荷,需通过结构优化降低起升载荷.
4.2 结构特性分析自动猫道起升拉力的增加要求液压绞车以及钢丝绳具有更好的性能,否则会导致机械故障增加,降低作业效率.为了得到部分结构尺寸对起升拉力的影响,给自动猫道的设计提供参考,采用控制变量的方法进行分析,变量的取值范围需保证支撑臂的最大偏转角小于90°,并防止结构发生自锁[18].所控制的变量应易于加工和调整且保持移送臂AC的长度不变,包括基座上挡块与坡道底端的距离e,移送臂与支撑臂的铰接位置即BC的长度,支撑臂BE的长度.
1)根据设计要求现控制e的取值分别为-1,-0.5,0,0.5,1 m,当e的取值为负时,挡块位于O点的左端.计算得到全过程钢丝绳的受力如图 10所示.
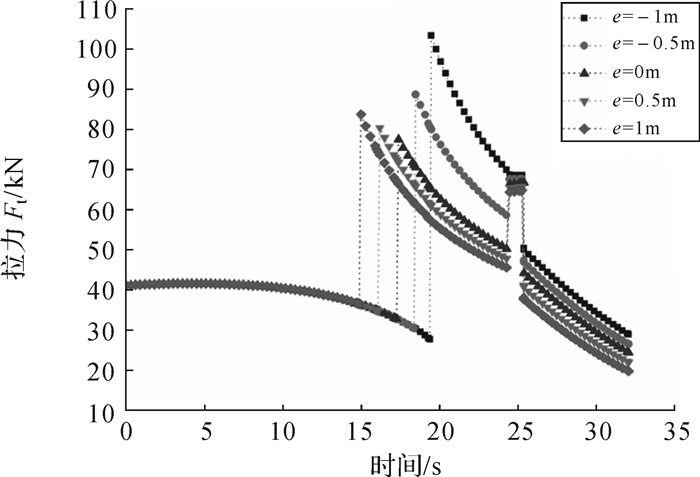
|
| 图 10 e对运动全过程拉力Ft的影响 Fig.10 Effect of e on the tension Ft in the whole process of motion |
2)控制BC的长度分别为1.7,2.2,2.7,3.2,3.7 m,计算得到全过程钢丝绳的受力如图 11所示.
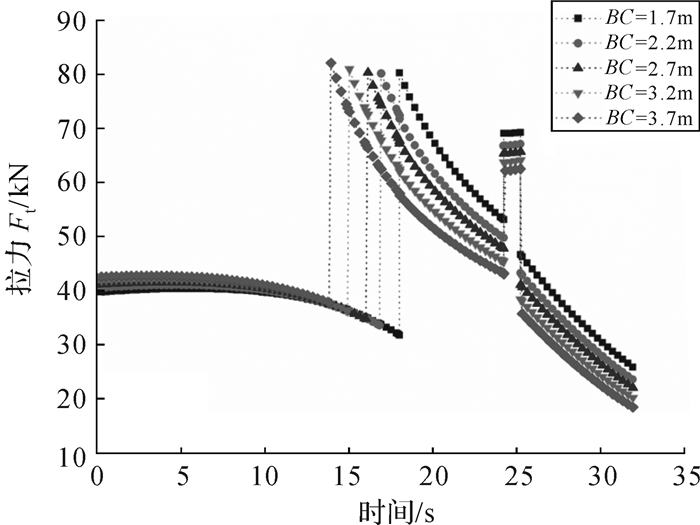
|
| 图 11 BC长度对运动全过程拉力Ft的影响 Fig.11 Effect of BC length on the tension Ft in the whole process of motion |
3)控制BE的长度分别为7.78,8.28,8.78,9.28,9.78 m,计算得到全过程钢丝绳的受力如图 12所示.
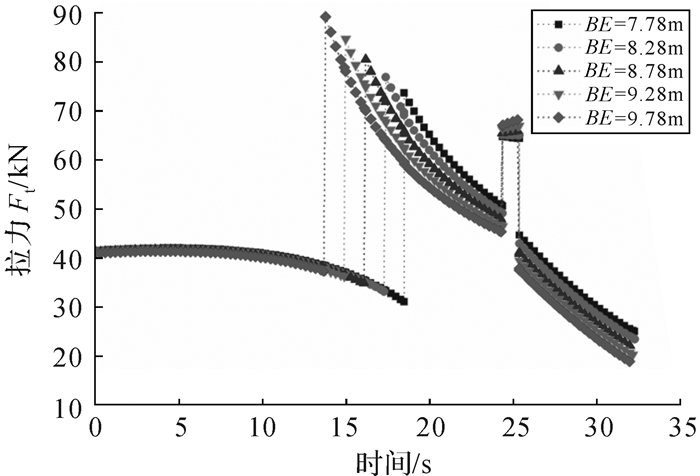
|
| 图 12 BE长度对运动全过程拉力Ft的影响 Fig.12 Effect of BE length on the tension Ft in the whole process of motion |
根据以上3组计算结果可以得到,e的变化对第3阶段的起升拉力影响不大,但增加e能减小第4阶段起升拉力,且当e=0时,即挡块位于坡道与基座的铰接位置时,能有效降低第2阶段的起升拉力;如果保持AC杆的总长不变,增加BC的长度,对第2阶段的起升拉力影响不大,但是能降低第3和第4阶段所需的起升拉力;增加BE杆的长度会导致第2阶段的起升拉力大幅度增加,第3阶段的起升拉力增加较少,但是第4阶段的起升拉力有所降低.
5 现场实验为减小起升过程中所需的最大拉力,采用枚举法对以上结构进行分析与讨论.根据分析结果将现有自动猫道结构进行调整,重新加工的支撑臂长度为7.78 m,并将基座上挡块调整至坡道底端,得到新的自动猫道结构.由于钢丝绳上不适合安装传感器,而钢丝绳由液压绞车驱动,液压绞车的驱动源为高压液压油,故液压绞车进油口的油压可有效地反映钢丝绳载荷大小.自动猫道实验现场见图 13.

|
| 图 13 自动猫道实验现场 Fig.13 Field experiment of automatic catwalk |
依据实际工况分别模拟输送3-1/2in钻杆、5in钻杆、13-3/8in套管、16in套管以及空载工况,其质量依次为218,358,811,1 250 kg,实验过程中对液压绞车的进油管线油压表数据进行记录.统计实验数据得到各组自动猫道起升全过程最大油压数据,如图 14所示.
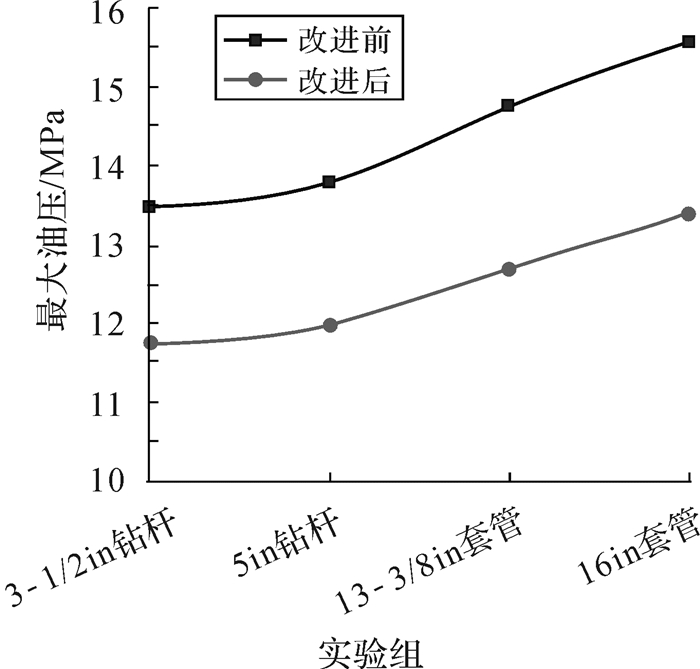
|
| 图 14 实验结果 Fig.14 Experimental results |
对比实验数据发现,改进后的自动猫道在起升过程中的最大油压均下降.以输送16in套管为例,起升最大油压下降2.2 MPa.同时,实验结果也表明自动猫道的空载运行时油压约为11.2 MPa,由此,建议在保证强度的条件下降低移送臂与支撑臂重量有助于降低液压绞车载荷.
6 结论1)通过分析自动猫道的运动特性,根据其几何关系以及钢丝绳拉力的作用形式,将自动猫道的运动过程分解成4个运动阶段并进行受力分析,依据实际工况对自动猫道进行简化,采用达朗贝尔原理建立了自动猫道在各个运动阶段的动力学模型.
2)计算并分析了部分结构尺寸对钢丝绳拉升式自动猫道起升拉力的影响,依据分析结果建议将挡块尽量靠近坡道底端,合理地增加移送臂尾端长度、减小支撑臂的长度.根据分析结果对自动猫道结构进行调整并进行实验,实验结果表明起升过程中所需液压绞车的载荷得到降低.
| [1] |
于兴军, 宋志刚, 魏培静, 等.
国内石油钻机自动化技术现状与建议[J]. 石油机械 , 2014, 42 (11) : 25–29.
YU Xing-jun, SONG Zhi-gang, WEI Pei-jing, et al. The technical status and recommendations on the domestic drilling rig automation[J]. China Petroleum Machinery , 2014, 42 (11) : 25–29. |
| [2] |
赵淑兰, 李文彪, 聂永晋, 等.
动力猫道技术国内外现状和发展趋势[J]. 石油矿场机械 , 2010, 39 (2) : 13–15.
ZHANG Shu-lan, LI Wen-biao, NIE Yong-jin, et al. Technology and developing trend of power catway at home and abroad[J]. Oil Field Equipment , 2010, 39 (2) : 13–15. |
| [3] |
刘强.石油钻机自动化猫道的研究与设计[D].大庆:东北石油大学机械科学与工程学院, 2013:2-3.
LIU Qiang. Research and design on automatic catwalk of oil drilling rig[D].Daqing: Northeast Petroleum University, School of Mechanical Science and Engineering, 2013:2-3. http://cdmd.cnki.com.cn/article/cdmd-10220-1013291107.htm |
| [4] |
高建强.全液压自动猫道提升系统研究[D].长春:吉林大学机械科学与工程学院, 2014:3-6.
GAO Jian-qiang. Research on hoisting system of hydraulic automatic catwalk[D]. Changchun: Jilin University, School of Mechanical Science and Engineering, 2014:3-6. http://cdmd.cnki.com.cn/article/cdmd-10183-1014270463.htm |
| [5] |
万晓鹏.自动排管机系统动力学分析与研究[D].长春:吉林大学机械科学与工程学院, 2014:6-7.
WAN Xiao-peng. Dynamics analysis and research of automatic pipe handing system[D]. Changchun: Jilin University, School of Mechanical Science and Engineering, 2014:6-7. |
| [6] |
张春鹏.全液压自动猫道举升系统研究[D].长春:吉林大学机械科学与工程学院, 2014:8-9.
ZHANG Chun-peng. Study on lifting system of full hydraulic automatic catwalk[D].Changchun: Jilin University, School of Mechanical Science and Engineering, 2014:8-9. http://cdmd.cnki.com.cn/article/cdmd-10183-1014295969.htm |
| [7] |
何鸿.
钻井平台钻杆自动化排放系统方案设计[J]. 石油矿场机械 , 2012, 9 (41) : 82–84.
HE Hong. Scheme design of automatic discharge pipe system of drilling platform[J]. Oil Field Equipment , 2012, 9 (41) : 82–84. |
| [8] |
郑元庆, 江正清, 裴俊峰, 等.
猫道机液压系统的可靠性分析[J]. 机床与液压 , 2014, 42 (19) : 199–203.
ZHENG Yuan-qing, JIANG Zheng-qing, PEI Jun-feng, et al. Reliability evaluation of catwalk hydraulic system[J]. Machine Tool & Hydraulics , 2014, 42 (19) : 199–203. |
| [9] |
崔学政, 刘全平, 肖文生, 等.
海洋钻井平台自动化猫道设计[J]. 石油矿场机械 , 2011, 40 (2) : 20–23.
CHUI Xue-zheng, LIU Quan-ping, XIAO Wen-sheng, et al. Design of automated catwalk-machine for offshore drilling platform[J]. Oil Field Equipment , 2011, 40 (2) : 20–23. |
| [10] |
谭志松, 于萍, 张春鹏, 等.
全液压自动猫道举升系统运动学分析[J]. 石油矿场机械 , 2015, 44 (7) : 24–27.
TAN Zhi-song, YU Ping, ZHANG Chun-peng, et al. Kinematics analysis of lifting system of full hydraulic automatic catwalk[J]. Oil Field Equipment , 2015, 44 (7) : 24–27. |
| [11] |
李艳娇, 于萍, 高建强, 等.
新型自动猫道提升系统动力学分析[J]. 石油矿场机械 , 2015, 44 (5) : 1–5.
LI Yan-jiao, YU Ping, GAO Jian-qiang, et al. Dynamic analysis of hoisting system of the new automatic catwalk[J]. Oil Field Equipment , 2015, 44 (5) : 1–5. |
| [12] |
任得勇, 刘雁蜀, 王元忠, 等.
自动猫道机起升钢丝绳受力特性研究[J]. 机械研究与应用 , 2014, 27 (4) : 54–57.
REN De-yong, LIU Yan-shu, WANG Yuan-zhong, et al. Research on the mechanical properties of automatic catwalk hoisting wire rope[J]. Mechanical Research & Application , 2014, 27 (4) : 54–57. |
| [13] |
哈尔滨工业大学理论力学教研室.
理论力学[M].6版. 北京: 高等教育出版社 ,2002 : 216 -220.
Theoretical Mechanics Department of Harbin Institute of Technology. Theoretical mechanics[M].6th ed. Beijing: Higher Education Press , 2002 : 216 -220. |
| [14] |
谢帆, 荆建平, 万召, 等.
基于有限差分法的径向滑动轴承油膜压力分布计算[J]. 润滑与密封 , 2012, 37 (2) : 12–15.
XIE Fan, JING Jian-ping, WAN Zhao, et al. Calculation of oil film pressure distribution of journal bearing based on finite difference method[J]. Lubrication Engineering , 2012, 37 (2) : 12–15. |
| [15] |
马良栋, 李增耀, 陶文铨.
高精度有限差分在湍流直接数值模拟中的应用[J]. 工程热物理学报 , 2007, 5 (28) : 859–961.
MA Liang-dong, LI Zeng-yao, TAO Wen-quan. The application of high resolution finite difference scheme in numerical simulation of turbulent[J]. Journal of Engineering Thermophysics , 2007, 5 (28) : 859–961. |
| [16] |
田亚平, 王小荣.
平面铰链五杆机构的Matlab动力学求解[J]. 机械研究与应用 , 2009 (5) : 26–29.
TIAN Ya-ping, WANG Xiao-rong. A dynamic solution for a planar linkage five-bar mechanism with Matlab[J]. Machine Research & Application , 2009 (5) : 26–29. |
| [17] |
张德丰, 杨文茵.
MATLAB仿真技术与应用[M]. 北京: 机械工业出版社 ,2002 : 73 -76.
ZHANG De-feng, YANG Wen-yin. MATLAB simulation technology and application[M]. Beijing: China Machine Press , 2002 : 73 -76. |
| [18] |
孙恒, 陈作模, 葛文杰.
机械原理[M]. 北京: 高等教育出版社 ,2006 : 69 -73.
SUN Heng, CHEN Zuo-mo, GE Wen-jie. Mechanical principles[M]. Beijing: Higher Education press , 2006 : 69 -73. |



