2. 中北大学机械与动力工程学院, 山西 太原 030051
2. School of Mechanical and Power Engineering, North University of China, Taiyuan 030051, China
永磁同步直线电机是直驱进给系统的重要组成部分.同滚珠丝杠驱动方式相比,直线电机具有高速高精和噪声低等优点.然而,由于永磁同步直线电机取消了机械转换环节,其更易受外界的扰动影响.摩擦力是影响永磁直线电机性能的重要因素之一.摩擦力会使电机在运行时出现粘滞滑动现象,产生噪声,并且影响电机运行的跟踪精度[1].因此,为了增强直线电机的跟踪效果,降低粘滑现象的影响,必须对摩擦力加以抑制.
针对永磁直线电机所受的摩擦力,可从改善电机的工作环境和加强控制等角度加以抑制.改善电机的工作环境包括提高电机导轨的润滑程度和优化结构等方面.然而,只通过改善电机的工作环境并不能完全消除摩擦力,需借助控制来弥补.运用现代控制方法进行摩擦抑制是一个重要的趋势.文献[2-5]采用自适应方法对摩擦力进行抑制,但此种方法使得系统复杂度增高并且增加了系统计算量,给系统的实时控制带来影响.文献[6-8]中以扰动观测器为基础的摩擦力补偿方式,占用了额外的系统资源,增加了控制的成本.本文通过调节控制器使电机在某一速度下匀速运行,由测得的输出电流推算出电机所受的摩擦力.首先在三环闭环控制的基础上设计速度前馈和加速度前馈控制器,保证电机具有较快的响应速度和较好的跟踪性能.基于测得的电机运行速度和对应速度下运用差分进化算法辨识出摩擦模型中的参数,建立起摩擦的数学模型.基于该模型设计摩擦前馈控制器,进而抑制直线电机所受的摩擦力.
1 Gauss摩擦模型通过对摩擦的深入研究发现,当永磁同步直线电机运行在低速区时,摩擦力随着电机运行速度的增加,先减小后增加,这种摩擦力先减小后增加的现象被称为Stribeck效应.Stribeck效应的存在使得直线电机在低速运行时易出现粘滑现象.LuGre模型引入了鬃毛模型的思想,使其可以更为精细地描述摩擦现象.但该模型由于引入了无法测量的状态变量z,影响了其动态参数辨识结果的精确性[9],进而影响该模型的精确性.同时,LuGre摩擦模型较复杂,增加了基于该模型的前馈补偿器的设计难度,也增加了控制系统的计算量和复杂度.相比之下,Gauss模型考虑了负斜率现象,使得该模型能以近90%的精度拟合出电机在低速时所受的摩擦力[9-10],且基于模型的前馈控制器易于设计,复杂度低,更易于添加到控制系统中.故本文选择Gauss模型作为辨识对象,并基于该模型设计前馈补偿器.其数学表达式如式(1)所示:
| ${{F}_{\text{f}}}=\left[ {{F}_{\text{c}}}+\left( {{F}_{\text{s}}}-{{F}_{\text{c}}} \right){{\text{e}}^{-{{\left( \frac{\upsilon }{{{\upsilon }_{\text{s}}}} \right)}^{2}}}} \right]\text{sgn} \left( \upsilon \right)+B\upsilon ,$ | (1) |
式中:Ff为永磁直线电机所受的摩擦力,Fc为库仑摩擦力,Fs为电机的最大静摩擦力,B为粘滞系数,vs为电机的Stribeck速度,v为电机运行时的速度.Gauss摩擦模型很好地描述了电机低速运行时的摩擦特性,其可以有效地消除粘滑现象.
2 摩擦模型的建立及补偿方法 2.1 摩擦力的测量当电机采用id=0矢量控制时,其电流环的输出电流同电磁推力成正比.电机运行时的受力情况可用式(2)和式(3)表示:
| $F=ma+{{F}_{\text{r}}}+{{F}_{\text{f}}},$ | (2) |
| $F=K{{i}_{q}},$ | (3) |
式中:F为直线电机的电磁推力,m为电机的动子质量,a为电机运行时的加速度,Fr为推力波动,K为力常数,iq为直线电机的q轴电流.
直线电机所受的推力波动可通过优化电机的设计结构以及采用合适的控制策略来降低,因此推力波动可忽略不计.故电机的受力情况可简化为
| $F=ma+{{F}_{\text{f}}},$ | (4) |
当电机匀速运行时,电机所受的摩擦力可认为与电机输出的电磁推力相等,即F=Ff.因此,调节控制器使永磁直线电机以不同的速度进行匀速运动,获取电机的力常数和永磁同步直线电机的输出电流,即可得到电机所受的摩擦力,以此可进行摩擦参数的辨识.
2.2 基于差分进化算法的模型参数辨识为了获取摩擦模型的具体数学函数表达式,需对模型中的Fc,Fs,B和vs等参数进行辨识.差分进化算法拥有较好的全局搜索能力,当待辨识的参数较多时,同最小二乘法相比,其较容易跳出局部最优解.与遗传算法相比,差分进化算法所特有的一对一的竞争法则,降低了其运算的复杂性,在保证辨识准确性的前提下,具有更快的收敛速度,从而节省了辨识时间[11-18].因此,本文选用差分进化算法来辨识摩擦模型中的参数.
取待辨识摩擦模型的4个参数向量为个体,差分进化算法在每一步迭代所得到的摩擦模型参数的辨识值为
| ${{{\hat{\mathit{\pmb{x}}}}}_{m}}={{\left[ {{{\hat{F}}}_{\text{c}}},{{{\hat{F}}}_{\text{s}}},\hat{B},{{{\hat{\upsilon }}}_{\text{s}}} \right]}^{\text{T}}},$ | (5) |
式中:m=1,2,…,M,M为初始群体的数量;
由下式可得对应摩擦模型的辨识值:
| ${{{\hat{F}}}_{\text{f}}}=\left[ {{{\hat{F}}}_{\text{c}}}+\left( {{{\hat{F}}}_{\text{s}}}-{{{\hat{F}}}_{\text{c}}} \right){{\text{e}}^{-{{\left( \frac{\upsilon }{{{\upsilon }_{\text{s}}}} \right)}^{2}}}} \right]\text{sgn} \left( \upsilon \right)+\hat{B}\upsilon ,$ | (6) |
式中:
差分进化算法的适应度函数取为
| $J=\frac{1}{2}{{\sum\limits_{i=1}^{N}{\left( {{F}_{\text{f}}}-{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}}}_{\text{f}}} \right)}}^{2}},$ | (7) |
式中:
算法的实现过程如下:
1)产生初始种群:在4维向量空间里随机生成满足约束条件的M个个体;
2)变异操作:在群体中随机产生3个个体进行差分操作;
3)交叉操作:基于交叉概率因子引入新个体以增加群体的多样性;
4)选择操作:以适应度函数为评价标准,在实验向量和目标向量中进行选择.
反复执行2)到4)步,直至达到最大迭代次数.经过数代的计算得到最优个体,将其作为最优个体输出,即可获得模型中参数的最优辨识值,并显示拟合曲线.
2.3 摩擦力前馈控制补偿若能够预测出控制系统的误差,则可采用前馈控制直接对误差进行消除.永磁同步直线电机所受的摩擦力具有同速度相关的特性,因此,可以通过采用基于摩擦模型的前馈补偿控制的方法对摩擦力进行抑制.由于电机所受的摩擦力可看作以速度为自变量的函数,需对在多种恒速运行情况下的摩擦模型进行如上运算,辨识出摩擦模型中的参数,即获得
|
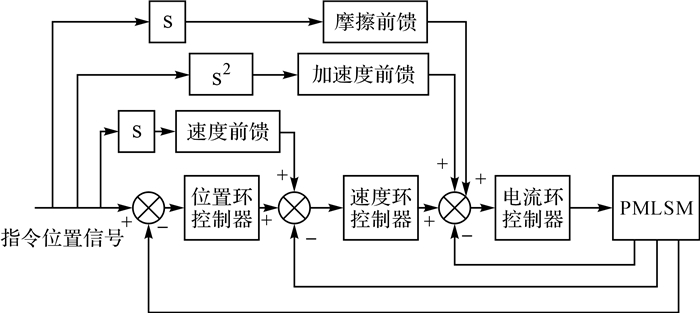
| 图 1 电机控制系统的结构框图 Fig.1 The structure diagram of the motor control system |
本文在MATLAB/Simulink中建立位置闭环、速度闭环和电流闭环的三环控制系统,将直线电机作为仿真对象,电机参数如表 1所示.
| 参数 | 量值 |
| 动子质量 | 2.3 kg |
| 力常数(N/A) | 63.9 |
| 行程 | 386 mm |
| 峰值推力 | 729 N |
| 连续推力 | 243 N |
| 极距 | 32 mm |
| 阻抗(L-L),25 ℃ | 7.8 Ω |
| 最大线圈温度 | 100 ℃ |
电机的摩擦特性可表示为与电机速度相关的函数,因此基于摩擦模型补偿时要求电机具有较高的跟踪能力.研究发现虽然通过负反馈可以提高永磁同步直线电机的稳定性,一定程度上减小电机的跟踪误差,但单纯采用负反馈控制很难满足定位精度高、响应时间快的要求且电机的跟踪性能仍不理想,不利于基于摩擦模型的前馈补偿.为提高直驱伺服系统的响应速度,可采用将速度和加速度的指令信号分别乘以Kv和Ka变为前馈信号补偿到速度环和电流环的输入端的方法,系统框图如图 1所示.
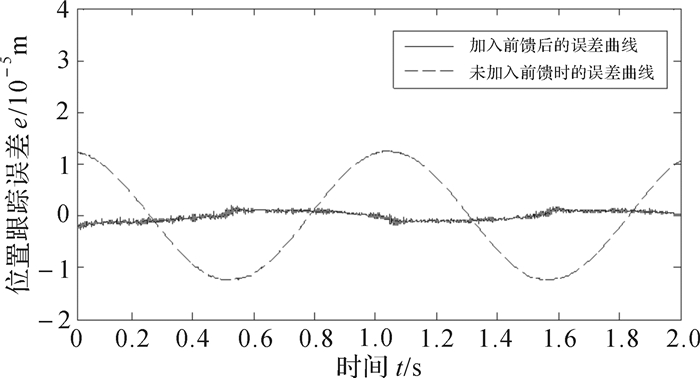
假设电机按正弦轨迹运动,且其最大速度为100 mm/s.其中Kv取值范围一般为0.85~1.1.通过对电机多次的调试比对,本文选用Kv=0.95.由式(2)可得,电机的加速度前馈控制器Ka应设为m/K,其中m为电机的运动质量,K为电机的电磁推力常数.加入速度前馈和加速度前馈前后的位置跟踪误差仿真曲线如图 2所示.由图 2易知,没加入速度前馈和加速度前馈时的位置跟踪误差是12.5 μm,加入速度前馈和加速度前馈后的位置跟踪误差是1.8 μm.由此可见,加入速度前馈和加速度前馈后,位置跟踪误差明显减小,增强了电机的跟踪性能.
|
| 图 2 速度前馈和加速前馈补偿前后的位置跟踪误差曲线 Fig.2 The tracking error curve before and after adding speed feed-forward and acceleration feed-forward compensation |
根据上述分析,摩擦力可以表示为同速度相关的函数.假设电机按正弦轨迹运动,且其最大速度为300 mm/s.按照式(1),设定直线电机摩擦力模型参数,表达式如式(8):
| $\begin{align} & {{F}_{\text{f}}}=\left[ 18.9272+8.0512{{\text{e}}^{-{{\left( \frac{\upsilon }{0.0172} \right)}^{2}}}} \right]\text{sgn} \left( \upsilon \right)+ \\ & \ \ \ \ \ \ \ 56.6223\upsilon , \\ \end{align}$ | (8) |
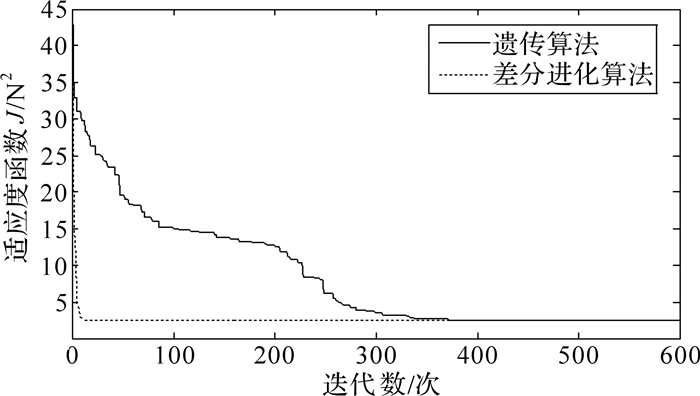
在Simulink中,构建直线电机三环控制模型,加入速度前馈控制器与加速度前馈控制器,并将上文提出的摩擦前馈补偿方法加入系统中,如图 1所示.Gauss摩擦模型中的未知参数分别用最小二乘法、遗传算法和差分进化算法进行辨识,辨识结果如表 2所示.其中,遗传算法和差分进化算法选择相同规模的初始种群数量和最大迭代次数.由表 2可知,运用最小二乘法辨识的模型参数误差较大,而用遗传算法和差分进化算法辨识的模型参数误差较小.遗传算法和差分进化算法的适应度函数J的优化过程如图 3所示.
| 待辨识 参数 |
设定值 | 差分进化 算法辨识值 |
遗传算法 辨识值 |
最小二乘法 辨识值 |
| Fc | 18.927 2 | 19.136 3 | 19.135 8 | 18.56 |
| Fs | 26.978 4 | 26.897 7 | 26.896 7 | 25.63 |
| vs | 0.017 2 | 0.017 3 | 0.017 3 | 0.021 8 |
| B | 56.622 3 | 57.358 4 | 57.761 9 | 59.26 |
|
| 图 3 遗传算法和差分进化算法的适应度函数J的优化过程 Fig.3 The optimization process of the fitness function J based on the genetic algorithm and the differential evolution algorithm |
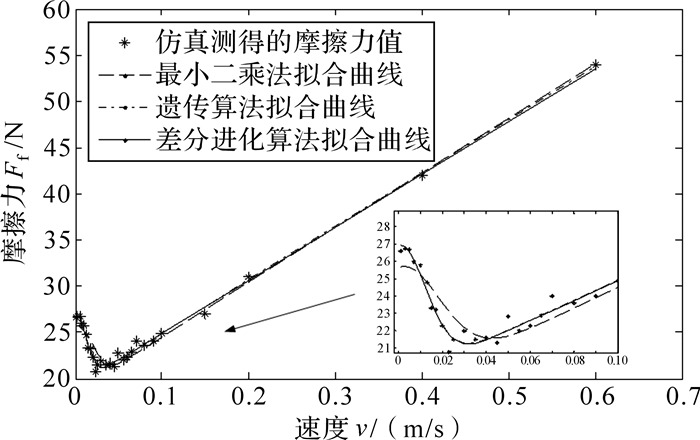
由图 3可以看出,相比于遗传算法,差分进化算法凭借其特有的一对一竞争法则能以更快的速度收敛.故本文采用的差分进化算法可以在保证辨识精度的前提下,节省辨识时间,对于需要进行多组辨识运算的实验来说是非常利的.基于3种辨识方法得到的摩擦力拟合曲线如图 4所示.
|
| 图 4 3种算法的摩擦力拟合曲线 Fig.4 The friction force fitting curves obtained by three algorithms |
从表 2和图 4可以看出,辨识出的摩擦力与给定摩擦力存在着差异,这是由于测得的输出电流受噪声干扰以及辨识方法存在误差所造成的.
3.3 仿真结果讨论在MATLAB/simulink中搭建电机的三环控制器以及速度前馈和加速度前馈控制器,将摩擦力变换成相应的电流值添加到电流环控制器中,以消弱摩擦对电机的影响.当电机运行以最高速度为300 mm/s作正弦运动时,其补偿前后的速度曲线和位置跟踪误差曲线如图 5(a)和(b)所示.
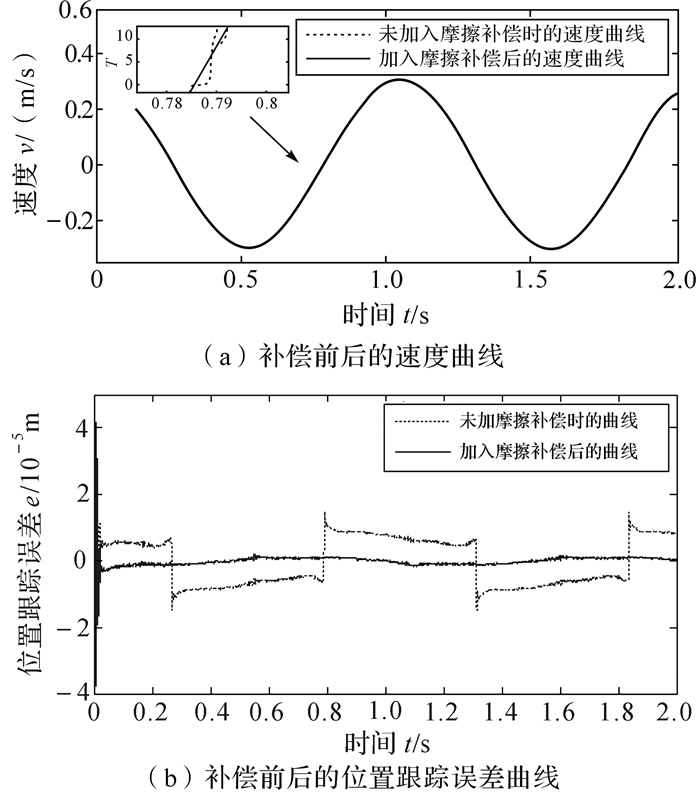
|
| 图 5 补偿前后的速度曲线和位置跟踪误差曲线 Fig.5 The speed curve and the position tracking error curve before and after compensation |
从图 5(a)可以看到,在没有摩擦力补偿时,永磁直线电机运行时受摩擦的影响较大,电机在速度转向处出现了粘滞滑动现象,而加入摩擦力补偿后电机的粘滞滑动现象被明显抑制.
由图 5(b)可知,没加入摩擦前馈补偿时电机运行的位置跟踪误差为14.5 μm.对直线电机进行摩擦补偿后,其运行的位置跟踪误差为2.5 μm.
从仿真实验结果可以看出,补偿后位置跟踪误差较未补偿降低80%以上,摩擦力的影响得到了明显削弱,验证了本文提出的辨识方法及前馈补偿策略是可行的.
应当指出的是,电机在运行时输出电流受噪声的影响,使得辨识出的摩擦数学模型存在误差,导致摩擦不能完全被抑制.下一步工作是探索更好的抑制电机噪声的方法,提高摩擦模型的辨识精度,使得补偿效果更好.
4 结论针对摩擦力对永磁直线电机动态特性的影响,本文建立了基于摩擦力数学模型的前馈补偿方法.首先建立电机的三环控制器以及速度前馈控制器和加速度前馈控制器,使电机具有良好的跟踪精度.其次,采取合适的控制策略使电机在某些速度下恒速运行,将测得的输出电流信号与电机的力常数相乘得到电机所受的摩擦力,然后采用差分进化算法辨识出摩擦模型中的参数,最后由辨识出的摩擦模型设计前馈控制器.仿真实验结果表明该方法明显抑制了直线电机速度转向时的粘滑现象和位置跟踪误差.且本文提出的摩擦前馈补偿方法实现过程较为简单,前馈控制器结构简单、计算量小并且可进行实时补偿.
| [1] | ARMSTRONG-HELOUVRY B, DUPONT P, DE-WIT C C. A survey of models, analysis tools and compensation methods for the control of machines with friction[J]. Automatica , 1994, 30 (7) : 1083–1138. DOI:10.1016/0005-1098(94)90209-7 |
| [2] |
向红标, 王收军, 张春秋, 等.
Stribeck模型自适应滑模摩擦补偿控制[J]. 中国测试 , 2015, 41 (9) : 92–95.
XIANG Hong-biao, WANG Shou-jun, ZHANG Chun-qiu, et al. Adaptive sliding friction compensation based on Stribeck model[J]. China Measurement & Test , 2015, 41 (9) : 92–95. |
| [3] | LEE T H, TAN K K, HUANG S. Adaptive friction compensation with a dynamical friction model[J]. IEEE/ASME Transactions on Mechatronics , 2011, 16 (1) : 133–140. DOI:10.1109/TMECH.2009.2036994 |
| [4] | LI Z, CHEN J, ZHANG G, et al. Adaptive robust control of servo mechanisms with compensation for nonlinearly parameterized dynamic friction[J]. IEEE Transactions on Control Systems Technology , 2013, 21 (1) : 194–202. DOI:10.1109/TCST.2011.2171966 |
| [5] |
路瑶, 何秋生, 苑伟华.
考虑摩擦伺服系统的补偿算法研究[J]. 微特电机 , 2015, 43 (7) : 71–74.
LU Yao, HE Qiu-sheng, YUAN Wei-hua. Research on compensation algorithm for servo system with friction[J]. Small & Special Electrical Machines , 2015, 43 (7) : 71–74. |
| [6] | XIA D, CHAI T, WANG L. Fuzzy neural-network friction compensation-based singularity avoidance energy swing-up to nonequilibrium unstable position control of pendubot[J]. IEEE Transactions on Control Systems Technology , 2014, 22 (2) : 690–705. DOI:10.1109/TCST.2013.2255290 |
| [7] |
王丽梅, 李兵.
基于摩擦观测器的直接驱动XY平台轮廓控制器设计[J]. 电机与控制学报 , 2013, 17 (1) : 31–36.
WANG Li-mei, LI Bing. Contour control design for direct drive XY table based on friction observer[J]. Electric Machines and Control , 2013, 17 (1) : 31–36. |
| [8] |
潘晴, 黄明辉, 李毅波.
大型液压机驱动系统摩擦补偿控制[J]. 机械科学与技术 , 2015, 34 (2) : 204–208.
PAN Qing, HUANG Ming-hui, LI Yi-bo. The friction compensation for giant hydraulic press[J]. Mechanical Science and Technology for Aerospace Engineering , 2015, 34 (2) : 204–208. |
| [9] | PIATKOWSKI T. Dahl and LuGre dynamic friction models: the analysis of selected properties[J]. Mechanism and Machine Theory , 2014, 73 (7) : 91–100. |
| [10] |
李鹏勃, 赵飞, 梅雪松, 等.
基于进给系统反馈信号的摩擦辨识方法[J]. 组合机床与自动化加工技术 , 2012 (11) : 4–7.
LI Peng-bo, ZHAO Fei, MEI Xue-song, et al. A friction identification method based on feedback signals of servo feed system[J]. Modular Machine Tool & Automatic Manufacturing Technique , 2012 (11) : 4–7. |
| [11] |
胡超杰.差分进化算法及其在电机参数辨识中的应用研究[D].长沙:湖南大学电气与信息工程学院, 2013: 1-54.
HU Chao-jie. The research on differential evolution algorithm and its application in motor parameter identification[D]. Changsha: Hunan University, College of Electrical and Information Engineering, 2013: 1-54. |
| [12] |
吴亮红.差分进化算法及应用研究[D].长沙:湖南大学电气与信息工程学院, 2007:1-96.
WU Liang-hong. The research on differential evolution algorithm and its application[D]. Changsha: Hunan University, College of Electrical and Information Engineering, 2007: 1-96. |
| [13] |
刘柏希, 姚昊雄, 聂松辉.
基于区间分析的LuGre摩擦模型参数辨识方法[J]. 中国机械工程 , 2013, 24 (19) : 2647–2652.
LIU Bai-xi, YAO Hao-xiong, NIE Song-hui. Parameter identification of LuGre friction model based on interval analysis[J]. China Mechanical Engineering , 2013, 24 (19) : 2647–2652. |
| [14] | YANADA H, SEKIKAWA Y. Modeling of dynamic behaviors of friction[J]. Mechatronics , 2008, 18 (7) : 330–339. DOI:10.1016/j.mechatronics.2008.02.002 |
| [15] | ALONGE F, DIPPOLITO F, RAIMONDI F. Least squares and genetic algorithms for parameter identification of induction motors[J]. Control Engineering Practice , 2001, 9 (6) : 647–657. DOI:10.1016/S0967-0661(01)00024-7 |
| [16] |
刘强, 扈宏杰, 刘金琨, 等.
基于遗传算法的伺服系统摩擦参数辨识研究[J]. 系统工程与电子技术 , 2003, 25 (1) : 77–79.
LIU Qiang, HU Hong-jie, LIU Jin-kun, et al. Research on parameter identification of friction model for servo systems based on genetic algorithms[J]. Systems Engineering and Electronics , 2003, 25 (1) : 77–79. |
| [17] |
周林, 彭程, 梁青, 等.
直流伺服系统静态摩擦的最小二乘辨识[J]. 电子技术 , 2012 (10) : 31–33.
ZHOU Lin, PENG Cheng, LIANG Qing, et al. The least square identification of static friction in servo system[J]. Electronics Technology , 2012 (10) : 31–33. |
| [18] | GLUCL T, KEMMETMULLER W, TUMP C, et al. A novel robust position estimator for self-sensing magnetic levitation systems based on least squares identification[J]. Control Engineering Practice , 2011, 19 (2) : 146–157. DOI:10.1016/j.conengprac.2010.11.003 |



