2. 中南大学 机电工程学院, 湖南 长沙 410083
2. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China
燃气轮机长期在高温恶劣的环境下工作,导致其故障率较高.据德国Siemens公司统计,燃气轮机机组发生的故障,58%是组合转子造成的[1],因此研究组合转子性能退化规律具有重要的意义,且该研究领域也将成为未来航空发动机和燃气轮机“两机”科技重大专项中的核心部分.由于蠕变、裂纹、磨损、松弛等诸多因素,会导致组合转子性能退化[2],但目前有关组合转子退化的研究较少,仅有少量研究人员以轮盘与拉杆裂纹[3]、螺纹自松弛[4]、拉杆松弛[5]等局部微缺陷为切入点,对组合转子的退化机理进行了初步研究.
燃气轮机组合转子由于在高温环境下运行,且存在较大的离心应力,其轮盘会发生蠕变,使得组合转子性能退化,甚至破坏机组的正常运行,引发事故.例如:在1974年6月19日,在美国的Tennessee州,一台燃气轮机机组由于组合转子轮盘蠕变,组合转子叶片及轮盘的径向位移超出了叶片与机壳的间隙而发生顶心,引发事故[6].目前针对轮盘蠕变引起的组合转子性能退化研究较少.邬文睿等[7]、Hongyin等[8]针对汽轮机转子涡轮轮盘的高温强度进行了研究,针对组合转子产生轮盘蠕变效应的区域、考虑轮盘蠕变的必要性及蠕变对于轮盘内部应力分布进行了研究;李全通等[9]建立了轮盘蠕变应变的理论概率模型;Lagneborg等[10]、曾攀[11]针对轮盘蠕变及低周疲劳寿命可靠性进行了分析,并提出了考虑应力松弛的轮盘蠕变效应及两者共同作用下轮盘寿命的计算方法;孙燕平等[12]、崔亚辉等[13]考虑到转子的蠕变效应,研究了转轴偏心力、叶片离心力、初始弯曲等因素导致的蠕变弯曲,得到了转子发生蠕变的主要区域及蠕变弯曲量随时间的变化规律,从理论上证明了转子的弯曲原因为高温蠕变.
综上所述,目前并不清楚轮盘蠕变引起组合转子性能退化的机理.为此,本文拟针对某重型燃气轮机组合转子,通过建立考虑轮盘间结合面刚度的有限元模型,研究组合转子在额定工况下的轮盘蠕变效应及其对组合转子性能退化的影响规律.
1 组合转子有限元模型燃气轮机根据装机量以及型号的不同,其核心部件组合转子具有不同的拉杆数目及轮盘级数.本文以某型燃气轮机组合转子为对象展开研究.图 1所示为该组合转子有限元模型,组合转子由压气机、燃烧室、透平三部分组成,其中压气机端有17级轮盘,透平端有4级轮盘,中间为燃烧室,压气机端及透平端轮盘均由周向分布的12根拉杆通过预紧力紧密连接在一起,尺寸参数如表 1所示.根据工程实际,选取组合转子材质为GH4169,该材料密度为7 850 kg·m-3,弹性模量为210 GPa.

|
| 图 1 组合转子有限元模型 Fig.1 Finite element model of combined rotor |
| 尺寸参数 | 量值/mm |
| 转子总长lrotor | 11 582 |
| 压气机端4至7级轮盘厚度ldisk4-7 | 311 |
| 压气机端8至11级轮盘厚度ldisk8-11 | 301 |
| 压气机端12至14级轮盘厚度ldisk12-14 | 190 |
| 压气机端15至17级轮盘厚度ldisk15-17 | 150 |
| 燃烧室长度 | 1 905 |
| 透平端1,2级轮盘厚度 | 304 |
| 透平端3,4级轮盘厚度 | 295 |
| 轮盘直径ddisk | 1 424 |
| 拉杆直径drod | 80 |
| 拉杆长度lrod | 3 740 |
接触界面是组合转子中最特别的部位,组合转子结构完整性与接触界面密切相关,深入研究组合转子接触界面的特性,对于精确地分析组合转子的动态特性具有积极的意义[14].因拉杆穿越孔与拉杆螺栓及轮盘与轴端拉杆螺母之间的接触界面刚度对组合转子弯曲振动的影响较小,因此本文主要考虑两轮盘间结合面刚度这一重要因素.
通过综合运用GW模型研究方法及有限元法来计算两轮盘间的接触刚度[15].首先建立能体现轮盘表面粗糙度的微元体模型,并对微元体的接触刚度进行分析计算,然后通过公式(1)、(2)得到轮盘结合面的法向刚度.
| $ K = \frac{{{S_1}}}{{{S_2}}}{k_{\rm{n}}}, $ | (1) |
| $ F = P \times {S_1}, $ | (2) |
式中:S1为轮盘结合面面积,S2为微元体模型结合面面积,kn为微元体模型法向刚度,K为轮盘界面法向刚度,P为预紧后的界面压力,F为预紧力.
组合转子轮盘间结合面接触属于非线性问题,因此对于结合面的处理无法直接利用有限元法进行解决[16].本文采用将结合面等效为虚拟材料层的方法(如图 2所示).基于上述对轮盘结合面法向接触刚度的计算结果,利用应变能相等原则,真实轮盘结合面总的法向应变能应与等效为虚拟材料层后的总法向应变能相等,可得到虚拟材料层弹性模量与结合面的法向刚度关系式:

|
| 图 2 虚拟材料层等效示意图 Fig.2 The equivalent diagram of virtual material layer |
| $ \bar E = Kh/{S_1}, $ | (3) |
式中:h为虚拟材料层的厚度,S1为结合面面积.
本文主要研究组合转子的弯曲振动特性,将虚拟材料层厚度设置为2 mm,模型中轮盘与虚拟材料层间的接触采用多点约束技术,其他接触界面均采用No Separation接触.所建立模型的计算结果与该重型燃气轮机的实测结果[17]如表 2所示,结果表明所建立模型与实际模型偏差小,模型可靠.
| 对比项 | 1阶弯振频率 | 2阶弯振频率 | 3阶弯振频率 |
| 模型计算结果 | 20.8 | 43.1 | 57.5 |
| 实测结果 | 17.5 | 41.7 | 55.8 |
组合转子长期在高温环境下运行,组合转子轮盘由于承受离心力作用将发生蠕变.本节将对组合转子轮盘蠕变变形量进行计算.
2.1 蠕变模型及参数蠕变一般分为3个阶段:初始阶段、稳定阶段、加速阶段[6].因为燃气轮机组合转子蠕变时间长,大部分时间处于蠕变稳定阶段,因此本文采用Norton蠕变模型(蠕变的第2阶段),本构方程如式(4)所示:
| $ {{\dot \varepsilon }_{\rm{C}}} = {C_1}{\sigma ^{{C_2}}}{{\rm{e}}^{\left( { - {C_3}/T} \right)}}, $ | (4) |
式中:$ \dot \varepsilon $C为应变求导;σ为加载应力;T为热力学温度;C1,C2,C3为蠕变公式参数.
根据文献[18]中针对GH4169材料的蠕变试验,采用最小二乘法计算式(4)中的蠕变参数,得到Norton蠕变模型的参数,如表 3所示.
参考文献[19],本文不考虑单级轮盘之间的轴向温差,对其进行热分析,得到组合转子运行过程中的温度分布如图 3所示,图 4给出了蠕变数据采集点位置.

|
| 图 3 组合转子运行温度分布 Fig.3 Operation temperature distribution of combined rotor |

|
| 图 4 蠕变量数据采集点示意图 Fig.4 Sketch map of acquisition point of creep data |
以组合转子运行转速为3 000 r/min为例进行计算,利用ANSYS对组合转子进行蠕变分析,运行时应力分布如图 5所示,图 6为各采集点蠕变伸长量曲线.

|
| 图 5 组合转子应力分布图 Fig.5 Stress distribution diagram of combined rotor |
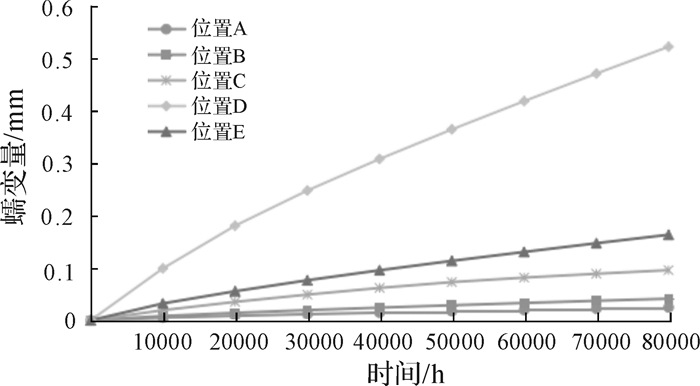
由图 6可以看出:1)组合转子蠕变速率随着时间的增加而减小;2)透平端第1级蠕变速率最快,在80 000 h时蠕变量达到了0.5 mm,这可以为燃气轮机组合转子结构设计中顶隙大小的确定提供参考.
|
| 图 6 各采集点蠕变伸长量曲线 Fig.6 Creep elongation curves of each acquisition point |
组合转子在不同的转速下运行,会产生不同的离心应力作用,这对于组合转子轮盘蠕变速率将产生重要影响,因此本节将重点研究转速对组合转子轮盘蠕变速率的影响.
因透平端第1级蠕变速率最快,该位置(即位置D)的蠕变伸长量最大,将对组合转子的运行产生较大影响,能够反映整个组合转子的轮盘蠕变伸长量变化速率,所以取该位置不同转速下的蠕变伸长量曲线进行分析.
由图 7可知:不同转速下,轮盘蠕变伸长量均随时间的增加缓慢增加,且蠕变速率逐渐减小;转速对于组合转子轮盘蠕变速率影响较大,转速变化300 r/min,轮盘蠕变速率成倍变化.在工程实际中,若增加转速,需重点考虑其对轮盘蠕变速率的影响.

|
| 图 7 转速对轮盘蠕变速率的影响 Fig.7 Effect of rotating speed on creep rate of turbine discs |
从轮盘蠕变导致组合转子整体刚度及结构变化的角度出发,揭示轮盘蠕变导致组合转子性能退化的机理,研究方法如图 8所示.组合转子轮盘在高温和离心应力作用下将发生蠕变,轮盘变薄,致使拉杆预紧力降低,结合面刚度发生变化,基于本文提出的利用虚拟材料层对轮盘间结合面刚度进行等效的方法,研究其动力学特性,定量地研究组合转子性能退化轨迹,并研究不同转速及拉杆数目下组合转子性能退化速率的变化规律.

|
| 图 8 轮盘蠕变引起组合转子性能退化的研究方法 Fig.8 Research method on the performance degradation of combined rotor caused by turbine discs creep |
根据图 8的研究方法,在转速为3 000 r/min和额定温度环境下,取拉杆初始预紧力为拉杆长度的1/1 000,且假定拉杆预紧力与伸长量呈线性相关,研究轮盘蠕变引起的拉杆预紧力变化规律,对组合转子进行动力学分析,如表 4所示为轮盘蠕变引起的组合转子前3阶弯曲频率随时间的变化关系.发现随着时间的增加,轮盘蠕变量增加,导致组合转子的前3阶弯振频率均发生漂移.
| 时间 t/h |
1阶弯振 频率/Hz |
2阶弯振 频率/Hz |
3阶弯振 频率/Hz |
| 0 | 19.128 | 44.103 | 58.535 |
| 10 000 | 19.107 | 44.049 | 58.468 |
| 20 000 | 19.091 | 44.006 | 58.411 |
| 30 000 | 19.078 | 43.982 | 58.382 |
| 40 000 | 19.068 | 43.958 | 58.359 |
| 50 000 | 19.06 | 43.939 | 58.334 |
| 60 000 | 19.053 | 43.923 | 58.312 |
| 70 000 | 19.047 | 43.911 | 58.293 |
| 80 000 | 19.041 | 43.899 | 58.272 |
组合转子的性能退化对燃气轮机的影响主要是振动造成的.组合转子的振动特性可由弯振频率表征,且弯振频率在工程上易于测量,因此,定义弯振固有频率作为性能退化参数,退化量定义式为
| $ \eta = \frac{{{f_0} - {f_t}}}{{{f_0}}}, $ | (9) |
式中:f0为初始时刻弯振频率,ft为t时刻弯振频率.
依照表 4中组合转子前3阶弯振频率随时间的变化关系,得到性能退化数据,对数据进行拟合,得到退化轨迹(图 9).

|
| 图 9 组合转子性能退化轨迹 Fig.9 Performance degradation trajectory of combined rotor |
由图 9可知,轮盘蠕变引起的组合转子性能退化量随时间缓慢增加,组合转子性能退化速率随时间增加而降低.
3.3 不同转速下轮盘蠕变引起组合转子性能退化速率的变化组合转子轮盘在不同转速下具有不同的应力分布及蠕变速率,保持组合转子的温度、拉杆数目、轮盘级数不变,考虑到工程实际,分别对2 400,2 700,3 000,3 300,3 600 r/min转速下的组合转子进行蠕变及动力学分析,得到不同转速下组合转子退化数据,拟合出退化轨迹(见图 10).

|
| 图 10 不同转速下组合转子性能退化轨迹 Fig.10 Performance degradation trajectory of combined rotor under different rotating speed |
由图 10可知:不同转速下,轮盘蠕变速率及退化速率均逐渐减小;转速对于组合转子轮盘蠕变速率影响较大,转速变化300 r/min时,轮盘蠕变速率及退化速率成倍变化.在工程实际中,若增加转速,需重点考虑其对轮盘蠕变速率及使用寿命的影响.
3.4 不同拉杆数目下轮盘蠕变引起组合转子性能退化速率的变化保持温度、转速、轮盘级数及拉杆初始总预紧力不变,分别对12,16,24根拉杆预紧的组合转子进行蠕变及动力学分析,分别得出不同拉杆数目下组合转子退化数据,拟合出退化轨迹(图 11).

|
| 图 11 不同拉杆数目下组合转子性能退化轨迹 Fig.11 Performance degradation trajectory of combined rotor under different number of rod |
由图 11可以看出:不同拉杆数目下,组合转子退化速率均逐渐减小;随着拉杆数目的增加,组合转子退化速率均加快.
4 组合转子性能退化模型验证实验组合转子轮盘蠕变时间较长,且其引起的退化过程十分缓慢,难以进行基于组合转子蠕变特性的实验研究.因此采用间接法进行实验研究.研究组合转子在不同预紧力条件下(轮盘蠕变引起)的固有频率变化规律,将实验结果与仿真结果对比,从而论证理论分析结果的正确性.
由于研究对象为真实组合转子模型,尺寸大、结构复杂,不易进行实验研究,因此,在组合转子简化模型上进行研究.该模型实物图及示意图如图 12所示,各尺寸参数如表 5.

|
| 图 12 组合转子实验模型 Fig.12 Experimental model of combined rotor |
| 尺寸参数 | 量值/mm |
| 转子总长lrotor | 1 972 |
| 轮盘宽度ldisk | 91 |
| 轮盘部分直径Ddisk | 317 |
| 转轴部分直径dshaft | 50 |
| 拉杆周向直径Drod | 269 |
| 拉杆直径drod | 80 |
首先对实验模型进行轮盘蠕变分析,得到不同时刻压气机端与透平端预紧力的大小,然后分别利用实验方法与有限元理论分析方法对组合转子固有特性进行测试与计算.实验研究时采用锤击法在组合转子上施加脉冲激励,引起组合转子自由振动,然后利用位移传感器采集组合转子的响应,分析得到组合转子的固有频率[20].表 6所示为组合转子在不同时刻弯振频率的实验与仿真结果对比.
| 时间/h | 透平端 预紧力/N |
压气机端 预紧力/N |
仿真值/ Hz |
实验值/ Hz |
| 0 | 42 000 | 42 200 | 48.91 | 48.08 |
| 10 000 | 41 850 | 42 000 | 48.83 | 48.00 |
| 20 000 | 41 150 | 41 850 | 48.76 | 47.93 |
| 30 000 | 40 600 | 41 700 | 48.71 | 47.88 |
| 40 000 | 40 100 | 41 550 | 48.67 | 47.84 |
| 50 000 | 39 650 | 41 450 | 48.64 | 47.82 |
| 60 000 | 39 250 | 41 350 | 48.61 | 47.79 |
| 70 000 | 38 850 | 41 250 | 48.59 | 47.76 |
| 80 000 | 38 450 | 41 150 | 48.57 | 47.74 |
按照前面对于组合转子性能退化量的定义式,取1阶弯振频率为退化参数,实验与仿真的退化轨迹如图 13.

|
| 图 13 实验与仿真的退化轨迹对比 Fig.13 Comparison of experimental and simulation degradation traigectories |
根据图 13可知,实验方法得到的模型性能退化轨迹与仿真分析结果相差很小,这在一定程度上验证了轮盘蠕变引起组合转子性能退化研究理论与方法的正确性.
5 结论本文提出了轮盘蠕变引起组合转子性能退化特性的研究思路及方法,研究了不同转速、拉杆数目下轮盘蠕变引起组合转子性能退化速率的变化规律,并对理论分析结果进行了一定的实验验证.研究结果表明:在高温、高转速共同作用下燃气轮机组合转子轮盘势必会发生蠕变,组合转子蠕变速率随着时间的增加而减小,透平端第1级蠕变速率最快;随着时间的增加,轮盘蠕变将引起组合转子性能退化,且轮盘蠕变引起的组合转子性能退化对于转速、拉杆数目的敏感性不容忽视,转速越大、拉杆数目越多,组合转子退化速率越快,在工程上需予以重点关注.
| [1] | HALL D K. Performance Limits of turbomachines[D]. Massachusetts: Massachusetts Institute of Technology, 2010: 102-113. |
| [2] | LEE J. Measurement of machine performance degradation using a neural network model[J]. Computers in Industry , 1996, 30 (3) : 193–209. DOI:10.1016/0166-3615(96)00013-9 |
| [3] |
李雪鹏, 王艾伦.
拉杆疲劳裂纹导致的组合转子性能退化研究[J]. 工程设计学报 , 2014, 21 (4) : 382–388.
LI Xue-peng, WANG Ai-lun. Research on performance degradation of combined rotor considering the fatigue crack in the rod[J]. Chinese Journal of Engineering Design , 2014, 21 (4) : 382–388. |
| [4] |
何竞飞, 万闯建.
螺栓联接在偏心载荷下螺纹载荷分布规律研究[J]. 机械科学与技术 , 2015, 20 (8) : 1149–1152.
HE Jing-fei, WAN Chuang-jian. Study on load distribution in the screw thread of bolt-joint subjected to eccentric loading[J]. Mechanical Science and Technology for Aerospace Engineering , 2015, 20 (8) : 1149–1152. |
| [5] |
苏永雷, 王艾伦, 李雪鹏, 等.
拉杆松弛对燃气轮机组合转子性能退化的影响[J]. 工程设计学报 , 2014, 21 (3) : 245–250.
SU Yong-lei, WANG Ai-lun, LI Xue-peng, et al. Effect of rod relaxation upon performance degradation of combined rotor for gas turbine[J]. Chinese Journal of Engineering Design , 2014, 21 (3) : 245–250. |
| [6] |
穆霞英.
蠕变力学[M]. 西安: 西安交通大学出版社 ,1990 : 87 -98.
MU Xia-ying. Creep mechanics[M]. Xi'an: Xi'an Jiaotong University Press , 1990 : 87 -98. |
| [7] |
邬文睿, 王炜哲.
660 MW超超临界汽轮机高压转子的高温蠕变强度分析[J]. 动力工程学报 , 2009, 29 (2) : 99–103.
WU Wen-rui, WANG Wei-zhe. Strength analysis of high-temperature creep for a 660 MW ultra supercritical steam turbine high-pressure rotor[J]. Journal of Chinese Society of Power Engineering , 2009, 29 (2) : 99–103. |
| [8] | HONGYIN Mao, SANKARAN Mahadevan. Probabilistic analysis of creep-fatigue failure[J]. International Journal of Fatigue , 2000, 22 (1) : 789–797. |
| [9] |
李全通, 景小宁, 吕文林.
基于人工神经网络的涡轮盘蠕变可靠性分析方法[J]. 航空动力学报 , 2003, 18 (2) : 211–215.
LI Quan-tong, JING Xiao-ning, LV Wen-lin. Artificial neural networks-based creep reliability analysis method of turbine disk[J]. Journal of Aerospace Power , 2003, 18 (2) : 211–215. |
| [10] | LAGNEBORG R, ATTRMO R. The effect of combined low-cycle fatigue and creep on the life of Austenitic stainless steels[J]. Meta1Trans , 1971, 18 (2) : 1821–1827. |
| [11] |
曾攀.
蠕变-疲劳交互作用下的结构分析[J]. 固体力学学报 , 1994, 15 (1) : 65–70.
ZENG Pan. Structural analysis under creep-fatigue interaction[J]. Chinese Journal of Solid Mechanics , 1994, 15 (1) : 65–70. |
| [12] |
孙燕平, 庞春凤.
弯曲残余应力对转子蠕变性能的影响研究[J]. 机械工程学报 , 2014, 50 (10) : 162–165.
SUN Yan-ping, PANG Chun-feng. Research on rotor creep properties under bending residual stress[J]. Journal of Mechanical Engineering , 2014, 50 (10) : 162–165. |
| [13] |
崔亚辉, 张俊杰, 蒋东翔.
超临界600MW机组汽轮机转子蠕变特性分析[J]. 热力发电 , 2013, 42 (12) : 69–71.
CUI Ya-hui, ZHANG Jun-jie, JIANG Dong-xiang, et al. Research on creep characteristic of a supercritical 600MW unit turbine rotor[J]. Thermal Power Generation , 2013, 42 (12) : 69–71. |
| [14] | GOERKE D, WILLNER K. Normal contact of fractal surfaces-experimental and numerical investigations[J]. Wear , 2008, 264 (7) : 589–598. |
| [15] |
李辉光, 刘恒, 虞烈.
粗糙机械结合面的接触刚度研究[J]. 西安交通大学学报 , 2011, 45 (6) : 69–74.
LI Hui-guang, LIU Heng, YU Lie. Contact stiffness of rough mechanical joint surface[J]. Journal of Xi'an Jiaotong University , 2011, 45 (6) : 69–74. |
| [16] |
艾延廷, 翟学, 王志, 等.
法向接触刚度对装配体振动模态影响的研究[J]. 振动与冲击 , 2012, 31 (6) : 171–174.
AI Yan-ting, ZHAI Xue, WANG Zhi, et al. Influence of normal stiffness on an assembly's vibration modes[J]. Journal of Vibration and Shock , 2012, 31 (6) : 171–174. |
| [17] |
李辉光, 刘恒, 虞烈.
考虑接触刚度的燃气轮机拉杆转子动力特性研究[J]. 振动与冲击 , 2012, 31 (7) : 4–8.
LI Hui-guang, LIU Heng, YU Lie. Dynamic characteristics of a rod fastening rotor for gas turbine considering contact stiffness[J]. Journal of Vibration and Shock , 2012, 31 (7) : 4–8. |
| [18] |
李玲.涡轴发动机转子连接螺栓的强度与蠕变寿命研究[D].南京:南京航空航天大学能源与动力学院, 2008:58-65.
LI Ling. Research on strength and creep life of connecting bolts in turboshaft engine rotors[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, College of Energy and Power Engineering, 2008:58-65. |
| [19] |
刘少权, 张艳春, 杜兆钢, 等.
温度场对燃气轮机拉杆转子临界转速的影响[J]. 燃气轮机技术 , 2011, 24 (2) : 20–23.
LIU Shao-quan, ZHANG Yan-chun, DU Zhao-gang, et al. Prediction of the influence of temperature field on the critical speeds of a rod-fastened rotor[J]. Gas Turbine Technology , 2011, 24 (2) : 20–23. |
| [20] |
李雪鹏, 王艾伦.
频繁启停过程中拉杆微裂纹引起的组合转子性能退化研究[J]. 工程设计学报 , 2015, 22 (2) : 129–136.
LI Xue-peng, WANG Ai-lun. Research on performance degradation of combined rotor considering the micro crack on the rod caused by frequent start-up and stop-down[J]. Chinese Journal of Engineering Design , 2015, 22 (2) : 129–136. |



