1. School of Automobile and Transportation, Qingdao University of Technology, Qingdao 266520, China
;
2. Institute of Power Machinery and Vehicle Engineering, Zhejiang University, Hangzhou 310027, China
车辆主动安全系统中,稳定性控制的研究一直占据着重要的地位.较为成熟的方法是以理想横摆角速度和质心侧偏角追踪[1-4],而相平面法是研究车辆稳定性的重要方法,也有很多学者进行了研究.Samsundar等建立了横摆角速度与侧向速度的相平面[5],Pacejka建立了前后轴侧偏角相平面[6],郭孔辉建立了转弯动能与前进动能之比的相平面[7-8],应用这些相平面能够解释实验现象,进行定量分析后能产生很好的效果.此外,Ono等通过质心侧偏角-横摆角速度β-r相平面对车辆稳定性进行了研究[9],Shen等通过引入所谓的关节点轨迹方法,分析了车辆系统β-r相平面的平衡点和相关的稳定性能[10].Inagaki等研究了质心侧偏角-质心侧偏角速度β-begin{document}$ \dot \beta $相平面,进行了车辆稳定性控制[11-12],He等用β-$ {\dot \beta } $相平面方法进行了车辆稳定性的集成控制[13],张晨晨等研究了β-begin{document}$ \dot \beta $相平面的影响因素[14].刘伟等将质心侧偏角相图在ESC系统中进行了稳定性控制的应用[15],刘飞和熊璐等用五菱形法研究了β-begin{document}$ \dot \beta $相平面在极限工况下车辆行驶的稳定性判据[16-17].以上对相平面的研究,大部分是采用简单的二自由度车辆模型,轮胎模型也不能够反映真实轮胎的侧向力,同时仅考虑了β-begin{document}$ \dot \beta $相平面或β-r单一相平面与车辆稳定性的关系.
因此,在前人研究工作的基础上,通过建立更加精确且同时考虑轮胎载荷转移和侧偏角变化的非线性整车模型,提出一种集成β-begin{document}$ \dot \beta $和β-r这2种相平面的优势,对车辆稳定性进行控制的方法.
1 车辆模型的建立
1.1 整车模型
针对某紧凑型轿车,建立二自由度扩展的整车模型,如图 1所示.忽略空气阻力以及转向系统和悬架系统的影响,考虑4个车轮在非线性域内的侧偏角和垂直载荷的变化,分别计算各个轮胎的侧向力.
由整车模型可以得到系统运动方程:
|
$
m\left( {\dot v + ur} \right) = \left( {{F_{y1}} + {F_{y2}}} \right)\cos \delta + {F_{y3}} + {F_{y4}},
$
|
(1) |
|
$
{{\dot I}_z}\dot r = a\left( {{F_{y1}} + {F_{y2}}} \right)\cos \delta - b\left( {{F_{y3}} - {F_{y4}}} \right),
$
|
(2) |
|
$
\beta = \arctan \left( {v/u} \right).
$
|
(3) |
各个轮胎的侧偏角如下:
|
$
{\alpha _1} = \arctan \left( {\frac{{v + ar}}{{u - rt/2}}} \right) - \delta ,
$
|
(4) |
|
$
{\alpha _2} = \arctan \left( {\frac{{v + ar}}{{u - rt/2}}} \right) - \delta ,
$
|
(5) |
|
$
{\alpha _3} = \arctan \left( {\frac{{v + br}}{{u - rt/2}}} \right) - \delta ,
$
|
(6) |
|
$
{\alpha _4} = \arctan \left( {\frac{{v + br}}{{u - rt/2}}} \right) - \delta ,
$
|
(7) |
为了研究轮胎非线性,考虑到载荷的转移,4个轮胎的垂直载荷分别是:
|
$
{F_{z1}} = \frac{{mgb}}{{2l}} - \frac{{ma{}_yhb}}{{tl}},
$
|
(8) |
|
$
{F_{z2}} = \frac{{mgb}}{{2l}} - \frac{{ma{}_yhb}}{{tl}},
$
|
(9) |
|
$
{F_{z3}} = \frac{{mgb}}{{2l}} - \frac{{ma{}_yha}}{{tl}},
$
|
(10) |
|
$
{F_{z4}} = \frac{{mgb}}{{2l}} - \frac{{ma{}_yha}}{{tl}},
$
|
(11) |
式(1)至式(11)中:δ是前轮转角,u是整车的纵向速度,v是整车的侧向速度,β是质心侧偏角,r是横摆角速度,αi(i=1,2,3,4)分别是4个轮胎的侧偏角,Fyi(i=1,2,3,4)分别是4个轮胎的侧向力,整车的其他参数如表 1.
表 1 整车的部分参数
Table 1 The main parameters of vehicle
| 参数 |
数值 |
| 整车质量m/kg |
1 563 |
| 整车绕z轴的转动惯量Iz/(kg·m2) |
2 796 |
| 整车质心到前轴的距离a/mm |
1 016 |
| 整车质心到后轴的距离b/mm |
1 444 |
| 质心高度h/mm |
556.6 |
| 轮距t/mm |
1 540 |
| 轴距l/mm |
2 550 |
| 轮胎的规格 |
205/55 R16 |
1.2 轮胎模型
由于稳定性控制是在轮胎的非线性区域内发生,需要对轮胎实际的侧向力进行拟合.考虑轮胎力的有效性和计算的简洁性,采用简化的MF公式进行拟合[6].
轮胎侧向力由下式给出:
|
$
{F_y} = \mu {F_z}\sin \left( {D\arctan \left( {B{\alpha _i}} \right)} \right),
$
|
(12) |
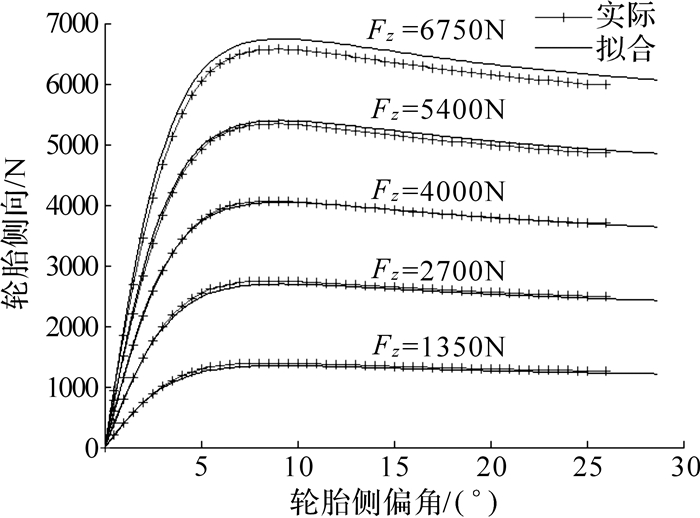
式中:Fy是轮胎的侧向力,μ是路面的附着系数,Fz是轮胎的垂直载荷,B和D是待拟合系数.拟合结果如图 2.
在μ=1时,通过对不同垂直载荷下轮胎侧向力的拟合,发现随着轮胎侧偏角的变化,可得到公式(12)的拟合系数:B=1.438,D=0.210 8.
拟合的轮胎侧向力最大偏差为2%,但是经过估算,单个轮胎的主要垂直载荷工作区域是在5 000 N之内,所以通过拟合而得到的参数能够满足相平面的要求.
2 相平面边界
由于路面附着系数和车速对相平面的边界影响很大,故需计算不同车速和路面附着系数下的稳定性边界,再根据此结果拟合出能够随着车速和路面附着系数变化的边界函数.
2.1 相平面稳定边界
所建立的整车模型方程可以表示为公式(13)和(14)所示的二阶自治系统:
|
$
\dot \beta = {f_1}\left( {\beta ,r} \right),
$
|
(13) |
|
$
\dot r = {f_2}\left( {\beta ,r} \right).
$
|
(14) |
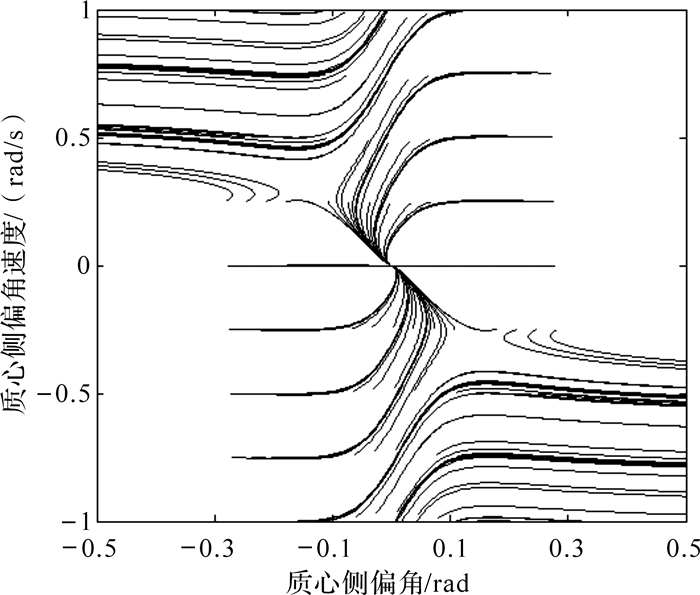
车速u0=100 km/h,前轮转角δ =0°时,路面附着系数μ0=0.8,赋予不同初始值(β(0),r(0)),运用相平面图的理论[18],得到β-begin{document}$ \dot \beta $相平面、β-r相平面如图 3和图 4.
通过观察图 3相平面的轨迹线变化,根据能回到稳定相点(0,0)的轨迹线划分稳定区域,划分的相平面稳定区域为图 5中的2条对称虚直线包围的区域,这2条虚直线可以用方程(15)表示:
|
$
\left| {\dot \beta + {k_1}\beta } \right| \le {c_1},
$
|
(15) |
式中k1,c1为边界系数.
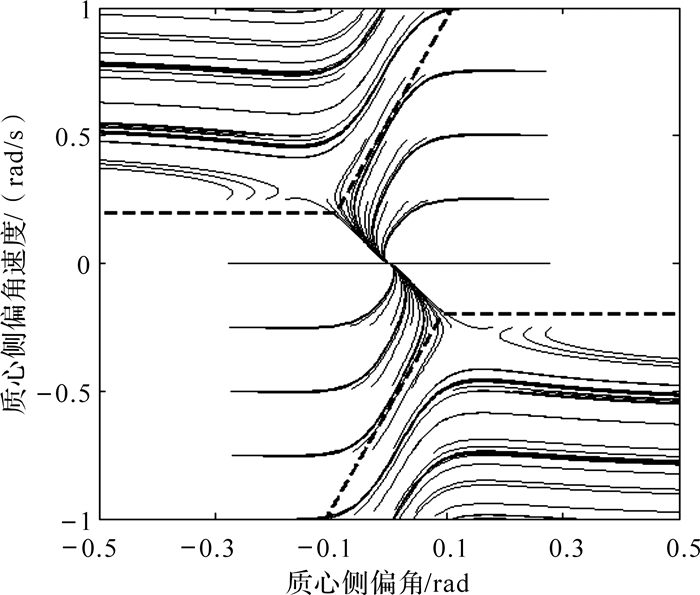
类似地,根据图 4能够回到原点的相轨迹,用2条对称的双折线划分稳定区域,如图 6中的虚线所示,并可用方程(16)和(17)同时表示:
|
$
\left| {r + {k_2}\beta } \right| \le {c_2},
$
|
(16) |
|
$
\left| r \right| \le {c_3},
$
|
(17) |
式中k2,c2和c3都是此稳定域的边界系数.
2.2 不同路面附着系数的影响
整车速度u0不变时,通过改变附着系数,获得2种相平面的稳定边界的参数,获得的数据对应表 2和表 3.
表 2 不同路面附着系数下β-begin{document}$ \dot \beta $\end{document}相平面的边界参数
Table 2 Boundary parameters of the β-begin{document}$ \dot \beta $\end{document} phase plane under different road friction coefficients
| 序号 |
μ |
k1 |
c1 |
| 1 |
0.1 |
1.0 |
0.08 |
| 2 |
0.2 |
2.4 |
0.18 |
| 3 |
0.3 |
4.0 |
0.22 |
| 4 |
0.4 |
5.0 |
0.28 |
| 5 |
0.5 |
5.5 |
0.40 |
| 6 |
0.6 |
6.6 |
0.45 |
| 7 |
0.7 |
7.5 |
0.55 |
| 8 |
0.8 |
8.0 |
0.65 |
| 9 |
0.9 |
8.5 |
0.70 |
| 10 |
1.0 |
9.8 |
0.85 |
表 3 不同路面附着系数下β-r 相平面的边界参数
Table 3 Boundary parameters of β-r phase plane under different road friction coefficients
| 序号 |
μ |
k2 |
c2 |
c3 |
| 1 |
0.1 |
0.7 |
0.08 |
0.021 2 |
| 2 |
0.2 |
1.3 |
0.15 |
0.042 4 |
| 3 |
0.3 |
2.0 |
0.25 |
0.063 6 |
| 4 |
0.4 |
2.2 |
0.32 |
0.084 8 |
| 5 |
0.5 |
2.7 |
0.42 |
0.106 9 |
| 6 |
0.6 |
3.0 |
0.49 |
0.127 1 |
| 7 |
0.7 |
3.8 |
0.50 |
0.148 3 |
| 8 |
0.8 |
4.1 |
0.60 |
0.169 5 |
| 9 |
0.9 |
4.5 |
0.70 |
0.190 7 |
| 10 |
1.0 |
5.0 |
0.80 |
0.211 9 |
运用多项式拟合表 2的数据,得到拟合公式(18)和(19):
|
$
{k_1} = - 4.28{\mu ^2} + 13.83\mu - 0.1283,
$
|
(18) |
|
$
{c_1} = 0.2197{\mu ^2} + 0.5814\mu + 0.03167.
$
|
(19) |
拟合表 3中的数据,得到拟合公式(20),(21)和(22):
|
$
{k_2} = 4.618\mu + 0.38,
$
|
(20) |
|
$
{c_2} = 0.757\mu + 0.0107,
$
|
(21) |
|
$
{c_3} = 0.212\mu .
$
|
(22) |
2.3 不同车速的影响
在附着系数μ0=0.8时,不同车速下β-begin{document}$ \dot \beta $和β-r两种相平面图的边界结果如表 4和表 5.
表 4 不同车速下β-begin{document}$ \dot \beta $\end{document}相平面的边界参数
Table 4 Boundary parameters of β-begin{document}$ \dot \beta $\end{document} phase plane under different vehicle speeds
| 序号 |
u/(km/h) |
k1 |
c1 |
| 1 |
60 |
8.05 |
0.75 |
| 2 |
70 |
8.05 |
0.76 |
| 3 |
80 |
8.01 |
0.75 |
| 4 |
90 |
8.01 |
0.77 |
| 5 |
100 |
8.00 |
0.75 |
| 6 |
110 |
7.95 |
0.76 |
| 7 |
120 |
8.02 |
0.74 |
| 8 |
130 |
8.00 |
0.74 |
| 9 |
140 |
8.01 |
0.76 |
| 10 |
150 |
8.00 |
0.76 |
表 5 不同车速下β-r相平面的边界参数
Table 5 Boundary parameters of β-r phase plane under different vehicle speeds
| 序号 |
u/(km/h) |
k2 |
c2 |
c3 |
| 1 |
60 |
5.0 |
1.0 |
0.282 5 |
| 2 |
70 |
4.8 |
0.90 |
0.242 2 |
| 3 |
80 |
4.5 |
0.80 |
0.211 9 |
| 4 |
90 |
4.3 |
0.70 |
0.188 4 |
| 5 |
100 |
4.1 |
0.60 |
0.169 5 |
| 6 |
110 |
3.9 |
0.55 |
0.154 1 |
| 7 |
120 |
3.7 |
0.56 |
0.141 3 |
| 8 |
130 |
3.5 |
0.50 |
0.130 4 |
| 9 |
140 |
3.0 |
0.45 |
0.121 1 |
| 10 |
150 |
2.8 |
0.40 |
0.113 0 |
分析表 4数据可知,k1值一直在[7.95,8.05]区间浮动,c1值一直在[0.74,0.77]区间浮动,由此可知车速对相平面边界的斜率和截距的影响在有限的范围内,所以车速对β-begin{document}$ \dot \beta $相平面边界的影响可以不考虑.
从图表 5可知,车速u与3个参数成反比关系,通过数据得到边界参数的拟合公式(23),(24)和(25):
|
$
{k_2} = \frac{{6586}}{{{u^2} - 20.11u + 1388}},
$
|
(23) |
|
$
{c_2} = \frac{{3319}}{{{u^2} + 131.2u + 820.6}},
$
|
(24) |
|
$
{c_3} = \frac{{4710}}{{1000u + 3.3}}.
$
|
(25) |
2.4 边界函数
综合以上对相平面边界的讨论,得到的路面附着系数和车速的关系及β-begin{document}$ \dot \beta $相平面的稳定边界可以用方程(26)来表示:
|
$
\left. {\begin{array}{*{20}{l}}
{\left| {\dot \beta + {k_1}\beta } \right| \le {c_1},}\\
{{k_1} = - 4.28{\mu ^2} + 13.83\mu - 0.1283,}\\
{{c_1} = 0.2197{\mu ^2} + 0.5814\mu + 0.03167.}
\end{array}} \right\}
$
|
(26) |
β-r相平面边界方程的参数与μ成正比关系,而与车速成反比关系,通过路面附着系数和车速拟合的方程,可以得到β-r相平面的边界函数:
|
$
\left. {\begin{array}{*{20}{l}}
{\left| {r + {k_2}\beta } \right| \le {c_2},}\\
{{k_2} = \frac{{7604\mu + 626}}{{ - 20.11u + 1388}},}\\
{{c_2} = \frac{{4188\mu + 59.2}}{{{u^2} + 131.2u + 820.6}},}\\
{\left| r \right| \le {c_3},}\\
{{c_3} = \frac{{5891\mu }}{{1000u + 3.3}}.}
\end{array}} \right\}
$
|
(27) |
3 车辆主动稳定性控制器的设计
所设计的横摆力矩双路相平面联合控制系统总体架构如图 7所示.稳定性控制系统中,β-begin{document}$ \dot \beta $相平面的误差是不稳定的相点到稳定边界的最短距离,通过PID控制算法计算得到其中一个横摆力矩Mβ-begin{document}$ \dot \beta $;类似地,可根据β-r相平面误差,通过PID控制算法计算另一个横摆力矩Mβ-r,系统所需的横摆力矩Mzc由两者联合产生.
3.1 基于β-begin{document}$ \dot \beta $\end{document}相平面的横摆力矩的计算
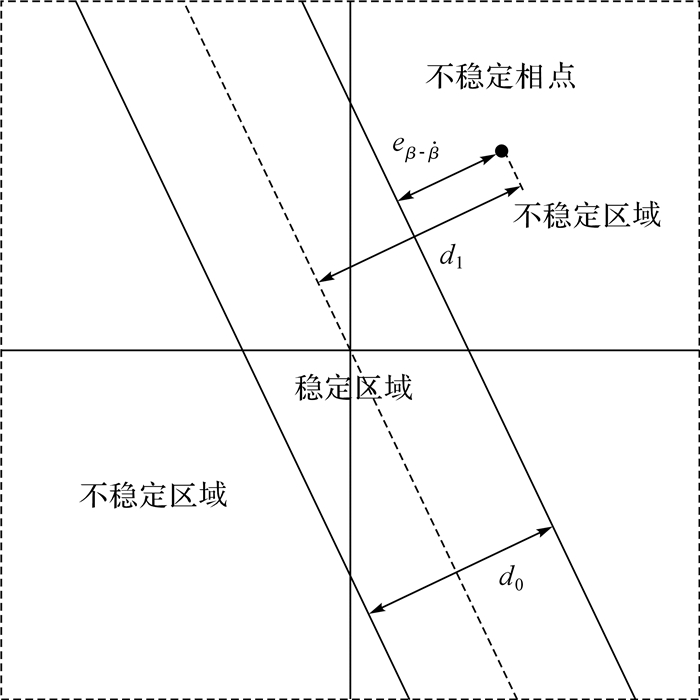
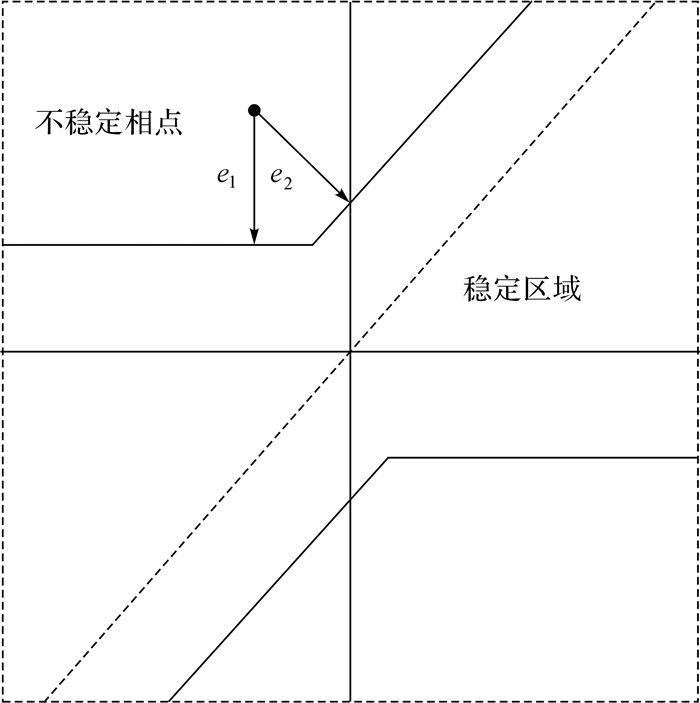
对图 5相平面中划分的稳定性区域进行处理,如图 8.
由图 8得到相平面的误差计算公式:
|
$
{d_1} = \frac{{\left| {\dot \beta + k\beta } \right|}}{{\sqrt {1 + {k^2}} }},
$
|
(28) |
|
$
{d_0} = \frac{{\left| {2{c_1}} \right|}}{{\sqrt {1 + {k^2}} }},
$
|
(29) |
|
$
{e_{\beta - \dot \beta }} = {d_1} - {d_0}/2,
$
|
(30) |
式中:eβ-begin{document}$ \dot \beta $是不稳定的相点到稳定边界的距离,且eβ-begin{document}$ \dot \beta $;d1是不稳定的相点到边界的中间线垂直距离;d0是2条稳定边界线之间的距离.
运用PID控制算法得到横摆力矩:
|
$
{M_{\beta - \dot \beta }} = {K_{{\rm{p}}\beta }}{e_{\beta - \dot \beta }} + {K_{{\rm{i}}\beta }}\int {{e_{\beta - \dot \beta }}{\rm{d}}t} {\rm{ + }}{K_{{\rm{d}}\beta }} + \frac{{{\rm{d}}{e_{\beta - \dot \beta }}}}{{{\rm{d}}t}},
$
|
(31) |
式中:Kpβ是β-begin{document}$ \dot \beta $相平面的比例参数,Kiβ是积分的参数,Kdβ是微分的参数.
3.2 基于β-r相平面的横摆力矩的计算
对图 6相平面划分的稳定区域进行处理,得到简化的相平面图边界,如图 9.
通过图 9获得β-r相平面的误差eβ-r:
|
$
{e_1} = \left| r \right| - {c_3},
$
|
(32) |
|
$
{e_2} = \frac{{\left| {r + {k_2}\beta } \right| - {c_2}}}{{\sqrt {1 + {k_2}} }},
$
|
(33) |
|
$
{e_{\beta - r}} = \min \left( {{e_1},{e_2}} \right),
$
|
(34) |
式中:e1是不稳定相点到水平线的距离且e1≥0,e2是不稳定相点到斜线的距离且e2≥0.
运用PID控制算法得到β-r相平面图的横摆力矩如下:
|
$
{M_{\beta - r}} = {K_{{\rm{p}}r}}{e_{\beta - r}} + {K_{{\rm{i}}r}}\int {{e_{\beta - r}}{\rm{d}}t} + {K_{{\rm{d}}r}}\frac{{{\rm{d}}{e_{\beta - r}}}}{{{\rm{d}}t}},
$
|
(35) |
式中:Kpr是β-r相平面比例参数,Kir是积分的参数,Kdr是微分的参数.
3.3 期望的横摆力矩的计算
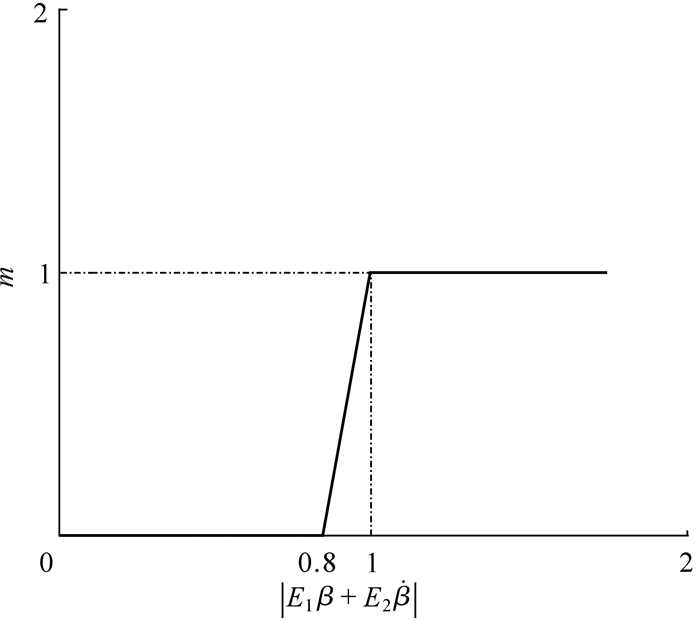
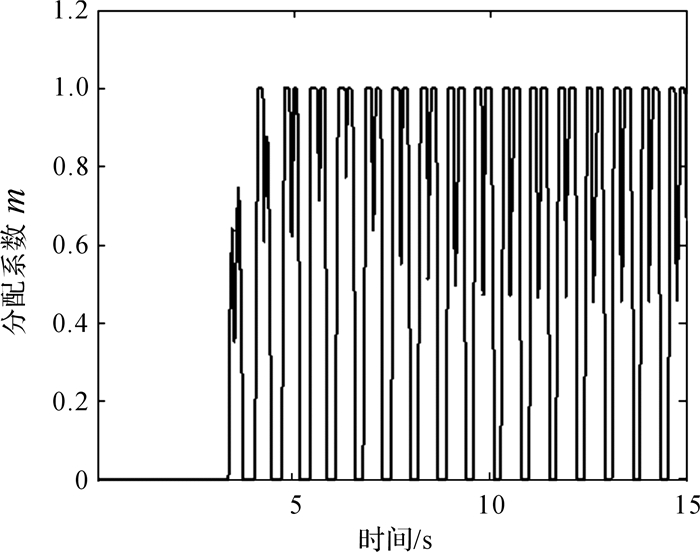
考虑到相点在β-begin{document}$ \dot \beta $相图的稳定域内,但是不在β-r相图稳定域内,所以将2个相图结合起来计算整车所需要的横摆力矩.通过方程(36)计算整车所需的横摆力矩Mzc,为了实现横摆力矩平滑地过渡,将分配系数m取值定为在横坐标值为0.8时开始变化,如图 10.
|
$
{M_{zc}} = m{M_{\beta - \dot \beta }} + \left( {1 - m} \right){M_{\beta - r}}.
$
|
(36) |
图 10横坐标中的E1和E2都是β-begin{document}$ \dot \beta $相平面稳定区域方程(15)的变形表达,且有
|
$
\left| {{E_1}\beta + {E_2}\beta } \right| \le 1,
$
|
(37) |
式中:
|
$
{E_1} = 1/{c_1},
$
|
(38) |
|
$
{E_2} = {k_1}/{c_1}.
$
|
(39) |
4 仿真验证
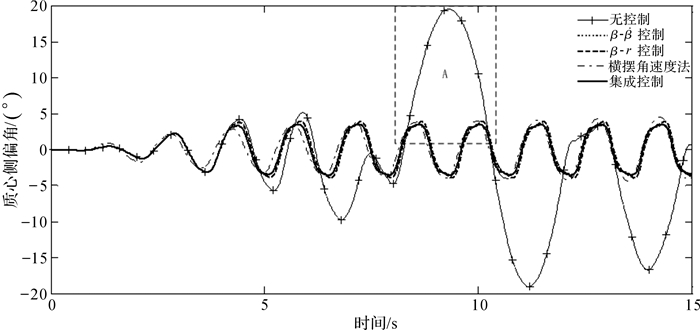
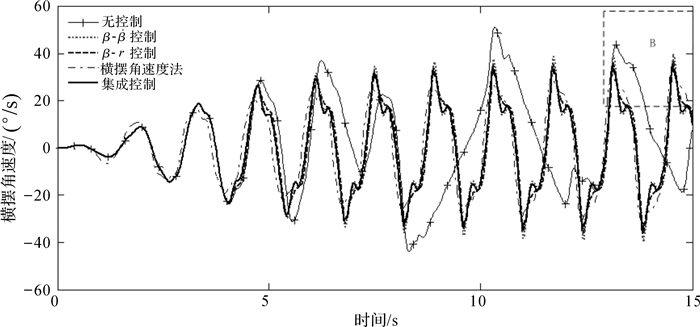
为了验证稳定性控制器效果,建立Simulink与Carsim联合仿真平台.仿真车辆以120 km/h的车速,在附着系数为0.8的路面上匀速行驶,然后输入频率为0.7 Hz增幅正弦变化的方向盘转角,如图 11,方向盘达到一定转角后,车辆将会出现失稳现象.图 12中给出了无控制、β-begin{document}$ \dot \beta $控制、β-r控制、基于PID的横摆角速度跟踪控制的结果[1].
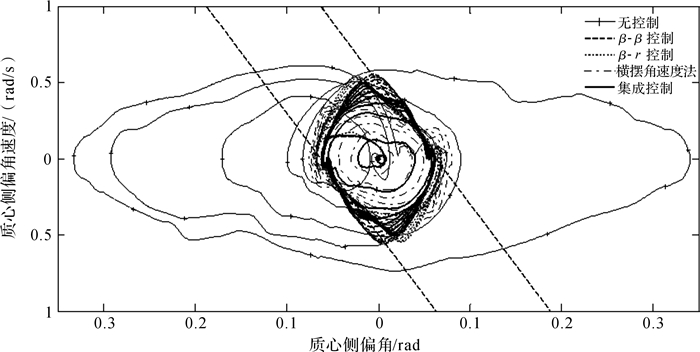
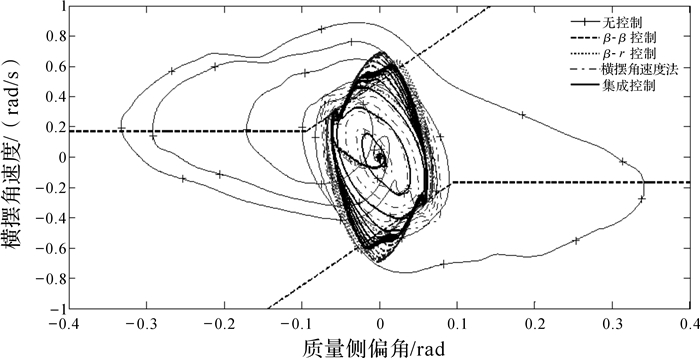
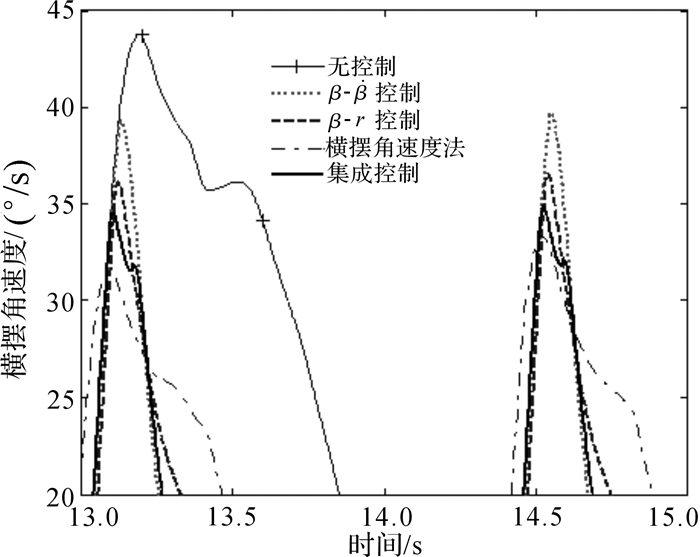
对于质心侧偏角,图 12和图 13结果表明:相平面的集成控制与β-r控制对比,集成控制峰能降低约10%;与横摆角速度法相比较,具有一定的优势;相平面集成控制可将无控制车辆的质心侧偏角最大峰值降低约80%,将无序的质心侧偏角控制到有序的状态.类似地,对于横摆角速度,图 14和图 15表明,集成控制要优于β-begin{document}$ \dot \beta $控制与β-r控制,分别在原有控制的基础上降低约8%和4%,稍弱于横摆角速度法的控制效果,可将无控制的车辆横摆角速度最大的峰值降低约36%,横摆角速度的运动状态从无规律的运动控制成有规律.
由图 16可知,分配系数m=1时,以β-begin{document}$ \dot \beta $相平面控制为主;m < 1时,运用β-r控制为主.所设计的集成控制器能够利用2种相平面进行稳定性的控制.
图 17和图 18表明,对于β-begin{document}$ \dot \beta $与β-r相平面中相轨迹围成的区域,集成控制的区域小于β-begin{document}$ \dot \beta $控制、β-r控制和横摆角速度方法的区域,在三者的相轨迹区域之内.无控制的车辆远离稳定区域,处于失稳的状态,集成控制能够将无控制车辆的相轨迹拉到稳定边界之内.
5 结论
通过建立二自由度整车扩展模型以及拟合实际车辆运行时轮胎的侧向力,获得了β-begin{document}$ \dot \beta $和β-r相平面稳定区域.通过不同的路面附着系数和车速,获得了稳定区域的边界函数.据此,用PID控制算法设计了集成2种相平面的车辆稳定性控制器,并在建立的Simulink和Carsim的联合仿真平台上,进行车辆稳定性控制的验证.仿真结果表明:能在单一的β-begin{document}$ \dot \beta $控制基础上降低横摆角速度峰值;在β-r控制基础上降低质心侧偏角和横摆角速度峰值;集成控制相平面的区域小于单一相平面控制的区域;能降低无控制车辆的质心侧偏角和横摆角速度峰值,将车辆不稳定的状态拉到稳定的区域;与横摆加速度方法相比较,具有一定的优势.本文设计的车辆稳定性控制器,能够显著提高车辆的稳定性.