Download PDF  
文章快速检索  
  高级检索
引用本文
刘文光,林炜彦,颜龙,舒斌. 基于抗振动疲劳的薄板加筋设计分析[J]. 工程设计学报, 2016, 23(4): 385-390.
LIU Wen-guang, LIN Wei-yan, YAN Long, SHU Bin. Analysis on stiffen design of a skin plate by anti-vibration fatigue[J]. Chinese Journal of Engineering Design, 2016, 23(4): 385-390.
基于抗振动疲劳的薄板加筋设计分析
刘文光,林炜彦,颜龙,舒斌     
南昌航空大学 航空制造工程学院, 江西 南昌 330063
收稿日期: 2015-09-24 .
作者简介: 刘文光(1978—),男,江西泰和人,副教授,博士,从事飞行器结构动力学及疲劳寿命预测研究,E-mail:liuwg14@nchu.edu.cn. http://orcid.org//0000-0002-4218-0287
摘要: 振动是航空薄板常见的载荷形式，通常采用加强筋来减小振动幅度，从而提高薄板寿命.研究薄板的抗振动疲劳加筋方法，探讨加强筋与板的连接方式以及加强筋的布置方向对薄板振动与疲劳的影响机制.首先，基于振动理论和板筋变形协调条件，建立加筋薄板的运动方程.然后，建立铆接、点焊和滚焊连接形式的加筋薄板有限元模型，探讨连接单元的动力学建模方法；在此基础上，研究连接形式和加筋安装方向对薄板结构动力学特性的影响；最后，结合动力响应分析探讨板筋连接方式和加筋安装方向对疲劳寿命的影响.研究结果表明，双向加筋薄板在低频振动时刚度高于单向加筋薄板，双向加筋有利于提高结构抗疲劳强度，铆接单向加筋薄板的振动疲劳寿命最短.
关键词: 加筋薄板     动力学特性     振动疲劳    

基金项目: 国家自然科学基金资助项目（51565039）
Analysis on stiffen design of a skin plate by anti-vibration fatigue
LIU Wen-guang, LIN Wei-yan, YAN Long, SHU Bin     
School of Aeronautic Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China
Abstract: Vibration is one of the common loading types to aircraft plate.It is frequent to use the stiffen method to reduce the vibration amplitude so as to improve the vibration fatigue life of thin plate.In order to study the anti-vibration fatigue method by stiffen,it is aimed to reveal the impacts of connecting method and connecting direction of stiffen on the vibration fatigue life of a thin plate.Firstly,the kinetic equation of a stiffen plate was set up by combining the vibration theory of thin plate and the deformation compatibility condition of plate and stiffen.Then the typical stiffen plate was employed to study the modeling method of the link element between the plate and the stiffen beam via building up the finite element dynamics model of stiffened plate structure with rivet,spot-weld and rolling-weld.Therefore,the dynamics properties of single-direction and double-direction stiffened plate were studied and the impacts of stiffen on the vibration properties were discovered.Finally,the fatigue life of the structure was estimated based on the analysis of the dynamic response.Meanwhile,the influence of the connection mode and the direction of the connection on the fatigue life was studied.Results indicate that the stiffness of the single-direction stiffened plate is higher than that of the double-direction stiffened plate.Double-direction stiffened plate is benefit to the strength of vibration fatigue for the thin plate and the fatigue life of the rivet stiffened plate is the minimum.
Key words: stiffened plate     dynamics characteristic     vibration fatigue    

在特定的条件下,飞机机翼、发动机叶片、机身、进气道壁板和航炮支架等都可简化为薄板模型来研究,而这些薄板经常在振动环境下工作,甚至要承受宽频振动的激励,可能一直处于共振状态[1].因为薄板所处振动环境十分复杂,极易导致疲劳问题,所以防止薄板疲劳尤为重要.提高薄板振动疲劳强度的方法有很多,比如增加薄板厚度或者更换薄板材料.但是在航空领域内,薄板重量最小是提高薄板强度的重要约束条件,所以通常采用加筋的方法来提高薄板的承载能力和抗疲劳强度[2].

薄板加筋是一种常见的提高结构强度和刚度的设计方法,广泛运用于航空领域[3-4].飞机尤其是军用飞机在高速飞行过程中,最容易受到高速气流的扰动,而民航客机的飞行环境虽然没有军用飞机的恶劣,但民航客机的机身结构更加宽大,运载能力更强，由此引发的结构疲劳破坏直接危及飞机蒙皮等薄板结构的可靠性[5].

对飞机蒙皮而言,加强筋承担薄板大部分垂直方向的载荷,并保证薄板有足够的稳定性来承受面内压力.当薄板所受的外载荷超过一定值时,加筋薄板或将失稳,或遭受疲劳破坏.对该问题,很多学者进行了相关的研究.Sakano等研究了变幅载荷下横向加筋构件焊接接头的疲劳强度,结合横向加筋构件2种变幅载荷作用试验,运用断裂力学准确分析了疲劳裂纹扩展问题[6].为了探讨加筋薄板振动对疲劳寿命的影响,刘文光等针对单向加筋薄板进行共振疲劳试验,分析了影响薄板振动疲劳寿命的若干因素[7],在此基础上,结合试验研究提出了一种加筋薄板的振动疲劳寿命计算方法[8].基于CAE仿真平台,廉政和顾超林应用损伤力学对飞行器上广泛使用的典型加筋薄板结构件进行了振动疲劳寿命估算[9-10].以加筋薄板为研究对象,王佳莹通过数值计算方法研究了高温环境下加筋薄板的振动疲劳寿命[11].

尽管研究者对薄板加筋的方法进行了一系列研究,但仍有很多关键技术没有厘清.对于不同部位的飞机薄板,它所处的振动环境不同,有时甚至会发生共振.为了减轻振动幅度,通常对薄板加筋以增强其刚度,进而提高其疲劳强度.为了进一步推动抗振动疲劳设计薄板加筋布置方法的发展,笔者研究了板筋的连接形式、加筋的安装方向等对薄板振动疲劳寿命的影响机制.

1 加筋薄板的运动方程

薄板和加强筋都是工程中的基本构件,但是两者的连接导致薄板几何上的不连续性和结构上的各向异性.为了准确预测加筋薄板的振动响应及其疲劳寿命,如何建立加筋薄板的运动方程成为关键问题之一.飞机运行时,薄板的振动幅度与其厚度不在一个数量级,所以建立加筋薄板的运动方程时采用大挠度弯曲理论更符合实际.

由薄板大挠度弯曲理论可知,板的中面应变表达式为

$\left\{ \begin{align} & {{\varepsilon }_{xp}}=\frac{\partial u}{\partial x}+\frac{1}{2}{{\left( \frac{\partial w}{\partial x} \right)}^{2}}, \\ & {{\varepsilon }_{yp}}=\frac{\partial v}{\partial y}+\frac{1}{2}{{\left( \frac{\partial w}{\partial y} \right)}^{2}}, \\ & {{\lambda }_{xyp}}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{{{\partial }^{2}}w}{\partial x\partial y}. \\ \end{align} \right.$

式中：εxp,εyp,γxyp表示薄板的中面应变；u,v分别表示薄板的中面沿x,y方向的位移；w表示薄板的中面沿z方向的总挠度.

薄板中面的内力表达式为

$\left\{ \begin{align} & {{N}_{x}}=\frac{{{E}_{p}}{{h}_{p}}}{1-v_{p}^{2}}({{\varepsilon }_{xp}}+v{{\varepsilon }_{yp}}), \\ & {{N}_{y}}=\frac{{{E}_{p}}{{h}_{p}}}{1-v_{p}^{2}}({{\varepsilon }_{yp}}+v{{\varepsilon }_{xp}}), \\ & {{N}_{xy}}=\frac{{{E}_{p}}{{h}_{p}}}{2(1+{{v}_{p}})}{{\gamma }_{xyp}}, \\ & {{M}_{x}}=-\frac{{{E}_{p}}h_{p}^{3}}{12(1-v_{p}^{2})}\left( \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+{{v}_{p}}\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}} \right), \\ & {{M}_{y}}=\frac{{{E}_{p}}h_{p}^{3}}{12(1-v_{p}^{2})}\left( \frac{{{\partial }^{2}}w}{\partial {{y}^{2}}}+{{v}_{p}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}} \right), \\ & {{M}_{xy}}=-\frac{{{E}_{p}}h_{p}^{3}}{12(1+{{v}_{p}})}\frac{{{\partial }^{2}}w}{\partial x\partial y}. \\ \end{align} \right.$

式中：Nx,Ny,Nxy,Mx,My,Mxy分别表示薄板沿x和y方向的面力与沿x和y轴的弯矩；hp为薄板厚度；Ep为薄板材料弹性模量；vp为薄板材料泊松比.

假定有一等截面加强筋和薄板刚性连接,基于板筋之间的变形协调条件,x和y方向上第K，L根加强筋上中面应变εxK，εyL的表达式为

$\left\{ \begin{align} & {{\varepsilon }_{xK}}={{\varepsilon }_{x}}-t\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}, \\ & {{\varepsilon }_{yL}}={{\varepsilon }_{y}}-t\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}}. \\ \end{align} \right.$

x方向第K根加强筋中面上的内力为

$\left\{ \begin{align} & {{N}_{xK}}={{E}_{K}}{{A}_{K}}{{\varepsilon }_{xK}}, \\ & {{M}_{xK}}={{E}_{K}}{{A}_{K}}t{{\varepsilon }_{xK}}-{{E}_{K}}{{I}_{xK}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}, \\ & {{M}_{xyK}}=-{{G}_{K}}{{J}_{xK}}\frac{{{\partial }^{2}}w}{\partial x\partial y}. \\ \end{align} \right.$

y方向第L根加强筋中面上的内力为

$\left\{ \begin{align} & {{N}_{yL}}={{E}_{L}}{{A}_{L}}{{\varepsilon }_{yL}}, \\ & {{M}_{yL}}={{E}_{L}}{{A}_{L}}t{{\varepsilon }_{yL}}-{{E}_{L}}{{I}_{yL}}\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}}, \\ & {{M}_{xyL}}=-{{G}_{L}}{{J}_{yL}}\frac{{{\partial }^{2}}w}{\partial x\partial y}. \\ \end{align} \right.$

式中：t为加强筋的厚度；IxK和JxK分别为x方向上第K根加强筋的转动惯量和扭转惯性矩；IyL和JyL分别为y方向上第L根加强筋的转动惯量和扭转惯性矩；AK和AL表示x方向第K根加强筋和y方向第L根加强筋的截面面积；EK,EL和GK,GL分别表示x方向第K根加强筋和y方向第L根加强筋材料的弹性模量和剪切弹性模量.

忽略薄板和加强筋之间的转动惯量、两向加强筋之间的耦合及加强筋的切向力,可推导出加筋薄板运动方程的一般表达式为

$\begin{align} & \frac{{{\partial }^{2}}{{M}_{x}}}{\partial {{x}^{2}}}+2\frac{{{\partial }^{2}}{{M}_{xy}}}{\partial x\partial y}+\frac{{{\partial }^{2}}{{M}_{y}}}{\partial {{y}^{2}}}+{{P}_{D}}+{{Q}_{D}}+ \\ & {{N}_{x}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+2{{N}_{xy}}\frac{{{\partial }^{2}}w}{\partial x\partial y}+{{N}_{y}}\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}}+q\left( t \right)= \\ & \rho h\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}+{{P}_{t}}+{{Q}_{t}}, \\ \end{align}$

其中:

$\begin{align} & {{P}_{D}}=\sum\limits_{K=1}^{{{m}_{K}}}{{}}\left( \frac{{{\partial }^{2}}{{M}_{xK}}}{\partial {{x}^{2}}}+2\frac{{{\partial }^{2}}{{M}_{xyK}}}{\partial x\partial y}+{{N}_{xK}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}} \right)\delta \left( y-{{b}_{K}} \right), \\ & {{Q}_{D}}=\sum\limits_{L=1}^{{{m}_{L}}}{{}}\left( \frac{{{\partial }^{2}}{{M}_{yL}}}{\partial {{y}^{2}}}+2\frac{{{\partial }^{2}}{{M}_{xyL}}}{\partial x\partial y}+{{N}_{yL}}\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}} \right)\delta \left( x-{{b}_{L}} \right), \\ & {{P}_{t}}=\sum\limits_{K=1}^{{{m}_{K}}}{{}}{{\rho }_{K}}{{A}_{K}}\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}\delta \left( y-{{b}_{K}} \right), \\ & {{Q}_{t}}=\sum\limits_{L=1}^{{{m}_{L}}}{{}}{{\rho }_{L}}{{A}_{L}}\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}\delta \left( x-{{b}_{L}} \right), \\ \end{align}$

式中：PD和QD分别表示x和y方向加强筋引起的弹性项；Pt和Qt分别表示x和y方向加强筋引起的惯性项;bK,bL分别为x和y方向上第K,L根加强筋的坐标；mK,mL分别为沿x和y方向加强筋的数量；δ(y- bK)和δ(x- bL)表示Dirac函数.

对加筋薄板动力响应的求解,实际上就是对上述方程组进行求解.研究单向加筋薄板时,忽略其中的QD和Qt项即可.

2 加筋薄板的数值建模

薄板加筋有单向和双向加筋之分,且板筋的连接形式可以是铆接、点焊或滚焊等.由于薄板的加筋布置方法不同,加强筋对薄板的刚度影响和惯性影响肯定不同,从而导致结构的动力学特性有所差异.

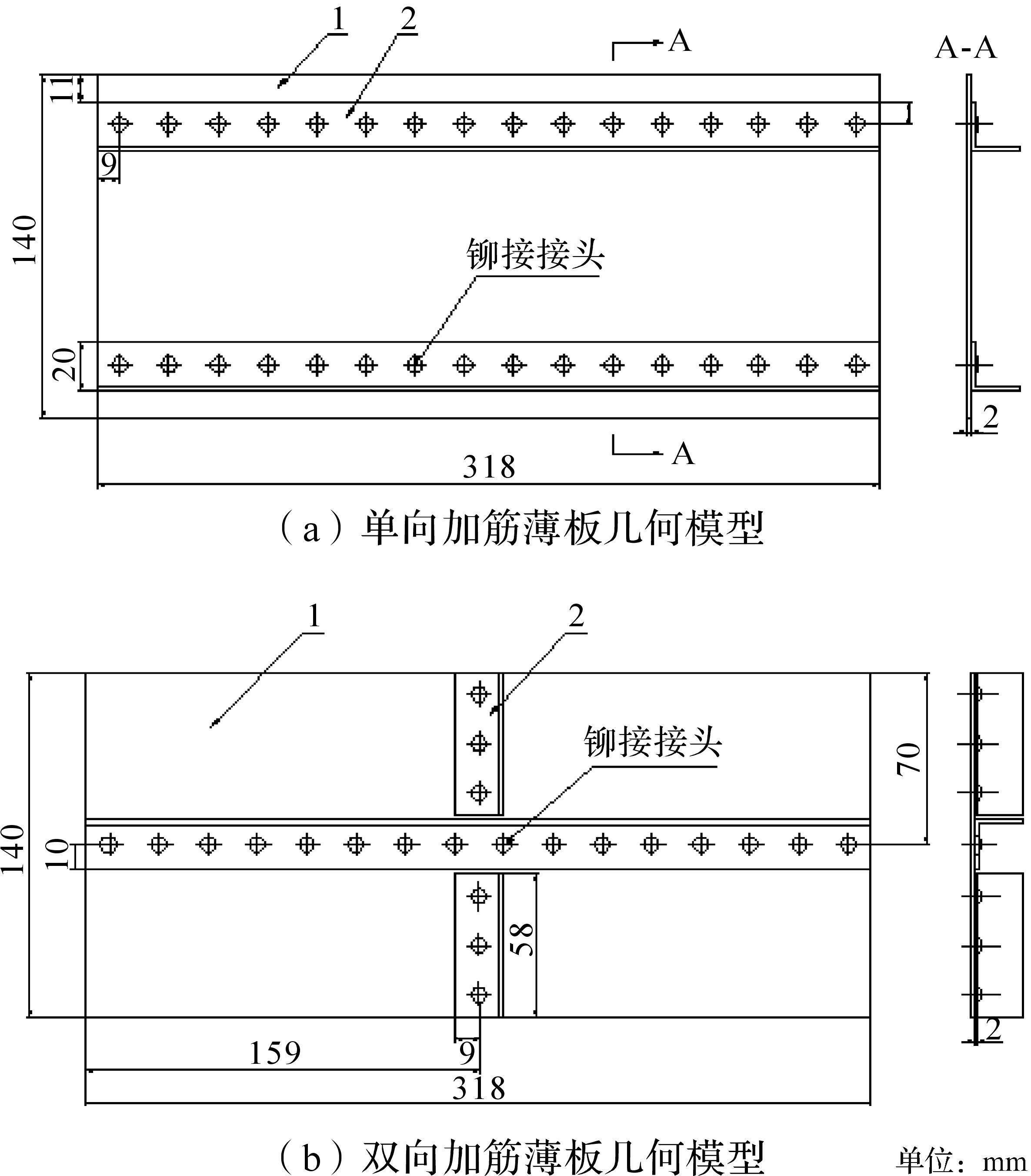
为了深入揭示加强筋对薄板振动疲劳寿命的影响机制,首先需要通过加筋薄板的动力学模型进行响应分析,然后结合Miner线性疲劳累积损伤理论预测结构总疲劳寿命.以国内某研究所设计的加筋薄板为对象进行研究[9],薄板和加强筋的材料均采用LY12CZ铝合金,弹性模量E=71.7 GPa,泊松比μ=0.33,密度ρ=2 740 kg/m3.薄板与L型加强筋的连接方法为铆接、点焊和滚焊三种,铆接和点焊的布置方法一样,而且L型加强筋的装配分为单向和双向两种.图 1所示的是单向和双向铆接加筋薄板的几何模型.

1-薄板；2-L型筋条. 图 1 铆接结构 Fig.1 Rivet structure
图选项

考虑薄板和加强筋的几何关系,薄板和加强筋简化为板壳单元,建立铆接、点焊和滚焊三种加筋薄板的有限元模型.对于铆接连接形式,铆钉选用CWELD单元；对于点焊连接,薄板与加强筋通过CERIG创建刚性连接；对于滚焊连接,由于薄板和加强筋连接的区域比较大,可将2个板筋节点重合简化处理.根据以上方法可建立3种连接形式的加筋薄板有限元模型.

图 2描述了不同连接形式加筋薄板前4阶次自由模态固有频率的比较.结果表明,铆接结构固有频率最小,点焊结构固有频率次之,滚焊薄板固有频率最大,计算模态振型与文献[9]中的试验模态振型基本吻合.

图 2 单向加筋薄板计算模态频率比较 Fig.2 Comparison of calculation frequency of single direction stiffen plate
图选项

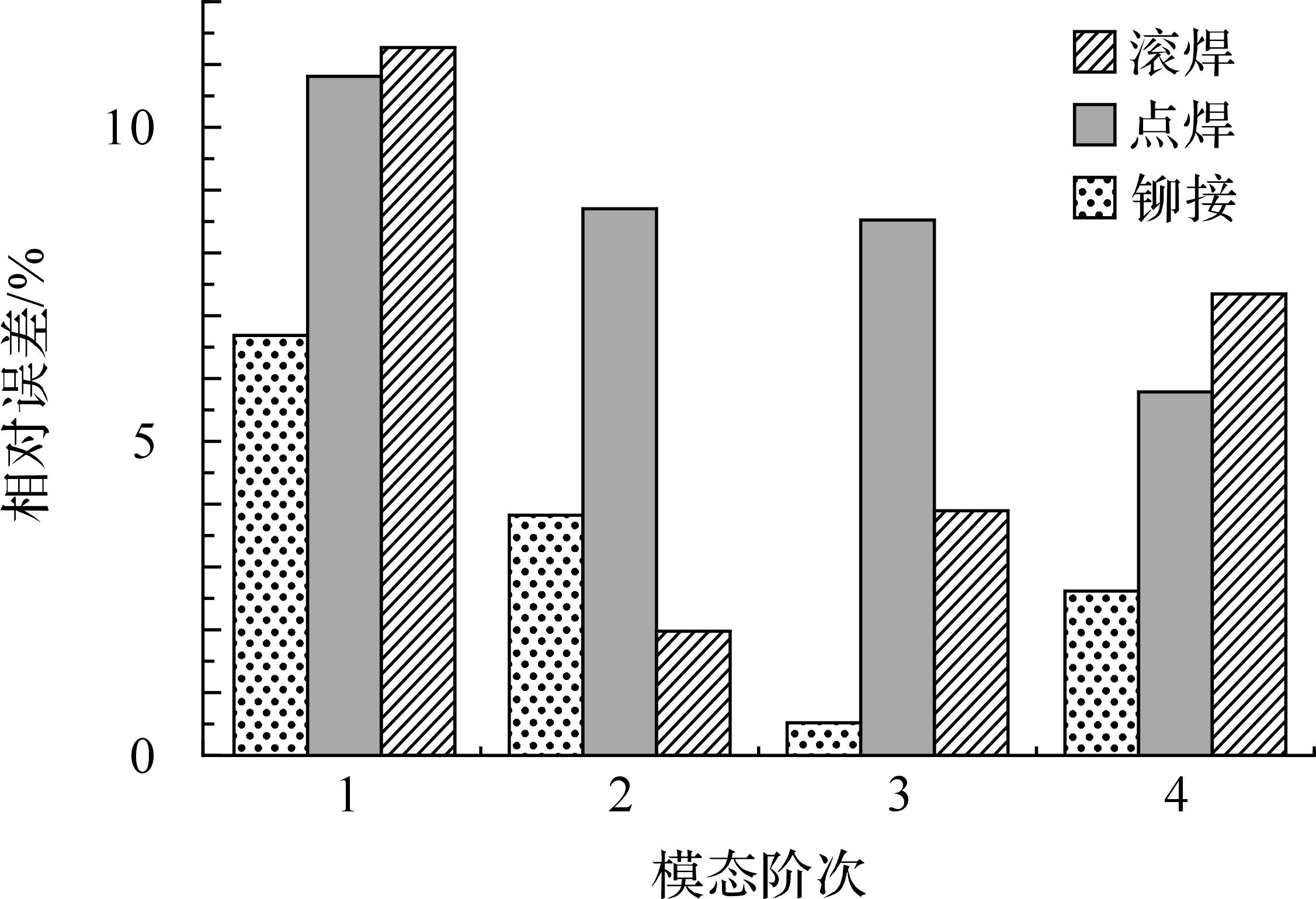
对各种连接形式加筋薄板的计算模态频率与试验模态频率进行比较,得到单向加筋薄板计算频率与试验频率的误差图,如图 3所示.

图 3 单向加筋薄板计算频率和试验频率的相对误差 Fig.3 Relative error of calculation frequency and test frequency of single direction stiffen plate
图选项

分析表明,在第1阶模态频率上,3种加筋薄板的相对误差比较大,而其它模态频率的相对误差比较小，可能是外部载荷的干扰对试验第1阶频率影响较大导致.虽然3种加筋薄板有限元模型的计算模态与试验模态存在误差,但是误差值在一定的范围之内,表明利用本文方法建立的铆接、点焊、滚焊薄板动力学有限元模型与物理实际基本吻合,即所建立的有限元模型可用于动力响应分析.

3 加筋薄板的动力响应分析

为了预测加筋薄板的动力响应,需要对薄板施加一定的载荷.而为了更准确模拟蒙皮载荷,基于损伤容限设计理论,假定蒙皮的检修周期为1 000 h,蒙皮的平均振动频率为100 Hz,由此可以推算出蒙皮的目标疲劳寿命为3.6×108次.

假定飞机蒙皮在服役过程中所承受的载荷为分布式压力,依据目标疲劳寿命,由公式(1)可得到蒙皮危险位置的最大应力控制水平[12]为

$\sigma _{rN}^{m}N=C,$ (1)

式中： σmrN是有限寿命疲劳极限值,其中LY12CZ的材料常数m=3.6[9],r为循环应力比；N是相应的应力循环次数；C为常数.

结果表明,对称加载下采用LY12CZ的对称循环极限σ-1=12.66 MPa.假定飞机运行时所受载荷为分布式正弦载荷,载荷幅值为1 800 Pa,计算可知加筋薄板危险位置等效应力在12.66 MPa左右.该结果为后续疲劳计算提供了疲劳载荷.

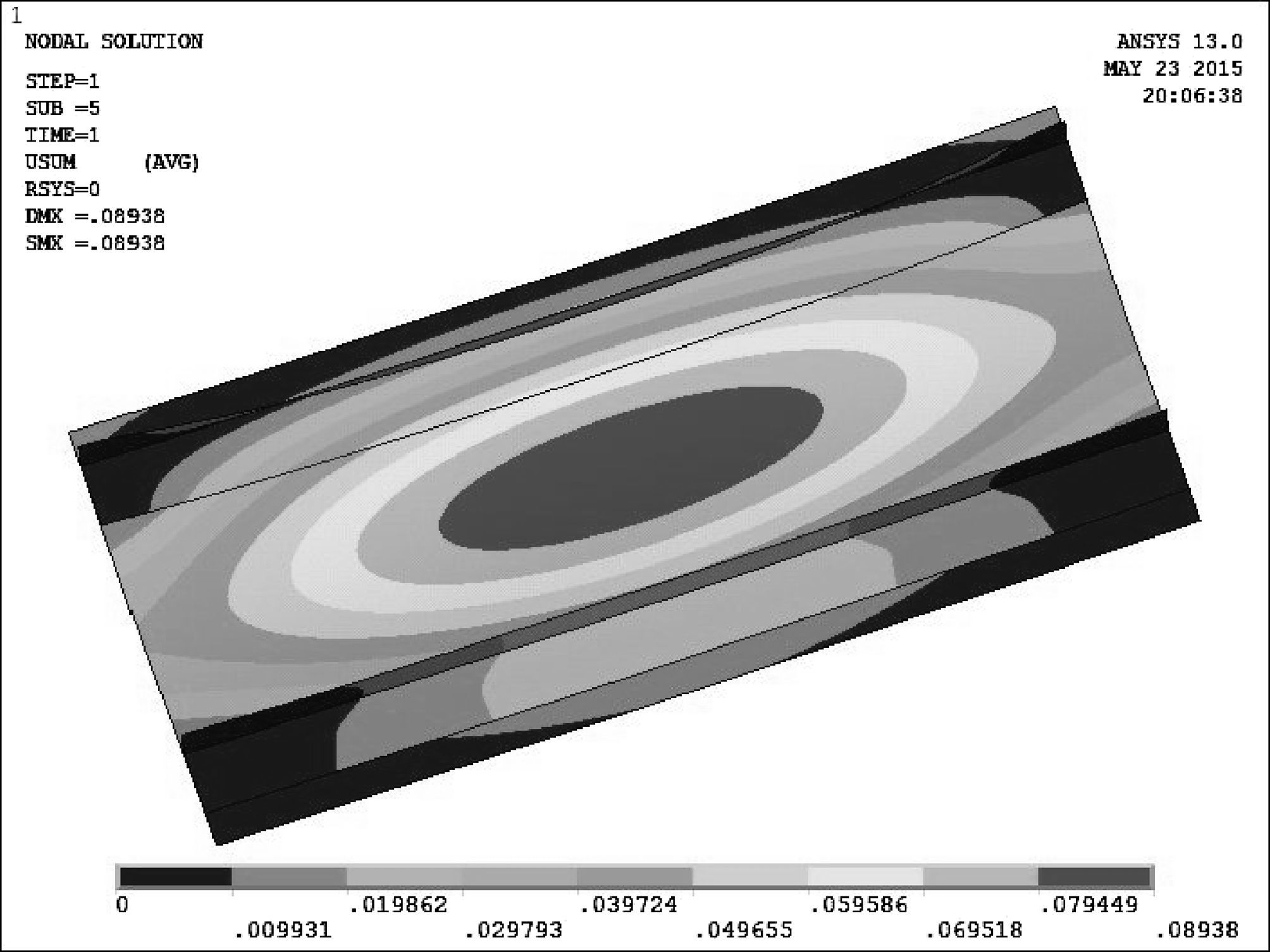
薄板加筋后,其动力响应将发生变化.考虑到飞机蒙皮实际上是固定在骨架上的,即：加强筋固定在骨架上,所以分析时对加强筋两端采用固支处理.选择瞬态求解,得到单向和双向铆接加筋薄板第1秒时的等效应变云图,如图 4、图 5所示.结果发现,加强筋的安装方向不同,薄板振动疲劳危险位置显著不同,说明加筋安装方向对振动疲劳寿命具有重要的影响.

图 4 单向铆接薄板的等效应变图 Fig.4 Equivalent strain of single rivet plate
图选项
图 5 双向铆接薄板的等效应变图 Fig.5 Equivalent strain of double rivet plate
图选项

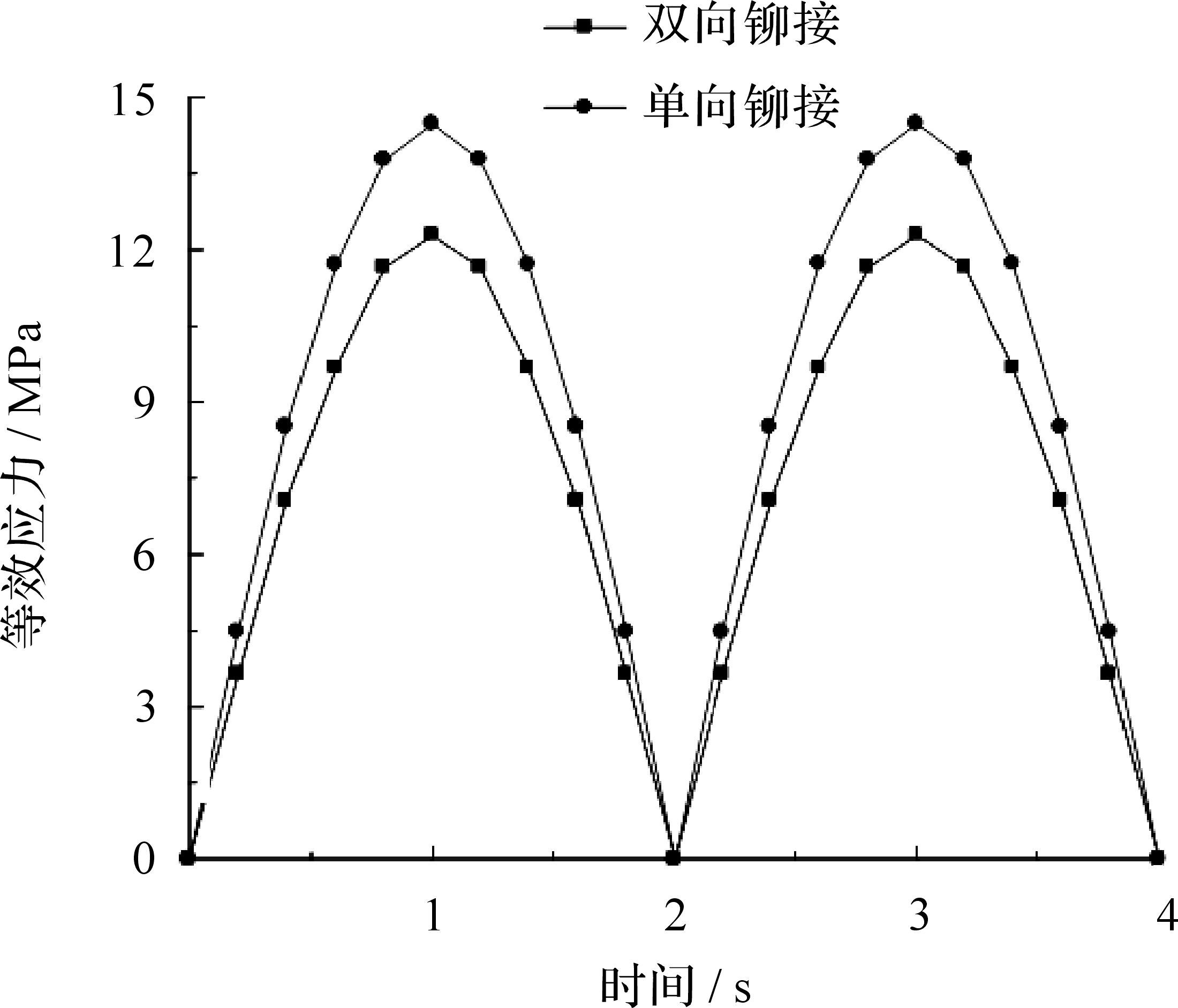
图 6描述了分布压力载荷作用下加强筋安装方向对最大应力的影响.分析表明,单向加筋薄板的最大应力高于双向加筋薄板的最大应力.造成这种差异性的原因可能是：加筋形式不同,薄板的刚度也有不同.结果说明,采用双向加筋更有利于提高加筋薄板构件的振动疲劳强度.

图 6 加筋薄板最大应变处节点应力变化曲线 Fig.6 Curve of stress variation in the maximum strain node of stiffened plate
图选项

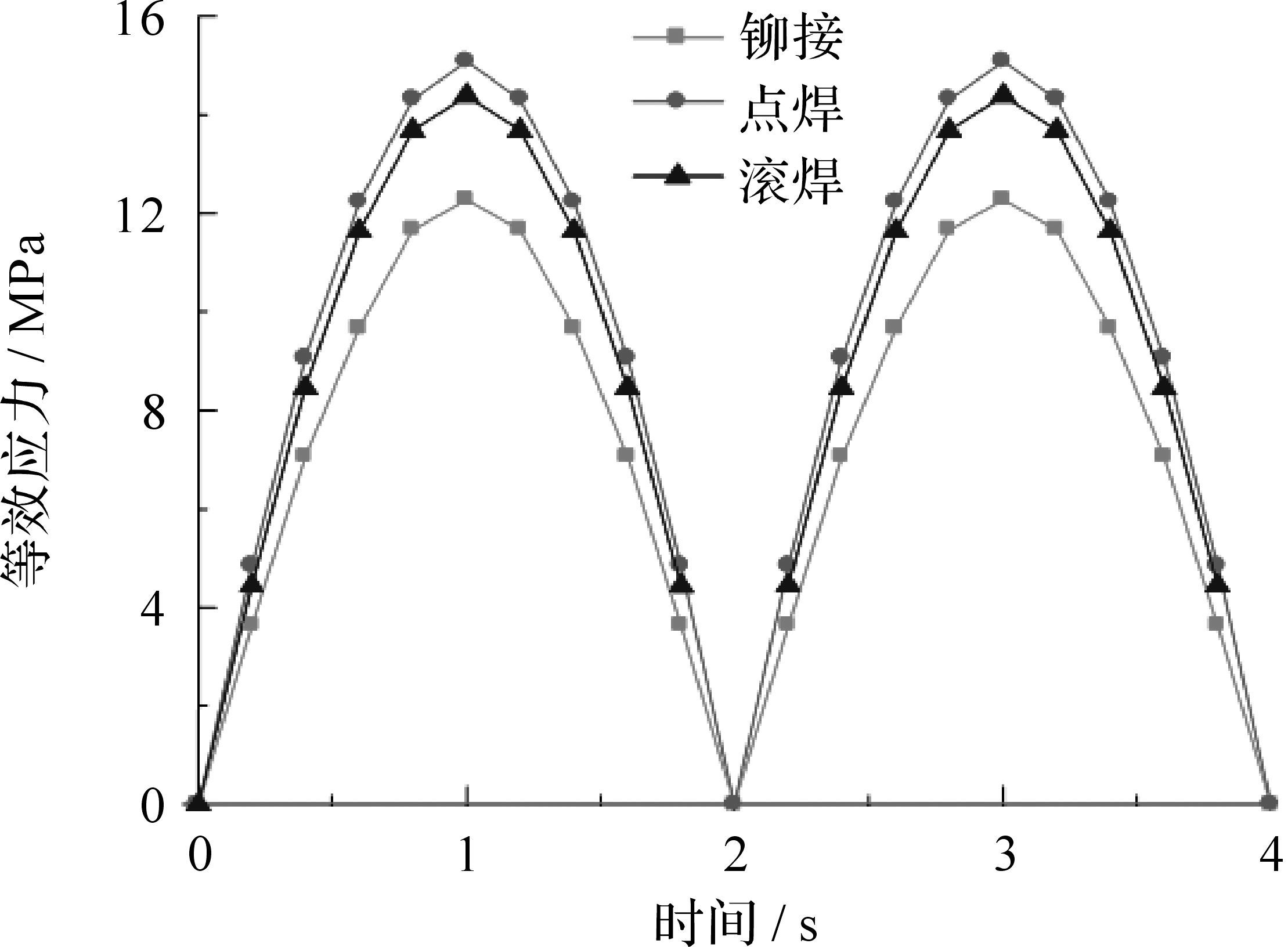
图 7描述了板筋不同连接形式对薄板最大应力的影响规律.分析发现,点焊薄板加筋构件的最大应力最大,其次是滚焊薄板加筋构件,铆接薄板加筋构件的最大应力最小.该变化规律与固有频率的变化规律不一致,即：滚焊薄板加筋构件的固有频率虽然最大,但其应力未必最大.结果表明,振动模态与结构响应之间的关系十分复杂,对振动疲劳寿命的影响机制更复杂.分析发现,应力最大的点都是连接点,原因在于连接点容易造成应力集中.点焊处的应力变化程度高于其它两种连接.点焊、滚焊的等效应力高于铆接连接的等效应力，但是，由于点焊连接加筋薄板中2个焊点之间存在缝隙，更容易造成应力集中，所以导致了点焊形式的等效应力变化大于滚焊形式.

图 7 3种连接形式下最大应变处节点应力变化曲线 Fig.7 Curve of stress variation by the three connection methods in the maximum strain node
图选项
4 加筋薄板的振动疲劳寿命

在加筋薄板构件动力响应计算的基础上,预测加筋薄板构件振动疲劳寿命的关键是振动疲劳寿命曲线的选取.因为动态疲劳S—N曲线是通过动态疲劳试验测得,受研究条件的限制,本文采用文献提供的LY12CZ铝合金的正弦振动疲劳寿命曲线方程[13]

$log~N=20.2053-6.8432log~S.$

实际疲劳寿命取决于材料的疲劳性能和应力水平.加筋薄板在正弦载荷作用下,不同类型的加筋薄板,连接点受拉压作用不同,危险点也不同,这就造成了疲劳寿命的不同.各种连接形式的加筋薄板疲劳破坏主要在连接部位,这是由于连接部位容易引起应力集中造成的.

在实际工程应用中,连接部位在连接过程还会对材料产生破坏,如：铆接会影响裂纹的扩展，点焊、滚焊引起的局部高温会影响材料的晶体结构.这些都会影响结构的实际寿命.

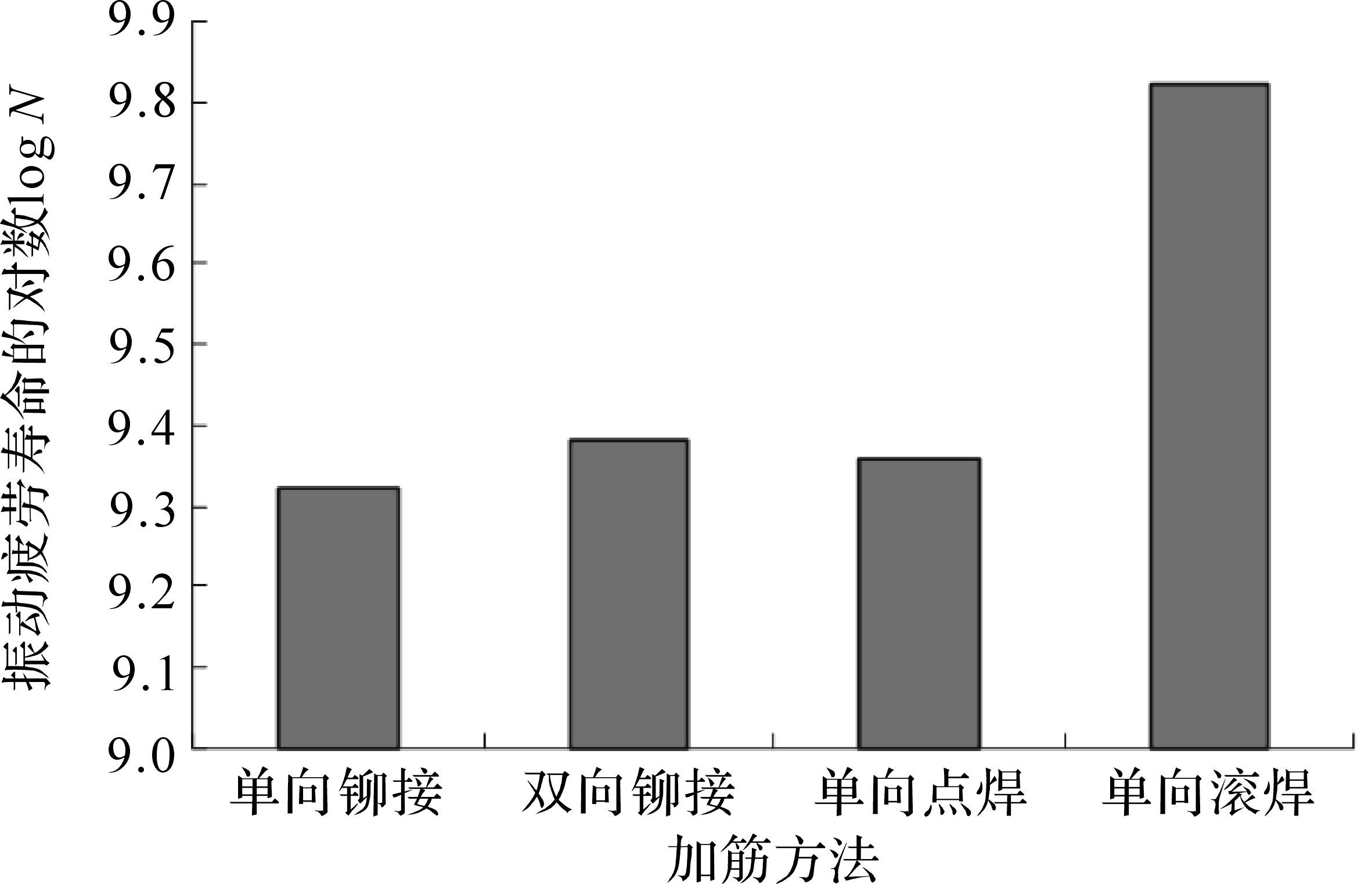
结合动力响应分析结果和LY12CZ的振动疲劳寿命曲线方程,可计算得到各种加筋薄板的实际寿命,如图 8所示.分析发现：各种加筋薄板的疲劳寿命与加筋薄板最大应力无对应的关系,对于单向加筋薄板构件,滚焊连接加筋薄板构件的振动疲劳寿命最大,点焊连接加筋薄板构件的振动疲劳寿命最小；而在动力响应方面,铆接连接加筋薄板构件的最大应力最大.分析认为,这是因为加筋薄板在振动过程中,薄板上疲劳应力并不是任意位置都按r=-1循环.

图 8 加筋布置对振动疲劳寿命的影响 Fig.8 Impacts of stiffen method on vibration fatigue life
图选项
5 结 语

以LY12CZ铝合金加筋薄板为对象,基于变形协调条件,建立加筋薄板的运动方程.为探讨板筋连接形式对薄板振动疲劳寿命的影响,通过仿真计算得出加筋薄板相应的固有频率和固有振型,并利用试验结果验证了3种连接形式的加筋薄板有限元模型的可靠性.在建立3种连接形式的单、双向加筋薄板数值模型的基础上,结合现已有的单向加筋薄板试验数据验证动力学模型的可靠性,对单、双向结构进行分析,研究加筋布置对结构振动疲劳寿命的影响.主要结论如下：

1) 加筋布置的改变,会影响加筋薄板的模态振型和模态频率,而且双向加筋薄板的第1阶模态频率会升高,相反其它3阶则降低，双向加筋薄板在低频振动时刚度高于单向加筋薄板；

2) 加筋布置对加筋薄板的动力响应明显,双向加筋薄板的最大动应力明显低于单向加筋薄板的最大动应力,结果表明双向加筋有利于提高结构抗振动疲劳强度；

3) 3种布置加筋薄板构件中,在相同载荷下铆接连接的单向加筋薄板的振动疲劳寿命最小,即安全系数最低.

参考文献
[1] 刘文光, 陈国平, 贺红林, 等. 结构振动疲劳研究综述[J]. 工程设计学报 , 2012, 19 (1) : 1–8. LIU Wen-guang, CHEN Guo-ping, HE Hong-lin, et al. Review of studying on vibration fatigue[J]. Chinese Journal of Engineering Design , 2012, 19 (1) : 1–8.
[2] 周江贝, 孙秦. 复合材料薄壁加筋结构局部稳定性分析的谱单元法[J]. 机械科学与技术 , 2014, 33 (2) : 1912–1915. ZHOU Jiang-bei, SUN Qin. The spectral element method of the local stability for the stiffened thin-walled structure of the composite[J]. Mechanical Science and Technology for Aerospace Engineering , 2014, 33 (2) : 1912–1915.
[3] 杨竣博, 宋笔锋, 钟小平. 曲加筋条壁板优化设计研究[J]. 机械强度 , 2014, 36 (6) : 904–910. YANG Jun-bo, SONG Bi-feng, ZHONG Xiao-ping. Research on optimal design of curvilinearly stiffened panels[J]. Journal of Mechanical Strength , 2014, 36 (6) : 904–910.
[4] 郑洁, 任善. 复合材料加筋壁板稳定性分析方法研究[J]. 航空科学技术 , 2015, 26 (3) : 44–48. ZHENG Jie, REN Shan. Study on stability analysis method of composite stiffened plates[J]. Aeronautical Science and Technology , 2015, 26 (3) : 44–48.
[5] 王富生, 张钧然, 郑涵天, 等. 复合材料加筋壁板鸟撞动响应分析[J]. 振动与冲击 , 2013, 32 (4) : 6–10. WANG Fu-sheng, ZHANG Jun-ran, ZHENG Han-tian, et al. Dynamic response of a composite reinforced panel to bird strike[J]. Journal of Vibration and Shock , 2013, 32 (4) : 6–10.
[6] SAKANO M, WAHAB M A. Fatigue strength of welded transverse stiffener joints under variable amplitude loading[J]. International Journal of Pressure Vessels and Piping , 1998, 75 (15) : 1037–1045. DOI:10.1016/S0308-0161(98)00108-2
[7] 刘文光, 贺红林. 单向双筋板结构件共振疲劳试验及分析[J]. 实验力学 , 2012, 27 (3) : 361–367. LIU Wen-guang, HE Hong-lin. Resonance fatigue testing and analysis of one-way double-stiffened plate[J]. Journal of Experimental Mechanics , 2012, 27 (3) : 361–367.
[8] 刘文光. 考虑结构裂纹扩展的振动疲劳寿命计算方法[J]. 振动工程学报 , 2012, 25 (1) : 79–82. LIU Wen-guang. Calculation method of vibration fatigue life with structure crack growth[J]. Journal of Vibration Engineering , 2012, 25 (1) : 79–82.
[9] 顾超林.加筋板连接件的振动疲劳仿真研究[D].南京:南京航空航天大学航空宇航学院,2009:1-69. GU Chao-lin.Research on vibration fatigue of stiffened aluminum alloy panel [D].Nanjing:Nanjing University of Aeronautics and Astronautics,College of Aerospace Engineering,2009:1-69.
[10] 廉政.典型结构件的振动疲劳分析[D].南京:南京航空航天大学航空宇航学院,2010:1-55. LIAN Zheng.Vibration fatigue analysis of typical structure [D].Nanjing:Nanjing University of Aeronautics and Astronautics,College of Aerospace Engineering,2010:1-64.
[11] 王佳莹.考虑温度影响下结构振动疲劳寿命估算[D].南昌:南昌航空大学航空制造工程学院,2012:1-56. WANG Jia-ying.Estimation of structural vibration fatigue life with temperature involved [D].Nanchang:Nanchang Hangkong University,School of Aeronautic Manufacturing Engineering,2012:1-56.
[12] 濮良贵, 纪名刚. 机械设计[M].7版. 北京: 高等教育出版社 ,2001 : 1 -210. PU Liang-gui, JI Ming-gang. Design of machinery[M].7th ed. Beijing: Higher Education Press , 2001 : 1 -210.
[13] 肖寿庭, 杜修德. LY12CZ铝合金悬臂梁动态疲劳 S—N曲线的试验测定[J]. 机械强度 , 1995, 17 (3) : 21–24. XIAO Shou-ting, DU Xiu-de. Measurement of a dynamic fatigue S-N curve for LY12CZ Al alloy cantilever specimens[J]. Journal of Mechanical Strength , 1995, 17 (3) : 21–24.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.014
教育部主管，浙江大学和中国机械工程学会主办
0

文章信息

刘文光, 林炜彦, 颜龙, 舒斌
LIU Wen-guang, LIN Wei-yan, YAN Long, SHU Bin
基于抗振动疲劳的薄板加筋设计分析
Analysis on stiffen design of a skin plate by anti-vibration fatigue
工程设计学报, 2016, 23(4): 385-390.
Chinese Journal of Engineering Design, 2016, 23(4): 385-390.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.014

文章历史

收稿日期: 2015-09-24

相关文章

工作空间