Download PDF  
文章快速检索  
  高级检索
引用本文
杨金川,田茂君,姚智慧,陈浩. 滚动汇流环装配力学特性分析与优化设计[J]. 工程设计学报, 2016, 23(4): 364-370.
YANG Jin-chuan, TIAN Mao-jun, YAO Zhi-hui, CHEN Hao. Analysis of mechanical characteristics and optimum design on assembling of rolling collector ring[J]. Chinese Journal of Engineering Design, 2016, 23(4): 364-370.
滚动汇流环装配力学特性分析与优化设计
杨金川1,2,田茂君1,姚智慧2,陈浩3     
1. 中国工程物理研究院 材料研究所, 四川 绵阳 621700;
2. 哈尔滨工业大学 机电工程学院, 黑龙江 哈尔滨 150001;
3. 海军装备部 重庆军代局, 重庆 400062
收稿日期: 2016-01-12 .
作者简介: 杨金川(1988—),男,四川阆中人,工程师,从事精密仪器设计和制造研究,E-mail:yangjinchuan@caep.cn. http://orcid.org//0000-0002-2313-5055
通讯作者: 姚智慧(1955—),男,硕士,教授,从事精细工艺、曲面加工与精密制造技术等研究,E-mail:yaozhizhi@hit.edu.cn.
摘要: 汇流环安装于具有相对转动的内、外环道之间，受到内、外环道的预紧压缩，形成与环道之间的微小面积接触，并通过接触面实现电传输.为了明确薄壁圆柱形滚动汇流环的装配力学特征及其压缩状态，基于汇流环装配后产生的变形状态，运用弯曲力学理论建立汇流环装配压缩后的弯曲变形模型，结合赫兹接触理论以及电接触理论得出汇流环压缩变形、接触电阻以及结构尺寸三者之间的关系.根据装配约束条件，得出汇流环预紧压缩量的预设范围.通过设计实例的计算分析与ABAQUS有限元验证，其结果表明有限元仿真结果与理论模型的计算结果相差微小.汇流环装配压缩的力学模型及其预设范围具有良好的合理性与正确性，能够为滚动汇流环的优化设计提供重要参考.
关键词: 滚动汇流环     装配压缩     结构设计     约束条件     仿真    

基金项目: 中国工程物理研究院材料研究所重点基金资助项目（SJZ201501）
Analysis of mechanical characteristics and optimum design on assembling of rolling collector ring
YANG Jin-chuan1,2, TIAN Mao-jun1, YAO Zhi-hui2, CHEN Hao3     
1. Institute of Materials, China Academy of Engineering Physics, Mianyang 621700, China ;
2. School of Mechanical and Electrical Engineering, Harbin Institute of Technology, Heilongjiang 150001, China ;
3. Chongqing Military Representative Bureau, Naval Equipment Department, Chongqing 400062, China
Abstract: The collector ring under compression is installed between a exterior orbit and a interior one that produces contact zone between ring and orbits and obtains electro-transport.Aiming to define character of rolling collector ring mechanics and its compression state,based on the distortion of ring after assembling,a bending deformation model of ring under compression was established with bending principle. Hertz contact theory and electrical contact theory were used to obtain the relationship among contact deformation,contact resistance and design size of the ring.According to the constraint conditions of assembling,the rational preinstalling and discriminant range of compression of collector ring were determined.By means of calculation and validation of design living example and simulation of software ABAQUS,the result of mechanics after simulation almost kept the same with calculation of theory model.The research provides reference for the development and optimum design of rolling collector ring.
Key words: rolling collector ring     assembling compression     structural design     constraint condition     simulation    

汇流环是装配于相对旋转的内、外两个环道之间,并在两者之间滚动，用以长时间传递电功率及电信号的精密输电装置，两者合称滚动汇流环，简称滚环.它由汇流环(柔性环)与内、外环道组成,通过径向预紧后的汇流环与内、外环道之间的接触面来传递电信号或功率,通常应用于国防或者航空航天等高精尖的系统设备[1-2].汇流环虽然是较小的零部件,但是其性能质量和工作状态会影响整套系统设备的性能和可靠性.所以,国内外在研制汇流环时,对其各项性能指标(主要指电接触性能与使用寿命)必须给予足够的重视[3].而汇流环径向压缩量的设计计算将直接关系到其接触状态,进而影响输电性能[4-5].

当前,国内外关于汇流环设计及其压缩定量方面的文献较少.其中,国内关于汇流环方面的研究多集中于滑动汇流环,其一般采用电刷与汇流环接触,两者之间不需要准确计算和确定压缩量.滑动汇流环存在一定的使用缺陷,例如滑动摩擦会引起汇流环和电刷的重度磨损、使用寿命短、安装预紧不稳定等[6-8].而国外自20世纪80年代起,便开始了滚动汇流环的研究,以解决滑动汇流环的固有缺陷.其中,以美国航空航天局为主导力量,开展并成功设计了多种不同构型的滚动汇流环[9-13].滚动汇流环的出现克服了原先滑动汇流环的许多短板，例如,采用滚动模式能够大幅减小甚至消除滑动磨损,从而提高汇流环的使用寿命.但由于其预紧压缩量直接关系到电传递的波动性,甚至影响信号传递的准确性,所以在设计与制造过程中需要严格准确地计算并规定汇流环与内、外环道之间的预紧压缩量,并进行合理性与可行性的判定.

因此,有必要基于滚动汇流环的设计要素,包括材料、使用寿命、力学状态等方面,结合材料力学与有限元仿真技术,给出滚动汇流环预紧压缩量计算方法与定量理论,并论证其合理性与可行性.

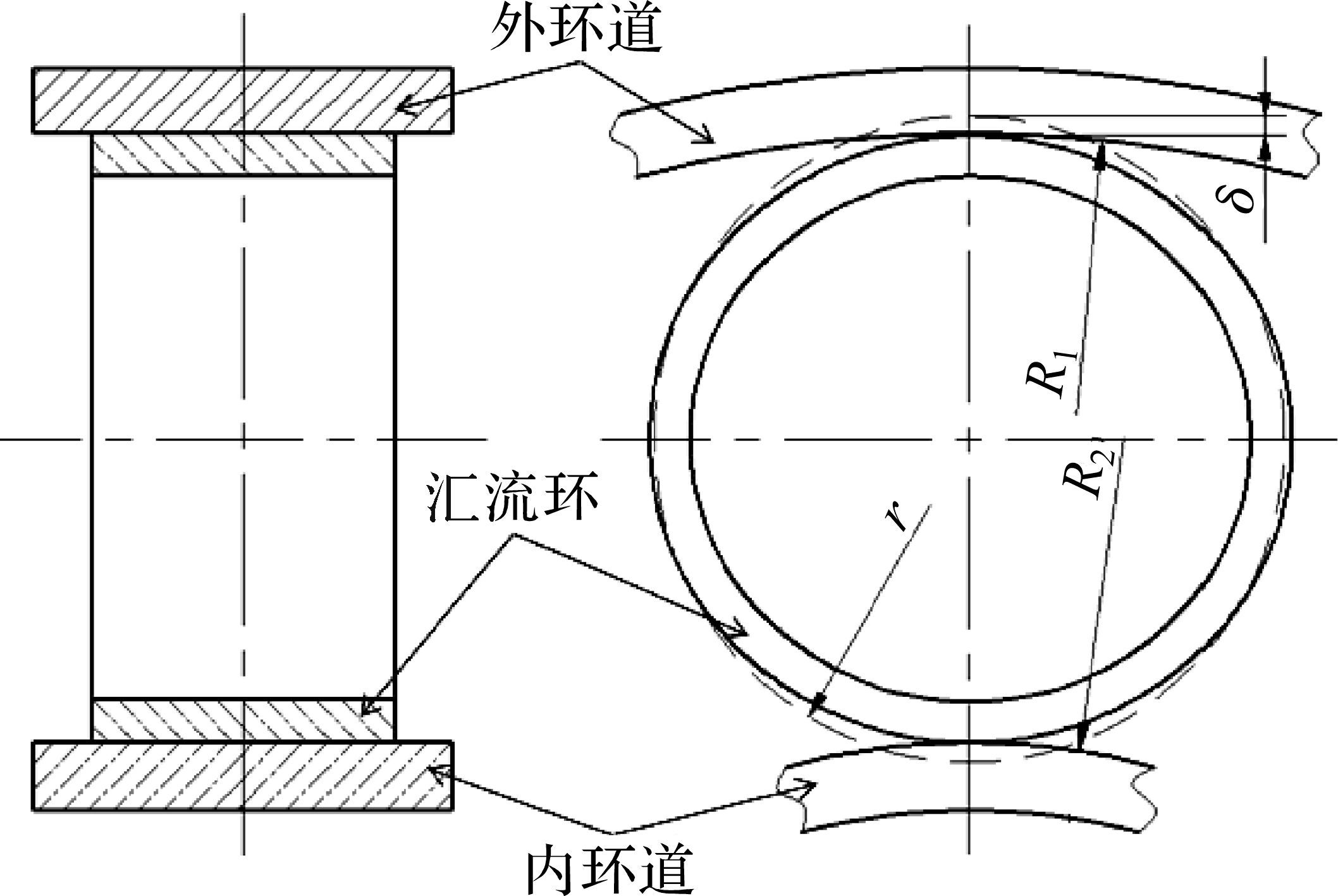
1 汇流环装配及力学解析模型

根据理论力学以及材料力学分析,圆柱形汇流环经过预加载(即由内、外环道尺寸决定形变与加载力)会出现整体以及局部形变.本文所研究的滚动汇流环结构如图 1所示.

图 1 滚动汇流环结构 Fig.1 Structure of rolling collector ring
图选项

由图 1可知,汇流环装配于内、外环道之间,由于受到环道的径向压缩加载力而发生了整体与局部的变形.由于装配前的汇流环与环道存在设计尺寸的差异,使得内外环对汇流环形成了预紧压缩而造成变形.因此,实际径向压缩量 (半径量)为

$\delta ={{Y}_{R}}=2r-\frac{\left( {{R}_{1}}-{{R}_{2}} \right)}{2},$ (1)

式中：r为汇流环未压缩前外圆半径；R1为外环道内半径；R2 为内环道外半径.

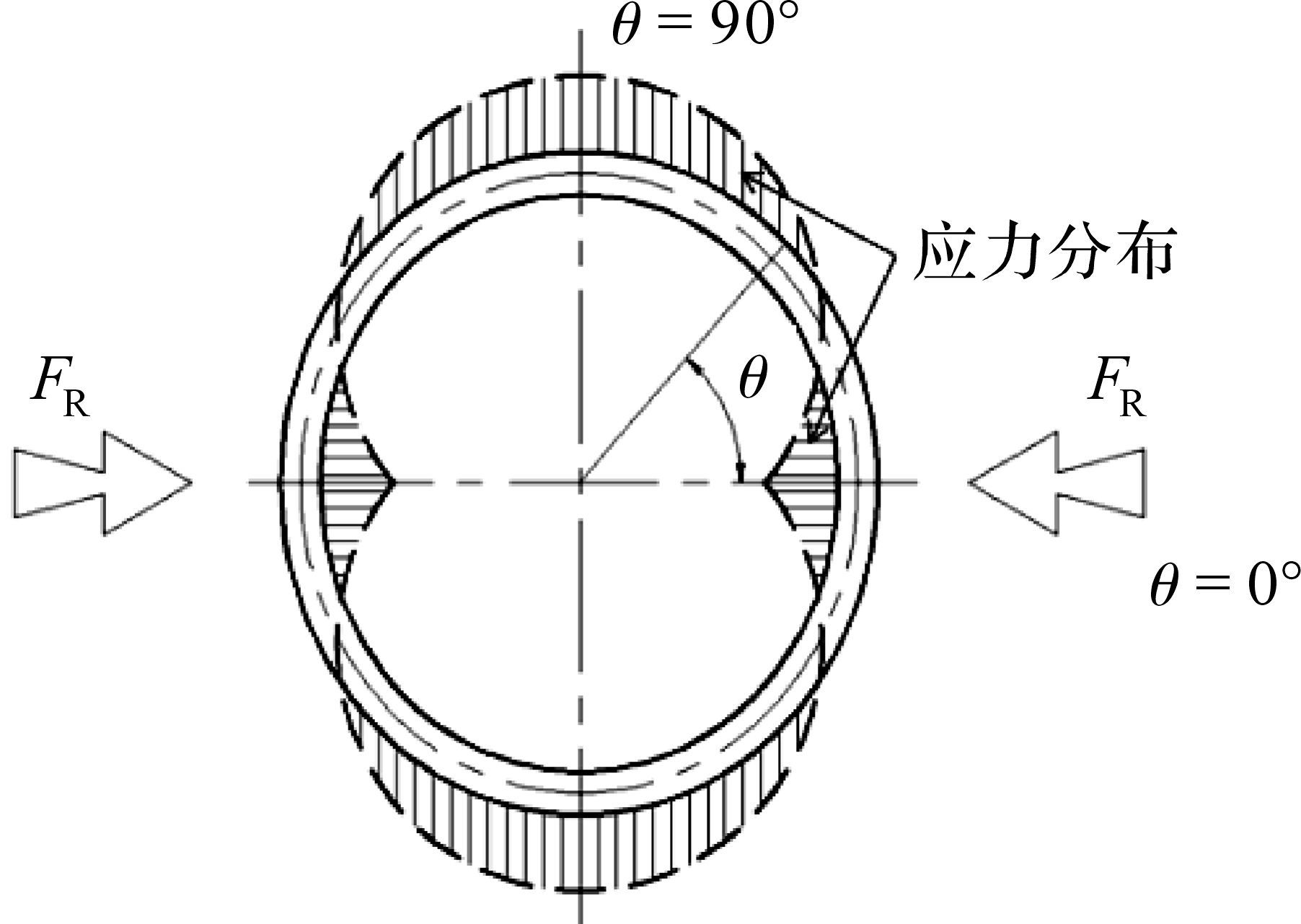
由图 1中三环结构尺寸可知,汇流环的变形与3个环的设计尺寸和接触位置有关.当三者之间形成预紧压缩时,汇流环在不同位置产生了不同的弹性应变与变形应力,其整体压缩后的力学状态如图 2所示.

图 2 汇流环压缩应变及其应力分布状态 Fig.2 Compression strain and stress distribution of collector ring
图选项

图 2中,FR为汇流环压缩时所受径向预紧力.在三环接触点附近(即θ=0°)时,根据相关计算可以得出以下力学关系：

1) 从接触点开始到垂直于接触点(即从0°到90°)变化时[14],不同点的压缩量为

${{Y}_{R}}=\frac{{{F}_{R}}{{r}^{3}}}{{{E}_{1}}I}\left( -\frac{1}{\pi }+\frac{sin~\theta }{4}+\frac{\pi cos~\theta }{8}-\frac{\theta cos~\theta }{4} \right),$ (2)

式中：E1为汇流环弹性模量；I为汇流环截面对中性轴的惯性矩；θ为汇流环上某点径向夹角.

2) 根据材料力学[15],汇流环经过压缩后,在环的截面内和内、外弧面上的任意点将受到由压缩引起的弯矩作用,该任意点所受弯矩大小为

$M={{F}_{R}}r\left( \frac{sin~\theta }{2}-\frac{1}{\pi } \right),$ (3)

式中r为环上任一点与圆心距离(压缩后).

由材料力学可知，弯曲应力计算公式为

${{\sigma }_{B}}=\frac{My}{I},$ (4)

式中y为计算应力点到截面中性轴的距离.

联立式(3)和式(4),再根据图 2所示,弯曲应力的最大值产生在汇流环θ=0°与θ=90°位置,可以分别得出这2个特殊位置的弯曲应力值，为

$\left. \begin{align} & {{\sigma }_{B0}}=\pm \frac{0.318{{F}_{R}}r{{c}_{0}}}{I}\text{ }\left( \theta =0{}^\circ \right), \\ & {{\sigma }_{B90}}=\pm \frac{0.182{{F}_{R}}r{{c}_{0}}}{I}\text{ }\left( \theta =90{}^\circ \right). \\ \end{align} \right\}$ (5)

其中：“+”表示为弯曲拉应力,在汇流环内圆弧上；“-”表示为弯曲压应力,在汇流环外圆弧上；c0为汇流环外圆到截面中性轴的距离.

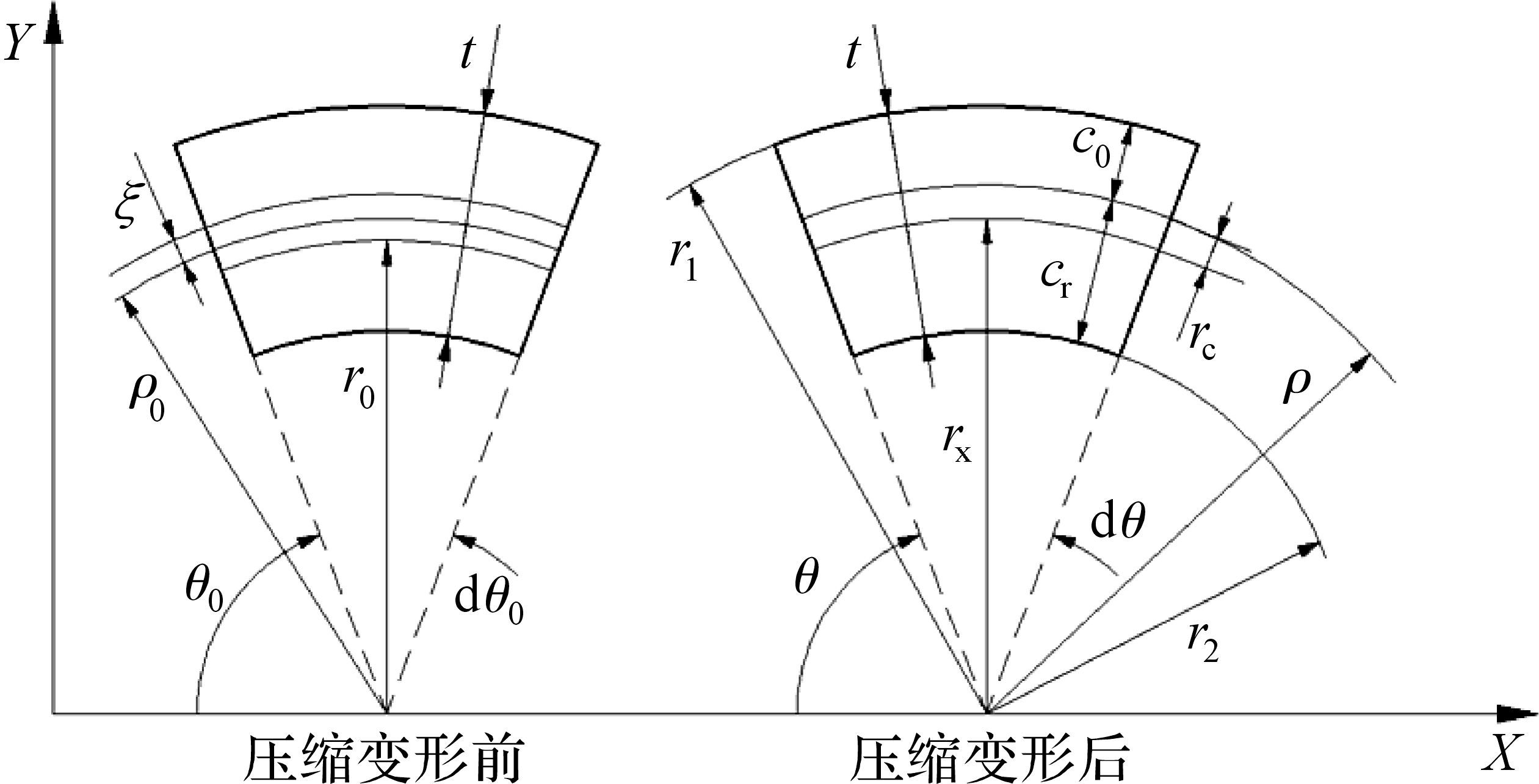
根据图 1,汇流环某微元段产生压缩前后的变形状态如图 3所示.

图 3 变形前后汇流环微段模型 Fig.3 Infinitesimal section of collector ring before and after assembling
图选项

图 3中：ρ为汇流环压缩后中性层的曲率半径,ρ0为汇流环压缩前中性层的曲率半径；ξ 为截面上任意一点到中性层的距离；r1和r2分别为压缩后截面的外、内弧面曲率半径；r0和rx分别为压缩前、后截面的形心层曲率半径；rc为形心层与中性层之间的距离.因此,有如下尺寸关系：

$\left\{ \begin{align} & {{\rho }_{0}}={{r}_{0}}+{{r}_{c}}, \\ & \rho ={{r}_{x}}+{{r}_{c}}. \\ \end{align} \right.$ (6)

假设已知横截面面积A,且汇流环压缩前后的厚度t不变,有如下截面力矩关系[16]：

$M={{\int }_{A}}\sigma \xi dA=\frac{E\left( {{r}_{0}}-{{r}_{x}} \right)I}{{{\rho }_{0}}\rho }.$ (7)

将式(3)与式(7)联立求解,可得汇流环内弧面距中性轴距离cr为

${{c}_{r}}=\frac{t}{2}+\frac{{{t}^{2}}12}{{{r}_{x}}}.$ (8)

令横截面形心层压缩前的形心圆半径为

${{r}_{3}}=r-\frac{t}{2},$ (9)

又可根据图 1和压缩后形成的椭圆及其计算公式[17],在汇流环压缩位置形成的横截面形心层短半轴和长半轴分别为

$\left. \begin{align} & {{r}_{a}}=\frac{{{R}_{1}}-{{R}_{2}}}{2}-\frac{t}{2}, \\ & {{r}_{b}}=\sqrt{2r_{3}^{2}-r_{a}^{2}}. \\ \end{align} \right\}$ (10)

从而可推出压缩后汇流环接触点处的横截面形心层曲率半径rx为

${{r}_{x}}=\frac{r_{b}^{2}}{{{r}_{a}}}.$ (11)

根据图 3和式(8)所示,可知汇流环外圆与横截面中性轴之间的距离c0为

${{c}_{0}}=t-{{c}_{r}}.$ (12)

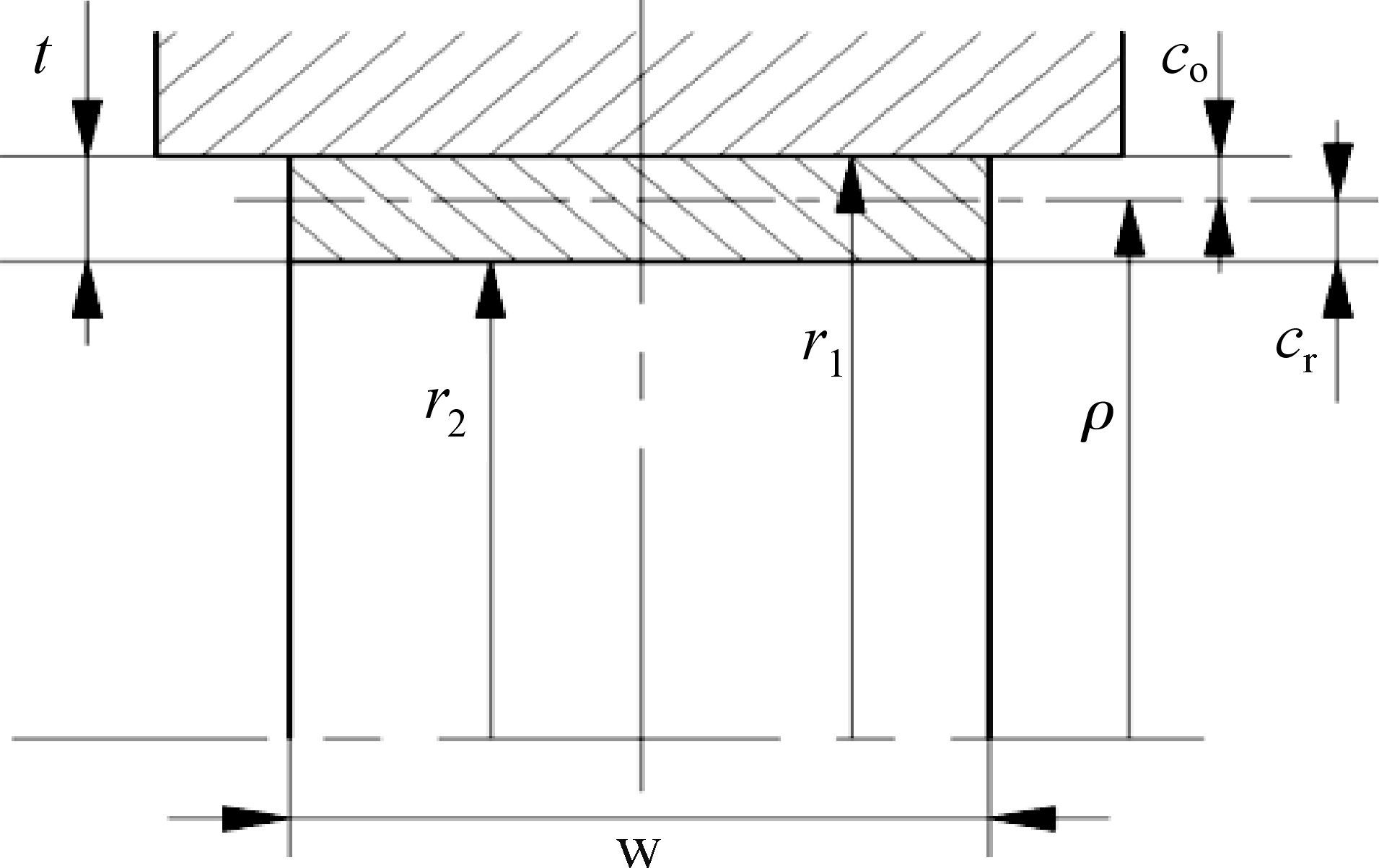
根据式(1)至式(3)所示受力状态,汇流环装配后预紧压缩的计算重要参量为汇流环截面对中心轴的惯性矩I.根据图 1,汇流环环接触时的横截面属性如图 4所示.

图 4 变形后汇流环横截面 Fig.4 Cross section of collector ring after assembling
图选项

图 4中,w为汇流环宽度.汇流环的横截面面积A为

$A=wt.$ (13)

根据材料力学,可知滚环横截面惯性矩Ir为

${{I}_{r}}=A\cdot \left[ {{\left( {{r}_{2}}+\frac{t}{2} \right)}^{2}}+\frac{{{t}^{2}}}{12} \right],$ (14)

则汇流环横截面的等效惯性矩I为

$I={{I}_{r}}-A\cdot {{\rho }^{2}}.$ (15)

以上各式便可以表征汇流环装配及力学状态,并可作为确定预紧压缩的定量理论与压缩量计算方法.但是,在确定汇流环预紧压缩量之前,还需要明确部分汇流环的约束条件,以明确压缩的定量范围.

2 汇流环装配装配约束条件

根据汇流环的功能作用,可以将用以确定滚动汇流环预装配的约束条件分为2种：一是力学约束条件，二是性能约束条件.

2.1 力学约束条件

根据汇流环装配后的压缩状态,其力学约束条件主要为汇流环材料应力疲劳极限及其对应的循环寿命极限.

其中,应力极限主要指汇流环装配后形成预紧压缩的环内弯曲应力不能大于满足设计要求的循环寿命对应的弯曲应力疲劳极限.

根据图 2和式(5),汇流环弯曲应力的最大值分布在θ=0°与θ=90°位置，又因为最大弯曲应力处内、外弧面的表面分别受拉伸应力和压缩应力，因此,汇流环在循环寿命范围内的最大弯曲应力应该小于对应的应力疲劳极限.设对应循环寿命的许用应力疲劳极限为σfN0,即存在如下限制关系：

$\left. \begin{align} & {{\sigma }_{B0}}\le {{\sigma }_{f{{N}_{0}}}}, \\ & {{\sigma }_{B90}}\le {{\sigma }_{f{{N}_{0}}}}. \\ \end{align} \right\}$ (16)

其中,材料在特定循环寿命次数N0时的疲劳强度极限为

${{\sigma }_{f{{N}_{0}}}}={{\sigma }_{r}}{{\cdot }^{m}}\sqrt{\frac{{{N}_{0}}}{N}},$ (17)

式中：σr为持久应力疲劳极限；m为汇流环材料系数；N为σr所对应的最小循环次数.

将式(16)和式(17)联立式(2)和式(5),可得

${{Y}_{R}}\le \frac{{{\sigma }_{f{{N}_{0}}}}{{r}^{2}}}{0.318{{c}_{0}}{{E}_{1}}}\left( \frac{\pi }{8}-\frac{1}{\pi } \right).$ (18)

其中,c0与YR之间的关系可以根据式(1)、式(8)到式(12)联立得出,为

$\frac{{{t}^{2}}}{6\left( t-2{{c}_{0}} \right)}=\frac{2r_{3}^{2}-\left( {{r}_{3}}-{{Y}_{R}} \right)}{{{r}_{3}}-{{Y}_{R}}}.$ (19)

将式(18)与式(19)联立,便可以得出汇流环装配后预紧压缩的预设上限.

2.2 性能约束条件

已知汇流环依靠其预紧压缩后的外圆弧面和环道弧面形成接触面来传导电信号与电功率,且该接触面面积的大小由汇流环预紧压缩量大小所决定[18-20].同时,该接触面面积的大小又决定了汇流环电传输性能的优劣.

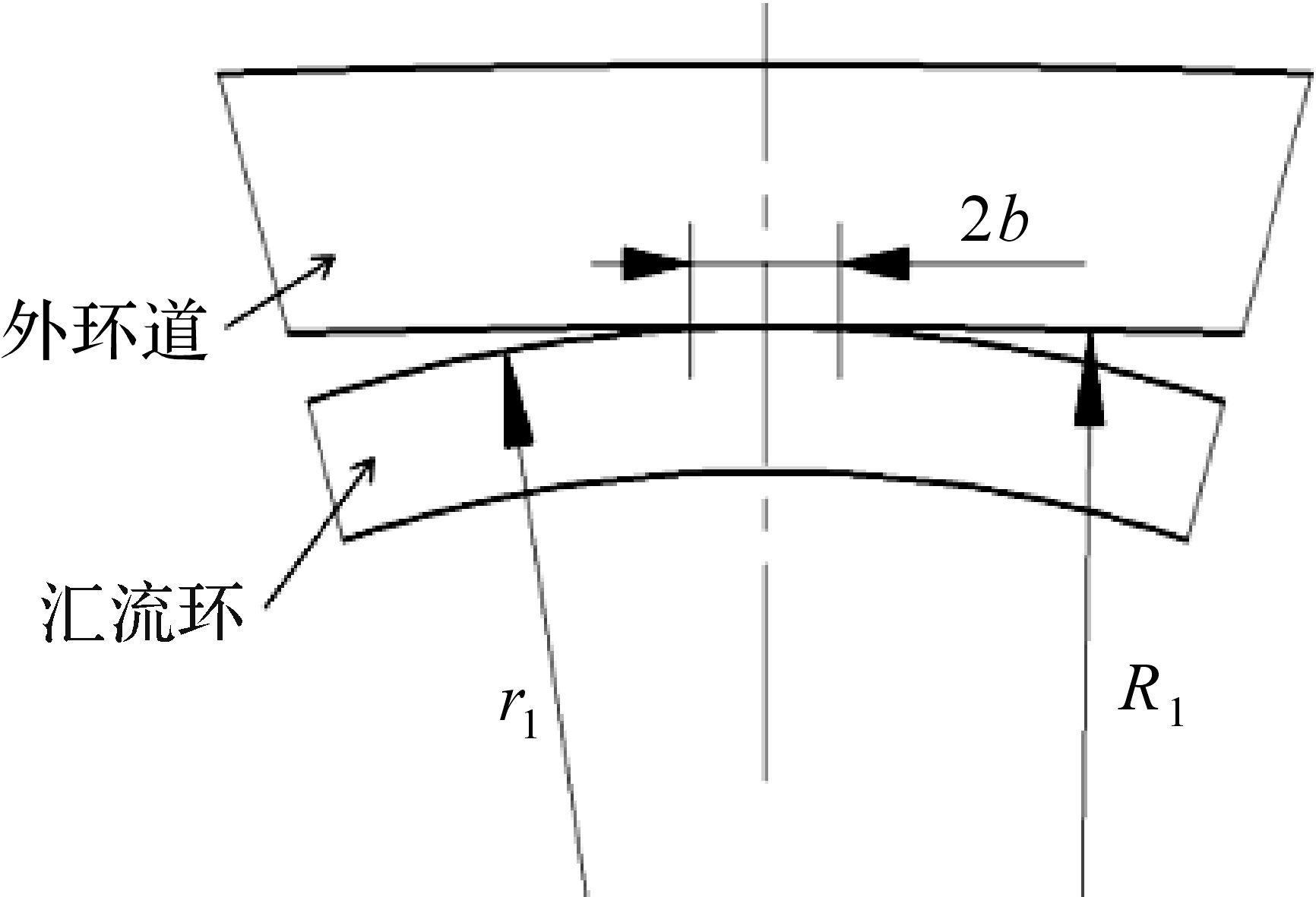
设定汇流环与内、外环道的接触均为弹性接触,可运用弹性接触(Hertz)理论对其进行研究.现将汇流环与环道的接触模型进行简化,如图 5所示.

图 5 压缩后汇流环接触尺寸 Fig.5 Contact size of collector ring after assembling
图选项

图 5中,2b为汇流环与环道之间的实际接触宽度.根据赫兹接触经典理论[21-22],可得出汇流环与环道之间的半接触宽度b为

$b=\sqrt{{{F}_{R}}\frac{\Delta }{\pi \cdot r}},$ (20)

其中,

$\Delta =\left( \frac{1-V_{1}^{2}}{{{E}_{1}}}+\frac{1-V_{2}^{2}}{{{E}_{2}}} \right)/\left( \frac{1}{2{{R}_{1}}}+\frac{1}{2{{r}_{1}}} \right),$ (21)

式中：V1和V2分别为汇流环材料与环道材料的泊松比；E1和E2分别为各自材料的弹性模量；r1可由图 3以及式(6)到式(12)计算推导.

根据式(20),可得汇流环在预紧压缩后与环道之间的接触面积Ac为

${{A}_{c}}=2b\cdot w.$ (22)

已知接触面积Ac和接触电阻RJ的关系[23]为

${{R}_{J}}=\frac{P}{2}\cdot \sqrt{\frac{\pi }{{{A}_{c}}}},$ (23)

式中P为汇流环电接触材料的电阻率.

根据航空航天领域以及工业标准的汇流环使用环境,汇流环的设计尺寸一般在 10～100 mm范围内.根据汇流环接触电阻的标准限值范围[24],汇流环的接触电阻应小于等于电接触设计标准,即

${{R}_{J}}\le {{R}_{b}}\in 0.1\tilde{\ }3~m\Omega $ (24)

由式(20)到式(24)可知,在汇流环和环道材料、汇流环宽度与厚度确定的情况下,径向预紧力与汇流环接触面积成正比.同时,接触面积又和接触电阻成反比[25].

由于接触电阻是影响汇流环电传输性能的直接原因[26],由式(24)联立式(20)到式(23)可计算得出汇流环装配压缩的预设下限量为

${{Y}_{R}}\ge \frac{{{P}^{4}}{{\pi }^{3}}{{r}^{4}}}{64{{R}^{4}}_{b}{{w}^{2}}{{E}_{1}}I\cdot \Delta }\left( \frac{\pi }{8}-\frac{1}{\pi } \right),$ (25)

式中,I与YR之间的关系可根据式(1)、式(6)到式(15)联立得出,为

$I={{I}_{r}}-A{{\left[ \frac{t}{2}+\frac{{{t}^{2}}}{12\left[ \frac{2{{({{Y}_{R}}+{{r}_{a}})}^{2}}-r_{a}^{1}}{{{r}_{a}}} \right]} \right]}^{2}}$ (26)

将式(26)与式(25)联立,便可以得出汇流环预紧压缩的预设下限.

由式(18)和式(25)可给出汇流环装配压缩的预设范围,在该范围内可设计并判定汇流环与环道之间尺寸预先设计的合理性.

3 实例分析计算及有限元验证

根据式(1)可知,汇流环的压缩量是由汇流环与内、外环道的装配所决定.因此,当汇流环原始直径确定后,以内、外环尺寸计算得出的压缩量为变量,可以得出压缩量与最大弯曲应力、接触电阻和循环寿命三者之间的关系.

根据图 2所示,汇流环的最大弯曲应力出现在θ=0°处.因此,将式(2)和式(5)联立,可得出最大弯曲应力σBmax与压缩量YR之间的关系为

${{\sigma }_{Bmax}}=\frac{0.318\cdot {{c}_{0}}\cdot {{Y}_{R}}\cdot {{E}_{1}}}{{{r}^{2}}\left( \frac{\pi }{8}-\frac{1}{\pi } \right)}.$ (27)

再联立式(2)、式(20)至式(23),可得出接触电阻RJ与压缩率YR之间的关系为

${{R}_{J}}=\frac{P}{2}\cdot \sqrt{\frac{\pi }{2w\cdot \sqrt{\frac{{{Y}_{R}}\cdot {{E}_{1}}\cdot I}{\pi \cdot {{r}^{4}}\left( \frac{\pi }{8}-\frac{1}{\pi } \right)\cdot \Delta }}}}.$ (28)

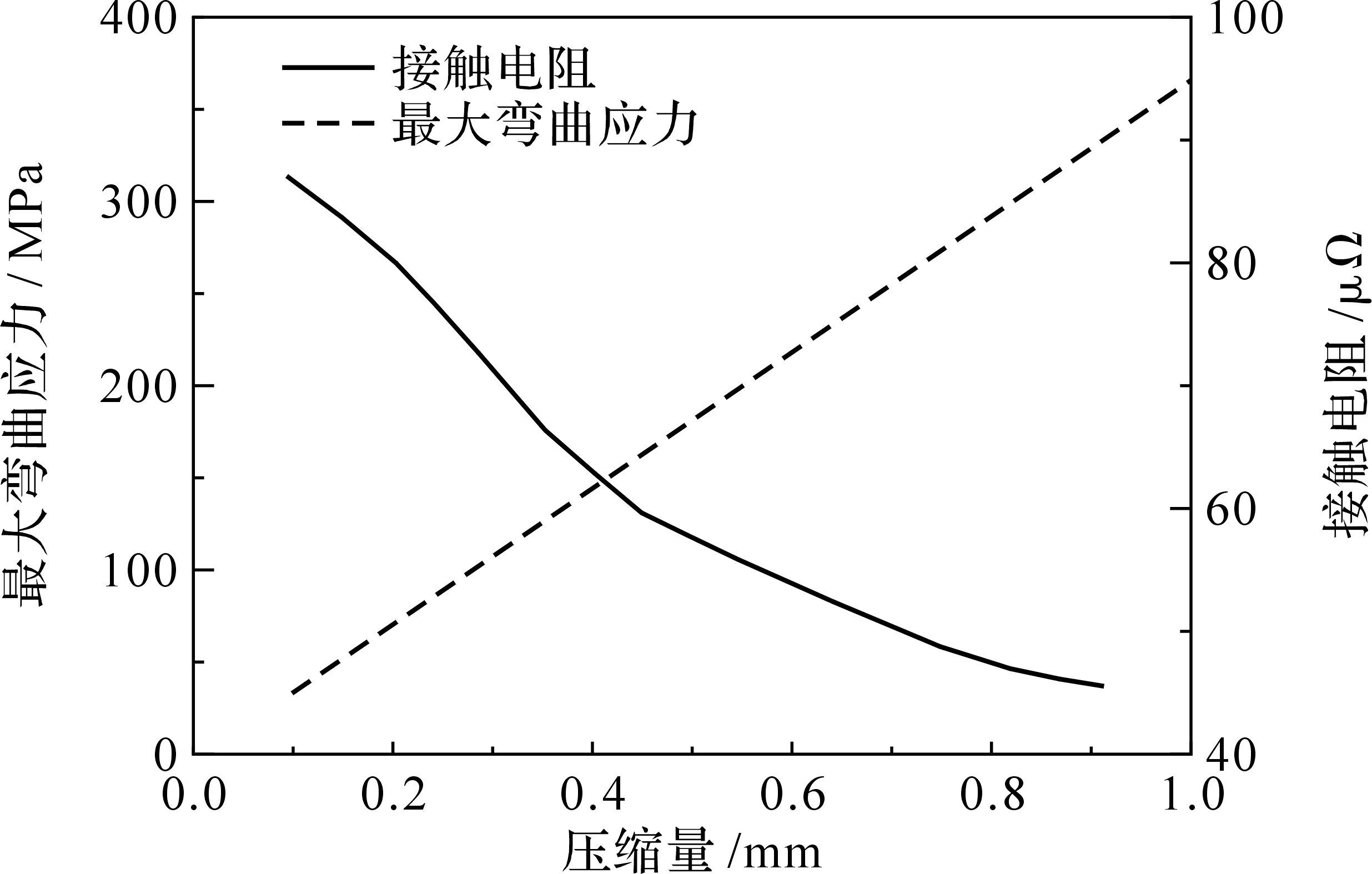
根据式(27)及式(28),可得出压缩量与汇流环最大弯曲应力及接触电阻之间的关系,如图 6所示.

图 6 压缩量与最大弯曲应力及接触电阻关系 Fig.6 Relationship among compression,maximum bending stress and contact resistance
图选项

根据式(27),将最大弯曲应力等效为对应循环寿命的最大许用应力疲劳极限σNf0,即

${{\sigma }_{Bmax}}={{\sigma }_{f{{N}_{0}}}}.$ (29)

则根据式(17),可得出在对应最大弯曲应力(疲劳极限)状态下的最大循环寿命为

${{N}_{Bmax}}=N\cdot {{\left( \frac{{{\sigma }_{Bmax}}}{{{\sigma }_{r}}} \right)}^{m}}.$ (30)

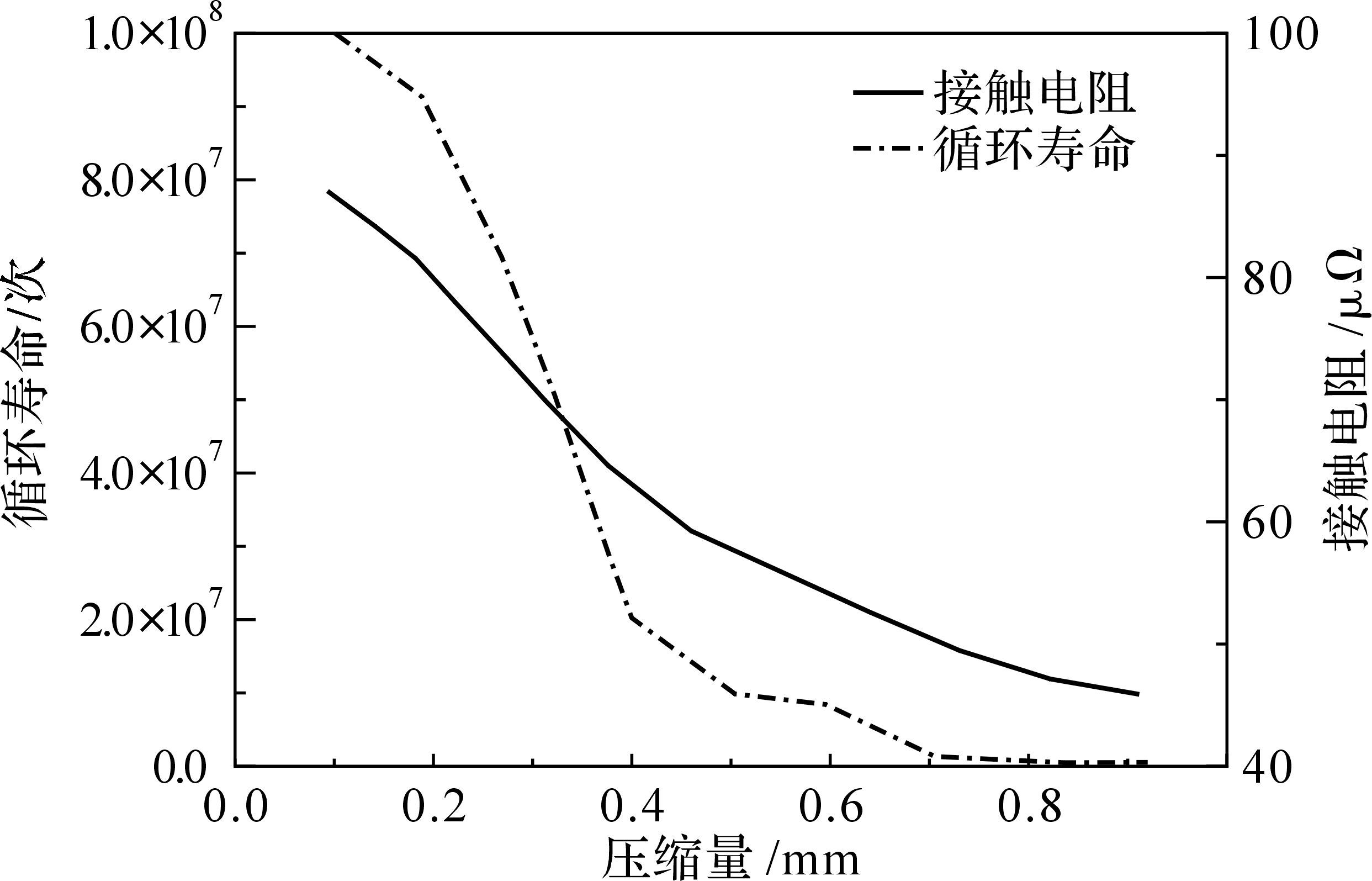
由式(30)和式(27)可得出压缩量与循环寿命之间的关系,如图 7所示.

图 7 压缩量与循环寿命及接触电阻关系 Fig.7 Relationship among compression,cycle times and contact resistance
图选项

由图 6和图 7可知,汇流环压缩量增大,使得装配后的最大弯曲应力增大，而接触电阻减小；同时,压缩量增大，使得循环寿命次数降低.

根据得出的汇流环预紧压缩量的理论上下限,可通过仿真计算对其范围进行实例验证.

已知某滚动汇流环设计实例的相关预设数据如表 1所示[25].

表 1 滚动汇流环设计实例数据 Table 1 The design data of rolling collector ring
参 数数 值
汇流环原始直径r/mm32.6
汇流环宽度w/mm4
汇流环厚度t/mm28.5
外环道内半径R1/mm76.58
内环道外半径R2/mm45
表选项

已知滚动汇流环所用材料为铍青铜,其材料牌号为QBe2.4,密度为8.06 g/cm3.该牌号铍青铜的电阻率P=6.63×10-6Ω·cm,弹性模量为E1=1.31×105 N/mm,泊松比为0.25.该汇流环设计要求的压缩受力循环寿命n=2.15×107次,其对应许用应力疲劳极限σfN0=210 MPa.

根据式(1)可得出汇流环的预设压缩量为

$\delta ={{Y}_{R}}=0.54~mm.$

再根据式(2)到式(26)可得出汇流环装配后预紧压缩YR的假设定量范围为

${{Y}_{R}}\in \left( 0.3154,0.5767 \right)~mm.$

由上述假设范围可知,预设的预紧压缩量为0.54 mm,正好在假设定量范围之内.可以判定,实例的预设内、外环道半径和计算得出的预紧压缩量是符合设计要求与约束条件的.

再次,将预设压缩量代入式(5)和式(23)可以得出对应的预紧最大弯曲应力为

${{\sigma }_{B0}}=198.52~MPa\le {{\sigma }_{f{{N}_{0}}}}=210~MPa.$

接触电阻RJ为

${{R}_{J}}=56.46~\mu \Omega \le {{R}_{b}}=100~\mu \Omega .$

根据以上结果可知,设计使用寿命和性能均满足设计标准与使用要求.

根据预设汇流环尺寸及其与内、外环道之间的装配关系,将汇流环与环道的设计尺寸进行虚拟样机的力学接触仿真.

采用ABAQUS接触仿真模型对汇流环的装配接触状态进行分析.

1) 整个模型网格单元类型为C3D10的六面体结构；

2) 将接触部分的内、外环道作为对汇流环施加装配压缩力的主接触面，汇流环外表面为副接触面；

3) 分别将汇流环外表面-内环道外表面、汇流环外表面-外环道内表面设定为表面-表面(standard)光滑接触模式(可分离)；

4) 内、外环道分别对汇流环施加径向方向0.54 mm的压缩量,内、外环道只具备径向自由度；

5) 选择S(Mises)与接触面积作为仿真输出的结果,代入运算.

整个模型结构和仿真结果下图 8和图 9所示.

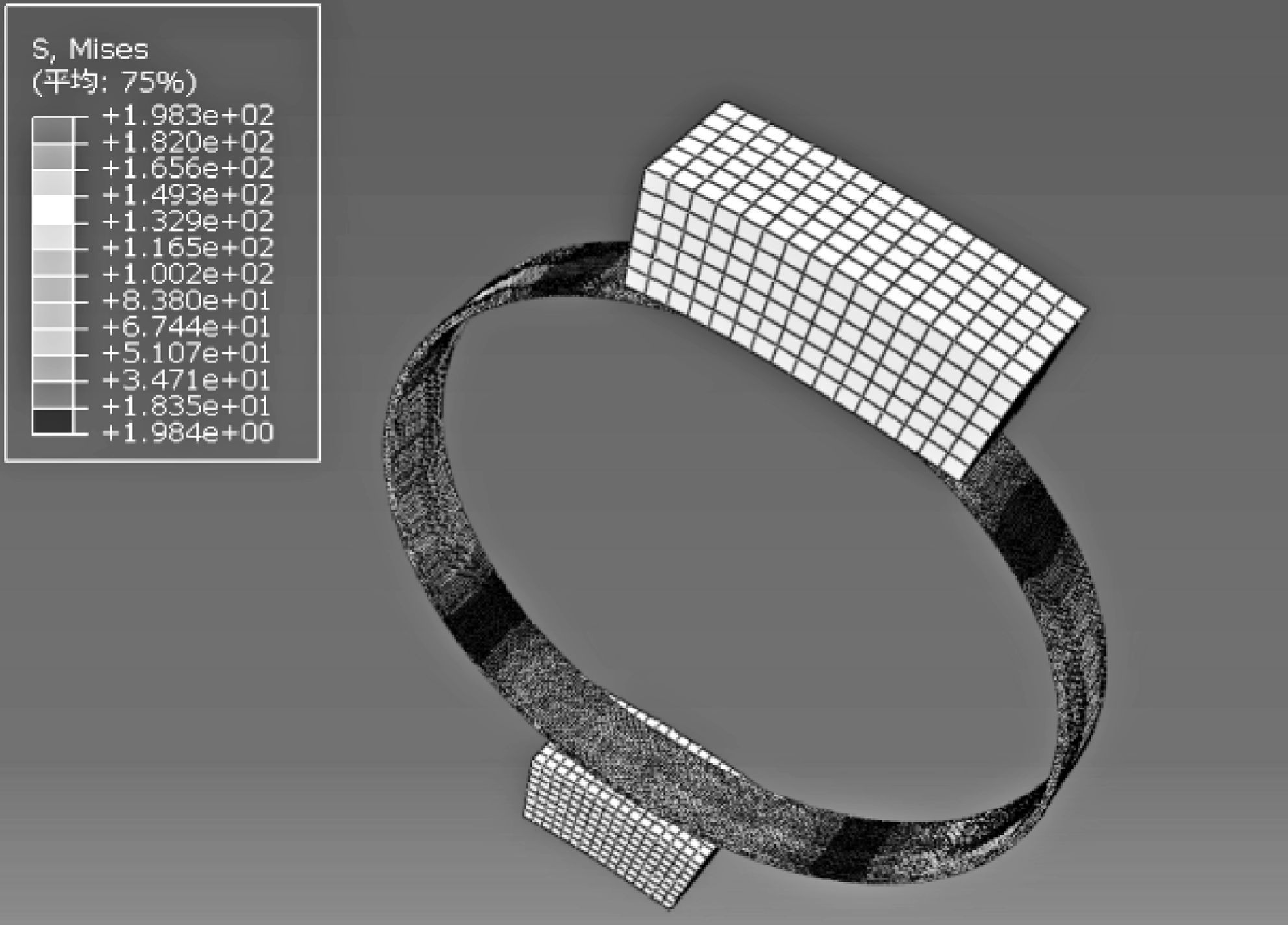
图 8 汇流环压缩后应力分布状态 Fig.8 Stress distribution of collector ring after assembling
图选项
图 9 汇流环压缩接触状态 Fig.9 Contact state of collector ring after assembling
图选项

从图 8和图 9所示仿真结果中可以看出,汇流环的压缩应力最大值达到了198 MPa(与理论计算值误差为±0.5 MPa),表面光滑状态下的接触面积为1.047 3 mm2.根据仿真得出的接触面积，经计算后的接触电阻值为57.70 μΩ，与力学模型计算得出的接触电阻值56.46 μΩ相比，误差为1.24 μΩ.

考虑到仿真和计算误差,说明之前的理论分析及其数值仿真模型是有效的.因此,经过理论分析和仿真,可以判定汇流环的预设尺寸和预紧压缩量设计是合理可行的.

4 结 论

通过理论力学与材料力学分析了滚动汇流环装配及力学状态,并在已知约束条件下,得到如下结论：

1) 汇流环的力学压缩状态与接触状态影响汇流环的使用循环寿命与接触电阻.压缩量越大，接触状态越好,接触电阻越小；但压缩形成的弯曲应力越大,使用循环寿命就越短.即压缩量和使用循环寿命两者之间为反比关系.

2) 建立了薄壁圆柱形滚动汇流环装配力学状态的等效数学理论模型,并在力学和性能约束条件下确定了环道内预紧压缩量的预设范围,能够为汇流环的前期优化设计提供重要参考.

3) 通过该理论模型可以求得汇流环在光滑接触的理想状态下的装配压缩的预设原则与判定分析,并以实例计算和仿真分析进行了验证.

参考文献
[1] 孙丽, 王秀伦, 王丽颖. 滚环的优化设计[J]. 大连铁道学院学报 , 1999, 20 (3) : 56–60. SUN Li, WANG Xiu-lun, WANG Li-ying. Optimum design on roll ring[J]. Journal of Dalian Railway Institute , 1999, 20 (3) : 56–60.
[2] 郑传荣, 赵克俊. 滚环中弹性环设计技术研究[J]. 电子机械工程 , 2011, 27 (3) : 24–27. ZHENG Chuan-rong, ZHAO Ke-jun. Study on flexible ring design of roll ring[J]. Electro-Mechanical Engineering , 2011, 27 (3) : 24–27.
[3] 张会林, 张凤山. 精密导电环在高速高温真空环境中输电特性研究[J]. 红外与毫米波学报 , 2003, 22 (6) : 461–463. ZHANG Hui-lin, ZHANG Feng-shan. Electric transportation properties of the high speed rotating exact electric ring under high temperature and vacuum environment[J]. Journal of Infrared and Millimeter Waves , 2003, 22 (6) : 461–463.
[4] 任万滨, 武剑, 陈宇, 等. 电触点材料接触电阻高精密测量技术[J]. 电工技术学报 , 2014, 29 (1) : 31–35. REN Wan-bin, WU Jian, CHEN Yu, et al. Precision measuring technique for contact resistance of contact materials[J]. Transactions of China Electrotechnical Society , 2014, 29 (1) : 31–35.
[5] MILENKO B, VALERY V K, NIKOLAI K M. Electrical contacts fundamentals, applications and technology[M]. Boca Raton: CRC Press , 2007 : 414 -420.
[6] 薛萍, 陈少兵, 刘丽. 电滑环中的导电环和电刷[J]. 光纤与电缆及其应用技术 , 2012, 11 (1) : 11–13. XUE Ping, CHEN Shao-bing, LIU Li. The Ring and brush in the slip-ring[J]. Optical Fiber & Electric Cable , 2012, 11 (1) : 11–13.
[7] 常健, 赵克俊, 郑传荣, 等. 浅谈电刷-导电环摩擦副使用寿命的影响因素[J]. 火控雷达技术 , 2014, 43 (1) : 101–104. CHANG Jian, ZHAO Ke-jun, ZHENG Chuan-rong, et al. Discussion on factors influencing service life of friction pairs composed of electric brush and conductive ring[J]. Fire Control Radar Technology , 2014, 43 (1) : 101–104.
[8] 郑冀, 欧阳锦林, 朱家佩. 真空长寿命自润滑电刷-滑环材料的研究[J]. 摩擦学学报 , 1997, 17 (2) : 129–139. ZHENG Ji, OUYANG Jin-lin, ZHU Jia-pei. Study on long life electrical brush slip-ring in vacuum[J]. Journal of Tribology , 1997, 17 (2) : 129–139.
[9] NIITSU T,HOSHIKAWA S, MAKINO K. Rotary connector: US, US 20090246976 A1[P].2010-07-29.
[10] JACOBSON P E. Multi-hundred kilowatt roll ring assembly[J]. NASA STI/Recon Technical Report N , 1985, 89 (4) : 24–29.
[11] ALLEN T S,JACOBSON P E.High current transfer roll ring assembly:US4372633[P].1983-01-25.
[12] JACOBSON P E. Advanced high-power transfer through rotary interfaces[J]. NASA STI/Recon Technical Report N , 1984, 85 (11) : 341–348.
[13] KIKUCHI,MA SAO,MITSUBISHI Denki K.K.Rotating electric machine integral with control device:EP1768236A1[P].2007-12-15.
[14] 王兆清, 李淑萍, 唐炳涛. 圆环变形及屈曲的重心插值配点法分析[J]. 机械强度 , 2009, 31 (2) : 245–249. WANG Zhao-qing, LI Shu-ping, TANG Bing-tao. Deformation and buckling analysis of ring by barycentric interpolation collocation method[J]. Journal of Mechanical Strength , 2009, 31 (2) : 245–249.
[15] YE Kai-yuan, TANG Ren-ji, ZHEN Ji-qing. The bending of elastic circular ring of non-homogeneous and variable cross section under the actions of arbitrary loads[J]. Applied Mathematics and Mechanics , 2004, 2 (1) : 1–13.
[16] 彭兴黔, 水运震, 周志宏. 活塞环结构设计研究[J]. 江汉石油学院学报 , 1996, 18 (2) : 89–92. PENG Xing-qian, SHUI Yun-zhen, ZHOU Zhi-hong. Research on structure design of piston ring[J]. Journal of Jianghan Petroleum Institute , 1996, 18 (2) : 89–92.
[17] 贾慧青. 椭圆周长的近似计算公式[J]. 甘肃联合大学学报 , 2012, 26 (3) : 26–29. JIA Hui-qing. Approximate formula on the circumference of an ellipse[J]. Journal of Gansu Lianhe University , 2012, 26 (3) : 26–29.
[18] MIDHA A, HOWELLl L L, NORTON T W. Limit positions of compliant mechanisms using the pseudo-right-body model concept[J]. Mechanism and Machine Theory , 2000, 35 (1) : 99–115. DOI:10.1016/S0094-114X(98)00093-7
[19] TRINH K E,RAMOS-MOORE E,MUECHLICH F.The role of microstructure and surface topography in the electrical behavior of sn-coated cu contacts[C]//Proceedings of the 27th International Conference on Electrical Contacts.Dresden, Germany, 2014:243-248.
[20] WINGERT P C, ALLEN S E, BEYINGTON C. The effects of graphite particle size processing on the performance of silver graphite contacts[J]. IEEE Transactions Components Hybrids and Manufacturing Technology , 1992, 15 (2) : 154–159. DOI:10.1109/33.142888
[21] HEINRIC Hertz. On the contact of elastic solids[J]. J Reineund Angewandte Mathematik , 1882, 92 (3) : 156–171.
[22] 田红亮, 朱大林, 方子帆, 等. 赫兹接触129年[J]. 三峡大学学报 , 2011, 33 (6) : 61–71. TIAN Hong-liang, ZHU Da-lin, FANG Zi-fan, et al. 129 years of Hertz contact[J]. Journal of China Three Gorges University , 2011, 33 (6) : 61–71.
[23] HOLM R. Electric contacts[M]. Berlin: Springer Press , 2010 : 43 -77.
[24] 哈尔滨工业大学精细工艺研究室. 新型滚动电传输装置的设计制造[M]. 哈尔滨: 哈尔滨工业大学出版社 ,1995 : 131 -157. Laboratory of Fine Processing of HIT. The design and manufacturing of new type of electric transmission device for rolling[M]. Harbin: Harbin Engineering University Press , 1995 : 131 -157.
[25] YUNUS E M,MCBRIDE J W,SPEARING S M.The relationship between contact resistance and contact force on au coated carbon nanotube surfaces[C]//Proceedings of the 53rd IEEE Holm Conference on Electrical Contacts.Pittsburgh, PA,2007:167-174.
[26] TIMSIT R S. Electrical contact resistance:properties of stationary interfaces[J]. IEEE Transactions on Components and Packaging Technology , 1999, 22 (1) : 85–98. DOI:10.1109/6144.759357
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.011
教育部主管，浙江大学和中国机械工程学会主办
0

文章信息

杨金川, 田茂君, 姚智慧, 陈浩
YANG Jin-chuan, TIAN Mao-jun, YAO Zhi-hui, CHEN Hao
滚动汇流环装配力学特性分析与优化设计
Analysis of mechanical characteristics and optimum design on assembling of rolling collector ring
工程设计学报, 2016, 23(4): 364-370.
Chinese Journal of Engineering Design, 2016, 23(4): 364-370.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.011

文章历史

收稿日期: 2016-01-12

相关文章

工作空间