由于冲击破岩掘进机(以下简称掘岩机)工作环境恶劣、工况复杂,工作过程中载荷变化剧烈,使其工作机构长时间受高速、高频冲击载荷作用,会产生强烈的冲击和振动,直接影响其结构强度、动态特性和使用寿命[1-6],所以对该机工作机构进行动态特性优化具有重要的意义.
传统动态优化方法通常是基于灵敏度的结构动力学修改,但对于维数较高、设计变量较多、优化目标不唯一的非线性系统,难以得到满意的结果.本文利用BP神经网络极强的非线性映射功能,建立该掘岩机工作机构设计变量与设计参数的映射关系,利用遗传算法对所建立的神经网络模型寻优,获取其动态特性最优时的设计变量和目标值[7-10],为该工作机构的进一步改进提供依据.
1 工作机构动态分析图 1为该掘岩机工作机构有限元模型:5,6,7分别为一、二、三级臂;8为破碎锤;3,4为工作机构举升液压缸,9为破碎锤竖直面转角液压缸,10是控制7伸缩的液压缸,11为控制6竖直面转角的液压缸;12为连接1,2,3,4,5的转动支座;各部分通过销轴连接.

|
| 图 1 工作机构有限元模型 Fig.1 Finite element model of working mechanism |
取对称面为纵向面,对工作机构进行模态分析,得到固有频率和模态振型如表 1所示.为了解其动载荷的响应情况,取输入载荷为1 099.14 kN[1],频率为0~60 Hz,步长为2,得应力、位移随频率变化曲线,分别如图 2(a),2(b)所示.由图可见,位移—频率响应的最大峰值和应力—频率的最大峰值处频率均在2阶固有频率处,所以2阶固有频率易引起工作机构共振[11-12].由表 1可知,2阶固有频率是工作机构的纵向弯曲振动,因此本文以提高工作机构的弯曲动刚度为优化目标.
| 阶数 | 频率/Hz | 最大变形量/m | 振型描述 |
| 1 | 5.852 9 | 0.030 691 | 破碎锤、三级臂、二级臂1阶纵向弯曲振动 |
| 2 | 7.014 3 | 0.032 01 | 破碎锤、三级臂、二级臂2阶纵向弯曲振动 |
| 3 | 24.941 | 0.061 631 | 破碎锤、三级臂3阶纵向弯曲振动 |
| 4 | 41.915 | 0.033 042 | 一级臂4阶纵向弯曲振动,整体扭转 |
| 5 | 48.036 | 0.040 231 | 一级臂5阶纵向弯曲振动,整体扭转 |
| 6 | 79.969 | 0.037 078 | 一级臂6阶纵向弯曲振动,整体扭转 |

|
| 图 2 应力、位移响应曲线 Fig.2 Response curve of stress and displacement |
灵敏度是指结构动态评价指标g(x1,x2,…,xn)对设计变量X=[x1,x2,…,xn]的敏感性程度,表达式为
由于工作机构几何参数较多,在进行灵敏度分析时,为了提高效率需对一些次要的参数进行缩减.
本文利用ANSYS自带的gradient evaluation tool对工作机构相关参数进行灵敏度分析,具体方法如下:
当设计变量在某一参考点改变±1%时,求解评价指标的变化量或变化梯度.ANSYS的求导计算用差商代替,灵敏度计算公式为
式中,e为n维单位向量,Δxi为变量xi的变化量.这里将优化参数的指标转化为评价函数的最小值问题,以工作机构拐点和铰点的相对位置为优化变量,选出灵敏度最高的24个变量为优化变量,表示为
X=[Loa,Lbf,Lac,Lce,Lcf,Lcf,Lfr,Lel,Lji,Ljn,Lmi,Lgp,Loh,Lhq,∠JKM,∠ODQ,D1,D2,D3,D4,d1,d2,d3,d4]T.
各变量灵敏度如表 2,参数分布见图 3.其中:Lce,Lef,Lcf为铰点间距,Loa为一级臂底端到铰点A的距离,Lji为铰点F到二级臂上轴线距离,Ljn为液压缸9伸出长度,Lbf,Lfr分别为一级臂、二级臂上轴线长度,Loh,Lgp,Lmi分别为一级臂、二级臂、三级臂下轴线长度,Lhq,Lel,Lac分别为液压缸3,4,10,11的全伸长度,D1,D2,D3,D4和d1,d2,d3,d4为缸3,9,10,11的缸筒内径和活塞杆直径.
| 设计变量 | 灵敏度 |
| Loa | 0.243 |
| Lbf | -0.436 |
| Lce | 0.034 |
| Lcf | -0.108 |
| Ljn | -0.085 |
| Lmi | -0.326 |
| Lgp | -0.156 |
| Loh | 0.375 |
| D1 | -0.268 |
| D3 | -0.154 |
| d1 | 0.064 |
| d3 | 0.072 |
| Lfr | -1.145 |
| Lel | 0.815 |
| Lji | -0.052 |
| Lef | -0.028 |
| Lhq | -1.315 |
| Lac | -0.492 |
| ∠JKM | 0.485 |
| ∠ODQ | -0.523 |
| D2 | -0.339 |
| D4 | -0.256 |
| d2 | 0.051 |
| d4 | 0.025 |

|
| 图 3 工作机构参数分布 Fig.3 Parameter distributions of working mechanism |
建立的该机工作机构非线性多目标优化模型为
式中:[σ],[χ],[f2]分别为许用应力、工作机构许用挠度和2阶固有频率的许用最大值.
对于该多目标的优化,采用权重和法来将其转化为单目标优化问题,有
根据Δδmax,Δχmax,Δf2在结构优化中的重要性,分别取ω1,ω2,ω3为0.4,0.4和0.2.设计变量约束条件为各几何尺寸上下限.
2.2 BP神经网络及结构设计由于工作机构参数较为复杂,其神经网络结构采用双隐含层的四层神经网络结构m-i-j-p.输入层神经元共计24个以x表示,输出记为y,隐含层单元数由公式
因传统BP神经网络在修正ω(k)时,仅按k是负梯度方式修正,未考虑之前所累积的经验,易陷入局部最优,所以这里采用增加动量项的方法[7],步骤如下:
1) 设置权值和阈值的初始值:ωij(0),θj(0)为数值较小的随机数.ωij为前一层第i层与第j层神经元的权重,θj为第j层神经元的阈值.
2) 提供训练样本.设输入矢量为Xk(k=1,2,…,M),期望输出为Tk,其中:Xk=(xk1,xk2,…,xkm),M是输入向量的维数;Tk为第k个样本的输出,Tk=(tk1,tk2,…,tkn),N为输出向量维数.
3) 计算神经网络实际输出及隐含层各单元的状态:
式中:Xkj表示第k个样本、第j个神经元的输出,fi()为神经元的激发函数.
4) 计算输出层和隐含层的训练误差:
5) 修正权值和阈值:
式中,η是学习速率(0<η<1),α是一个常数,决定过去权重的变化对目前权重变化的影响程度.
6) 当k经历1至24后,判断所给指标是否满足精度要求.
7) 结束.
图 4为工作机构动态性能映射及附加动量项的神经网络结构.

|
| 图 4 工作机构动态性能映射BP网络 Fig.4 BP network of dynamic performance for working mechanism |
利用ANSYS Workbench储存的数据构造正交表,样本总数为60个,分训练集和测试集两部分,因素数为为24个,每个因素分为5个水平级,如表 3所示.
| No. | Loa/mm | Lbf/mm | Lac/mm | Lcf/mm | Lce/mm | Lfr/mm | Lel/mm | Lji/mm | D1/mm | D2/mm | d1/mm | d2/mm | Δf2/Hz | Δxmax/mm | Δδmax/MPa | Ljn/mm | Lmi/mm | Lgp/mm | Lef/mm | Loh/mm | Lhq/mm | ∠JKM | ∠ODQ | D3/mm | D4/mm | d3/mm | d4/mm | Δf2/Hz | Δxmax/mm | Δδmax/MPa |
| 1 | 473.5 | 1 058.3 | 1 130.0 | 212.4 | 203.5 | 1 400.0 | 1 590.0 | 403.0 | 115 | 100 | 60 | 48 | 4.465 7 | 7.99 | 3.5 | 1 200.0 | 1 500.0 | 1 350.0 | 185.7 | 1 450.7 | 1 350.0 | 170.0° | 20.0° | 100 | 115 | 48 | 60 | 4.465 7 | 7.99 | 3.5 |
| 2 | 483.5 | 1 028.3 | 1 100.0 | 211.6 | 205.5 | 1 350.0 | 1 630.0 | 402.0 | 113 | 98 | 60.5 | 49 | 4.025 3 | 7.74 | 3.2 | 1 195.0 | 1 480.0 | 1 340.0 | 185.2 | 1 470.7 | 1 300.0 | 171.0° | 19.0° | 99 | 113 | 48.4 | 61 | 4.025 3 | 7.74 | 3.2 |
| 3 | 493.5 | 998.3 | 1 070.0 | 211.4 | 207.5 | 1 300.0 | 1 670.0 | 401.0 | 111 | 96 | 61 | 48.2 | 3.862 1 | 7.27 | 3.6 | 1 190.0 | 1 460.0 | 1 330.0 | 187.3 | 1 490.7 | 1 250.0 | 172.0° | 18.0° | 98 | 111 | 48.9 | 58 | 3.862 1 | 7.27 | 3.6 |
| 4 | 503.5 | 968.3 | 1 040.0 | 214.3 | 209.5 | 1 250.0 | 1 710.0 | 400.0 | 109 | 94 | 59.4 | 47 | 3.236 4 | 8.14 | 3.4 | 1 185.0 | 1 440.0 | 1 320.0 | 188.1 | 1 510.7 | 1 200.0 | 173.0° | 17.0° | 97 | 109 | 47.6 | 59.3 | 3.236 4 | 8.14 | 3.4 |
| 5 | 513.5 | 938.3 | 1 010.0 | 213.7 | 211.5 | 1 200.0 | 1 750.0 | 399.0 | 107 | 92 | 58 | 47.2 | 3.047 5 | 7.67 | 2.8 | 1 180.0 | 1 420.0 | 1 310.0 | 184.4 | 1 530.7 | 1 150.0 | 174.0° | 16.0° | 96 | 107 | 47 | 60.2 | 3.047 5 | 7.67 | 2.8 |
为提高神经网络预测的精度,将设计参数和目标函数值转化成[0,1]之间的数,具体方法[8]如下:
式中:xmin,ymin和xmax,ymax分别为样本数据序列中的最小数和最大数,xk,yk为归一化后的数据.求得预测函数最优值及对应的设计参数后,进行反归一化处理,有
从60组样本中选出30组作为测试集,其余作为训练集来建立预测目标函数的BP神经网络.经过2 000次测试训练,网络均方误差为0.007 224,30组测试样本的预测误差≤3.2%.神经网络精度较高.通过训练集对网络的训练,解出设计参数与目标函数的关系为
式中:sim表示神经网络仿真函数,net为训练好的模型.
3 工作机构动态性能优化因GA算法的搜索始终涉及整个解的空间,擅长全局搜索.因此本文采用遗传算法找寻该非线性函数的最优解集[13-14].遗传算法的计算步骤主要有染色体编码、初始化种群、适应度计算、选择、交叉以及变异等过程.本文优化目标为2阶固有频率最大值,其适应度函数为
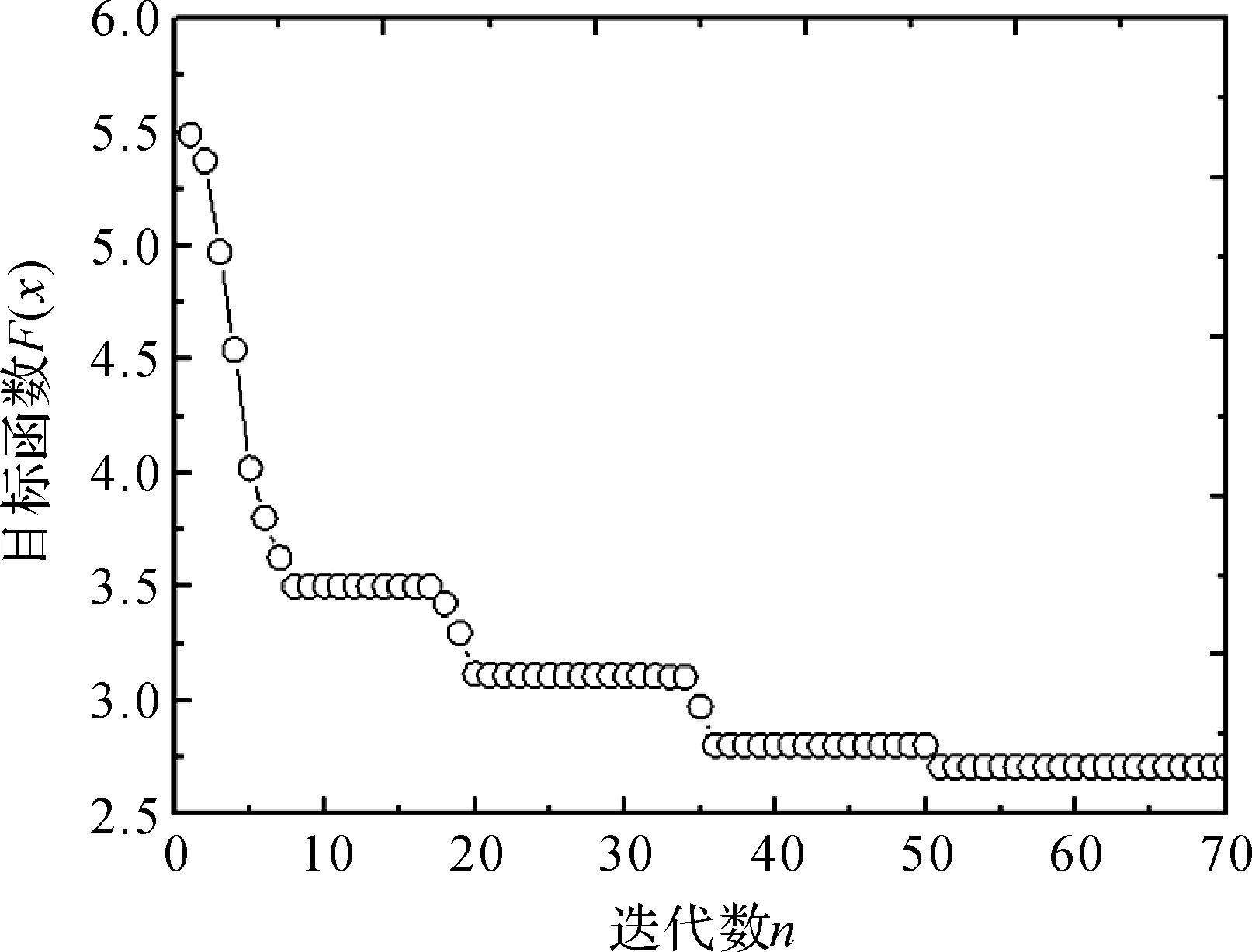
GA算法的基本参数设置为:种群规模为100,交叉概率Pc=0.65,变异概率Pm=0.01,终止进化代数为70.目标函数与迭代数的变化曲线如图 5所示.
|
| 图 5 目标函数与迭代次数关系 Fig.5 Relationship between objective function and iterations |
优化后:目标函数最优值Δf2=2.0132 Hz,增大24.7%;Δχ max=6.53 mm,减小27.5%,Δδmax=2.2 MPa,减小43.07%.对应的设计参数对比见表 4.图 6为优化前后工作机构的位移、应力分布云图.可见,优化后,各阶频率的应力及变形(图 6(b)、(d))较优化前(图 6(a)、(c))普遍降低,动态性能明显改善.

|
| 图 6 优化前后应力与位移对比 Fig.6 Contrast of stress and displacement before and after optimization |
| 参数 | 优化前 | 优化后 |
| Loa/mm | 473.5 | 486.7 |
| Lbf/mm | 1 058.3 | 1 013.5 |
| Lac/mm | 1 130.0 | 1 080.0 |
| Lce/mm | 203.5 | 205.8 |
| Lfr/mm | 1 400.0 | 1 230.0 |
| Lcf/mm | 212 | 210 |
| d1/mm | 60 | 59.3 |
| d3/mm | 48 | 47.8 |
| Lel/mm | 1 590.0 | 1 650.0 |
| Lji/mm | 403.0 | 392.0 |
| D1/mm | 115 | 110 |
| D2/mm | 100 | 92 |
| Ljn/mm | 1 200.0 | 1 185.0 |
| Lmi/mm | 1 500.0 | 1 404.2 |
| Lgp/mm | 1 350.0 | 1 280.0 |
| Loh/mm | 1 450.7 | 1 600.1 |
| Lhq/mm | 1 350.0 | 1 177.0 |
| Lef/mm | 185 | 182 |
| d2/mm | 48 | 47.7 |
| d4/mm | 60 | 59.5 |
| ∠JKM | 170.0° | 176.6° |
| ∠ODQ | 20.0° | 18.6° |
| D3/mm | 100 | 97 |
| D4/mm | 115 | 112 |
1) 建立了掘岩机工作机构的有限元模型,通过模态分析和谐响应分析,确定了影响其机构动态性能的模态频率,为工作机构动态性能优化奠定了基础.
2) 通过灵敏度分析,确定了影响工作机构动态性能的主要设计参数,利用BP神经网络模型,确定设计参数与最大动应力、弯曲动刚度和钎杆顶端动位移间的映射关系,建立了2阶固有频率最大的优化目标.
3) 将有限元法、正交实验法、BP神经网络算法和遗传算法相结合的动态优化方法用于掘岩机工作机构的动态优化,使工作机构的固有频率提高,最大动变形和最大动应力大大降低,动态性能明显改善.
| [1] | 李晓豁, 郭娜, 郑有山, 等. 典型工况下冲击破岩掘进机工作机构力学特性研究[J]. 工程设计学报 , 2014, 21 (5) : 439–443. LI Xiao-huo, GUO Na, ZHENG You-shan, et al. Study on mechanical properties of working mechanism for impacting and crushing rock roadheader under typical conditions[J]. Chinese Journal of Engineering Design , 2014, 21 (5) : 439–443. |
| [2] | FARID M, LUKASIEWICZ S A. Dynamic modeling of spatial manipulators with flexible links and joints[J]. Computers & Structures , 2000, 75 (4) : 419–437. |
| [3] | 于兰峰, 王金诺. 塔式起重机结构系统动态优化设计[J]. 西南交通大学学报 , 2007, 42 (2) : 206–210. YU Lan-feng, WANG Jin-nuo. Dynamic optimum design of tower crane structures[J]. Journal of Southwest Jiaotong University , 2007, 42 (2) : 206–210. |
| [4] | JONES K, TURCOTTE J. Finite element model updating using antiresonant frequencies[J]. Journal of Sound and Vibration , 2002, 252 (4) : 717–727. DOI:10.1006/jsvi.2001.3697 |
| [5] | 张颚, 许林安, 刘中华, 等. 多自由度坐姿人体上体系统动力学建模与振动特性研究[J]. 工程设计学报 , 2008, 15 (4) : 74–79. ZHANG E, XU Lin-an, LIU Zhong-hua, et al. Dynamic modeling and vibration characteristics of multi DOF upper part system of seated human body[J]. Chinese Journal of Engineering Design , 2008, 15 (4) : 74–79. |
| [6] | 李晓豁, 吴云, 王新, 等. 井下移动式液压破碎机工作机构疲劳寿命分析[J]. 广西大学学报(自然科学版) , 2013, 38 (5) : 1027–1032. LI Xiao-huo, WU Yun, WANG Xin, et al. Fatigue life analysis for underground mobile hydraulic crusher working mechanism[J]. Journal of Guangxi University(Natural Science Edition) , 2013, 38 (5) : 1027–1032. |
| [7] | 童水光, 王相兵, 钟崴, 等. 基于BP-HGA的起重机刚性支腿动态优化设计[J]. 浙江大学学报(工学版) , 2013, 47 (1) : 122–130. TONG Shui-guang, WANG Xiang-bing, ZHONG Wei, et al. Dynamic optimization design for rigid landing leg of crane based on BP-HGA[J]. Journal of Zhejiang University(Engineering Science) , 2013, 47 (1) : 122–130. |
| [8] | 李晓豁, 吴云, 刘藏泽, 等. 不同工况移动式液压破碎机工作机构有限元分析[J]. 机械设计 , 2014, 31 (9) : 40–43. LI Xiao-huo, WU Yun, LIU Cang-ze, et al. Finite element analysis of mobile hydrahlic crusher working mechanism under working conditions[J]. Journal of Machine Design , 2014, 31 (9) : 40–43. |
| [9] | MANSOUR A E, WIRSCHING P H. Sensitivity factors and their application to marine structures[J]. Marine Structures , 1995, 8 (3) : 229–255. DOI:10.1016/0951-8339(94)00001-9 |
| [10] | SHEN Y, LÜ Y M. Neural network for nonlinear programming with linear constraints[J]. Computer Engineering & Applications , 2006, 44 (23) : 75–77. |
| [11] | 李晓豁, 刘藏泽, 孟冉, 等. 井下移动式破碎机垂直方向随机振动相应的研究[J]. 工程设计学报 , 2014, 21 (1) : 56–61. LI Xiao-huo, LIU Cang-ze, MENG Ran, et al. Study on vertical random vibration response of underground mobile crusher[J]. Chinese Journal of Engineering Design , 2014, 21 (1) : 56–61. |
| [12] | YAO Y X, SUN L W. Structural optimization of precision instruments through modal analysis[J]. Journal of Harbin Institute of Technology , 2002, 9 : 161–165. |
| [13] | TAO Q, REN F X, SUN D M. Neural network for nonlinear programming problems with hybrid constraints[J]. Journal of Software , 2002, 13 (2) : 304–310. |
| [14] | LANGLOIS R G, ANDERSON R J. Multibody dynamics of very flexible damped systems[J]. Multibody System Dynamics , 1999, 3 (2) : 109–136. DOI:10.1023/A:1009898425669 |


