2. 山河智能装备股份有限公司 国家级企业技术中心, 湖南 长沙 410100
2. National Enterprise R & D Center, Sunward Intelligence Equipment Co., Ltd., Changsha 410100, China
潜孔钻机是冲击器潜入孔内而回转机构在孔外带动钻杆旋转,主动轮持续提供推进力使其向矿岩钻进的设备[1].它广泛应用于钻凿炮孔中,具有钻孔直径大、钻孔深、钻孔效率高、适用范围广等特点,是当前通用的大型凿岩钻孔设备[1-2].因此,研究潜孔钻机关键部件具有十分重要的理论意义和实用价值.机架平台作为潜孔钻机重要的承载结构件,不同作业环境影响其受力,并且因误操作而导致的极限工况对平台的破坏程度大.目前,对潜孔钻机平台的研究主要集中在钻进和提钻工况下平台受力分析和改进方面[3],而未对误操作导致的极限工况下的平台进行研究,因此具有一定的片面性.基于此,本文对正常和极限工况下的平台进行受力分析和有限元分析,找到危险区域,为平台结构的设计提供参考.
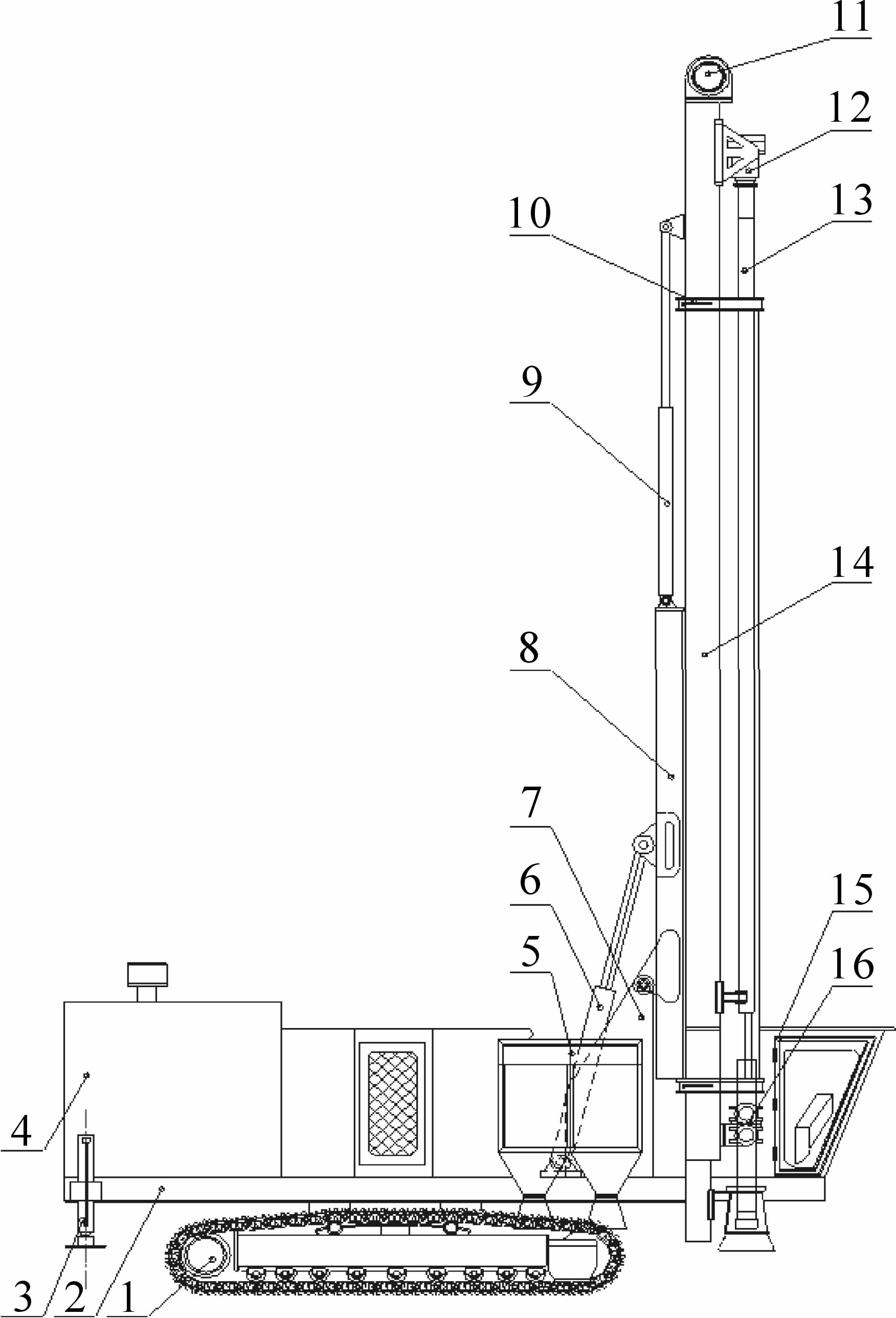
1 潜孔钻机的工作原理及工况分析 1.1 潜孔钻机的结构及工作原理架式潜孔钻机的结构如图 1所示.潜孔钻机行走至指定钻孔位置后,根据钻孔作业环境调整支撑平台的支腿个数,通过操作举升油缸和补偿油缸,调整潜孔钻机工作装置姿态使钻架垂直于地面并且下支点支撑在作用面,潜孔钻机即可钻孔作业.冲击器潜入孔内给钻头施加冲击力而回转机构在孔外带动钻杆回转,同时主动轮持续提供推进力.钻孔作业产生的岩渣和粉尘由高风压排出孔底.待主钻杆完全钻入孔内后,卸杆装置将钻杆库中的副钻杆与主钻杆连接而继续钻孔作业,直至钻孔达到指定要求,提升钻杆并将副钻杆卸至钻杆库,操作举升油缸和补偿油缸至初始姿态,最后提升支腿离地即可行走.
|
| 1—底盘;2—平台;3—支腿;4—空压机;5—除尘系统;6—举升油缸;7—滑架支座;8—滑架体;9—补偿油缸;10—卸杆库;11—主动轮;12—回转器;13—钻杆;14—钻架;15—司机室;16—卸杆器. 图 1 潜孔钻机结构 Fig.1 Structure of down-the-hole drill |
根据潜孔钻机实际作业环境,操作者可调整支腿油缸支撑平台来确保在作业过程中平台的相对稳定性,因此支撑平台的支腿数量可从0增至4,论文仅详细分析1个支腿支撑平台的正常工况和极限工况.在潜孔钻机钻孔作业完成后,正常操作为提升钻杆、钻架以及支腿油缸,才能行走,此为正常工况;但有时因操作不当导致钻架或支腿油缸未提升而潜孔钻机已行走,此为极限工况.极限工况因操作者的疏忽导致,在潜孔钻机实际钻孔作业中不常发生,但对平台的破坏程度高,需着重加以分析.
2 数学模型的建立潜孔钻机机架平台受力分为三大部分:平台上零部件的重力(恒定的),工作装置对平台的作用力(由滑架体与滑架体支座处的约束反力和举升油缸提供的主动力构成),支腿油缸对平台的支撑反力(由实际工况决定).本文以湖南山河智能机械股份有限公司研制的SWDA200C型潜孔钻机为研究对象.
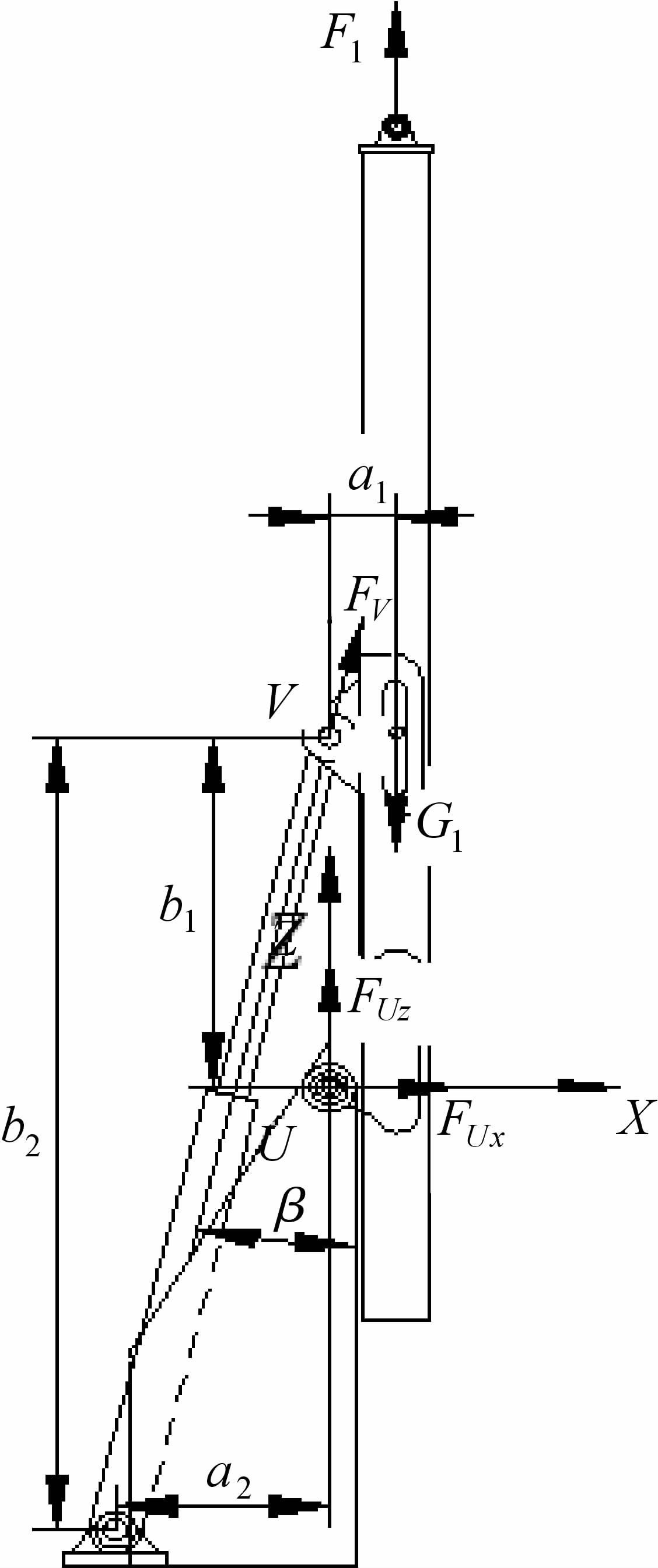
在潜孔钻机作业过程中,整个工作装置垂直于地面并且下支点支撑在作用面,补偿油缸的压力取12 MPa,以滑架体为研究对象,进行受力分析[4-8],如图 2所示.
|
| 图 2 滑架受力分析图 Fig.2 Mechanical analysis of the carriage device |
∑FX=0,即
∑FZ=0,即
∑MU(F)=0,即
式中:FUx,FUz为滑架支座与滑架体处约束反力在X,Z轴上的分量;FV为举升油缸的载荷;F1为补偿油缸对滑架体的作用力,F1=53 694 N;G1为滑架体重量,G1=10 519.8 N;β=arctan(a2/b2),为举升油缸与滑架体之间的夹角,β=12.72°;a1,a2,b1,b2的定义见图 2,a1=254 mm,a2=524 mm,b1=1 500 mm,b2=3 382 mm.
可得:
整个潜孔钻机重心O点相对O′(平台与底盘焊接中心点)的位置为:
式中:Gi为平台上零部件(如空压机、发动机等)的重量,其总重为251 368.7 N;Xi,Yi为零部件的重心与中心O′点间的距离在X,Y轴上的分量.
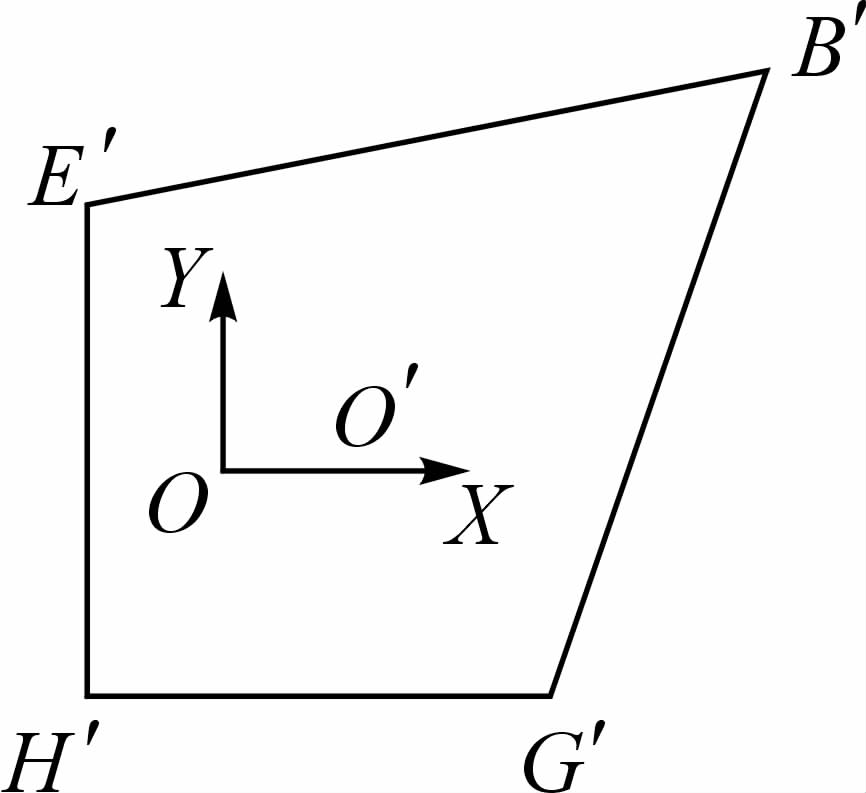
2.1 正常工况仅1个支腿和3/4履带支撑即可保证平台稳定的工况下,又可分为4种情况,本文只讨论其中一种,其余3种类似.平台上各关键点位置分析如图 3,重心O点相对O′的位置坐标为(-457 mm,-48 mm),B′为支腿支撑点,相对O′点位置坐标为(2 150 mm,1 839 mm);E′,G′,H′为履带支撑点,相对O′点位置坐标分别为(-1 113 mm,1 195 mm),(1 110 mm,-1 195 mm),(-1 113 mm,-1 195 mm).
|
| 图 3 平台上各关键点位置 Fig.3 Locations of key-points of the platform |
此力系属于空间平衡力系,支腿和履带支撑反力平行于Z轴(Z轴垂直于XOY平面),可知各支撑反力在X,Y轴上的分量以及对于Z轴的矩都为零,即∑FX≡0,∑FY≡0,∑MZ(F)≡0,因此,空间平衡力系只有3个平衡方程:
∑FZ=0,即
∑MX(F)=0,即
∑MY(F)=0,即
式中:FB′z为支腿支撑反力,FE′z,FG′z,FH′z为履带支撑反力,为未知量;lOE′x,lOE′y为重心O点和履带支撑点E′间距离在X,Y轴上的分量,lOE′x=656 mm,lOE′y=1 243 mm(由O,E′之间位置坐标得出),其余lOB′x,lOB′y,lOG′x,lOG′y,lOH′x,lOH′y亦是如此.由平衡方程可知,未知量个数多于方程个数属于超静定问题,为求解上述平衡方程可通过变形相容条件建立与平衡方程线性无关的方程[9].
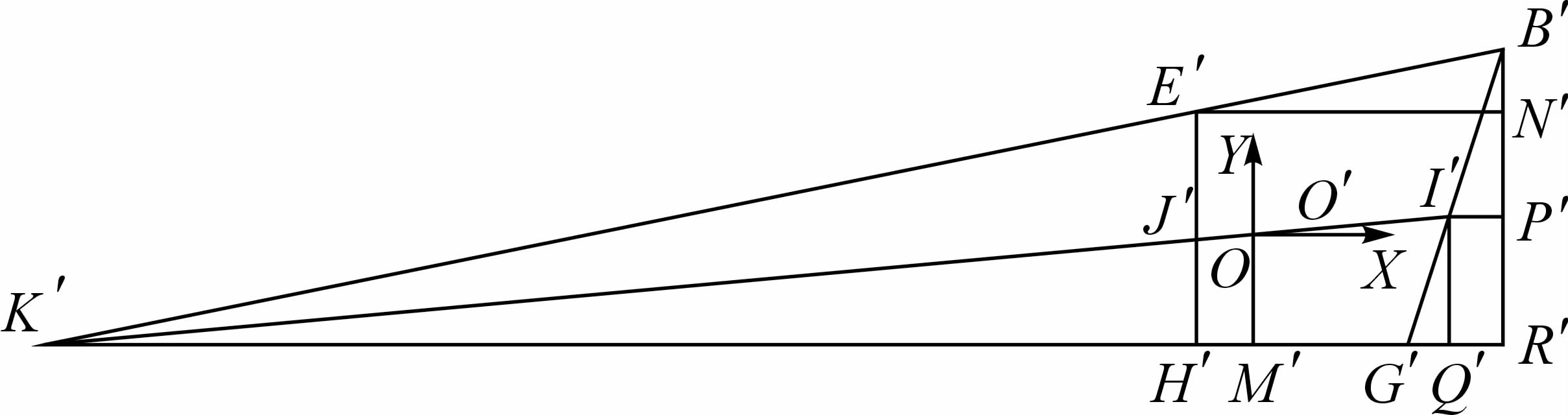
现假设平台是绝对刚性以简化计算.由图 3中分析可知:如果潜孔钻机重心O在4个支腿包围的支撑面内,则支撑反力FE′z和FH′z合力FE′H′z的作用点J′在E′H′线段上,同理支撑反力FB′z和FG′z合力FB′G′z的作用点I′在B′G′线段上,并且J′,O,I′三点必在一条直线上,其延长线必与E′B′,H′G′延长线交于K′点,过O,I′,B′点分别作直线垂直于线段H′G′并相交于M′,Q′,R′点,过E′,I′点分别作直线垂直于线B′R′并相交于N′,P′点,如图 4所示.
|
| 图 4 平台受力分析图 Fig.4 Mechanical analysis of the platform |
由图 4几何关系即可得出履带支撑反力FE′z和FH′z的合力FE′H′z与FE′z,以及支腿支撑反力FB′z和履带支撑反力FG′z的合力FB′G′z与FB′z的比例关系:
式中:
lB′N′为B′点与N′点之间的距离,其余lE′N′,lE′H′,lK′H′,lOM′,lJ′H′,lH′M′,lH′G′,lG′R′,lB′R′定义亦是如此.
将式(9)或(10)联合式(6)至式(8)可得:
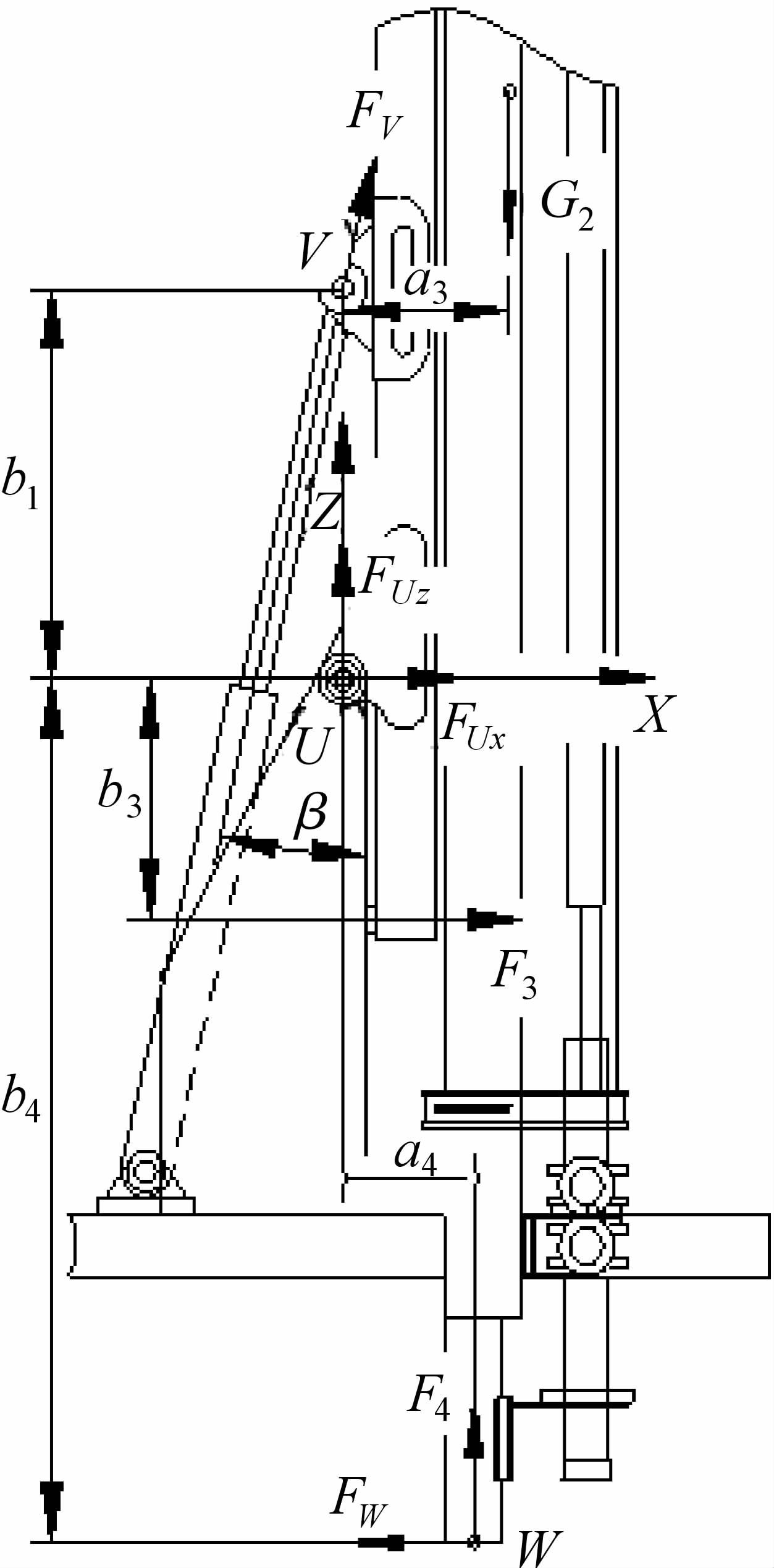
由于操作者的疏忽未提升钻架和支腿,此时钻架和支腿的下支点支撑于作用面而潜孔钻机已行走.滑架体与滑架支座处铰点主要承担使工作装置转动的作用力,而滑架体底部侧面垫板承受滑架支座对其的作用力,因此滑架支座铰点的约束反力在X轴上的分量与正常工况相比变化范围很小,为简化计算,可视为不变.以整个工作装置为研究对象,其受力分析如图 5.列出平衡方程:
|
| 图 5 工作装置受力分析图 Fig.5 Mechanical analysis of the working device |
∑FX=0,即
∑FZ=0,即
∑MV(F)=0,即
式中:FW=μF4,为最大静摩擦力,可约等于动摩擦力,FW=51 574 N,F4= F1+G2-G1为作用面对钻架下支点的支撑反力,F4=97 310.2 N;μ为摩擦系数,取0.53;F3为滑架支座对滑架体垫板的作用力;G2为整个工作装置的重量,G2=54 136 N;a3,a4,b3,b4定义见图 5,其值分别为:a3=684 mm,a4=538 mm,b3=925 mm,b4=3 300 mm.
可得:
平台的重心因滑架支座与滑架体处约束反力FU以及举升油缸载荷FV的变化而不同,可根据式(4)至式(10)得出平台重心O点相对O′的位置坐标为(1 mm,-30 mm)和支腿、履带支撑反力:
支腿在水平方向的作用力为最大静摩擦力:
式中:μ为摩擦系数,取0.53;FB′z为此工况下支腿在B′点的支撑反力.
2.2.2 极限工况2当潜孔钻机处于钻架提升而支腿未提升的极限工况下,滑架体与滑架体支座处约束反力和举升油缸载荷因钻架离地而不同,当钻架刚离地时,整个工作装置下支点支撑反力以及因牵引力而产生的静摩擦力为零,其受力分析类似图 5,列出平衡方程:
∑FX=0,即
∑FZ=0,即
∑MV(F)=0,即
可得:
此时,平台的受力如图 4,支腿、履带支撑反力的计算方法如同正常工况,即可根据式(4)至式(10)得出平台重心O点相对O′的位置坐标为(318 mm,-72 mm)和支腿、履带支撑反力:
由式(14)得
式中:μ为摩擦系数;FB′z为此工况下支腿在B′点的支撑反力.
2.2.3 极限工况3当潜孔钻机处于支腿提升而钻架未提升的极限工况下,此时平台因支腿提升而出现局部不稳,但平台倾斜角度不大,为简化计算可视平台处于相对稳定状态,整个工作装置的受力分析如同非正常工况1,约束反力FU和举升载荷FV的结果一致,而支腿已提升,在水平方向未受力.
3 平台的有限元分析平台焊接件的材料为Q345,在常温下,屈服极限为345 MPa,弹性模量为2×105 MPa,泊松比为0.3,密度为7.85×103 kg/m3.
3.1 平台的有限元分析结果采用Inventor绘制潜孔钻机平台三维实体模型,将其导入ANSYS中进行有限元分析.建模时应尽量保证平台的力学模型与实际结构相似,可简化或忽略对平台没有较大影响的结构(如小倒角、圆角以及圆孔).在ANSYS中单元类型采用SOLID285,对几何实体模型采用自由网格划分方法,并在应力集中区域进一步细化网格.在平台底端与底盘焊接处施加X,Y,Z方向的位移和转动约束,将上述各个工况的力加载至相应位置.
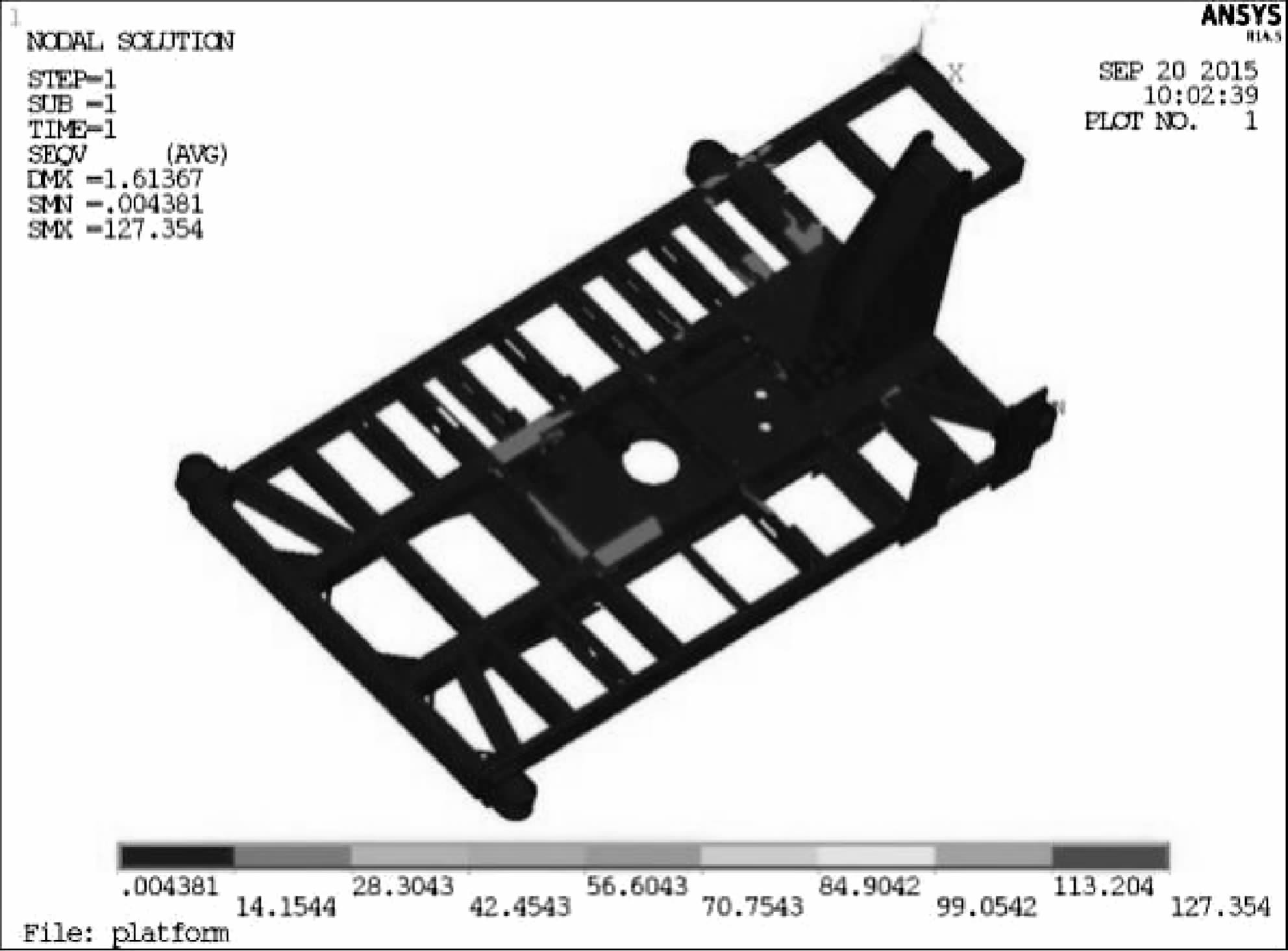
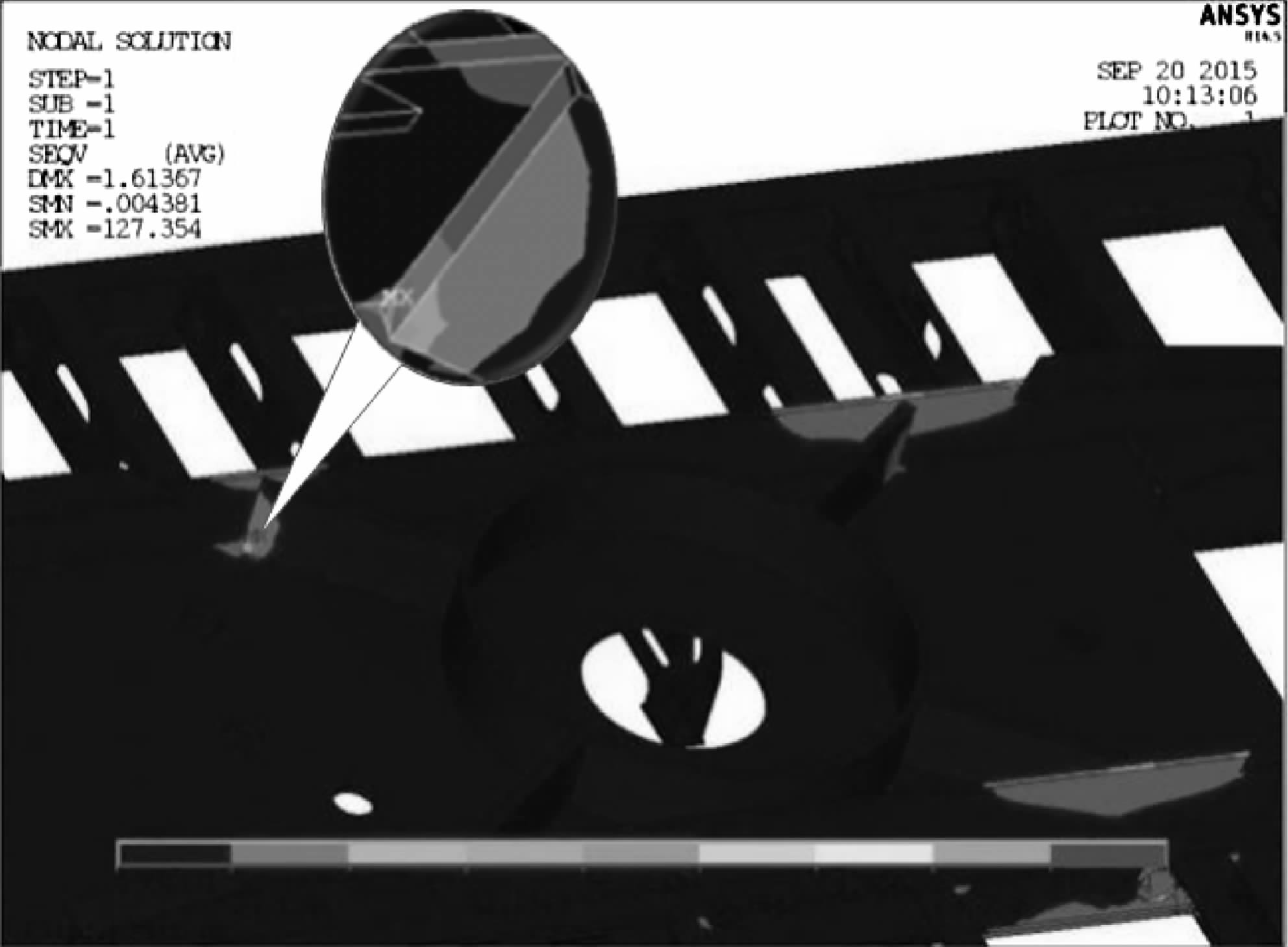
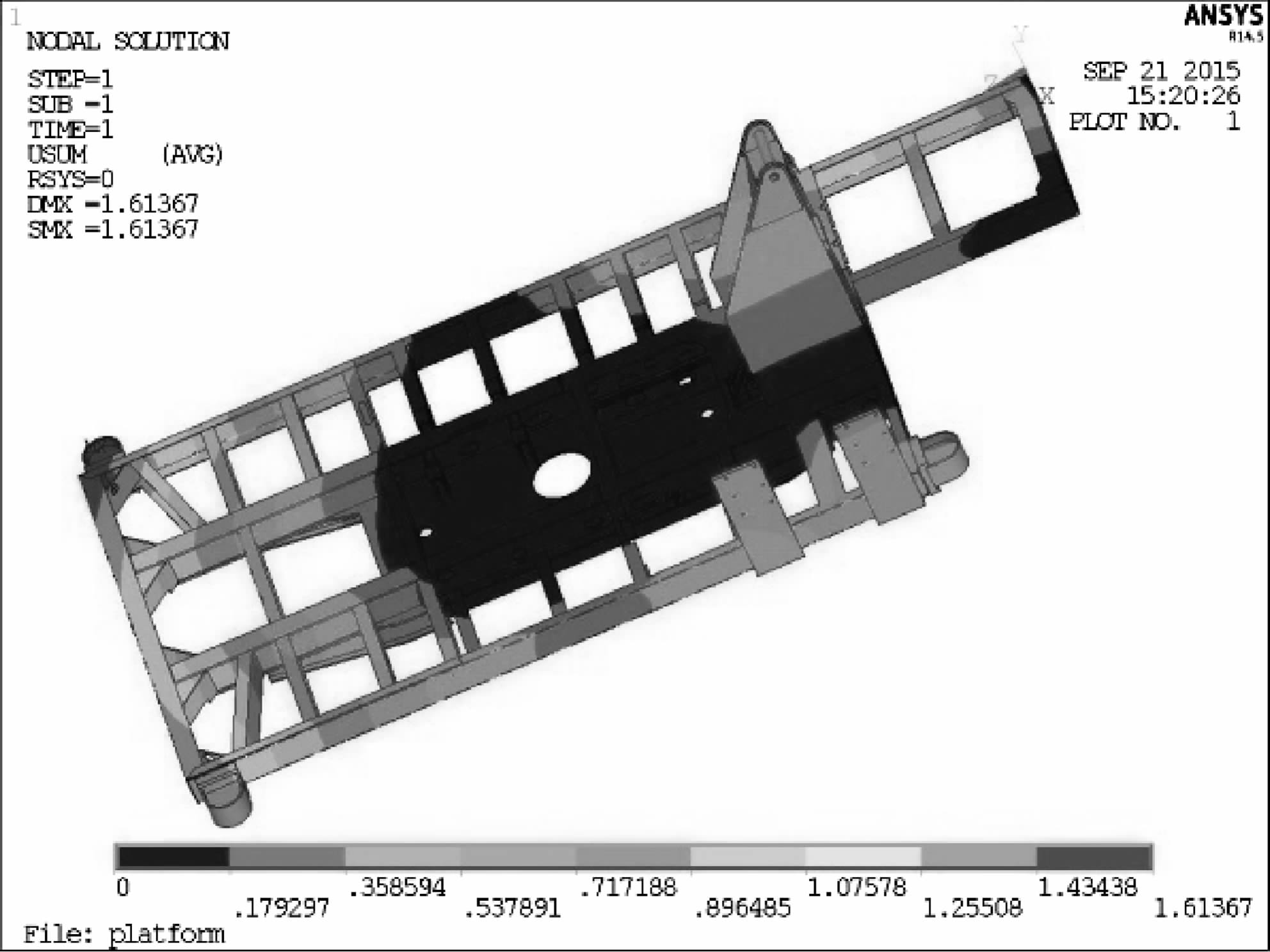
正常工况:潜孔钻机钻架下支点支撑在作用面上,冲击器潜入孔内钻凿炮孔.此时平台的等效应力云图如图 6、图 7,平台大部分区域处于低应力状态,应力最大值发生在平台底部左筋板与主底板的连接处,其值为127.354 MPa,平台中部和支腿2附近横梁是局部应力较大的区域.如图 8,最大位移出现在支腿1安装座处,其值为1.613 67 mm.
|
| 图 6 正常工况时平台的应力云图 Fig.6 The stress plot of platform under normal condition |
|
| 图 7 正常工况时平台的局部应力云图 Fig.7 The part stress plot of platform under normal condition |
|
| 图 8 正常工况时平台的位移云图 Fig.8 The deformation plot of platform under normal condition |
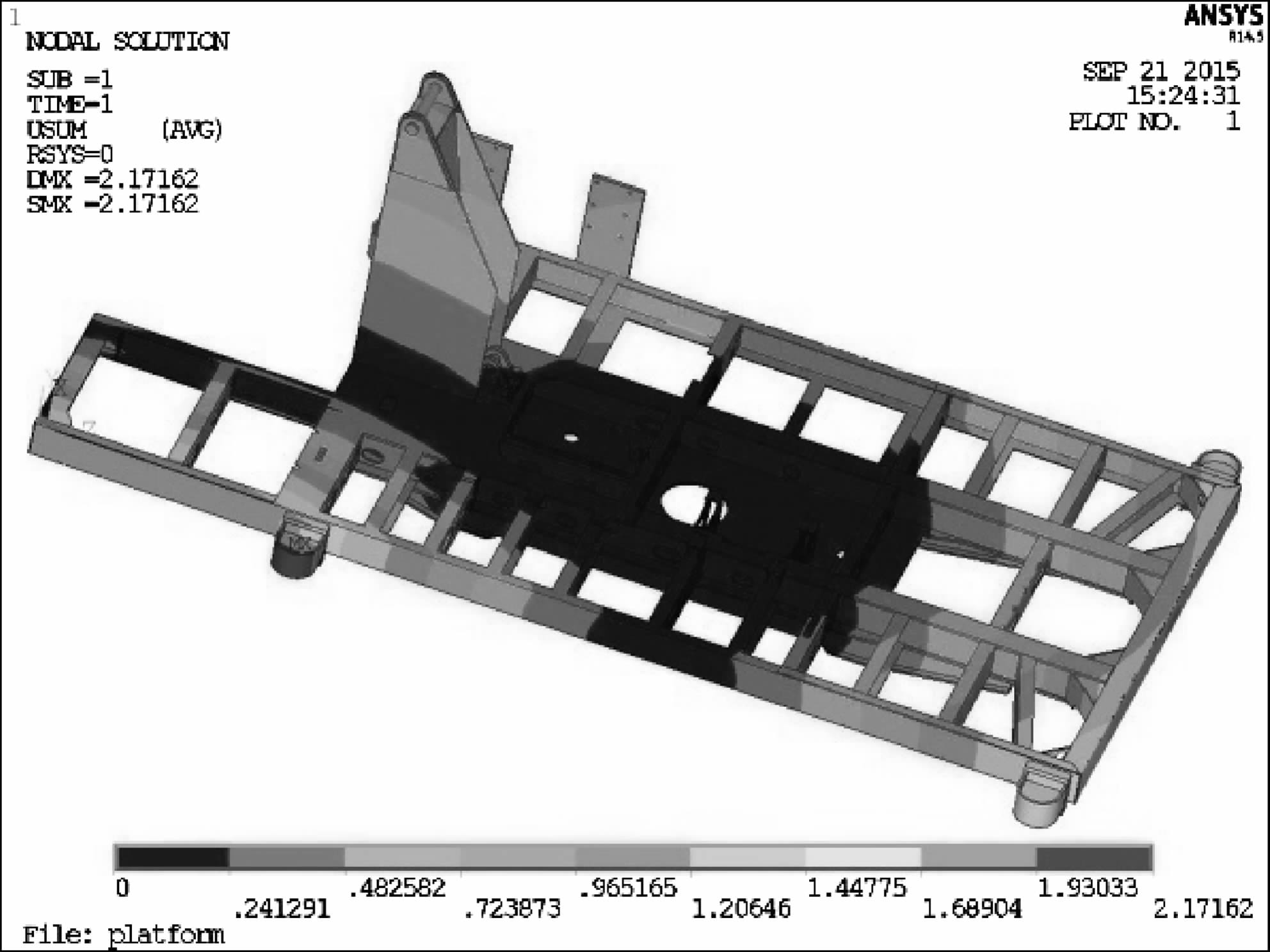
极限工况1:潜孔钻机作业达到指定要求后,未提升钻架和支腿而向前行走.平台的等效应力云图如图 9、图 10,平台大部分区域处于低应力状态,应力最大值位于平台底部右筋板与主底板连接处,其值为158.282 MPa,中间平台的中部与前部以及平台的左前侧部分横梁是局部应力较大的区域.如图 11,最大位移出现在支腿2安装座处,其值为2.171 62 mm.

|
| 图 9 极限工况1时平台的应力云图 Fig.9 The stress plot of platform under ultimate condition 1 |

|
| 图 10 极限工况1时平台的局部应力云图 Fig.10 The part stress plot of platform under ultimate condition 1 |
|
| 图 11 极限工况1时平台的位移云图 Fig.11 The deformation plot of platform under ultimate condition 1 |
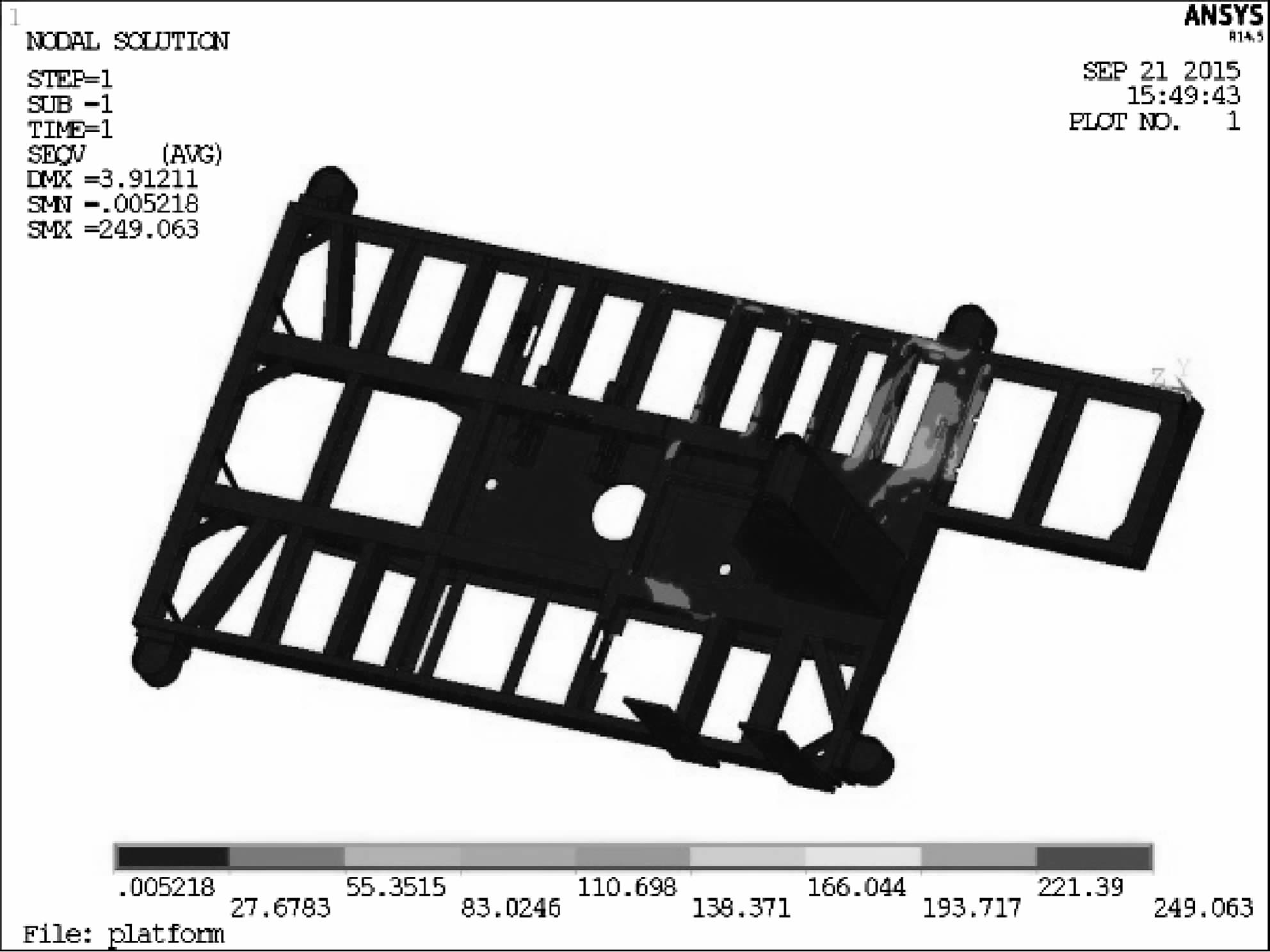
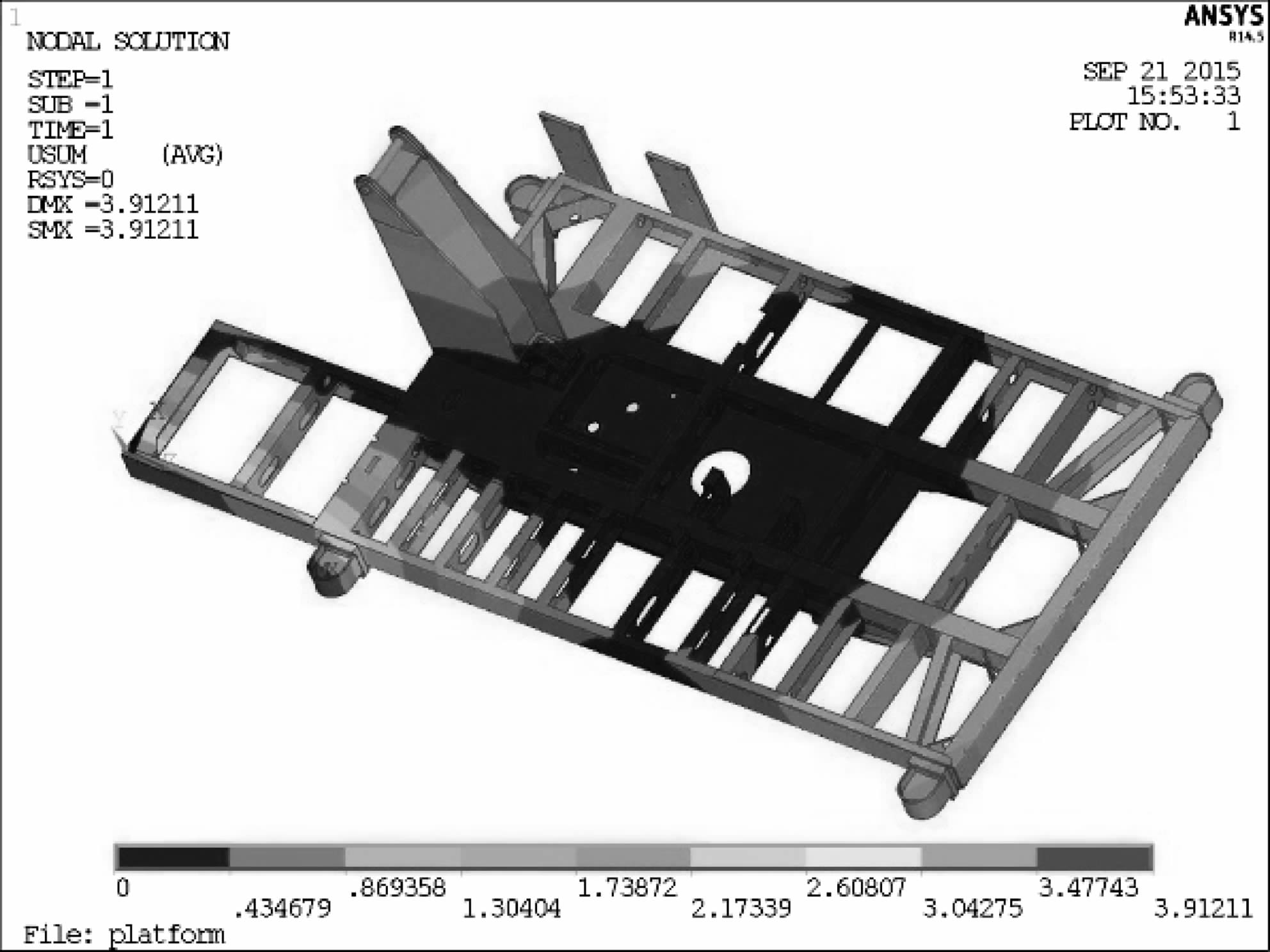
极限工况2:潜孔钻机作业达到指定要求后,仅提升钻架而支腿未提升.此时平台的等效应力云图如图 12、图 13,平台的大部分区域处于低应力状态,应力最大值位于平台底部左筋板与主底板连接处,其值为249.063 MPa,局部应力较大区域出现在平台的中前部两侧和支腿2附近的横梁.如图 14,最大位移出现在支腿2安装座处,其值为3.912 11 mm.
|
| 图 12 极限工况2时平台的应力云图 Fig.12 The stress plot of platform under ultimate condition 2 |

|
| 图 13 极限工况2时平台的局部应力云图 Fig.13 The part stress plot of platform under ultimate condition 2 |
|
| 图 14 极限工况2时平台的位移云图 Fig.14 The deformation plot of platform under ultimate condition 2 |
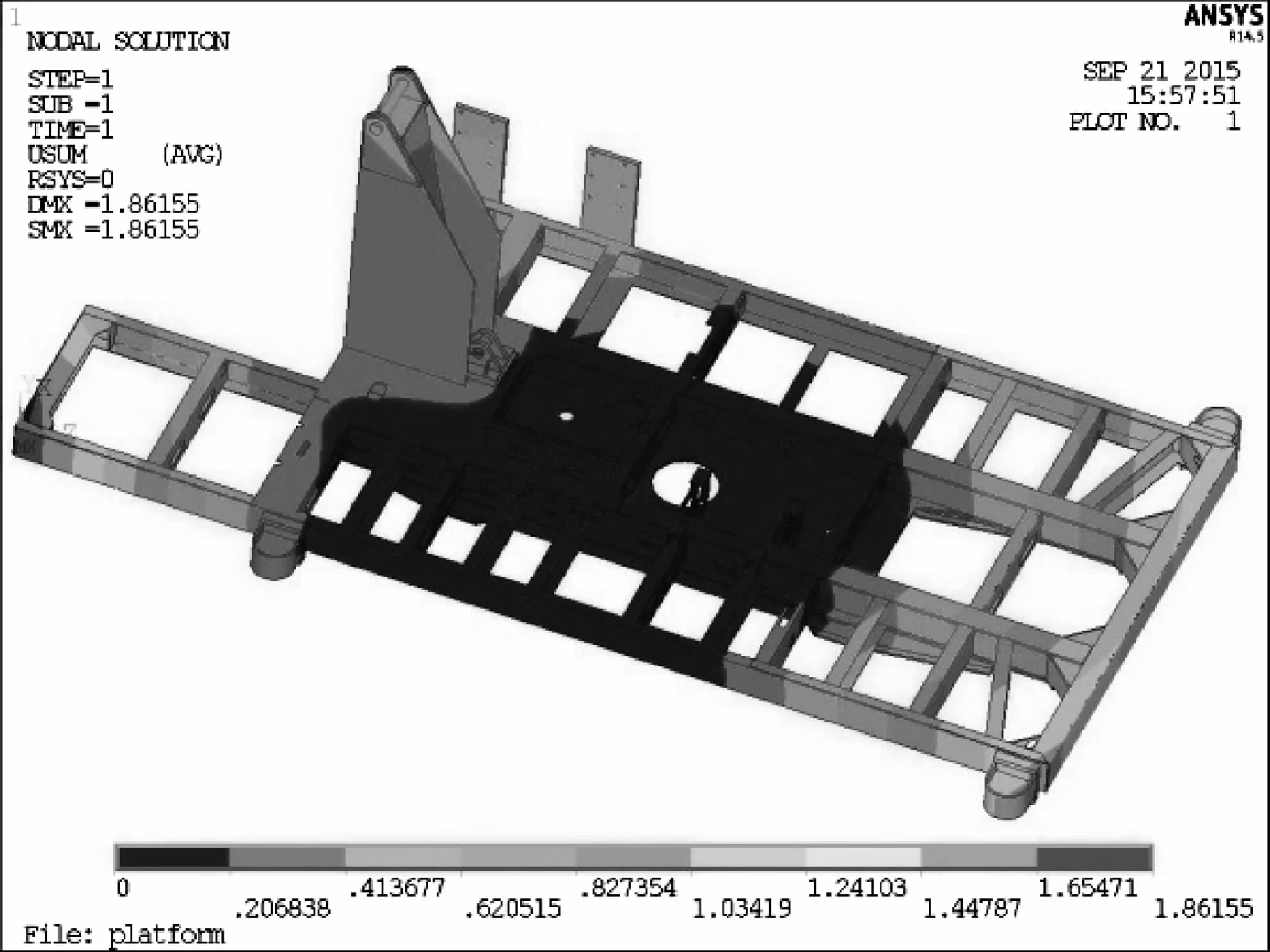
极限工况3:潜孔钻机作业达到指定要求后,仅提升支腿而钻架未提升.此时平台的等效应力云图如图 15、图 16,平台的大部分区域处于低应力状态,应力最大值位于滑架体支座与平台连接处,其值为143.124 MPa,局部应力较大区域出现在平台中部两侧主梁以及滑架体中部垫板周围和支座销轴上.如图 17,最大位移出现在平台的左前方,其值为1.861 55 mm.

|
| 图 15 极限工况3时平台的应力云图 Fig.15 The stress plot of platform under ultimate condition 3 |

|
| 图 16 极限工况3时平台的局部应力云图 Fig.16 The stress plot of platform under ultimate condition 3 |
|
| 图 17 极限工况3时平台的位移云图 Fig.17 The deformation plot of platform under ultimate condition 3 |
综上所述,极限工况对平台的破坏程度高于正常工况,在平台结构设计时应着重考虑极限工况.根据不同工况下的平台应力云图可知,平台大部分区域的应力远低于材料的屈服极限,结构设计较为合理,但在保证平台结构静强度足够的前提下可合理地优化,以减轻平台的质量和减少材料的消耗.而在危险区域和应力集中部位,可采取相应的措施,如采用加强筋、圆弧过渡、零件加厚等方法.
4 结 论本文通过分析潜孔钻机支撑平台和工作装置的结构和受力特点,确定了单支腿支撑平台的正常工况和极限工况,建立其力学模型,利用力学平衡理论和变形相容条件,得出各个工况下平台的力载荷,然后在Inventor中绘制三维实体模型,将其导入ANSYS进行有限元分析,获得了相应工况下的应力、位移云图,并加以分析,揭示了平台在各个工况下的最大应力值、变形值及其分布规律,其结果表明:
1) 平台的最大应力出现在平台底部两侧筋板与主底板的连接处以及滑架体与平台连接处;
2) 极限工况的最大应力均大于正常工况,两者都小于材料的屈服极限,因此平台结构静强度足够,满足设计要求;
3) 平台的最大变形出现在极限工况2时左前支腿安装座处,其值小于4 mm,符合设计要求.
| [1] | 赵宏强, 林宏武, 陈欠根, 等. 国内外液压潜孔钻机发展概况[J]. 工程机械与维修 , 2006 (4) : 72–73. ZHAO Hong-qiang, LIN Hong-wu, CHEN Qian-gen, et al. The development of the hydraulic DTH at home and abroad[J]. Construction Machinery & Maintenance , 2006 (4) : 72–73. |
| [2] | 吴双斌.潜孔钻机钻臂运动学与动力学研究及优化设计[D].长沙:中南大学机电工程学院,2011:1-2. WU Shuang-bin.The dynamics and kinematics study and optimization of the boom of down-the-hole drill[D].Changsha:Central South University,College of Mechanical and Electrical Engineering, 2011:1-2. |
| [3] | 杨天兵, 张韬. 露天潜孔钻机平台的结构改进和有限元分析[J]. 建筑机械 , 2008 (23) : 77–80. YANG Tian-bin, ZHANG Tao. The finite element analysis for the platform of open-air dived holes drilling machine[J]. Construction Machinery , 2008 (23) : 77–80. |
| [4] | 李立新, 江玉刚, 曹谊勃. 基于精确齿面建模的ZA蜗杆蜗轮有限元接触分析[J]. 工程设计学报 , 2011, 18 (1) : 38–42. LI Li-xin, JIANG Yu-gang, CAO Yi-bo. Finite element analysis of contact between ZA worm and worm gear based on precise tooth surface model[J]. Chinese Journal of Engineering Design , 2011, 18 (1) : 38–42. |
| [5] | 王艳, 徐信芯, 焦生杰. 旋挖钻机回转平台的有限元分析[J]. 设备管理与维修 , 2013 (5) : 97–101. WANG Yang, XU Xin-xin, JIAO Sheng-jie. Static finite element analysis for rotating platform of rotary drilling[J]. Road Machinery & Construction Mechanization , 2013 (5) : 97–101. |
| [6] | 周宏兵, 王世怀, 康辉梅, 等. 旋挖钻机的三角形连接架的有限元分析[J]. 现代制造工程 , 2011 (2) : 70–75. ZHOU Hong-bing, WANG Shi-huai, KANG Hui-mei, et al. The finite element analysis for the triangular connecting frame of rotary drilling rig[J]. Modern Manufacturing Engineering , 2011 (2) : 70–75. |
| [7] | 康辉梅, 何清华, 谢嵩岳, 等. 提钻工况下旋挖钻机的受力分析[J]. 工程力学 , 2010, 27 (10) : 214–218. KANG Hui-mei, HE Qing-hua, XIE Song-yue, et al. Mechanics analysis of rotary drilling rig under drilling bucket lifting conditions[J]. Engineering Mechanics , 2010, 27 (10) : 214–218. |
| [8] | 李明宝. 理论力学[M]. 武汉: 华中科技大学出版社 ,2007 : 92 -95. LI Ming-bao. Theoretical mechanics[M]. Wuhan: Press of Huazhong University of Science Technology , 2007 : 92 -95. |
| [9] | 郑兰霞, 胡修池, 等. 一种新的汽车起重机支腿受力计算方法[J]. 华北水利水电学院学报 , 2004, 25 (4) : 49–51. ZHENG Lan-xia, HU Xiu-chi, et al. A new calculating method for the force in supporting legs of mobile crane[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power , 2004, 25 (4) : 49–51. |


