Download PDF  
文章快速检索  
  高级检索
引用本文
周镇宇,唐进元,董建雄. 同功重比修形斜齿和直齿面齿轮性能对比研究[J]. 工程设计学报, 2016, 23(4): 338-344.
ZHOU Zhen-yu, TANG Jin-yuan, DONG Jian-xiong. Comparative study on the performance of modified face gears with helical pinion and spur pinion in the case of same power density[J]. Chinese Journal of Engineering Design, 2016, 23(4): 338-344.
同功重比修形斜齿和直齿面齿轮性能对比研究
周镇宇,唐进元,董建雄     
中南大学 高性能复杂制造国家重点实验室, 湖南 长沙 410083
收稿日期: 2016-01-20 .
作者简介: 周镇宇(1991—),男,江西宜春人,硕士生,从事齿轮传动及数字化制造研究,E-mail:zhenyuzhou@csu.edu.cn. http://orcid.org//0000-0001-5888-2892
通讯作者: 唐进元(1962－),男,湖南长沙人,教授,从事齿轮传动及数字化制造研究,E-mail:jytangcsu@163.com
摘要: 为深入了解同功重比修形斜齿与直齿面齿轮的性能差异，选择更适合于高速重载工况下的面齿轮传动.基于啮合原理推导了修形斜齿与直齿面齿轮齿面方程，基于CATIA建立了修形斜齿与直齿面齿轮三维模型，采用有限元接触分析方法，以接触应力、弯曲应力和重合度为面齿轮传动性能指标展开研究.研究结果表明：修形斜齿面齿轮相比修形直齿面齿轮接触应力大幅降低，算例最大接触应力降低16.3%；修形斜齿面齿轮相比修形直齿面齿轮弯曲应力大幅降低，算例最大弯曲应力降低32.4%；修形斜齿面齿轮相比修形直齿面齿轮重合度大幅提高，算例重合度提高10.3%.所以同功重比情况下，修形斜齿面齿轮传动性能优于修形直齿面齿轮，前者更适合于高速重载工况下的轻量化设计.
关键词: 轻量化     功重比     接触应力     弯曲应力     重合度     修形    

基金项目: 国家自然科学基金资助项目（51535012，51305462，51275530）
Comparative study on the performance of modified face gears with helical pinion and spur pinion in the case of same power density
ZHOU Zhen-yu, TANG Jin-yuan, DONG Jian-xiong     
State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China
Abstract: In order to know the performance difference of the modified face gears with helical pinion and spur pinion under the same power density better and choose a more suitable kind of face gear drive for high speed and heavy load conditions. Based on meshing theory, the tooth surface equations of the modified face gears with helical pinion and spur pinion were derived. The three-dimensional models of the modified face gears with helical pinion and spur pinion were built by CATIA. The finite element contact analysis method was used and the contact stress, bending stress and contact ratio were considered as performance indexes of the face gears to expand the research. Researches proved that the contact stress of modified face gear with helical pinion was much lower than that of modified face gear with spur pinion. The maximum contact stress was reduced by 16.3% in the case. The bending stress of modified face gear with helical pinion was much lower than that of modified face gear with spur pinion. The maximum bending stress was reduced by 32.4% in the case. The contact ratio of modified face gear with helical pinion was much higher than that of modified face gear with spur pinion. The contact ratio was increased by 10.3% in the case. So the transmission performance of the modified face gear with helical pinion is better than that of modified face gear with spur pinion under the same power density, the former is more suitable for the lightweight design under high speed and heavy load condition.
Key words: lightweight     power density     contact stress     bending stress     contact ratio     modification    

面齿轮传动是一种相对较新的齿轮传动方式.正交面齿轮传动中,与直齿轮啮合传动的称为直齿面齿轮,与斜齿轮啮合传动的称为斜齿面齿轮.面齿轮目前主要应用于武装直升机主传动中,而轻量化设计已成为飞机、汽车设计的一大趋势[1].对直升机主减速器而言,高功率密度是其主要性能指标,因此研究面齿轮功重比(单位质量所承载的功率)非常有必要.

斜齿面齿轮和直齿面齿轮均易出现边缘接触.为改善接触轨迹的齿面分布,避免边缘接触,得到均匀的载荷分布,需对面齿轮进行修形.Litvin等[2-8]率先提出抛物线齿廓修形方法,并在斜齿面齿轮接触分析中提出点接触形成条件和安装误差坐标系,得到均匀的齿面接触轨迹；初步给出面齿轮重合度的定义,但未给出具体计算方法.雷敦财[9]研究了有限元分析中轮毂结构对啮合刚度的影响.

本文基于有限元分析方法,在相同功重比工况下对修形斜齿面齿轮和修形直齿面齿轮进行接触应力、弯曲应力和重合度对比研究.

1 修形斜齿和直齿面齿轮齿面方程

齿轮啮合传动中主、被动齿轮的基节必须处处相等,从理论上讲,精确的渐开线刚性齿轮是能够实现上述目标的.但实际的齿轮副均为弹性体,在一定啮合力作用下会产生相应弹性变形,使处于啮合线位置的主动轮和被动轮基节出现变化,啮合过程中产生啮合冲击.为了消除轮齿啮合冲击,通常采用齿廓修形方法,即沿齿高方向从齿面上去除部分材料,从而改变齿廓形状,消除啮合冲击,减小啮合过程中的最大应力,提高齿轮副的传动平稳性和使用寿命.而抛物线齿廓是常用的修形齿廓.

考虑到标准的斜齿面齿轮和直齿面齿轮在啮合传动过程中均易产生边缘接触,故对这2种面齿轮均进行抛物线齿廓修形.修形面齿轮的齿面由修形产形轮齿面包络得到[10],而修形产形轮齿面由修形齿条刀具包络得到的,修形齿条齿廓直线被抛物线代替.

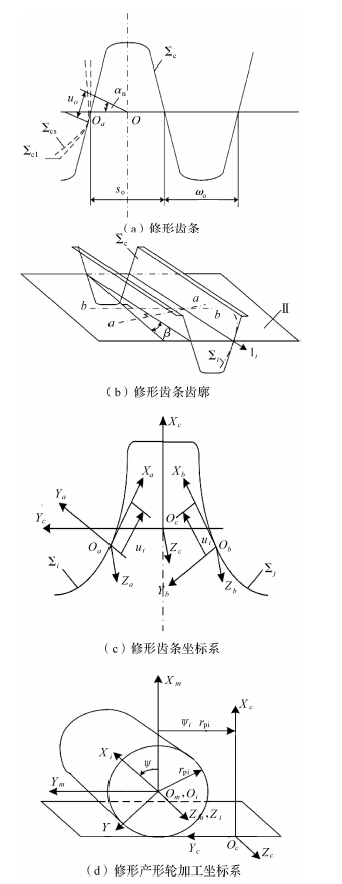
1.1 修形斜齿面齿轮齿面方程

传统加工斜齿轮的齿条刀刃∑c是直线,端面如图 1(a)所示,虚线所示∑cs和∑c1为修形抛物线齿廓,顶点Oa的位置由uo决定；空间齿廓如图 1(b)所示,∑i(i=cs,cl)为修形齿条齿面,li(i=cs,cl)为齿宽纵向变量参数；图 1(c)为抛物线修形齿条端面两侧齿廓,Sc(xc,yc,zc)为齿条动标系,Sa(xa,ya,za)和Sb(xb,yb,zb)为辅助坐标系,ui(i=s,l)为坐标系Sa(xa,ya,za)中横向变量参数；图 1(d)所示为修形齿条加工修形产形轮的坐标系,Sm(xm,ym,zm)为静标系,rpi(i=s,l)为节圆半径,Si(xi,yi,zi)为产形轮(i=s)和传动轮(i=l)动标系.

图 1 修形斜齿轮加工坐标系 Fig.1 The processing coordinate system of the modified helical pinion
图选项

图 1(c)中修形齿条刀具左右两侧齿面∑i和∑j(i,j=cs,cl)方程为(符号和±均按左右顺序表示)

${{r}_{al}}({{u}_{i}},{{l}_{i}})=\left[ \begin{align} & {{u}_{i}}{{l}_{i}}\mp sin~\beta ~sin~{{\alpha }_{n}} \\ & \pm {{a}_{i}}{{u}_{i}}^{2}+{{l}_{i}}sin~\beta cos~{{\alpha }_{n}} \\ & -{{l}_{i}}cos~\beta \\ \end{align} \right].$ (1)

动标系Sa到Sc的转换矩阵[11]为Mca，得Sc中修形齿条刀具齿面∑i(i=cs,cl)方程为

${{r}_{cl}}({{u}_{i}},{{l}_{i}})={{M}_{ca}}{{r}_{al}}({{u}_{i}},{{l}_{i}})$ (2)

其齿面法向量为ncl；Sc到Ss的转换矩阵为Msc(ψs)；得Ss中∑i(i=cs)包络的修形产形轮齿面∑s1方程为

$\left\{ \begin{align} & {{r}_{s1}}({{u}_{s}},{{l}_{s}})={{M}_{sc}}({{\psi }_{s}}){{r}_{cl}}({{u}_{s}},{{l}_{s}}), \\ & {{f}_{1}}({{u}_{s}},{{l}_{s}},{{\psi }_{s}})=0. \\ \end{align} \right.$ (3)

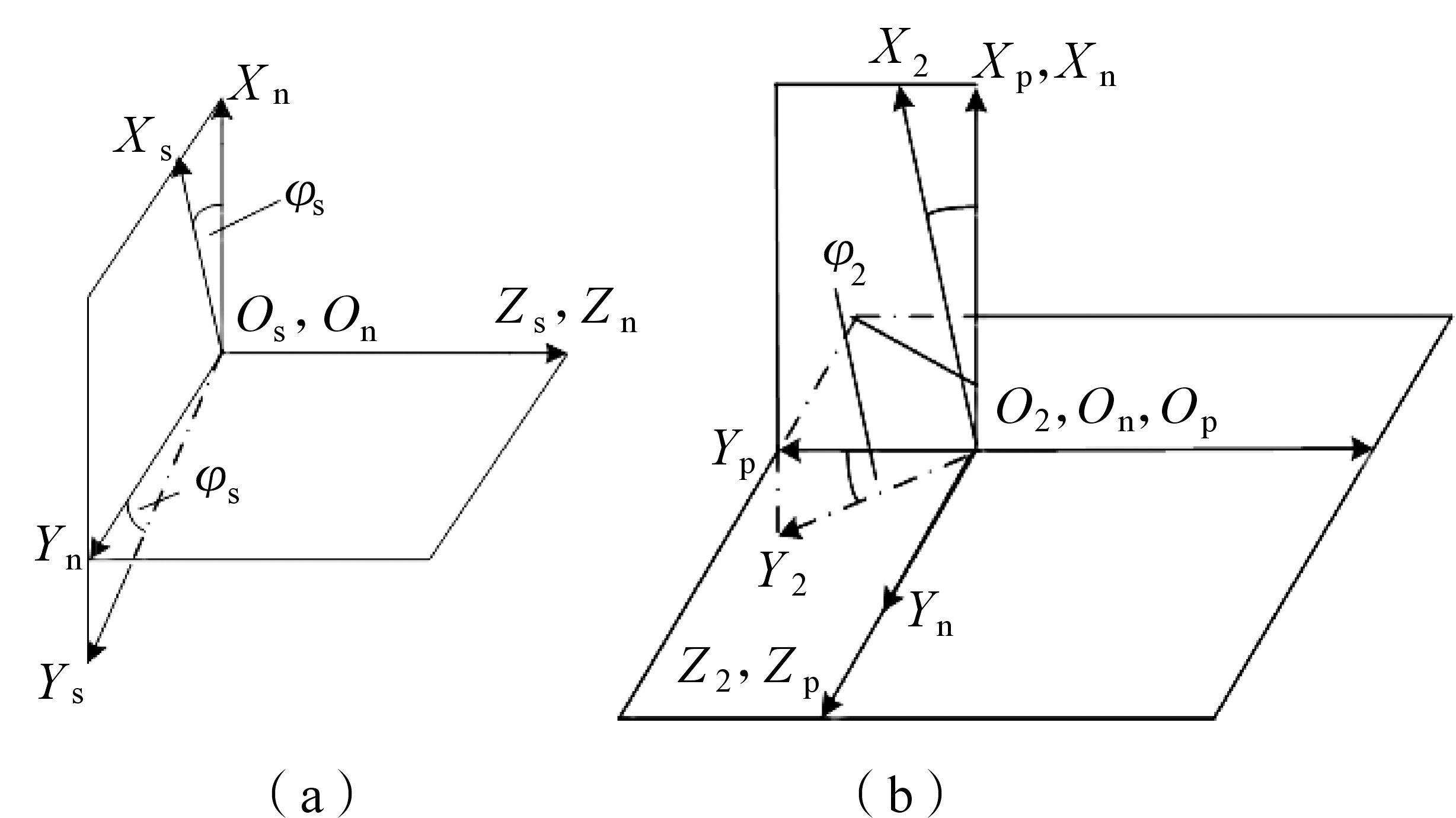
其齿面法向量为 ns2；图 2为修形斜齿面齿轮加工坐标系；Ss到S2转化矩阵为M2s；φs和φ2满足以下关系,其中Z2为面齿轮齿数:

图 2 修形斜齿面齿轮加工坐标系 Fig.2 The processing coordinate system of the modified face gear with helical pinion
图选项
$\frac{{{\phi }_{2}}}{{{\phi }_{s}}}=\frac{{{Z}_{s}}}{{{Z}_{2}}}={{m}_{2s}}.$ (4)

修形产形轮齿面∑s1包络的修形斜齿面齿轮齿面∑1在动标系S2中的方程为

$\left\{ \begin{align} & {{r}_{2}}({{u}_{s}},{{l}_{s}})={{M}_{2s}}{{r}_{s1}}({{u}_{s}},{{l}_{s}}), \\ & {{f}_{21}}({{u}_{s}},{{l}_{s}},{{\phi }_{s}})=0. \\ \end{align} \right.$ (5)

用同样方法可由修形齿条右侧刀刃包络得到修形产形轮齿面,进而包络求出修形斜齿面齿轮另一齿面的方程.

1.2 修形直齿面齿轮齿面方程

与修形斜齿面齿轮不同的是,修形直齿面齿轮两侧齿面是对称的,故只需推导一面的方程即可.此处所述修形直齿面齿轮的修形方法跟1.1节方法一致,推导过程也基本相同,不赘述其过程,在图 2所示加工坐标系中可求得动标系S2中修形面齿轮方程为

$\left\{ \begin{align} & {{r}_{2}}({{u}_{s}},{{l}_{s}})={{M}_{2s}}{{r}_{s1}}({{u}_{s}},{{l}_{s}}), \\ & f({{u}_{s}},{{l}_{s}},{{\phi }_{s}})=0. \\ \end{align} \right.$ (6)

其中rs(us,ls)为修形直齿产形轮方程.

2 修形斜齿和直齿面齿轮高精度几何建模

有限元仿真对几何模型精度要求较高.表 1和表 2为修形斜齿和直齿面齿轮设计参数.

表 1 修形斜齿面齿轮设计参数 Table 1 The design parameters of the modified face gear with helical pinion
设计参数传动小轮产形轮修行斜齿面齿轮
齿数Z2528160
压力角α/(°)2525—
模数m/mm6.356.356.35
旋向左旋左旋右旋
螺旋角β/(°)151515
外径/mm——582
内径/mm——497
轴交角γ/(°)909090
修形系数as0.0020.003—
齿顶系数1.01.251.0
齿底系数1.251.251.25
比值so/ωo0.90.9—
表选项
表 2 修形直齿面齿轮设计参数 Table 2 The design parameters of the modified face gear with spur pinion
设计参数参数值
小齿轮齿数Z119
产形轮齿数Zs21
面齿轮齿数Z273
名义压力角α/(°)25
模数m/mm4.5
面齿轮内径/mm158
面齿轮外径/mm189
抛物线位置参数Uo/mm3.035
轴交角γ/(°)90
产形轮齿顶高系数as1.25
产形轮齿根高系数bs1
小轮齿顶高系数a11
小轮设计齿根高系数bm1
表选项

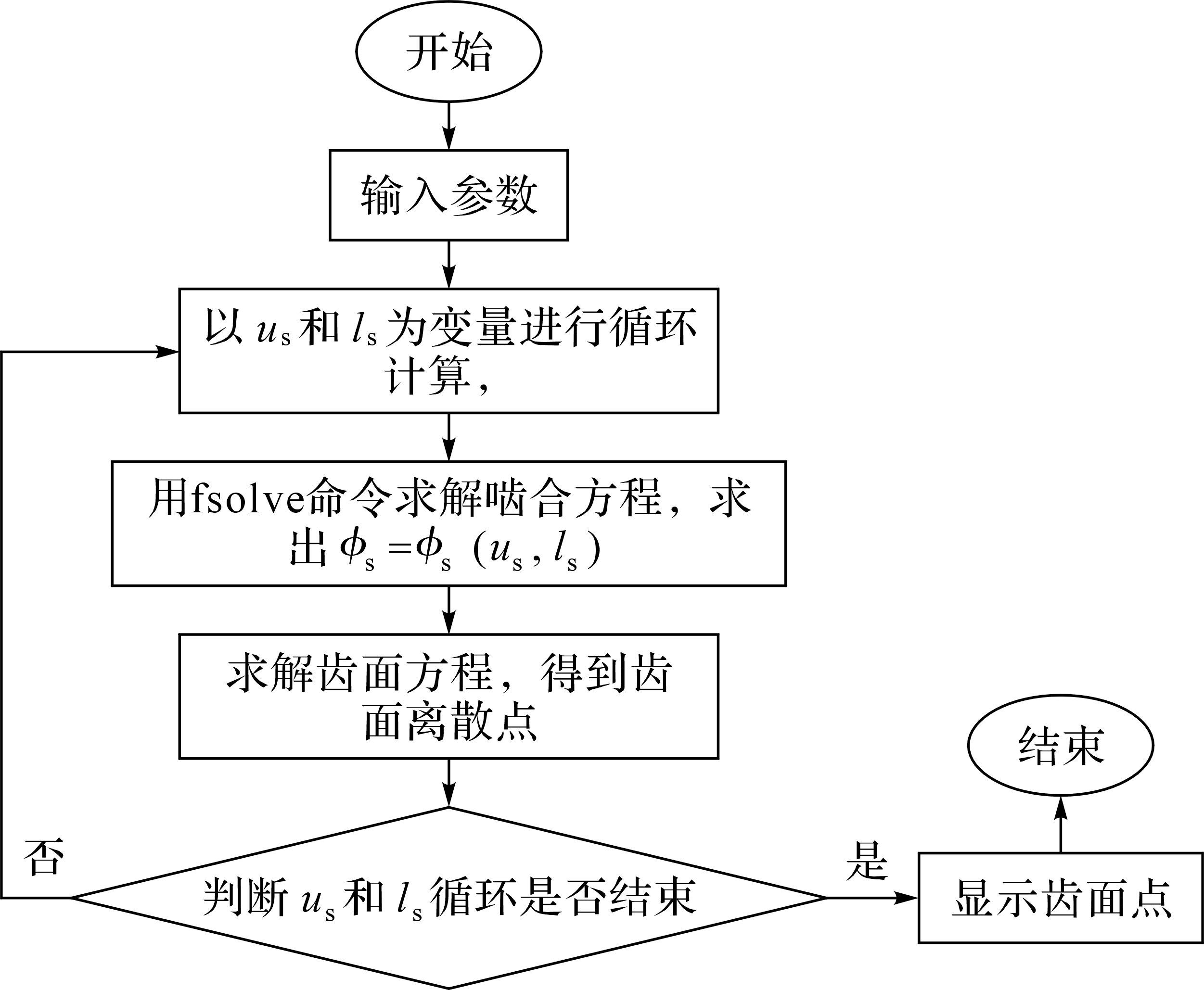
根据修形斜齿和直齿面齿轮方程,利用MATLAB计算功能计算得到齿面离散点,计算流程如图 3所示.

图 3 修形斜齿面齿轮齿面离散点计算流程图 Fig.3 The calculation flow chart of the tooth surface discrete points of the modified face gear with helical pinion
图选项

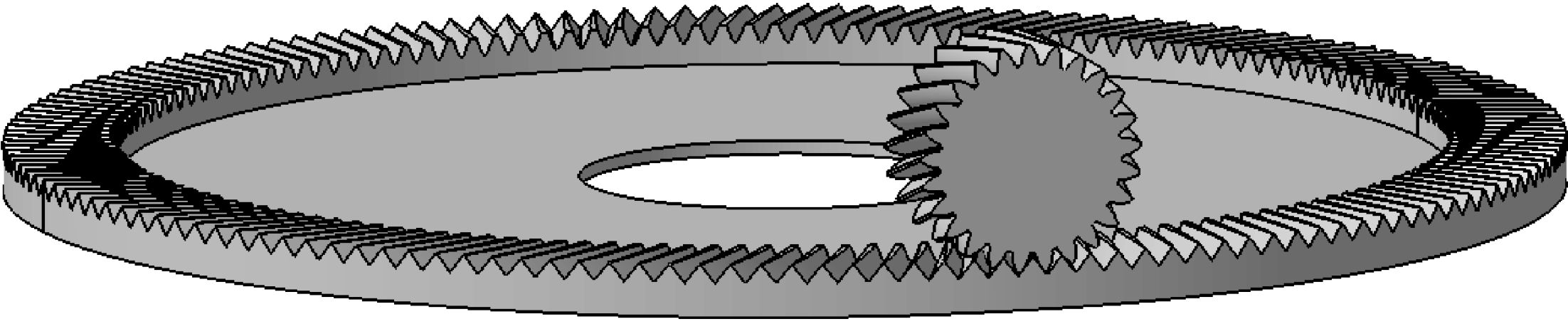
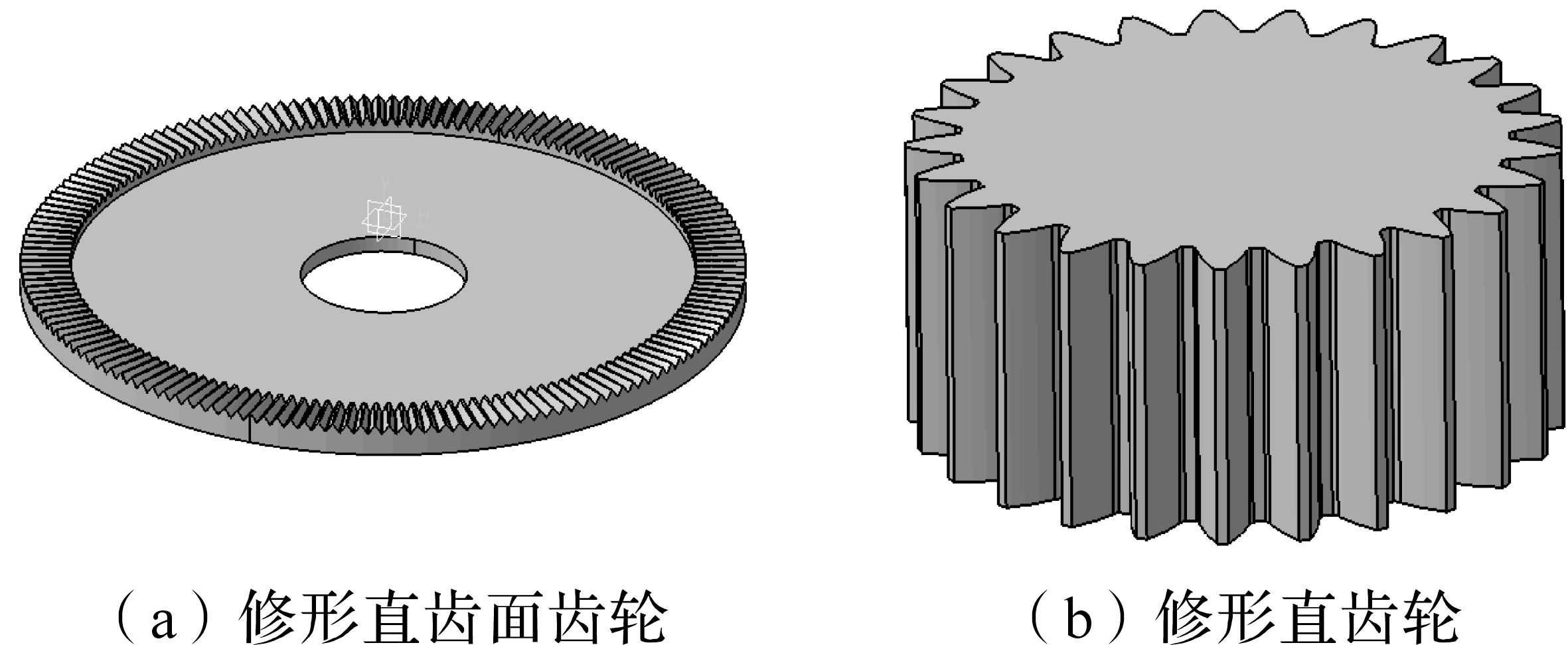
计算得到的齿面点数据,导入CATIA中进行拟合,经分割、阵列、去除等步骤可得到高精度修形斜齿面齿轮几何模型装配图，如图 4所示[12-13].同样方法可得修形直齿面齿轮几何模型装配图，如图 5所示.

图 4 修形斜齿面齿轮 Fig.4 The modified face gear with helical pinion
图选项
图 5 修形直齿面齿轮 Fig.5 The modified face gear with spur pinion
图选项
3 修形斜齿和直齿面齿轮功重比对比分析

功重比为承载功率和质量的比值,因2组齿轮采用相同材料,质量等价于体积.本文采用有限元分析的方法,对比相同功重比的修形斜齿面齿轮和修形直齿面齿轮的承载能力.在CATIA中测得修形斜齿面齿轮大小轮体积总和为22 900 000 mm3，修形直齿面齿轮大小轮体积总和为31 320 000 mm3.

3.1 修形斜齿和直齿面齿轮有限元建模

基于ABAQUS有限元软件[14-17],对图 4和图 5的2组面齿轮进行有限元建模,其建模过程按以下步骤进行：1)几何模型导入；2)网格划分；3)装配；4)设置材料属性：E=2.06×105 MPa,v=0.3；5)设置分析步；6)建立接触与约束；7)定义边界条件和载荷；8)设置网格类型以及创建并提交作业.

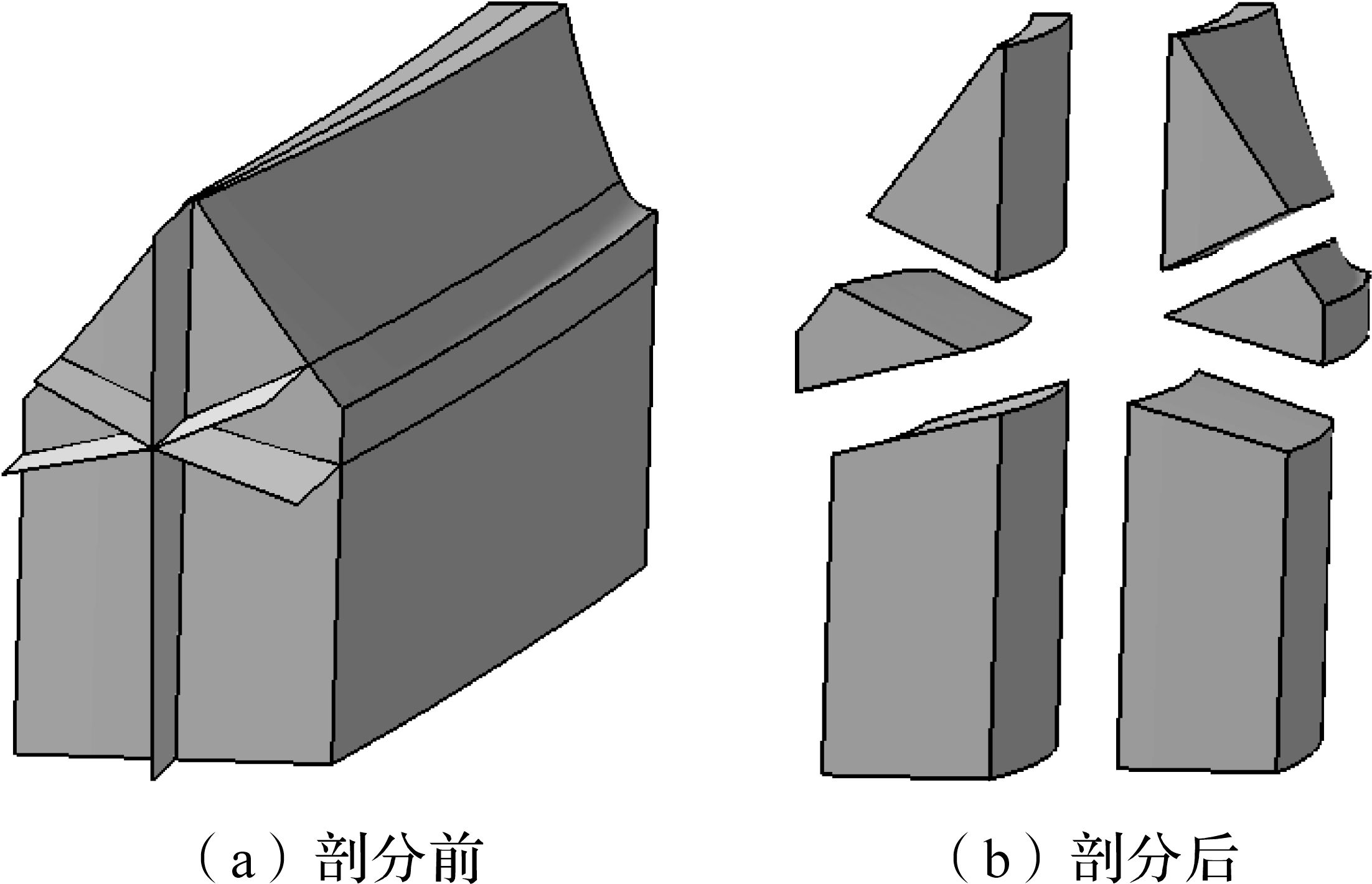
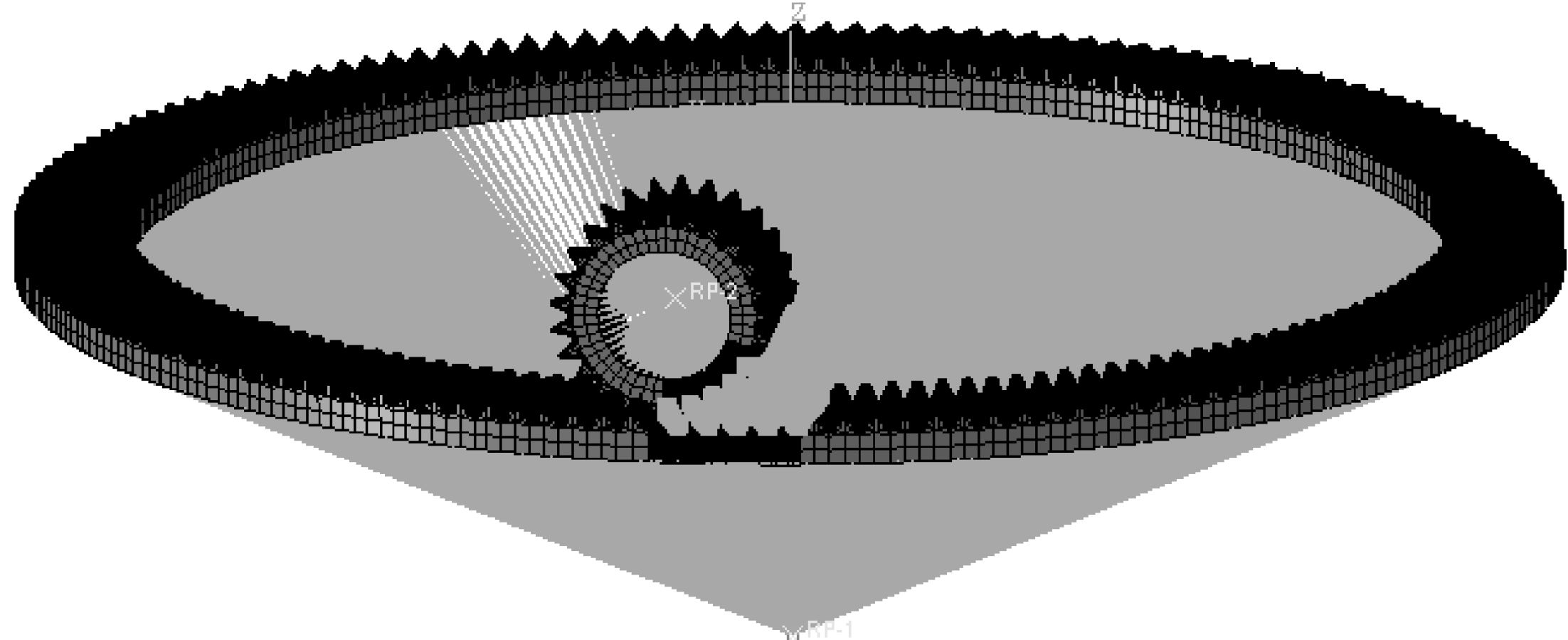
对修形斜齿面齿轮进行网格划分时,需先在CATIA中将修形斜齿面齿轮的单齿进行剖分,过程如图 6所示.有些情况下,若齿轮内外端粗细不均,还需在齿宽方向进行剖分,把分块同时导入ABAQUS进行网格划分,再把划分好网格的分块进行接合.修形斜齿面齿轮有限元网格如图 7所示.

图 6 CATIA中剖分单齿 Fig.6 The partition of single gear in CATIA
图选项
图 7 修形斜齿面齿轮有限元网格模型 Fig.7 The finite element mesh model of the modified face gear with helical pinion
图选项

修形直齿面齿轮有限元建模过程相比修形斜齿面齿轮更加简单,不具体介绍.

修形斜齿面齿轮转速为5 000 r/min，功率为524 kW，计算得大轮扭矩为1 000 N·m.在相同转速下,根据测得的体积,可求得同功重比的修形直齿面齿轮承载功率为716.7 kW，大轮扭矩为1 368 N·m.把已建好的2组齿轮有限元模型定义载荷后即可提交计算.

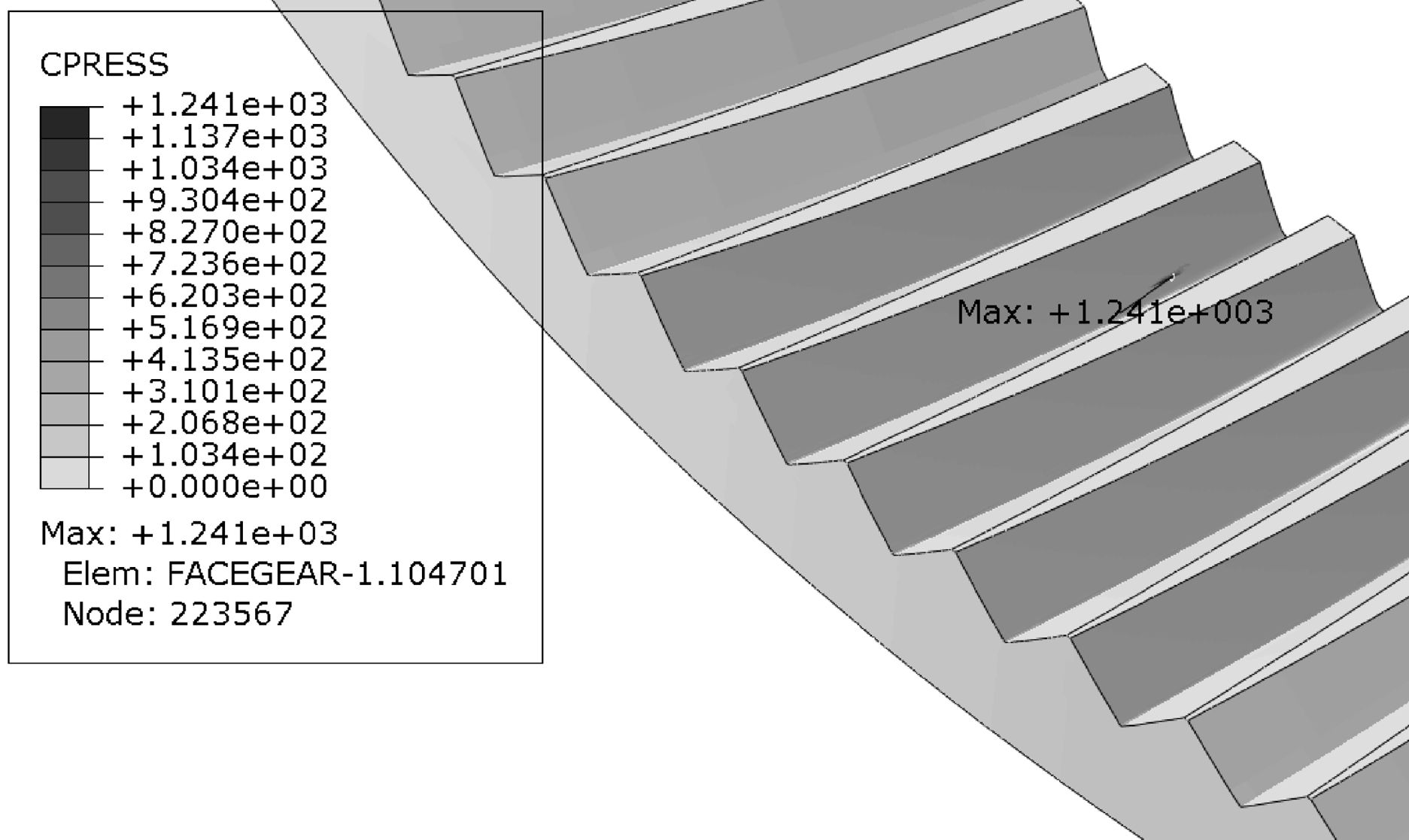
3.2 接触应力对比

2组齿轮经有限元分析后,得到同功重比情况下修形斜齿面齿轮最大接触应力如图 8所示,修形直齿面齿轮最大接触应力如图 9所示.

图 8 修形斜齿面齿轮最大接触应力云图 Fig.8 The maximum contact stress cloud chart of the modified face gear with helical pinion
图选项
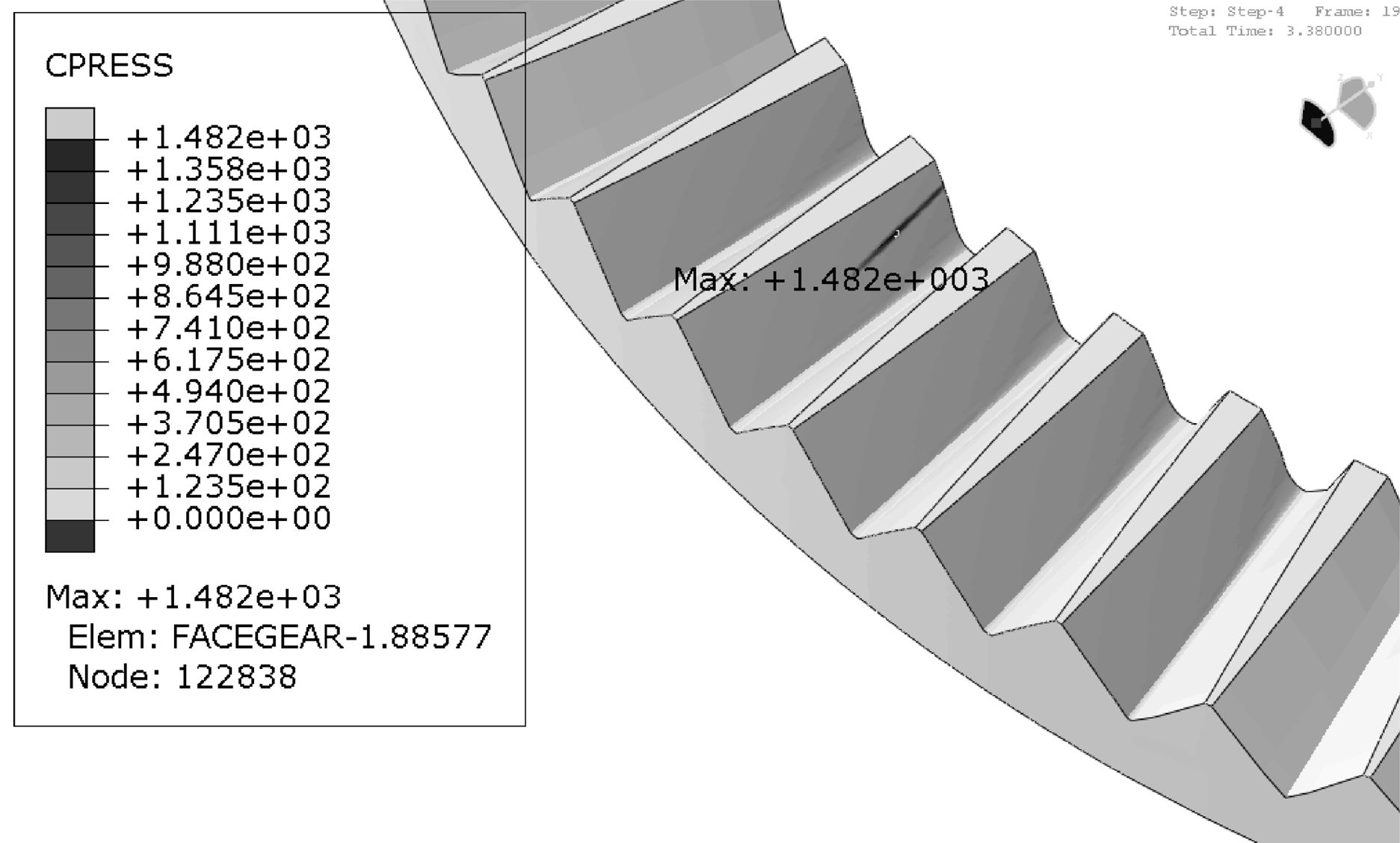
图 9 修形直齿面齿轮最大接触应力云图 Fig.9 The maximum contact stress cloud chart of the modified face gear with spur pinion
图选项

由图 8和图 9可知修形斜齿面齿轮最大接触应力为1 241 MPa，修形直齿面齿轮最大接触应力为1 482 MPa.对比分析可知：同功重比工况下，修形斜齿面齿轮相比修形直齿面齿轮最大接触应力降低16.3%((1482-1241)/1482×100%).

3.3 弯曲应力对比

修形斜齿面齿轮最大弯曲应力如图 10所示,修形直齿面齿轮最大弯曲应力如图 11所示.

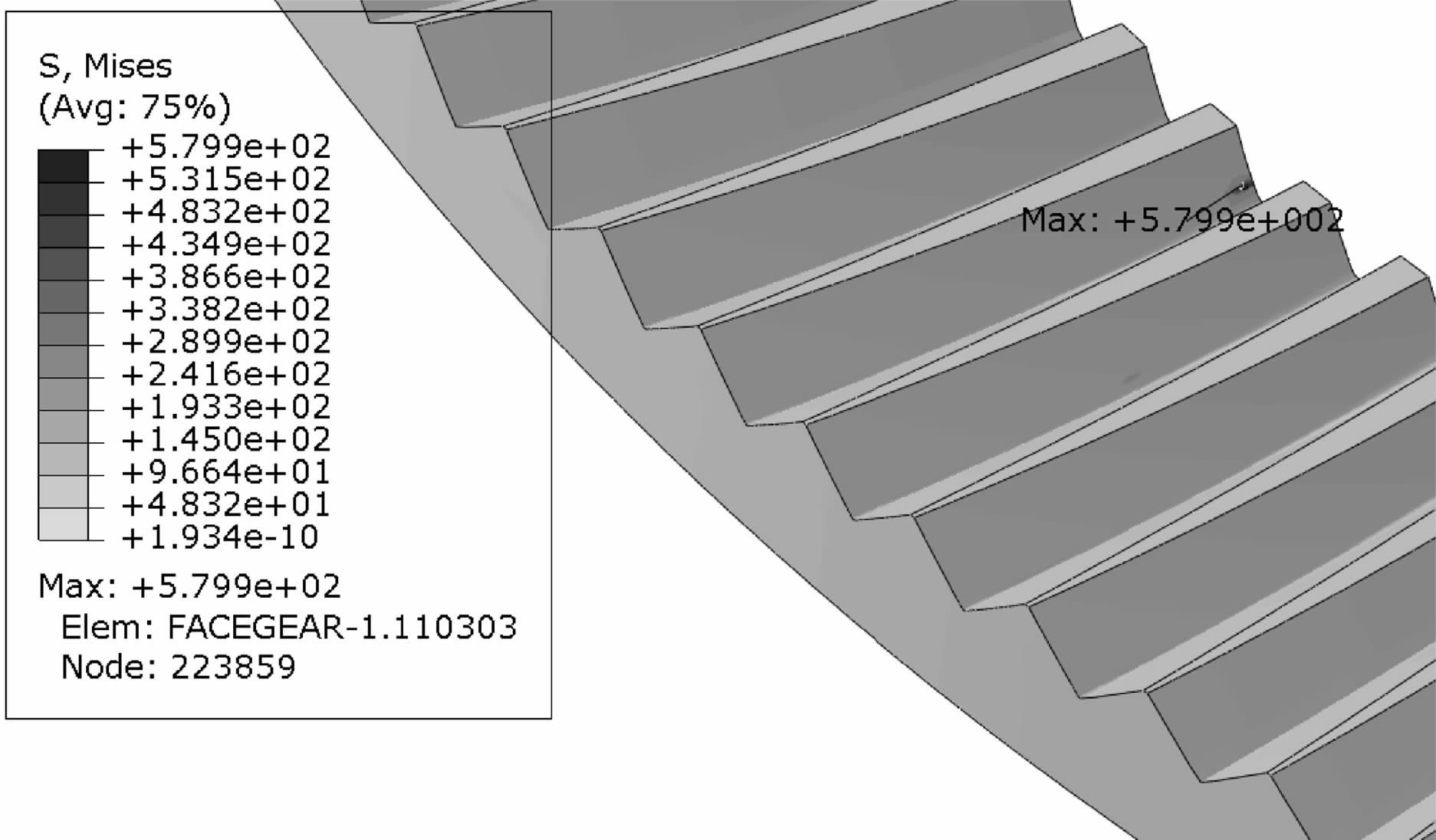
图 10 修形斜齿面齿轮最大弯曲应力云图 Fig.10 The maximum bending stress cloud chart of the modified face gear with helical pinion
图选项
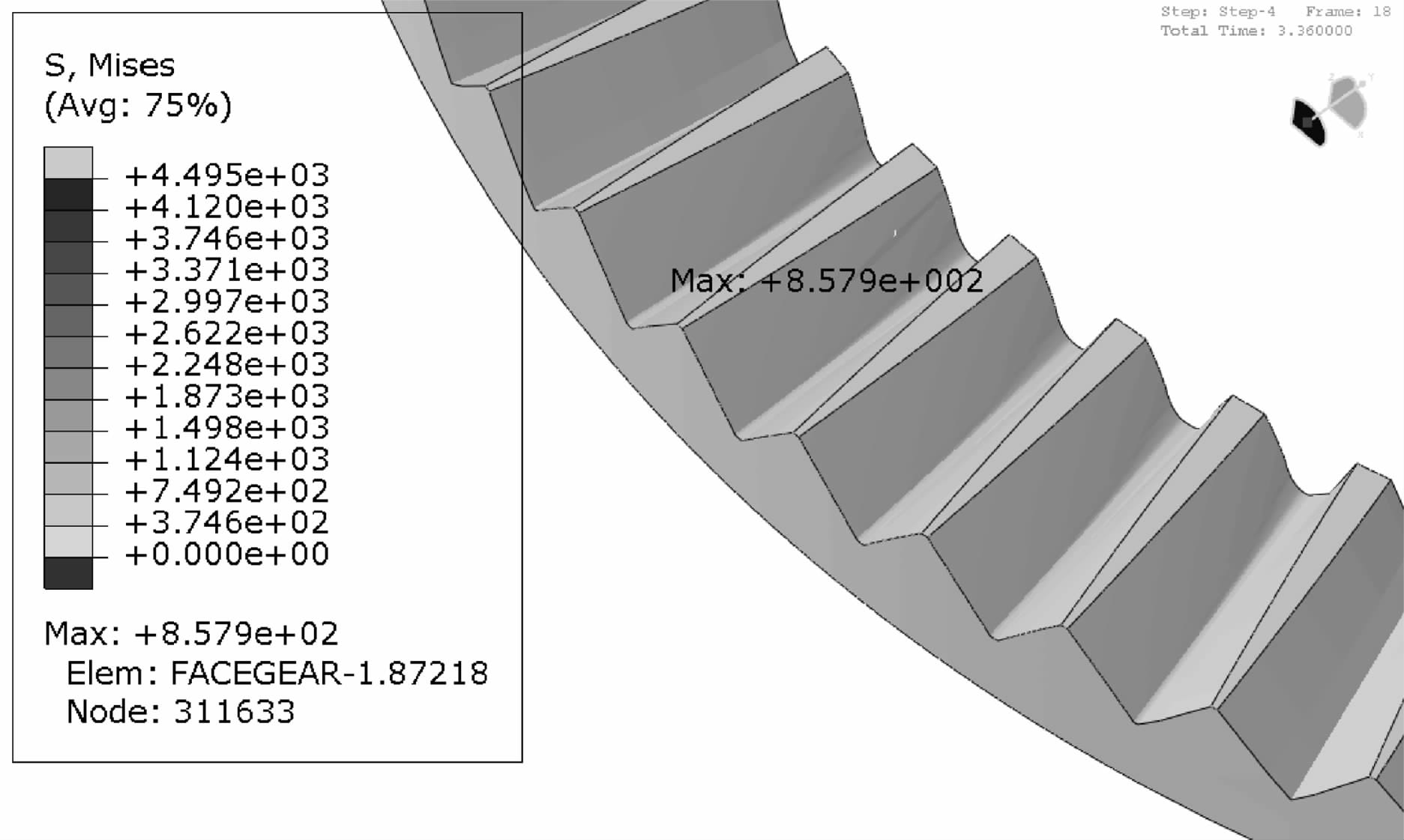
图 11 修形直齿面齿轮最大弯曲应力云图 Fig.11 The maximum bending stress cloud chart of the modified face gear with spur pinion
图选项

由图 10可知修形斜齿面齿轮最大弯曲应力为579.9 MPa，由图 11可知修形直齿面齿轮最大弯曲应力为857.9 MPa.对比可知：相同功重比工况下,修形斜齿面齿轮相比修形直齿面齿轮最大弯曲应力降低32.4%((857.9-579.9)/857.9×100%).

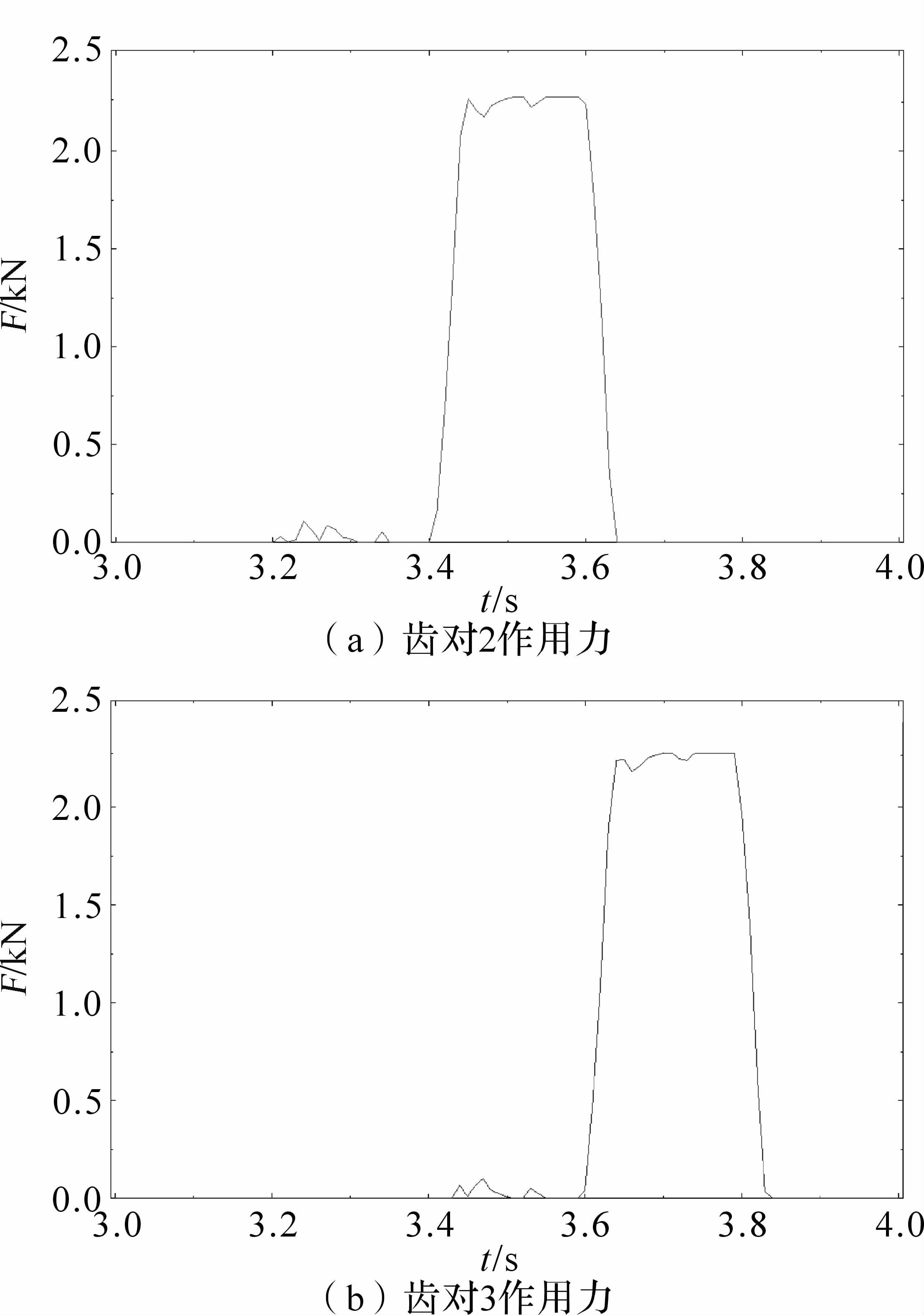
3.4 重合度对比

修形斜齿面齿轮有限元仿真结果的齿对接触力随时间分布如图 12所示.

图 12 修形斜齿面齿轮接触力 Fig.12 The contact force diagram of the modified face gear with helical pinion
图选项

由图 12可知：齿对2从t=3.21 s进入啮合,t=3.64 s退出啮合；齿对3从t=3.44 s进入啮合,t=3.84 s退出啮合；可得单个齿啮合时间段t2=3.64-3.21=0.43 s,t3=3.84-3.44=0.40 s,=(t2+t3)/2=0.415 s；相邻齿对进入啮合时间差Δt=3.44-3.21=0.23 s；由时间差法[18]计算可得加载重合度ε=/Δt=1.804.

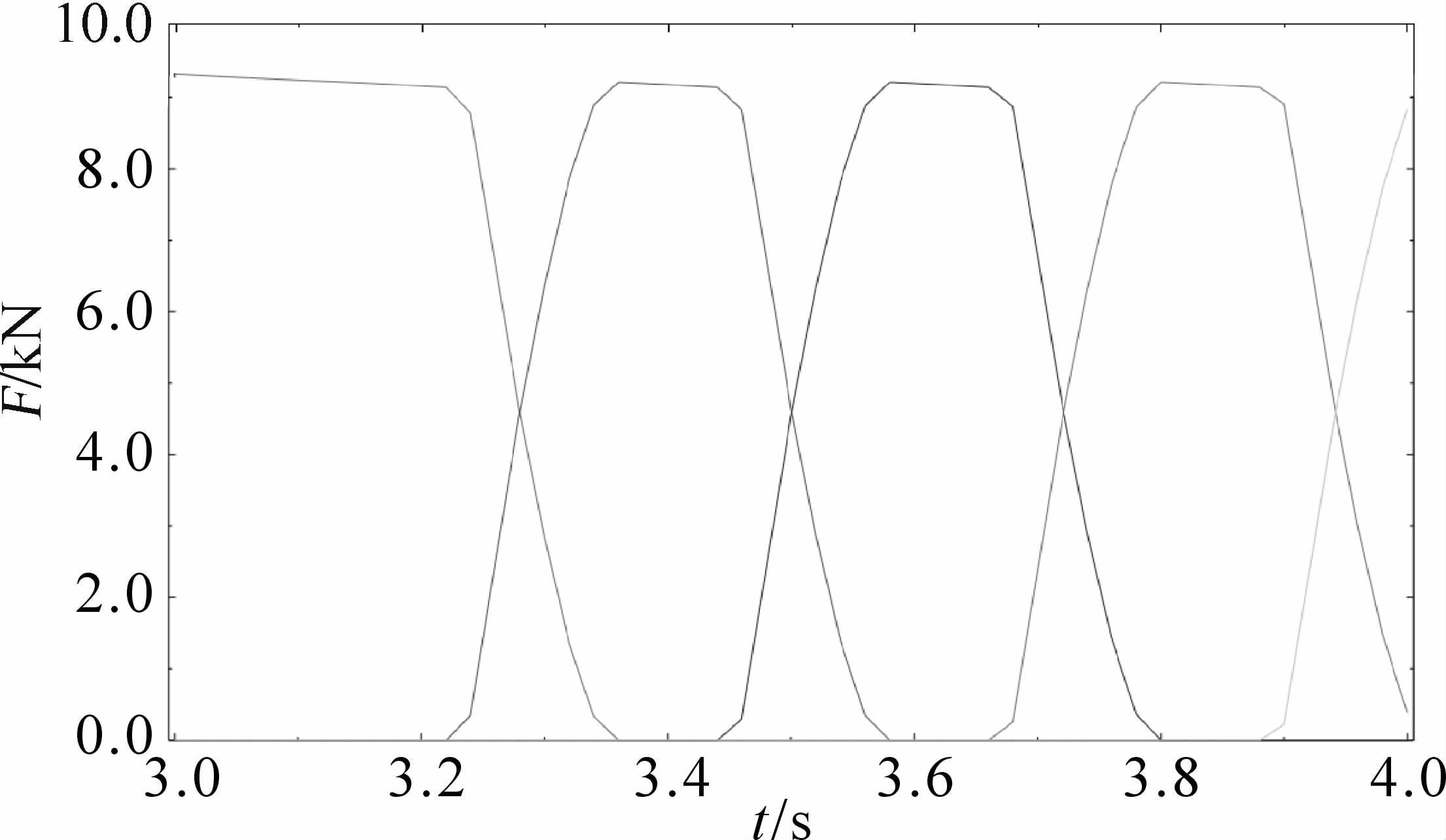
修形直齿面齿轮齿对接触力随时间分布如图 13所示.

图 13 修形直齿面齿轮接触力 Fig.13 The contact force diagram of the modified face gear with spur pinion
图选项

同样方法算得同功重比的修形直齿面齿轮传动重合度为1.636.

对比分析可知：在上述同功重比工况下,修形斜齿面齿轮相比修形直齿面齿轮重合度提高10.3%((1.804-1.636)/1.636×100%).

4 结 论

同功重比工况下,修形斜齿面齿轮相比修形直齿面齿轮：最大接触应力降低16.3%,最大弯曲应力降低32.4%,重合度提高10.3%.修形斜齿面齿轮比修形直齿面齿轮承载能力更强,重合度更高,更加符合高速重载工况下的轻量化设计要求.

参考文献
[1] 王征兵. 大型偏航变桨齿轮箱轻量化设计技术研究[D]. 郑州:机械科学研究总院郑州机械研究所,2012:28-30. WANG Zheng-bing. Research on lightweight design technology for large scale yaw and pitch gearboxes [D]. Zhengzhou: China Academy of Machinery Science & Technology, Zhengzhou Research Institute of Mechanical Engineering, 2012: 28-30.
[2] LITVIN F L, ZHANG Y, WANG J C, et al. Design and geometry of face-gear drives[J]. Journal of Mechanical Design , 1992, 114 (4) : 642–647. DOI:10.1115/1.2917055
[3] LITVIN F L.Development of face-gear technology for industrial and aerospace power transmission[R].Washington D.C.:NASA/CR-2002-211320.
[4] HEATH G F,BOSSLER R B.Advanced Rotorcraft Transmission (ART) Program-Final Report[R].Washington D.C.:NASA/CR-1993-191057.
[5] LITVIN F L, FUENTES A, ZANZI C. Design,generation and stress analysis of two versions of geometry of face-gear drives[J]. Mechanism and Machine Theory , 2002, 37 (10) : 1179–1211. DOI:10.1016/S0094-114X(02)00050-2
[6] LITVIN F L, GONZALWZ-PEREZ I, FUENTES A. Design,generation and stress analysis of face-gear drive with helical pinion[J]. Computer Methods in Applied Mechanics and Engineering , 2005, 194 (36/38) : 3870–3902.
[7] LITVIN F L, FUENTES A, HOWKINS M. Design,generation and TCA of new type of asymmetric face-gear drive with modified geometry[J]. Computer Methods in Applied Mechanics and Engineering , 2001, 190 (43/44) : 5837–5865.
[8] LITVIN F L, VECCHIATO D, GUROVICH E. Computerized developments in design,generation,simulation of meshing,and stress analysis of gear drives[J]. Meccanica , 2005, 40 (3) : 291–323. DOI:10.1007/s11012-005-4020-y
[9] 雷敦财.面齿轮时变啮合刚度计算及动态啮合性能研究[D].长沙:中南大学机电工程学院,2013:42-46. LEI Dun-cai.Study of time varying mesh stiffness and dynamic performance of face-gear pair [D].Changsha: Central South University,School of Mechanical and Electrical Engineering,2013:42-46.
[10] 李特文.齿轮几何学与应用理论[M].国凯,叶凌云,范琳,等,译.上海:科学技术出版社,2008:484-516. LITVIN F L.Gear geometry and applied theory [M].Translated by GUO Kai,YE Ling-yun,FAN Lin,et al.Shanghai:Science and Technology Press,2008:484-516.
[11] 李瑰贤. 空间几何建模及工程应用[M]. 北京: 高等教育出版社 ,2007 : 135 -137. LI Kui-xian. Spatial geometry modeling and its application in engineering[M]. Beijing: Higher Education Press , 2007 : 135 -137.
[12] 丁仁亮. CATIA V5教程[M]. 北京: 机械工业出版社 ,2007 : 2 -30. DING Ren-liang. CATIA V5 Course[M]. Beijing: China Machine Press , 2007 : 2 -30.
[13] 陈兴明.含安装误差的修形直齿面齿轮传动齿面接触分析的研究[D].长沙:中南大学机电工程学院,2012:21-24. CHEN Xing-ming.Tooth contact analysis of modified spur face gear drives with alignment errors[D].Changsha:Central South University,School of Mechanical and Electrical Sngineering, 2012:21-24.
[14] 刘艳平.直齿面齿轮加载接触分析及弯曲应力和接触应力计算方法研究[D].长沙:中南大学机电工程学院,2012:29-32. LIU Yan-ping.The loaded tooth contact analysis and bending stress and contact stress calculating method research of face gear drive with spur involute pinion[D].Changsha:Central South University,School of Mechanical and Electrical Engineering, 2012:29-32.
[15] 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社 ,2007 : 24 -32. SHI Yi-ping, ZHOU Yu-rong. Detailed answers of instances by ABAQUS finite element analysis[M]. Beijing: China Machine Press , 2007 : 24 -32.
[16] 罗希年.齿轮弯曲应力计算的优化[D].西安:长安大学机械工程学院,2012:42-47. LUO Xi-nian.The optimization of calculation of gear bending stress[D].Xi'an: Chang'an University,School of Mechanical Engineering,2012:42-47.
[17] 戈红霞, 吕庆军, 张志凯. 关于面齿轮接触和弯曲应力有限元计算方法的研究[J]. 新技术 新工艺 , 2014 (1) : 43–47. GE Hong-xia, LÜ Qing-jun, ZHANG Zhi-kai. Research on finite element method of face gear contact and bending stress calculation[J]. New Technology & New Process , 2014 (1) : 43–47.
[18] 董建雄, 唐进元. 基于轮齿接触分析的修形面齿轮传动重合度计算研究[J]. 机械传动 , 2015, 39 (4) : 8–10. DONG Jian-xiong, TANG Jin-yuan. Study on contact ratio calculation of modified face gears based on contact analysis[J]. Mechanical Transmission , 2015, 39 (4) : 8–10.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.007
教育部主管，浙江大学和中国机械工程学会主办
0

文章信息

周镇宇, 唐进元, 董建雄
ZHOU Zhen-yu, TANG Jin-yuan, DONG Jian-xiong
同功重比修形斜齿和直齿面齿轮性能对比研究
Comparative study on the performance of modified face gears with helical pinion and spur pinion in the case of same power density
工程设计学报, 2016, 23(4): 338-344.
Chinese Journal of Engineering Design, 2016, 23(4): 338-344.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.007

文章历史

收稿日期: 2016-01-20

相关文章

工作空间