Download PDF  
文章快速检索  
  高级检索
引用本文
刘小龙,赵彦峻,葛文庆,王滢,张忠东. 医疗助力下肢外骨骼设计及动力学仿真分析[J]. 工程设计学报, 2016, 23(4): 327-332.
LIU Xiao-long, ZHAO Yan-jun, GE Wen-qing, WANG Ying, ZHANG Zhong-dong. Design and dynamics simulation analysis of medical disabled lower limb exoskeleton[J]. Chinese Journal of Engineering Design, 2016, 23(4): 327-332.
医疗助力下肢外骨骼设计及动力学仿真分析
刘小龙1,赵彦峻1,葛文庆2,王滢1,张忠东1     
1. 山东理工大学 机械工程学院, 山东 淄博 255049;
2. 山东理工大学 交通与车辆工程学院, 山东 淄博 255049
收稿日期: 2015-10-13 .
作者简介: 刘小龙(1992—),男,山东济南人,硕士生,从事外骨骼机器人建模、仿真与优化等研究,E-mail:876853834@qq.com. http://orcid.org//0000-0001-8291-0814
通讯作者: 赵彦峻(1970—),女,山东淄博人,博士,副教授,硕士生导师,从事外骨骼机器人,多体复杂系统建模、仿真及多学科优化等研究,E-mail:zyj6270110@163.com
摘要: 针对人体下肢受伤康复等问题，设计了医疗助力下肢外骨骼机器人.对下肢外骨骼系统进行了基本结构设计，把下肢运动分单腿、双腿支撑的不同时期，进行了下肢外骨骼系统动力学计算.通过Lagrange方程，得到各关节力矩计算公式，建立了三维模型，利用基于接口的协同仿真技术并结合ADAMS和MATLAB软件对外骨骼进行联合仿真，得到单腿支撑时期各关节角度变化曲线及力矩变化曲线，对比仿真数据和理论计算数据，验证了理论模型的合理性.通过下肢外骨骼仿真分析设计，为后期下肢外骨骼运动控制及模型制造提供重要数据与理论基础.
关键词: 下肢外骨骼     动力学计算     Lagrange方程     仿真分析    

基金项目: 国家自然科学基金青年基金资助项目（51505263）；山东省科技发展计划资助项目（2014GGX103007）；山东省高等学校科技计划项目（J15LB08）
Design and dynamics simulation analysis of medical disabled lower limb exoskeleton
LIU Xiao-long1, ZHAO Yan-jun1, GE Wen-qing2, WANG Ying1, ZHANG Zhong-dong1     
1. School of Mechanical Engineering, Shandong University of Technology, Zibo 255049, China ;
2. School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China
Abstract: Aiming at the problems such as lower extremity injury, the medical assistive limb exoskeleton robot is designed. The basic structure of lower limb exoskeleton system was designed. The lower limb movement was divided into different periods, such as single leg support period and two legs support period. The dynamics computation of lower limb exoskeleton system was made. By the use of the Lagrange equation, the calculation formula of each joint torque was made. The three-dimensional model was established. Based on the collaborative simulation technology of the interface, the exoskeleton was unitedly simulated united simulation by ADAMS and MATLAB software. The curves of each joint's angle and torque in the single leg support period were made. It showed the correctness of the theoretical analysis by comparing the simulation data with the theoretical calculation date. By the simulation analysis of the lower limb exoskeleton, it provides important data and theoretical basis for the motion control and model manufacturing of lower extremity exoskeleton.
Key words: lower limb exoskeleton     dynamics calculation     Lagrange equation     simulation analysis    

根据研究调查显示,我国老龄化人群中偏瘫患者众多,车祸等因素造成的下肢瘫痪者也有所增多,而其中大多数经过有效治疗并辅以康复训练可以恢复基本行走能力,最后逐渐康复,由此,医疗下肢外骨骼进入了人们的视线并发挥越来越大的作用[1-2].外骨骼机器具有强大的能量但不具有人类所特有的智慧,将人类智能与外骨骼强大的机械能量结合起来,这就是外骨骼机器人的设计思想[3].在早期外骨骼研究中,上肢外骨骼的研究较为成熟[4-5],但下肢外骨骼的成熟设计鲜见.目前,国外的BLEEX系列[6]与HAL系列[7]外骨骼分别应用于军事和医疗,我国清华大学、浙江大学和中国科学院等科研院所也有下肢外骨骼项目的研究[8-10].

医疗下肢外骨骼的设计目的是控制外骨骼进行辅助人类康复行走,而仿真分析可以为实际模型提供理论依据[11-13],因此提出下肢外骨骼基本结构设计和动力学及理论计算联合仿真分析.

1 原理分析及设计 1.1 基本尺寸设计

由于人的身高各不相同,若想使下肢外骨骼能适应于不同的穿戴者,就必须将下肢外骨骼的大小腿连杆及腰部连杆设计成可调节的形式.查询人体躯干长度GB 10000—88(中国成年人人体尺寸)进行设定,将下肢外骨骼的合理可调尺寸大致设定为：小腿杆长度l1=300～420 mm；大腿杆长度l2=390～520 mm；腰部长度l3=270～360 mm.

参考人体的运动参数,结合下肢外骨骼工作情况的需要,确定各关节转动范围,设θc为髋关节的屈/伸角度(伸为正,屈为负),θk为膝关节的屈/伸角度,则：髋关节的屈/伸角度(竖直向下为0°)θc=-30°～30° ；膝关节的屈/伸角度θk=-30°～0°.

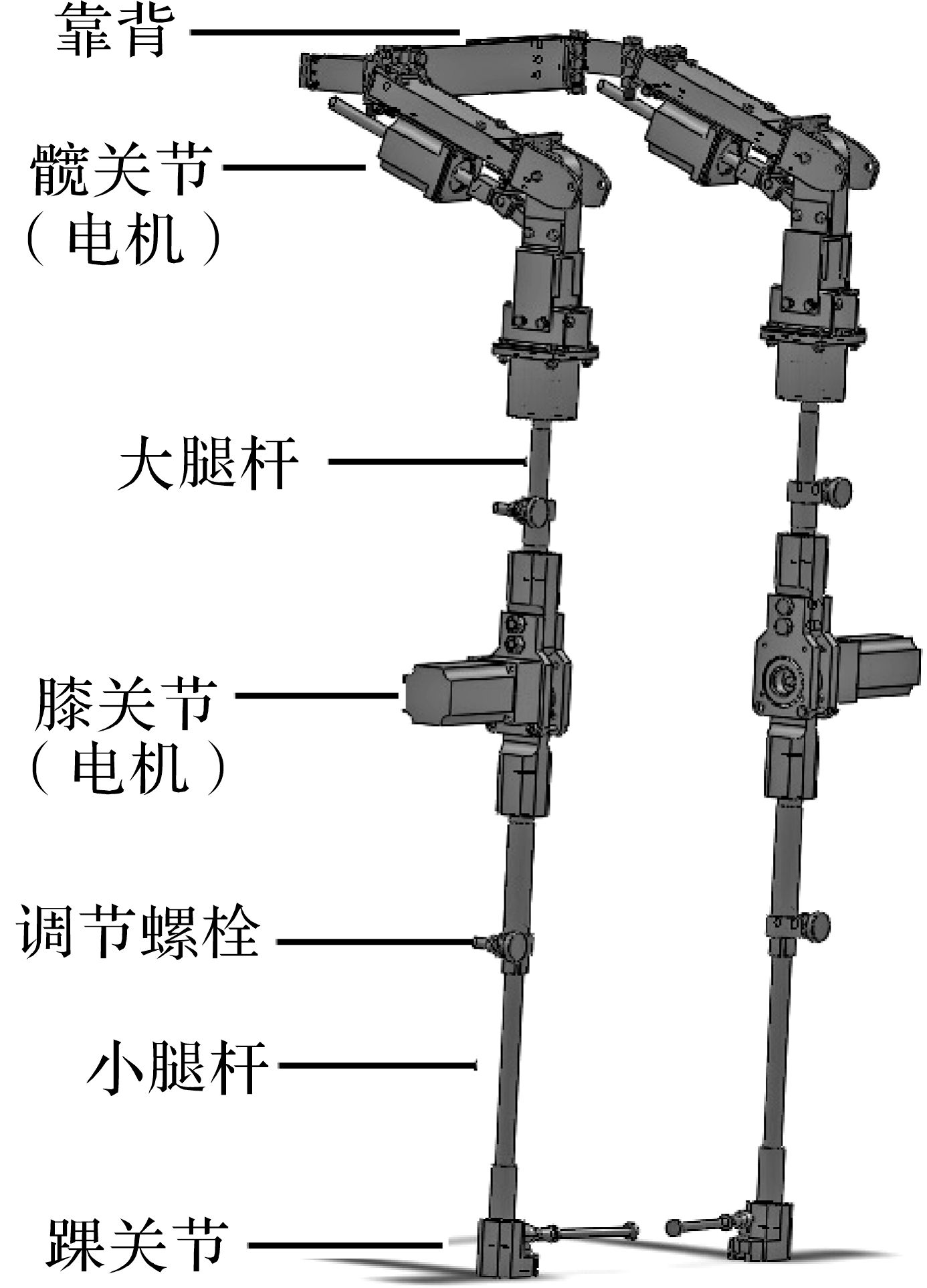
1.2 结构设计

该可穿戴式下肢外骨骼机器人采用轻质合金材料,利用电机驱动,具有使用方便、成本低廉、控制精确及响应迅速等优点.该机构单边自由度分别为：髋关节，2个；膝关节，1个；踝关节，3个.整个机构由2个直线电机和2个旋转电机驱动.下肢外骨骼三维整体结构模型如图 1所示,腰部、大腿、小腿的长度均可实现无级可调,机构穿戴时,用系带将人体与外骨骼耦合连接,通过控制系统控制电机带动人体,辅助人体行走动作.

图 1 下肢外骨骼三维结构模型 Fig.1 Three dimensional structure model of lower limb exoskeleton
图选项

在外骨骼机器人髋关节处需要实现的自由度有2个,即髋关节的前后屈/伸和左右转动.膝关节处所确定的自由度只有膝关节的屈/伸.在大腿和小腿之间用12 mm铝板连接,犹如人体的韧带,同时12 mm厚铝板还可以做轴承座用.膝关节的伸展角度与人正常行走时膝关节的角度相同,如果过度伸展则会造成膝关节反关节折断,使穿戴者的膝关节严重受伤.基于这一方面的考虑,本设计采用了一个接触式自动限位装置.

下肢外骨骼机构的腰背部及大、小腿部需要具有可调功能.腰背架不仅要能够承载一定的重物,并且结构需要具有一定的柔韧性,通过调节螺栓来调节背部的宽度,可以由最为常见的腰带实现.大、小腿部分主要由外杆和内杆组成,内杆套在外杆内部,可以通过螺栓松开/锁紧来调节腿部的长度,共同实现无级调节.

2 建模及动力学分析

外骨骼机器人,实质上是由一系列关节连接而成的空间连杆开环式机构[14],因而双足外骨骼机器人分析中通常采用连杆模型进行动力学分析.以往的研究中,针对不同的应用环境,简化的外骨骼模型有七杆机构[15]与五杆机构[16]两种.本设计用于医疗康复辅助行走,需要外骨骼提供一定动力带动人体,在髋关节、膝关节处安装电机,因此采用五杆机构更为合理.由此,建立矢状面内的五杆机构来分析关节的力矩.动力学仿真多采用的Lagrange函数为

$L={{E}_{K}}-U.$ (1)

本文采用基于Lagrange函数的多自由度机械系统建模方法,下肢外骨骼系统动力学表达式可表述为

$\frac{d}{dt}\left( \frac{\partial L}{\partial {{q}_{i}}} \right)-\frac{\partial L}{\partial {{q}_{i}}}=\frac{d}{dt}\left( \frac{{{E}_{K}}}{\partial {{q}_{i}}} \right)-\frac{{{E}_{K}}}{{{q}_{i}}}+\frac{\partial U}{\partial {{q}_{i}}}={{Q}_{i}}.$ (2)

其中：qi(i=1，2，…，5)表示第i个广义坐标,EK表示系统的动能,U表示系统的势能,Qi表示第i个广义坐标的广义力.

下文中,将分别对单腿与双腿支撑两部分进行动力学分析.

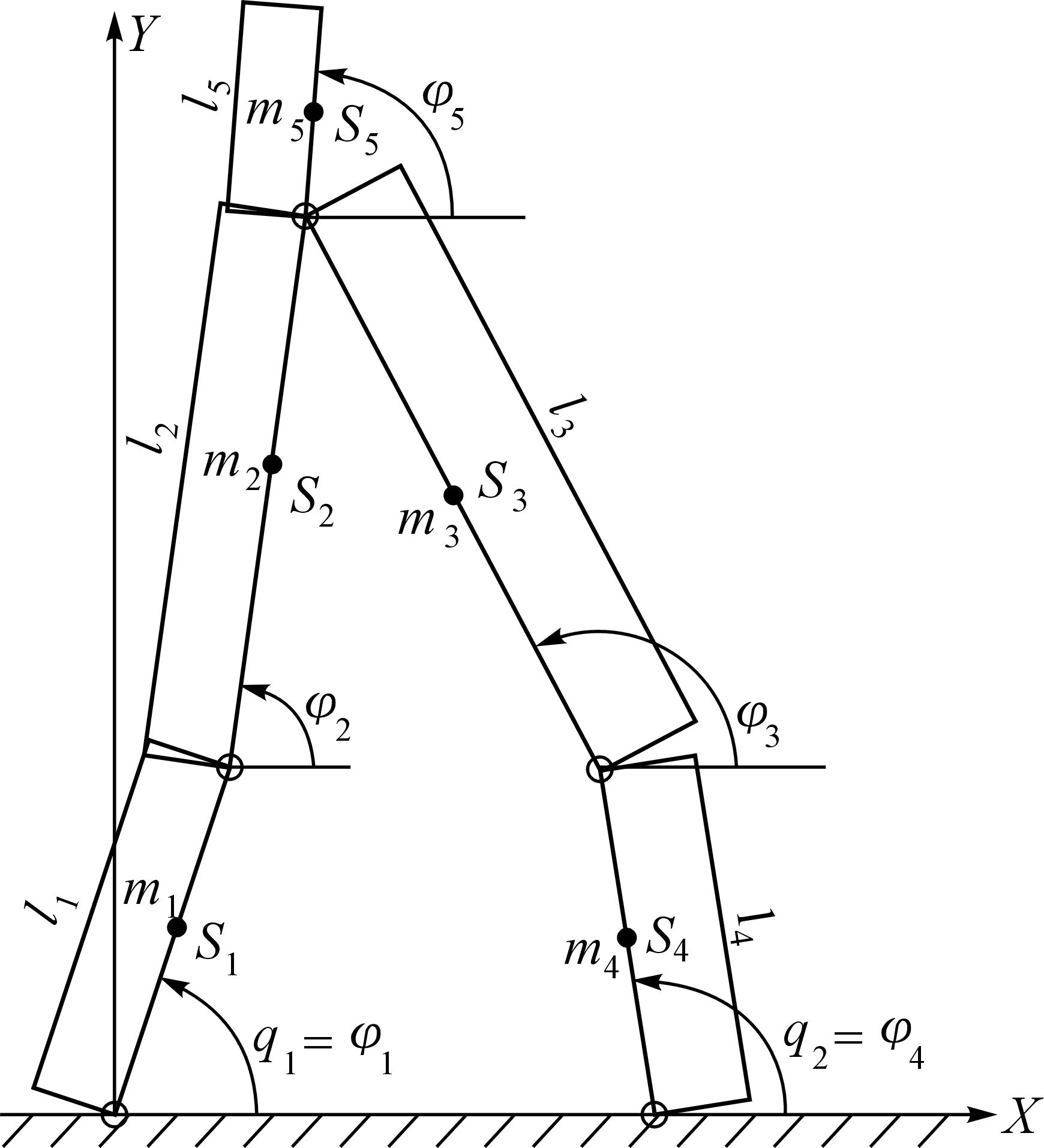
2.1 双腿支撑动力学分析

下肢外骨骼双腿支撑模型如图 2所示,此运动状态各构件分别对应于上肢、大腿、小腿，共五部分.图中li(i=1，2，…，5)表示各杆件的长度,Si表示各杆件的质心位置,φi表示各关节屈伸角度的大小,mi表示各杆件质量.在此将广义坐标建立在构件1，4上,q1=φ1,q2=φ4,则其他构件的运动可以表达为q1，q2的函数.

图 2 下肢外骨骼双腿支撑模型 Fig.2 Double support model of lower limb exoskeleton
图选项

设各构件质心Si的坐标为xi，yi,转角为φi,则有

$\left. \begin{align} & {{x}_{i}}={{x}_{i}}({{q}_{1}},{{q}_{2}}) \\ & {{y}_{i}}={{y}_{i}}({{q}_{1}},{{q}_{2}}) \\ & {{\varphi }_{i}}={{\varphi }_{i}}({{q}_{1}},{{q}_{2}}). \\ \end{align} \right\}$ (3)

相应的速度为

$\left. \begin{align} & {{{\dot{x}}}_{i}}=\frac{\partial {{x}_{i}}}{\partial x{{q}_{1}}}{{{\dot{q}}}_{1}}+\frac{\partial {{x}_{i}}}{\partial x{{q}_{2}}}{{{\dot{q}}}_{2}}=u_{xi}^{\left( 1 \right)}{{{\dot{q}}}_{1}}+u_{xi}^{\left( 2 \right)}{{{\dot{q}}}_{2}}, \\ & {{{\dot{y}}}_{i}}=\frac{\partial {{y}_{i}}}{\partial y{{q}_{1}}}{{{\dot{q}}}_{1}}+\frac{\partial {{y}_{i}}}{\partial y{{q}_{2}}}{{{\dot{q}}}_{2}}=u_{yi}^{\left( 1 \right)}{{{\dot{q}}}_{1}}+u_{yi}^{\left( 2 \right)}{{{\dot{q}}}_{2}}, \\ & {{{\dot{\varphi }}}_{i}}=\frac{\partial {{\varphi }_{i}}}{\partial \varphi {{q}_{1}}}{{{\dot{q}}}_{1}}+\frac{\partial {{\varphi }_{i}}}{\partial \varphi {{q}_{2}}}{{{\dot{q}}}_{2}}=u_{\varphi i}^{\left( 1 \right)}{{{\dot{q}}}_{1}}+u_{\varphi i}^{\left( 2 \right)}{{{\dot{q}}}_{2}}. \\ \end{align} \right\}$ (4)

式中uki(1)，uki(2) (i=1，2，…，5；k=x,y,φ)为第i个构件对广义坐标q1，q2的偏类速度,等于2=0,1=1 s-1和1=0,2=1 s-1时各构件相应点的速度和构件角速度,其值为

$\left. \begin{align} & {{u}^{(1)}}_{ki}={{{\dot{k}}}_{i}}\left| {{_{{{{\dot{q}}}_{2}}=0,}}_{{{{\dot{q}}}_{1}}=1,}} \right., \\ & {{u}^{(2)}}_{ki}={{{\dot{k}}}_{i}}\left| {{_{{{{\dot{q}}}_{1}}=0,}}_{{{{\dot{q}}}_{2}}=1,}} \right. \\ \end{align} \right\}$ (5)

则得到下肢外骨骼系统的动能为

$\begin{align} & {{E}_{K}}=\frac{1}{2}\sum\limits_{i}^{5}{\left[ {{m}_{i}}\left( \dot{x}_{i}^{2}+\dot{y}_{i}^{2} \right)+{{J}_{i}}\dot{\varphi }_{i}^{2} \right]}= \\ & \frac{1}{2}{{J}_{11}}^{2}{{{\dot{q}}}_{1}}+\frac{1}{2}{{J}_{22}}{{^{2}}_{2}}+{{J}_{12}}{{{\dot{q}}}_{1}}{{{\dot{q}}}_{2}}, \\ \end{align}$ (6)

式中J11，J22，J12为等效转动惯量,其值为

$\left. \begin{align} & {{J}_{11}}=\sum\limits_{i=1}^{5}{\left\{ {{m}_{i}}\left[ {{\left( {{u}^{(1)}}_{{{x}_{i}}} \right)}^{2}}+{{\left( {{u}^{(1)}}_{{{y}_{i}}} \right)}^{2}} \right] \right.}+\left. {{J}_{i}}{{\left( {{u}^{(1)}}_{\varphi i} \right)}^{2}} \right\}, \\ & {{J}_{22}}=\sum\limits_{i=1}^{5}{\left\{ {{m}_{i}}\left[ {{\left( {{u}^{(2)}}_{{{x}_{i}}} \right)}^{2}}+{{\left( {{u}^{(2)}}_{{{y}_{i}}} \right)}^{2}} \right] \right.}+\left. {{J}_{i}}{{\left( {{u}^{(2)}}_{\varphi i} \right)}^{2}} \right\}, \\ & {{J}_{12}}=\sum\limits_{i=1}^{5}{\left\{ {{m}_{i}}\left[ {{\left( {{u}^{(1)}}_{{{x}_{i}}} \right)}^{2}}+{{\left( {{u}^{(1)}}_{{{y}_{i}}} \right)}^{2}} \right] \right.}+\left. J{{u}^{(1)}}_{\varphi i}{{u}^{(2)}}_{\varphi i} \right\}. \\ \end{align} \right\}$ (7)

下肢外骨骼系统的势能为

$U=\sum\limits_{i=1}^{5}{{{m}_{i}}g{{y}_{i}}}$ (8)

式中：g=9.8 m/s2；yi为各构件质心高度,由式(3)知其为q1，q2的函数.

将上述得到的式(6)和式(8)代入式(2)中,得到动力学方程为

$\left. \begin{align} & {{J}_{11}}{{{\ddot{q}}}_{1}}+{{J}_{12}}{{{\ddot{q}}}_{2}}+\frac{1}{2}\frac{\partial {{J}_{11}}}{\partial {{q}_{1}}}\dot{q}_{1}^{2}+\left( \frac{\partial {{J}_{12}}}{\partial {{q}_{2}}}-\frac{1}{2}\frac{\partial {{J}_{22}}}{\partial {{q}_{1}}} \right)\dot{q}_{2}^{2}+\frac{\partial {{J}_{11}}}{\partial {{q}_{2}}}+\sum\limits_{i=1}^{5}{{{m}_{i}}gu_{yi}^{\left( 1 \right)}{{{\dot{q}}}_{1}}}={{Q}_{1}} \\ & {{J}_{12}}{{{\ddot{q}}}_{1}}+{{J}_{22}}{{{\ddot{q}}}_{2}}+\frac{1}{2}\frac{\partial {{J}_{22}}}{\partial {{q}_{2}}}\dot{q}_{2}^{2}+\left( \frac{\partial {{J}_{12}}}{\partial {{q}_{1}}}-\frac{1}{2}\frac{\partial {{J}_{11}}}{\partial {{q}_{2}}} \right)\dot{q}_{1}^{2}+\frac{\partial {{J}_{22}}}{\partial {{q}_{1}}}+\sum\limits_{i=1}^{5}{{{m}_{i}}gu_{yi}^{\left( 2 \right)}{{{\dot{q}}}_{2}}}={{Q}_{1}}. \\ \end{align} \right\}$ (9)

上式中广义力Qi可表示为

$\left. \begin{align} & {{Q}_{1}}=\sum\limits_{i=1}^{4}{\left( {{F}_{ix}}{{u}^{(1)}}_{xi}+{{F}_{iy}}{{u}^{(1)}}_{yi} \right)}+\sum\limits_{i=1}^{4}{{{M}_{i}}{{u}^{(1)}}_{\varphi i}} \\ & {{Q}_{2}}=\sum\limits_{i=1}^{4}{\left( {{F}_{ix}}{{u}^{(2)}}_{xi}+{{F}_{iy}}{{u}^{(2)}}_{yi} \right)}+\sum\limits_{i=1}^{4}{{{M}_{i}}{{u}^{(2)}}_{\varphi i}} \\ \end{align} \right\}$ (10)

其中：Fix，Fiy为关节受到的重力在x，y方向上的分力；Mi为关节受到的驱动力矩.

本设计中研究髋关节和膝关节加载力矩进行辅助行走,因此只取4个力与力矩进行分析.上述得到的动力学方程中,将已知的参数代入,可由式(3)开始逐步解出关节速度、力矩等参数,因篇幅限制不一一列出.

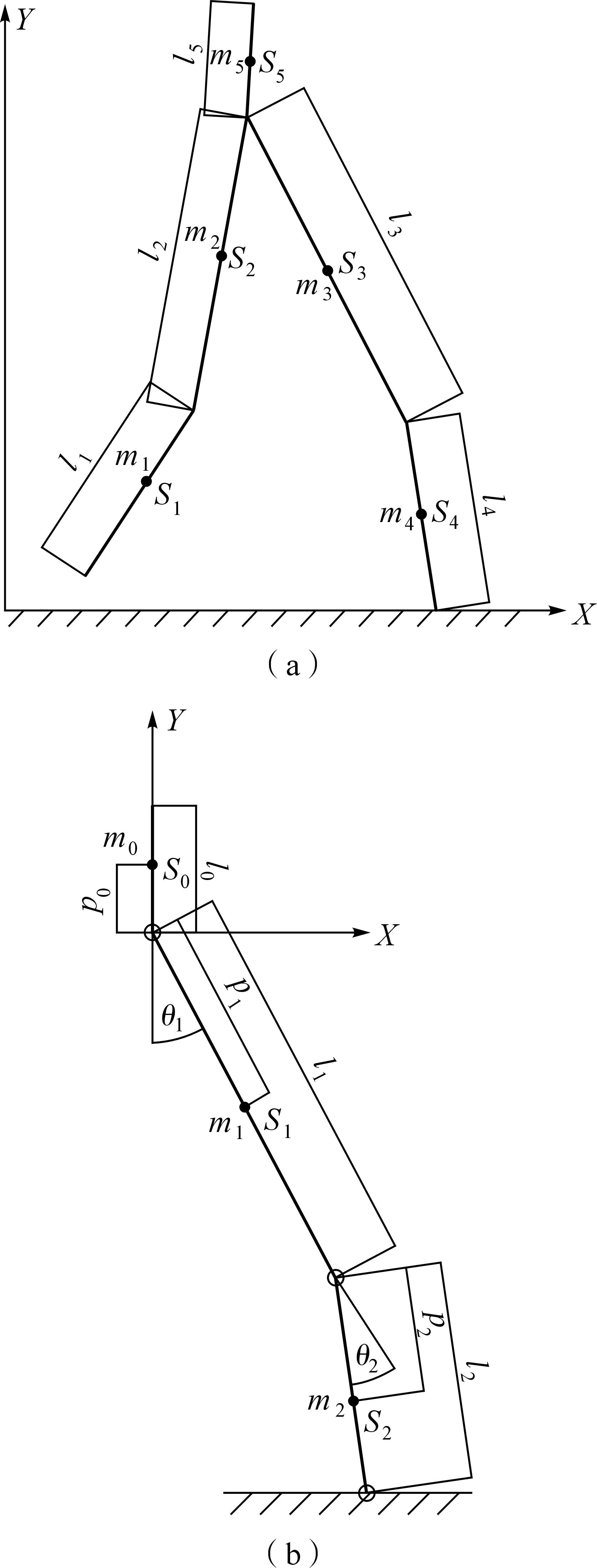
2.2 单腿支撑动力学分析

下肢外骨骼行走周期中单腿支撑时期,可建立相应模型,如图 3(a)所示.单腿支撑期间,人体大部分重量集中于支撑腿,支撑腿电机负载最大,因此可以对模型进行简化,建立模型如图 3(b)所示.图中关节变量θi(i=1,2)为构件的转角,pi (i=1,2)为质心到关节中心的距离,其余参数同2.1节.

图 3 下肢外骨骼单腿支撑模型 Fig.3 Single support model of lower limb exoskeleton
图选项

设各构件质心Si的坐标为xi，yi,则：

$\left. \begin{align} & {{x}_{1}}={{p}_{1}}sin~{{\theta }_{1}} \\ & {{y}_{1}}=-{{p}_{1}}cos~{{\theta }_{1}}. \\ \end{align} \right\}$ (11)
$\left. \begin{align} & {{x}_{2}}=-{{l}_{1}}sin~{{\theta }_{1}}-{{p}_{2}}\sin {{\theta }_{1}}-{{\theta }_{2}}, \\ & {{y}_{2}}=-{{l}_{1}}cos~{{\theta }_{1}}-{{p}_{2}}cos{{\theta }_{1}}-{{\theta }_{2}}. \\ \end{align} \right\}$ (12)

杆1，2质心速度平方为：

${{{\dot{x}}}^{2}}_{1}+{{{\dot{y}}}^{2}}_{1}={{\left( {{p}_{1}}{{{\dot{\theta }}}_{1}} \right)}^{2}},$ (13)
${{{\dot{x}}}^{2}}_{1}+{{{\dot{y}}}^{2}}_{1}={{{\dot{l}}}^{2}}{{_{1}}_{1}}\dot{\theta }_{1}^{2}+p_{2}^{2}-\left( {{{\dot{\theta }}}_{1}}-{{{\dot{\theta }}}_{2}} \right)+2{{l}_{1}}{{p}_{2}}\left( \dot{\theta }_{1}^{2}-{{{\dot{\theta }}}_{1}}{{{\dot{\theta }}}_{2}} \right)\cos {{\theta }_{2}}.$ (14)

可以得到下肢外骨骼系统的动能为

$\begin{align} & {{E}_{K}}=\sum\limits_{i=1}^{2}{{{E}_{i}}}=\frac{1}{2}{{m}_{1}}{{p}^{2}}_{1}\dot{\theta }_{1}^{2}+\frac{1}{2}{{m}_{2}}{{l}^{2}}_{1}\dot{\theta }_{1}^{2}+\text{ }\frac{1}{2}{{m}_{2}}{{p}^{2}}_{2}{{\left( {{{\dot{\theta }}}_{1}}-{{{\dot{\theta }}}_{2}} \right)}^{2}} \\ & +{{m}_{2}}{{l}_{1}}{{p}_{2}}\left( \dot{\theta }_{1}^{2}-\dot{\theta }_{1}^{2} \right)cos~{{\theta }_{2}}. \\ \end{align}$ (15)

下肢外骨骼系统的势能为

$\begin{align} & U=\sum\limits_{i=1}^{3}{=}{{U}_{i}}={{m}_{0}}g{{p}_{0}}+{{m}_{1}}g{{p}_{1}}\left( 1-cos~{{\theta }_{1}} \right)+{{m}_{2}}g{{l}_{1}}\left( 1-cos~{{\theta }_{1}} \right)+ \\ & {{m}_{2}}g{{p}_{2}}\left[ 1-cos{{\theta }_{1}}-{{\theta }_{2}} \right] \\ \end{align}$ (16)

式中g=9.8 m/s2.将式(15)和式(16)代入动力学方程(2),可得到关节1，2的转矩如下：

${{T}_{1}}={{D}_{11}}{{{\ddot{\theta }}}_{1}}+{{D}_{12}}{{{\ddot{\theta }}}_{2}}+{{D}_{112}}{{{\dot{\theta }}}_{1}}{{{\dot{\theta }}}_{2}}+{{D}_{122}}\dot{\theta }_{2}^{2}+{{D}_{1}},$ (17)
${{T}_{2}}={{D}_{21}}{{{\ddot{\theta }}}_{1}}+{{D}_{22}}{{{\ddot{\theta }}}_{2}}+{{D}_{212}}{{{\dot{\theta }}}_{1}}{{{\dot{\theta }}}_{2}}+{{D}_{222}}\dot{\theta }_{1}^{2}+{{D}_{2}}.$ (18)

对上式中参数分析可知,$\ddot \theta $1或$\ddot \theta $2是由加速度引起的关节力矩项,$\dot \theta $12或 $\dot \theta $22是由向心力引起的关节力矩项,$\dot \theta $1$\dot \theta $2是由科氏力引起的关节力矩项,只含有θ1或θ2的为重力引起的关节力矩项.

可以看出此动力学方程较为复杂,包含很多因素,这些因素都影响外骨骼的动力学特性.因下肢外骨骼系统关节速度不大,不是高速机构,故分析仿真时可以省略含有$\dot \theta $12，$\dot \theta $22及$\dot \theta $1$\dot \theta $2的项.

3 下肢外骨骼仿真

利用基于接口的协同仿真技术并结合ADAMS和MATLAB软件对外骨骼进行联合仿真.

按照前文设计要求,在三维CAD建模软件SOLIDWORKS中构建简化的下肢外骨骼模型,将建好的模型保存为 Parasolid(*.x_t)格式的文件,直接导入 ADAMS中.在 ADAMS 中对下肢外骨骼进行设定并仿真[17-18]：为满足虚拟样机质量要求,可以选择“Define Mass By User Input”,即直接设定构件的质量；按照行走的运动方式设定各关节的约束；把行走支撑面与大地固连；修改下肢助力外骨骼脚底与支撑地面间的硬度、渗透度及粗糙度.

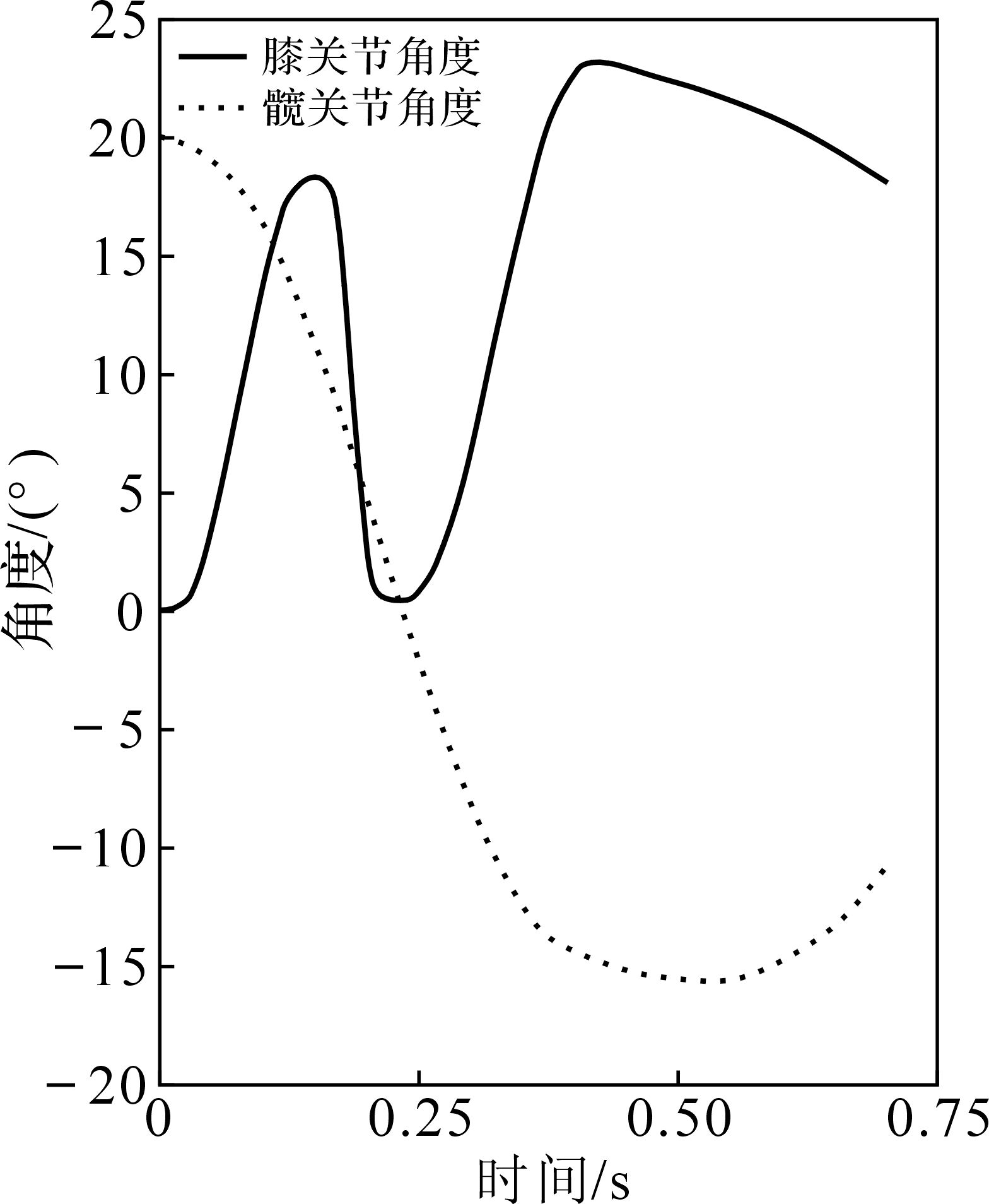
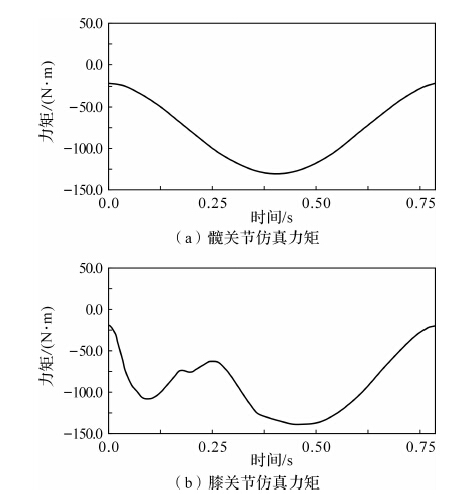
对下肢外骨骼模型进行仿真分析.由于本设计应用于康复辅助行走,主要研究关节的最大转矩用于结构设计,所以仅对单腿支撑时期进行分析,得到一个运动周期中髋关节与膝关节的角度变化曲线和运动力矩曲线,如图 4、图 5所示.图 4中的角度与图 3(b)中θ1，θ2相对应.将关节角度变化数据导出为.txt格式,导入MATLAB进行理论计算,并输入质量长度等参数,具体见表 1,得到下肢外骨骼运动力矩变化的理论计算值如图 6所示.具体数值可以参见表 2.

图 4 髋关节和膝关节角度变化曲线 Fig.4 Hip and knee joint angle change curves
图选项
图 5 ADAMS仿真力矩 Fig.5 ADAMS simulation torque
图选项
表 1 下肢外骨骼系统理论计算各参数值 Table 1 The theoretical calculation parameters of lower limb exoskeleton
参数m1p1l1m2p2l2
量值55.26 kg0.30 m0.52 m23.4 kg0.20 m 0.44m
表选项
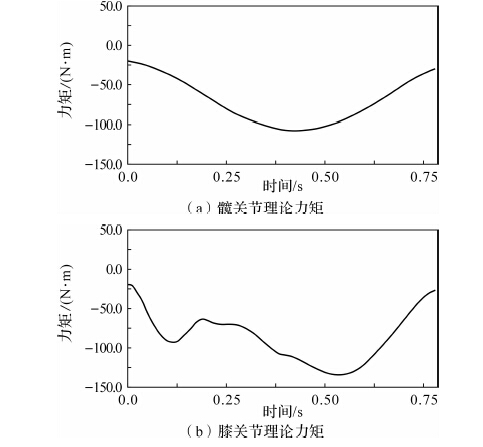
图 6 MATLAB计算力矩 Fig.6 MATLAB computed torque
图选项
表 2 髋关节与膝关节力矩值 Table 2 The hip joint and knee joint torque values
时间/ s00.10.250.50.75
髋关节仿真力矩/(N·m)23-52-107-113-32
髋关节理论力矩/(N·m)24-46-76-92-30
膝关节仿真力矩/(N·m)22-110-61-133-27
膝关节理论力矩/(N·m)23-96-74-120-29
表选项

分析表 2可知,2种结果中的力矩变化存在一定误差,理论结果数据偏小,且理论曲线较为平缓,但俩方法力矩变化总体相差不大,在可接受范围之内,同时也说明理论模型分析的正确性.仿真分析与理论计算存在误差的主要原因是：外骨骼虚拟样机设计及参数设定过程中存在误差,理论计算中模型结构处理及公式简化与实际运动情况存在误差.

4 总 结

设计了一款医疗助力下肢外骨骼,完成了外骨骼的基本结构设计,其中可调节机构的设计简单方便,适合于不同高度人群.针对行走的不同时期,主要分为单腿与双腿支撑两种模型,通过理论计算对下肢外骨骼进行了动力学分析.根据实际应用环境,对单腿支撑时期进行仿真,利用基于接口的协同仿真技术并结合ADAMS和MATLAB软件对外骨骼进行联合仿真,得到髋关节及膝关节角度变化数据和俩关节力矩变化数据,仿真结果与理论计算结果基本一致.研究结果可以为实际模型设计及其他后续工作提供理论基础和数据依据.

参考文献
[1] 杨巍, 张秀峰, 杨灿军, 等. 基于人机5杆模型的下肢外骨骼系统设计[J]. 浙江大学学报(工学版) , 2014, 48 (3) : 430–435. YANG Wei, ZHANG Xiu-feng, YANG Can-jun, et al. The design of lower extremity exoskeleton man-machine system based on 5 bar model[J]. Journal of Zhejiang University (Engineering Science) , 2014, 48 (3) : 430–435.
[2] ZHAO Yan-jun, ZHANG Yan-qing, GE Wen-qing, et al. Finite element Simulation of Soldier Lower Extremity[J]. Journal of Multimedia , 2013, 8 (6) : 705–711.
[3] YANG Can-jun,NIU Bin,CHEN Ying.Adaptive neuro-fuzzy control based development of a wearable exoskeleton leg for human walking power augmentation[C]//Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Monterey,California,USA,July 24-28,2005:24-28.
[4] 曹电锋, 杨启志, 庄佳奇, 等. 一种六自由度上肢康复机器人的结构设计及运动学分析[J]. 工程设计学报 , 2013, 20 (4) : 338–343. CAO Dian-feng, YANG Qi-zhi, ZHUANG Jia-qi, et al. Structure design and analysis of kinematics of a 6-DOF upper-limbed rehabilitation robot[J]. Chinese Journal of Engineering Design , 2013, 20 (4) : 338–343.
[5] 杨启志, 曹电锋, 赵金海. 上肢康复机器人研究现状的分析[J]. 机器人 , 2013, 35 (5) : 630–640. DOI:10.3724/SP.J.1218.2013.00630 YANG Qi-zhi, CAO Dian-feng, ZHAO Jin-hai. Analysis on state of the art of upper limb rehabilitation robots[J]. Robot , 2013, 35 (5) : 630–640. DOI:10.3724/SP.J.1218.2013.00630
[6] ANDREW CHU,H KAZEROONI,ADAM ZOSS.On the mechanical design of the Berkeley Lower Extremity Exoskeleton (BLEEX)[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Edmonton, Canada, August 2-6, 2005: 3132-3139.
[7] 王伟. 可穿戴机器人的研究现状和面临的挑战[J]. 机器人技术与应用 , 2013 (4) : 12–16. WANG Wei. Study status and challenges of wearable robot[J]. Robot Technique and Application , 2013 (4) : 12–16.
[8] 陈鹍, 刘启栋, 王人成, 等. 一种减重步行训练机器人的研制[J]. 中国康复医学杂志 , 2011 (9) : 847–851. CHEN Kun, LIU Qi-dong, WANG Ren-cheng, et al. The development of a gait training robot[J]. Chinese Journal of Rehabilitation Medicine , 2011 (9) : 847–851.
[9] 隋立明, 张立勋. 气动肌肉驱动步态康复训练外骨骼装置的研究[J]. 哈尔滨工程大学学报 , 2011, 32 (9) : 1244–1248. SUI Li-ming, ZHANG Li-xun. Development of an actuated exoskeleton with pneumatic muscles for gait rehabilitation training[J]. Journal of Harbin Engineering University , 2011, 32 (9) : 1244–1248.
[10] 孙健, 余勇, 葛运健, 等. 可穿戴下肢助力机器人感知系统研究[J]. 微纳电子技术 , 2007 (7) : 353–357. SUN Jian, YU Yong, GE Yun-jian, et al. Research on sensing systems of wearable power assist leg[J]. Micronano Electronic Technology , 2007 (7) : 353–357.
[11] 沈凌, 孟青云, 喻洪流. 基于虚拟样机技术的下肢假肢结构设计与仿真[J]. 工程设计学报 , 2011, 18 (1) : 34–37. SHEN Ling, MENG Qing-yun, YU Hong-liu. Design and simulation of leg prosthesis structure based on virtual prototype technology[J]. Chinese Journal of Engineering Design , 2011, 18 (1) : 34–37.
[12] 刘娟秀, 吴益飞, 郭健, 等. 一种平地楼梯两用助行机器人的建模与仿真分析[J]. 工程设计学报 , 2015, 22 (4) : 344–350. LIU Juan-xiu, WU Yi-fei, GUO Jian, et al. Modeling and simulation analysis of a walking assistant robot for both plane and stair[J]. Chinese Journal of Engineering Design , 2015, 22 (4) : 344–350.
[13] 刘方圆, 吕传毅, 贺磊. 模块化护理床的下肢机构设计与运动分析[J]. 工程设计学报 , 2014, 22,21 (16) : 583–588. LIU Fang-yuan, LÜ Chuan-yi, HE Lei. Design and motion analysis of nursing bed lower limbs mechanism based on modularity[J]. Chinese Journal of Engineering Design , 2014, 22,21 (16) : 583–588.
[14] 刘极峰, 丁继斌. 机器人技术基础[M]. 北京: 高等教育出版社 ,2006 : 68 -99. LIU Ji-feng, DING Ji-bin. Fundamentals of robot techniques[M]. Beijing: Higher Education Press , 2006 : 68 -99.
[15] 唐志勇, 谭振中, 裴忠才. 下肢外骨骼机器人动力学分析与设计[J]. 系统仿真学报 , 2013, 25 (6) : 1338–1344. TANG Zhi-yong, TAN Zhen-zhong, PEI Zhong-cai. Analysis and design of lower extremity exoskeleton robot dynamics[J]. Journal of System Simulation , 2013, 25 (6) : 1338–1344.
[16] 王健美, 付成龙, 黄元林, 等. 基于Matlab的双足机器人动力学仿真及仿生控制平台[J]. 系统仿真学报 , 2011, 23 (5) : 977–983. WANG Jian-mei, FU Cheng-long, HUANG Yuan-lin, et al. Dynamics simulation and bionic control platform for biped robot with Matlab[J]. Journal of System Simulation , 2011, 23 (5) : 977–983.
[17] 惠记庄, 魏芳胜, 高凯, 等. 基于ADAMS的冗余驱动并联机器人动力学仿真研究[J]. 工程设计学报 , 2012, 19 (5) : 362–365. HUI Ji-zhuang, WEI Fang-sheng, GAO Kai, et al. Study on dynamics simulation of redundantly actuated parallel robot based on ADAMS[J]. Chinese Journal of Engineering Design , 2012, 19 (5) : 362–365.
[18] 李增刚. ADAMS入门详解与实例[M]. 北京: 国防工业出版社 ,2010 : 59 -154. LI Zeng-gang. ADAMS introduction explain in detail and example[M]. Beijing: National Defense Industry Press , 2010 : 59 -154.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.005
教育部主管，浙江大学和中国机械工程学会主办
0

文章信息

刘小龙, 赵彦峻, 葛文庆, 王滢, 张忠东
LIU Xiao-long, ZHAO Yan-jun, GE Wen-qing, WANG Ying, ZHANG Zhong-dong
医疗助力下肢外骨骼设计及动力学仿真分析
Design and dynamics simulation analysis of medical disabled lower limb exoskeleton
工程设计学报, 2016, 23(4): 327-332.
Chinese Journal of Engineering Design, 2016, 23(4): 327-332.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.005

文章历史

收稿日期: 2015-10-13

相关文章

工作空间