Download PDF  
文章快速检索  
  高级检索
引用本文
金闪闪,邹航,郭桦. 绳锯线弓角静态测量方法的研究[J]. 工程设计学报, 2016, 23(4): 309-315.
JIN Shan-shan, ZOU Hang, GUO Hua. Research on static measuring method of wire saw deflection angle[J]. Chinese Journal of Engineering Design, 2016, 23(4): 309-315.
绳锯线弓角静态测量方法的研究
金闪闪1,2,邹航1,2,郭桦1,2     
1. 华侨大学 脆性材料加工技术教育部工程研究中心, 福建 厦门 361021;
2. 华侨大学 制造工程研究院, 福建 厦门 361021
收稿日期: 2016-04-08 .
作者简介: 金闪闪(1991—),女,河南商丘人,硕士生,从事高效精密加工研究,E-mail:1400203013@hqu.edu.cn. a href="http://orcid.org//0000-0003-2618-8972">http://orcid.org//0000-0003-2618-8972
通讯作者: 郭桦(1956—),男,湖南常德人,教授,硕士生导师,博士,从事超硬材料及相关设备的研究,E-mail:guoh1214@hqu.edu.cn
摘要: 金刚石绳锯在切割圆弧板材时，受到进给方向的阻力，形成“线弓角”，使板材中部产生“过切”，严重时导致材料报废.为解决这一问题，提出了线弓角的概念，从理论上提出了一种基于悬臂式力传感器的绳锯线弓角的静态测量方法，通过轴力传感器输出的电压值计算出线弓角度.试验在自行设计和搭建的绳锯线弓角测量平台上进行，用钢丝绳模拟串珠绳产生线弓角，并进行导轮受力与线弓角关系的静态测量试验分析，以验证该方法测量线弓角的可行性.试验结果表明：在一定范围内，串珠绳初始张紧力越大，线弓角的计算值越接近理论值.因此，采用所提出的测量方法，当装有轴力传感器的导轮处在刚好与钢丝绳接触的状态下，选择合适的初始张紧力，可以测得较准确的角度值.
关键词: 绳锯     轴力传感器     线弓角    

基金项目: 国家自然科学基金资助项目（51175193）；国家科技支撑计划资助项目（2012BAF13B04）；华侨大学研究生科研创新能力培育计划资助项目（1400203013）
Research on static measuring method of wire saw deflection angle
JIN Shan-shan1,2, ZOU Hang1,2, GUO Hua1,2     
1. Engineering Research Center for Machining of Brittle Materials of Ministry of Education, Huaqiao University, Xiamen 361021, China ;
2. Institute of Manufacturing Engineering, Huaqiao University, Xiamen 361021, China
Abstract: When diamond wire saw cuts circular arc, wire saw deflection angle will be formed due to resistance in the feed direction. If the bending is serious enough, the center of the circular plate will be cut excessively and leads to material scrap. In order to solve the problem, wire saw deflection angle is defined. The static measuring methodology of wire saw deflection angle was proposed. This methodology was based on cantilever type axis force sensor. Through the axis force sensor, voltage values were output and recorded to calculate wire saw deflection angle. Static measuring experiments were carried out in the physical equipment designed and built by authors. In the experiments, the steel rope was used to simulate diamond wire saw and created wire saw deflection angle. The static measuring experiments were carried out to study the relationship between the force of guide wheel and wire saw deflection angle. It was found that, the measured angle was close to the theoretical angle with the increase of initial tension within certain range. Therefore, when the edge of guide wheel whose axis assembles the force sensor is just contacted with steel cable, the wire saw deflection angle can be measured relative accurately by this method.
Key words: wire saw     axis force sensor     wire saw deflection angle    

金刚石绳锯加工技术具有资源利用率高、环境影响小、锯切效率高、荒料质量好、施工简单、人工成本低及适用石材范围广等一系列优点，因此能实现各种异形面加工、大型土建拆迁、管道施工等工程领域的高效切割以及适用于如海底构件的维修、核电厂的拆除等特殊领域的工作，可支撑石材矿山的可持续开采，推进石材制品更加规模化、艺术化[1-6].

许多学者对金刚石串珠绳及绳锯切割过程作了大量研究.刘宝昌等[7]从理论上分析了金刚石绳锯的锯切轨迹及锯切机理，得出金刚石绳锯的锯切轨迹近似为圆的渐开线，但没有提出线弓角的概念.张进生等[8]结合金刚石串珠锯在石岛红花岗石高效回采中的应用试验研究，讨论了串珠锯的磨损形式和锯切线速度、串珠绳预紧力等工作参数之间的关系，忽略了串珠绳线弓角对石材切割的影响.章兼植[9]探讨了绳锯在锯切时的受力情况及锯切轨迹，并着重分析了承载钢丝绳的应力组成，及钢丝绳作业时的曲率对寿命的影响，但没有测量钢丝绳作业时的受力值.黄国钦等[10]建立了串珠绳锯切弧区内单颗磨粒平均切削深度与锯切参数之间的理论关系，在此基础上采用单因素法和正交法进行锯切参数对锯切力和锯切功率的影响试验研究.王飞等[6]分析了串珠的磨(破)损、锯切力与加工参数的关系，认为单载荷作用时串珠磨损取决于金刚石出刃、串珠组分与锯切参数；锯切力随着进给速度与锯切长度增大而增大，随着串珠绳线速度增加而降低.Turchetta[11]提出了金刚石磨粒在不同磨损条件下的切削力模型.王海波等[12]强调了金刚石串珠绳的张紧力对绳锯机的切割效率和使用寿命具有非常直接的影响.以上研究中，研究者主要针对金刚石串珠绳锯的锯切参数等进行研究，很少关注串珠绳在切割石材过程中产生的线弓角.Liedke等[13]描述了金刚石线锯在切割硅片时形成的线弓的形状.Teomete[14]采用柯达DX 7630 6.1像素的数码相机对金刚石线锯在切割硅片时产生的线弓角进行拍摄，然后测量线弓角，其虽然可以作为串珠绳线弓角测量方法的参考，但这种方法还未用于串珠绳线弓角的测量.闫先华[15]阐述了异型绳锯机加工误差产生的主要原因是金刚石绳锯在切割过程中出现的挠度，也提出当金刚石绳锯两端的进给运动由垂直(水平)转变为水平(垂直)时停止进给，进行延时切割或完成延时切割后沿进给轨迹反方向回退以减少挠度，但是没有对这种挠度进行准确描述，也没有提出挠度所对应转角的测量方法.Turchetta等[16]研究了一种新型金刚石绳锯机，金刚石绳锯在加工石材时可以保持弯曲状态切割，且曲率会随着绳锯张紧力及切割力增加而增大，从而成倍地提高石材的去除率，这说明绳锯曲率会对石材的切割产生一定影响，但文中并未提出测量办法.实际上，在金刚石绳锯切割圆弧板材时，绳锯以一定的进给速度从板材的边缘切入，当绳锯越过圆弧板材中心线回走时，由于进给方向阻力的存在会使得绳锯发生弯曲变形，严重时会使圆弧板材在中心线处产生“过切”现象，导致材料报废.本文将绳锯在产生过切现象时的弯曲挠度定义为“线弓角”.

本文提供了一种绳锯线弓角的静态测量方法，用钢丝绳模拟串珠绳产生线弓角并对其进行测量试验，分析了钢丝绳初始张紧力的大小及装有传感器的导轮轴的高度对测量结果的影响.拟通过该方法测得准确线弓角，根据线弓角的大小调整进给速度，避免产生过切现象，进而保证绳锯加工的精度，对提高圆弧等异型板材加工质量具有重要意义.

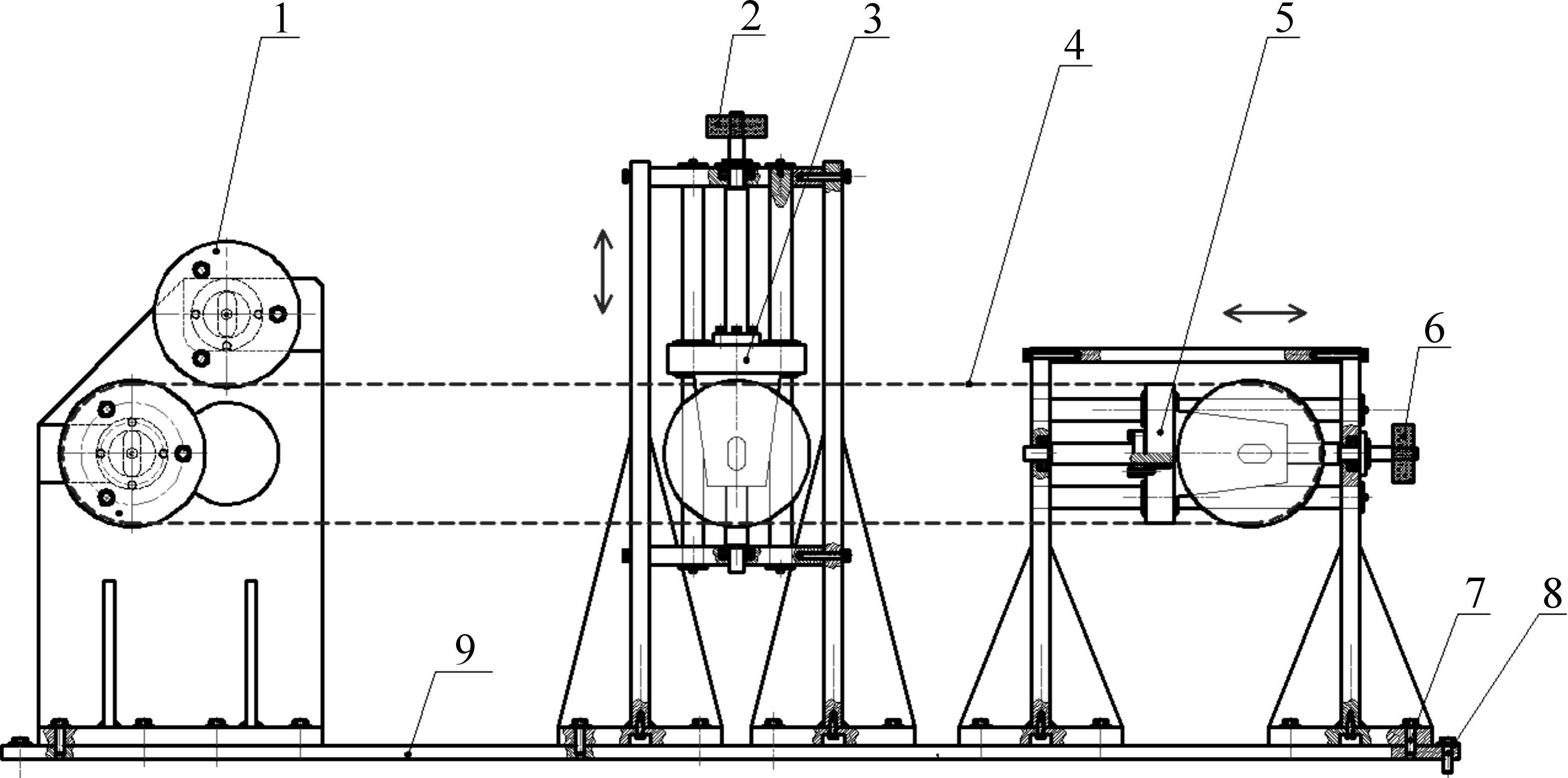
1 导轮受力与角度关系的理论分析

试验在自行设计和搭建的绳锯线弓角测量平台上进行.如图 1所示，左侧导轮、中间导轮、右侧张紧导轮在同一平面内；左导轮与右侧张紧导轮在同一高度.图中竖直进给装置3和水平张紧装置5均采用丝杠与光轴配合的直线运动装置，旋转手柄2可使装置3对串珠绳起到向上顶的作用，模拟串珠绳切割石材的过程；串珠绳受到导轮1的阻力形成线弓角，以此模拟绳锯线弓角的产生.水平张紧装置5用来对绳锯进行张紧.图中导轮1的轴上装有力传感器，用来测量串珠绳在形成线弓角之后串珠绳水平方向的力Fx和竖直方向的力Fy.图 2所示是线弓角测量平台.

1—导轮(轴上装有传感器)；2—竖直进给手轮；3—竖直进给装置；4—串珠绳；5—水平张紧装置；6—水平张紧手轮；7—螺栓；8—膨胀螺栓；9—底板. 图 1 线弓角测量装置示意图 Fig.1 Measure device schematic diagram of wire saw deflection angle
图选项
图 2 线弓角测量平台 Fig.2 he equipment of measuring wire saw deflection angle
图选项

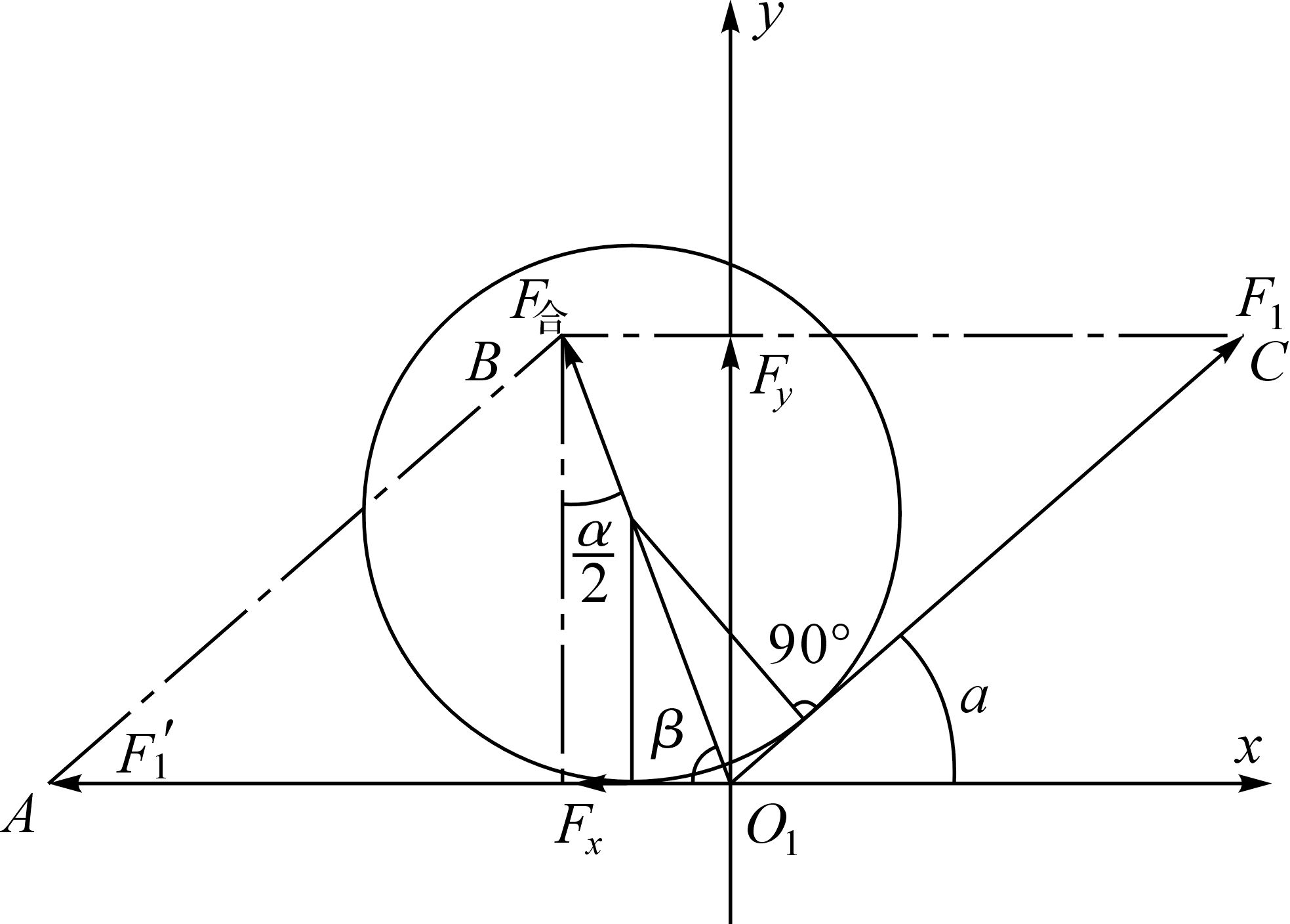
由于金刚石绳锯是具有一定弹性的连续体，在锯切过程中不会产生折点，为简化起见，把金刚石绳锯看作是一条连续的锯切线[7].故本试验选用钢丝绳代替串珠绳进行线弓角静态测量试验.导轮受力分析如图 3所示，F1为钢丝绳或串珠绳的张力且处处相等，根据实际绳锯机的工作情况，F1一端应为水平方向，另一端会随着角α(即线弓角)的改变而改变；F合为绳子对导轮的合力，指向圆心；Fx,Fy分别是F合在水平方向和竖直方向的分力.通过Fx，Fy求出绳子与水平方向的夹角α.具体推导过程如下：

图 3 导轮1受力分析图 Fig.3 The force analysis of guide wheel 1
图选项

因为F1=F′1，F合过圆心，所以AO1=CO1，ABCO1是菱形，根据几何知识可知：

$\beta =90{}^\circ -\frac{\alpha }{2}$ (1)
$cot~\beta =\frac{{{F}_{x}}}{{{F}_{y}}}$ (2)
$tan\frac{\alpha }{2}=\frac{{{F}_{x}}}{{{F}_{y}}}$ (3)
$\alpha =2arctan\frac{{{F}_{x}}}{{{F}_{y}}}.$ (4)

可以利用公式(4)，通过测得Fx，Fy求出串珠绳与水平方向的夹角α.

2 试验条件与方案 2.1 试验条件

试验设备：钢丝绳、自行设计和搭建的测量平台.

试验仪器：福禄克数字万用表F101/F101KIT、数显角度尺、数显式拉力计和直流开关电源NES-200-24 200W 24V LED(将220 V交流电转化为24 V直流电).

试验平台的测力系统组成如图 4所示.

图 4 试验平台测力系统组成 Fig.4 The composition of force measuring system of test platform
图选项

导轮的轴上安装悬臂式轴力传感器，材料为42CrMo，调质处理，保证硬度220~240 HBS.由于传感器在室温下使用，导轮旋转引起的温度变化不大，所以传感器温度补偿范围为20~70 ℃.本试验中所设计的轴力传感器量程为：水平方向为150 N，竖直方向为1 500 N；又根据多个传感器加工厂家提供的数据，将传感器综合精度设计为0.5%；传感器的采样频率设定为200 Hz.

传感器配接的信号放大器的参数如表 1，水平方向输出电压0～5 V代表 0～150 N的力，竖直方向输出电压0～5 V代表 0～1 500 N的力.

表 1 与传感器配接的信号放大器的参数 Table 1 The parameters of signal amplifier connected with sensor
放大器供电24 V DC
Fx=±150 N输出信号±5 V DC
Fy=±1 500 N输出信号±5 V DC
表选项

传感器受力大小与输出电压成线性关系，但实际上，传感器的最大量程与电压输出的最大值并不正好对应，即传感器存在标定系数.将实际加载力与传感器测量的力的比值定义为标定系数λ,则有:

${{F}_{x}}=({{U}_{x}}-{{U}_{x0}})\times 30\times {{\lambda }_{1}},$ (5)
${{F}_{y}}=({{U}_{y}}-{{U}_{y0}})\times 300\times {{\lambda }_{2}}.$ (6)

式中：λ1，λ2分别是传感器水平和竖直方向的标定系数；Ux0，Uy0分别是传感器在水平方向和竖直方向的初始电压；Ux，Uy分别是水平方向和竖直方向的最终输出电压.

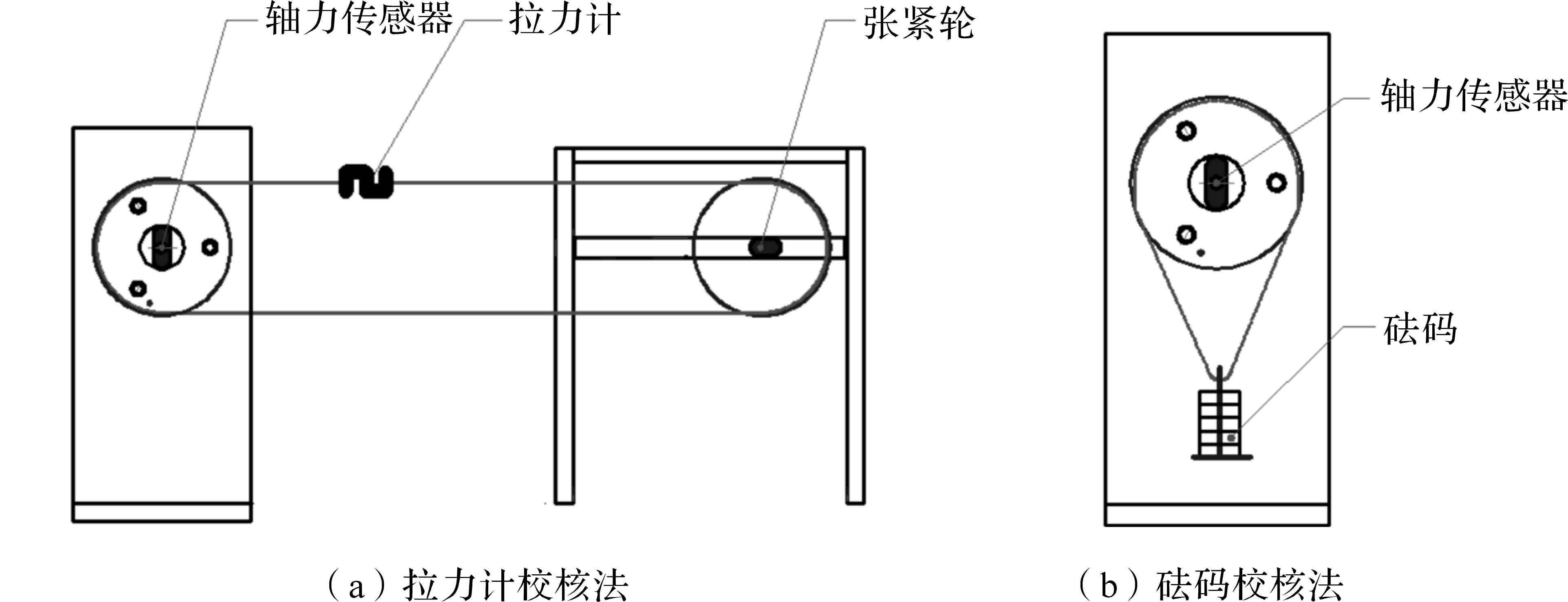
在本试验提供的测量平台上，采用2种方法对传感器进行校核.如图 5所示，(a)是在串珠绳上加装数显式拉力计，(b)是在导轮(导轮轴上装有力传感器)上直接加载砝码.(a)的具体实施方法是：转动水平张紧手轮以改变加载力大小，标定水平方向时，初始张紧力从0 N开始，记下轴力传感器初始电压值Ux0，每次加载20 N，记下每次拉力计示数Fx以及轴力传感器输出电压值Ux，根据公式(5)计算出水平方向标定系数λ1.标定竖直方向时，方法相同，每次加载200 N，利用公式(6)计算λ2；(b)的具体实施方法与(a)类似，通过加减砝码改变加载力大小，水平方向每次加载20 N，竖直方向每次加载200 N.通过多次标定得出：水平方向标定系数λ1在1.188～1.189之间；竖直方向标定系数在0.985～1.000之间.虽然标定系数不为1，但是用传感器测量的力与实际加载力之间具有很好的线性关系.通过调整信号放大器内部旋钮，将传感器初始值归零，可以使标定系数约等于1.后续试验中标定系数均按1计算.

图 5 传感器校核示意图 Fig.5 Configuration of sensor calibrating
图选项
2.2 试验方案

本试验选用钢丝绳代替串珠绳进行导轮受力与线弓角关系的静态测量试验.将钢丝绳安装于测量平台的左右导轮上，转动水平张紧手轮6，使钢丝绳达到预定的初始张紧力，分别记下初始位置时传感器水平和竖直方向输出电压Ux0，Uy0.再转动竖直进给手轮2，每次转动一定的圈数，使角度上升1°，记下各次传感器水平(x轴)方向输出电压Ux和竖直(y轴)方向的输出电Uy.因传感器输出的电压信号与受到的压力成线性关系，可利用式(5)，(6)和(4)计算出角度值α1.

另一方面，理论上升角度α2与丝杠总进给圈数n(n为转动竖直进给手轮的圈数)的关系为

$tan~{{\alpha }_{2}}=\frac{n\times p}{L},$ (7)

式中：p为丝杠螺距，p=6 mm；L为竖直进给手轮与导轮1的水平距离，L=700 mm.因此可得理论上升角度α2与丝杠总进给圈数n的关系，如表 2所示.

表 2 理论上升角度α2与圈数n的关系 Table 2 The relationship between theoretical angle α2 and number of turns n
α2/(°)1234567
n/圈2.04.16.18.210.212.314.3
α2/(°)891011121314
n/圈16.418.520.622.724.826.929.1
表选项

因此，可以通过改变n的大小来改变理论上升角度α2的大小.使用数显角度尺测量实际线弓角度α3，将其与理论角度α2比较，如表 3所示.

表 3 实际角度α3与理论角度α2对比 Table 3 The contrast of practical angle α3 and theoretical angle α2
α2/(°)α3/(°)
1.01.10.80.80.91.0
2.02.12.11.92.11.8
3.03.22.93.03.03.0
4.04.14.24.03.94.0
5.05.15.15.15.15.2
6.06.06.06.26.26.2
7.07.27.27.27.27.1
8.08.08.18.17.98.1
9.09.09.19.29.29.1
10.010.310.010.010.39.9
11.011.111.211.211.311.2
12.012.112.112.112.212.1
13.013.013.113.113.213.2
表选项

从表 3中可以看出，实际角度与理论角度基本吻合，所以试验中只对计算角度α1和理论角度α2的误差作分析，计算角度α1与实际角度α3的误差不再详细分析.记μ为计算角度α1和理论角度α2的误差，则有

$\mu =\frac{{{\alpha }_{1}}-{{\alpha }_{2}}}{{{\alpha }_{2}}}\times 100%.$ (8)

另外，由于传感器精度为0.5%，Fx的误差值为±0.75 N，实际上，在0～2°范围内，Fx的值小于0.5 N，小于其传感器本身测量精度，所以0～2°范围内的角度测量必定不准确.又根据实际绳锯加工过程中出现过切现象时线弓角一般不小于7°，所以不测量2°范围以内的角度不会影响整个试验.后续试验所测角度均从3°开始.

在钢丝绳上加装数显式拉力计以明确张紧力大小，手摇水平张紧丝杠的手轮对钢丝绳进行张紧.本文加装轴力传感器的导轮与钢丝绳刚好接触，手动旋转该导轮，钢丝绳基本保持不动，肉眼看不出导轮与钢丝绳间隙的位置定义为零点，记此时装有传感器的导轮轴(以下简称传感器轴)的位置为H=0 mm处.

为了验证本文提出的线弓角测量方法的可行性，并考虑到实际试验中出现的情况，针对不同的钢丝绳初始张紧力和传感器轴的高度，分别进行角度测量试验.试验方案如表 4.

表 4 试验方案 Table 4 The experiment scheme
影响因素量值
钢丝绳初始张紧力F800，1 000，1 200，1 400 N
传感器轴的高度H-4，0，4 mm
表选项
3 试验结果与分析 3.1 钢丝绳初始张紧力大小对角度测量的影响

将钢丝绳安装在测量平台上，保证导轮不倾斜，取传感器轴的高度H=-4，0，4 mm，进行3组试验，每组试验的初始张紧力F又分别为800，1 000，1 200，1 400 N，进行4次线弓角静态测量试验.α1是计算角度，α2是理论角度，μ为两者误差，测量结果如表 5所示.

表 5 H=-4 mm，初始张紧力F改变时的α1和μ Table 5 H=-4 mm，the α1 and μ when the initial tension F changes
α2/(°)F/N
8001 0001 2001 400
α1/(°)μ/%α1/(°)μ/%α1/(°)μ/%α1/(°)μ/%
3.02.89-3.82.63-12.32.85-5.03.217.1
4.03.89-2.63.66-8.53.88-3.04.358.7
5.04.31-13.74.59-8.15.295.75.285.6
6.05.02-16.35.47-8.96.172.96.172.8
7.05.59-20.16.46-7.77.192.77.040.6
8.06.51-18.67.39-7.68.303.78.162.0
9.07.80-13.38.42-6.49.404.49.030.4
10.08.72-12.89.29-7.110.484.810.121.2
11.09.89-10.110.33-6.111.575.211.565.1
12.011.06-7.811.42-4.812.473.912.242.0
13.012.18-6.312.57-3.313.362.713.342.6
表选项

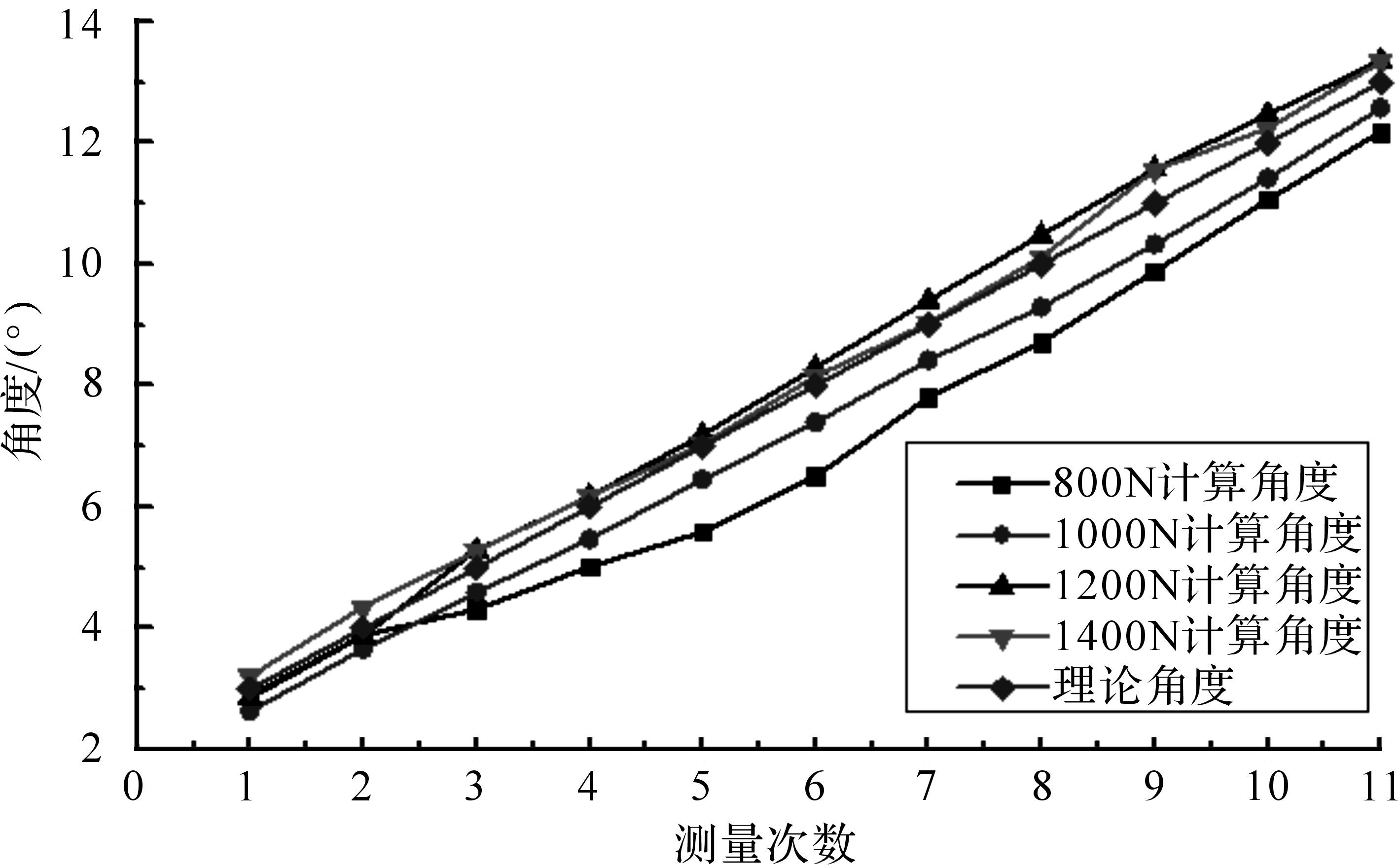
由表 5和图 6可知，当传感器轴在-4 mm的位置时，初始张紧力为800，1 000 N时，计算角度会比理论值小；初始张紧力为1 200，1 400 N时，计算角度基本上比理论角度略大；计算角度与理论角度的误差值随着张紧力的增大而减小.由图 6可以看出，随着初始张紧力的增加，计算角度会逐渐向理论角度靠近.

图 6 H=-4 mm，F改变时α1的变化规律 Fig.6 H=-4 mm，the change rule of α1 when F changes
图选项

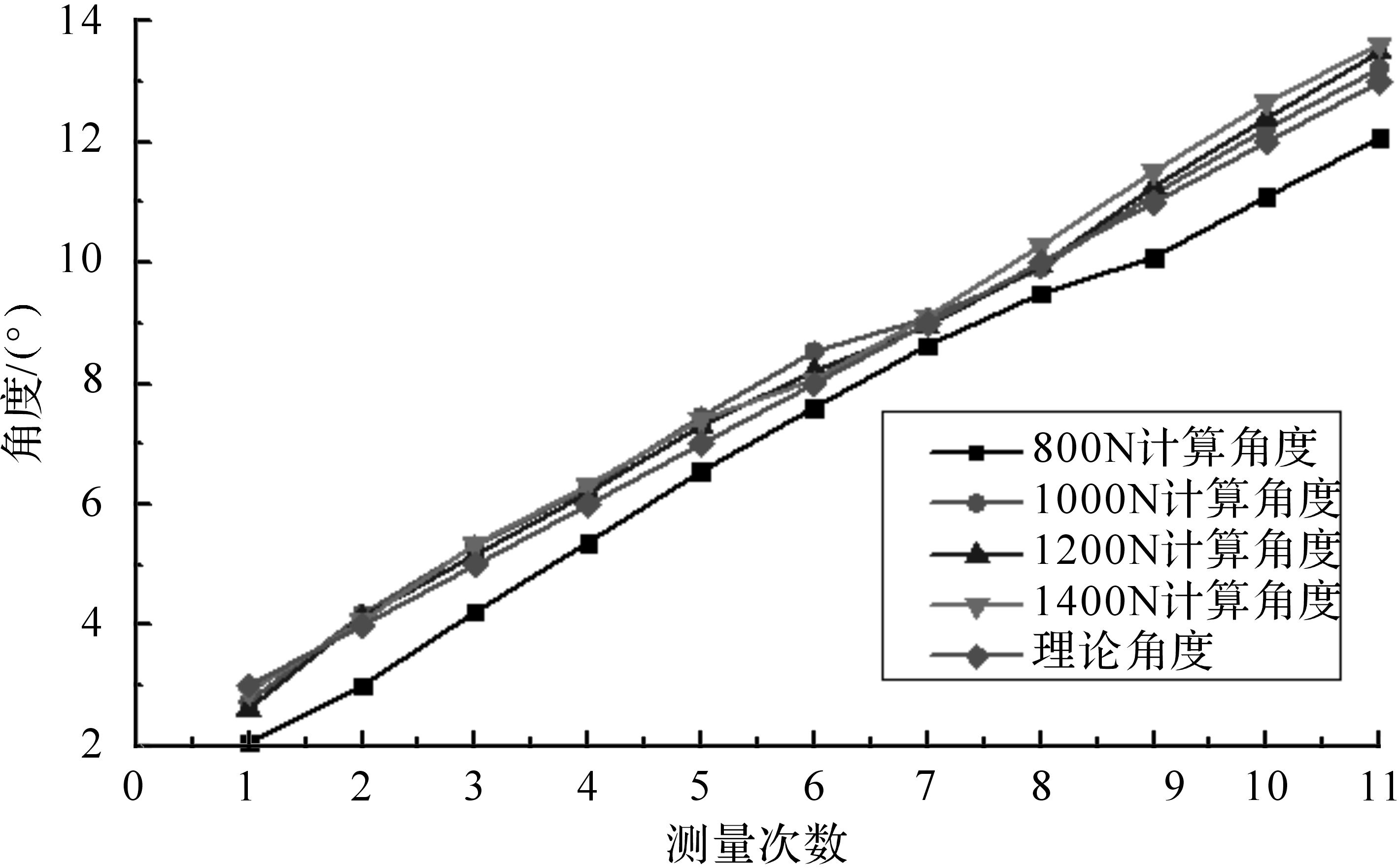
由表 6和图 7可知，当传感器轴在0 mm位置时，计算角度与理论角度比较接近：800 N时，计算角度会比理论值小；初始张紧力为1 000，1 200，1 400 N时，计算角度基本上比理论角度略大；计算角度与理论角度的误差值随着张紧力的增大而逐渐减小.由图 7可以看出，随着初始张紧力的增加，计算角度逐渐向理论角度靠近.初始张紧力为1 000 N及以上时，测量得到的计算角度相对准确.

表 6 H=0 mm，初始张紧力F改变时的α1和μ Table 6 H=0 mm，the α1 and μ when the initial tension F changes
α2/(°)F/N
8001 0001 2001 400
α1/(°)μ/%α1/(°)μ/%α1/(°)μ/%α1/(°)μ/%
3.02.07-31.02.73-8.82.62-12.62.90-3.2
4.03.00-25.04.184.44.133.34.071.8
5.04.22-15.65.326.55.173.35.346.9
6.05.37-10.56.274.46.193.16.325.3
7.06.55-6.57.466.67.314.57.415.8
8.07.61-4.98.536.78.212.78.070.9
9.08.63-4.19.091.08.96-0.49.111.2
10.09.49-5.19.90-1.09.95-0.510.292.9
11.010.09-8.311.141.211.262.511.524.7
12.011.09-7.612.221.912.393.312.654.6
13.012.07-7.213.221.713.493.813.624.7
表选项
图 7 高度H=0 mm，F改变时α1的变化规律 Fig.7 H=0 mm，the change rule of α1 when F changes
图选项

由表 7和图 8可知：当传感器轴在4 mm位置时，计算角度会比理论角度略大；初始张紧力为800 N时，计算角度与理论角度的误差值为13.6%～25.5%，初始张紧力为1 400 N时，误差值为0.1%～12.2%，所以，随着张紧力的增大，计算角度与理论角度的误差值逐渐减小，计算角度逐渐向理论角度靠近.

表 7 H=4 mm，初始张紧力F改变时的α1和μ Table 7 H=4 mm，the α1 and μ when the initial tension F changes
α2/(°)F/N
8001 0001 2001 400
α1/(°)μ/%α1/(°)μ/%α1/(°)μ/%α1/(°)μ/%
3.03.0718.33.268.83.093.13.000.1
4.04.9222.94.7418.64.399.84.041.1
5.06.1022.05.7214.55.6212.35.5811.5
6.07.5325.256.8213.76.6010.06.7312.2
7.08.5021.48.0014.37.639.07.8512.2
8.09.5219.09.0913.68.669.58.699.6
9.010.5016.710.1813.19.869.59.869.6
10.011.3613.611.1211.211.1311.310.939.3
11.012.5013.612.2010.912.1510.412.059.5
12.013.5412.813.2410.313.2110.113.119.3
13.014.6412.614.269.714.199.214.199.2
表选项
图 8 H=4 mm，F改变时α1的变化规律 Fig.8 H=4 mm，the change rule of α1 when F changes
图选项

根据上述试验结果可知，通过测量电压值计算得出的角度会随着初始张紧力的增加更加接近理论值.一方面，当初始张紧力较小时，轴力传感器测量出的力也较小，甚至低于传感器精度而引起误差产生，这就导致测量角度不准确；另一方面是由钢丝绳本身的性质决定的，钢丝绳是一种柔性的空间螺旋结构钢制品，具有柔软性、阻尼吸收和强度高的特点[17].钢丝绳随着拉力的增加，弹性模量先是增加，当拉力增加到一定值时，弹性模量值不增反降[18].因此，当初始张紧力较小时，钢丝绳的长度变化不与所受载荷成线性关系，这会导致计算角度与理论角度有一定偏差.在一定范围内，初始张紧力增大，线性关系越好，测量计算出的角度就更接近理论值.

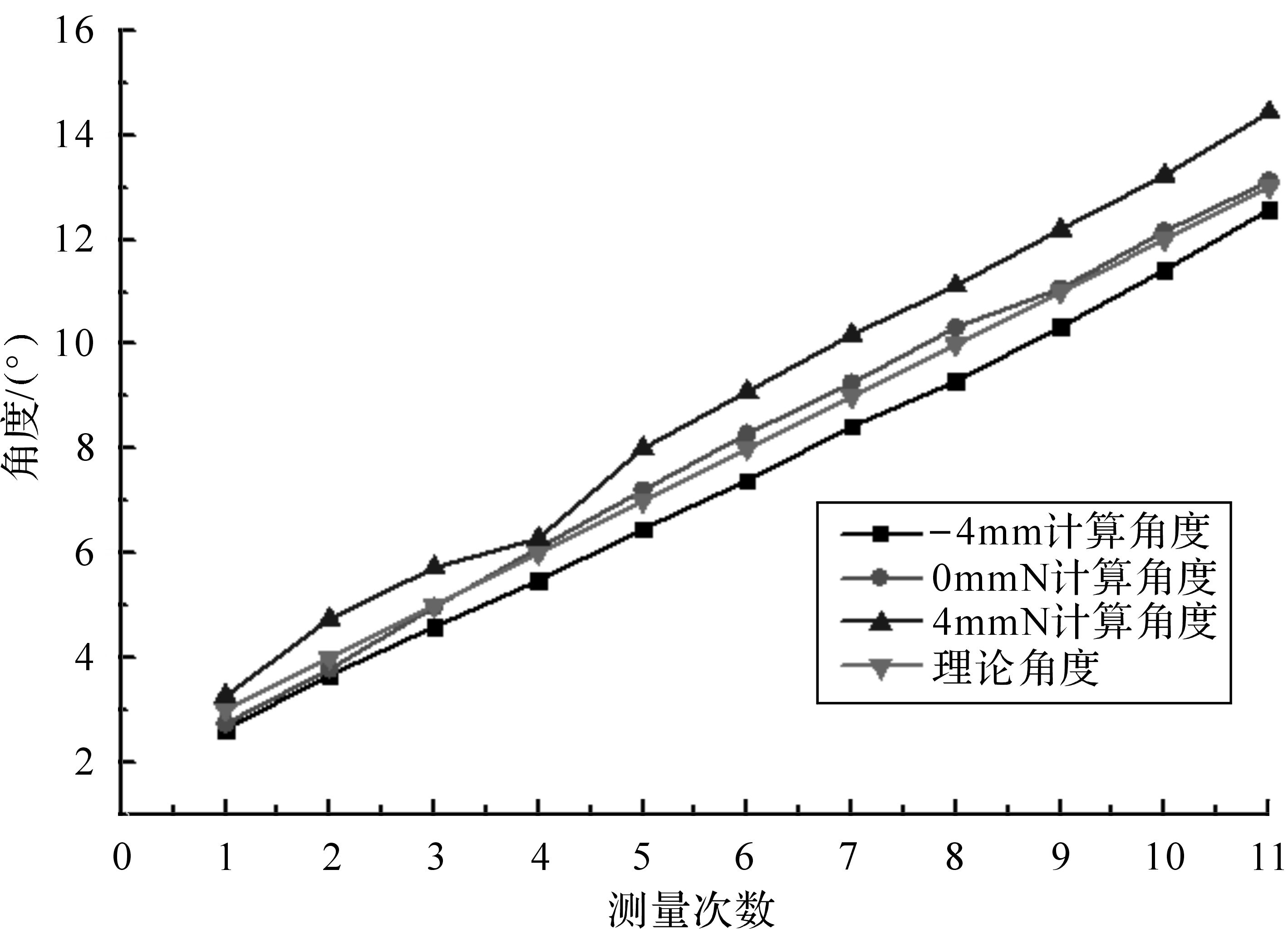
3.2 传感器轴的高度对角度测量的影响

根据以上试验可得出，传感器轴的高度也会影响计算角度与理论角度的偏差.以F=1 000 N为例，分别测量H=-4，0，4 mm时的线弓角度.

由表 8和图 9可知：当传感器轴在-4 mm位置时，计算角度比理论角度小3.3%～12.3%；传感器轴在4 mm位置时，计算角度比理论角度大8.8%～18.6%；传感器轴在0 mm位置时，计算角度与理论角度最接近，且5°以上的误差控制在3.5%以内.因此，传感器轴在0 mm位置时测得的角度最接近真实值.

表 8 F=1 000 N，改变H时的α1和μ Table 8 F=1 000 N，the α1 and μ when H changes
α2/(°)H/mm
-404
α1/(°)μ/%α1/(°)μ/%α1/(°)μ/%
3.02.63-12.32.73-9.03.268.8
4.03.66-8.53.78-5.64.7418.6
5.04.59-8.14.97-0.55.7214.5
6.05.47-8.96.101.76.2813.7
7.06.46-7.77.212.98.0014.3
8.07.39-7.68.283.59.0913.6
9.08.42-6.49.252.810.1813.1
10.09.29-7.110.323.211.1211.2
11.010.33-6.111.070.612.2010.9
12.011.42-4.812.161.413.2310.3
13.012.57-3.313.120.914.4411.1
表选项
图 9 F=1 000 N，改变H时α1的变化规律 Fig.9 F=1 000 N，the change rule of α1 when H changes
图选项
4 结 论

本文提出了一种绳锯线弓角的静态测量方法，用钢丝绳模拟串珠绳产生线弓角并对其进行测量试验，分析了钢丝绳初始张紧力的大小和传感器轴的高度对测量结果的影响.试验表明：随着初始张紧力的增加，计算角度会逐渐向理论角度靠近，一方面可能是由于传感器精度较低，导致张紧力较低时测量不准，另一方面是钢丝绳本身的特点决定的；当传感器轴的位置在0 mm时，计算角度最接近理论值.因此，当导轮处在刚好与钢丝绳接触的状态下，选择合适的初始张紧力，可以测得准确的角度值.这证明了自行设计和搭建的测量平台的合理性，也验证了文中线弓角测量方法的可行性.

参考文献
[1] SPIELVOGEL E. An investigation into the economics of wire saws[J]. Industrial Diamond Review , 1999, 59 : 178–182.
[2] GARRARD R, PEACOCK S R, HORI M. The future role of diamond in the construction industry[J]. Industrial Diamond Review , 2001 (2) : 121–129.
[3] TÖNSHOFF H K. Diamond tools for wire sawing metal components[J]. Diamond and Related Materials , 2002, 250 (3/6) : 742–748.
[4] WRIGHT D N, ENGELS J A. The environment and cost benefits of using diamond wire for quarrying and processing of natural stone[J]. Industrial Diamond Review , 2003 (4) : 16–24.
[5] 王慧.水下金刚石绳锯机关键技术研究与样机研制[D].哈尔滨:哈尔滨工程大学机电工程学院,2008: 1-8. WANG Hui. Key technology and model machine research on underwater diamond wire saw[D]. Harbin: Harbin Engineering University, School of Mechanical and Electrical Engineering, 2008: 1-8.
[6] 王飞, 张进生, 王志. 金刚石串珠绳锯锯切技术研究现状与发展[J]. 金刚石与磨料磨具工程 , 2013, 33 (1) : 36–42. WANG Fei, ZHANG Jin-sheng, WANG Zhi. Current situation and development of diamond wire saw cutting technology[J]. Diamond & Abrasives Engineering , 2013, 33 (1) : 36–42.
[7] 刘宝昌, 张祖培, 孙友宏, 等. 金刚石绳锯的锯切轨迹及锯切机理研究[J]. 金刚石与磨料磨具工程 , 2002 (6) : 17–20. LIU Bao-chang, ZHANG Zu-pei, SUN You-hong, et al. Research on sawing trajectory and mechanism of diamond wire saw[J]. Diamond & Abrasives Engineering , 2002 (6) : 17–20.
[8] 张进生, 王志, 黄波, 等. 金刚石串珠锯在花岗岩高效回采中的应用[J]. 金刚石与磨料磨具工程 , 2004 (6) : 12–15. ZHANG Jin-sheng, WANG Zhi, HUANG Bo, et al. Application research of diamond wire-saw in high efficiency quarrying of granite[J]. Diamond & Abrasives Engineering , 2004 (6) : 12–15.
[9] 章兼植. 金刚石串珠绳锯的受力分析[J]. 石材 , 2005 (1) : 38–43. ZHANG Jian-zhi. Analysis of the force of diamond wire saw[J]. Stone , 2005 (1) : 38–43.
[10] 黄国钦, 黄辉, 郭桦, 等. 串珠绳锯切花岗石过程中锯切参数对锯切力和能耗的影响[J]. 机械工程学报 , 2009, 45 (3) : 234–239. DOI:10.3901/JME.2009.03.234 HUANG Guo-qin, HUANG Hui, GUO Hua, et al. Influences of sawing parameters on forces and energy in wire sawing of granite[J]. Journal of Mechanical Engineering , 2009, 45 (3) : 234–239. DOI:10.3901/JME.2009.03.234
[11] TURCHETTA S. Cutting force and diamond tool wear in stone machining[J]. International Journal of Advanced Manufacturing Technology , 2012, 61 (5/8) : 441–448.
[12] 王海波, 张岚, 孟庆新, 等. 水下绳锯机切割油气管道锯切参数优化研究[J]. 机床与液压 , 2016, 44 (7) : 36–39. WANG Hai-bo, ZHANG Lan, MENG Qing-xin, et al. Sawing parameters optimization study of underwater wire saw cutting oil and gas pipelines[J]. Machine Tool & Hydraulics , 2016, 44 (7) : 36–39.
[13] LIEDKE T, KUNA M. A macroscopic mechanical model of the wire sawing process[J]. International Journal of Machine Tools & Manufacture , 2011, 51 (9) : 711–720.
[14] TEOMETE E. Investigation of long waviness induced by the wire saw process[J]. Proceedings of the Institution of Mechanical Engineers, Prat B: Journal of Engineering Manufacture , 2011, 225 (7) : 1153–1162. DOI:10.1177/2041297510393620
[15] 闰先华. 怎样提高金刚石异型绳锯机的加工精度[J]. 石材 , 2013 (2) : 18–19. RUN Xian-hua. How to improve the machining precision of diamond wire saw machine in special shape cutting[J]. Stone , 2013 (2) : 18–19.
[16] TURCHETTA S, POLINI W, GELFUSA G, et al. A new sawing machine by diamond wire[J]. The International Journal of Advanced Manufacturing Technology , 2014, 70 (1/4) : 73–78.
[17] 刘玉辉.钢绳绳内在特性和力学性能研究[D].太原:太原理工大学机械工程学院,2014: 2-5. LIU Yu-hui. Research on inherent properties and mechanical performances of wire rope[D]. Taiyuan: Taiyuan University of Technology, School of Mechanical Engineering, 2014: 2-5.
[18] 倪松远.钢丝绳机械性质的研究[D].哈尔滨:东北林业大学工程技术学院,2004: 11-12,47. NI Song-yuan. The study of the steel wire rope mechanical character[D]. Harbin: Northeast Forestry University, College of Engineering and Technology, 2004: 11-12,47.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.002
教育部主管，浙江大学和中国机械工程学会主办
0

文章信息

金闪闪, 邹航, 郭桦
JIN Shan-shan, ZOU Hang, GUO Hua
绳锯线弓角静态测量方法的研究
Research on static measuring method of wire saw deflection angle
工程设计学报, 2016, 23(4): 309-315.
Chinese Journal of Engineering Design, 2016, 23(4): 309-315.
http://dx.doi.org/10.3785/j.issn.1006-754X.2016.04.002

文章历史

收稿日期: 2016-04-08

相关文章

工作空间