2. 山河智能装备股份有限公司 国家级企业技术中心, 湖南 长沙 410100
2. National Enterprise R & D Center, Sunward Intelligence Equipment Co., Ltd., Changsha 410100, China
液压凿岩机因其效率高、能耗低、安全等优势,逐步应用于隧道、矿山、水电工程等钻凿工况中[1, 2].作为液压凿岩机的重要组成部分,配流阀通过行程反馈,和活塞形成一个快速匹配系统,而阀芯的开口量会随着活塞控制边的运动发生很大变化.这种变化很多时候会使系统产生很大的压差,甚至发生二次冲击和零位泄漏的现象[3],降低凿岩机的工作效率.因此,阀芯开口的设计与研究对液压凿岩机的整机性能有着重要作用.目前,对阀芯开口的研究主要集中在正开口和正开口量方面[4, 5, 6, 7, 8],对阀芯开口形式和配流阀的导向、制造工艺的研究很少,而对零位负开口情况下阀芯开口运动进行非线性建模、动力学仿真的研究则更少.为了研究和改善液压凿岩机配流阀的性能,本文结合阀芯的制造工艺和定位导向的分析,基于液压凿岩机的配流控制原理和阀芯的运动规律,耦合蓄能器,建立了阀芯开口运动的数学模型,对阀芯开口进行设计和运动学仿真研究,最后分析了阀芯开口对液压凿岩机冲击性能的影响.
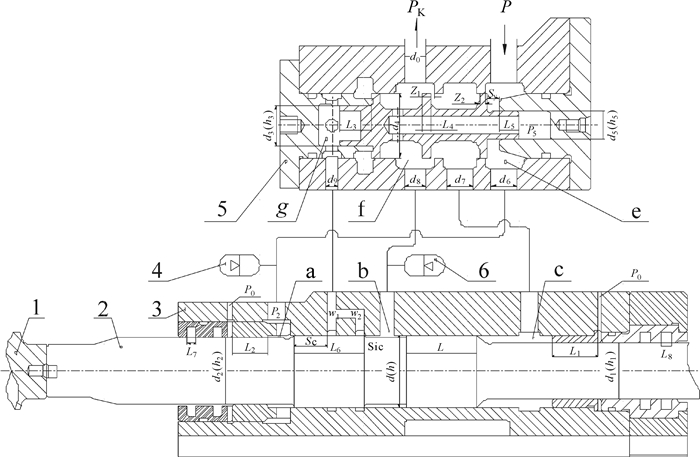
液压凿岩机的配流原理及相关参数如图 1所示.阀芯和活塞的运动匹配是一个行程位置反馈系统,阀芯的运动实质上可以理解为阀芯开口量Z0=Z1-Z2的变化过程.因此作为配流阀的重要参数之一,零位开口对凿岩机工作效率、后腔压力峰值和配流阀的制造难度有很大的影响.当图示的Z2=0时,阀芯处于零位状态,此时,若Z0>0,则阀芯的零位状态为正开口,在此开口状态时,阀芯右控制腔、活塞后腔和回油腔有一个短暂的三腔沟通状态;若Z0 <0,则阀芯的零位状态为负开口,在此开口状态时,活塞后腔和回油腔不会沟通,因此,活塞后腔因不能直接回油而出现憋压,压力上升.相关研究表明,阀芯的正开口设计消除了后腔压力峰值[4].但由上述分析可知,这个短暂的三腔沟通状态不是凿岩机的有效工作状态,所以其在一定程度上降低了液压凿岩机的工作效率.同时,在此开口状态下,阀芯的定位导向由配流阀的左右端盖来实现,但由于阀芯、左右端盖和阀体的同轴度都存在误差,这种误差的累积在很大程度上增加了配流阀的导向精度要求和加工难度.而零位负开口设计能保证阀芯和阀体时刻有两端接触,这直接实现了阀芯的导向要求,同时降低了配流阀的加工难度.同时,由于不存在三腔沟通的状态,只要控制后腔压力峰值在系统允许的范围内,负开口设计能提高液压凿岩机的工作效率.
|
| 图 1 液压凿岩机配流原理及相关参数 Fig. 1 The distributing principle and related parameters of hydraulic rock drill 1—钎尾;2—活塞;3—缸体;4—高压蓄能器;5—配流阀;6—低压蓄能器.a—活塞前腔;b—活塞回油腔;c—活塞后腔;e—配流阀右控制腔;f—配流阀回油腔;g—配流阀左控制腔. |
为了便于分析,这里认为零位状态下活塞的后腔压力峰值等效为后腔的压力和压力增量之和.所以,本文从阀芯运动出发,耦合蓄能器,建立压差模型,计算后腔压力;基于油液压缩,分析阀芯零位状态,计算压力增量,从而建立阀芯运动开口状态的数学模型.
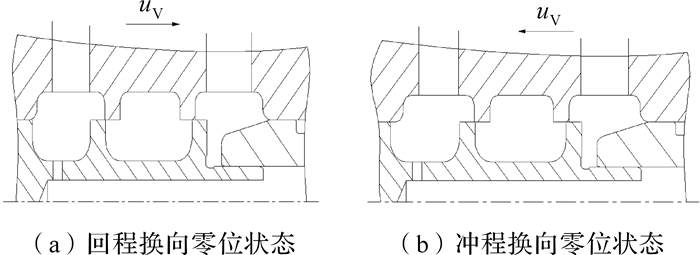
当回程反馈油道打开时,如图 2(a)所示,阀芯开始右移,当阀芯位移yv逐渐趋于Z2,即阀芯处于零位状态时,活塞后腔与阀体右控制腔开始沟通,阀芯开始回程减速,此时供给液压凿岩机的压力油,只有一部分用于阀芯的换向和活塞的回程,其余进入高压蓄能器蓄能,此外,后腔的回油也进入蓄能器,所以,进入蓄能器的油液体积Vh1为
|
| 图 2 零位状态下阀芯运动简化模型 Fig. 2 Simplified model of the core at zero position |
| $ {{V}_{\text{hl}}}=\int{\left( Q+{{\mu }_{p}}\left( {{A}_{1}}-{{A}_{2}} \right)-{{\mu }_{\text{v}}}{{A}_{3}} \right)\text{d}t,} $ | (1) |
由气体状态方程,可得此状态下的蓄能器工作压力Ph1为
| $ {{P}_{\text{hl}}}={{P}_{AH}}{{\left( \frac{{{V}_{\text{ah}}}}{{{V}_{\text{ah}}}-{{V}_{\text{hl}}}} \right)}^{\lambda }}, $ | (2) |
此时,阀芯的右控制腔直接和高压蓄能器、活塞后腔连通,后腔进油通道逐步打开.因此,考虑局部阻力损失,建立蓄能器和活塞后腔的压差模型[9],可得此状态下活塞后腔的压力P1为
| $ {{P}_{\text{l}}}={{P}_{\text{hl}}}-\frac{{{\xi }_{6}}\rho }{2}{{\left( \frac{{{\mu }_{\text{p}}}{{A}_{1}}}{{{A}_{7}}} \right)}^{2}}, $ | (3) |
当活塞反向冲程运动打开冲程反馈油道后,如图 2(b),阀芯左控制腔与活塞回油腔连通,在压力差的作用下,阀芯开始冲程换向,和上述不同的是,有小部分回油将用来控制阀芯的运动,冲程运动所需的压力油远大于系统所供给的压力油,所以,蓄能器所排出油液体积Vh2为
| $ {{V}_{\text{h2}}}=\int{\left( {{u}_{\text{p}}}\left( {{A}_{1}}+{{A}_{2}} \right)+{{u}_{v}}\left( {{A}_{4}}-{{A}_{3}} \right)-Q \right)\text{d}t}, $ | (4) |
同理,可得此状态下蓄能器的工作压力Ph2为
| $ {{P}_{\text{hl}}}={{P}_{\text{ah}}}{{\left( \frac{{{V}_{\text{ah}}}}{{{V}_{\text{ah}}}+{{V}_{\text{h2}}}} \right)}^{\lambda }}, $ | (5) |
在此状态中,后腔进油通道逐步关闭,阀口开口随之减小,所以,可得到此状态下活塞后腔的压力P2为
| $ {{P}_{2}}={{P}_{\text{h2}}}-\frac{{{\xi }_{6}}\rho }{2}{{\left( \frac{{{\mu }_{\text{p}}}{{A}_{1}}}{{{A}_{7}}} \right)}^{2}}. $ | (6) |
由于系统的局部阻力损失在上述分析过程进行了计算,这里可不考虑,所以在零位时,阀芯的速度uv0为
| $ {{u}_{v0}}=\frac{1}{{{m}_{v}}}\int\limits_{0}^{t}{\left( {{P}_{q}}{{A}_{4}}-{{P}_{q}}\left( {{A}_{4}}-{{A}_{5}} \right)-{{P}_{a}}{{A}_{5}}-{{F}_{\text{sv}}}-{{F}_{\text{lv}}} \right)}\text{d}t, $ | (7) |
由于阀芯速度uv0与阀芯负开口量Z0的比值很大,这里认为阀芯在此状态下,阀芯以速度uv0作匀速运动,则阀芯在零位开口状态下的时间tv0为
| $ {{t}_{v0}}=\frac{\left| {{Z}_{2}}-{{Z}_{1}} \right|}{{{u}_{v0}}}. $ | (8) |
同理,活塞在时间tv0内的运动也可作匀速运动处理,则活塞的速度up0为
| $ {{u}_{\text{p}0}}=\frac{1}{{{m}_{\text{P}}}}\int\limits_{0}^{t}{\left( {{P}_{2}}{{A}_{2}}-{{P}_{1}}{{A}_{1}}-{{F}_{\text{s}}}-{{F}_{1}}-{{F}_{\text{f}}} \right)}\text{d}t, $ | (9) |
所以基于油液的可压缩性,在该状态下,活塞后腔的液压油压缩量ΔV为
| $ \Delta V=\frac{\pi }{4}{{u}_{\text{P0}}}{{t}_{v0}}\left( {{d}^{2}}-d_{1}^{2} \right)-{{Q}_{\text{l1}}}{{t}_{v}}-{{Q}_{\text{l2}}}{{t}_{v}}, $ | (10) |
根据偏心环形缝隙的流量计算公式,可知活塞后腔内外圆柱面的泄漏量Ql为
| $ {{Q}_{1}}=\left( 1+5{{\varepsilon }^{2}} \right)\frac{\pi {{d}_{i}}h_{i}^{3}}{12\mu \cdot {{l}_{i}}}\Delta {{P}_{i}}\pm \frac{\pi {{d}_{i}}{{h}_{i}}}{2}{{\mu }_{0}}, $ | (11) |
式(11)中,当相对运动方向与压差方向相同时,“±”取“+”,反之取“-”,所以结合活塞运动状态,如图 1所示,可得到活塞后腔内外圆柱面的泄漏量Ql1,Ql2为:
| $ 12 $ | (12) |
| $ {{Q}_{12}}=\left( 1+5{{\varepsilon }^{2}} \right)\frac{\pi {{\text{d}}_{1}}{{h}_{1}}^{3}}{12\mu \cdot {{l}_{1}}}\Delta {{P}_{1}}-\frac{\pi {{\text{d}}_{1}}{{h}_{1}}}{2}{{u}_{\text{p}0}}. $ | (13) |
因此,根据油液的压缩方程,可得零位状态下后腔的压力增量ΔP为
| $ \Delta P=-K\frac{\Delta V}{{{V}_{0}}}0-K\frac{\frac{\pi }{4}{{u}_{p0}}{{t}_{v}}\left( {{d}^{2}}-d_{1}^{2} \right)-{{Q}_{11}}{{t}_{v}}-{{Q}_{12}}{{t}_{v}}}{{{V}_{0}}}, $ | (14) |
综上所述,联立式(1)至式(14),可以用来计算活塞后腔的压力峰值P′1,并将P′1代入式(15)进行校验,即
| $ P{{'}_{1}}={{P}_{1}}+\Delta P<[{{P}_{\max }}], $ | (15) |
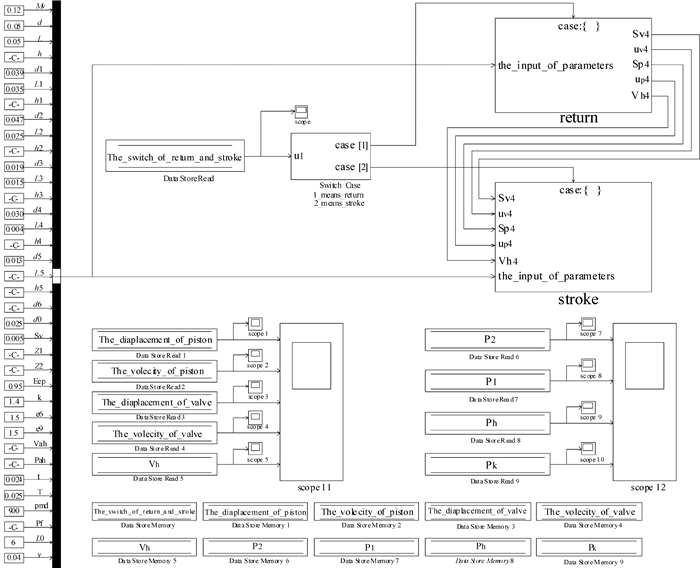
前面通过对阀芯零位状态下的运动和蓄能器充排油分析,并结合气体状态方程和蓄能器耦合,得到后腔压力P1的方程,共计6个方程,这6个方程一起构成了一组非线性代数方程组,用来描述零位状态下阀芯的运动学特征和后腔的压力变化;通过对阀芯零位状态的分析,获得6个描述系统在零位状态下压力增量ΔP的计算方程,并通过代入和积分变换,得到后腔的压力增量ΔP计算方程式(14).仿真模型分为2个模块,模块1用于求解P1,模块2用于求解ΔP.考虑到使用Simulink建立动态仿真后,每个状态进行切换时,都需要对活塞位移yp进行1次求解和判断,所以,为了实现模型的参数化仿真,利用MATLAB强大的数值计算功能,编写MATLAB函数实现yp的求解和判定[10].在Simulink平台建立的基于MATLAB函数的液压凿岩机动力学仿真模型如图 3所示.
|
| 图 3 基于Simulink的液压凿岩机仿真模型 Fig. 3 The simulation model of hydraulic rock drill based on Simulink |
通过以上仿真模型,可以对配流阀阀芯开口状态进行分析,特别是不同开口形式对液压凿岩机的整机特性的研究.由于液压凿岩机常处在高频、强冲的工况,流量和压力的变化是其显著的特点,所以将主要对系统压力和单次最大冲击能等特性进行研究,并分析开口形式对其的影响.
以山河智能机械股份有限公司研制的某型液压凿岩机为研究对象,主要的结构参数设定如表 1所示.
| 参数 | 量值 | 参数 | 量值 | |
| mv | 0.12 kg | d | 50 mm | |
| mp | 5.5 kg | d1 | 39 mm | |
| V0 | 14.98 mL | L1 | 50 mm | |
| Pah | 5.5 MPa | L2 | 35 mm | |
| Vah | 116 mL | h | 0.03 mm | |
| Pmax | 20 MPa | h1 | 0.02 mm |
为了增强正开口和负开口两种形式下液压凿岩机冲击性能和运动匹配的可比性,保证运动参数和结构参数不变,对MATLAB函数和Simulink仿真模型的输入进行相应修改,即可得到开口量Z0分别为0.2 mm和-0.2 mm时2种形式下的仿真模型.同时,采用仿真结果与实测结果进行比对的方式来验证模型的可靠性.
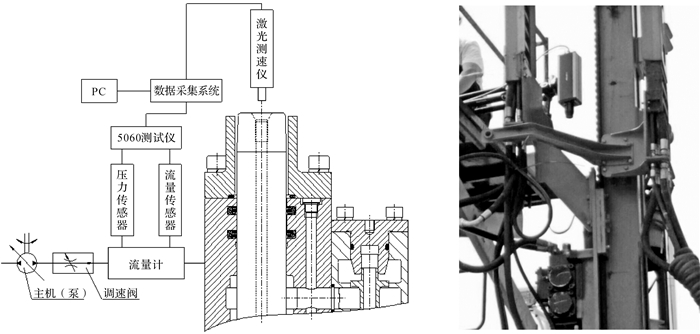
冲击能和系统压力是评定液压凿岩机性能的重要指标,所以同仿真一样,实测对象包括不同开口形式下的液压凿岩机后腔压力和冲击能,实验测试方案和现场实验如图 4所示.方案中,以钻机为平台,系统供给流量由调速阀控制,主要包括2个测试模块,分别是以5060测试仪为主的流量压力测量模块和以多普勒激光测试仪为主的活塞速度测量模块,冲击能是通过活塞速度换算得到的.2个模块共用PC机的数据采集系统.其中在测试活塞速度时,后缸体尾部开孔并贴有防油聚光的膜片,以保证测试的准确性.
|
| 图 4 测试方案和现场实验 Fig. 4 Experimental scheme and field experimentExperimental scheme and field experiment |
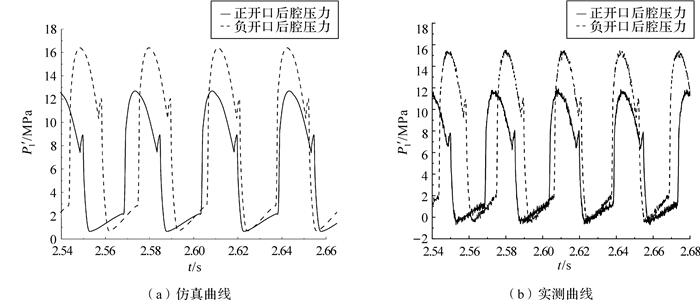
液压凿岩机工作的主要特点是流量和压力的变化.在行程位置反馈中,阀芯的开口量会随着活塞控制边的运动发生很大变化[4].这种变化很多时候会使系统产生很大的压差.所以,保证输入流量不变,进行仿真,可得不同开口形式下后腔的压力曲线,并与实测曲线进行比较,如图 5所示.
|
| 图 5 不同开口形式下后腔压力的仿真曲线和实测曲线 Fig. 5 Simulating and measured curve of pressure in back cavity under different opening types |
由图 5(a)仿真曲线可知,在正开口情况下,后腔的压力峰值约为12.6 MPa,而在负开口情况下,后腔的压力峰值约为16.4 MPa.这是因为在零位负开口状态时,活塞后腔因不能回油而憋压,因此,后腔的压力会有一个增量,但这个峰值压力是在系统的最大允许范围内.而对比图 5(b),可以发现正开口设计的后腔压力峰值约为13.2 MPa,负开口设计的后腔峰值压力可以达到17.1 MPa.但曲线的整体变化情况是一样的,峰值压力误差约为4.7%,这是因为在实际工况中,存在配流阀和胶管的蓄能效应[7],故该模型是合理的.这表明了配流阀负开口设计的可行性.同时,由于缸体后腔憋压时间较短,出现峰值压力的状态是一个很短暂的过程,也就是说只要采取合适的负开口设计,后腔的压力峰值是可以控制在系统的最大压力允许范围内的.
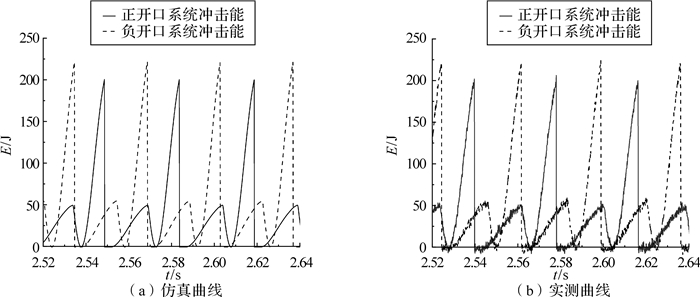
由上述分析可知,采用负开口设计的配流阀会有一个很大的压力峰值,这主要是负开口设计避免了正开口的三腔沟通状态,这样,系统的内泄量将减小,而这在一定程度上将会影响液压凿岩机的冲击性能.所以,保证输入流量不变,进行仿真,可得不同开口形式下系统冲击能曲线,并与实测曲线进行比较,如图 6所示.
|
| 图 6 不同开口形式下液压凿岩机冲击能的仿真曲线和实测曲线 Fig. 6 Simulating and measured curve of impact-energy of hydraulic rock drill under different opening types |
由图 6(a)仿真曲线可知,当配流阀采用零位负开口设计时,活塞的冲击末速度约为9.12 m/s,单次冲击最大冲击能可达到225 J,而在同等输入的情况下,采用正开口设计,活塞的冲击末速度约为8.2 m/s,冲击能约为200 J.同时,在频率上,采用负开口设计可达到33.85 Hz,而采用正开口设计,其频率约为31 Hz.而对比实测曲线图 6(b),可以看出负开口设计的液压凿岩机单次最大冲击能约为218 J,正开口情况下,冲击能也略有下降,同时频率也有一定程度的减小,这是因为仿真过程中忽略了油液泄漏和冲击应力波在凿岩机机体上的耗散等因素,但误差仅为3.2%,是在可以允许的范围内.这表明了在同等情况下,采用负开口设计的液压凿岩机的单次冲击最大冲击能约提高12.5%,工作效率约提高9.2%.
通过对配流阀定位导向和配流控制原理的分析,提出了零位负开口的设计方法,建立了阀芯开口运动的非线性方程和后腔峰值压力的计算方法,快速准确地计算了后腔峰值压力.仿真和实验分别研究了在不同开口形式下,液压凿岩机的后腔峰值压力和冲击能的特性变化.仿真和实验结果为液压凿岩机配流阀的设计提供理论依据.研究表明:
1)零位负开口设计的配流阀比零位正开口设计的配流阀的加工难度低,工艺性能要好.
2)由于阀芯的换向速度较快,且负开口量一般较小,缸体后腔憋压时间较短,只要进行合理的开口设计,便可将后腔的压力峰值控制在系统允许的范围之内.
3)在同等情况下,相比正开口设计,负开口设计的液压凿岩机的单次冲击最大冲击能约提高12.5%,工作效率约提高9.2%.
| [1] | BARTELS R J.Recent finding in the development of hydraulic hammer and hydraulic demolition cutters[J].Tech Mitt Krupp,1992,2(1):23-35. |
| [2] |
丁问司,黄晓东.自配流型液压冲击器建模与仿真[J].振动与冲击,2010,29(2):103-106. DING Wen-si,HUANG Xiao-dong.Modeling and simulation for a self-distributing flow hydraulic impactor[J].Journal of Vibration and Shock,2010,29(2):103-106. |
| Cited By in Cnki (16) | Click to display the text | |
| [3] |
章海,裴翔,陈胜,等.数字缸的静态特性分析[J].工程设计学报,2004,11(1):27-30. ZHANG Hai, PEI Xiang,CHEN Sheng,et al.Analysis on static characteristics of digital servo cylinder[J].Chinese Journal of Engineering Design,2004,11(1):27-30. |
| Cited By in Cnki (4) | Click to display the text | |
| [4] |
何清华.液压冲击机构研究设计[M].长沙:中南大学出版社,2009:74-85. HE Qing-hua.Research and design of hydraulic impact mechanism[M].Changsha:Central South University Press,2009:74-85. |
| [5] |
齐仁贤,刘仕勋,唐焕斌,等.液压凿岩机控制阀研究[J].有色金属(矿山部分),1986,6(8):22-29. QI Ren-xian,LIU Shi-xun,TANG Huan-bin,et al.Study on the control valve of hydraulic rock drill[J].Nonferrous Metals (Mining),1986,6(8):22-29. |
| Cited By in Cnki (8) | |
| [6] |
刘万灵,赵记尚,高澜庆.液压凿岩机换向阀的分析与测试[J].凿岩机械气动工具,1990,2(8):55-60. LIU Wan-ling,ZHAO Ji-shang,GAO Lan-qing,et al.Analysis and experiment of revering valve of hydraulic rock drill[J].Drilling Machinery & Pneumatic Tool,1990,2(8):55-60. |
| Cited By in Cnki (2) | |
| [7] |
舒敏飞,何清华,赵宏强,等.液压凿岩机冲击压力及冲击性能仿真研究[J].武汉理工大学学报,2011,33(8):133-137. SHU Min-fei,HE Qing-hua,ZHAO Hong-qiang,et al.Study on simulation of impact performance and working pressure of hydraulic drifter[J].Journal of Wuhan University of Technology,2011,33(8):133-137. |
| Cited By in Cnki (5) | |
| [8] |
赵宏强.新型液压冲击器仿真与优化研究[J].凿岩机械气动工具,2001(1):12-26. ZHAO Hong-qiang.Simulation and optimization research of a new type of hydraulic impact machines[J].Drilling Machinery & Pneumatic Tool,2001(1):12-26. |
| Cited By in Cnki (23) | |
| [9] | BORUTZKY W,BARNARD B,THOMA J U.Describing bond graph models of hydraulic components in Modelica[J].Mathematics and Computers in Simulation.2000,25(4):37-41. |
| Click to display the text | |
| [10] |
黎明安. MATLAB/Simulink动力学系统建模与仿真[M]. 西安: 国防工业出版社,2012:113-137. LI Ming-an. The model and simulation of dynamic system based on MATLAB/Simulink[M]. Xi'an: National Defense Industry Press, 2012:113-137. |


