2. 江苏大学 电气信息工程学院, 江苏 镇江 212013
2. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China
调速型鼠笼式异步磁力联轴器即永磁调速器[1],是在普通永磁磁力联轴器的基础上发展而来的一种新型的调速传动装置.永磁调速器作为一种新兴的节能调速设备,在国外已经被成功应用于工业与军事上[2, 3, 4],在国内也被应用于石化、电力等行业.与变频调速设备相比,永磁调速器采用纯机械式结构,消除了电力谐波及电磁干扰,实现了软启动及过载保护,有助于提高系统的稳定性和可靠性[5, 6].
调速型异步磁力联轴器作为一种新型传动调速装置,具有结构简单、过载保护、节能效果显著等优点[1, 5].如图 1所示,调速型鼠笼式异步磁力联轴器机械结构主要由永磁转子和导体转子组成.磁力联轴器在非完全啮合时,由于模型并不对称,会有一定的轴向力产生,并且由于啮合长度的变化,轴向力会随之变化.轴向力的大小直接关系到磁力联轴器工作时的稳定性,尤其是在进行连续调速的情况下,用来调节啮合长度的执行机构承受交变载荷会影响磁力联轴器调速的精确性.因此,轴向力的研究对于调速型磁力联轴器的理论研究、参数设计与优化及其应用都有着一定的理论及实际意义.
|
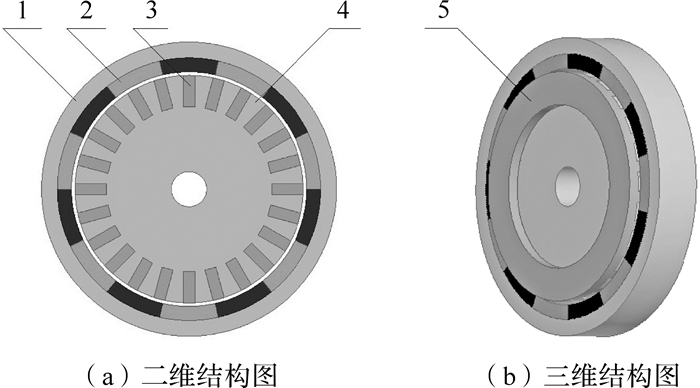
| 图 1 调速型鼠笼式异步磁力联轴器 Fig. 1 Adjustable speed squirrel-cage asynchronous magnetic coupling 1—外转子轭铁; 2—永磁体; 3—铜导条; 4—内转子轭铁; 5—铜导体端环. |
调速型鼠笼式异步磁力联轴器的结构如图 1所示,主要由永磁体2、铜导体3、外轭铁1及内轭铁4组成.各永磁体均为径向充磁,但相邻永磁体间充磁方向相反,其工作原理是铜导体切割永磁体磁场产生感应电流,感应电流产生的感应磁场与原永磁磁场相互耦合来传递动力[7].通过调节内外转子的轴向位置可改变永磁体2与导体3之间的啮合长度,从而控制其传递动力的能力,从而实现负载转速、转矩的调节.
本文轴向力是指调速型鼠笼式异步磁力联轴器内外转子上受到的沿轴方向的力,内外转子受到的轴向力大小相等、方向相反.调速型鼠笼式异步磁力联轴器通过调节内外转子轴向的啮合长度改变转速,为了系统可以精确并稳定地运行,内外转子的轴向位置必须控制精确,因而轴向力的存在对磁力联轴器的工作性能有较大影响.为了磁力联轴器精确稳定地运行,需对轴向力进行研究分析.
计算永磁体磁场的方法有解析法、有限元法、等效磁网络法和数值解析结合法[8].目前,对磁场及磁力计算主要采用有限元等数值计算法以及有限几种典型结构的经验公式法[9].有限元等数值计算法虽然具有较高的计算精度,但计算较为繁杂而且不能显式表达磁场或磁力与各参数之间的相互关系.故本文通过引入等效面电流法,解析出动态空间磁场分布,进而求解出轴向力的计算表达式.
如图 1所示,磁力联轴器由内、外两个转子组成,其中内转子为铜导体,外转子为永磁体.联轴器工作时,外转子转动形成旋转磁场,内转子导体切割磁力线形成感应电流,感应电流产生感应磁场,与外转子永磁体的旋转磁场耦合产生转矩,通过调节永磁体与导体之间的啮合长度就可以控制传递的转矩,从而实现负载转速的调节.
基于等效面电流法作出如下假设:
1)永磁体径向均匀磁化,气隙是均匀的;
2)轭铁将磁力线封闭,有较高的磁导率且未磁化饱和,忽略边缘效应及漏磁;
3)永磁体的退磁曲线为一直线,回复线与退磁曲线重合,即永磁体磁导率为定值;
4)导磁材料被永磁体径向均匀磁化,不存在体电流,只存在面电流;
5)理论计算中只考虑联轴器工作在静态下的情况,故忽略铜导体切割磁力线产生的感应磁场对气隙磁场的影响.
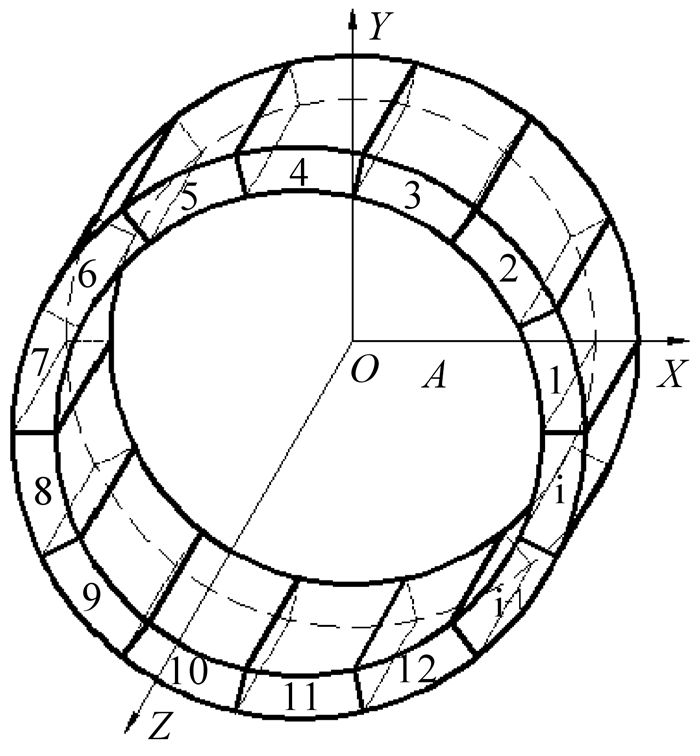
根据毕奥-沙伐定理,建立异步磁力联轴器的直角坐标系,见图 2,坐标原点在磁力联轴器端面的中点处.利用永磁体等效面电流法,可得永磁体在空间磁场中任意场点的磁感应强度表达式为[10]
| $ B = \frac{{{\mu _0}}}{{4\pi }}\int\limits_S {\frac{{{\delta _{\rm{s}}} \times r}}{{{r^3}}}} {\rm{d}}S = \frac{{{M_r}{\mu _0}}}{{4\pi }}\int\limits_S {\frac{{{e_\rho } \times n \times r}}{{{r^3}}}} {\rm{d}}S $ | (1) |
|
| 图 2 永磁转子模型 Fig. 2 Model of permanent magnet rotor |
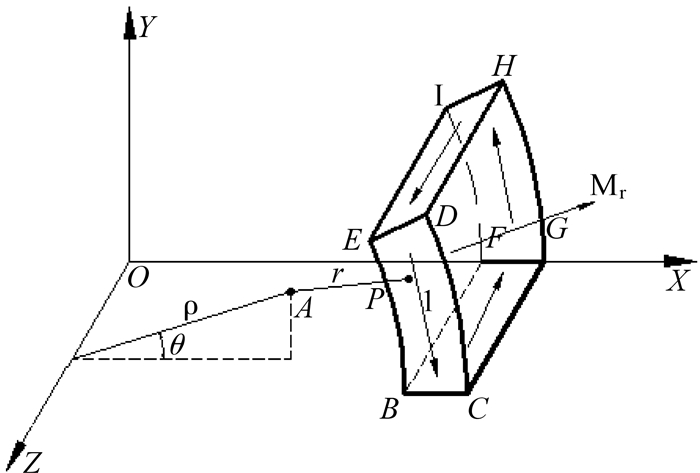
为了便于分析计算,应用等效面电流法将单极永磁体模型等效为永磁体4个表面BCDE,FGHI,BCFG,EDHI的等效面电流,分别求出各等效面电流在气隙中任一点A产生的磁感应强度B,见图 3.
|
| 图 3 单块永磁体的数学模型 Fig. 3 Mathematical model of single block permanent magnet |
1)永磁体BCDE面上等效面电流在A点产生的磁感应强度B1为[11]
| $ {B_1} = {\left( { - 1} \right)^{i + 1}}\frac{{{M_r}{\mu _0}}}{{4\pi }}\int_{(i - 1)\beta }^{i\beta } {\frac{{{{\rm{A}}_1}}}{{{{\left| {{r_1}} \right|}^3}}}} {\rho _1}{{\rm{d}}_1}{\rho _1}{\rm{d}}{\theta _1}, $ | (2) |
A1=(Z1-Z-vt)cos(θ1+ωt)x+(Z1-Z-vt)sin(θ1+ωt)y+[ρcos(θ-θ1-ωt)-ρ1]z;
R1为永磁体内部半径;R2为永磁体外部半径;β为单块永磁体的磁极张角;ω为永磁转子的角速度;v为永磁转子的轴向进给速度;i为永磁体编号,i=1,2,…,np,np为磁极对数.2)永磁体FGHI面上等效面电流在A点产生的磁感应强度B2为
| $ {B_2} = {\left( { - 1} \right)^{i + 2}}\frac{{{M_{r1}}{\mu _0}}}{{4\pi }}\int_{(i - 1)\beta }^{i\beta } {\int_{{R_{}}}^{{R_2}} {\frac{{{A_2}}}{{{{\left| {{r_2}} \right|}^3}}}{\rho _1}} } {\rm{d}}{\rho _1}{\rm{d}}{\theta _1}, $ | (3) |
A2=(Z1-Z-vt)cos(θ1+ωt)x+(Z1-Z-vt)sin(θ1+ωt)y+[ρcos(θ-θ1-ωt)-ρ1]z.
3)永磁体BCFG面上等效面电流在A点产生的磁感应强度B3为
| $ {B_3} = {\left( { - 1} \right)^{i + 1}}\frac{{{M_{r1}}{\mu _0}}}{{4\pi }}\int_0^L {\int_{{R_1}}^{{R_2}} {\frac{{{A_3}}}{{{{\left| {{r_3}} \right|}^3}}}{\rho _1}} } {\rm{d}}{\rho _1}{\rm{d}}{Z_1}, $ | (4) |
A3=[ρsin θ-ρ1sin((i-1)β+ωt)]x-[ρcos θ-ρ1cos((i-1)β+ωt)]y.
4)永磁体EDHI面上等效面电流在A点产生的磁感应强度B4为
| $ {B_4} = {\left( { - 1} \right)^{i + 2}}\frac{{{M_{r1}}{\mu _0}}}{{4\pi }}\int_0^L {\int_{{R_1}}^{{R_2}} {\frac{{{A_4}}}{{{{\left| {{r_4}} \right|}^3}}}{\rho _1}} } {\rm{d}}{\rho _1}{\rm{d}}{Z_1}, $ | (5) |
A4=[ρsin θ-ρ1sin(iβ+ωt)]x-[ρcos θ-ρ1cos(iβ+ωt)]y.
故可以得到所有永磁体在A点产生的磁感应强度,为
| $ B = \sum\limits_i^{{n_p}} {\left( {{B_1} + {B_2} + {B_3} + {B_4}} \right)} . $ | (6) |
假设磁场在导磁材料区域的分布均匀,故可得到简化的电磁力[11, 12]为
| $ F=\frac{{{\mu }_{r}}-1}{2{{\mu }_{0}}{{\mu }_{r}}}\iint_{s}{{{B}^{2}}\text{d}S=\frac{{{\mu }_{r}}-1}{2{{\mu }_{0}}{{\mu }_{r}}}}{{B}^{2}}S. $ | (7) |
根据式(6)计算得到的磁感应强度,由式(7)及式(1)可以得出单块永磁体对于点A处的电磁力为 [13]
| $ {{F}_{A}}=\frac{{{\mu }_{r}}-1}{2{{\mu }_{0}}{{\mu }_{r}}}B_{A}^{2}{{S}_{A}}, $ | (8) |
| $ {{F}_{z}}=m{{F}_{A}}\sin \ \varphi =\frac{m{{F}_{A}}\Delta L}{\sqrt{{{\left( \frac{{{r}_{1}}+{{r}_{2}}+{{r}_{3}}+{{r}_{4}}}{2} \right)}^{2}}+\Delta {{L}^{2}}}} $ | (9) |
由于调速型磁力联轴器在工作时做双自由度运动,既绕水平轴旋转,又沿水平轴轴向移动(见图 4),故选用Magnet电磁场仿真软件,分析调速型鼠笼式异步磁力联轴器从完全啮合状态至脱离状态的轴向力.联轴器模型的主要结构参数如下:永磁转子磁极对数为7,内转子槽数为24,槽深为18 mm,槽宽为6.5 mm,永磁体轴向长度为26 mm,端环轴向长度为6 mm.

|
| 图 4 调速器运动示意图 Fig. 4 Motion diagram of the machine |
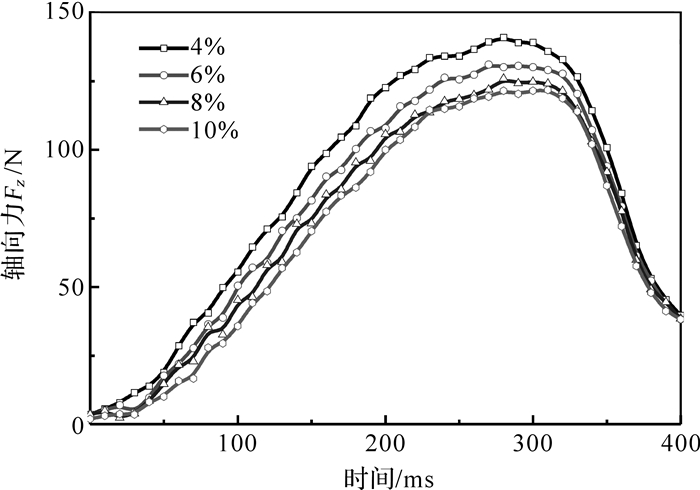
如图 5所示为主动转子转速为1 500 r/min、轴向退出速度为0.08 m/s时,不同转差率下的螺旋退出轴向力随时间的变化曲线.从图 5可知,4条曲线都以零点为起点.这是由于在完全啮合状态,联轴器处于平衡位置,各个方向的合力为0.螺旋进给的轴向力随着时间的增加先增大后减小,在260—280 ms即轴向偏移为20.8~22.4 mm时达到最大值,在400 ms时刻即脱离状态时达到最小值.轴向力在到达峰值前,4条曲线较为稀疏,转差率对其影响较大;但在到达峰值后,4条曲线变得较为紧密,转差率对其影响逐渐下降;在400 ms时刻,各转差率的轴向力相差无几.
|
| 图 5 螺旋退出轴向力时变图 Fig. 5 Time varying axial force diagram in the process of the screw out |
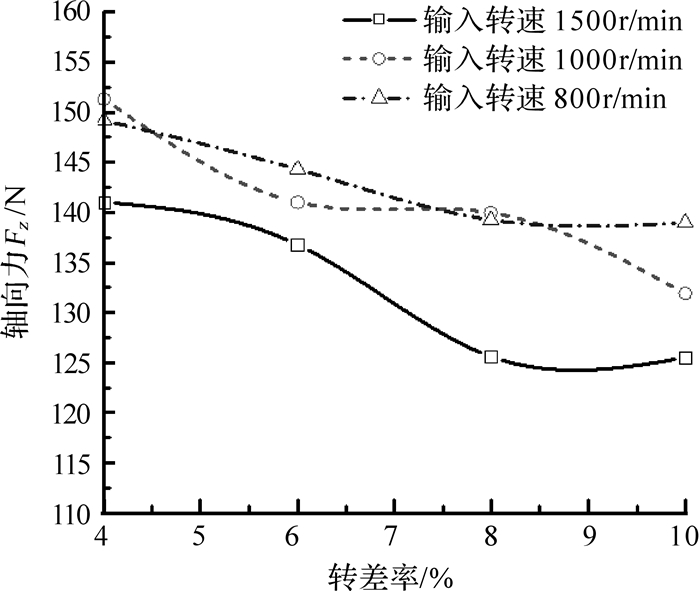
图 6为4%,6%,8%,10%转差率下轴向力的最大值.1 500 r/min时最大值分别为141,136.77,125.6,124.5 N;1 000 r/min时最大值分别为151.3,141,139.97,131.9 N;800 r/min时的最大值分别为149.17,144.3,139.25,138.97 N.随着输入转速的增加,轴向力逐渐降低.
|
| 图 6 不同转速下的最大轴向力 Fig. 6 Maximum axial force with different input speed |
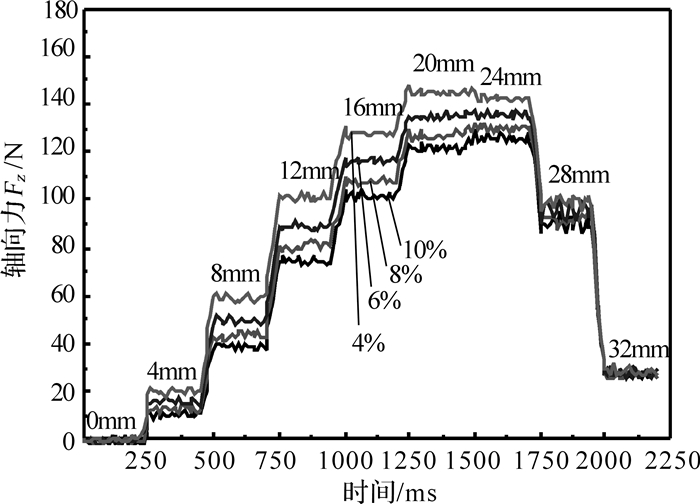
图 7为调速型鼠笼式异步磁力联轴器输入转速为1 500 r/min、轴向退出速度为0.08 m/s时,不同转差率下的螺旋退出至固定轴向偏移长度0,4,8,12,16,20,24,28,32 mm的连续轴向力时变图.如图 7所示,随着时间的变化,轴向力先增大后减小,曲线呈现阶梯状爬升而后下降的趋势.其中,轴向力最大值位于固定轴向偏移长度20~24 mm区间,分别为128.6,131.17,138.15,147.1 N;轴向力最小值位于固定轴向偏移长度32 mm处,分别为25.8,25.9,26.1,26.2 N.由图中曲线可以看出:轴向力在到达峰值前,处于负加速度爬升状态,相邻固定轴向偏移长度的轴向力之差不断减小;当运动至固定偏移长度并仅做旋转运动时,轴向力波动类似于正弦波作周期性振动;在越过峰值后,轴向力急速下降至最小值.同时,从图中可以看出,在同一轴向偏移长度的情况下,轴向力随着转差率的变大而变小.这是由于随着调速器主从转子间的转差率的变大,导体转子切割磁力线引起的感应电流所产生的反磁势会随之变大,从而削弱了气隙磁场强度,使得轴向力变小.当轴向偏移长度为32 mm时,此时调速器处于脱离状态,导体转子几乎不能切割磁力线产生感应电流形成反磁势,故转差率对其影响降至最低.
|
| 图 7 螺旋退出过程中的轴向力 Fig. 7 The axial force in the process of the screw out |
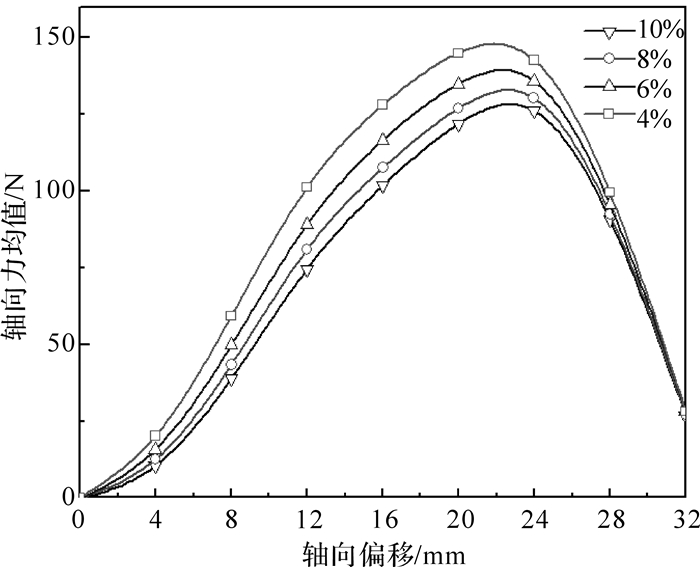
图 8为主动转子转速为1 500 r/min、不同转差率下的轴向力均值随不同轴向偏移长度的变化曲线图.从图中可知,轴向力均值曲线呈现先增大后减小的趋势.随着转差率的增大,轴向力也随之变小.在轴向偏移长度32 mm即脱离状态时,各转差率下的轴向力均值趋于稳定值26 N.由公式(9)可知,啮合长度ΔL=0时,轴向力Fz=0,随着ΔL的增加,Fz逐步增大,但同时BA随啮合长度的增加逐步减小,导致FA逐步减小,当FA减小到一定程度,会抵消ΔL增大对FA的影响,此时出现轴向力最大值,随着FA进一步减小,轴向力Fz逐步减小至0,趋势与模拟一致.
|
| 图 8 固定轴向偏移的轴向力均值 Fig. 8 Mean axial force for fixed axial deviation |
从等效面电流理论出发,推导出调速型鼠笼式异步磁力联轴器在低转差率下的动态空间磁场分布及螺旋进给/退出轴向力计算表达式,然后进行模拟分析,得到结论如下:
1)调速型鼠笼式异步磁力联轴器由完全啮合状态至脱离状态过程中,轴向力呈现先增大后减小的趋势,最大值出现在脱离过程中;
2)调速型鼠笼式异步磁力联轴器在相同输入转速情况下,转差率越大,轴向力越小,在脱离状态时趋于稳定值;
3)调速型鼠笼式异步磁力联轴器由完全啮合状态至脱离状态过程中,转差率对轴向力的影响逐渐变小,在同一轴向偏移长度的情况下,轴向力随着转差率的变大而变小.
| [1] | WALLACE A,von JOUANNE A,JEFFRYES R,et al.Comparison testing of an adjustable-speed permanent-magnet eddy-current coupling[C].IEEE Pulp and Paper Industry Technical Conference.Atlanta:IEEE Service Center,2000:73-78. |
| [2] | WALLACE A,von JOUANNE A.Industrial speed control:are PM couplings an alternative to VDFs[J].IEEE Industry Applications Magazine,2001,7(5):57-63. |
| Click to display the text | |
| [3] | HIGHFILL G S,HALÜERSON L A.Lowering total cost of ownership with breakthrough magnetic torque transfer technology[C].2006 IEEE Cement Industry Technical Conference Record.Atlanta:IEEE Service Center,2006:15. |
| Click to display the text | |
| [4] | POTGIETER Johannes H J,KAMPER M J.Optimum design and comparison of slip permanent-magnet couplings with wind energy as case study application[J].IEEE Transactions on Industry Applications,2014,50(5):3223-3234. |
| Click to display the text | |
| [5] | LUBIN T,REZZOUG A.Steady-state and transient performance of axial-field eddy-current coupling[J].IEEE Transactions on Industrial Electronics,2015,62(4):2287-2296. |
| [6] |
王旭,王大志,刘震,等.永磁调速器的涡流场分析与性能计算[J].仪器仪表学报,2012,33(1):155-160. WANG Xu,WANG Da-zhi,LIU Zhen,et al.Eddy current field analysis and performance calculations for adjustable permanent magnetic coupler[J].Chinese Journal of Scientific Instrument,2012,33(1):155-160. |
| Cited By in Cnki (12) | Click to display the text | |
| [7] | MOHAMMADI S,MIRSALIM M,VAEZ-ZADEH S,et al.Analytical modeling and analysis of axial-flux interior permanent-magnet couplers[J].IEEE Transactions on Industrial Electronics,2014,11(61):5940-5947. |
| Click to display the text | |
| [8] |
章跃进,江建中,屠关镇.应用数值解析结合法计算旋转电机磁场[J].电工技术学报,2004,19(1):7-11. ZHANG Yue-jin,JIANG Jian-zhong,TU Guan-zhen.Research on numerical and analytical combined method of magnet field computation for rotational electrical machines[J]. Journal of Electrotechnics,2004,19(1):7-11. |
| Cited By in Cnki (25) | Click to display the text | |
| [9] |
田录林,贾嵘,杨国清,等.永磁铁磁贴合体的磁场及磁力[J].电工技术学报,2008,23(6):7-13. TIAN Lu-lin,JIA Rong,YANG Guo-qing,et al.The magnetic field and magnetic force of permanent magnet affixed to a plane magnetizer[J].Journal of Electrotechnics,2008,23(6):7-13. |
| Cited By in Cnki (12) | Click to display the text | |
| [10] | 管春松.盘式异步磁力联轴器的电磁特性与温度场性能研究[D].镇江:江苏大学机械工程学院,2012:31-33. GUAN Chun-song.Study on electromagnetic properties and thermal field in axial asynchronous permanent magnet couplings[D].Zhenjiang:Jiangsu University,School of Mechnical Engineening,2012:31-33. |
| [11] | 王晶晶.双层实心异步磁力联轴器涡流及温度场分析[D].镇江:江苏大学机械工程学院,2009:24-25. WANG Jing-jing. Double solid induction magnetic coupling eddy current and temperature field analysis[D].Zhenjiang:Jiangsu University,School of Mechanical Engineering,2009:24-25. |
| [12] | 张宏.新型节能调速设备永磁磁力耦合调速器的原理及应用[J].中国电力教育,2009,2(14):552-553. ZHANG Hong. New energy-saving equipment principle and application of permanent magnetic coupling[J].China Power Education,2009,2(14):552-553. |
| Cited By in Cnki (9) | |
| [13] | 王瑜.永磁装置中磁场力的计算[J].磁性材料及器件,2007,38(5):49-52. WANG Yu.Calculation of magnet force of permanent magnet devices[J].Magnetic Materials and Devices,2007,38(5):49-52. |
| Cited By in Cnki (30) |



