世界上每年因肿瘤死亡的人数约500万.我国每年新发现的肿瘤患者约100万人以上[1].目前,手术、放射和药物治疗是3种主要治疗方法.随着放射治疗技术的快速进步,肿瘤放疗向着精确放疗方向快速发展,从而取得了更好的治疗效果[2].
常规放疗床如西门子550TxT、CyberKnife放射治疗床[3,4]均为串联结构,只能实现3个自由度的运动,且刚度较差,定位精度不高,承载能力较差,空间自由度受到限制.而并联机构由于刚度大、精度高、动态性能好、承载能力强等优点,在机器人领域得到了越来越广泛的重视[5],本文提出的六自由度放疗床可以有效满足放疗设备使用要求,达到精确放疗的效果.
放疗床用于对患者进行定位,因此对于其平稳性和安全性有严格要求.六自由度并联机构结构参数复杂,工作空间小,因此,通过分析各参数对放疗床受力的影响,对放疗床进行结构设计和参数优化就成为极其重要的环节.针对放疗床的使用要求,本文提出一种多目标协调的机构参数优化方法,考虑工作空间、放疗床受力、雅克比矩阵条件数,以及构建关于条件数全域均值、条件数波动情况的目标函数,进行参数的具体优化.
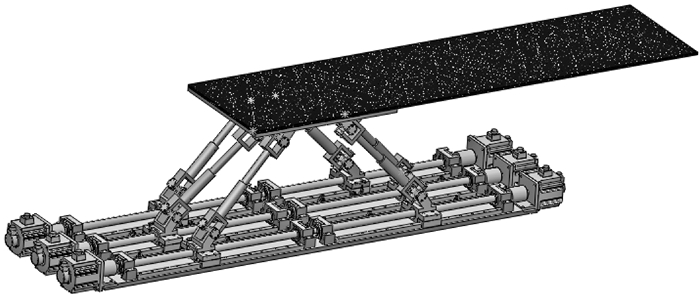
1 运动学模型根据精确放射治疗的要求,选用如图 1所示的6-HTRT结构形式.该构型沿着导轨方向的运动即纵向运动的范围仅受导轨长度限制,可以轻易得到放大,且结构整体宽度较小,可以与床板宽度保持一致,结构的整体体积也较小.因此,该并联构型能够很好地满足放疗床的使用要求.
|
| 图 1 6-HTRT放射治疗床 Fig. 1 Radiotherapy bed of 6-HTRT |
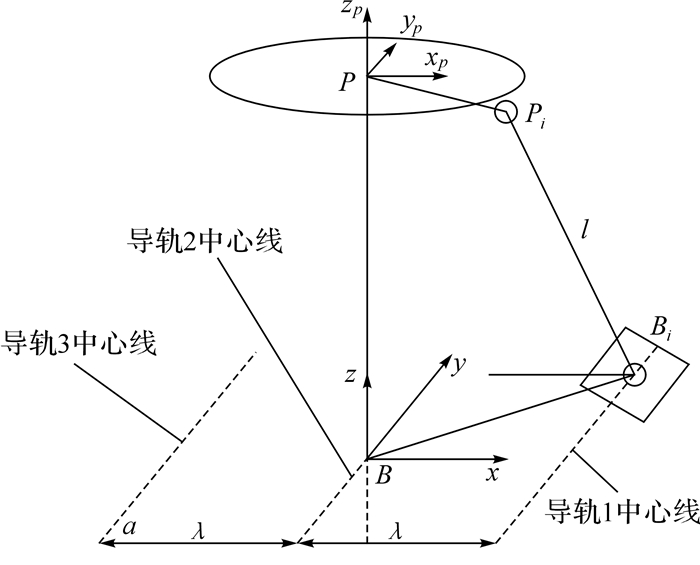
如图 2所示:Bi,Pi(i=1,2,…,6)分别表示定平台虎克铰中心点和动平台虎克铰中心点;各Pi在同一圆上,圆心为点P.定平台处的3条导轨在同一平面内,定义该平面为α.机构在初始状态下,动平台与定平台的3条导轨所确定的α平面平行.机构在初始位置时过点P做α的垂线,与Bi所在平面的交点为B.在B点建立基座坐标系,简计为B,z轴与平面α垂直,方向向上,x轴与3条导轨的中心线垂直,且指向导轨1.y轴即可由右手定则得到.在点P建立与动平台固连的坐标系P-xpypzp,简计为{P},坐标原点设为动平台铰链点所在圆的圆心P,动平台处于初始安装状态时其坐标系与基座坐标系方位完全相同[6,7].
|
| 图 2 放疗床坐标系 Fig. 2 Coordinate system of radiotherapy bed |
设动平台中心到铰链中心的矢径与该组铰链轴线间的夹角为θp,将θp定义为动平台铰链分布角度.
用Φpi表示动平台坐标系{P}中x正半轴到矢径PPi沿逆时针方向需要旋转的角度,则有下述公式:
| ${\Phi _{pi}}=\frac{2}{3}\pi \left[{\frac{{i - 1}}{2}} \right]+{\left({ - 1} \right)^i} \cdot {\theta _p}.$ | (1) |
定平台虎克铰中心点Bi沿着基座坐标系的y轴方向作平移运动,将其移动量Si作为放疗床的输入量.动平台虎克铰中心点Pi在动平台坐标系中的矢量描述为
| ${}^P{P_i}={\left[{r\cos \;{\varphi _{pi}},r\;\sin \;{\varphi _{pi}},0\;} \right]^{\rm{T}}},$ | (2) |
式中:r为动平台半径,mm.
定平台铰链中心点Bi在{B}中的矢量描述为
| $^B{B_i}={\left[{{x_{Bi}},{y_{Bi}},0\;} \right]^{\rm{T}}}.$ | (3) |
xBi与yBi的表达式如下:
| ${x_{Bi}}=\left\{ \begin{array}{l} \lambda,i=1,2,\\ 0,i=3,6,\\ - \lambda,i=4,5. \end{array} \right.\;\;\;{y_{Bi}}=\left\{ \begin{array}{l} \left({{k_1},{k_2}} \right),i=1,2,\\ \left({{k_3},{k_6}} \right),i=3,6,\\ \left({{k_4},{k_5}} \right),i=4,5, \end{array} \right.$ | (4) |
式中:λ为相邻2条导轨中心线之间的距离,mm;ki与动平台中心点的空间位置和姿态有关.
设动平台坐标系绕基座坐标系3个主轴的转角分别为θx,θy,θz,得到的合成旋转变换矩阵来表示动平台坐标系相对于基座坐标系的姿态,具体表达式如式(5):
| $\begin{array}{l} ^B{Q_p}=\left[{\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{{c_{13}}}\\ {{c_{21}}}&{{c_{22}}}&{{c_{23}}}\\ {{c_{31}}}&{{c_{32}}}&{{c_{33}}} \end{array}} \right]={\rm{Rot}}\left({z,{\theta _z}} \right)\cdot {\rm{Rot}}\left({y,{\theta _y}} \right)\cdot {\rm{Rot}}\left({x,{\theta _x}} \right)=\\ \left[{\begin{array}{*{20}{c}} {C{\theta _z}}&{ - S{\theta _z}}&0\\ {S{\theta _z}}&{C{\theta _x}}&0\\ 0&0&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {C{\theta _y}}&0&{S{\theta _y}}\\ 0&1&0\\ { - S{\theta _y}}&0&{C{\theta _y}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} 1&0&0\\ 0&{C{\theta _x}}&{ - S{\theta _x}}\\ 0&{S{\theta _x}}&{C{\theta _x}} \end{array}} \right]=\\ \left[{\begin{array}{*{20}{c}} {C{\theta _z}C{\theta _y}}&{C{\theta _z}S{\theta _y}S{\theta _x} - S{\theta _z}C{\theta _x}}&{C{\theta _z}S{\theta _y}C{\theta _x}+S{\theta _z}S{\theta _x}}\\ {S{\theta _z}C{\theta _y}}&{S{\theta _z}S{\theta _y}S{\theta _x}+C{\theta _z}C{\theta _x}}&{S{\theta _z}S{\theta _y}C{\theta _x} - C{\theta _z}S{\theta _x}}\\ { - S{\theta _y}}&{C{\theta _y}S{\theta _x}}&{C{\theta _y}C{\theta _x}} \end{array}} \right], \end{array}$ | (5) |
式中:Sθx=sinθx,Sθy=sinθy,Sθz=sinθz,Cθx=cosθx,Cθy=cosθy,Cθz=cosθz.
动平台在基座坐标系中的位姿矢量用Xp=[P,Ω]T描述,其具体表达式如下:
| ${X_p}={\left[{{P_x},{P_y},{P_z},{\theta _x},{\theta _y},{\theta _z}} \right]^{\rm{T}}}.$ | (6) |
在对放疗床进行位置控制时,当给定床板在空间内某一位姿,需要利用其位姿逆解来得到各个滑块的输入值,进而得到电机输入的参考值.对于本文研究的放疗床,当给定动平台几何中心的位置和姿态后,通过结构的几何关系求出各个滑块的位移,进而得到电机的转角,即为其位姿逆解.设点Pi在基座坐标系中的位置矢量为
| $^B{P_i}={\left[{{x_{pi}},{y_{pi}},{z_{pi}}\;} \right]^{\rm{T}}}.$ | (7) |
由BBi=[xBi,yBi,0]T及丨BPi-BBi丨=l可得定平台铰链点在基座坐标系中沿y方向的坐标表达式[8],为
| ${y_{Bi}}=\left\{ \begin{array}{l} {y_{pi}} - \sqrt {{L^2} - {{\left({{x_{Bi}} - {x_{pi}}} \right)}^2} - z_{pi}^2},i=1,5,6,\\ {y_{pi}}+\sqrt {{L^2} - {{\left({{x_{Bi}} - {x_{pi}}} \right)}^2} - z_{pi}^2},i=2,3,4 \end{array} \right.$ | (8) |
设向量P为动平台中心点在基座坐标系中的矢量描述,由此可得动平台虎克铰中心点在基座坐标系中的矢量描述为
| $^B{P_i}{=^B}{Q_p}{ \cdot ^P}{P_i}+P.$ | (9) |
根据上述表达式可得到放疗床的位姿逆解yBi,对于表达式中的正负号的选取,结合了动平台几何中心的位置和各滑块所在的位置.
1.3 影响工作空间的因素放疗床的位置工作空间可描述为,在不考虑动平台姿态转角情况下,即动平台平动时动平台中心点能够到达的最大空间范围[9,10].
1)影响放疗床工作空间的主要结构参数:r,为动平台虎克铰中心点Pi所在圆的半径;l(杆长参数),为定平台虎克铰中心点Bi与动平台虎克铰中心点Pi间的距离;λ,为相邻导轨间的距离;θp,为动平台虎克铰铰链分布角度.机构的工作空间可由r,l,λ,θp完全确定,因此,对以上4个参数进行初选、调整和优化来满足所需位置和姿态工作空间以及放疗床性能的要求.
2)逆解约束条件包括:①各虎克铰的转角应在允许的转动范围之内,即动平台中心运动到工作空间内的各个位姿,各虎克铰之间均不发生干涉;②连杆之间不发生干涉,即动平台在运动过程中相邻两杆之间的最短距离应大于连杆的直径[11];③定平台滑块的移动应在允许的行程范围内;④放疗床凸性限制,即各滑块沿导轨方向应在其相应动平台铰链点的外侧.
2 放疗床参数优化由于受到放射治疗使用过程和系统整体布局的限制,要求放疗床床板宽度及整体外形具有较小的尺寸,但并联机构本身工作空间较小,因此,需要通过优化参数来满足工作空间.基于以上限制,本文提出一种多目标协调机构参数优化方法,考虑工作空间、放疗床受力情况、雅可比矩阵条件数[12,13],以及构建关于条件数全域均值、条件数波动情况的目标函数,进行参数优化.
2.1 虎克铰初始安装角度优化在动平台所需的工作空间确定之后,可以通过优化虎克铰的初始安装角度的方法来减小虎克铰绕自身动坐标系x′轴和y′所需要的转角极限值,这样可以有效减小虎克铰的尺寸,进一步提高虎克铰的强度和刚度,在相同的受力情况下减小虎克铰的变形,提高放疗床的整体刚度[14,15].
先假设定平台各虎克铰绕基座坐标系x,z轴的初始安装角度均为零度,式(10)所示为动平台处于任意位姿时定平台每对虎克铰绕其自身坐标系的摆角α和β:
| $\left[\begin{array}{l} ^{Fi}x\\ ^{Fi}y\\ ^{Fi}z\\ 1 \end{array} \right]=\left[\begin{array}{l} l \cdot {\sin ^{Fi}}\beta \\ - l \cdot {\sin ^{Fi}}\alpha \cdot {\cos ^{Fi}}\beta \\ l \cdot {\cos ^{Fi}}\alpha \cdot {\cos ^{Fi}}\beta \\ 1 \end{array} \right].$ | (10) |
因此,遍历放疗床整个使用工作空间,求得各个位姿的定平台虎克铰的2个摆角,并找出每个虎克铰的摆角在整个遍历空间内所取得的最大值和最小值.在此,取最大与最小值的平均值作为虎克铰的初始安装角度,公式如下:
| $\alpha Fi=\frac{{^{Fi}{\alpha _{\max }}{+^{Fi}}{\alpha _{\min }}}}{2},$ | (11) |
| $\beta Fi=\frac{{^{Fi}{\beta _{\max }}{+^{Fi}}{\beta _{\min }}}}{2},$ | (12) |
得到定平台虎克铰的初始安装角度后,进行相应的圆整,数据见表 1.
| 虎克铰序号 | 绕x轴初始 安装角度/(°) | 绕z轴初始 安装角度/(°) |
| 定平台虎克铰1 | -41 | 2 |
| 定平台虎克铰2 | 41 | 2 |
| 定平台虎克铰3 | 35 | -7.5 |
| 定平台虎克铰4 | 35 | 5.5 |
| 定平台虎克铰5 | -35 | 5.5 |
| 定平台虎克铰6 | -35 | -7.5 |
同理,按照上述方法得到动平台各对虎克铰的初始安装角度后,进行相应的圆整,数据见表 2.
| 虎克铰序号 | 绕x轴初始 安装角度/(°) | 绕z轴初始 安装角度/(°) |
| 动平台虎克铰1 | -41 | -2 |
| 动平台虎克铰2 | 41 | -2 |
| 动平台虎克铰3 | 34 | 7.5 |
| 动平台虎克铰4 | 34 | -5.5 |
| 动平台虎克铰5 | -34 | -5.5 |
| 动平台虎克铰6 | -34 | 7.5 |
没考虑虎克铰初始安装角度时,在工作空间内,以动平台各对虎克铰为例,其绕自身坐标系轴线的转角范围如表 3所示.
| 虎克铰序号 | 绕x′轴的 转角范围/(°) | 绕y′轴的 转角范围/(°) |
| 动平台虎克铰1 | -72.2~-8.9 | -24.6~20.8 |
| 动平台虎克铰2 | 8.9~72.2 | -24.6~20.8 |
| 动平台虎克铰3 | -5.1~72.2 | -17.7~32.6 |
| 动平台虎克铰4 | -3.9~72.8 | -29.7~18.7 |
| 动平台虎克铰5 | -72.8~3.9 | -29.7~18.7 |
| 动平台虎克铰6 | -72.2~5.1 | -17.7~32.6 |
考虑虎克铰初始安装角度之后,在工作空间内,以动平台各对虎克铰为例,其绕自身坐标系轴线的转角范围如表 4所示.
| 虎克铰序号 | 绕x′轴的 转角范围/(°) | 绕y′轴的 转角范围/(°) |
| 动平台虎克铰1 | -31.2~32.1 | -22.6~22.8 |
| 动平台虎克铰2 | -32.1~31.2 | -22.6~22.8 |
| 动平台虎克铰3 | -39~38.2 | -25.5~25.1 |
| 动平台虎克铰4 | -37.9~38.8 | -24.2~24.2 |
| 动平台虎克铰5 | -38.8~37.9 | -24.2~24.2 |
| 动平台虎克铰6 | -38.2~39.1 | -25.2~25.1 |
通过上述分析得到,虎克铰绕z轴的初始安装角度较小,考虑绕z轴的初始安装角度后虎克铰的转角极限减小程度较小,且会给零件的加工和装配带来困难,因此,本文只考虑虎克铰绕x轴的初始安装角度,在保证满足工作空间的条件下,减小了虎克铰绕自身坐标系x轴的转角极限值,因此,可以有效减小虎克铰的结构尺寸.优化后虎克铰尺寸参数如表 5所示.
首先给定各几何参数一个初值,使这几个参数构成的放疗床模型满足其所需工作空间的要求.然后,固定除动平台半径r以外的其他几何参数,进一步通过工作空间分析可得,增大r可以增大放疗床的工作空间.但由于其实际的使用要求,床板宽度不能超过800 mm,进而r的取值受到一定的限制.
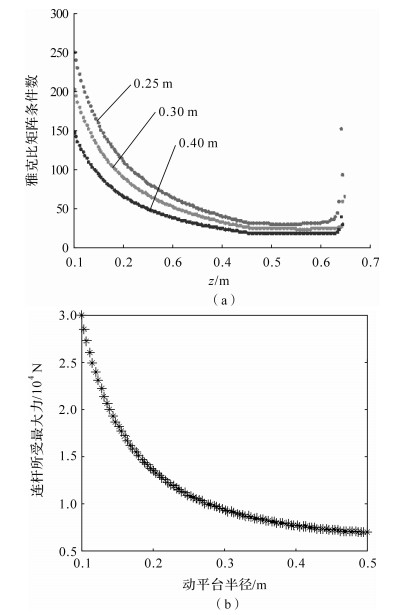
利用上述指标对放疗床的r进行优化.如图 3(a)所示,增大动平台半径r可以减小放疗床雅可比矩阵的条件数,且动平台的高度越大,机构的雅可比矩阵条件数越小.
|
| 图 3 动平台半径对放疗床性能影响 Fig. 3 Influence of moving platform radius on radiotherapy bed performance |
杆件所受的最大力在一定范围内随着动平台半径的增大而减小,如图 3(b)所示.因此,在床板宽允许的范围内,增大放疗床的动平台半径,可以起到增大工作空间、减小机构雅可比矩阵条件数以及减小杆件所受最大力的作用.进而,可以初步确定r较好的取值范围为300~400 mm.
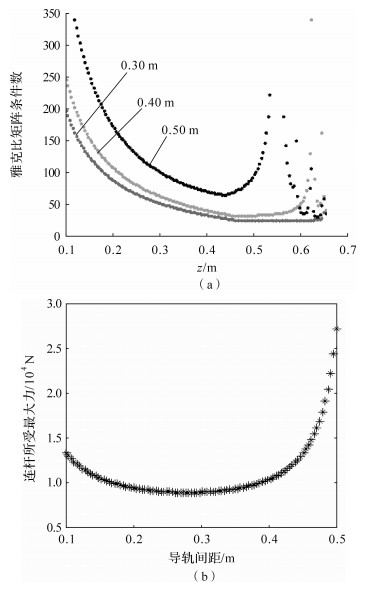
2.2.2 导轨间距λ固定除导轨间距λ以外的其他几何参数,进一步通过工作空间分析可得,当导轨间距λ略小于动平台半径时,放疗床的工作空间较大.如图 4(a)所示,导轨间距λ越小,动平台的高度越高,放疗床的雅克比矩阵条件数越小.
|
| 图 4 导轨间距对放疗床性能影响 Fig. 4 Influence of guide spacing on radiotherapy bed performance |
杆件所受的最大力在一定范围内随导轨间距的变化规律如图 4(b)所示,导轨间距在200~300 mm范围内变化时,杆件所受的最大力较小.因此,可以确定导轨间距较好的取值范围为200~300 mm.
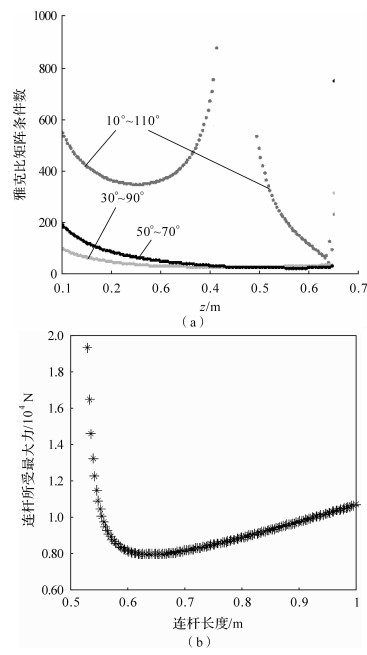
2.2.3 动平台铰链分布角度θp固定除θp以外的其他几何参数,进一步通过工作空间分析可得,θp对放疗床工作空间的影响很小,但主要对工作空间内雅可比矩阵条件数大小及分布产生影响.如图 5(a),30°~90°与50°~70°的铰链分布角度时雅可比矩阵条件数较小,并且随着动平台中心高度的增加条件数逐渐减小.在MATLAB中得到放疗床30°~90°的分布角度比50°~70°分布杆件所受的最大力要小,因此初步选30°~90°作为放疗床的铰链分布角度.
|
| 图 5 动平台铰链分布角度和杆长对放疗床性能的影响 Fig. 5 Influence of moving platform hinge distribution angle and rod length on radiotherapy bed performance |
固定除杆长l以外的其他几何参数,进一步通过工作空间分析可得,增大杆长l可以较大程度地增大放疗床的工作空间,但结构的整体尺寸会变得很大.根据放疗床的使用要求,床板前段下方要留出一定的空间放置影像板,用于X射线的成像,以便实时跟踪病灶部位,因此导轨长度受到制约,此情况下,在一定范围内减小连杆长度反而可以增大放疗床的工作空间.结合工作空间、雅可比矩阵条件数以及连杆受力对l进行优化显得尤为重要,如图 5(b),连杆长度在600~700 mm范围内时,连杆所受的最大力较小.因此,可以确定连杆长度较好的取值范围为600~700 mm.
2.3 放疗床几何参数最终确定以上通过对工作空间、雅可比矩阵条件数和连杆受力情况进行的分析,得到放疗床各几何参数较佳的取值范围.在此,通过建立目标函数对各参数进行最终的确定[16].将雅可比矩阵条件数的全域均值作为放疗床性能的评价指标,其反映了放疗床在整个工作空间内性能的平均水平[17,18],具体表达式如式(13)所示,
| $\bar \eta=\frac{{\sum\limits_{i=1}^n {{\rm{cond}}\left({{J_i}} \right)} }}{n}.$ | (13) |
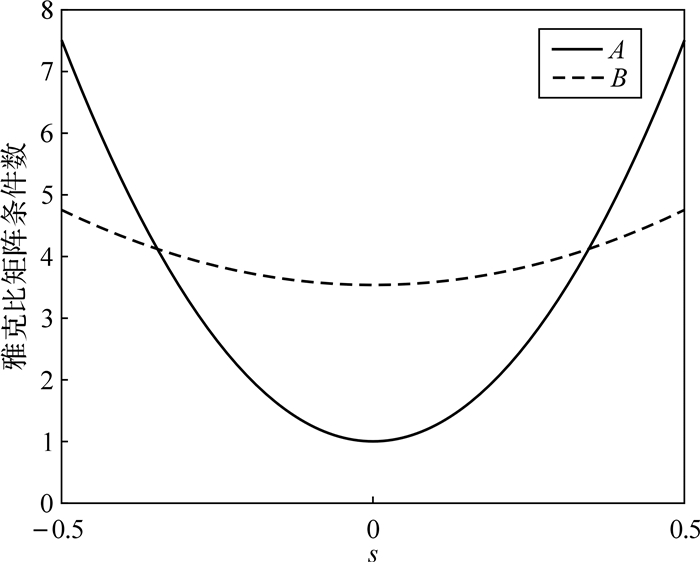
通过MATLAB编程,遍历以上分析得到的较佳的参数取值范围,对应每组参数均求取条件数的全域均值.此处应该指出,条件数的全域均值仅能反映全域上条件数的均值情况,不能反映其波动情况,故难于完整地表达放疗床全域操作性能.上述情况可通过一个图例加以说明.如图 6所示,设曲线A和曲线B分别表示A和B两个机构在归一后工作空间s⊂[-0.5,0.5]中雅可比矩阵条件数的变化,并用 ${{\bar \eta }_A}$>和 ${{\bar \eta }_B}$>分别表示它们的全域均值,并且可以由图中相应的曲线与s轴间的面积表示.由图可知, ${{\bar \eta }_A}$>小于 ${{\bar \eta }_B}$>,但是在边界处,机构A的雅可比矩阵条件数远高于机构B,因而不能说机构A的操作性能优于机构B.即雅可比矩阵的条件数在工作空间内有较大波动时,同样影响放疗床的操作性能,故不能完整表达放疗床全域性能.为此,构造一个能体现条件数波动情况的指标:
| $\tilde \eta=\frac{{\max \left({{\rm{cond}}\left(J \right)} \right)}}{{\min \left({{\rm{cond}}\left(J \right)} \right)}}$ | (14) |
|
| 图 6 机构A与机构B性能比较 Fig. 6 Performance comparison between institution A and institution B |
公式(14)中max(cond(J))和min(cond(J))分别表示在工作空间截面内雅可比矩阵条件数的最大值与最小值,因此 ${\tilde \eta }$>可以反映条件数在全域上的波动情况.为了综合考虑 ${\bar \eta }$>和 ${\tilde \eta }$>对放疗床性能的影响,构造如下目标函数:
| ${\eta _s}={{\bar \eta }^2}+{\left({\delta \tilde \eta } \right)^2},$ | (15) |
式中:σ表示加权因子,其值根据 ${\bar \eta }$>值的数量级确定,即若两者在同一数量级下,σ取值为1.
通过MATLAB编程,对上述得到的各参数较佳的取值范围进行遍历,求解各参数组合下ηs的值.此时,参数优化变为求解目标函数的最小值问题,即
| ${\eta _s}={{\bar \eta }^2}+{\left({\delta \tilde \eta } \right)^2} \to \min.$ | (16) |
通过上述优化得到各参数的取值,对得到的值进行圆整,最终得到放疗床的参数,见表 6.
| 参数 | 连杆长度 l/mm | 动平台半径 r/mm | 导轨间距 λ/mm | 动平台铰链分布 角度θp/(°) |
| 数值 | 650 | 309 | 281 | 29~91 |
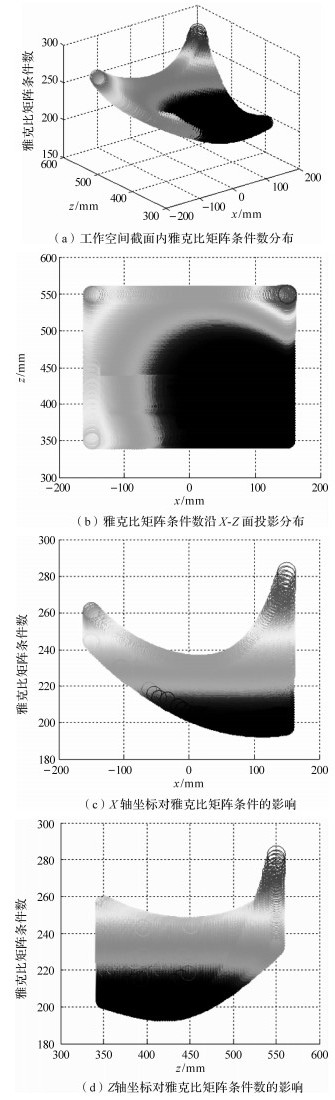
根据最终确定的几何参数,在MATLAB中得到放疗床雅可比矩阵条件数在工作空间截面内的分布,如图 7.由此可以看出,雅可比矩阵条件数在工作空间内较小且总体分布比较均匀,只有在工作空间截面内的边界部位,雅可比矩阵的条件数稍大些.
|
| 图 7 雅可比矩阵条件数分布 Fig. 7 Jacobian matrix condition number distribution |
为了实现放疗床的精确治疗,本文提出了一种多目标协调的机构参数优化方法,对参数进行具体优化,最终得到了放疗床各参数,使得放疗床在工作空间内雅可比矩阵条件数较小且分布均匀.
本文首先建立了放疗床的运动学模型,分析了各对虎克铰的运动范围,求得了放疗床在确定位姿下各虎克铰的确切摆角.对双端虎克铰形式的并联放疗床进行了工作空间的精确分析,得到了机构各参数对工作空间的影响,为放疗床的参数优化提供依据.之后提出了一种优化虎克铰初始安装角度的方法,在满足工作空间的条件下,可以有效减小虎克铰绕各轴的转角极限,进而减小虎克铰的尺寸.根据放疗床使用特性的要求,提出了一种多目标协调的机构参数优化方法,考虑工作空间、放疗床受力、雅可比矩阵条件数,以及构建关于条件数全域均值、条件数波动情况的目标函数,进行参数的具体优化,最终得到了放疗床各参数,使得放疗床在工作空间内雅可比矩阵条件数较小且分布均匀.
| [1] | 杨瑞杰,王俊杰.放射治疗质量保证与患者安全:2013北美放射肿瘤年会进展[J].中国医疗设备,2014(29):163-164. YANG Rui-jie,WANG Jun-jie.Radiotherapy quality assurance and patient safety:the progress of 2013 ASTRO annual meeting[J].China Medical Device,2014(29):163-164. |
| Cited By in Cnki (4) | |
| [2] | 甄鑫.自适应放射治疗中的图像变形配准关键技术研究[D].广州:南方医科大学生物医学工程学院,2013:1-10. ZHEN Xin.Research of deformable image registration for adaptive radiation therapy[D].Guangzhou:Southern Medical University,School of Biomedical Engineering,2013:1-10. |
| Cited By in Cnki (4) | |
| [3] | SPEZI E,FERRI A.Dosimetric characteristics of the Simens IGRT carbon fiber tabletop[J].Med Dos,2007,32(4):295-298. |
| Click to display the text | |
| [4] | SINCLAIR J,CHANG S D,GIBBS I C,et al.Multisession Cyberknife radiosurgery for intramedullary spinal cord arteriovenous malformations[J].Neurosurgery,2006,58(6):1081-1089. |
| Click to display the text | |
| [5] | 彭忠琦.并联机构的发展及应用[J].光机电信息,2011,28(12):45-50. PENG Zhong-qi.Development and application of parallel mechanism[J].Ome Information,2011,28(12):45-50. |
| Cited By in Cnki (37) | Click to display the text | |
| [6] | 黄鹏,汪劲松,王立平,等.3-PRS并联机构误差运动学分析及辨识[J].清华大学学报(自然科学版),2010,50(11):1811-1814. HUANG Peng,WANG Jing-song,WANG Li-ping,et al.Kinematical error analysis and identification of a 3-PRS parallel mechanism[J].Journal of Tsinghua University (Science & Technology),2010,50(11):1811-1814. |
| Cited By in Cnki (6) | Click to display the text | |
| [7] | 谢志江,史浩明.6-HUS并联机构位置逆解与运动学优化设计[J].机械设计,2011,12(12):26-30. XIE Zhi-jiang,SHI Hao-ming.Inverse positions solution and kinematics optimal design based on a 6-HUS parallel mechanism[J].Journal of Machine Design,2011,12(12):26-30. |
| Cited By in Cnki (3) | Click to display the text | |
| [8] | 皮阳军,王骥,胡玉梅.并联六自由度机构运动学与动力学标定对比[J].哈尔滨工程大学学报,2014,35(11):1422-1426. PI Yang-jun,WANG Ji,HU Yu-mei.Comparison of dynamic and kinematic calibrations for the 6-DOF parallel mechanism[J].Journal of Harbin Engineering University,2014,35(11):1422-1426. |
| Cited By in Cnki (2) | |
| [9] | 于凌涛,孙立宁,杜志江.并联机器人胡克铰工作空间的研究与应用[J].机械工程学报,2006,42(8):120-124. YU Ling-tao,SUN Li-ning,DU Zhi-jiang.Study and application of workspace on Hooke joint in parallel robot[J].Journal of Mechanical Engineering,2006,42(8):120-124. |
| Cited By in Cnki (24) | Click to display the text | |
| [10] | 刘玉斌,赵杰,杨永刚,等.一种新型6-PRRS并联机器人工作空间分析[J].机械与电子,2007(2):53-56. LIU Yu-bin,ZHAO Jie,YANG Yong-gang,et al.Workspace analysis of a novel 6-PRRS parallel robot[J].Machinery & Electronics,2007(2):53-56. |
| Cited By in Cnki (2) | Click to display the text | |
| [11] | DASGUPTA B,MRUTHYUNJAYS T S.The stewart platform manipulator:a review[J].Mech Mach Theory,2000,35(1):15-40. |
| Click to display the text | |
| [12] | 孙立宁,于晖,祝宇虹,等.机构影响系数和并联机器人雅克比矩阵的研究[J].哈尔滨工业大学学报,2002,34(6):810-814. SUN Li-ning,YU Hui,ZHU Yu-hong,et al.Influence coefficient of mechanism and Jacobia matrix of parallel robot[J].Journal of Harbin Institute of Technology,2002,34(6):810-814. |
| Cited By in Cnki (60) | Click to display the text | |
| [13] | 兰陟,李振亮,李亚,等.基于旋量理论的5-DOF上肢康复机器人雅克比矩阵求解[J].机械设计,2011,28(5):51-53,74. LAN Zhi,LI Zhen-liang,LI Ya,et al.Calculation of Jacobin matrix of a 5-DOF upper limb re-habilitation robot based on screw theory[J].Journal of Machine Design,2011,28(5):51-53,74. |
| Cited By in Cnki (6) | |
| [14] | 盖永军,王静泉.虎克铰在6-UPU运动平台中的应用[J].电子测试,2014(z1):52-54. GAI Yong-jun,WANG Jing-quan.Application of Hooke Joints in 6-UPU motion platform[J].Electronic Test,2014(z1):52-54. |
| Cited By in Cnki | |
| [15] | 赵强,阎绍泽.双端虎克铰型六自由度并联机构的动力学模型[J].清华大学学报(自然科学版),2005,45(5):610-613. ZHAO Qiang,YAN Shao-ze.Dynamic model of a 6-DOF parallel mechanism with Hooke's joints at both chain ends[J].Journal of Tsinghua University(Science and Technology),2005,45(5):610-613. |
| Cited By in Cnki (34) | Click to display the text | |
| [16] | 孙小勇,郑彬,鲍捷,等.高速6-PSS并联机器人参数优化设计[J].农业机械学报,2015,46(5):372-378. SUN Xiao-yong,ZHEN Bin,BAO Jie,et al.Parameter optimization design of high-speed 6-PSS parallel robot[J].Transactions of the Chinese Society for Agricultural Machinery,2015,46(5):372-378. |
| Cited By in Cnki (1) | Click to display the text | |
| [17] | 黄府,刘会议.基于雅可比矩阵条件数的并联机构参数优化[J].机械,2012,39(12):41-45. HUANG Fu,LIU Hui-yi.Parameters optimization of parallel mechanism based on the condition of Jacobian matrix[J].Machinery,2012,39(12):41-45. |
| Cited By in Cnki (9) | Click to display the text | |
| [18] | 魏永庚,袁明,石勇,等.基于雅克比矩阵的并联机构结构参数优化设计[J].黑龙江大学工程学报,2015(1):87-91. WEI Yong-kang,YUAN Ming,SHI Yong,et al.Structure parameters optimization design of parallel mechanism based on Jacobian matrix[J].Journal of Engineering of Heilongjiang University,2015(1):89-91. |
| Cited By in Cnki (2) | Click to display the text |



