全柔性并联机构具有分辨率高、运动灵活、动态特性好等优点,在生物工程、集成电路制造、光学微处理等微观领域得到了广泛应用.随着微观领域技术的不断拓展,对机构的性能提出了更高的要求,因此设计出一种操作行程大、动态响应速度快和运动精度高的新型全柔性并联机构具有重要意义[1].机构的“型”是研究的理论基础,也是提高其刚度和定位精度的重要因素[2].目前,大多是通过将并联机构各运动铰链的运动副以柔性铰链代替,再用柔性连杆连接各柔性铰链,从而设计出全柔性并联机构,即为柔性铰链替换法.例如王硕[3]设计的3-RPR柔性并联微位移机构,杨启志等[4]设计的非对称3-RPRR全柔性平移微动并联机构.为了克服空间全柔性并联机构构型设计的缺陷,Howell[5]将柔性铰链和机构构型集成在一整体材料上,采用线切割加工方式得到类平面全柔性并联机构支链及其构型,但该方法仍未解决柔性铰链在整体材料上的配置问题.拓扑优化方法[6]能够在一定的约束条件下,删除一些不必要的单元并保持机构的原有特性,该方法只需设定好原始的设计区域、机构的约束位置以及驱动力的加载位置,系统就会根据受力情况自动地在设计空间内寻找出最佳的应力应变分布形式,避免了全柔性机构铰链设计的随机性.本文首先基于全柔性并联机构原型,采用型综合法[7,8],设计与并联机构原型空间运动特性一致的3-RPRR类平面全柔性机构;然后对3-RPRR类平面全柔性机构进行拓扑优化,去除随机性设计的柔性铰链,找到其整体柔度最小时的应力应变分布位置,根据优化结果设计出最优配置的3-RPRR类平面全柔性并联机构;最后利用Hyperworks/Radioss软件分别对2种类平面全柔性并联机构进行静力学分析和模态分析.
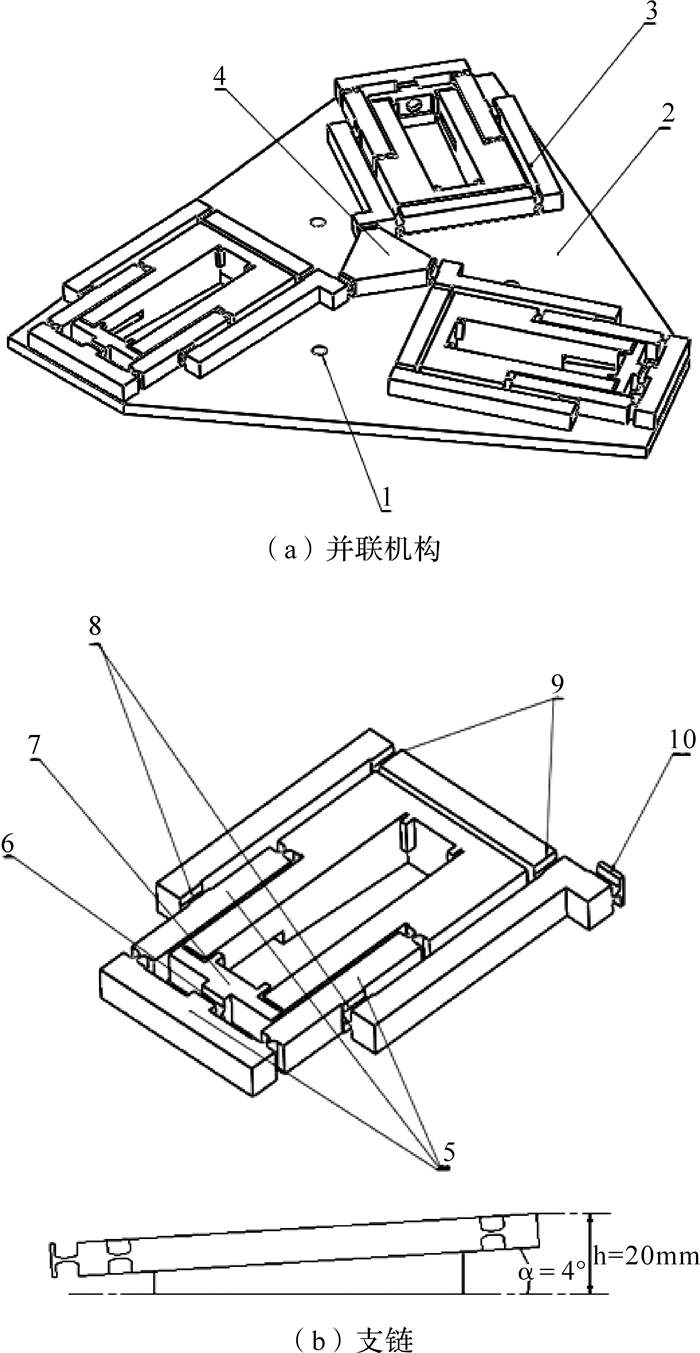
1 3-RPRR类平面全柔性并联机构设计基于3-RPRR并联机构原型,以型综合法为理论依据,通过研究传统并联原型机构的空间几何矢量约束关系,在整体板材上通过先进的线切割技术切出与原型机构各运动副相对应的柔性运动副,将各柔性运动副运动轴线的相对几何关系与并联原型机构各运动副运动轴线的相对几何关系保持一致,设计出3-RPRR类平面全柔性机构及其支链,如图 1所示.3-RPRR类平面全柔性机构有3条支链,每条支链由3个转动副(R副)和一个移动副(P副)组成.在全柔性支链中,以柔性移动副7作为驱动副,为了使RPRR全柔性支链具有良好的运动特性,设计2组相对于移动副7的辅助转动副8和9,共同实现支链转动副的运动特性.
|
| 1—固定螺栓孔;2—静平台;3—柔性支链;4—动平台;6,8,9,10—柔性转动副;5,7—柔性移动副. 图 1 3-RPRR类平面全柔性并联机构及其支链 图 1 3-RPRR类平面全柔性并联机构及其支链 Fig. 1 3-RPRR planar fully compliant parallel mechanism and its branched chains |
3-RPRR类平面全柔性并联机构为三输入三输出的机构,根据类平面全柔性并联机构理论的输入输出映射关系,以材料密度为设计变量,柔度最小为目标函数,优化前后的材料体积比以及驱动端的合位移为约束条件,构建3-RPRR类平面全柔性并联机构的优化模型为
| $\left\{ \begin{array}{l} \min \;c=\sum\limits_{i=1}^3 {\sum\limits_{j=1}^3 {\tilde U_j^{\rm{T}}K{U_i}=\sum\limits_{e=1}^N {\sum\limits_{i=1}^3 {\sum\limits_{j=1}^3 {\rho _e^p\tilde U_{ej}^{\rm{T}}{K_e}{U_{ei}},} } } } } \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;K{{\tilde U}_i}={{\tilde F}_i},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;K{U_i}=U{F_i},\\ \tilde F={J_i}F,\\ \int_\Omega {{\rho _e}{\rm{d}}\Omega \le V,} \\ i,j - 1,2,3,;e=1,2,\ldots,N. \end{array} \right.$ |
式中:${\tilde U}$为伴随位移的转置矩阵;K为优化后类平面全柔性并联机构的整体刚度;U为实际载荷下的位移;ρe为第e个单位的相对密度;p为中间材料的密度惩罚因子,在工程实际应用中,一般取3≤p≤5;${{\tilde U}_{ej}}$为第j个虚载荷下单元e的位移;Ke为单元e的刚度;${{\tilde U}_{ei}}$为第i个实际载荷下单元e的位移;${\tilde F}$为第i个虚载荷;Fi为第i个实际载荷;V为类平面全柔性并联机构优化后的体积.
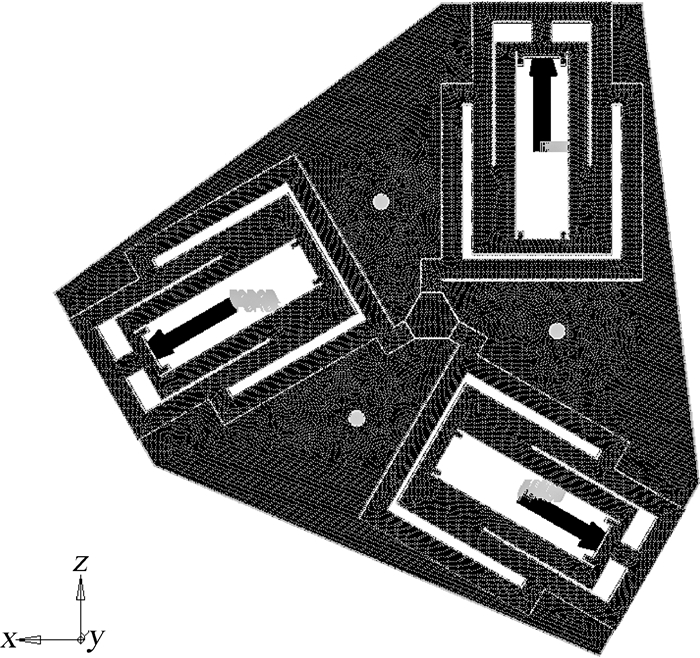
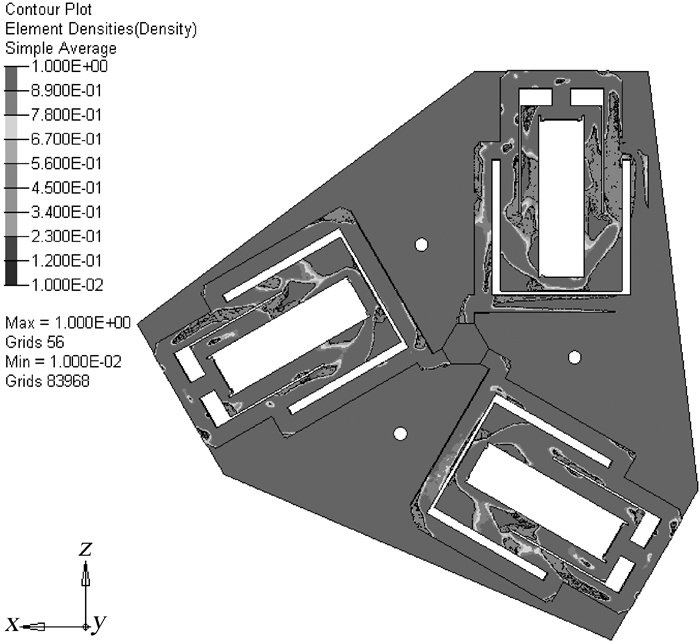
2.2 仿真实验及优化结果在综合考虑机构的柔度和刚度的情况下,机构的材料选用65Mn(弹簧钢),弹性模量E=207 GPa,泊松比μ=0.3,密度为7 900 kg/m3.采用四面体网格,网格尺寸定义为1.将支链部分设置成设计域,动、静平台设置成非设计域,设计域离散为1 582 243个四面体单元和351 600个节点.在3个输入端分别施加1 000 N的静载荷,在动平台的中心处定义沿着X,Y,Z三个轴的平动的3个输出,有限元模型如图 2所示.以柔度最小为目标函数,优化前后材料的体积比为约束条件进行拓扑优化.经过7次拓扑优化迭代,可得拓扑优化后的材料分布情况,如图 3所示.
|
| 图 2 3-RPRR拓扑优化有限元模型 Fig. 2 Topology optimization finite element model of3-RPRR |
|
| 图 3 3-RPRR类平面全柔性并联机构拓扑优化结果 Fig. 3 Topology optimization results of 3-RPRR planar fully compliant parallel mechanism |
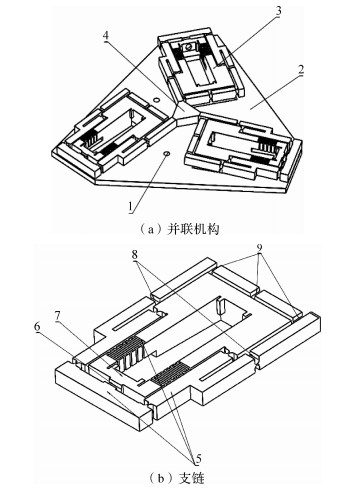
在实现运动特性的前提下,从图 3可以看出3-RPRR类平面全柔性并联机构在支链柔度最小时的应力应变分布情况.根据应力应变分布图,适当地去除部分多余材料,设计出铰链最优配置的3-RPRR类平面全柔性并联机构及其支链,如图 4所示.
|
| 1—固定螺栓孔;2—静平台;3—柔性支链;4—动平台;6,8,9—柔性转动副;5,7—柔性移动副. 图 4 优化后3-RPRR类平面全柔性并联机构及其支链 Fig. 4 Optimized 3-RPRR planar fully compliant parallel mechanism and its branched chains |
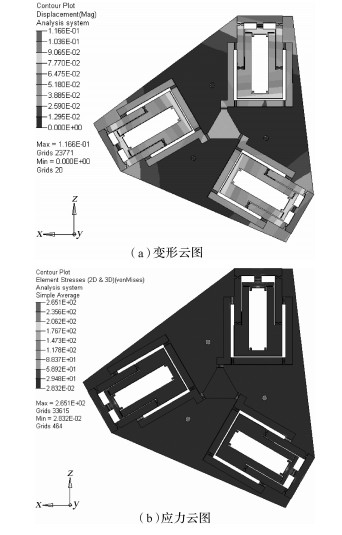
在Solidworks中建立2种3-RPRR类平面全柔性并联机构的三维模型,并且导入Hyperworks中进行有限元分析.采用四面体网格划分,2种机构的材料均选用65Mn(弹簧钢),其弹性模量为207 GPa,泊松比为0.3,密度为7 850 kg/m3.设定构型固定螺栓处的自由度为0,对其3个分支的驱动端上分别施加500 N的载荷[9,10].2种机构的变形云图以及应力云图分别如图 5和图 6所示.
3.2 刚度分析经过有限元分析,得到2种机构在受到外力作用时的位移矩阵分别为:
|
| 图 5 优化前机构变形云图以及应力云图 Fig. 5 Deformation cloud and stress cloud of mechanism before optimization |
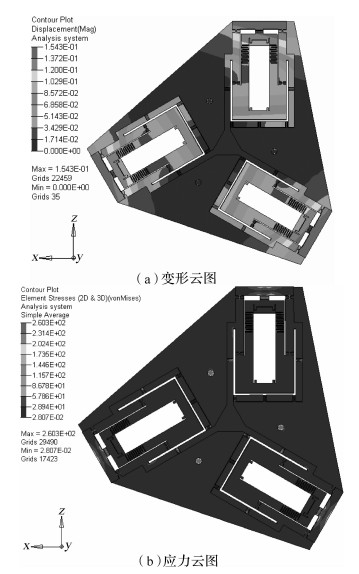
|
| 图 6 优化后机构变形云图以及应力云图 Fig. 6 Deformation cloud and stress cloud of optimized mechanism |
| $\begin{array}{l} {\delta _1}=\left[{\begin{array}{*{20}{c}} {0.0183}&{ - 0.0715}&{ - 0.0326}\\ {0.01810}&{ - 0.0722}&{0.0347}\\ { - 0.0394}&{ - 0.0731}&{ - 0.0156} \end{array}} \right],\\ {\delta _2}=\left[{\begin{array}{*{20}{c}} { - 0.0114}&{ - 0.0674}&{ - 0.112}\\ {0.0975}&{ - 0.0756}&{0.0478}\\ { - 0.0882}&{ - 0.0753}&{0.0568} \end{array}} \right]. \end{array}$ |
将施加在机构上的载荷分解为如下所示的3个线性独立的力螺旋:
| ${F_1}=\left[\begin{array}{l} {f_x}\\ 0\\ 0 \end{array} \right],{F_2}=\left[\begin{array}{l} 0\\ {f_y}\\ 0 \end{array} \right],F3=\left[\begin{array}{l} 0\\ 0\\ {f_z} \end{array} \right],$ | (1) |
式中:fx,fy和fz分别代表施加在X轴、Y轴和Z轴上的力.
在静平衡条件下,由虚功原理可以得到2种方案的类平面全柔性并联机机构静刚度模型为[11]:
| $K=\delta \cdot {F^{ - 1}}$ | (2) |
令K1,K2分别为优化前和优化后支链构成的3-RPRR类平面全柔性并联机构的静刚度矩阵,则由式(1)和式(2)可得:
| $\begin{array}{l} {K_1}=\left[{\begin{array}{*{20}{c}} {830}&{3340}&{1670}\\ {920}&{3270}&{1460}\\ {1940}&{3350}&{710} \end{array}} \right],\\ {K_2}=\left[{\begin{array}{*{20}{c}} {520}&{3460}&{500}\\ {4640}&{3540}&{2410}\\ {4350}&{3620}&{2700} \end{array}} \right]. \end{array}$ |
由上述数据可以得出,在去除部分材料后K2仍略大于K1,说明优化后的3-RPRR类平面全柔性并联机构在刚度方面更优.因此优化后的3-RPRR类平面全柔性支链构成的整体机构的动态性能和定位精度更好.
4 基于Hyperworks/Radioss的模态分析模态分析的目的是识别出系统的模态参数,为系统的振动特性分析、振动故障诊断和预报以及机构动力特性的优化设计提供依据.相比有预应力的情况,类平面全柔性并联机构在无预应力的条件下固有频率数值较小且变化不大.因此,只研究在无预应力条件下的2种类平面全柔性并联机构构型的前3阶振动频率.2种机构的前3阶固有频率值和前3阶振型图分别如表 1、图 7和图 8所示.
| 优化前后 | 固有频率/Hz | ||
| 1阶 | 2阶 | 3阶 | |
| 优化前 | 289.66 | 314.89 | 456.67 |
| 优化后 | 365.66 | 366.67 | 380.1 |
| 提高率/% | 26.24 | 16.45 | 20.22 |
由表 1、图 7和图 8可以看出,铰链优化配置后的类平面全柔性并联机构与优化配置前的机构相比,前3阶固有频率均提高15%以上,并且其动态特性也稍有提高.说明铰链优化后的3-RPRR类平面全柔性并联机构在抗振性和抗干扰性方面更优.

|
| 图 7 优化前机构的前3阶振型图 Fig. 7 Former three order vibration model charts of mechanism before optimization |

|
| 图 8 优化后机构的前3阶振型图 Fig. 8 Former three order vibration model charts ofoptimized mechanism |
本文首先基于3-RPRR并联机构原型,采用型综合法设计出3-RPRR类平面全柔性机构及其支链.然后,运用拓扑优化的方法,得到支链柔度最小时的应力应变图,设计出铰链最优配置的3-RPRR类平面全柔性并联机构及其支链.最后,利用Hyperworks/Radioss分别对2种机构进行静力学和模态分析,得到机构在受到驱动力后的位移和应力分布云图以及机构的前3阶固有频率和阵型,仿真结果表明:
1) 2种类平面全柔性并联机构都能实现空间三平移运动,验证了设计的有效性、正确性;
2) 铰链优化配置后的3-RPRR类平面全柔性并联机构相比于优化前具有较大的整体刚度、更优的抗干扰性及抗振性,并且更省材料;
3) 基于拓扑优化的铰链最优配置方法更适用于精密加工和微定位操作等研究领域.
| [1] | 国家自然科学基金委员会工程与材料科学部.机械工程学科发展战略报告(2011—2020)[M].北京:科学出版社,2010:10-16. National Natural Science Foundation of Engineering and Materials Science Department.Report on development strategy of mechanical engineering discipline (2011—2020)[M].Beijing:Science Press,2010:10-16. |
| [2] | 于靖军,宗光华,毕树生.全柔性机器人机构的结构构型研究[J].机器人,2003,25(4):367-372. YU Jing-jun,ZONG Guang-hua,BI Shu-sheng.Fully compliant robotic mechanisms and their configurations[J].Robot,2003,25(4):367-372. |
| Cited By in Cnki (16) | Click to display the text | |
| [3] | 王硕.3-RPR柔性并联微位移机构的设计与分析[D].北京:北京交通大学机械与电子控制工程学院,2007:19-25. WANG Shuo.Design and analysis of 3-RPR flexible parallel micro-displacement mechanism[D].Beijing:Beijing Jiaotong University,School of Mechanical,Electronic and Control Engineering,2007:19-25. |
| Cited By in Cnki (10)Click to display the text | |
| [4] | 杨启志,马履中,郭宗和,等.全柔性并联机器人支链静刚度矩阵的建立[J].中国机械工程,2008,19(10):1156-1159. YANG Qi-zhi,MA Lü-zhong,GUO Zong-he,et al.Establishing the static stiffness matrix of compliant chain for a fully compliant parallel robot using D-H transformation method[J].China Mechanical Engineering,2008,19(10):1156-1159. |
| Cited By in Cnki (12) | Click to display the text | |
| [5] | HOWELL L L.Complaint mechanisms[M].New York:Wiley Interscience,2001:1-47. |
| [6] | BENDSOE M P,SIGMUND O.Topology optimization[M]. Germany:Springer,2004:56-82. |
| [7] | CHARLES J Kim.A conceptual approach to the computa-tional synthesis of compliant mechanisms[D].Michigan:University of Michigan,School of Engineering,2005:113-132. |
| Click to display the text | |
| [8] | 李守忠,于靖军,宗光华.基于旋量理论的并联柔性机构构型综合与主自由度分析[J].机械工程学报,2010,46(13):54-60.LI Shou-zhong,YU Jing-jun,ZONG Guang-hua.Type synthesis and principal freedom analysis of parallel flexure mechanisms based on screw theory[J].Journal of Mechanical Engineering,2010,46(13):54-60. |
| Cited By in Cnki (21) | Click to display the text | |
| [9] | BOUDEWIJN R,DANNIS M B,MEINT J,et al.Design and fabrication of a planar three-DOFs manipulator[J].Journal of Microelectromechanical Systems,2010,19(5):1116-1130. |
| Click to display the text | |
| [10] | 刘庆玲.柔性对称微位移放大机构性能分析方法的研究[J].工程设计学报,2013,20(4):345-347.LIU Qing-ling.Study on the performance analysis methods of the compliant symmetric micro-displacement magnifying mechanism[J].Chinese Journal of Engineering Design,2013,20(4):345-347. |
| Cited By in Cnki (10) | Click to display the text | |
| [11] | 朱春霞.基于有限元的3-TPT并联机床结构特性研究[D].沈阳:东北大学机械工程与自动化学院,2006:44-58.ZHU Chun-xia.Research on 3-TPT parallel machine tool structural characteristics based on finite element analysis[D].Shenyang:Northeastern University,School of Mechanical Engineering and Automation,2006. |
| Cited By in Cnki (12) |


