从20世纪到如今21世纪,微电子封装技术一直是微电子厂家核心竞争力的重要体现之一[1].为实现微电子封装高效、稳定、经济的目的,世界各地的研究人员在创新封装方式、建立封装过程模型以及优化控制算法等方面进行了大量的研究.随之微电子封装中的关键技术——流体点胶技术得到了空前的发展[2,3].
点胶是一种将封装用胶液如环氧树脂、硅胶等分配到芯片、集成电路所需位置的技术[4,5,6,7].目前盛行4种形式的点胶技术,包括螺旋泵式、时间压力式、活塞泵式和喷射式点胶[8,9,10,11].前3种形式的点胶技术均为接触式,而喷射式点胶为非接触式的点胶技术.非接触式喷射点胶能大大提高胶液的分配速度,并且胶点均匀.因其具有高效、非接触等优点而被普遍认为是最具发展潜力的新一代点胶技术[12,13].
喷射式点胶技术虽已被提出并发展了很长一段时间,但是在喷射高黏度微量胶滴的工况下,其喷射性能尚未完全达到工业界的要求.其原因之一在于现有关键点胶设备——点胶阀喷射高黏胶液能力不足,这就会导致喷嘴口挂胶现象严重甚至无法喷射等.目前通常采用加温的方式降低胶液的黏度,进而间接地提高点胶阀喷射能力,但该方式又带来了胶液性质变化、固化速度加快等问题.所以加温不能完全解决点胶阀喷射能力不足的问题.因此,优化喷射阀本身以提高其高黏胶液喷射能力成为必要.
影响点胶阀喷射能力的一个非常重要的因素是其流道的尺寸.特别是占据大部分流道空间的回流腔,其可认为回流间隙是喷射阀流道尺寸中一项关键尺寸.其原因是回流间隙与供胶压力决定了回流阻力的大小,而回流阻力影响撞针撞击喷嘴基座的速度,进而影响挤压腔内流体压强的大小.挤压腔内的压强则直接决定了胶滴喷落速度.然而,对于点胶阀流道尺寸方面的优化,目前所做的研究工作非常少.Nguyen,Shan等从机理出发分别建立了点胶阀体内部流体稳态、非稳态模型[14,15,16],Chen等为喷嘴外部胶液拉丝断裂机理建立了模型[17].这些工作均侧重于胶液喷射机理的研究,目的在于更深入地了解喷射阀的工作机理.但模型的完备性与准确性不足,使得以上工作尚不能直接用于阀体的流道尺寸优化.
本文基于数值仿真进行点胶阀流道尺寸的优化.文章首先简单介绍了喷射点胶阀的工作原理.然后根据流体本构方程建立了点胶阀的胶液喷射模型,并结合Fluent软件实现点胶阀的胶液喷射动态仿真.相应的点胶阀喷射实验验证了仿真模型的正确性.最后采用仿真模型进行了回流间隙的优化分析,与此同时,建立回流间隙与胶滴滴落速度的高斯拟合模型.通过对该模型的极值求解获得回流腔的最优回流间隙.进一步的仿真结果显示:优化后的回流腔相比未优化的,其喷射能力有了明显的提升.
1 气动喷射阀简介与实验平台目前市场上的非接触式喷射点胶阀产品众多,按撞针的驱动原理可以分为以下4类:气动弹簧式、超磁伸缩式、压电陶瓷式、电磁弹簧式.各种类型的喷射阀各有优缺点,本文实验中所用的气动喷射阀具有结构简单、经济等特点[18].因此,气动式是电子封装工业使用较普遍的类型.无论何种喷射点胶阀,其喷射出胶均靠阀内撞针快速撞击挤压作用,所以文中优化回流间隙的思路与方法具有普遍适用性.
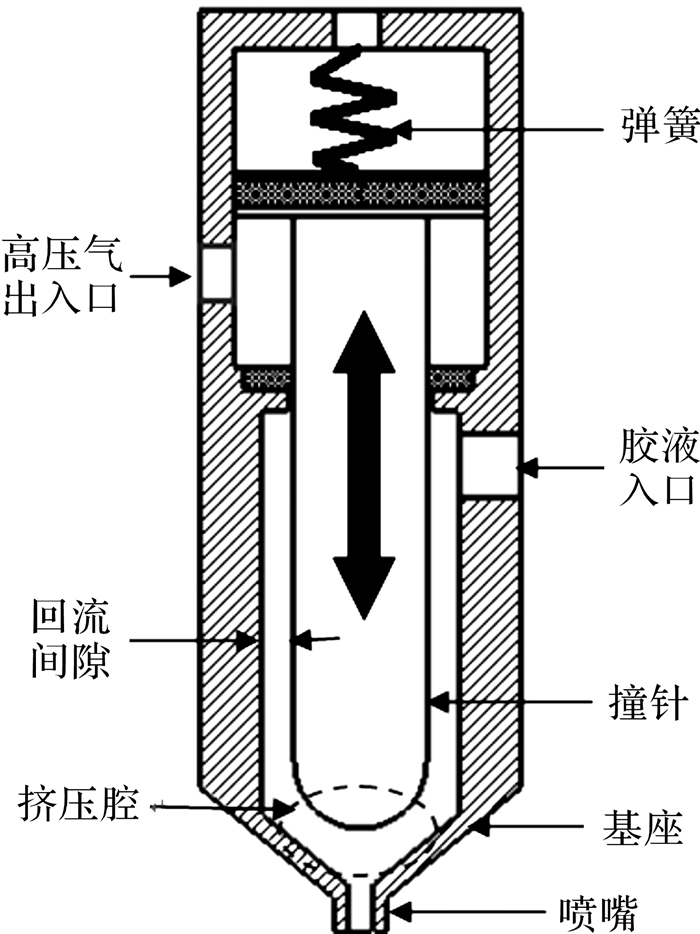
气动式喷射的工作原理比较简单,其工作原理如图 1所示.首先,高压气体进入阀体空腔并推动撞针上移进而压缩弹簧,同时胶液进入撞击腔内进行胶液补充;然后,释放高压气体,此时压缩弹簧迅速推动撞针下移并撞击基座,撞击过程中撞击腔内将形成极高压强;最后,微量胶液因高压喷射而出.
|
| 图 1 喷射阀结构简图 Fig. 1 Schematic structure of jetting valve |
实验平台搭建如图 2所示,其中:控制器用于点胶阀的3个轴向运动控制,以及对点胶频率、气压、温度等工作参数的控制;高速摄像仪采用的是FAST-CAM SA1.1(由Photron生产),它能以1 024×1 024的高分辨率和5 400帧/s的高速进行拍摄;监视器用于显示并记录高速摄像仪所拍摄的图片;撞针位移测量系统能时刻记录阀体内部撞针的位移数据.

|
| 图 2 实验平台 Fig. 2 Experiment setup |
1)连续性方程为
| $\frac{{\partial \rho }}{{\partial t}}+\frac{\partial }{{\partial x}}\left({\rho {u_x}} \right)+\frac{\partial }{{\partial r}}\left({\rho {u_r}} \right)+\frac{{\rho {u_r}}}{r}=0,$ |
其中:ρ为胶液密度,由于不考虑胶液可压缩,式中ρ为常值;x为轴向坐标,r为径向坐标;ux为轴向速度,ur为径向速度.
2)动量守恒方程为
| $\begin{array}{l} \frac{{\partial \left({\rho {u_x}} \right)}}{{\partial t}}+\frac{1}{r}\;\frac{{\partial \left({r\rho {u_x}{u_x}} \right)}}{{\partial x}}+\frac{1}{r}\;\frac{{\partial \left({r\rho {u_r}{u_x}} \right)}}{{\partial r}}=\\ - \frac{{\partial P}}{{\partial x}}+\frac{1}{r}\frac{\partial }{{\partial x}}\;\left[{r\mu \left({\frac{{2\partial {u_x}}}{{\partial x}} - \frac{2}{3}\left({\nabla \cdot u} \right)} \right)} \right]+\\ \frac{1}{r}\frac{\partial }{{\partial r}}\;\left[{r\mu \left({\frac{{\partial {u_x}}}{{\partial r}}+\frac{{\partial {u_x}}}{{\partial x}}} \right)} \right],\\ \frac{{\partial \left({\rho {u_r}} \right)}}{{\partial t}}+\frac{1}{r}\;\frac{{\partial \left({r\rho {u_x}{u_r}} \right)}}{{\partial x}}+\frac{1}{r}\;\frac{{\partial \left({r\rho {u_r}{u_r}} \right)}}{{\partial r}}=\\ \frac{2}{3}\frac{\mu }{r}\left({\nabla \cdot u} \right)+\frac{1}{r}\frac{\partial }{{\partial r}}\;\left[{r\mu \left({\frac{{2\partial {u_r}}}{{\partial r}} - \frac{2}{3}\left({\nabla \cdot u} \right)} \right)} \right] - \\ \frac{{\partial P}}{{\partial r}}+\frac{1}{r}\frac{\partial }{{\partial x}}\;\left[{r\mu \left({\frac{{\partial {u_r}}}{{\partial x}}+\frac{{\partial {u_x}}}{{\partial r}}} \right)} \right] - 2\mu \frac{{{u_r}}}{{{r^2}}}, \end{array}$ |
其中:
| $\nabla \cdot u=\frac{{\partial {u_x}}}{{\partial x}}+\frac{{\partial {u_r}}}{{\partial r}}+\frac{{{u_r}}}{r},$ |
P为流体压强,μ为胶液黏度.
3)流体体积函数(VOF)为
| $\begin{array}{l} \frac{1}{{\rho q}}\left[{\frac{\partial }{{\partial t}}\left({{\alpha _q}{\rho _q}} \right)+\nabla \cdot \left({{\alpha _q}{\rho _q}{\mu _q}} \right)} \right]=\sum\limits_{p=1}^n {\left({{{\dot m}_{pq}} - {{\dot m}_{q\;\;\;\;}}_p} \right)},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{p=1}^n {{\alpha _q}=1,} \end{array}$ |
其中:q,p分别意味着第q,p相;αq是q相在单元格的体积分数,αq=0表明单元格q相为空,αq=1表示单元格全为q相,0<αq<1则表明单元格包含边界;ρq为q相密度;}$ {m_{pq}} $为p相至q相的质量传递;n为仿真中出现的总的相数.
2.2 数值仿真模型实现本文要仿真的对象为气动喷射阀内被弹簧驱动的撞针开始运动到撞击基座这一运动而导致的物理出胶过程.实验所用气动喷射阀胶液入口以下为轴对称结构,而喷射阀的喷嘴又离胶液入口较远,所以胶液入口以下流体区域可以轴对称结构进行等效近似.表 1为笔者实验所用的某公司生产的气动喷射阀部分参数.
| 序号 | 名称 | 数值 |
| 1 | 回流间隙 | 0.15 |
| 2 | 撞针直径 | 2.7 |
| 3 | 回流腔长 | 18.8 |
| 4 | 喷嘴直径 | 0.35 |
| 5 | 基板距离 | 5 |
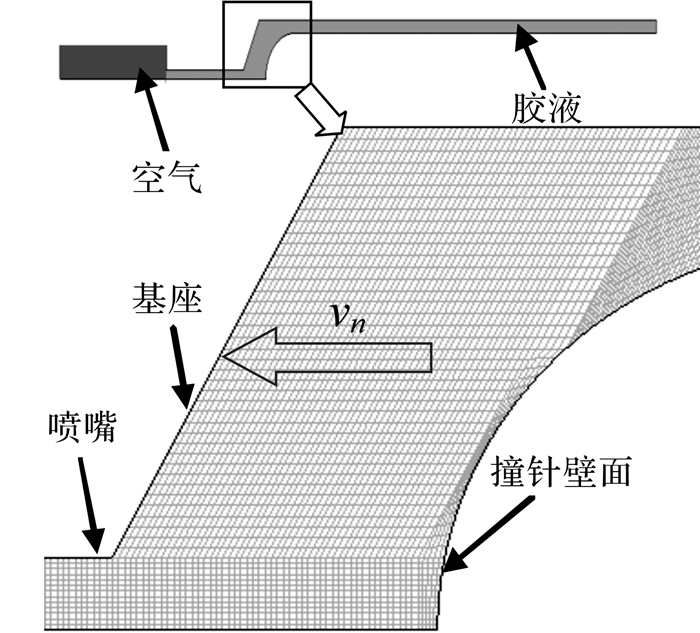
选用当下被广泛认可并使用的CFD仿真软件Fluent进行数值仿真.数值仿真计算时需要相应网格对流体计算域进行离散,网格质量的优劣直接决定了仿真中每步迭代的收敛性,同时也影响着仿真结果的好坏.而且,由于仿真过程中撞针下撞挤压流体,仿真过程必须使用动网格技术.不合理的网格将使动网格预览无法正确进行,这就对网格划分提出了更严格的要求.本文选用ICEM CFD对流体计算域进行细致的结构化网格划分,具体如图 3所示.仿真中选用2D轴对称瞬态求解器,并用VOF模型来捕捉胶滴的自由表面.同时使用了Fluent提供的动网格技术,网格更新方式为Layering.
|
| 图 3 流体域结构化网格 Fig. 3 Structured grid of fluid domain |
撞针的耦合运动速度计算依靠UDF中的DIFINE_CG_MOTION实现,其中主要还包括F_STORAGE_R_N3V,F_P,它们分别用来计算撞针所受的剪切力和流体压强作用于撞针的压力.由这些宏计算得到的力以及当前时刻的撞针速度以及位移,下一个时间步的撞针速度就可以计算得出,最后通过DIFINE_CG_MOTION赋值给撞针壁面.具体撞针运动数学模型如下所示:
| $\left\{ \begin{array}{l} \Delta v=\frac{{{F_0} - k{s_n} - {f_{{\rm{fluid}}}} - f}}{m} \cdot {\rm{d}}t,\\ {v_{n+1}}={v_n}+\Delta v,\\ {s_{n+1}}={s_n}+\frac{{{v_n}+{v_{n+1}}}}{2} \cdot {\rm{d}}t \end{array} \right.$ |
其中:F0与k分别为弹簧预紧力和刚度系数;s为撞针位移;ffluid与f分别为流体阻力和阀内轨道阻力;m为运动部件质量,主要为撞针的质量;dt为仿真时间步长.为了获得胶液滴落速度,还需用C_VOF获取胶滴低端位置并输出记录到文本文件.
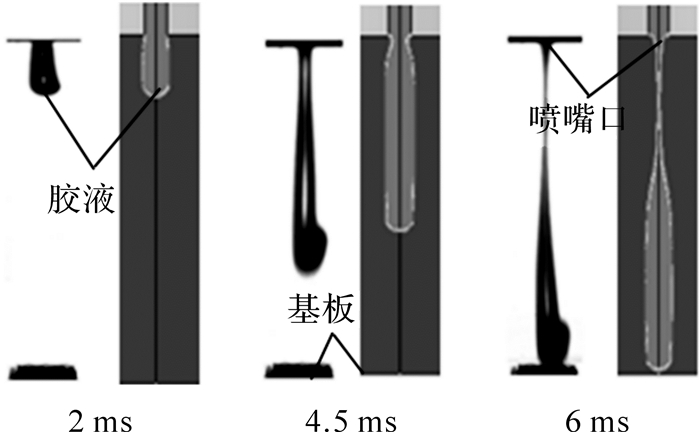
2.3 模型验证模型建立后需经与实验进行对比校核以验证所建模型的可靠性.本文的校核方法为:1)利用高速摄像仪拍摄记录实验中的出胶过程并将其与仿真结果对比;2)利用撞针位移测量系统获取实验中撞针动态位移并将其与仿真结果对比.为此,本文设计了相应的喷胶实验,实验平台前文已有所简介.仿真中的相关参数与实验中气动喷射点胶阀相应工作参数保持一致.在胶液喷射过程中,用高速摄像仪记录了喷嘴口胶滴形成过程.所拍摄的出胶图片可与仿真中胶液形态进行比对.图 4为仿真与实验中在各时刻胶滴自由表面变化情况.由图可以看出喷射出胶过程:首先是喷嘴口圆柱形出胶,圆柱半径大约为喷嘴口半径;然后胶柱靠近喷嘴端开始缩颈并逐渐变细至最终掉落.从图 4可以看出,仿真与实验中胶液自由表面除一些具体细节外,其主要出胶过程大体相似.
|
| 图 4 出胶状态对比(左:实验;右:仿真) Fig. 4 Comparison on droplet profile(left:experiment,right:simulation) |
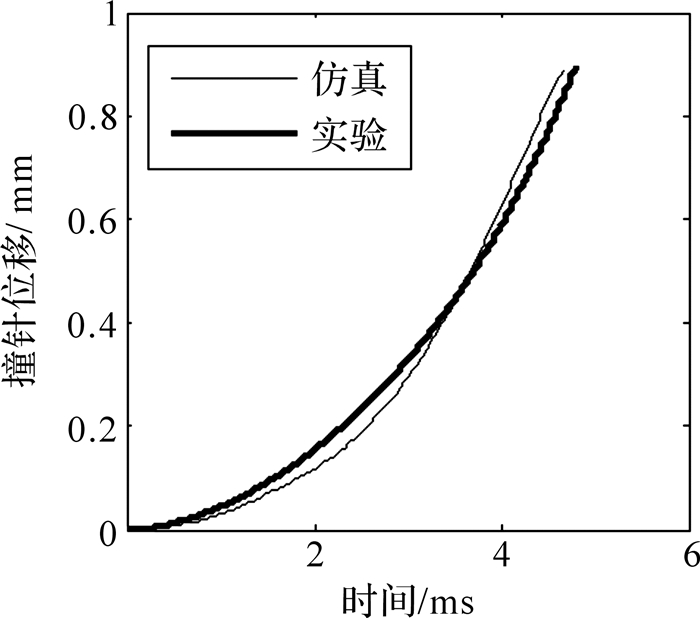
整个喷胶过程的发生靠的是撞针的运动,因此比较仿真与实验中各自的撞针位移对于验证仿真模型也具有十分可靠的参考意义.实验中撞针位移的测量可以通过本文设计的撞针位移测量系统得以实现.最终获得的位移对比效果如图 5所示.
|
| 图 5 撞针位移对比 Fig. 5 Comparison on needle displacement |
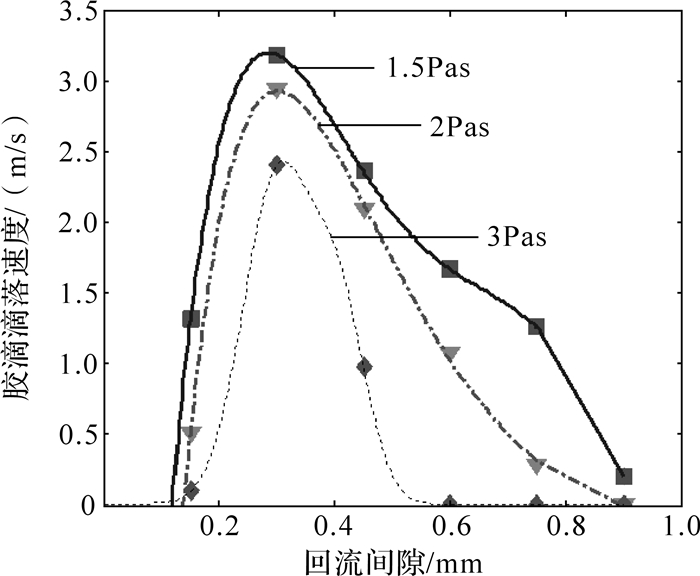
不同的回流间隙将对喷射阀的出胶速度产生较大的影响,本节通过仿真深入研究其影响程度.仿真过程中,除了黏度与回流间隙外,其它边界条件与相关参数均保持不变.图 6中离散数据点均为各回流间隙不同黏度胶液下的胶滴喷落速度.由图可以看出,当间隙相同时,随着胶液黏度的增加,胶液速度逐渐减小,这是由于黏度的增加导致撞针加速困难,进而减小了撞针喷射动力.相同黏度下,不同的回流间隙表现出极大的喷射差异.间隙过大或者过小均使得喷射速度降低.间隙过小使得回流阻力极大,这同样导致撞针加速困难.而间隙过大时,前期胶液能快速回流,腔内压强难以上升,所以前期缓慢出胶.后期撞击时,虽因撞针高速而形成高压,但撞击那一刻也是阀门关闭之时,这导致此刻喷出的高速胶液的质量极其微小.这部分胶液所拥有的动能会被喷嘴外做负功的胶液阻力如表面张力迅速消耗.所以其喷射速度仍不能提高.由此可以得出一定存在最优间隙使得喷射速度最大.
|
| 图 6 滴落速度对比 Fig. 6 Comparison on dropping speed |
通过以上分析可知,回流间隙逐渐增大或减小,滴落速度都趋向并最终等于0.为拟合具有此特征的数据,本文选择高斯函数.据最小二乘思想,该拟合可转为如下数学优化问题:
| $\begin{array}{l} \min \;S\left(\beta \right)=\left\| {\left({{f_1}\left(\beta \right),\ldots,{f_2}\left(\beta \right)} \right)} \right\|_2^2,\\ {f_1}\left(\beta \right)={\beta _1}{{\rm{e}}^{{\rm{ - }}\frac{{{{\left({{x_i} - {\beta _2}} \right)}^2}}}{{{\beta _3}}}}}+{\beta _4}{{\rm{e}}^{{\rm{ - }}\frac{{{{\left({{x_i} - {\beta _5}} \right)}^2}}}{{{\beta _6}}}}} - {y_i}, \end{array}$ |
式中,(xi,yi)为仿真数据,β=(β1,…,β6)为待定系数.将原目标函数用给定信赖域的二次模型进行逼近,具体如下:
| $\left\{ \begin{array}{l} \min {q^{\left(k \right)}}\left(d \right)=S\left({{\beta ^{\left(k \right)}}} \right)+g_k^{\rm{T}}d+\frac{1}{2}{d^{\rm{T}}}{G_k}d,\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\left\| d \right\|_2} \le \Delta k. \end{array} \right.$ |
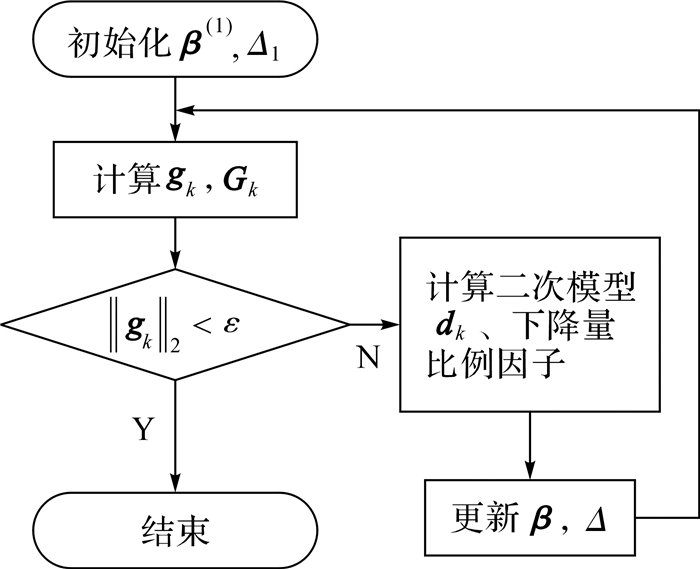
并用信赖域算法进行迭代计算,其中gk为目标函数S在当前迭代点β(k)处的梯度,Gk为S在β(k)处的Hessen矩阵.d为二次模型求解出的步长,即β(k+1)=β(k)+d.图 7描述了本文所用算法的总体概要流程.最终拟合效果如图 7所示.
|
| 图 7 算法概要流程 Fig. 7 Algorithm general flowchart |
通过拟合结果,本文得到各黏度下的最优回流间隙,具体如表 2所示.由表 2可以看出,随着胶液黏度的增加,相应的最优回流间隙也呈现细微的变大.这是由于黏度的增加必定加大胶液的回流阻力,为了获得最大的喷胶速度则需保证撞针的加速不能受太大阻扰,所以间隙要细微增加来避免回流阻力的过度增大.
| 黏度/Pas | 1.5 | 2 | 3 |
| 最优回流间隙/mm | 0.285 | 0.302 | 0.311 |
为验证表 2中所取最优值的准确性,本文对各黏度下最优回流间隙附近值进行仿真计算,结果如图 8所示.由图可以看出,表 2中最优尺寸在各黏度对应的滴落速度均比附近所选两点大.所以表 2中数据比较准确.

|
| 图 8 峰值点验证 Fig. 8 Confirmation of peak points |
由于微电子封装胶液的黏度一般小于3 Pas或者在3 Pas左右,所以选择高黏度3 Pas下的最优尺寸0.311 mm比较合理.另外可以计算得到,1.5 Pas下0.311 mm的胶液滴落速度比0.28 mm的少了1.2%,而2 Pas下0.311 mm与0.30 mm的相比只少了0.2%.所以选择0.311 mm能兼顾低黏度下的胶液滴落速度.
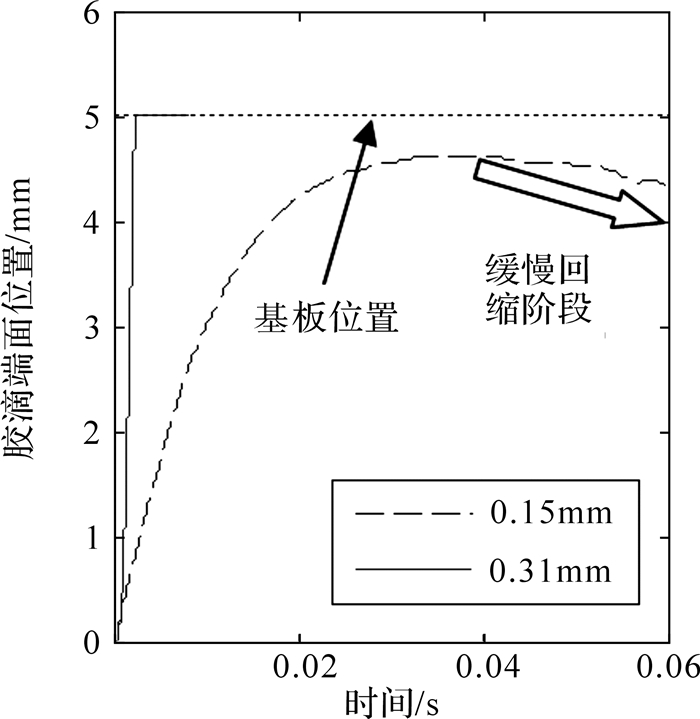
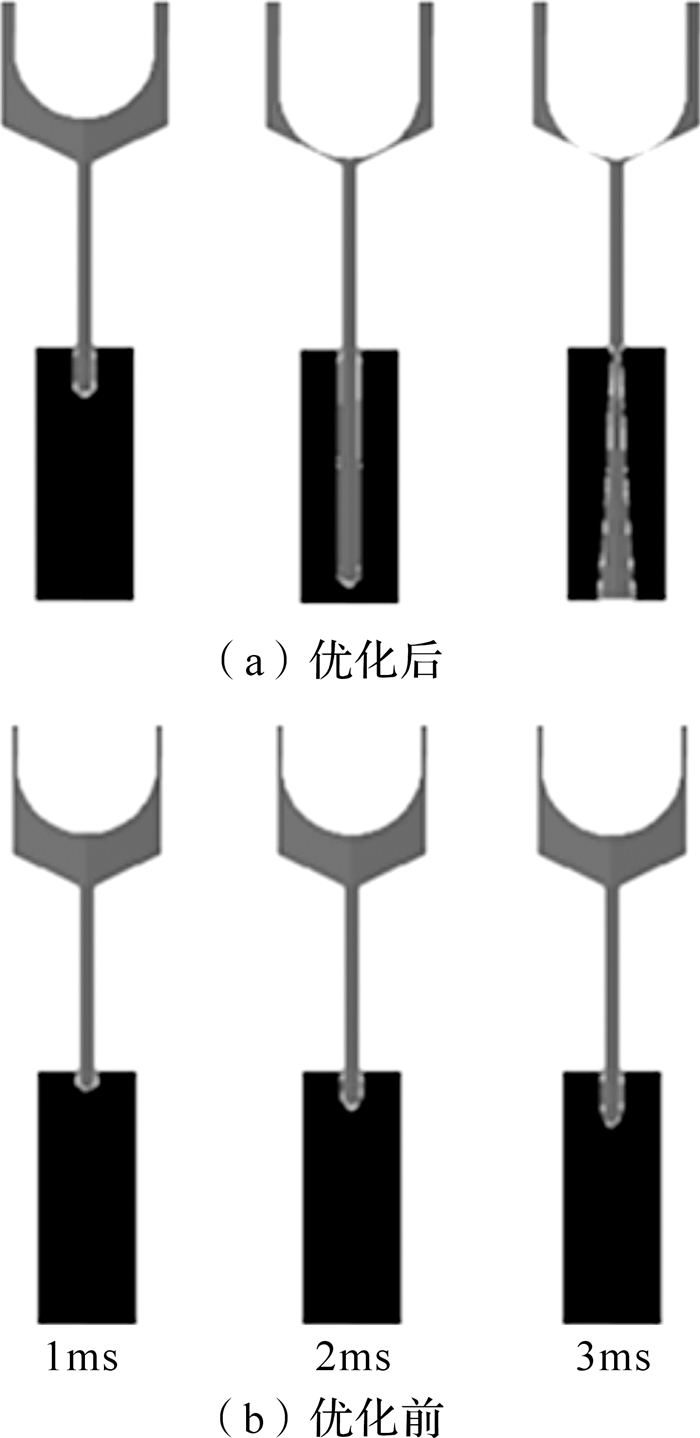
3.2 优化前后对比图 9表示的是3 Pas下0.311 mm与0.15 mm回流间隙的胶滴喷射对比.可以看出,优化前出胶速度十分缓慢,且胶滴不能顺利滴落到基板上面.而优化尺寸下的喷射情况完全相反.对于2 Pas,0.311 mm下的喷射胶液滴落速度是0.15 mm下的6倍,1.5 Pas下为2.5倍.图 10为优化前后各时刻出胶状态的对比.显然,对回流间隙优化后,现有阀的喷射能力显著提高.
|
| 图 9 优化前后胶滴运动对比 Fig. 9 Comparison on droplet movement between before optimization and after |
|
| 图 10 优化前后出胶状态对比 Fig. 10 Comparison on droplet profile between before optimization and after |
为提高现有喷射阀的喷射能力,本文首先分析了回流间隙的重要性.通过仿真分析各回流间隙下的喷射胶滴滴落速度,发现不同间隙下的喷射性能差异很大.然后根据仿真数据建立了回流间隙与胶滴滴落速度的高斯拟合模型.通过对该模型的极值求解,获得回流腔的最优间隙.对比发现,优化前后胶液喷射速度相差数倍.所以此优化结果极大地增强了现有喷射阀的喷射能力.由于市场上各种形式喷射点胶阀的喷射出胶均靠阀内撞针快速撞击挤压作用,其流道结构基本相似,所以本文优化思路具有普遍适用性.
| [1] | 高尚通.跨世纪的微电子封装[J].半导体情报,2000,37(6):1-7. GAO Shang-tong.Microelectronics packaging marching towards the new century[J].Semiconductor Information,2000,37(6):1-7. |
| Cited By in Cnki (30) | |
| [2] | BABIARZ A J.Jetting small dots of high viscosity fluids for packaging applications[J].Semiconductor International,2006,29(9):2-8. |
| [3] | NGUON B,JOUANEH M.Design and characterization of a precision fluid dispensing valve[J].The International Journal of Advanced Manufacturing Technology,2004,24(3/4):251-260. |
| Click to display the text | |
| [4] | KOIDE A,SASAKI Y,YOSHIMURA Y,et al.Micromachined dispenser with high flow rate and high resolution[C]//Proceedings IEEE 13th Annual International Conference on Micro Electro Mechanical Systems.Miyavaki,Jan.23-27,2000. |
| [5] | LEWIS A,BABIARZ A.Conductive adhesive dispensing process considerations[C]//Proceedings of the Technical Program:National Electronic Packaging and Production Conference.Anaheim,Feb.26-Mar.1,1999. |
| [6] | MARONGELLI S R,DIXON D,PORCARIET S,et al.Practical production uses of SMT adhesives[C]//Proceeding of the IEEE/CPMT International Electronic Manufacturing Technology (IEMT) Symposium.Tokyo,1998:147-155. |
| Click to display the text | |
| [7] | 孙道恒,高俊川,杜江,等.微电子封装点胶技术的研究进展[J].中国机械工程,2011,22(20):2513-2519. SUN Dao-heng,GAO Jun-chuan,DU Jiang,et al.Advances in fluid dispensing technology for micro-electronics packaging[J].China Mechanical Engineering,2011,22(20):2513-2519. |
| Cited By in Cnki (37) | Click to display the text | |
| [8] | 赵翼翔,陈新度,陈新.微电子封装中的流体点胶技术综述[J].液压与气动,2006(2):52-54. ZHAO Yi-xiang,CHEN Xin-du,CHEN Xin.An overview of fluid dispensing technology for micro-electronics packaging[J].Chinese Hydraulics & Pneumatics,2006(2):52-54. |
| Cited By in Cnki (36) | Click to display the text | |
| [9] | CHEN X B.Modeling and control of fluid dispensing process:a state-of-the-art review[J].The International Journal of Advanced Manufacturing Technology,2009,43(3/4):276-286. |
| Click to display the text | |
| [10] | 李章平,邓圭玲.精密点胶螺杆泵胶液流动分析与数值仿真[J].中国机械工程,2007,18(17):2102-2107. LI Zhang-ping,DENG Gui-ling.Numerical simulations and analysis of three-dimensional flows in the archimedes pump on dispensing[J].China Mechanical Engineering,2007,18(17):2102-2107. |
| Cited By in Cnki (20) | Click to display the text | |
| [11] | PIRACCI A F.Advantages of non-contact dispensing in SMT assembly processes[C]//SMTA International Conference Proceedings.Asymtek,2000-09-24. |
| Click to display the text | |
| [12] | PIRACCI A F.Practical production applications for jetting technology[C]//Proceedings of APEX Conference.Long Beach,CA,2000:1-6. |
| Click to display the text | |
| [13] | QUINONES H,BABIARZ A,DECK C,et al.Fluid jetting for next generation packages[C]//Proceedings of Packaging Technolog.Berlin,2002:1-8. |
| [14] | NGUYEN Q H,CHOI S B.Modeling of unsteady laminar flow based on steady solution in jetting dispensing process[J].IEEE Transactions on Electronics Packaging Manufacturing,2008,31(2):134-142. |
| Click to display the text | |
| [15] | SHAN X Y,CHEN Y,PENG X,et al.Modeling of laminar fluid flow in jet dispensing process[C].15th International Conference on Electronic Packaging Technology (ICEPT).Chengdu,Aug.12-15,2014. |
| Click to display the text | |
| [16] | QUOC H N,HAN Y M,CHOI S B,et al.Dynamic characteristics of a new jetting dispenser driven by piezostack actuator[J].IEEE Transactions on Electronics Packaging Manufacturing,2008,31(3):248-259. |
| Click to display the text | |
| [17] | CHEN Y,WANG F L,LI H X,et al.Experimental and modeling study of high-viscosity silicone jet dispensing process for LED packaging[C].15th International Conference on Electronic Packaging Technology (ICEPT).Chengdu,Aug.12-15,2014. |
| Click to display the text | |
| [18] | 彭先安.面向高性能LED封装的气动喷射阀喷胶性能研究[D].长沙:中南大学机电工程学院,2014:85-90. PENG Xian-an.Research on the performance of pneumatic jetting valve in the dispensing of high-performance LED package[D].Changsha:Central South University,College of Mechanical and Electrical Engineering,2014:85-90. |
| Cited By in Cnki |



