2. 中国煤矿装备有限责任公司, 北京 100011
2. China National Coal Mining Equipment Co., Ltd., Beijing 100011, China
采煤机作为综采成套装备中的关键设备,其动态性能直接影响着自身的可靠性和煤炭开采产量,所以研究工况下采煤机的动力学性能是提升采煤机质量的一个重要基础[1].对采煤机的载荷和动态特性方面的研究主要有:文献[2, 3]分析了滚筒截割载荷下摇臂壳体的应力、应变;文献[4]分析了滚筒阶跃负载下摇臂的动力学响应;文献[5, 6]建立了随机截割载荷激励下的采煤机整机力学模型;文献[7]研究了考虑滚筒偏心载荷作用下采煤机的横、纵向振动特性;文献[8, 9]对采煤机的摇臂及行走部的动力性能进行了研究;文献[10]采用LS-DYNA对驱动轮与销排间的动态啮合特性进行了分析;文献[11]研究了截割臂齿轮传动系统的振动响应;文献[12]采用蒙特卡洛法对采煤机的动态特性进行了研究;文献[13]对滚筒的可靠性、寿命进行了预测.
以上研究中,多研究单一激励下采煤机整机或工作装置的动力学特性,而采煤机的动力学模型具有多输入、非线性等特点,特别是滚筒的振动量较大,而这种振动又会引起滚筒的阻力载荷产生变化,两者之间存在着耦合.基于以上原因,本文综合运用锋利截齿截割阻力模型、含间隙齿轮啮合模型及库伦摩擦模型描述采煤机工作载荷,采用拉格朗日动力学方程建立采煤机动力学模型,采用ode45对模型求解,研究采煤机工作过程中的动力学特性,研究结果为采煤机性能和结构优化提供依据.
1 动力学模型建立根据采煤机各零部件间的结构尺寸和联接方式,作如下假设:
1) 左、右滚筒与左、右摇臂的联接刚度,左、右摇臂与机身间的联接刚度,左、右摇臂举升油缸的支撑刚度,都视为无穷大;
2) 左、右导向滑靴和左、右平滑靴与机身的联接刚度视为无穷大;
3) 驱动轮与各销排间的啮合间隙相等;
4) 摇臂各个截面形状、尺寸相同,截面极惯性矩为I,弹性模量为E.
令:坐标原点为O;m1,x1为机身的质量和位移;m2,m3为右、左摇臂的质量;δ,γ为右、左摇臂的摆角;b为摇臂质心与摇臂回转点的距离;k2,k3为右、左摇臂质心点的等效刚度,根据材料力学弯曲变形的挠度公式[14]有 $ {k_2} = {k_3} = \frac{{3EI}}{{{b^3}}}$;m4,m5为右、左滚筒的质量;e为滚筒质心与摇臂回转点的距离;k4,k5为右、左滚筒的等效刚度,${k_4} = {k_5} = \frac{{3EI}}{{{e^3}}}$;F1,F2为右、左驱动轮与销排之间的驱动力;Fu为平滑靴和导向滑靴与刮板机之间的摩擦力之和;F3,F4为右滚筒的牵引阻力、截割阻力;F5,F6为左滚筒的牵引阻力、截割阻力.采煤机动力学模型如图 1所示.
系统的动能为
| $\begin{array}{l} T = \frac{1}{2}{m_1}\dot x_1^2 + \frac{1}{2}{m_2}\left( {\dot x_2^2 + \dot y_2^2} \right) + \frac{1}{2}{m_3}\left( {\dot x_3^2 + \dot y_3^2} \right) + \\ \;\;\;\;\;\frac{1}{2}{m_4}\left( {\dot x_4^2 + \dot y_4^2} \right) + \frac{1}{2}{m_5}\left( {\dot x_5^2 + \dot y_{\rm{5}}^{\rm{2}}} \right) \end{array}$ | (1) |
式中: $ {{\dot x}_2},{{\dot y}_2},{{\dot x}_3},{{\dot y}_3}$为右、左摇臂的水平和竖直速度; $ {{\dot x}_4},{{\dot y}_4},{{\dot x}_5},{{\dot y}_5}$为右、左滚筒的水平和竖直速度.
因右、左摇臂振动摆角相对摇臂工作时的举升角Φ1,Φ2也是很小的,令:cos Φ1≈cos(Φ1+δ),sin Φ1≈sin(Φ1+δ),cos Φ2≈cos(Φ2+γ),sin Φ2≈sin(Φ2+γ),则有:
| $\left. \begin{array}{l} {{\dot x}_2} = {{\dot x}_1} - b \times \dot \delta \cos {\phi _1},\\ {{\dot y}_2} = b \times \dot \delta \sin {\phi _1}. \end{array} \right\}$ | (2) |
| $\left. \begin{array}{l} {{\dot x}_3} = {{\dot x}_1} - b \times \dot \gamma \cos {\phi _2},\\ {{\dot y}_3} = b \times \dot \gamma \sin {\phi _2}. \end{array} \right\}$ | (3) |
| $\left. \begin{array}{l} {{\dot x}_4} = {{\dot x}_1} - e \times \dot \delta \cos {\phi _1},\\ {{\dot y}_4} = b \times \dot \delta \sin {\phi _1}. \end{array} \right\}$ | (4) |
| $\left. \begin{array}{l} {{\dot x}_5} = {{\dot x}_1} - e \times \dot \gamma \cos {\phi _2},\\ {{\dot y}_5} = e \times \dot \gamma \sin {\phi _2}. \end{array} \right\}$ | (5) |
整理后得
| $\begin{array}{l} T = \frac{1}{2}\dot x_1^2\left( {{m_1} + {m_2} + {m_3} + {m_4} + {m_5}} \right) - \\ \;\;\;\;\;\;{{\dot x}_1}\dot \delta \left( {{m_2}b + {m_4}e} \right)\cos \;\;{\phi _1} - {{\dot x}_1}\dot \gamma \left( {{m_3}b + } \right.\\ \;\;\;\;\;\left. {{m_5}e} \right)\cos {\phi _2} + \frac{1}{2}{{\dot \delta }^2}\left( {{m_2}{b^2} + {m_4}{e^2}} \right) + \\ \;\;\;\;\;\frac{1}{2}{{\dot \gamma }^2}\left( {{m_3}{b^2} + {m_5}{e^2}} \right). \end{array}$ | (6) |
令w2,w3,w4,w5为右、左摇臂和滚筒的切向位移,因为摇臂的挠度较小,所以有:w2=bδ,w3=bγ,w4=eδ,w5=eγ.
系统的势能为
| $U = \frac{1}{2}{k_2}\omega _2^2 + \frac{1}{2}{k_3}\omega _3^2 + \frac{1}{2}{k_4}\omega _4^2 + \frac{1}{2}{k_5}\omega _5^2,$ | (7) |
整理后得
| $U = \frac{1}{2}{k_2}{b^2}{\delta ^2} + \frac{1}{2}{k_3}{b^2}{\gamma ^2} + \frac{1}{2}{k_4}{e^2}{\delta ^2} + \frac{1}{2}{k_5}{e^2}{\gamma ^2}.$ | (8) |
将式(6)和式(8)代入Lagrange动力学方程,整理后得
| $M\ddot X + KX = F,$ | (9) |
其中: $X = \left[{\begin{array}{*{20}{c}} {{x_1}}\\ \delta \\ \gamma \end{array}} \right],$
| $\begin{array}{l} M = \left[ {\begin{array}{*{20}{c}} {{M_{11}}}&{{M_{12}}}&{{M_{13}}}\\ {{M_{21}}}&{{M_{22}}}&0\\ {{M_{31}}}&0&{{M_{33}}} \end{array}} \right],\\ {M_{11}} = {m_1} + {m_2} + {m_3} + {m_4} + {m_5},\\ {M_{12}} = - \left( {{m_2}b + {m_4}e} \right)\cos {\phi _1},\\ {M_{13}} = - \left( {{m_3}b + {m_5}e} \right)\cos {\phi _2},\\ {M_{21}} = - \left( {{m_2}b + {m_4}e} \right)\cos {\phi _1},\\ {M_{22}} = {m_2}{b^2} + {m_4}{e^2},\\ {M_{31}} = - \left( {{m_3}b + {m_5}e} \right)\cos {\phi _2},\\ {M_{33}} = {m_3}{b^2} + {m_5}{e^2},\\ K = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&{{k_2}{b^2} + {k_4}{e^2}}&0\\ 0&0&{{k_3}{b^2} + {k_5}{e^2}} \end{array}} \right],\\ F = \left[ {\begin{array}{*{20}{c}} {{F_1} + {F_2} - {F_3} - {F_5} - {F_u}}\\ {{F_3}e\sin {\phi _1} + {F_4}e\cos {\phi _1}}\\ {{F_5}e\sin {\phi _2} + {F_6}e\cos {\phi _2}} \end{array}} \right]. \end{array}$ |
如图 2所示,QN1,QN2为右、左驱动轮啮合力,根据含间隙齿轮非线性啮合模型,有[15, 16]
| $\left. \begin{array}{l} {Q_{N1}} = Kf\left( {{x_1} - {e_1}\left( t \right),d} \right) + C\left( {{{\dot x}_1} - {{\dot e}_1}\left( t \right)} \right),\\ {Q_{N2}} = Kf\left( {{x_2} - {e_2}\left( t \right),d} \right) + C\left( {{{\dot x}_2} - {{\dot e}_2}\left( t \right)} \right). \end{array} \right\}$ | (10) |
式中:ei(t)=eisin(ωqt+ηi)为齿频误差,ηi齿频误差初始相位角,ωq为驱动轮角速度;d为齿轮啮合间隙;K为啮合刚度;C为啮合阻尼.
| $\begin{array}{l} f\left( {{x_i} - {e_i}\left( t \right),d} \right) = \\ \left\{ \begin{array}{l} {x_i} - {e_i}\left( t \right) - d,\;\;{x_i} - {e_i}\left( t \right) > d,\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - d \le {x_i} - {e_i}\left( t \right) \le d,\\ {x_i} - {e_i}\left( t \right) + d,\;{x_i} - {e_i}\left( t \right) < - d. \end{array} \right. \end{array}$ | (11) |
式中i=1,2.
啮合刚度K等于平均啮合刚度Kn与时变啮合刚度之和,为
| $K = {K_n} + {K_a}\cos \left( {{\omega _q}t + {\eta _i}} \right).$ | (12) |
设驱动轮和销排啮合角为a,则右、左行走部驱动轮与销排间的啮合力在行走方向的分力分别为F1=QN1cos a,F2=QN2cos a.
2.2 摩擦激励采煤机行走截割过程中,起支撑作用的平滑靴和导向滑靴将与刮板机产生一定的摩擦,采用库伦摩擦定律描述该摩擦载荷,有
| ${F_u} = \left\{ \begin{array}{l} {F_P}u,\;\;\;{x_i} > 0,\\ 0,\;\;\;\;\;\;\;{x_1} = 0,\\ - {F_P}u,\;\;\;{x_1} < 0. \end{array} \right.$ | (13) |
式中:u为平滑靴与刮板中部槽的摩擦系数;FP为采煤机滑靴支撑力,FP=mg-F4-F6,mg为采煤机总重量.
2.3 滚筒截割激励根据文献[2, 3]可知:单个截齿在截割煤岩过程中,受到截割阻力、牵引阻力和侧向阻力三个作用力,其中截割阻力和牵引阻力可表示为
| $\left. \begin{array}{l} Z = \frac{{{K_y}A}}{{\cos {\beta _0}}}\frac{{0.35{b_p} + 0.3}}{{{b_P} + B{h^{0.5}}}}ht{K_m}{K_a}{K_f}{K_p},\\ Y = {K_q}Z. \end{array} \right\}$ | (14) |
式(14)中各参数所表示的意思及取值见参考文献[2, 3],除切削厚度h和平均截距t外,其余值的大小均取决于煤岩的物理特性和截齿的结构尺寸,切削厚度h和平均截距t与采煤机的截割速度有关,表示为
| $h = \frac{v}{{nm}}\sin {\varphi _i}.$ | (15) |
如考虑滚筒的x向振动,则有
| $h = \left( {\frac{v}{{nm}} + {x_c}} \right)\sin {\varphi _i},$ | (16) |
式中:xc为滚筒的x方向振动量,对于图 1中的右侧滚筒,有xc=x4,左侧滚筒的xc=x5;m为螺旋滚筒上安装的截齿数;n为螺旋滚筒的转速;v为采煤机的牵引速度;φi为螺旋滚筒上第i个截齿的位置角.
|
| 图 1 采煤机动力学模型 Fig. 1 Mechanical model of shearer |

|
| 图 2 行走驱动激励 Fig. 2 Driving load of road wheel |
| $t = \left( {1.25h + {b_q} + 1.25} \right)\frac{{1.47B}}{{B + 1.2}},$ |
式中B为煤岩的脆性程度系数.
当采煤机的滚筒结构和截割煤岩的物理性质确定后,单个截齿截割阻力是采煤机牵引速度、滚筒x向振动量、位置角函数:
| $\left. \begin{array}{l} Z = f\left( {v,{x_c},{\varphi _i}} \right),\\ Y = {K_q}f\left( {v,{x_c},{\varphi _i}} \right). \end{array} \right\}$ | (17) |
如将单个截齿的截割阻力和牵引阻力沿x,y方向分解并依次叠加便可得到右、左滚筒在牵引方向和竖直方向的载荷为:
| $\left. \begin{array}{l} {F_3} = \sum\limits_{i = 1}^{{N_1}} {\left( { - Z\sin {\varphi _i} - Y\cos {\varphi _i}} \right)} ,\\ {F_4} = \sum\limits_{i = 1}^{{N_1}} {\left( {Z\cos {\varphi _i} - Y\sin {\varphi _i}} \right)} . \end{array} \right\}$ | (18) |
| $\left. \begin{array}{l} {F_5} = \sum\limits_{i = 1}^{{N_2}} {\left( { - Z\sin {\varphi _i} - Y\cos {\varphi _i}} \right)} ,\\ {F_6} = \sum\limits_{i = 1}^{{N_2}} {\left( {Z\cos {\varphi _i} - Y\sin {\varphi _i}} \right)} . \end{array} \right\}$ | (19) |
式(18)、式(19)中,N1,N2为右、左两侧滚筒参与截割的截齿数.
再令
| $\left. \begin{array}{l} \Delta {F_3} = F{'_3} - {F_3},\\ \Delta {F_4} = F{'_4} - {F_4},\\ \Delta {F_5} = F{'_5} - {F_5},\\ \Delta {F_6} = F{'_6} - {F_6}. \end{array} \right\}$ | (20) |
式(20)中:F′3,F′4,F′5,F′6为未考虑摇臂振动时的右、左滚筒牵引和截割载荷;ΔF3,ΔF4,ΔF5,ΔF6为未考虑摇臂振动时滚筒载荷与考虑摇臂振动时的载荷差值.
3 模型求解式(9)中质量矩阵存在耦合,为了求解方便,采用模态坐标法对其解耦,将质量矩阵M和刚度矩阵K代入系统频率方程Δ(ω2)=|kij-ω2mij|=0中,可求系统的特征值和自然频率,再将其代入([k]-ω2[m]){u}=0,可得到系统的模态向量矩阵U,令
| $\left. \begin{array}{l} \left\{ x \right\} = U\left\{ q \right\},\\ \left\{ {\dot x} \right\} = U\left\{ {\dot q} \right\},\\ \left\{ {\ddot x} \right\} = U\left\{ {\ddot q} \right\}, \end{array} \right\}$ | (21) |
对式(9)进行坐标变换,得
| ${U^T}MU\left\{ {\ddot q} \right\} + {U^T}KU\left\{ q \right\} = {U^T}F.$ | (22) |
式(22)中,各参数大小可通过查询采煤机的设计资料和工艺参数获得,主要参数如表 1所示.设置仿真时间为200 s,仿真步长为0.01 s,采用ode45对式(22)进行求解后,再代入式(21)中,可得式(9)的解.
| 参数 | 数值 | 参数 | 数值 |
| 采高/m | 3 | 摇臂长度/m | 2.56 |
| 煤质硬度f | 3 | 滚筒转速/(r/min) | 35 |
| 整机质量/t | 54 | 滚筒质量/t | 2.2 |
| 摇臂质量/t | 9.8 | 牵引速度/(m/min) | 3 |
| 滚筒直径/m | 1.8 | 右、左摇臂摆角/(°) | 15,-10 |
截取仿真的稳态阶段(160-170 s),如图 3所示.

|
| 图 3 时域振动曲线 Fig. 3 Vibration curves of time domain |
图 3(a)中因初始设置时采煤机行走轮与销排间存在6 mm的间隙,当采煤机工作时,行走轮与销排啮合,逐渐产生-6 mm的位移,受采煤机工作负载的影响,行走轮与销排间产生接触变形,最大接触变形量为0.035 mm,机身的振动幅值约为0.2 mm.
图 3(b)、(c)中,右侧摇臂的振动要大于左侧摇臂,其中右侧摇臂在1.74 ×10-3 rad上下波动,振动幅值约为0.8×10-4 rad,左侧摇臂在6.32 ×10-4 rad上下波动,振动幅值约为0.4×10-5 rad.引起右侧摇臂振动较大的原因:一是摇臂的举升角大于左侧;二是右侧滚筒参与截割的截齿数大于左侧滚筒,使右侧滚筒工作阻力大于左侧滚筒.
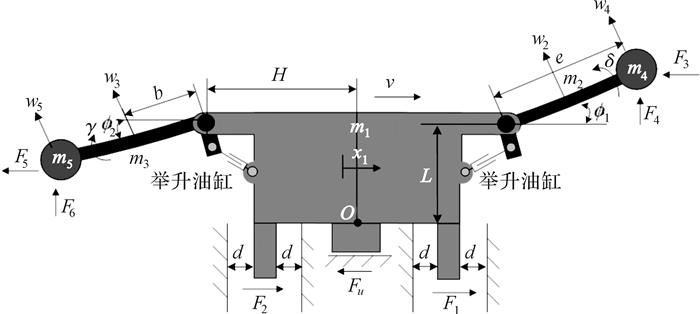
4.2 振动相图由图 4(a)知:机身的相图较规则,可近似为周期振动,机身振动速度在-1.4~+1.4 mm/s间波动;由图 4(b)、(c)知:右、左摇臂的振动相图不规则,曲线间存在交叉和重叠,右、左摇臂的振动角速度在-1×10-3~+1×10-3 rad/s和-4.5×10-4~+4.5×10-4 rad/s间波动.
|
| 图 4 振动相图 Fig. 4 The vibration phase diagram |
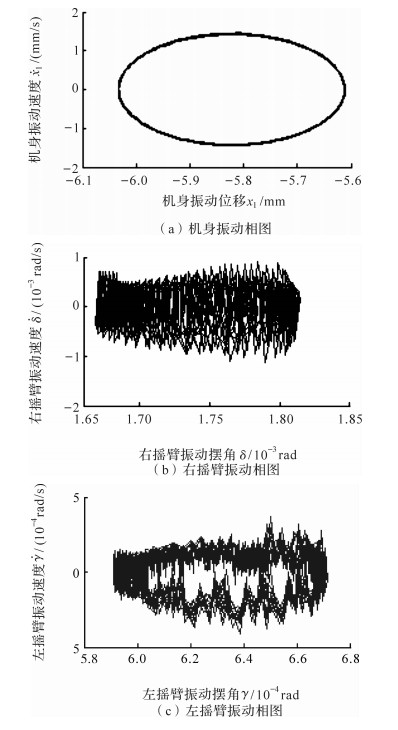
由图 5(a)、(b)可知:与未考虑滚筒截割过程中的滚筒振动相比,当考虑两侧滚筒的振动影响时,右、左滚筒截割力相对较小,两者的差值见图 5(c),右滚筒的牵引载荷减小量均值约为8 000 N,截割载荷减小量均值约为9 500 N;左滚筒的牵引载荷减小量均值约为5 000 N,截割载荷减小量均值约为7 000 N.以上分析说明受摇臂振动的影响,当采煤机以相同速度截割时,考虑滚筒振动时的阻力载荷要小于未考虑滚筒振动的,这也说明了滚筒的振动有利于煤岩的截割.
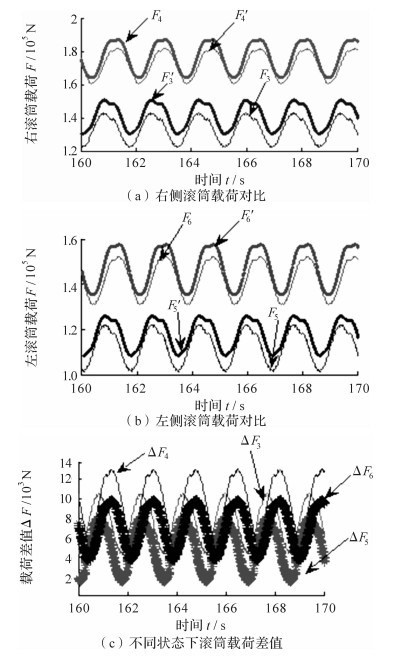
|
| 图 5 滚筒载荷分析 Fig. 5 Drum load analysis |
为了对采煤机的动力学模型及其求解结果的准确性进行验证,利用中煤张家口煤矿机械有限责任公司“国家能源煤矿采掘机械装备研发(实验)中心”对采煤机截割过程中右侧摇臂的振动量进行测量.实验中采煤机型号为MG500/1180,测试时其采煤机牵引速度为3 m/min;假煤壁硬度f=3,高度为3 m;测试传感器为北京必创的无线A301三向加速度传感器,将其安装在摇臂行星减速器壳体中心外侧,该位置与滚筒轴线同轴;信号采集系统为BeeData,从实验数据中,截取1 000个数据点作为样本进行分析,结果如图 6所示.

|
| 图 6 滚筒振动实验值与仿真值 Fig. 6 Simulation value and test value of drum |
由于实验条件下行走驱动激励、滑靴摩擦激励、滚筒截割激励均具有一定的随机性,采煤机与刮板机的相互接触和工作状态也比模型的边界条件复杂,所以,实验测量所得滚筒振动加速度的变化状态与仿真值是不同的,但从两者时域特征值上,仍可进行对比分析.如图 6所示:滚筒x向振动加速度约在-500~+500 mm/s2间波动,y向约在500~1 500 mm/s2间波动,说明仿真结果与实验结果的波动范围基本相同;滚筒在x,y向振动加速度实测结果的均值为-97.15和941.29 mm/s2,仿真结果为-52.44和911.24 mm/s2,实验测量均值要大于仿真计算均值,其中x方向相差较大,为45.17 mm/s2,约占测量值的46%,但y方向相差很小,约占测量值的3.2%.引起x方向振动误差较大的最主要原因是实验中刮板机上的销排节距误差,特别是2个销排连接处的距离误差较大,采煤机在销排上行走时产生较大的振动冲击,而本文没有考虑以上2种误差的影响,故在x方向仿真与实验的均值存在较大的偏离.
5 结 论采用拉格朗日动力学方程建立多激励下采煤机整机动力学模型,利用ode45对模型求解,分析了MG500/1180采煤机在煤壁硬度f=3、高度为3 m、牵引速度为3 m/min时的动力学特性,结果表明:
1) 机身的振动幅值约为0.2 mm;右摇臂振动幅值约为0.8×10-4 rad,左摇臂振动幅值约为0.4×10-5 rad,右侧摇臂振动较大的原因是其摇臂举升角较大、滚筒载荷较大.
2) 通过对比摇臂有、无振动两种状态下滚筒工作载荷表明:当采煤机以相同速度截割时,考虑滚筒振动时的阻力载荷要小于未考虑滚筒振动的.
3) 对右侧摇臂的振动量进行了实验测量,实验结果表明:在x方向仿真与测量结果的均值相差较大,差值约占测量值的46%;在y方向的均值相差很小,差值仅占测量值的3.2%;虽然仿真与实验结果存在一定误差,但仿真与实验结果的波动范围基本相同.实验结果可以验证采煤机的动力学模型具有一定的准确性,特别是其在y方向的分析结果较为准确.
| [1] | 张世洪.我国综采采煤机技术的创新研究[J].煤炭学报,2010,35(11):1988-1994. ZHANG Shi-hong.Study on the innovation of fully mechanized coal shearer technology in China[J].Journal of China Coal Society,2010,35(11):1988-1994. |
| Cited By in Cnki | Click to display the text | |
| [2] | 赵丽娟,王乘云.采煤机截割部建模与动力学仿真研究[J].工程设计学报,2010,17(2):119-124. ZHAO Li-juan,WANG Cheng-yun.Modeling and dynamic simulation of shearer cutting unit [J].Chinese Journal of Engineering Design,2010,17(2):119-124. |
| Cited By in Cnki (19) | Click to display the text | |
| [3] | 赵丽娟,宋朋,谢波.新型薄煤层采煤机截割部振动特性研究[J].广西大学学报(自然科学版),2014,39(2):265-274. ZHAO Li-juan,SONG Peng,XIE Bo.Vibration performance research of a new shearer cutting unit in shin coal seam[J].Journal of Guangxi University (Natural Science Edition),2014,39(2):265-274. |
| Cited By in Cnki | Click to display the text | |
| [4] | 廉自生,刘楷安.采煤机摇臂虚拟样机及其动力学分析[J].煤炭学报,2005,30(6):801-804. LIAN Zi-sheng,LIU Kai-an.Virtual proto type of shearer ranging arm and its dynamics analysis[J].Journal of China Coal Society,2005,30(6):801-804. |
| Cited By in Cnki (44) | Click to display the text | |
| [5] | 刘春生,李德根,戴淑芝.随机载荷对双滚筒采煤机整机力学特性的影响[J].煤矿机电,2012(6):45-49. LIU Chun-sheng,LI De-gen,DAI Shu-zhi.Fluency of random load on mechanical properties of double-drum shearer[J].Coal Mine Electromechanical,2012(6):45-49. |
| Cited By in Cnki | |
| [6] | 刘春生.滚筒式采煤机理论设计基础[M].徐州:中国矿业大学出版社,2003:85-90. LIU Chun-sheng.Design basis of drum shearer design theory[M].Xuzhou:China University of Mining and Technology Press,2003:85-90. |
| [7] | 李晓豁,李萍,刘春生.采煤机在行走方向上的动力学行为研究[J].黑龙江科技学院学报,2002,12(4):1-4. Ll Xiao-huo,Ll Ping,LIU Chun-sheng.Study of shearer dynamic behaviors along the traction[J].Journal of Heilongjiang Institute of Science & Technology,2002,12(4):1-4. |
| Cited By in Cnki (14) | Click to display the text | |
| [8] | LIU Song-yong.Model test of the cutting properties of a shearer drum [J].Mining Science and Technology,2009,19(1):74-78. |
| Click to display the text | |
| [9] | LIU Song-yong,LUO Chen-xu.Vibration experiment of shearer walking unit[J].Applied Mechanics & Materials,2012,268:1257-1261. |
| Click to display the text | |
| [10] | 周甲伟,刘瑜,刘送永,等.采煤机行走机构动态啮合特性分析[J].工程设计学报,2013,20(3):230-237. ZHOU Jia-wei,LIU Yu,LIU Song-yong,et al.Characteristic analysis of dynamic meshing for shearer walking mechanism[J].Chinese Journal of Engineering Design,2013,20(3):230-237. |
| Cited By in Cnki (6) | Click to display the text | |
| [11] | LI Jian-ping, GUO Hui-zhen.Vibration characteristics of shearer cutting unit based on multibody dynamics[J].Electronic Journal of Geotechnical Engineering,2014,19(4):3195-3208. |
| Click to display the text | |
| [12] | SEYED Hadi Hoseinie,MOHAMMAD Ataei,REZA Khalokakaie, et al.Reliability analysis of drum shearer machine at mechanized longwall mines[J].Journal of Quality in Maintenance Engineering,2012,18(1):98-119. |
| Click to display the text | |
| [13] | TIRYAKI B.In situ studies on service life and pick consumption characteristics of shearer drums[J].Journal of the South African Institute of Mining and Metallurgy,2004,104(2):107-121. |
| Click to display the text | |
| [14] | 单祖辉.材料力学[M].北京:高等教育出版社,2010:152-159. SHANG Zu-hui.Mechanics of materials[M].Beijing:Higher Education Press,2010:152-159. |
| [15] | 盛冬平,朱如鹏,靳广虎,等.考虑摩擦的多间隙直齿弯扭振动建模和分岔特性[J].航空动力学报,2015,30(2):498-506. SHENG Dong-ping,ZHU Ru-peng,JIN Guang-hu,et al.Bifurcation characteristic and modeling of transverse-torsional spur gear vibration considering friction and multiple clearances[J].Journal of Aerospace Power,2015,30(2):498-506. |
| Cited By in Cnki | Click to display the text | |
| [16] | 黄冠华,周宁,张卫华,等.动态激励下高速列车齿轮传动系统振动特性分析[J].铁道学报,2012,36(12):20-27. HUAN Guan-hua,ZHOU Ning,ZHANG Wei-hua,et al.Vibration characteristics of gear transmission system of high speed train under dynamic excitation[J].Journal of the China Railway Society,2012,36(12):20-27. |
| Cited By in Cnki (1) | Click to display the text |


