拆解是废旧产品再制造的前提[1].可拆卸性评估和拆卸序列规划是当前再制造工程的研究热点.产品拆解时间和拆解能量分析是开展上述研究的2个重要方面.研究者从拆解时间方面对产品可拆卸性和拆卸序列规划进行了大量研究,如:于随然等提出了产品的可拆卸性评价指标和基于拆解时间的评价方法[2];孙有朝等考虑拆卸效率问题,提出基于零件故障率和拆解时间的产品拆卸性定量评估方法[3];Kroll等对以拆解时间为参数的拆解评估问题进行了研究[4];Go等提出基于遗传算法的拆卸序列优化方法,并得到拆卸时间最短的拆卸序列[5];Beatriz等以最小拆解时间为优化目标,建立了复杂产品的拆卸优化模型[6];郭希旺等以最小拆解时间和最大拆解收益为优化目标,建立了多目标优化数学模型[7];张雷等为了提高复杂产品拆解效率、缩短拆解时间,提出了针对复杂产品的并行拆解建模及规划方法[8].上述研究均没有考虑产品的拆解能量消耗.而在实际生产中,产品拆解能量的分析往往更能直接评估产品的可拆卸性能,优化产品的拆卸序列.此外,产品拆解能量分析,可为对应拆解设备的设计(如力、力矩、运动距离等方面)提供参考;反过来,也可对已有产品进行结构优化,使其具有更好的拆卸性能.目前对产品拆解能量分析评估方面研究较少,尽管田广东等基于拆解过程存在的不确定特性,提出了产品拆解能量分析方法[9],但没有考虑到产品拆解能量与零部件间连接方式、物理化学变化以及拆卸序列等之间的关系.事实上,一个相同的功能实现,零部件间可有不同的连接方式,对应不同的拆解方法和装置,对拆解能量影响较大.而且同一种产品,产品的拆卸序列往往不唯一,产品的拆解能量值也不尽相同.
综合考虑零部件间连接方式、物理化学变化以及拆卸序列等因素对拆解能量的影响,本文提出了一种拆解能量分析方法.以工程液压油缸为研究对象来分析评估其拆解能量,以拆解约束图模型构建液压油缸的拆解信息模型并生成相应的拆卸序列;通过定义零部件拆解能量的组成并讨论液压油缸中零部件间连接方式和拆解能量间的数学关系,分析规划以拆解所需最小能量为目标的液压油缸拆卸优化序列.
为使研究问题简单化,在对液压油缸拆解能量评估之前做出假设:①液压油缸的拆解为无损拆解;②液压油缸拆解中不考虑零部件的磨损、腐蚀、断裂和变形等,为理想拆卸.实际拆解时,根据产品的实际损耗程度评估,将理论值赋予一个大于1的修正系数,可大体反映产品的实际拆解能量值.
1 液压油缸拆解约束模型图 1所示为某工程液压油缸结构简图.本文基于拆解混合图理论来构建液压油缸拆解约束矩阵和拆解约束图[10].为避免产生没有价值的液压油缸拆卸序列,将典型联结元拆卸优先级规则[11]引入拆解混合图中,构建液压油缸的拆解约束图,在图中这类零件之间用虚有向边表示.
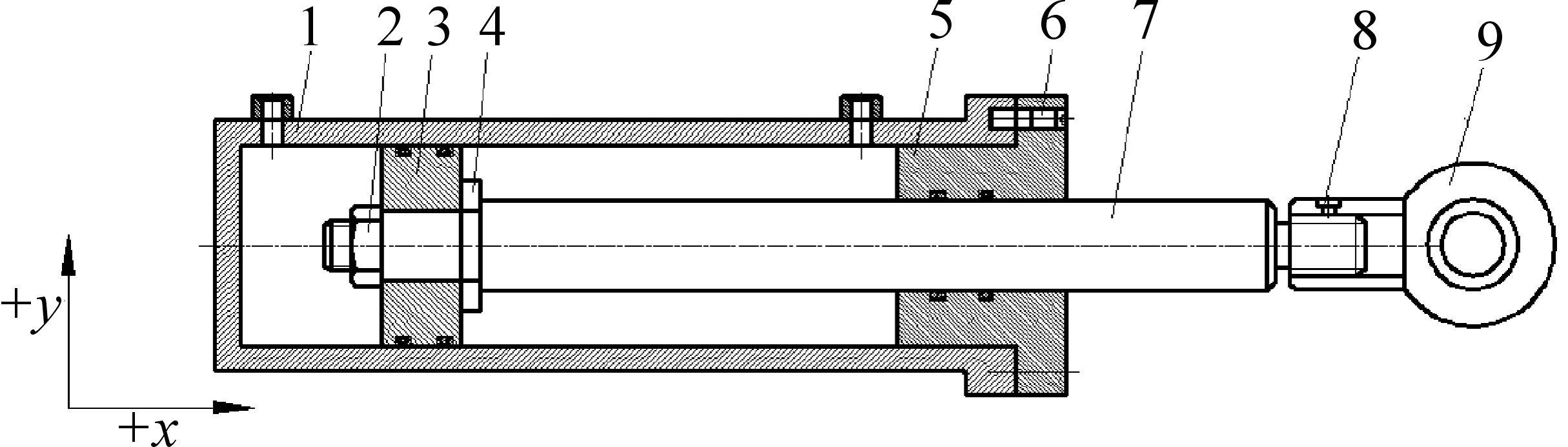 |
| 1—油缸缸体;2—锁紧螺母;3—活塞组;4—缓冲套;5—缸盖件;6—缸盖螺钉;7—活塞杆;8—紧定螺钉;9—耳轴.图 1 某工程液压油缸结构简图 Fig. 1 Structure diagram of engineering hydraulic cylinder |
构建的约束图矩阵为
| ${\rm{R = }}\left[ \begin{array}{l} {\rm{0 0 1 0 1 1 0 0 0}}\\ {\rm{0 0 3 2 0 0 4 0 0}}\\ {\rm{1 1 0 3 0 0 4 0 0}}\\ {\rm{0 0 1 0 0 0 4 0 0}}\\ {\rm{1 0 0 0 0 1 1 0 0}}\\ {\rm{4 0 0 0 3 0 0 0 0}}\\ {\rm{0 1 1 1 1 0 0 1 1}}\\ {\rm{0 0 0 0 0 0 3 0 3}}\\ {\rm{0 0 0 0 0 0 4 1 0}} \end{array} \right]{\rm{,}}$ | (1) |
根据拆解约束矩阵(1),构建拆解约束图,如图 2所示.
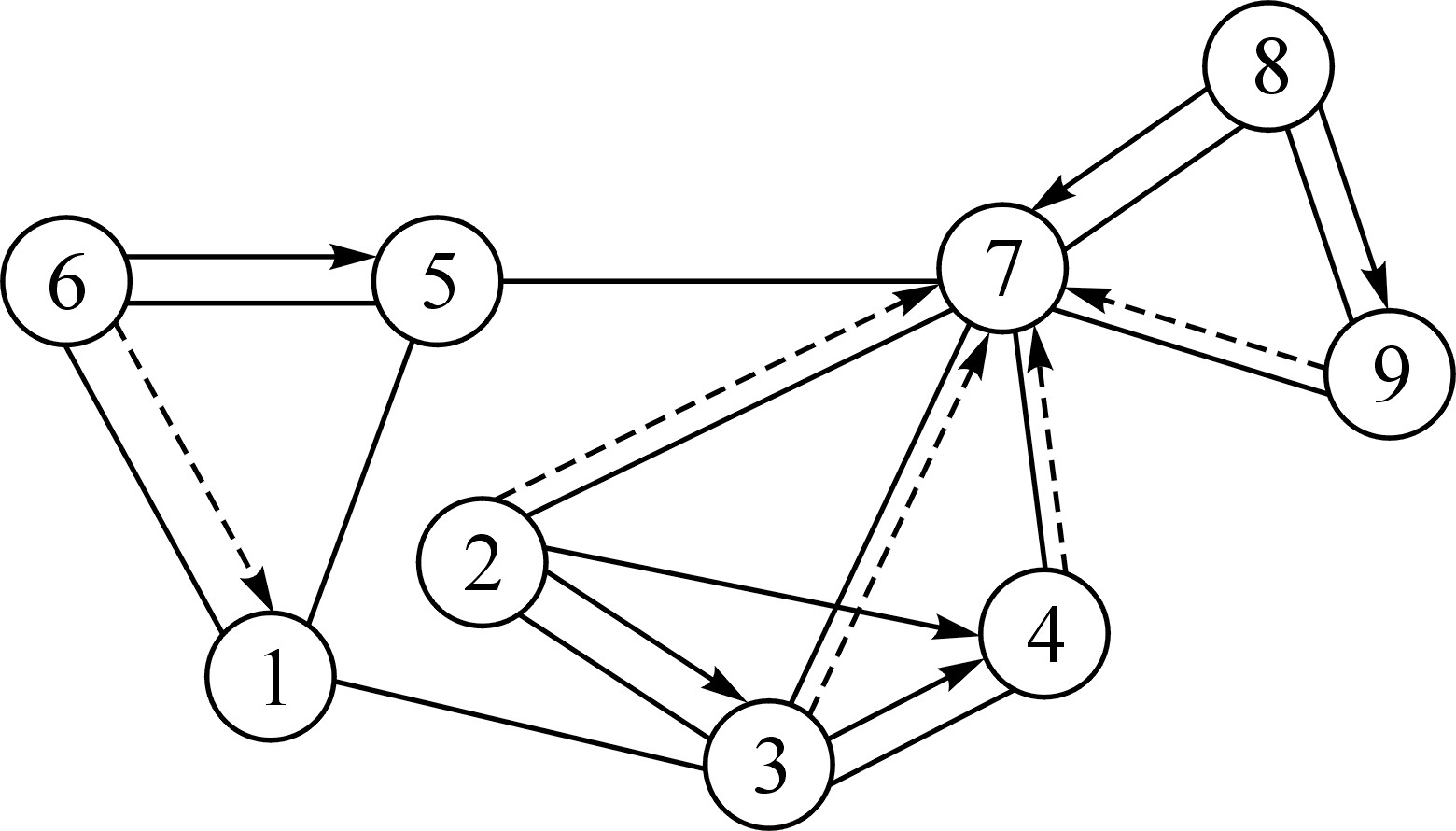 |
| 图 2 液压油缸拆解约束图 Fig. 2 Constraint graph of hydraulic cylinder |
由图 2得到2条完整的油缸可行拆卸序列:
Ⅰ:6-1-2-3-4-5-8-9-7;
Ⅱ:8-9-6-1-2-3-4-5-7.
2 液压油缸拆解能量分析 2.1 拆解能量与拆卸能量
拆解能量指组成拆卸序列的多个拆卸过程所消耗的功,拆卸能量是指定零件在某次拆卸过程中所消耗的功,故有
| ${{\rm{E}}_{\rm{Z}}}{\rm{ = }}\sum\limits_{i = 1}^n {{{\rm{E}}_i}},$ | (2) |
零件拆卸过程大体可分为定位、夹紧、解除约束和零件移出等.理论上零件拆卸能量是上述几个动作消耗能量之和.目前由于零件的拆卸大部分是手动或半自动,零件定位与夹紧消耗能量的多少与零件的拆卸熟练程度和零件拆解工具等相关.当拆卸很熟练时,零件定位夹紧能量几乎不变;不同的拆解工具,在定位和夹紧过程中消耗能量会有些差异.因此,本文在计算零件拆卸能量时,只计算零件约束解除和零件移出所消耗的能量.零件拆卸消耗能量可表示为
| ${E_{{i_{}}}} = {E_{ci}} + {E_{yi}},$ | (3) |
拆卸能量的构成与拆卸路径相关,计算零件拆卸能量时必须考虑这点.图 3所示拆卸零件路径图中,拆卸零件1时,拆卸路径A-B仅为零件1拆卸路径中的一条,在零件1拆卸过程中,其他零部件对其约束作用并没有做功,Eci为零,故在计算拆卸能量时只需计算移出消耗能量,这类零件的特点是可拆卸方向不唯一;在拆卸零件2时,拆卸路径为C-D-F,路径C-D段的拆卸方向唯一,需克服其他零部件对其约束作用,应计算解除约束消耗能量Eci;路径D-F段拆卸路径不唯一,无需克服其他零部件对其约束作用,只计算移出消耗能量Eyi;该零件拆卸能量是解除约束消耗能量和移出消耗能量之和.判定零件可拆卸方向的具体方法可参考文献[12]和文献[13].
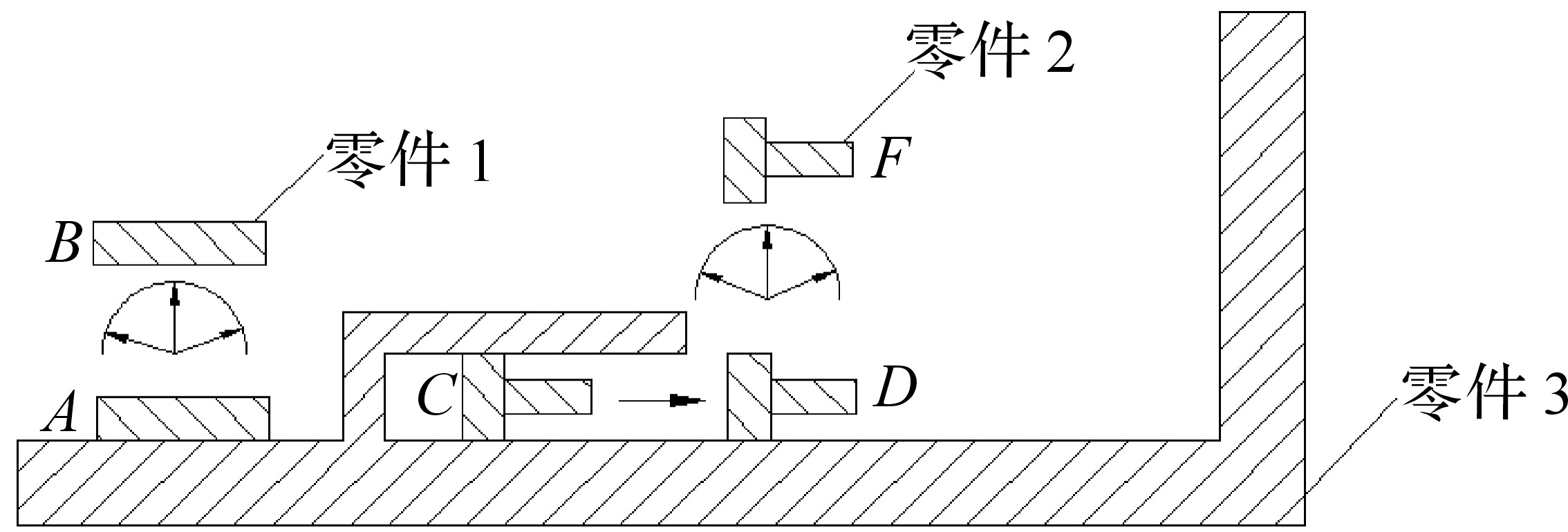 |
| 图 3 零件拆卸路径图 Fig. 3 Parts disassembly path diagram |
零件移出能量是指零件解除约束后,移到零件放置区域需消耗的能量.移出方式可以是专用车(如行车和叉车等)搬运、传送带运输以及人力搬运,采用不同的零件移出方式,零件移出能量计算方法不尽相同.为了更有效、简单地评估零件移出消耗能量,本文提出传送带模型.假设解除约束后的零件全部采用传送带运输到零件放置区域;传送带在运输过程中速度平稳,零件在传送带上从无初速释放,至到达零件放置区域前与传递带速度同步,之后零件和传送带保持相对静止到达零件放置区域.在零件运输过程中,零件与传送带从相对运动到相对静止,依据能量守恒定律,传送带额外多输出的能量等同于移出零件消耗的能量,近似等于零件获得的动能和零件与传送带间摩擦力做功产生的热能.零件移出能量为
| ${E_{yi}} = \frac{1}{2}m{v^2} + {Q_{re}},$ | (4) |
| $\sum\limits_{i = 1}^n {{E_{yi}}} = \sum\limits_{i = 1}^n {{m_{yi}}} {v^2},$ | (5) |
在液压油缸中,螺纹连接是最典型的连接之一,而螺钉连接是最常见的螺纹连接.以螺钉拆卸为例分析螺纹约束解除消耗的能量.目前,螺钉拆卸大部分通过扳手拆卸.螺钉拆卸过程分为螺钉约束解除和螺钉移出两部分.螺钉约束解除过程按照螺钉受力情况可分为松动过程和空转过程,松动过程中始终有预紧力存在,空转过程是无预紧力下螺钉自螺纹孔中旋出过程.理论上,螺钉解除约束消耗的能量为松动过程和空转过程所消耗能量之和.但空转过程消耗能量相比于松动过程消耗能量较小[14],因此,这部分能量可忽略不计.在螺钉松动过程中,松动力矩是拧紧力矩的0.8倍[15],表示为
| ${T_s} = 0.8T,$ | (6) |
则松动过程中消耗能量为
| ${E_{cs}} = {T_s}\theta = 0.8T\theta ,$ | (7) |
图 1液压油缸中缸体与缸盖连接、活塞杆与活塞连接、活塞杆与锁紧螺母连接、耳轴和活塞杆的连接、紧定螺钉与活塞杆的连接都是螺纹连接,其约束的解除能量计算均可参考上述分析.
2.3.2 非刚性过盈配合约束解除非刚性过盈配合是指过盈连接的零件能相对平动或转动的配合,常见于高分子材料零件与金属零件之间,如活塞上密封圈与缸筒间、缸盖上密封圈与活塞杆间的非刚性过盈配合.目前拆卸非刚性配合约束一般是手动拆卸或者用专用拉锯拆卸.以活塞上密封圈和缸筒间非刚性过盈配合约束解除为例来分析此类约束.
图 4所示为液压油缸局部结构图,箭头表示拆卸方向.该非刚性过盈配合约束解除过程分为活塞一直在缸筒内移动和活塞脱离缸筒两部分,采用专用拆卸工具将活塞移出缸筒外.
 |
| 图 4 液压油缸局部结构图 Fig. 4 Local structure diagram of hydraulic cylinder |
解除约束力为缸筒对密封圈的作用力F:
| $F = l\mu \pi D\vartheta ,$ | (8) |
活塞整体在缸筒内移动过程消耗的能量为
| ${E_{cm}} = Fx = l\mu \pi D\vartheta x,$ | (9) |
活塞逐渐脱离缸筒过程消耗的能量为
| ${E_{ct}} = \sum\limits_{i = 1}^l {i\mu \pi D\vartheta {x_i}} ,$ | (10) |
| ${x_h} = {x_1} + {x_2} + {x_3} + \ldots {\rm{ + }}{x_l},$ | (11) |
活塞上密封圈和缸筒间非刚性过盈配合约束解除消耗的能量为
| ${E_{ch}} = {E_{cm}} + {E_{ct}}.$ | (12) |
图 1中液压油缸缸盖上密封圈与活塞杆间的连接也是非刚性过盈配合,其约束的解除能量计算可参考上述分析.
2.4 液压油缸拆解能量
综合分析,液压油缸理论拆解能量Ez为
| ${E_z} = \sum\limits_{i = 1}^n {{E_i}} = \sum\limits_{i = 1}^n {\left( {{E_{ci}} + {E_{yi}}} \right)} ,$ | (13) |
| $\sum\limits_{i = 1}^n {{E_{ci}}} = {E_{c1}} + {E_{c2}} + \ldots {E_{cn}},$ | (14) |
实际的液压油缸拆解能量值E′z估计为
| $E{'_z} = K{E_z},$ | (15) |
以图 1某工程液压油缸为例,表 1为液压油缸零件结构参数及数值,表 2为油缸中非刚性过盈配合约束解除参数及数值.按图 2的可行拆卸序列来计算该油缸拆解能量.
| 零件名称 | 数量/个 | 拧紧力矩/ (N·m) | 旋转角度/ (°) | 质量/kg |
| 缸盖螺钉 | 10 | 210 | 90 | 不计 |
| 锁紧螺母 | 1 | 175 | 90 | 2.5 |
| 活塞组件 | 1 | 120 | 60 | 20 |
| 耳轴 | 1 | 150 | 90 | 25 |
| 紧定螺钉 | 1 | 15 | 45 | 不计 |
| 缸盖组件 | 1 | — | — | 20 |
| 活塞杆 | 1 | — | — | 100 |
| 缸筒 | 1 | — | — | 150 |
| 参数 | 非刚性过盈配合名称 | |
| 活塞密封圈 与缸筒 | 缸盖密封圈 与活塞杆 | |
| 密封圈数目/个 | 3 | 2 |
| 摩擦系数 | 0.3 | 0.3 |
| 配合直径/mm | 360 | 255 |
| 配合长度/mm | 210 | 360 |
| 单元圆周正压力/Pa | 1 200 | 1 200 |
| 移动距离/mm | 1 400 | 800 |
由表 1和表 2中液压油缸相关参数及数值,计算可行拆卸序列Ⅰ中零件约束解除和移出消耗能量,见表 3.由于缓冲套与活塞杆为间隙配合,且缓冲套质量很小,解除缓冲套所消耗的能量很小,忽略不计.
|
油缸零件及 拆卸顺序i | 解除约束消耗 能量Eci/J | 零件移出消耗 能量Eyi/J |
| 缸盖螺钉:1 | 176 | 质量太小,忽略不计 |
| 缸筒:2 | 1 838 | 600 |
| 锁紧螺母:3 | 220 | 10 |
| 活塞组件:4 | 100 | 80 |
| 缸盖组件:6 | 565 | 80 |
| 紧定螺钉:7 | 19 | 质量太小,忽略不计 |
| 耳轴:8 | 188 | 100 |
| 活塞杆:9 | 0 | 400 |
| 消耗能量和 | ∑Eci=3 106 J | ∑Eyi=1 270 J |
由表 3可得,以该液压油缸的可行拆卸序列I来计算其拆解能量E1-z为
| ${E_{1 - z}} = \sum\limits_{i = 1}^n {{E_i}} = \sum\limits_{i = 1}^n {\left( {{E_{ci}} + {E_{yi}}} \right)} = 3106 + 1270 = 4376{\rm{J}}{\rm{.}}$ | (16) |
以可行拆卸序列Ⅱ来计算该油缸的拆解能量,参考拆卸序列Ⅰ中各参数值,其中缸盖组件在活塞杆上移动方向与序列I中缸盖组件移动方向相反,在活塞杆上一直移动的距离由800 mm变为210 mm,其他参数值几乎没有变化,则缸盖组件解除约束消耗能量由565 J变为151 J,其他零部件解除约束消耗能量几乎不变,则以该液压油缸可拆卸序列Ⅱ计算其拆解能量E2-z为
| ${E_{2 - z}} = \sum\limits_{i = 1}^n {{E_i}} = \sum\limits_{i = 1}^n {\left( {{E_{ci}} + {E_{yi}}} \right)} = 2692 + 1270 = 3962{\rm{J}}{\rm{.}}$ | (17) |
由E2-z<E1-z,可得该油缸以可行拆卸序列Ⅱ来拆解时,该油缸拆解过程中消耗能量较小,若依据拆解能量最小原则,可拆卸序列Ⅱ优于可行拆卸序列Ⅰ.
4 结 论本文基于拆解混合图构建了工程液压油缸拆解约束模型,得到了相应的拆卸序列;定义了拆解能量的组成,分析归纳了工程液压油缸的各种典型约束解除消耗能量计算公式,提出了用传送带模型来计算零部件移出消耗能量.以某工程液压油缸拆解为例,计算得出该液压油缸拆卸序列Ⅰ和Ⅱ的拆解能量值,通过比较分析可得到该液压油缸拆卸序列Ⅱ的拆解能量较小.通过对液压油缸拆解能量的分析评估,可为油缸的拆卸序列规划、专用拆卸设备设计和液压油缸的可拆卸性设计提供参考.
| [1] |
朱胜,姚巨坤.再制造设计理论及应用[M].北京:机械工业出版社,2009:43-50. ZHU Sheng,YAO Ju-kun.Remanufacturing design theory and application [M].Beijing:Mechanical Industry Press,2009:43-50. |
| [2] |
于随然,陶璟,陈泓,等.基于拆卸时间的产品可拆卸性评价及改进设计[J].上海交通大学学报,2007,41(9):1476-1478. YU Sui-ran,TAO Jing,CHEN Hong,et al.The time based evaluation of product disassemblibility and design improvement[J].Journal of Shanghai Jiaotong University,2007,41(9):1476-1478. |
| Click to display the text | |
| [3] |
孙有朝,黄进永,王伟,等.基于零件故障率和拆卸时间的产品拆卸性定量评估方法[J].机械工程学报,2010,46(13):148-154. SUN You-chao,HUANG Jin-yong,WANG Wei,et al.Quantitative evaluation method of product disassembly based on parts failure rate and disassembly time [J].Journal of Mechanical Engineering,2010,46(13):148-154. |
| Click to display the text | |
| [4] | KROLL E,CARVER B S.Disassembly analysis through time estimation and other metrics[J].Robotics and Computer-Integrated Manufacturing,1999,15(3):191-200. |
| Click to display the text | |
| [5] | GO T F,WAHAB D A,RAHMAN M N A,et al.Genetically optimised disassembly sequence for automotive component reuse [J].Expert Systems with Application,2012,39(5):5409-5417. |
| Click to display the text | |
| [6] | BEATRIZ G,BELARMINO A D.A scatter search approach to the optimum disassembly sequence problem [J].Computers & Operations Research,2006,33(5):1776-1793. |
| Click to display the text | |
| [7] |
郭希旺,刘士新,王大志,等.多目标拆卸序列优化问题的分散搜索算法[J].东北大学学报,2012,33(1):57-59. GUO Xi-wang,LIU Shi-xin,WANG Da-zhi,et al.Scatter search for solving multi-objective diassembly sequence optimization problems[J].Journal of Northeastern University,2012,33(1):57-59. |
| Click to display the text | |
| [8] |
张雷,彭宏伟,卞本阳,等.复杂产品并行拆解建模及规划方法研究[J].中国机械工程,2014,25(7):937-943. ZHANG Lei,PENG Hong-wei,BIAN Ben-yang,et al.Parallel disassembly modeling and planning method of complex products[J].China Mechanical Engineering,2014,25(7):937-943. |
| Click to display the text | |
| [9] |
田广东,储江伟,刘玉梅,等.产品拆解混合图模型构建与能量评估方法[J].计算机集成制造系统,2012,18(22):2614-2618. TIAN Guang-dong,CHU Jiang-wei,LIU Yu-mei,et al.Construction and energy evaluation method for hybrid graph model of product disassembly[J].Computer Integrated Manufacturing Systems,2012,18(22):2614-2618. |
| Click to display the text | |
| [10] | LI J R,TOR S B,KHOO L P.A hybrid disassembly sequence planning approach for maintenance[J].Journal of Computing and Information Science in Engineering,2002,2(1):28-37. |
| Click to display the text | |
| [11] |
张秀芬,胡志勇,蔚刚,等.基于联结元的复杂产品拆卸模型构建方法[J].机械工程学报,2014,50(9):123-130. ZHANG Xiu-fen,HU Zhi-yong,WEI Gang,et al.Disassembly modeling method for complex products based on connector structure units[J].Journal of Mechanical Engineering,2014,50(9):123-130. |
| Click to display the text | |
| [12] |
郭伟祥,刘光复,刘志峰,等.产品拆卸运动仿真与干涉分析[J].计算机集成制造系统,2006,12(4):517-519. GUO Wei-xiang,LIU Guang-fu,LIU Zhi-feng,et al.Product disassembly motion simulation & interference analysis[J].Computer Integrated Manufacturing Systems,2006,12(4):517-519. |
| Click to display the text | |
| [13] |
江吉彬,许明三,曾寿金,等.废旧机电产品再制造的拆卸路径规划[J].农业机械学报,2009,40(10):204-206. JIANG Ji-bin,XU Ming-san,ZENG Shou-jin,et al.Disassembly path planning method of waste electromechanical products in remanufacturing[J].Journal of Agricultural Machinery,2009,40(10):204-206. |
| Click to display the text | |
| [14] | 李辰,朱勇军,侯兆欣,等.钢结构高强度螺栓连接紧固原理分析及螺母转角法的试验研究[J].建筑结构,2013,43(增刊):449-452. LI Chen,ZHU Yong-jun,HOU Zhao-xin,et al.Theoretical and testing study on tigtening behavior of high-strength bolts and turn-of-nut method [J].Building Structure,2013,43(supplement):449-452. |
| Click to display the text | |
| [15] | SUGA T,SANESHIGE K,FUJIMOTO J.Quantitative disassembly evaluation[C]//Proc IEEE Symp Electronicsand Environment.Dallas,May.6-8,1996. |


