2. 中国联合通信网络有限公司 江苏省分公司, 江苏 南京 210024;
3. 江苏金冠立体停车股份有限公司, 江苏 南通 226003
2. Jiangsu Branch, China United Network Communications Group Co., Ltd., Nanjing 210024, China;
3. Jiangsu Jinguan Solid Parking System Engineering Co., Ltd., Nantong 226003, China
汽车保有量的急剧增加伴随着泊车位供应不足与泊车位需求增长过快的过剩矛盾日益凸显,造成了城市交通拥挤、停车困难等社会问题,成为制约城市经济和社会发展的瓶颈.而基于AGV平面移动式智能停车库的出现,则很好地解决了这一难题.与传统平面车库和机械式立体车库相比,该智能车库具有停车占地面积少、有效存车数量多、车辆存取自动化程度高、性价比高以及安全可靠性高等优点,可实现无人自动存取车、AGV自动充电以及车库自动计费等诸多功能[1].研究平面移动式智能停车库的核心是解决AGV存取车路径规划问题.目前,针对路径规划问题,国内外相关学者已做了大量研究工作,并相继提出了禁忌搜索算法[2]、模拟退火算法[3]、遗传算法[4]、蚁群算法[5]以及粒子群算法[6]等.
粒子群算法(PSO)是由Eberhart和Kennedy于1995年基于鸟群捕食行为而提出的一种群体智能优化算法.该算法保留了种群的全局搜索策略,可通过速度—位移模型和自身记忆特性实现动态跟踪及实时调整搜索策略等功能,具有算法设计简单、易于实现、需调整参数较少、收敛速度快、全局搜索能力强等优点,一经提出便引起了学者的关注和研究,并在函数优化、路径规划、神经网络训练以及自动控制等领域得到了广泛应用.樊明等[4]通过建立惯性权重系数、认知系数与收缩因子三者之间的联动关系和引入遗传算法的交叉与变异操作对粒子群算法进行了改进,并将改进算法用于智能存取系统,解决了存取系统的路径优化问题;王波等[6]通过引入遗传算法的交叉与变异操作对粒子群算法进行了改进,并将改进的粒子群算法用于云计算任务调度中,通过仿真测试验证了算法的可行性和有效性;乔俊飞等[7]提出采用改进的动态自适应粒子群算法解决给水管网优化问题,仿真试验结果显示改进算法具有较强的全局搜索能力和较快的收敛速度.
遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索优化方法,该算法借鉴了达尔文的进化论和孟德尔的遗传学说,具有易于实现、可处理复杂问题、可实现并行搜索、算法效率高以及鲁棒性强等特点,被广泛用于解决图像处理、人工智能、路径规划以及生产调度等领域的问题.Imen等[5]针对机器人在静态环境中的路径规划问题,提出将蚁群算法与遗传算法进行有效结合,并通过仿真测试验证了算法的可行性和有效性;雷伟军等[8]提出将改进的遗传算法用于解决多模型加工路径规划问题,缩短了多模型的整体加工路径长度;徐翔等[9]通过引入新的交叉变异概率公式对基本遗传算法进行了改进,然后将改进算法运用到智能体路径规划中,仿真结果显示改进算法的收敛性能和全局搜索能力都有明显提高.
针对智能停车库AGV存取车路径规划问题,结合粒子群和遗传算法的优点,提出了一种融合粒子群和遗传算法的自适应混合算法(APSOGAA).该混合算法在标准粒子群算法和遗传算法的基础上,通过引入动态自适应调整策略分别对惯性权重系数、学习因子以及交叉变异概率公式来进行优化.进化初期,为平衡算法全局和局部搜索能力,提高搜索效率和改善收敛性能,通过在惯性权重系数和学习因子之间建立动态联动关系,实现对粒子速度和位置的实时有效更新;进化后期,为防止粒子陷入局部最优,出现早熟问题,通过引入自适应遗传算法的交叉、变异操作来增强粒子多样性,拓展粒子解空间,增强算法全局搜索能力,提高算法进化速度和收敛精度.为验证混合算法的可行性和有效性,最后选用MATLAB软件对其进行了仿真测试.
1 问题描述及数学模型当AGV从预存停车位出发到目标停车位取出车辆,然后再将其运回到预存车位,这个过程可简化为TSP问题.TSP作为优化组合领域的经典NP难题,备受国内外学者关注和研究.Basu[2]提出用禁忌搜索算法解决TSP问题;Wang等[3]提出用改进的模拟退火算法解决TSP问题;Aditi等[10]提出用粒子群蚁群混合算法来解决TSP问题.此处AGV路径规划的TSP问题可定义为:在已知AGV可行路径节点的前提下,AGV从预存停车位出发,遍历各个可行路径节点1次,然后将目标车辆运送至预存停车位,在此过程中确定一条可使AGV运行距离最短的可行路径.数学模型可描述为:根据可行路径节点坐标,建立赋权图G=(Q,E),其中,Q表示节点集合,Q={1,2,…,n },E表示各节点间形成的可行路径,dij表示i,j节点间的欧式距离,可按照式(1)计算得到,对于不连通节点间的权值可赋值inf (无穷大).数学模型可表示为:
| $ {d_{ij}} = \sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2}} , $ | (1) |
| $ D = \sum\limits_i^{n - 1} {{d_{ij}}} + {d_{n1}}, $ | (2) |
式中:i,j表示可行路径上的节点;D表示整个循环路径总长度.
2 粒子群算法设计 2.1 基本粒子群算法粒子群算法(PSO)是一种基于迭代搜寻最优解的随机优化技术,其基本思想是通过群体中个体间的协作和信息共享来寻找最优解[11].在PSO算法中,首先将问题的可行解空间初始化为一群粒子,每个优化问题的潜在最优解均可视为搜索空间中的一个粒子,通过适应度函数评价种群中粒子的优劣,对比粒子当前适应度值及其所经过的个体极值点pbest和全局极值点pgbest的适应度值,更新粒子当前最优个体极值点和全局最优极值点,然后按照方程式(3)和(4)分别对粒子的速度和位置进行更新,最终实现粒子在可行解空间中的寻优.
在d维搜索空间中,粒子i的位置和速度可分别表示为Xi ={xi1,xi2,…,xin}和Vi={vi1,vi2,…,vin}.粒子i的速度和位置可按照式(3)和式(4)进行更新:
| $ \begin{array}{l} {v_{id}}\left( {t + 1} \right) = {v_{id}}\left( t \right) + {c_1}{r_1}[{p_{{\rm{best}}}}\left( t \right) - {x_{id}}\left( t \right)] + \\ {c_2}{r_2}[{p_{{\rm{gbest}}}}\left( t \right) - {x_{id}}\left( t \right)], \end{array} $ | (3) |
| $ {x_{id}}\left( {t + 1} \right) = {x_{id}}\left( t \right) + {v_{id}}\left( {t + 1} \right),j = 1,2,\ldots ,d, $ | (4) |
式中:j表示粒子的搜索空间,i表示当前粒子;参数c1和c2表示学习因子;r1和r2为随机数,r1∈[0, 1],r2∈[0, 1];xid和vid分别表示粒子i在d维的当前位置和当前速度;pbest为粒子i在d维的个体极值点位置,pgbest为当前整个粒子群在d维中的全局极值点位置.
2.2 基本遗传算法遗传算法是由美国Holland教授借鉴生物界进化规律而提出的一种启发式随机搜索方法,主要由编码、选择、交叉、变异以及解码操作组成.该算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象,从任意初始种群出发,通过随机选择、交叉和变异等操作,按照“适者生存、优胜劣汰”的进化原则,产生一群更适应环境的个体.优化群体经过多代繁衍进化,最后收敛到一群最适应环境的个体,通过对优化个体解码,可得到问题的最优解或次最优解.
3 粒子群遗传算法设计在AGV存取车路径规划中,选用标准粒子群算法和遗传算法虽然能够使AGV规划出一条从起始位置到目标位置的强鲁棒性优化路径,但依然存在诸多不足,主要表现为收敛速度慢、搜索效率较低、易出现早熟或停滞以及易陷入局部最优等.针对上述问题,通过引入动态自适应调整策略,设计了一种动态自适应混合算法.
3.1 惯性权重优化由标准粒子群算法中粒子速度更新方程可知,粒子的飞行速度直接影响着算法全局搜索能力.粒子飞行速度越大,则搜索能力就越强,其飞到全局最优解区域的可能性就越大.但当飞行速度过大时,粒子极易飞越最优解而转向其他区域;当飞行速度过小时,粒子会因无法找到解空间的最佳位置而陷入局部最优.为对粒子飞行速度进行有效控制和约束,Shi等在标准粒子算法模型中引入了惯性权重系数ω,粒子的速度和位置更新公式可更改为[12]:
| $ \begin{array}{l} {v_{id}}\left( {t + 1} \right) = w{v_{id}}\left( t \right) + {c_1}{r_1}[{p_{{\rm{best}}}}\left( t \right) - {x_{id}}\left( t \right)] + \\ {c_2}{r_2}[{p_{{\rm{gbest}}}}\left( t \right) - {x_{id}}\left( t \right)], \end{array} $ | (5) |
| $ {x_{id}}\left( {t + 1} \right) = {x_{id}}\left( t \right) + {v_{id}}\left( {t + 1} \right),j = 1,2,\ldots ,d, $ | (6) |
惯性权重系数ω是PSO算法中一个极为重要的控制参数,直接影响着粒子的搜索能力和算法的收敛速度.较大的惯性权重系数有利于增强算法的全局搜索能力和提高收敛速度,但会降低算法局部搜索能力且不易得到精确全局最优解;较小的惯性权重系数有利于提高收敛精度和得到精确最优解,但会削弱全局搜索能力和降低收敛速度.因此,选择合理的惯性权重系数ω对增强算法搜索能力和提高收敛速度是极为重要的.为平衡粒子群算法的全局和局部搜索能力,选用非线性动态惯性权重对粒子群算法进行了改进,更改后的权重系数公式如下[13]:
| $ w = \left\{ {\begin{array}{*{20}{c}} {{w_{\min }} - \frac{{\left( {{w_{\max }} - {w_{\min }}} \right)\left( {f - {f_{\min }}} \right)}}{{{f_{avg}} - {f_{\min }}}},f \le {f_{avg}},}\\ {{w_{\max ,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f > {f_{avg}},} \end{array}} \right. $ | (7) |
式中:ωmax为ω的最大值,ωmin为ω的最小值,一般取ωmax=0.9,ωmin=0.4;f表示粒子当前的适应度值,favg和fmin分别表示当前所有粒子的平均适应度值和最小适应度值.
3.2 学习因子优化学习因子c1和c2是PSO算法的另外一组重要参数,决定了粒子自我认知和社会认知对粒子运行轨迹的影响,反映了群体中各粒子间的信息交流[14].当学习因子c1取较大值时,过多的粒子会聚集在局部区域内徘徊;当学习因子c2取较大值时,会促使粒子在局部最小值范围内过早收敛.因此,选择合适的学习因子对增强算法搜索能力和提高收敛精度与速度极为重要.在PSO算法中,学习因子一般为常数,取值通常为c1=c2=2,但在实际应用中,学习因子也存在其他取值方式,常见的有同步变化和异步变化,此处采用异步变化的学习因子对PSO算法进行改进,以实现对学习因子的动态调整.更改后的学习因子公式如下[15]:
| $ {c_1} = {c_{1,s}} + \frac{{{c_{1,e}} - {c_{1,s}}}}{{{t_{\max }}}} \cdot t, $ | (8) |
| $ {c_2} = {c_{2,s}} + \frac{{{c_{2,e}} - {c_{2,s}}}}{{{t_{\max }}}} \cdot t, $ | (9) |
式中:参数c1,s和c2,s分别表示学习因子c1和c2的初始值,c1,e和c2,e分别表示学习因子c1和c2的迭代终值;t表示当前迭代次数,tmax表示最大迭代次数.多数情况下,上式中的参数进行如下设置可取得较好效果:c1,s=c2,s=2.5,c1,e=c2,e=0.5.
由更改后的学习因子公式和速度与位置更新公式分析可知:在算法进化初期,粒子具有较强的自我学习能力和较弱的社会学习能力,有利于强化粒子全局搜索能力;在进化后期,粒子具有较强的社会学习能力和较弱的自我学习能力,有利于提高粒子的收敛速度和收敛精度,确保粒子能够收敛到全局最优.
3.3 交叉和变异概率调整公式在算法进化后期,为防止粒子陷入局部最优及出现早熟问题,此处通过引入自适应遗传算法的交叉、变异操作来增强PSO算法的全局搜索能力,提高算法的收敛速度和收敛精度.
交叉、变异操作是产生新个体的关键环节,分别影响着遗传算法的全局和局部搜索能力,通常情况下交叉概率Pc取较大值,变异概率Pm取较小值.对于交叉概率Pc,取值越大,则产生新个体的速度就越快,但过大的Pc会使得群体优良模式被破坏的可能性增大,致使具有高适应度的优良个体被破坏;Pc过小则会使得新个体产生速度变得缓慢,致使搜索过程停滞不前,影响算法的全局搜索能力.对于变异概率Pm,若取值过小,则不利于产生新个体结构,且算法易出现早熟;若取值过大,则会使得群体中具有较高适应度的个体被破坏的可能性增大,导致算法性能下降.因此,选择合理的交叉、变异概率对增强算法搜索能力和改善算法收敛性能有着极为重要的作用.
针对不同问题,Pc和Pm的确定工作异常繁琐、复杂,而且也很难找到理想通用的Pc和Pm.另外,固定的Pc和Pm无法保证算法在优化空间中搜索到全局最优解,也很难适应搜寻过程中不同取值需求.为此,Srinivas等人[16]提出了一种自适应遗传算法,在该算法中,Pc和Pm可根据适应度变化而自行调整.但在个体适应度和最大适应度取相同值的情况下,交叉、变异概率取值同时为零,易使算法出现早熟收敛,陷入局部最优解.基于此,对Srinivas提出的自适应算法作进一步改进,将群体中具有最大适应度的个体交叉、变异概率分别提高到Pc2和Pm2,以确保具有最大适应度的个体的交叉、变异概率在进化过程中不出现零值,避免算法出现停滞问题.在进化过程中,为确保每代优良个体不被破坏,可采用精英选择策略,将每次迭代产生的优良个体直接复制到下一代.改进后的交叉、变异概率公式如下[17]:
| $ {P_{\rm{c}}} = \left\{ {\begin{array}{*{20}{c}} {{P_{c1}} - \frac{{\left( {{P_{c1}} - {P_{c2}}} \right)\left( {f' - {f_{avg}}} \right)}}{{{f_{\max }} - {f_{avg}}}},f' \ge {f_{avg}},}\\ {{P_{c1}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f' < {f_{avg}},} \end{array}} \right. $ | (10) |
| $ {P_{\rm{m}}} = \left\{ {\begin{array}{*{20}{c}} {{P_{m1}} - \frac{{\left( {{P_{m1}} - {P_{m2}}} \right)\left( {{f_{\max }} - f} \right)}}{{{f_{\max }} - {f_{avg}}}},f \ge {f_{avg}},}\\ {{P_{m1}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f < {f_{avg}},} \end{array}} \right. $ | (11) |
式中:参数Pc1和Pm1分别表示交叉概率和变异概率的最大值;参数fmax和favg分别表示粒子群中最大适应度值和各次迭代的平均适应度值;参数f′和f分别表示要交叉个体中较大的适应度值和要变异个体的适应度值.多数情况下,上式中的参数进行如下设置可取得较好效果:Pc1=0.9,Pc2=0.6,Pm1=0.1,Pm2=0.001.
3.4 算法具体实施步骤Step 1:建立AGV运行环境模型,确定可行路径上各节点坐标位置,并对各节点坐标进行编号;
Step 2:初始化算法各参数,以整数方式对粒子个体进行编码,随机生成一个规模为m的粒子群,设定粒子的初始位置和初始速度;
Step 3:由适应度函数方程式计算出各粒子适应度值,对比分析各粒子适应度值,并根据适应度值优劣来更新粒子的个体最佳位置pbest和全局最佳位置pgbest;
Step 4:根据式(7)、(8)及式(9)分别对惯性权重系数ω和学习因子c1及c2进行更新;
Step 5:根据式(5)和式(6)更新粒子的速度和位置;
Step 6:由适应度函数方程式计算出各粒子适应度值,并根据适应度值优劣来更新粒子的个体最佳位置pbest和全局最佳位置pgbest;
Step 7:根据适应度函数计算各粒子适应度值,对比各粒子适应度值,按照交叉概率式(10)选择需要交叉的个体和群体,完成个体最优交叉和群体最优交叉操作;
Step 8:按照式(11),粒子进行变异操作,产生新粒子;
Step 9:由适应度函数方程式计算出新粒子适应度值,并根据适应度值优劣来更新粒子的个体最佳位置pbest和全局最佳位置pgbest;
Step 10:判断算法是否满足终止条件,若是,则算法结束,输出结果,否则转至Step 3.
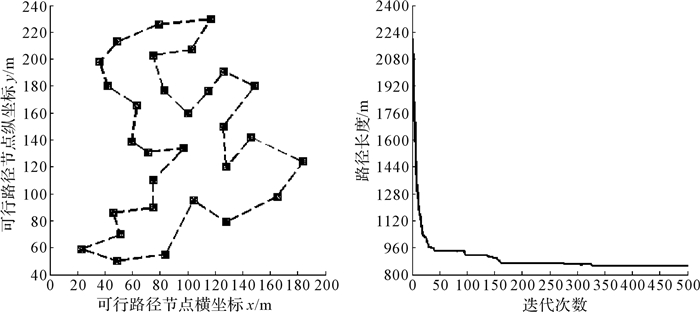
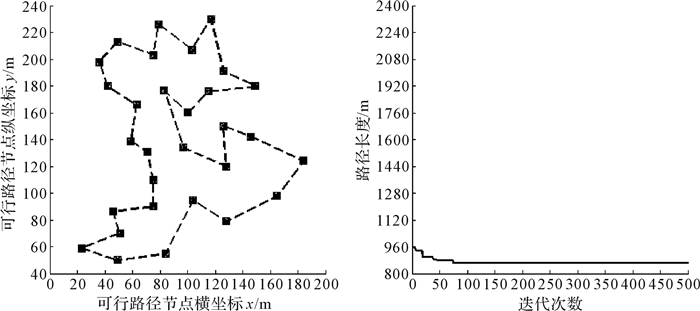
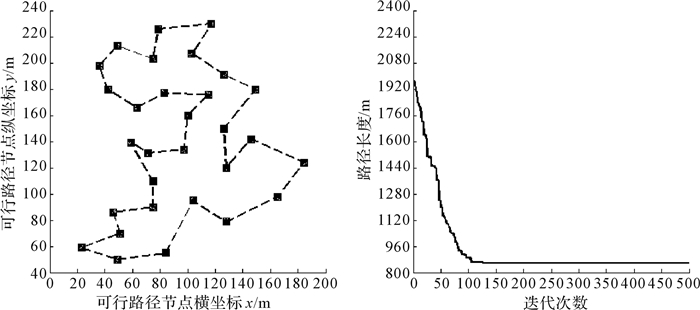
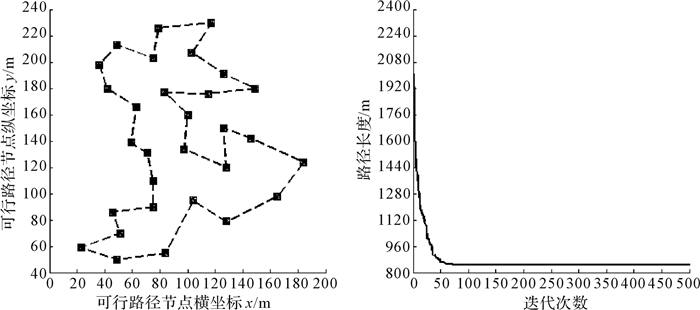
4 仿真及分析为验证算法在AGV路径规划中的合理性和有效性,以可行路径上30个坐标点的路径寻优为例,算法参数设置如下:在禁忌搜索算法中,禁忌长度为50,候选解为200,最大步数为500;蚁群算法中,蚂蚁数量为40,α=1,β=5,ρ=0.1,最大迭代次数为500;遗传算法中,种群规模为500,Pc=0.9,Pm=0.05,最大迭代次数为500;混合算法中,种群规模为500,最大迭代次数为500.在MATLAB环境下分别对禁忌搜索算法、蚁群算法、遗传算法及混合算法进行仿真测试.通过对比上述算法仿真数据,来验证混合算法的性能.仿真结果如图 1至图 4所示.
|
| 图 1 禁忌搜索算法路径轨迹迭代图 Fig. 1 Path trajectory iteration graph of TSA |
|
| 图 2 蚁群算法路径轨迹迭代图 Fig. 2 Path trajectory iteration graph of ACO |
|
| 图 3 遗传算法路径轨迹迭代图 Fig. 3 Path trajectory iteration graph of GA |
|
| 图 4 混合算法路径轨迹迭代图 Fig. 4 Path trajectory iteration graph of hybrid algorithm |
图 1至图 4所示为AGV在各算法下的存取车路径运行轨迹迭代图,图中虚线代表AGV存取车路径运行轨迹曲线,实线代表各算法下AGV的迭代路径变化曲线.由图可知,在遍历可行路径各节点的前提下,根据当前位置以及存取车位置,AGV运用上述算法均可快速搜索到一条自起点至终点的优化路径.
对比表 1数据,结合图中所示的AGV运行轨迹可知,AGV采用禁忌搜索算法规划的路径长度为852.59 m,蚁群算法为860.865 2 m,遗传算法为855.266 6 m,混合算法为847.492 3 m,在路径长度方面,混合算法比禁忌搜素算法减少了5.097 7 m,比蚁群算法减少了13.372 9 m,比遗传算法减少了7.774 3 m.在迭代次数方面,禁忌搜索算法在第329代开始收敛,蚁群算法为第80代,遗传算法为第127代,混合算法为第76代,很显然,混合算法具有较快的收敛速度.综上分析可知,混合算法在搜索路径长度和收敛速度方面都是最优的,表明混合算法具有较快搜索速度、较高搜索效率的优点.
| 算法 | 最短路径长度/m | 收敛代数 |
| 禁忌搜索算法 | 852.59 | 329 |
| 蚁群算法 | 860.865 2 | 80 |
| 遗传算法 | 855.266 6 | 127 |
| 混合算法 | 847.492 3 | 76 |
针对AGV存取车路径规划问题,有效地将粒子群算法和遗传算法进行了融合,在标准粒子群算法和遗传算法的基础上,通过引入动态自适应调整策略,设计了一种动态自适应混合算法,并在MATLAB环境下对该混合算法进行了仿真测试.由仿真测试结果可得如下结论:在遍历可行路径各节点的前提下,根据AGV自身当前位置,运用文中所提算法均可快速搜索到一条自起点至终点的无交叉优化路径;与禁忌搜索算法、蚁群算法以及遗传算法相比,混合算法规划的路径长度最短;路径迭代图显示混合算法具有较好收敛性能、较快搜索速度、较高搜索效率以及较短搜索路径长度的优点.
| [1] | CHARLES E B,BRIAN G P,CHRISTIAN A Y,et al.Automated automotive vehicle parking/storage system:US12855017[P].2014-05-27. |
| [2] | BASU S.Tabu search implementation on traveling salesman problem and its variations:a literature survey[J].American Journal of Operations Research,2012,2(2):163-173. |
| Click to display the text | |
| [3] | WANG Yong,TIAN De,LI Yu-hua.An improved simulated annealing algorithm for travelling salesman problem[J].International Journal of Online Engineering,2013,9(4):28-32. |
| Click to display the text | |
| [4] | 樊明,郭艺,贠超,等.基于自适应混合算法的智能存取系统动态路径规划[J].系统仿真学报,2013,25(7):1543-1548. FAN Ming,GUO Yi,YUN Chao,et al.Adaptive hybrid algorithm for dynamic path planning problem of intelligent access system[J].Journal of System Simulation,2013,25(7):1543-1548. |
| Cited By in Cnki (4) | Click to display the text | |
| [5] | IMEN C,ANIS K,SAHAR T,et al.Smartpath:an efficient hybrid ACO-GA algorithm for solving the global path planning problem of mobile robots[J].International Journal of Advanced Robotic Systems,2014,11(1):1-15. |
| Click to display the text | |
| [6] | 王波,张晓磊.基于粒子群遗传算法的云计算任务调度研究[J].计算机工程与应用,2015,51(6):84-88. WANG Bo,ZHANG Xiao-lei.Task scheduling algorithm based on particle swarm optimization genetic algorithms in cloud computing environment[J].Computer Engineering and Applications,2015,51(6):84-88. |
| Cited By in Cnki (7) | Click to display the text | |
| [7] | 乔俊飞,王超,刘昌芬.基于改进的自适应粒子群算法的给水管网优化设计[J].北京工业大学学报,2014,40(7):1035-1040. QIAO Jun-fei,WANG Chao,LIU Chang-fen.Optimal design of a water supply system based on improved self-adaptive particle swarm algorithm[J].Journal of Beijing University of Technology,2014,40(7):1035-1040. |
| Cited By in Cnki (3) | Click to display the text | |
| [8] | 雷伟军,程筱胜,戴宁,等.基于改进遗传算法的多模型加工路径规划[J].机械工程学报,2014,50(11):153-161. LEI Wei-jun,CHENG Xiao-sheng,DAI Ning,et al.Multi-model machining path planning based on improved genetic algorithm[J].Journal of Mechanical Engineering,2014,50(11):153-161. |
| Cited By in Cnki (7) | Click to display the text | |
| [9] | 徐翔,梁瑞仕,杨会志.基于改进遗传算法的智能体路径规划仿真[J].计算机仿真,2014,31(6):357-361. XU Xiang,LIANG Rui-shi,YANG Hui-zhi.Path planning for agent based on improved genetic algorithm[J].Computer Simulation,2014,31(6):357-361. |
| Cited By in Cnki (5) | |
| [10] | ADITI K,MAITI M K,MAITI M.Profit maximization of TSP through a hybrid algorithm[J].Computers and Industrial Engineering,2015,88:229-236. |
| Click to display the text | |
| [11] | PINKEY C,KUSUM D,MILLIE P.Novel inertia weight strategies for particle swarm optimization[J].Memetic Computing,2013,5(3):229-251. |
| Click to display the text | |
| [12] | SHI Y,EBERHART R.Monitoring of particle swarm optimization[J].Frontiers of Computer Science in China,2009,3(1):31-37. |
| Click to display the text | |
| [13] | AHMAD N,MEHDI E M,REZA S.A novel particle swarm optimization algorithm with adaptive inertia weight[J].Applied Soft Computing Journal,2011,11(4):3658-3670. |
| Click to display the text | |
| [14] | 马国庆,李瑞峰,刘丽.学习因子和时间因子随权重调整的粒子群算法[J].计算机应用研究,2014,31(11):3291-3294. MA Guo-qing,LI Rui-feng,LIU Li.Particle swarm optimization algorithm of learning factors and time factor adjusting to weights[J].Application Research of Computers,2014,31(11):3291-3294. |
| Cited By in Cnki (8) | Click to display the text | |
| [15] | 赵远东,方正华.带有权重函数学习因子的粒子群算法[J].计算机应用,2013,33(8):2265-2268. ZHAO Yuan-dong,FANG Zheng-hua.Particle swarm optimization algorithm with weight function's learning factor[J].Journal of Computer Applications,2013,33(8):2265-2268. |
| Cited By in Cnki (24) | Click to display the text | |
| [16] | SRINIVAS M,PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Transactions on Systems,Man and Cybernetics,1994,24(4):656-667. |
| Click to display the text | |
| [17] | 任子武,伞冶.自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报,2006,18(1):41-43. RRN Zi-wu,SAN Ye.Improved adaptive genetic algorithm and its application research in parameter identification[J].Journal of System Simulation,2006,18(1):41-43. |
| Cited By in Cnki (193) | Click to display the text |



