从20世纪70年代起,管路布局设计问题已经在诸如航空发动机、大规模集成电路及船舶机舱等工业领域成为一个热门的研究课题.管路设计是船舶设计过程中至关重要的部分.由于布局空间结构的复杂性、管路数量众多以及各种设计约束等,船舶管路布局工作复杂而耗时[1].因此,需要一种智能优化设计方法辅助设计人员提高设计效率,减少设计过程中的人为错误.
在路径规划问题的研究中,传统的搜索算法包括Dijkstra算法[2]、迷宫算法[3, 4]等.其中迷宫算法是经典的布线算法,在管路解存在的条件下,迷宫算法一定能找到最优解;但当搜索空间的范围增大时,迷宫算法则需要大量的数据存储空间,其搜索效率降低.对此,Hightower[5]提出了逃逸算法,有效提高了算法的搜索效率,但是难以保证搜索到最短路径.近年来,现代优化算法[6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]的发展推动了管路路径规划算法的进一步研究,遗传算法[6, 7, 8, 9]是具有代表性的一种算法.Ito[6]应用遗传算法对二维空间的管路布局问题进行了系列的研究,提出变长度的编码方法,引入空间能量的概念,取得了较好的仿真验证结果.范小宁等[8]基于遗传算法提出了变长度编码的交叉变异方法,求解三维空间管路布局问题,其仿真实例也验证了算法的有效性.但是,变长度编码易产生过分冗长的管路,而这些管路对更优管路的搜索意义不大,造成程序设计复杂,影响算法效率.此外,专家系统法也被广泛应用于管路布局的实践中.
针对上述问题,本文在对简化布局空间进行网格划分并完成网格能量值分布的基础之上,构建了管路布局优化问题的数学模型.进一步将改进的迷宫算法与遗传算法相结合,提出一种优化设计方法解决管路路径规划问题.引入辅助点改进迷宫算法保证了初始种群的多样性,保证了管路编码的连续并且没有重复基因段.在此基础上,提出了定长度的管路染色体编码方法,并结合基于引入方向优先搜索策略的迷宫算法设计相应的操作算子,提高了遗传算法的性能.仿真试验验证了算法的有效性和可行性.
1 管路布局问题描述船舶舱室空间有限,布局环境复杂,而且管路系统复杂,在管路布局过程中需要满足多种约束.其中主要的约束有障碍躲避、管路长度最短、管路弯头数最少、保证管路间的安全距离及管路支架的公用性等.本文考虑的管路布局的评价标准为管路总长度最短、弯头数最少和管路的并行性好;将障碍躲避等作为管路布局优化问题的约束条件.针对以上的评价标准与约束条件,首先阐述了布局空间的数学描述方法,并在此基础之上构成了管路布局优化问题的数学模型.
1.1 布局空间表达船舶管路布局空间的表达指对布局环境中船舶设备、管路的实体模型的数学描述,其首要任务是进行空间划分.本文利用轴平行包围盒对布局空间进行包络,并将其分解为m×n×l个均等的网格细胞.选定包围盒某一顶点作为坐标原点,并设定其坐标值为(1,1,1),则其他各个网格细胞的坐标由其与原点网格的相对位置关系决定,换句话说,当前网格所处的行、列、层即为其坐标值.同时,各个网格细胞也被赋予了一个默认的标定值“0”,代表了布局环境中的可行布局空间.工作空间中的船舶设备、已生成的管路等都是布局过程中的障碍,其所占据的网格被赋予一个标定值“#”,代表工作环境中的不可行空间.完整地表达设备、管路的模型信息需要大量的存储空间,影响算法的运行效率.据此,本文利用轴平行包围盒对船舶设备进行包络,极大地简化了模型的表达;同时,对于生成的管路,本文也将其圆形横截面处理为矩形横截面.鉴于网格划分的精度和各障碍在工作空间中的位置差异性,每个网格细胞存在3种状态:空、完全被占据和部分被占据.文中将部分被占据的网格细胞视为完全占据,并赋予标定值“#”.图 1为一个简化布局空间网格划分后对布局障碍和生成管路进行表达的例子.

|
| 图 1 布局空间表达示例 Fig. 1 An example for representation of layout space |
基于上述空间划分方法,管路路径即被定义为一条从起始点到终止点、由一系列相互邻接网格组成的折线段,并假定管路的中轴线穿过各网格点的中心.一条管路路径的编码即与其所穿过的网格细胞相对应的坐标值构成的序列,其中,路径的始、末点即为船舶设备的进、出口.但是,采用上述的简化方法对设备模型进行简化之后,会导致设备进、出口被包含在模型内,因此,将设备的原进、出口沿中心轴线向外延伸至模型外部的邻接网格,并以此网格作为新的管路接口点.
1.2 能量值分布在管路布局设计过程中,2条或者多条管路并行时,可以共享管路支架,降低管路安装的费用.为了便于对管路并行性的优劣进行评价,文中对布局空间中划分的网格细胞赋予特定的能量值,表示该网格的优先权值[6].本文假定,能量值越低,管路穿过该区域的消耗越小,该网格的优先权值越大.对于不可行布局空间所包含的网格细胞,其默认能量值为E∞;对于可行布局空间包含的所有网格细胞,其能量值的默认值为E.当布局空间中存在已生成的管路时,管路本身所穿过的网格细胞的能量值为“无穷”,但其周围网格细胞的能量值根据距离差异被赋予不同的能量值Ei(Ei<E).图 2为一个对管路周围网格细胞能量值进行赋值的例子.

|
| 图 2 布局空间网格能量值评估示例 Fig. 2 An example for evaluation of energy value of grid cells |
有以上的介绍可知,船舶管路路径寻优问题是典型的多目标优化问题,其本质是寻找一组满足约束条件并使评价函数得到最优组合的解.本文根据工程设计经验,对各个评价目标赋予一个权值,将复杂的多目标优化问题转换为单目标优化问题,并将迷宫算法和遗传算法相结合对其进行求解.依据评价标准,确定优化问题的目标函数Obj(f),见式(1),并将此目标函数直接作为后文优化算法中的适应度函数.
| $ {\rm{Obj}}\left( f \right) = {c_1} \cdot {L_p} + {c_2} \cdot {B_p} + {c_3} \cdot {E_p}, $ | (1) |
其中:c1,c2和c3为与各目标函数相关的权重值,它们的值取决于优化问题中目标函数的重要性,且与设计人员对多个目标函数的权衡相关;Lp为管路路径的总长度,Bp为管路路径的拐弯次数,Ep为管路路径所穿过的网格细胞能量值的总和.
2 管路路径规划方法为解决方向优先搜索策略存在的易产生无效管路而导致需要大量修补工作的问题,本文将迷宫算法和遗传算法相结合,提出了一种新的管路路径规划方法.利用改进迷宫算法生成少量的初始种群,迷宫算法扩展编码的连续性有效保证了种群中个体的有效性;而且,相比单纯利用迷宫算法搜索所有可行路径后比较选出最优解的方法,遗传算法所需的种群规模非常小,用以生成初始种群的迷宫算法的搜索效率也是可以接受的.在此基础之上,利用遗传算法对初始种群进行优化,并最终得出综合最优解.图 3为利用优化算法进行路径规划的流程图,其中,gen表示遗传代数,max gen表示设定的最大遗传代数.

|
| 图 3 路径规划算法流程图 Fig. 3 Flow chart of pipe routing algorithm |
迷宫算法是经典的路径搜索算法,主要包括扩展搜索和回溯两个过程.
扩展搜索是指从一个网格细胞到另一个相邻网格细胞的扩张过程,并且对到达的网格赋予特定的标定值进行标记.扩展搜索持续进行直到找到目标网格点,其中扩展过程与网格标记的规则如下:
1)初始网格标记为1;
2)只有当前网格相邻的可行空间网格可以被标记,其标定值为当前网格标定值加1;
3)当前搜索到的网格已经标记,则取较小的值作为其标定值.
回溯过程是从目标点到起始点的反向搜索过程.回溯的方向取为网格标记值减少的方向,每次遍历1个网格细胞,直到找到起始网格点.则由起始点到终止点的网格坐标编码构成了一条可行并且无重复路径段的联通路径.
2.1.2 辅助点的引入由于迷宫算法的编码特性,直接利用迷宫算法可以对由以始、末点为对角顶点构成的空间S进行全局的搜索,但却难以到达除此之外的布局空间.另外,试验发现,在利用迷宫算法进行路径搜索过程中存在与单纯方向优先搜索策略相同的问题:可行解多集中于始、末点对角连接线附近,而无法均匀遍布布局空间[6].因此,本文在布局空间中引入了辅助点的概念.以图 4为例,空间S分别沿着坐标轴的方向进行适当扩充得到S′,为了能够遍历S′中所有的区域,增加管路多样性,在S′中的可行空间中随机产生一个辅助点P.以原起始点为起点,P点为终点,利用迷宫算法生成一条可行的辅助路径A-P1;然后以P点为起点,原终止点为终点,产生另一条可行的辅助路径A-P2;将2条路径连接,便构成了一条新的有效的路径.辅助点的引入扩大了迷宫算法的搜索范围,增加了可行管路的多样性,有助于算法搜寻到最优的管路段,提高算法的搜索效率.

|
| 图 4 辅助点的引入 Fig. 4 Introduction of auxiliary point |
在改进迷宫算法的基础之上,结合迷宫算法自身的特点,本文提出了管路染色体的定长度编码策略.一般地,在由始、末点所构成的布局空间S中可以搜索到有效的管路路径,因此本文假定扩展的空间即S′-S是无障碍的.由迷宫算法的搜索原理易知,利用其在布局空间S中搜索到的路径长度是相同的.但在扩展空间中,由于辅助点位置的差异性,管路路径的长度也会有所不同,并且有一个最大长度值.为了找到这个最大的长度值,分别选取扩展空间中的8个顶点作为辅助点,与原始末点共同构造出可行的联通路径,并比较其路径长度,得出最大值.此最大值即为遗传算法过程中染色体编码的固定长度值.
本文提出的定长度编码方法只需在遗传操作进行之前进行1次,不会显著增加算法的计算量,影响算法的运行效率.而且,定长度编码克服了变长度编码在遗传操作过程中程序设计复杂、运行效率低等缺陷,有助于提高算法的收敛效率.
2.3 遗传算子 2.3.1 选择算子本文采用的选择方法为随机联赛选择机制,其具体操作过程如下:从种群中随机选择N个个体进行适应度大小比较,将其中适应度最高的个体遗传到下一代,此处N=2;重复上述过程n次,便得到了包含n个个体的下一代种群.但是,单纯采用联赛选择机制可能会造成最优个体的丢失,因此,引入最优个体保留策略,不失种群多样性的同时保证了最优个体的优先权.
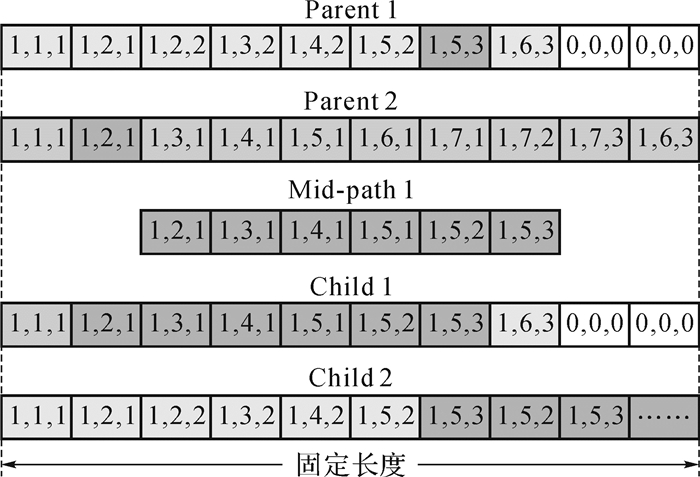
2.3.2 交叉算子传统的单点交叉操作是随机选择一个染色体串的节点位置,然后交换2个父代染色体节点右端部分来产生2个子代个体.在此基础之上,结合范小宁等[8]所提出的变长度编码交叉方法,本文提出了基于定长度编码的交叉策略.此部分以图 5为例来说明定长度编码的交叉策略:随机选定2个父代染色体Parent 1和Parent 2;分别在2个父代染色体上选择2个交叉点,本例假设Parent 1上的交叉点为(1,5,3),Parent 2上的交叉点为(1,2,1);分别以这2个交叉点为始、末点,利用改进迷宫算法生成一条辅助路径Mid-path 1,并与父代染色体重新结合生成2个子代个体Child 1和Child 2,结合方法如图 5所示.本例中,子代染色体Child 1长度在限定长度内,不足位置由0补充;子代染色体Child 2的长度超过了限定长度,直接删除.
|
| 图 5 定长度编码交叉方法 Fig. 5 Crossover based on fixed-length coding method |
其中,此处的迷宫算法不同于初始路径生成时采用的改进迷宫算法,在扩展过程结束后,算法的回溯过程采用方向优先的搜索策略:利用2个点的位置关系确定优选方向的矢量,随机选择初始方向,沿网格值减小的方向搜索,遇到障碍后改变回溯方向,直到找到终止点形成一条有效的联通路径作为子路径;若多次改变方向仍无法找到有效的联通路径,则重新选择交叉点,重复以上操作,直到找到可行的路径.
2.3.3 变异算子在基本位变异的思想的基础上,结合变长度编码变异方法[8],提出了基于定长度编码的变异策略.以图 6为例详细叙述该策略的实现过程:随机选定一个父代染色体Parent 3;在父代染色体上随机选择2个变异点,本例假设选定的变异点为(1,3,1)与(1,7,3);分别以这2个变异点作为始、末点,利用与交叉操作中相同的迷宫算法构造一条辅助路径Mid-path 2,并以该路径替换父代染色体Parent 3上变异点间的基因段,生成一个子代染色体Child 3.同样,若生成的子代个体长度超过了定长度编码限定的长度,则直接将其删除,不计入子种群当中.

|
| 图 6 定长度编码变异方法 Fig. 6 Mutation based on fixed-length coding method |
在Windows 7的环境下,利用MATLAB 2011b实现了上述管路路径规划算法.试验建立了一个三维模拟空间Space-test,空间对角坐标为(1,1,1)和(50,50,50).利用布置在模拟空间Space-test中的长方体块模拟布局过程中的障碍,各长方体块的对角坐标如表 1所示.
| 障碍标记 | 对角坐标 |
| 1 | (1,4,1;20,16,10) |
| 2 | (1,1,34;10,20,50) |
| 3 | (4,30,1;18,40,25) |
| 4 | (30,1,35;50,15,50) |
| 5 | (30,10,1;45,24,20) |
| 6 | (26,38,1;38,46,25) |
| 7 | (40,20,30;49,49,40) |
在确定了布局空间后,首先要对其进行网格划分.本例的模拟空间Space-test被划分为50×50×50个网格细胞,并赋予默认标定值和能量值.对于长方体障碍空间中的网格,则将其标记为“#”,赋予其能量值为“∞”.为充分检验算法的性能,在模拟空间Space-test加入一条“已生成”直管路G-pipe,假定该管路路径染色体编码为:[(25,1,1);(25,1,2);(25,1,3);…;(25,1,50)],并依据前文所述能量值赋值方法对该管路及其周围的网格细胞进行赋值.其中,默认能量值取为10,管路周围网格能量值的范围取为(2,6),偶数递增.至此,完成了管路布局空间的构建.
3.2 仿真、结果与分析对模拟空间Space-test进行参数设置的基础上,以公式(1)作为评价函数,利用本文提出的组合优化算法对以(1,1,1)和(50,50,50)为始、末点的管路路径进行规划求解.本例中各目标函数采用的计量单位均为1,多次试验发现,当各目标函数的权值相同时,由于管路路径的拐弯次数的取值相对于路径总长度值和路径穿过的网格细胞总能量值较小,其对总体适应度函数值的影响较小,易导致优化算法无法收敛到最优解.因此,需适当增加目标函数的Bp权值大小,并减小目标函数Lp和Ep权值的大小.基于大量的试验总结,并考虑到各目标函数对优化结果影响的均衡性,最终将各目标函数的权值c1,c2,c3依次确定为0.01,0.97,0.02.遗传算法的参数如表 2所示.
算法的进化过程如图 7所示,其中,图示中x,y,z坐标轴表示了布局空间中管路的位置坐标值.参考图 7(a)可知,辅助点的引入增加了初始种群的多样性,并使得管路能够遍布整个布局空间,为得出最优管路奠定了良好的基础.图 7(b)为算法收敛曲线图,其中横坐标为遗传代数,纵坐标为适应度函数值.可见,最优个体保留策略保留了当代的最优个体,有助于算法向最优解收敛;算法在23代左右收敛,证明了算法具有良好的收敛性能.图 7(c)为依据得到的最优路径编码绘制的三维路线图,作为比较,在布局空间Space-test中去除“已生成”管路G-pipe,则利用路径规划算法对其求解,得出的可能最优管路路径图如图 7(d)所示.比较发现,所提出的算法能够有效地找到一条长度最短、拐弯次数最少并且具有良好并行性的综合最优管路.

|
| 图 7 优化算法路径规划进程 Fig. 7 Optimization procedure of pipe routing algorithm |
为进一步验证算法的效率,采用文献[8]中的例子进行对比试验,如图 8所示.测试结果显示,在相同的测试条件下,本文的规划算法平均迭代10次即可收敛,文献[8]平均迭代60次;得到路径图如图 8(a)所示,图 8(b)为某次算法运行过程的收敛曲线图.对比试验结果,充分验证了改进迷宫算法对提高算法搜索效率的显著效果,也证明了所提出的路径规划算法具有较快的收敛速度和较高的搜索效率.

|
| 图 8 比较案例优化进程 Fig. 8 Optimization procedure of a comparative case |
结合布局空间参数设置和优化算法得到最优管路,其仿真试验三维实体模型示意图如图 9所示.应当注意,试验中的模型是对实际布局空间的一种简化,因此布局结果可能与实际的管路布局存在一定的差距.但试验结果表明了算法可以获得一定约束条件下的综合最优解,可以对设计人员的管路布局工作提供有效的参考,提高其工作效率,因此该算法对实际布局工作具有一定的指导意义.

|
| 图 9 仿真环境管路布局结果 Fig. 9 ipe layout result of simulation environment |
以上算法主要是针对两点管路进行路径规划,在此基础上,进行适当扩展即可对分支管路路径进行规划.在处理分支管路路径问题时,可以将分支管路视为若干个两点管路,以最短重合路径为评价标准并设计相应的遗传算子,利用优化算法进行优化,从而得出近优解.不难看出,本文所提出的算法为分支管路路径规划问题的研究奠定了良好的基础.
4 结 论本文将改进的迷宫算法与遗传算法相结合,提出了一种新的船舶管路布局方法.迷宫算法的应用保证了管路编码的连续性和无重复性,辅助点的引入增加了初始种群的多样性,有利于算法搜索效率的提升.基于此,提出了定长度的编码方法,结合基于引入方向优先搜索策略的迷宫算法,设计了相应的遗传操作算子.带方向优先策略的迷宫算法加快了遗传算法的收敛速度,提高了搜索算法的收敛性能.仿真试验也表明所提出的算法能够找到长度最短、拐弯次数最少及并行性好的综合最优路径,验证了其可行性和效率,以及对实际管路布局工作的指导意义.
| [1] | PARK J H,STORCH R L.Pipe-routing algorithm development:case study of a ship engine room design[J].Expert Systems with Applications,2002,23(3):299-309. |
| Click to display the text | |
| [2] | DIJKSTRA E W.A note on two problems in connexion with graphs[J].Numerische Mathematik,1959,1(1):269-271. |
| Click to display the text | |
| [3] | LEE C Y.An algorithm for path connections and its applications[J].Ire Transactions on Electronic Computers,1961,10(3):346-365. |
| Click to display the text | |
| [4] | 樊江,马枚,杨晓光.航空发动机外部管路自动敷设研究[J].机械设计,2003,20(7):21-23. FAN Jiang,MA Mei,YANG Xiao-guang.Research on automatic laying out for external pipeline of aero-engine[J].Journal of Machine Design,2003,20(7):21-23. |
| Cited By in Cnki (32) | Click to display the text | |
| [5] | HIGHTOWER D W.A solution to line routing problems on the continuous plane[C]//Proceedings of 6th Design Automation Workshop.IEEE,1969:1-24. |
| Click to display the text | |
| [6] | ITO T.A genetic algorithm approach to piping route path planning[J].Journal of Intelligent Manufacturing,1999,10(1):103-114. |
| Click to display the text | |
| [7] | ITO T.Developments in applied artificial intelligence[C].Berlin:Springer,2002:547-556. |
| [8] | 范小宁,林焰,纪卓尚.船舶管路三维布局优化的变长度编码遗传算法[J].中国造船,2007,48(1):82-90. FAN Xiao-ning,LIN Yan,JI Zhuo-shang.A variable length coding genetic algorithm to ship pipe path routing optimization in 3D space[J].Shipbuilding of China,2007,48(1):82-90. |
| Cited By in Cnki (17) | Click to display the text | |
| [9] | SANDURKAR Sunand,WEI Chen.GAPRUS—genetic algorithms based pipe routing using tessellated objects[J].Computers in Industry,1999,38(3):209-223. |
| Click to display the text | |
| [10] | REN Tao,ZHU Zhi-liang,DIMIROVSKI G M,et al.A new pipe routing method for aero-engines based on genetic algorithm[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2014,228(3):424-434. |
| Click to display the text | |
| [11] | JIANG Wen-ying,LIN Yan,CHEN Ming,et al.An ant colony optimization-genetic algorithm approach for ship pipe route design[J].International Shipbuilding Progress,2014,61(3):163-183. |
| Click to display the text | |
| [12] | 范小宁,林焰,纪卓尚.多蚁群协进化的船舶多管路并行布局优化[J].上海交通大学学报,2009,43(2):193-197. FAN Xiao-ning,LIN Yan,JI Zhuo-shang.Multi ant colony cooperative co-evolution for optimization of ship muti pipe parallel routing[J].Journal of Shanghai Jiaotong University,2009,43(2):193-197. |
| Cited By in Cnki (12) | |
| [13] | LIU Qiang,WANG Chen-gen.A discrete particle swarm optimization algorithm for rectilinear branch pipe routing[J].Assembly Automation,2011,31(4):363-368. |
| Click to display the text | |
| [14] | LIU Qiang,WANG Chen-gen.Pipe-assembly approach for aero-engines by modified particle swarm optimization[J].Assembly Automation,2010,30(4):365-377. |
| Click to display the text | |
| [15] | LIU Qiang,WANG Chen-gen.Multi-terminal pipe routing by Steiner minimal tree and particle swarm optimization[J].Enterprise Information Systems,2012,6 (3):315-327. |
| Click to display the text | |
| [16] | KIM S H,RUY W,JANG B S.The development of a practical pipe auto-routing system in a shipbuilding CAD environment using network optimization[J].International Journal of Naval Architecture and Ocean Engineering,2013,5(3):468-477. |
| Click to display the text |



