振动筛是工、农、土建等行业按照粒径大小对物料分级的主要设备.人们致力于提高振动筛筛分性能,而筛分实验是其理论研究的基础.若建立多种振动形式,及结构和工艺参数与筛分性能的定量关系,由于人力、物力、财力的限制,逐个考察参数影响的传统实验并不可取[1].借助计算机技术,利用离散单元法对复杂的筛分过程进行数值模拟,为支持向量机的非参数回归建模提供训练和测试用的输入/输出样本数据.
离散单元法可用来研究散体介质系统的力学行为,在振动筛分中取得了成功的应用.2002年,Cleary等利用离散单元法对不同大小的颗粒在倾斜筛面上筛分进行初步探索[2].2003年,li等基于离散单元法对颗粒在筛面上的运动形式进行分析[3].2006年,焦红光等用颗粒离散单元法模拟筛分过程[4].在2008年,刘光焕等介绍了离散单元法在振动筛分中的基本理论应用[1].2009年,Cleary等利用DEM对等厚筛分和双层筛板的颗粒流进行分析[5, 6],陈艳华等详细分析并建立单一筛分参数与筛分效率之间的关系模型[7, 8].学者们对颗粒在筛面上的运动状态、不同振动形式、进料率、筛分参数与筛分性能的关系作了详尽的分析[9].但是由于筛分参数的多元化,筛分问题呈高度复杂非线性,其输入与输出关系很难用一个表达式直接给出.同时参数优化过程需要大规模迭代计算,离散单元法计算时间长,亟待建立筛分综合模型,寻找筛分参数的优化组合来指导振动筛的设计及提高筛分性能[10].
支持向量回归机基于统计学理论集成凸二次规划、对偶表示和优化理论等技术,能够较好解决小样本学习问题,其核心内容由Vapnik等人于1995年提出[11, 12].支持向量回归机采用结构风险最小化原则,通过核函数把非线性问题转化为特征空间的线性问题,并具有很强的非线性处理能力,在回归建模方法研究方面表现出良好的性能,已被成功应用到系统辨识、非线性建模和系统预测等方面[13, 14, 15].为提高核函数的性能及回归预测能力,支持向量回归机由单核发展到多核学习.本文采用Rakotomamonjy提出的简单多核支持向量机(SimpleMKL)对振动筛的筛分模型进行非参数建模[16].同时筛机的参数优化是一个复杂多极值、多约束、非线性的混合多维空间优化问题,优化计算成本高,利用李晓磊等人2002年提出的群智能仿生人工鱼群优化算法进行参数优化[17].人工鱼群算法具有并行性、简单性、全局性、快速性和跟踪性等特点,以SimpleMKL模型为食物浓度函数计算手段,完成参数组合寻优.最终本文采取AFSA-SimpleMKL联合方法实现振动筛的建模与参数优化,为振动筛的设计与制造提供新思路.
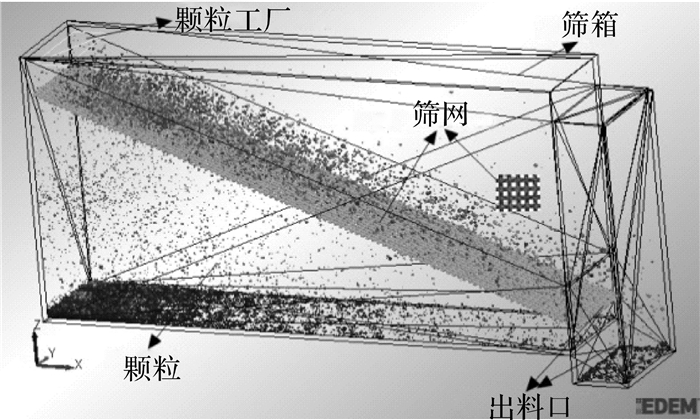
1 振动筛仿真实验将三维模型导入基于离散单元法的EDEM软件中,如图 1所示,简化模型主要由筛箱、筛网和颗粒工厂组成,其筛箱的长、宽、高分别为160,30.5和80 mm.从图 2中可看出,筛分过程准确模拟了颗粒运动、颗粒与颗粒之间的碰撞和颗粒透筛过程.筛分过程是一个快速过程,其碰撞过程中颗粒的磨损与变形量很小,故采用Mindlin等研究基础上建立的Hertz-Mindlin无滑动接触力学模型.离散单元法是将物料看作一系列离散的独立运动的单元,利用牛顿第二定律建立每个单元的运动方程,并用中心差分法求解,整个筛分过程由各个颗粒的运动和相互位置表达.任意时刻t下,作用在单元上的合力和合力矩的方程为:
| $ {{\ddot x}_i}\left( t \right) = \frac{{\partial {{\dot x}_i}\left( t \right)}}{{\partial t}} = {\left( {\sum {F\left( t \right)} } \right)_i}/{m_i}, $ | (1) |
| $ {{\ddot \theta }_i}\left( t \right) = \frac{{\partial {{\dot \theta }_i}\left( t \right)}}{{\partial t}} = {\left( {\sum {F\left( t \right)} } \right)_i}/{I_i}, $ | (2) |
|
| 图 1 3D-DEM简化筛分模型 Fig. 1 3D-DEM simplified screening model |

|
| 图 2 筛面上颗粒筛分过程 Fig. 2 Process of sieving simulation |
其中xi,∑F(t)和mi分别表示i单元的平动位移、作用合力和质量,θi,∑M(t)i和Ii分别表示
筛分过程的初始条件如表 1所示.筛分效率是评定筛分性能的主要指标,用来描述筛分的完成度.筛分效率γ表达式为
| $ \gamma = \left( {\frac{{{m_{{{\rm{S}}_1}}}}}{{{m_{{{\rm{S}}_2}}}}} - \frac{{{m_{{{\rm{G}}_1}}}}}{{{m_{{{\rm{G}}_2}}}}}} \right) \times 100\% , $ | (3) |
| 物料属性 | 泊松比 | 剪切模量 | 密度 |
| 颗粒 | 0.3 | 23 MPa | 2 678 kg/m3 |
| 筛面 | 0.29 | 79.92 GPa | 7 861 kg/ m3 |
| 碰撞属性 | 恢复系数 | 静摩擦系数 | 动摩擦系数 |
| 颗粒-颗粒 | 0.1 | 0.545 | 0.01 |
| 颗粒-筛面 | 0.2 | 0.5 | 0.01 |
其中,ms1,mG1分别是筛下物中小于分离粒径颗粒的质量和大于分离粒径的颗粒质量;ms2,mG2分别为待筛分物料中小于分离粒径和大于分离粒径的颗粒的质量.基于筛面上与筛面下所有小于分离粒径和大于分离粒径颗粒的混杂情况,筛分效率描述了筛分效果的综合能力.
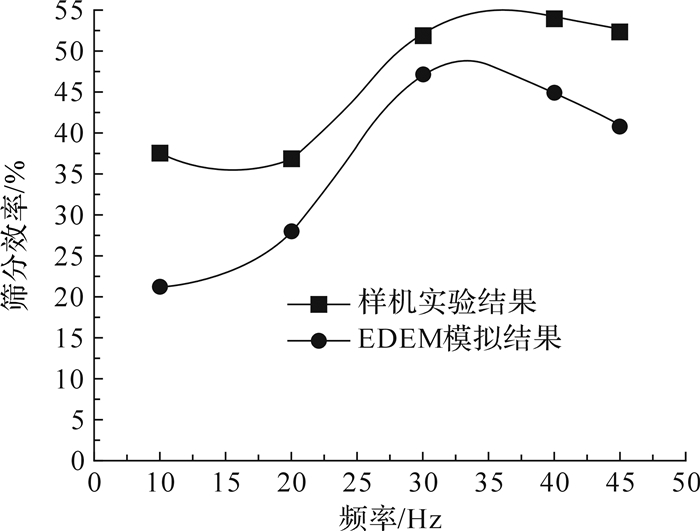
2 可调参数振动筛对仿真实验的验证选取沙子为筛分材料,为尽量符合EDEM仿真实验颗粒工厂的粒径分布,利用震击式标准振动筛(图 3)对入料颗粒进行筛分.图 4为大部分由螺栓螺母紧固的组合式可调参数振动筛样机,具备多参数可调等优点.为验证仿真的可靠性,进行了物理实验与仿真实验的对比.实验的主要条件如下:处理量约为0.5 t/h,筛孔大小为0.6 mm,筛丝直径为0.45 mm,筛面倾角为30°,振幅为2.3 mm,振动方向角为75°.在不同振动频率下,实验振动筛结果和模拟实验结果对比如图 5所示.

|
| 图 3 筛选不同粒径分布的实验颗粒 Fig. 3 Experimental particles with different size distributions |

|
| 图 4 振动筛实验样机 Fig. 4 Experimental prototype of vibrating screen |
|
| 图 5 可调实验振动筛与模拟实验筛分效率对比 Fig. 5 Comparison of screening efficiency by experiment and simulation |
因为碰撞系数、材料属性、进料量与模拟条件存在差距,物理实验与仿真实验不可能完全一致.同时Cleary提出颗粒形状对筛分过程也存在一定的影响[18],全面系统地表征随机颗粒的形状来减少真实颗粒与球类模型之间的差距以致EDEM仿真更接近真实的筛分现象逐渐被学者重视.利用震击式标准振动筛获得的具有特定粒径分布的入料颗粒与颗粒工厂产生的颗粒也存在误差.从图 5可以看出,筛分效率在数值上存在差距,但是两者在振动频率对筛分效率影响的规律上是一致的,这表明数值模拟实验能够反映筛分规律,可以运用数值模拟仿真方法对筛分进行机理性研究.
3 基于SimpleMKL振动筛回归模型引入核函数是支持向量机的核心部分.基于单个特征空间的单核方法,由于不同核函数或同一核函数的不同参数,其核映射能力差异明显.针对单个简单的核函数处理样本存在的问题,采用符合Mercer定理的多核代替单核的学习方法来增强决策函数的能力,提高学习性能.本文将SimpleMKL理论引入直线振动筛的建模,分析简单多核支持向量机的原始和对偶问题,采用梯度下降法进行权系数运算,以KKT条件作为算法的停止准则,建立直线振动筛的筛分回归模型.
3.1 SimpleMKL非线性回归方法T=x1,y1,x2,y2,…,xn,yn∈Rd×Yn,其中:R为实数集,xi∈R
| $ f\left( x \right) = \sum\limits_{m - 1}^M {\left( {{w_m},{\phi _m}\left( x \right)} \right) + b,} $ | (4) |
其中wm∈Fm.引入松弛因子ξ,函数拟合问题根据结构最小原则,原始问题转化为优化问题,描述如下:
| $ \min \psi ({w_m},b,\xi ,d) = \frac{1}{2}\sum\limits_{m - 1}^M {\frac{1}{{{d_m}}}{{\left\| {{w_m}} \right\|}^2}{H_m} + C\sum\limits_{i - 1}^n {{\xi _i}} } , $ | (5) |
| $ {\begin{array}{*{20}{c}} {^{s.t.}{y_i}\sum\limits_{m = 1}^M {{w_m} \cdot \varphi \left( {{x_i}} \right) + {y_i}b \ge 1 - {\xi _i},} }\\ {\sum\limits_{m = 1}^M {{d_m} = 1,{d_m} \ge 0,} }\\ {{\xi _i} \ge 0.} \end{array}} $ | (6) |
同单核支持向量机将上述问题转化为对偶问题类似,但对偶问题的目标函数式不可微,简单多核支持向量机利用二阶段交替优化技术将目标函数变形,由式(5)与(6)整理以dm为变量的优化问题为:
| $ \mathop {\min }\limits_{d \ge 0} J\left( d \right),\sum\limits_{m = 1}^M {{d_m} = 1} , $ | (7) |
| $ \left. {\begin{array}{*{20}{c}} {^{s.t.}\mathop {\min }\limits_{{w_m},b,\xi } \frac{1}{2}\sum\limits_{m = 1}^M {\frac{1}{{{d_m}}}{{\left\| {{w_m}} \right\|}^2}{H_m} + C\sum\limits_{i = 1}^n {{\xi _i}} ,} }\\ {{y_i}\sum\limits_{m = 1}^M {{w_m} \cdot \varphi \left( {{x_i}} \right) + {y_i}b \ge 1 - {\xi _i},} }\\ {{\xi _i} \ge 0.} \end{array}} \right\} $ | (8) |
| $ \begin{array}{l} L = \frac{1}{2}\sum\limits_{m = 1}^M {\frac{1}{{{d_m}}}{{\left\| {{w_m}} \right\|}^2}{H_m} + C\sum\limits_{i = 1}^n {{\xi _i}} } + \\ \;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{\alpha _i}\left( {1 - {\xi _i} - {y_i}\sum\limits_{m = 1}^M {{w_m} \cdot {\varphi _m}\left( {{x_i}} \right) + {y_i}b} } \right)} \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{\nu _i}{\xi _i}} , \end{array} $ | (9) |
其中αi,νi为拉格朗日算子.分别对wi,b,ξi求偏导数并令其等于0,将得到的极值条件代入拉格朗日函数式(9)中,即对偶问题变为
| $ \max \;Q\left( \alpha \right) = - \frac{1}{2}\sum\limits_{i,j = 1}^m {{\alpha _i}{\alpha _j}{y_i}{y_j}{K_d}\left( {{x_i},{x_j}} \right) + \sum\limits_{i = 1}^n {{\alpha _i}} } \;{\rm{s}}{\rm{.t}}{\rm{.}} $ | (10) |
| $ \left. {\begin{array}{*{20}{c}} {\sum\limits_i^n {{\alpha _i}{y_i}} }\\ {c \ge {\alpha _i} \ge 0,}\\ {{K_d}\left( {{x_i},{x_j}} \right) = \sum\limits_{m = 1}^M {{d_m}{k_m}\left( {{x_i},{x_j}} \right).} } \end{array}} \right\} $ | (11) |
利用梯度计算的方法对J(d)进行计算,假设d*是式(7)中的一个最优解,α*=(α1,α2,…,αn)是式(10)的最优解,那么简单多核支持向量机的非线性回归函数为
| $ f\left( x \right) = \sum\limits_{i = 1}^n {a_i^*{y_i}} \sum\limits_{m = 1}^M {{d_m}{K_d}\left( {{x_i},{x_j}} \right) + b.} $ | (12) |
利用SimpleMKL建模的目的是通过合理设计筛机的结构参数和振动参数,使得筛分效率最高.筛分效率可以由映射关系表达:
| $ \gamma = f({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},) $ | (13) |
式中:x1是振幅;x2是振频;x3是振动方向角;x4是筛孔直径;x5是筛丝直径;x6是筛面倾角.其函数关系呈高度非线性,很难用简单函数表达,利用机器学习语言的支持向量机模型可以有效地描述这种输入与输出的映射关系.
选用EDEM的仿真实验数据作为供训练和测试用的输入与输出样本数据.由于支持向量机能较好地解决小样本、非线性等问题,选取67组数据作为样本数据点,样本总量上满足回归建模的需要.振动筛分参数因素水平及筛分效率计算结果如表 2所示.
| 组号 | x1 | x2 | x3 | x4 | x5 | x6 | 筛分效率 | 组号 | x1 | x2 | x3 | x4 | x5 | x6 | 筛分效率 | |
| 1 | 0.5 | 20 | 100 | 0.8 | 0.5 | 21 | 0.380 81 | 34 | 4.5 | 30 | 40 | 1 | 0.7 | 21 | 0.444 17 | |
| 2 | 1.5 | 20 | 100 | 0.8 | 0.5 | 21 | 0.559 33 | 35 | 4.5 | 40 | 50 | 1 | 0.7 | 21 | 0.328 55 | |
| 3 | 2.5 | 20 | 100 | 0.8 | 0.5 | 21 | 0.604 37 | 36 | 4.5 | 20 | 50 | 1 | 0.7 | 21 | 0.469 46 | |
| 4 | 3.6 | 20 | 100 | 0.8 | 0.5 | 21 | 0.553 07 | 37 | 4.5 | 40 | 30 | 1 | 0.7 | 21 | 0.467 78 | |
| 5 | 4.5 | 20 | 100 | 0.8 | 0.5 | 21 | 0.498 73 | 38 | 2.55 | 24 | 75 | 1 | 0.3 | 21 | 0.530 00 | |
| 6 | 5.6 | 20 | 100 | 0.8 | 0.5 | 21 | 0.456 91 | 39 | 2.55 | 24 | 75 | 1 | 0.5 | 21 | 0.532 2 | |
| 7 | 7.0 | 20 | 100 | 0.8 | 0.5 | 21 | 0.459 65 | 40 | 2.55 | 24 | 75 | 1 | 0.7 | 21 | 0.465 13 | |
| 8 | 2.55 | 10 | 100 | 0.8 | 0.5 | 21 | 0.439 81 | 41 | 2.55 | 24 | 75 | 1 | 1.0 | 21 | 0.355 69 | |
| 9 | 2.55 | 15 | 100 | 0.8 | 0.5 | 21 | 0.556 14 | 42 | 2.55 | 24 | 75 | 1 | 1.2 | 21 | 0.315 12 | |
| 10 | 2.55 | 40 | 100 | 0.8 | 0.5 | 21 | 0.514 75 | 43 | 2.55 | 24 | 75 | 1 | 1.5 | 21 | 0.243 78 | |
| 11 | 2.55 | 30 | 100 | 0.8 | 0.5 | 21 | 0.556 06 | 44 | 2.55 | 21 | 100 | 0.6 | 0.7 | 21 | 0.555 2 | |
| 12 | 2.55 | 20 | 21 | 0.8 | 0.5 | 21 | 0.565 84 | 45 | 2.55 | 21 | 100 | 0.8 | 0.7 | 21 | 0.452 1 | |
| 13 | 2.55 | 20 | 31 | 0.8 | 0.5 | 21 | 0.586 83 | 46 | 2.55 | 21 | 100 | 1.0 | 0.7 | 21 | 0.558 4 | |
| 14 | 2.55 | 20 | 45 | 0.8 | 0.5 | 21 | 0.608 78 | 47 | 2.55 | 21 | 100 | 1.3 | 0.7 | 21 | 0.479 | |
| 15 | 2.55 | 20 | 51 | 0.8 | 0.5 | 21 | 0.582 87 | 48 | 2.55 | 21 | 100 | 1.5 | 0.7 | 21 | 0.340 03 | |
| 16 | 2.55 | 20 | 61 | 0.8 | 0.5 | 21 | 0.567 39 | 49 | 2.55 | 21 | 100 | 1.8 | 0.7 | 21 | 0.137 6 | |
| 17 | 2.55 | 20 | 71 | 0.8 | 0.5 | 21 | 0.582 59 | 50 | 2.55 | 21 | 100 | 2.0 | 0.7 | 21 | 0.097 | |
| 18 | 2.55 | 20 | 81 | 0.8 | 0.5 | 21 | 0.610 11 | 51 | 2.55 | 24 | 75 | 0.5 | 1 | 10 | 0.638 58 | |
| 19 | 2.55 | 20 | 91 | 0.8 | 0.5 | 21 | 0.550 23 | 52 | 2.55 | 24 | 75 | 0.5 | 1 | 15 | 0.603 88 | |
| 20 | 2.55 | 20 | 100 | 0.8 | 0.5 | 21 | 0.452 34 | 53 | 2.55 | 24 | 75 | 0.5 | 1 | 21 | 0.582 59 | |
| 21 | 1.5 | 20 | 40 | 1 | 0.7 | 21 | 0.476 81 | 54 | 2.55 | 24 | 75 | 0.5 | 1 | 25 | 0.555 16 | |
| 22 | 1.5 | 10 | 30 | 1 | 0.7 | 21 | 0.305 12 | 55 | 2.55 | 24 | 75 | 0.5 | 1 | 30 | 0.532 2 | |
| 23 | 1.5 | 30 | 50 | 1 | 0.7 | 21 | 0.635 70 | 56 | 2.55 | 24 | 75 | 0.5 | 1 | 35 | 0.458 72 | |
| 24 | 1.5 | 40 | 60 | 1 | 0.7 | 21 | 0.555 79 | 57 | 2.55 | 24 | 75 | 0.5 | 1 | 40 | 0.396 25 | |
| 25 | 1.5 | 10 | 40 | 1 | 0.7 | 21 | 0.403 34 | 58 | 2.55 | 24 | 75 | 0.5 | 1 | 45 | 0.335 47 | |
| 26 | 2.5 | 20 | 50 | 1 | 0.7 | 21 | 0.605 44 | 59 | 2.55 | 24 | 75 | 0.8 | 0.3 | 15 | 0.647 08 | |
| 27 | 2.5 | 30 | 60 | 1 | 0.7 | 21 | 0.524 06 | 60 | 2.55 | 24 | 75 | 1.0 | 0.5 | 15 | 0.641 94 | |
| 28 | 2.5 | 30 | 30 | 1 | 0.7 | 21 | 0.580 42 | 61 | 2.55 | 24 | 75 | 1.2 | 0.7 | 15 | 0.657 99 | |
| 29 | 3.5 | 10 | 50 | 1 | 0.7 | 21 | 0.490 47 | 62 | 2.55 | 24 | 75 | 1.0 | 0.3 | 20 | 0.673 46 | |
| 30 | 3.5 | 20 | 60 | 1 | 0.7 | 21 | 0.481 97 | 63 | 2.55 | 24 | 75 | 1.2 | 0.5 | 20 | 0.580 90 | |
| 31 | 3.5 | 30 | 30 | 1 | 0.7 | 21 | 0.490 34 | 64 | 2.55 | 24 | 75 | 0.8 | 0.7 | 20 | 0.518 95 | |
| 32 | 3.5 | 40 | 40 | 1 | 0.7 | 21 | 0.395 04 | 65 | 2.55 | 24 | 75 | 1.2 | 0.3 | 30 | 0.621 91 | |
| 33 | 4.5 | 40 | 60 | 1 | 0.7 | 21 | 0.420 32 | 66 | 2.55 | 24 | 75 | 0.8 | 0.5 | 30 | 0.497 12 | |
| 34 | 4.5 | 30 | 40 | 1 | 0.7 | 21 | 0.444 17 | 67 | 2.55 | 24 | 75 | 1.0 | 0.7 | 30 | 0.527 06 |
采用不同核函数及不同参数组成的简单多核支持向量机,基核函数主要采用RBF核函数和Poly核函数.
高斯核函数:
| $ k\left( {x,x'} \right) = \exp \left( { - {{\left\| {x - x'} \right\|}^2}/2{\sigma ^2}} \right). $ |
多项式核函数:
| $ k\left( {x,x'} \right) = {\left( {x \cdot x' + 1} \right)^p}. $ |
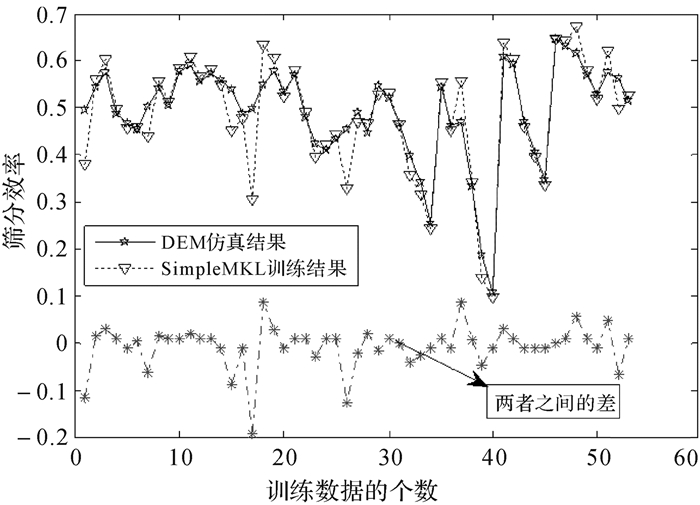
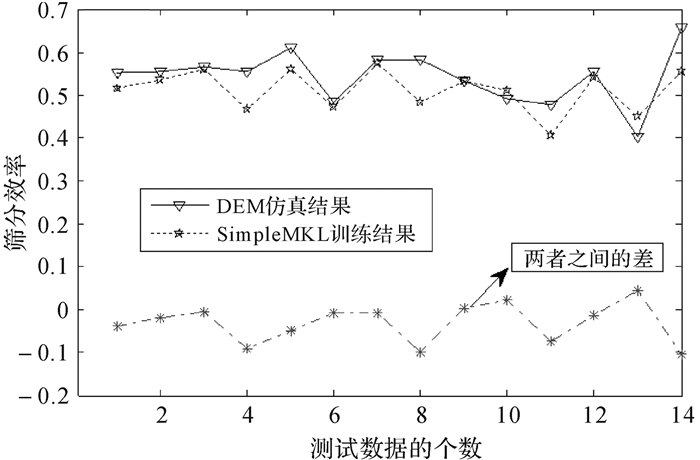
式中,σ是高斯核参数,p为多项式核函数中的阶数.SimpleMKL回归机的主要参数为惩罚系数C、高斯核参数σ、多项式核参数p以及多核权重系数dm.在本文中为了使得其模型学习能力较好,并保证良好的泛化预测能力,选取惩罚系数C为15,p的取值为1,2,3,σ的取值为0.01:0.05:0.2,0.5,1,2,5,7,10,12,15,17,通过梯度下降法选择最优的dm.其他主要参数ε=0.01,λ=1×10-8,最大迭代步数为500.随机选取53组为训练样本,剩余的14组为测试样本.训练与测试的结果如图 6和图 7所示.
|
| 图 6 训练结果与EDEM仿真对比 Fig. 6 Comparison between the training results and EDEM simulation results |
|
| 图 7 测试结果与EDEM仿真对比 Fig. 7 Comparison between the testing results and EDEM simulation results |
图 6表示出SimpleMKL对53组样本仿真数据的学习能力;从图 7可知,用14组测试数据与由SimpleMKL建立的筛分模型所得的预测结果进行比较,两者确有误差,但整体趋势和输出误差在可接受范围内.同时2幅图显示出由SimpleMKL建立的模型对样本的学习能力良好,对新鲜数据的泛化预测能力也较好.综上所述,可以利用上述建立的模型对筛机的振动参数和结构参数进行参数优化设计分析.
4 基于人工鱼群算法对回归模型参数寻优计算模型是一个高度非线性、多极值且不可微分的多参数大规模计算问题,传统的机械优化算法如鲍威尔法、梯度下降法等优化算法虽有所长,但很难满足其可微分连续等严格的数学条件,利用鲁棒性强和全局收敛性好的人工鱼群智能优化算法,模拟鱼类觅食、追尾和聚群行为,通过每条鱼的局部寻优达到全局寻优,以用于解决各种组合优化问题.根据上述建立的数学模型,需要优化的参数与优化目标的关系可表示为:
| $ \max \;\gamma = f({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},). $ | (14) |
| $ \left. {\begin{array}{*{20}{c}} {^{{\rm{s}}.t.}0.5 \le {x_1} \le 2.6{\rm{mm,}}}\\ {10 \le {x_2} \le 30{\rm{Hz}},}\\ {{{30}^ \circ } \le {x_3} \le {{75}^ \circ },}\\ {0.6 \le {x_4} \le 1.0{\rm{mm,}}}\\ {0.3 \le {x_5} \le 0.5{\rm{mm,}}}\\ {{{15}^ \circ } \le {x_6} \le {{26}^ \circ }} \end{array}} \right\} $ | (15) |
在实际振动筛分中,由于受到筛机振动强度和结构参数的限制,并且为了避免颗粒贴附筛面和过度扬尘等现象,将每个设计变量的可行域范围作为参数组合优化的约束条件,如式(15)所示.人工鱼群算法求解振动筛分模型的流程图如图 8所示,其初始参数如表 3所示.
|
| 图 8 人工鱼群算法对筛分模型寻优的流程图 Fig. 8 Flowchart of AFSA-SimpleMKL for optimization |
| 参数 | 取值 | 参数 | 取值 | |
| 人工鱼群 | 100 | 感知距离 | 2 | |
| 最大迭代次数 | 50 | 拥挤度因子 | 0.618 | |
| 觅食最大试探次数 | 100 | 移动步长 | 0.3 |
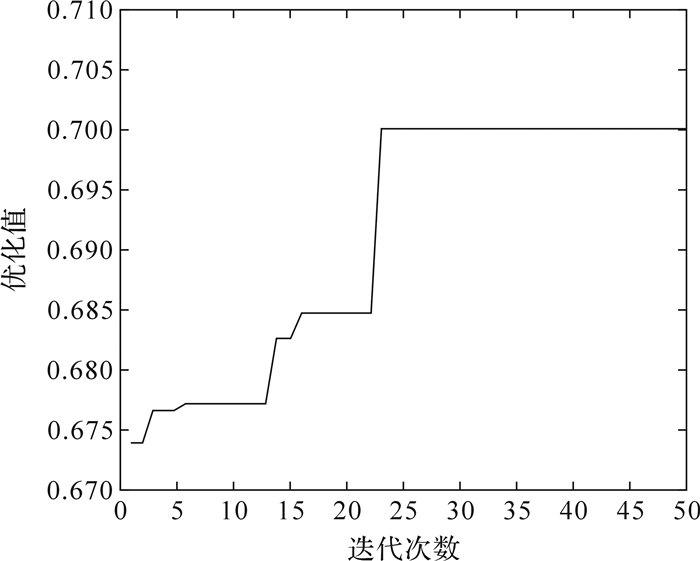
选取50次迭代过程,其迭代变化图如图 9所示.由人工鱼群对简单多核支持向量机的寻优结果:振幅为2.506 64 mm,振动频率为21.832 5 Hz,振动方向角为50.12005°,筛孔大小为0.940 82 mm,筛丝直径为0.395 72 mm,筛面倾角为21.641 19°,筛分效率为0.700 5.将所得的参数组合圆整后,振幅为2.5 mm,振动频率为22 Hz,振动方向角为50°,筛孔大小为0.9 mm,筛丝直径为0.4 mm,筛面倾角为21.6°,利用EDEM仿真计算得到筛分效率为0.696 7.

|
| 图 9 最优组合的变化过程 Fig. 9 Optimal combination process |
1)EDEM仿真能够根据筛分作业的实际工作条件得到筛分效率,替代费时费力的物理试验.由组合式可调参数的振动筛样机的实验结果表明模拟结果能够基本反映筛分作业的特性和趋势.
2)利用简单多核支持向量机对高度非线性的筛分过程进行建模.其综合统计学理论、对偶原则和最优化理论,基于结构风险性最小原则,对小样本数据进行训练并能对新样本进行预测.为振动筛分提供非参数建模,同时其模型也有利于对筛分参数的组合寻优.
3)利用人工鱼群智能寻优算法解决SimpleMKL筛分模型参数寻优时数学模型不可微分、高度非线性等问题,找到适于筛分的参数组合,对优化的参数组合利用DEM进行仿真,提高筛分效率,丰富了筛分理论,同时为制造振动筛提供新的设计思路.
4)对实验过程中由仿真颗粒形状带来的误差、简单多核支持向量机基核函数和核参数的初始值引起的偏差、人工鱼群初始参数的设置和迭代时间较长等问题,仍需进一步研究.
| [1] | 刘光焕,童昕,辛成涛.振动筛筛分过程的数值模拟及进展[J].金属矿山,2008(9):104-110. LIU Guang-huan,TONG Xin,XIN Chen-tao.Numerical simulation of vibration screening process and its process[J].Metal Mine,2008(9):104-110. |
| Cited By in Cnki (22) | Click to display the text | |
| [2] | CLEARY P W,SAWLEY M.DEM modelling of industrial granular flows:3D case studies and the effect of particle shape on hopper discharge[J].Applied Mathematical Modelling,2002,26(2):89-111. |
| Click to display the text | |
| [3] | LI J,WEBB C,PANDIELLA S S,et al.Discrete particle motion on sieves:a numerical study using the DEM simulation[J].Powder Technology,2003,133(1/3):190-202. |
| Click to display the text | |
| [4] | JIAO H G,MA J,ZHAO Y M.Study on the numerical simulation of batch sieving process[J].Journal of Coal Science & Engineering,2006,12(2):80-83. |
| Click to display the text | |
| [5] | CLEARY P W,SINNOTT M D,MORRISON R D.Separation performance of double deck banana screens:part 1:flow and separation for different accelerations[J].Minerals Engineering,2009,22 (14):1218-1229. |
| Click to display the text | |
| [6] | CLEARY P W,SINNOTT M D,MORRISON R D.Separation performance of double deck banana screens:part 2:quantitative predictions[J].Minerals Engineering,2009,22 (14):1230-1244. |
| Click to display the text | |
| [7] | CHEN Y H,TONG X.Modeling screening efficiency with vibrational parameters based on DEM 3D simulation[J].Mining Science and Technology,2010,20(4):615-620. |
| Click to display the text | |
| [8] | CHEN Y H,TONG X.Application of the DEM to screening process:a 3D simulation[J].Mining Science and Technology,2009,19(4):493-497. |
| Click to display the text | |
| [9] | 李菊,赵德安,沈惠平,等.基于输入优选的三维并联振动筛输出特性分析[J].中国机械工程,2014,25(14):1852-1857. LI Ju,ZHAO De-an,SHEN Hui-ping,et al.Analysis on output characteristics of three-dimensional parallel kinematics vibrating screen based on input optimization[J].China Mechanical Engineering,2014,25(14):1852-1857. |
| Cited By in Cnki (2) | Click to display the text | |
| [10] | LI Z F,TONG X.Modeling and parameter optimization for the design of vibrating screens[J].Minerals Engineering,2015,83:149-155. |
| Click to display the text | |
| [11] | VAPNIK V.The nature of statistical learning theory[M].New York:Springer,1995:84-90. |
| [12] | VAPNIK V N.An overview of statistical learning theory[J].IEEE Trans Neural Networks,1999,10 (5):988-999. |
| Click to display the text | |
| [13] | 李元诚,方廷健,于尔铿.短期负荷预测的支持向量机方法[J].中国电机工程学报,2003,23(6):55-59. LI Yuan-cheng,FANG Ting-jian,YU Er-keng.Study of support vector machines for short-term load forecasting[J].Proceedings of the CSEE,2003,23(6):55-59. |
| Cited By in Cnki (372) | Click to display the text | |
| [14] | 申中杰,陈雪峰,何正嘉,等.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测[J].机械工程学报,2013,49(2):183-189. SHEN Zhong-jie,CHEN Xue-feng,HE Zheng-jia,et al.Remaining life predictions of rolling bearing based on relative features and multivariable support vector machine[J].Chinese Journal of Mechanical Engineering,2013,49(2):183-189. |
| Cited By in Cnki (17) | Click to display the text | |
| [15] | 陆凤仪,王 爽,徐格宁,等.构建起重机载荷谱v-SVRM预测模型的改进方法[J].工程设计学报,2015,22 (5):412-419. LU Feng-yi,WANG Shuang,XU Ge-ning,et al.Improved modeling method for prediction model of crane load spectrum based on support vector regression machine[J].Chinese Journal of Engineering Design,2015,22 (5):412-419. |
| Cited By in Cnki | |
| [16] | RAKOTOMAMONJY A,BACH F R,CANU S,et al.SimpleMKL[J].Journal of Machine Learing Reseach,2008,9(11):2491-2521. |
| Click to display the text | |
| [17] | 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38. LI Xiao-lei,SHAO Zhi-jiang,QIAN Ji-xin.An optimizing method based on autonomous animats:fish-swarm algorithm[J].Systems Engineering—Theory & Practice,2002,22(11):32-38. |
| Cited By in Cnki (953) | Click to display the text | |
| [18] | CLEARY P W.DEM prediction of industrial and geophysical particle flows[J].Particuology,2010,8(2):106-118. |
| Click to display the text |



