2. 安徽机电职业技术学院, 安徽 芜湖 241002;
3. 江西理工大学 机电工程学院, 江西 赣州 341000
2. Anhui Technical College of Mechanical and Electrical Engineering, Wuhu 241002, China;
3. School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
并联机构的微运动分析是机构运动特性研究的重要组成部分,也是机构误差分析和控制仿真的基础[1].并联机构具有承载能力强、位置精度高、结构刚度大等优点,其早期的主要研究对象为Stewart平台[2].少自由度并联机构的构型简单易实现、动力学求解容易,因此少自由度并联机构的研究越来越普遍.Tsai等人[3]采用螺旋理论的方法求解出3-RPS并联机构的Jacobian矩阵,并列举了所有情况的奇异矩阵.但是,得到的Jacobian矩阵不是方阵,不能作为控制系统的参考输入值.Jacobian矩阵的正确与否直接影响着机构的轨迹跟踪精度,而轨迹跟踪精度是并联机构控制性能的重要指标,因此如何提高并联机构的轨迹跟踪精度逐渐成为学者们关注的焦点.朱大昌等人[4]基于广义Jacobian矩阵,采用模糊PID的控制方法,对3-RPC并联机构各支链位移的轨迹跟踪误差进行了研究.Park等人[5]提出了一种基于摄动观测器的变结构控制方法,探讨了机构在不确定项和非线性条件下的稳定性问题.Wu等人[6]将PI控制器与模糊自整定PD控制器相结合,设计了一种混合自整定的PID控制器,解决了控制器轨迹跟踪的稳定性和收敛性问题.为提高并联机构的轨迹跟踪精度,本文基于机构的动力学方程和比例切换控制律,设计了一种以3-RPS并联机构为研究对象的滑模变结构控制系统.首先,通过Solidworks与MATLAB软件的关联插件,将3-RPS并联机构的Solidworks三维模型转换为MATLAB/SimMechanics仿真分析模型,采用微位移法求解3-RPS并联机构的Jacobian矩阵,给控制系统提供参考输入值.其次,设计滑模变结构控制器(SMC),并证明控制器的稳定性.最后,分别采用PID和SMC控制方式对机构进行仿真分析,对比动平台的位置变化曲线和轨迹跟踪误差曲线,从而证明SMC控制的有效性.
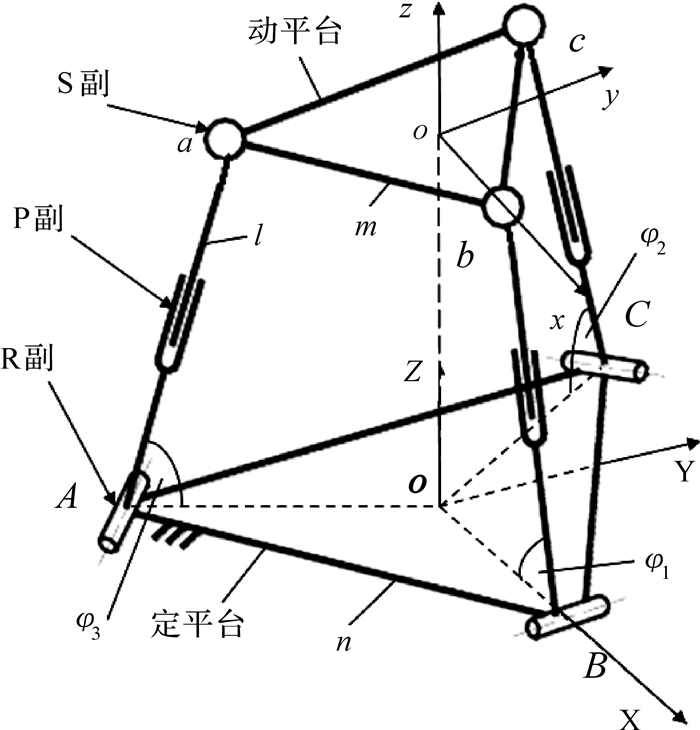
1 3-RPS并联机构MATLAB建模3-RPS是具有对称结构的三自由度并联机构,其构型简图如图 1所示.机构的动、定平台分别由2个等边三角形△abc和△ABC组成,动、定平台之间通过3条支链相连接,其中每条支链含有1个R副(转动副)、1个P副(移动副)和1个S副(球副).定平台与R副相连,动平台与S副相连,P副连接着R副和S副.分别建立机构的动、定平台坐标系o-xyz和O-XYZ,o和O表示动、定平台的中心.其中,动、定平台的边长分别为m和n,驱动杆长为l,支链与定平台的夹角为φi.
|
| 图 1 3-RPS并联机构构型简图 Fig. 1 Structure diagram of 3-RPS parallel mechanism |
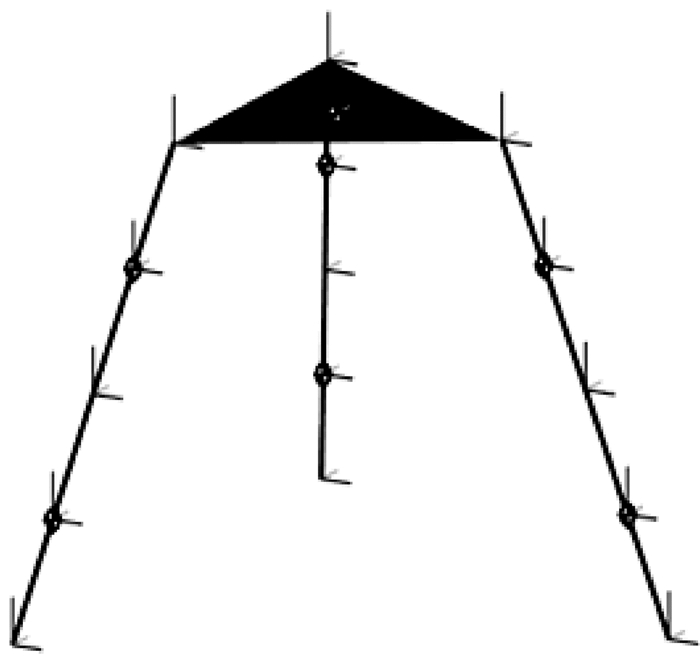
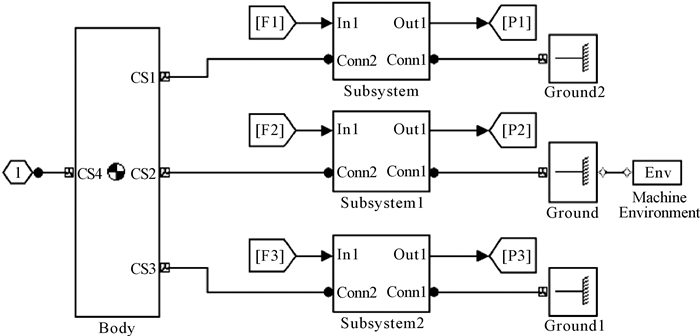
SolidWorks软件具备完善的三维建模功能,而MATLAB软件在机构运动学和动力学仿真领域具有优越性,通过插件(SimMechanics Link)可以很好地结合SolidWorks和MATLAB软件.运用SolidWorks建立3-RPS并联机构的三维模型,将装配体的.SLDASM文件另存为.XML文件;在MATLAB的命令窗口中输入mech_import命令,载入刚刚保存的.XML文件;在框图中添加所需的检测和驱动模块,并设置好相应构件的参数,即可建立机构的MATLAB/SimMechanics模型.3-RPS并联机构的MATLAB简图如图 2所示,机构的MATLAB/SimMechanics模型如图 3所示,其支链的MATLAB/SimMechanics模型如图 4所示.3-RPS并联机构各构件的坐标参数值如表 1所示.
|
| 图 2 3-RPS并联机构MATLAB简图 Fig. 2 MATLAB Diagram of 3-RPS parallel mechanism |
|
| 图 3 3-RPS并联机构SimMechanics模型 Fig. 3 SimMechanics model of 3-RPS parallel mechanism |

|
| 图 4 3-RPS并联机构支链SimMechanics模型 Fig. 4 SimMechanics model of 3-RPS parallel mechanism's branched chain |
| 模块组 | 支链1 | 支链2 | 支链3 |
| Ground | $ \left[ \frac{\sqrt{3}}{3}m,\text{0},0 \right] $ | $ \left[ -\frac{\sqrt{3}}{6}m,\frac{1}{2}m,0 \right] $ | $ \left[ -\frac{\sqrt{3}}{6}m,-\frac{1}{2}m,0 \right] $ |
| Revolute | $ \left[ \frac{\sqrt{3}}{4}(m+\frac{1}{3}n),0,\frac{l\sin {{\varphi }_{1}}}{4} \right]$ | $\left[ -\frac{\sqrt{3}}{8}(m+\frac{1}{3}n),\frac{3}{8}(m+\frac{1}{3}n),\frac{l\sin {{\varphi }_{2}}}{4} \right] $ | $ \left[ -\frac{\sqrt{3}}{8}(m+\frac{1}{3}n),-\frac{3}{8}(m+\frac{1}{3}n),\frac{l\sin {{\varphi }_{3}}}{4} \right] $ |
| dingliangan | $ \left[ \frac{\sqrt{3}}{6}(m+n),0,\frac{l\sin {{\varphi }_{1}}}{2} \right] $ | $\left[ -\frac{\sqrt{3}}{8}(m+\frac{1}{3}n),\frac{3}{8}(m+\frac{1}{3}n),\frac{l\sin {{\varphi }_{2}}}{4} \right] $ | $\left[ -\frac{\sqrt{3}}{8}(m+\frac{1}{3}n),-\frac{3}{8}(m+\frac{1}{3}n),\frac{l\sin {{\varphi }_{3}}}{4} \right] $ |
| Prismatic | $\left[ \frac{\sqrt{3}}{6}(m+n),0,\frac{l\sin {{\varphi }_{1}}}{2} \right] $ | $ \left[ -\frac{\sqrt{3}}{12}(m+n),\frac{3}{8}(m+\frac{1}{3}n),\frac{l\sin {{\varphi }_{2}}}{2} \right] $ | $ \left[ -\frac{\sqrt{3}}{12}(m+n),-\frac{3}{8}(m+\frac{1}{3}n),\frac{l\sin {{\varphi }_{3}}}{2} \right] $ |
| dongliangan | $ \left[ \frac{\sqrt{3}}{4}(\frac{1}{3}m+n),0,\frac{3l\sin {{\varphi }_{1}}}{4} \right] $ | $ \left[ -\frac{\sqrt{3}}{8}(\frac{1}{3}m+n),\frac{3}{8}(\frac{1}{3}m+n),\frac{3l\sin {{\varphi }_{2}}}{4} \right] $ | $ \left[ -\frac{\sqrt{3}}{8}(\frac{1}{3}m+n),-\frac{3}{8}(\frac{1}{3}m+n),\frac{3l\sin {{\varphi }_{3}}}{4} \right] $ |
| Spherical | $ \left[ \frac{\sqrt{3}}{3}n,\text{0},l\sin {{\varphi }_{1}} \right] $ | $ \left[ -\frac{\sqrt{3}}{6}n,\frac{1}{2}n,l\sin {{\varphi }_{2}} \right] $ | $ \left[ -\frac{\sqrt{3}}{6}n,-\frac{1}{2}n,l\sin {{\varphi }_{3}} \right] $ |
并联机构微运动分析的主要目的是得到其输入输出的Jacobian矩阵.对于多自由度的并联机构而言,可采用螺旋法求解Jacobian矩阵.但是,采用螺旋法求解少自由度并联机构的Jacobian矩阵,得到的Jacobian矩阵往往不是非奇异方阵,且不能避免求解超越方程组的问题.为了避免上述难题,本文提出了一种求解Jacobian矩阵的新方法,即微位移法.微位移法的基本思想为:在机构微运动分析的基础上,把无穷小量及其高阶无穷小量等价成零,将超越方程组简化,以利于提取机构的输入与输出量.当机构的转角δα,δβ,δγ或者移动距离dx,dy,dz较小时,
| $ \left\{ \begin{matrix} \underset{\delta v\to 0}{\mathop{\lim }}\,\sin \delta v=\delta v \\ \underset{\delta v\to 0}{\mathop{\lim }}\,\cos \delta v=1 \\ \end{matrix} \right. $ | (1) |
其中δv表示δα,δβ,δγ,dx,dy,dz及其高阶量.应用微位移法求解得到的Jacobian矩阵为非奇异方阵,可以直接作为并联机构仿真系统的理论参考输入值.
假设机构动平台坐标系的x,y,z轴相对于定平台分别转动了δγ,δβ,δα以及平移了dx,dy,dz,根据静坐标系变换原则,可得到相应的旋转变换矩阵Rα,β,γ和平移变换矩阵Ttrans.
| $ {R_{\alpha ,\beta ,\gamma }} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}\alpha {\rm{c}}\beta }&{{\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma - {\rm{s}}\alpha {\rm{c}}\gamma }&{{\rm{c}}\alpha {\rm{s}}\beta {\rm{c}}\gamma + {\rm{s}}\alpha {\rm{s}}\gamma }\\ {{\rm{s}}\alpha {\rm{c}}\beta }&{{\rm{s}}\alpha {\rm{s}}\beta {\rm{s}}\gamma + {\rm{c}}\alpha {\rm{c}}\gamma }&{{\rm{s}}\alpha {\rm{s}}\beta {\rm{c}}\gamma - {\rm{c}}\alpha {\rm{s}}\gamma }\\ { - {\rm{s}}\beta }&{{\rm{c}}\beta {\rm{s}}\gamma }&{{\rm{c}}\beta {\rm{c}}\gamma } \end{array}} \right] $ |
其中,c()=cos(),s()=sin(),下同.
| $ {{T}_{\text{trans}}}=\left[\begin{matrix} 1 & 0 & 0 & dx \\ 0 & 1 & 0 & dy \\ 0 & 0 & 1 & dz \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] $ |
综上,可得到齐次变换矩阵为:
| $ \begin{align} & T={{T}_{trans}}{{R}_{z,\alpha }}{{R}_{y,\beta }}{{R}_{x,\gamma }}= \\ & \left[ \begin{matrix} \operatorname{c}\alpha \operatorname{c}\beta & \operatorname{c}\alpha \operatorname{s}\beta \operatorname{s}\gamma -\operatorname{s}\alpha \operatorname{c}\gamma & \operatorname{c}\alpha \operatorname{s}\beta \operatorname{c}\gamma +\operatorname{s}\alpha \operatorname{s}\gamma & dx \\ \operatorname{s}\alpha \operatorname{c}\beta & \operatorname{s}\alpha \operatorname{s}\beta \operatorname{s}\gamma +\operatorname{c}\alpha \operatorname{c}\gamma & \operatorname{s}\alpha \operatorname{s}\beta \operatorname{c}\gamma -\operatorname{c}\alpha \operatorname{s}\gamma & dy \\ -\operatorname{s}\beta & \operatorname{c}\beta \operatorname{s}\gamma & \operatorname{c}\beta \operatorname{c}\gamma & dz \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \\ \end{align} $ |
定平台各铰链中心点A,B,C在O-XYZ中的坐标向量为:
| $ {{\left[\begin{matrix} A & B & C \\ \end{matrix} \right]}^{T}}=\left[\begin{matrix} \frac{\sqrt{3}n}{3} & -\frac{\sqrt{3}n}{6} & -\frac{\sqrt{3}n}{6} \\ 0 & \frac{n}{{}} & -\frac{n}{2} \\ 0 & 0 & 0 \\ \end{matrix} \right] $ |
动平台各铰链中心点a,b,c在o-xyz中的坐标向量为:
| $ {{\left[\begin{matrix} a & b & c \\ \end{matrix} \right]}^{T}}=\left[\begin{matrix} \frac{\sqrt{3}m}{3} & -\frac{\sqrt{3}m}{6} & -\frac{\sqrt{3}m}{6} \\ 0 & \frac{m}{2} & -\frac{m}{2} \\ 0 & 0 & 0 \\ \end{matrix} \right] $ |
由齐次变换矩阵T,根据公式P′=TP可得动平台各个铰链中心向量oa,ob,oc旋转变换后在基坐标O-XYZ中的齐次坐标向量形式,如式(2)所示.由于3-RPS并联机构实现的是绕x轴、y轴的转动
| $ \left[\begin{matrix} a' & b' & c' & 1 \\ \end{matrix} \right]=\left[\begin{matrix} \frac{\sqrt{3}}{3}n\operatorname{c}\alpha \operatorname{c}\beta & -\frac{\sqrt{3}}{6}n\operatorname{c}\alpha \operatorname{c}\beta +\frac{1}{2}n(\operatorname{c}\alpha \operatorname{s}\beta \operatorname{s}\gamma -\operatorname{s}\alpha \operatorname{c}\gamma ) & -\frac{\sqrt{3}}{6}n\operatorname{c}\alpha \operatorname{c}\beta -\frac{1}{2}n(\operatorname{c}\alpha \operatorname{s}\beta \operatorname{s}\gamma -\operatorname{s}\alpha \operatorname{c}\gamma ) & dx \\ \frac{\sqrt{3}}{3}n\operatorname{s}\alpha \operatorname{c}\beta & -\frac{\sqrt{3}}{6}n\operatorname{s}\alpha \operatorname{c}\beta +\frac{1}{2}n(\operatorname{s}\alpha \operatorname{s}\beta \operatorname{s}\gamma +\operatorname{c}\alpha \operatorname{c}\gamma ) & -\frac{\sqrt{3}}{6}n\operatorname{s}\alpha \operatorname{c}\beta -\frac{1}{2}n(\operatorname{s}\alpha \operatorname{s}\beta \operatorname{s}\gamma +\operatorname{c}\alpha \operatorname{c}\gamma ) & dy \\ -\frac{\sqrt{3}}{3}n\operatorname{s}\beta & \frac{\sqrt{3}}{6}n\operatorname{s}\beta +\frac{1}{2}n\operatorname{c}\beta \operatorname{s}\gamma & \frac{\sqrt{3}}{6}n\operatorname{s}\beta -\frac{1}{2}n\operatorname{c}\beta \operatorname{s}\gamma & dz \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] $ | (2) |
和沿z轴的平移,所以将机构绕x轴的转动δα、绕y轴的转动δβ和沿z轴的平移dz作为机构的输出量.根据δα,δβ,dz求解各杆的杆长变化,并将其作为机构的输入量.
将机构的所有参数写入MATLAB的m文件中,编写求解杆长变化量和输入输出Jacobian矩阵的程序.通过MATLAB计算各杆长的变化量,可得到Δli与δα,δβ,dz之间的关系,其齐次坐标形式如式(3)所示.
| $ \left[\begin{matrix} \Delta {{l}_{1}} \\ \Delta {{l}_{2}} \\ \Delta {{l}_{3}} \\ 1 \\ \end{matrix} \right]=\left[\begin{matrix} 0 & -\frac{\sqrt{3}m}{3}\sin {{\varphi }_{1}} & {{\sin }^{2}}{{\varphi }_{1}} & \frac{{{m}^{2}}}{nl}+\frac{{{n}^{2}}}{6l}-\frac{mn}{3l}+\frac{l}{2}\left( {{\sin }^{2}}{{\varphi }_{1}}-1 \right) \\ \frac{m}{2}\sin {{\varphi }_{2}} & \frac{\sqrt{3}m}{6}\sin {{\varphi }_{2}} & \sin {{\varphi }_{2}} & \frac{{{m}^{2}}}{nl}+\frac{{{n}^{2}}}{6l}-\frac{mn}{3l}+\frac{l}{2}\left( {{\sin }^{2}}{{\varphi }_{2}}-1 \right) \\ -\frac{m}{2}\sin {{\varphi }_{3}} & \frac{\sqrt{3}m}{6}\sin {{\varphi }_{3}} & \sin {{\varphi }_{3}} & \frac{{{m}^{2}}}{nl}+\frac{{{n}^{2}}}{6l}-\frac{mn}{3l}+\frac{l}{2}\left( {{\sin }^{2}}{{\varphi }_{3}}-1 \right) \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]\left[\begin{matrix} \delta \alpha \\ \delta \beta \\ dz \\ 1 \\ \end{matrix} \right] $ | (3) |
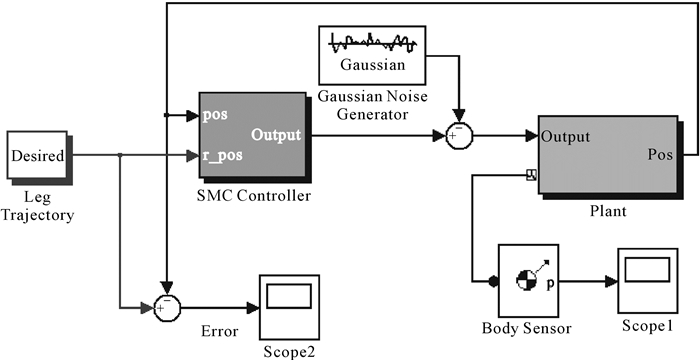
记Δl1 Δl2Δl31T=Qδαδβdz1T,根据Jacobian矩阵的定义δαδβdz1T=JΔl1 Δl2Δl31T,运用微位移法得到的机构输入输出Jacobian矩阵J=Q-1.将机构的Jacobian矩阵写入图 5的Leg Trajectory模块,为控制仿真提供参考输入.
|
| 图 5 3-RPS并联机构控制系统总框图 Fig. 5 Total block diagram of 3-RPS parallel mechanism’s control system |
3-RPS并联机构控制系统的总框图如图 5所示,其中:Controller为系统的控制器;Plant是机构的MATLAB/SimMechanics模型,即图 3所示的系统被控对象;Body Sensor是动平台传感器;Scope1和Scope2是示波器,分别显示动平台的位置和误差曲线;Gaussian Noise Generator为外加的高斯噪声干扰信号,用于验证控制器的抗干扰性;Leg Trajectory为机构的参考输入值,其主要作用是根据Jacobian矩阵计算出各杆杆长的变化量.其框图如图 6所示.其中,EulerXYZ为第2节计算的旋转变换矩阵,position matrix为位置矩阵,body_pts,pos_base,nominal leg length分别是由机构的尺寸参数组成的矩阵,Desired1为动平台的期望输入信号.

|
| 图 6 控制系统参考输入框图 Fig. 6 Block diagram of control system’s reference input |
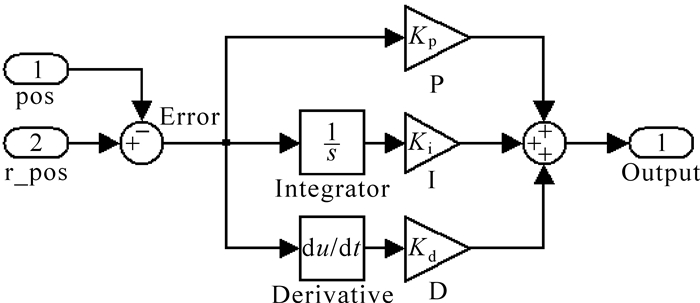
PID控制器因其控制算法成熟,已在工程设计中得到了普遍应用.但是,如何确定PID控制器的各个参数是控制器设计的关键问题之一.由于经验凑试法具有较强的适用性,可用于各种控制系统,本文采用经验凑试法来调整PID控制器的各个参数.3-RPS并联机构PID控制器MATLAB/Simulink框图如图 7所示.其中,Integrator为连续时间积分器,Derivative为连续时间微分器.
|
| 图 7 PID控制器MATLAB/Simulink框图 Fig. 7 MATLAB/Simulink model of PID controller |
根据拉格朗日方程,采用独立坐标描述的3-RPS并联机构的动力学方程[7]为
| $ M(q)\ddot{q}+{{V}_{m}}(q,\dot{q})\dot{q}+F(\dot{q})+G(q)+{{\tau }_{d}}=\tau $ |
其中:q和$ \dot{q} $分别表示机构的广义位移和广义速度,τ为驱动力矩向量;M(q)∈R4×4为机构的惯性矩阵;Vm(q,$ \dot{q} $)∈R4×4表示离心力和哥氏力矩阵;F($ \dot{q} $)∈R4×1为摩擦矩阵;G(q)∈R4×1为重力矩阵;τd∈R4×1为外加干扰.3-RPS并联机构的动力学方程有如下的基本性质:
1)对于任意的q和$ \dot{q} $,M(q)是正定对称矩阵,且矩阵M(q)和Vm(q,$ \dot{q} $)是一致有界的.
2)矩阵M(q)-2Vm(q,$ \dot{q} $)是斜对称矩阵,即对于任意的向量ξ,有
| $ {{\xi }^{T}}(M(q)-2{{V}_{m}}(q,\dot{q}))\xi =0 $ |
3)定义参数向量Ω,Ω表示M,Vm,F,G的定常系数,则存在一个适当的矩阵Φ(q,ω,ψ,$ \dot{q} $),使得M(q),Vm(q,$ \dot{q} $),F($ \dot{q} $)和G(q)满足线性关系:
| $ M(q)\omega +{{V}_{m}}(q,\dot{q})\psi +F(\dot{q})+G(q)+{{\tau }_{d}}=\Phi (q,\omega ,\psi ,\dot{q})\Omega $ |
在分析证明SMC控制器的Lyapunov稳定性过程中,需要利用上述性质.
设计滑模变结构控制器(SMC)主要包括设计滑动模态控制律u(x)和切换函数s(x)两个相对独立的部分.下面基于3-RPS并联机构动力学模型,结合比例切换控制律,设计机构的滑模变结构控制器,并根据Lyapunov函数证明SMC控制器的稳定性.
假设系统的理想位置信号为qd(t),误差信号为e(t)=q(t)-qd(t).设计的滑模函数为
| $ s=Ce+\dot{e} $ |
其中,$ C=diag({{c}_{1}},...,{{c}_{n}}),{{c}_{i}}>0 $选取的Lyapunov函数为$ V(x)=\frac{1}{2}{{s}^{T}}Ms $,则
| $ \dot{V}\text{=}\frac{1}{2}\left( {{{\dot{s}}}^{\text{T}}}Ms+{{s}^{\text{T}}}\dot{M}s+{{s}^{\text{T}}}M\dot{s} \right) $ |
由特性(1)可知,$ {{\dot{s}}^{\text{T}}}Ms\text{=}{{s}^{\text{T}}}M\dot{s} $,则
| $ \dot V{\rm{ = }}\frac{1}{2}{s^{\rm{T}}}\dot Ms + {s^{\rm{T}}}M\dot s = \frac{1}{2}{s^{\rm{T}}}(\dot M - 2{V_m})s + {s^{\rm{T}}}{V_m}s + {s^{\rm{T}}}M\dot s $ |
由特性(2)可知,$ {{s}^{\text{T}}}(\dot{M}-2{{V}_{m}})s\text{=}0 $,则
| $ \dot V{\rm{ = }}{s^{\rm{T}}}{V_m}s + {s^{\rm{T}}}M\dot s $ |
将动力学方程代入上式,则
| $ \dot{V}\text{=}{{s}^{T}}[{{V}_{m}}(Ce+{{\dot{q}}_{d}})+M({{\ddot{q}}_{d}}+C\dot{e})+F+G-{{\tau }_{d}}-\tau] $ |
由特性(3)可知,则
| $ \text{=}{{s}^{\text{T}}}[\Phi (t,q,{{q}_{d}},\dot{q},\ddot{q},{{\ddot{q}}_{d}})\Omega -\tau]. $ |
根据比例切换控制律$ u(x) = (\omega |e| + \psi \dot e){\mathop{\rm sgn}} (s(x)) $,可得滑模变结构控制器的控制律为
| $ \tau = \Phi {\Omega _0} + (\omega |e| + \psi \dot e){\rm{sgn}}(s(x)) $ | (4) |
其中,ΦΩ0为机构的精确函数矩阵,ω和ψ为控制律大于零的常数,即需要确定的控制参数.由式(4)可知
| $ \dot{V}\text{=}{{s}^{T}}[\Phi (\Omega -{{\Omega }_{0}})-(\omega |e|+\psi \dot{e})|s|]={{s}^{T}}[\Phi \Delta \Omega -|u(x)|]. $ |
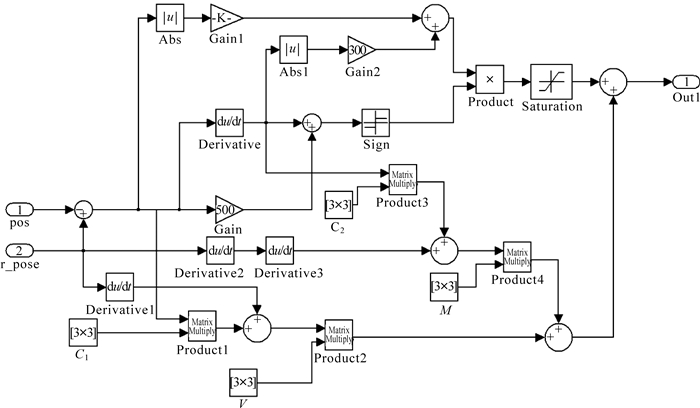
取ui(x)>Φ|ΔΩ|max,则$ \dot{V} $≤0.因此,控制系统具有稳定性.根据式(4)的控制律和$ {{u}_{i}}(x)>\Phi \text{ }\!\!|\!\!\text{ }\Delta \Omega {{\text{ }\!\!|\!\!\text{ }}_{\max }} $的约束条件,SMC控制器的MATLAB/Simulink框图如图 8所示.其中,Gain1和Gain2分别表示参数ω和ψ的设定值,M表示机构的惯性矩阵,V表示科氏力和离心力矩阵,C1为摩擦矩阵,C2为重力矩阵.
|
| 图 8 SMC控制器MATLAB/Simulink框图 Fig. 8 MATLAB/Simulink model of SMC controller |
设定初始参数:动平台的质量为1kg,转动惯量Ixx=11.7kg·m2,Iyy=11.8kg·m2,Izz=20.1kg·m2,φ1=φ2=φ3=60°,m=50mm,n=100mm,l=120mm.动平台的输入期望参考值:y=0.1sin(3πt),仿真时间为10s.根据经验凑试法,不断调整P,I,D的值,Kp=16,Ki=1,Kd=0.2;根据SMC控制器框图,不断调整ω和ψ的值,ω=1 540,ψ=53.PID和SMC控制动平台的位置变化曲线如图 9和图 10所示,轨迹跟踪曲线如图 11和图 12所示.为验证PID控制和SMC控制的抗干扰能力,在控制器的输出端添加一个高斯噪声干扰信号,则系统的轨迹追踪曲线如图 13和图 14所示.
|
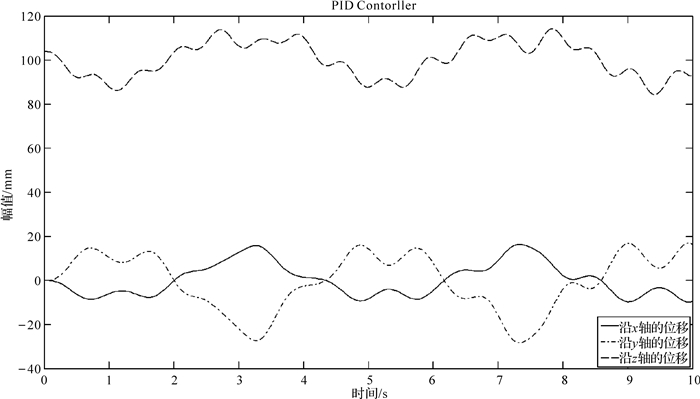
| 图 9 PID控制动平台位置变化曲线 Fig. 9 Position change curve of moving platform by PID controller |
|
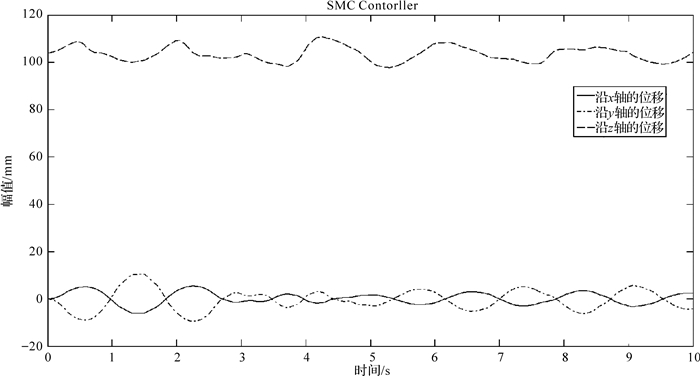
| 图 10 SMC控制动平台位置变化曲线 Fig. 10 Position change curve of moving platform by SMC controller |
|
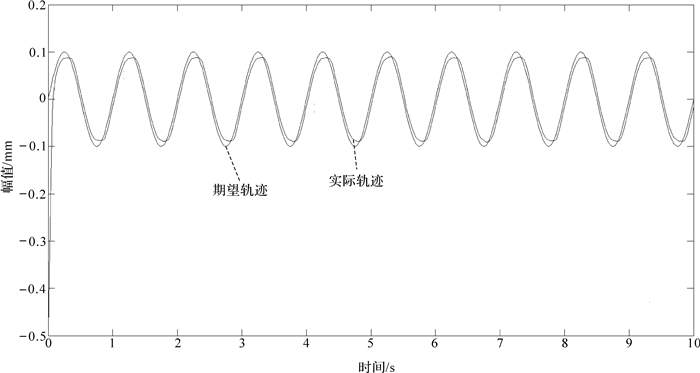
| 图 11 PID控制动平台轨迹跟踪曲线 Fig. 11 Trajectory tracking curve of moving platform by PID controller |
|
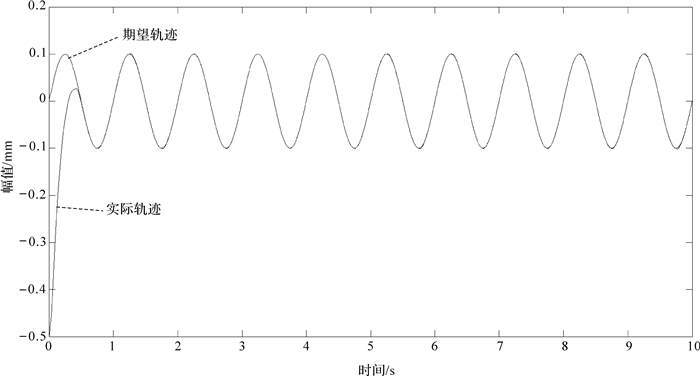
| 图 12 SMC控制动平台轨迹跟踪曲线 Fig. 12 Trajectory tracking curve of moving platform by SMC controller |
|
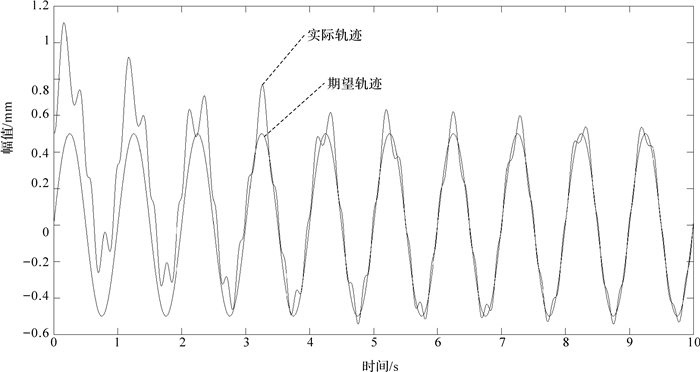
| 图 13 添加高斯噪声后PID控制动平台轨迹跟踪曲线 Fig. 13 Trajectory tracking curve of moving platform by PID controller after adding Gauss noise |
|
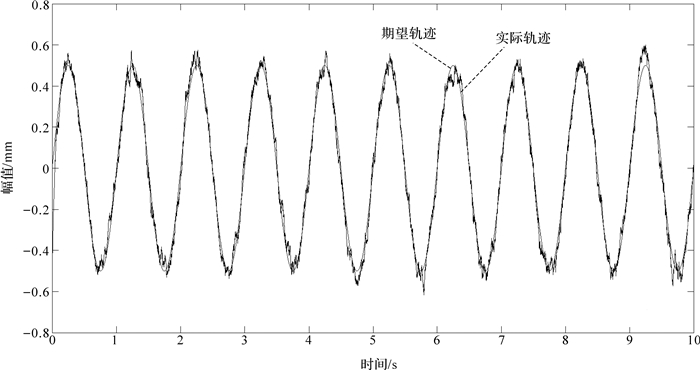
| 图 14 添加高斯噪声后SMC控制动平台轨迹跟踪曲线 Fig. 14 Trajectory tracking curve of moving platform by SMC controller after adding Gauss noise |
对比图 9和图 10可知,在相同的输入条件下,SMC控制动平台的位置变化相对于PID更平稳,运动更趋于稳定.对比图 11和图 14,机构在较短的时间内,2种控制方法都出现了一定的波动.PID控制虽有一定的调平能力,但抗干扰能力较差,机构的轨迹跟踪效果不好.SMC控制的抗干扰能力强,机构的轨迹跟踪效果相对于PID控制更好.
5 总 结通过微位移法分析了3-RPS并联机构的输入输出Jacobian矩阵,为机构的控制仿真提供理论的参考输入值.根据3-RPS并联机构的MATLAB仿真模型和动力学方程,设计了PID控制器和基于比例切换律的SMC控制器,并对其进行了仿真和对比.结果表明:SMC控制器与PID控制器相比,具有鲁棒性强、跟踪精度高、响应速度快、稳态误差小等优点,满足并联机构高精度的轨迹跟踪要求,在工程实践中具有重要的应用价值.
| [1] | 黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997:36-37. HUANG Zhen,KONG Ling-fu,FANG Yue-fa.Theory and control of parallel robot mechanism[M].Beijing:Mechanical Industry Press,1997:36-37. |
| [2] | STEWART D.A platform with six-degrees-of-freedom[J].Proceeding of the Institute of Mechanical Engineering,1965,180(5):371-386. |
| Click to display the text | |
| [3] | TSAI L W.Direct kinematic analysis of a 3-RPS parallel manipulator[J].Mechanical and Machine Theory,2003,38(1):71-83. |
| Click to display the text | |
| [4] | 朱大昌,刘云鸿,冯文结.3-RPC型并联机器人模糊PID控制系统研究[J].机械传动,2014,38(2):114-117. ZHU Da-chang,LIU Yun-hong,FENG Wen-jie.Research on the fuzzy PID control system of 3-RPC parallel robot[J].Mechanical Transmission,2014,38(2):114-117. |
| Cited By in Cnki (6) | |
| [5] | PARK Minkyn,LEE Min-cheol,GO Seok-jo.The design of sliding mode controller with perturbation observer for a 6-DOF parallel manipulator[C]//Proceedings of ISIE 2001.Pusan,Korea,March 10-14,2001:1502-1508. |
| Click to display the text | |
| [6] | WU Hua-peng,HANDROOS Heikki.Hybrid fuzzy self-tunning PID controller for a parallel manipulator[C]//Proceedings of the 5th Word Congress on Intelligent Control and Automation.Hangzhou,China,June 15-19,2004:2545-2550. |
| Click to display the text | |
| [7] | 杨香兰.6-DOF并联机器人动力学建模及模糊变结构控制[D].河北:燕山大学机械工程学院,2001:28-31. YANG Xiang-lan.The dynamics modeling and fuzzy variable structure control for 6-DOF parallel robot[D].Hebei:Yanshan University,College of Mechanical Engineering,2001:28-31. |
| Click to display the text | |
| [8] | SHIJING Li,ZUREN Feng,HAO Feng.Variable structure control for 6-6 parallel manipulators based on CMAC[C]// Proceedings of 4th World Congress on Intelligent Control and Automation.Shanghai,China,June 15-19,2002:1939-1944. |
| Click to display the text | |
| [9] | 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:25-30. LIU Jin-kun.MATLAB simulation for sliding mode variable structure control[M].Beijing:Tsinghua University Press,2005:25-30. |
| [10] | CHENG C,CHEN S H. Design of adaptive variable structure controllers with application to robot manipulators[C]// Proceedings of 5th World Congress on Intelligent Control and Automation.June 15-19,2004:4904-4908. |
| Click to display the text | |
| [11] | 张立勋.机电系统建模与仿真[M].哈尔滨:哈尔滨工业大学出版社,2009:140-147. ZHANG Li-xun.Modeling and simulation of mechanical and electrical systems[M].Harbin:Harbin Institute of Technology Press,2009:140-147. |
| [12] | 朱大昌,李培,顾起华.全柔顺并联机构理论[M].北京:冶金工业出版社,2013:153-163. ZHU Da-chang,LI Pei,GU Qi-hua.The theory of compliant parallel mechanism[M].Beijing:Metallurgical Industry Press,2013:153-163. |
| [13] | VICENTE P V,SUGURN A.Dynamic sliding PID control for tracking of robot manipulators:theory and experiments[J].IEEE Transaction on Robotics and Automation,2003,19(6):967-976. |
| Click to display the text |


