2. 中国煤矿机械装备有限责任公司, 北京100011;
3. 中煤张家口煤矿机械有限责任公司, 河北 张家口 076250
2. China National Coal Mining Equipment Co., Ltd., Beijing 100011, China;
3. China Coal Zhangjiakou Coal Mining Machinery Co., Ltd., Zhangjiakou 076250, China
刨煤机作为开采薄煤层与中厚煤层的采煤机械,可实现刨煤机械化与自动化.而刨煤机在矿井下工作过程中的动态特性十分复杂.针对刨煤机在动载荷作用下关键部件的可靠性问题,赵丽娟等[1, 2, 3]应用雨流法对刨煤机牵引块、回转接头以及刨刀进行了疲劳预测.康晓敏等[4]基于雨流法以及线性Miner疲劳累积损伤模型对刨链疲劳寿命进行了预测.刨头是刨煤机系统的工作机构,康晓敏等[5]对刨头的稳定性进行了分析.刨头与滑架之间间隙的存在,导致刨煤机在滑架上运行时产生碰撞,从而影响其动力特性、可靠性等.中部槽滑架体在大冲击载荷作用下将产生疲劳裂纹,严重情况下将导致刨煤机整个生产线停产.
针对间隙碰撞振动,卢绪祥等[6]应用Hertz接触理论研究了含对称间隙结构的接触碰撞动力学特性.Pashah等[7]应用弹簧质量模型以及三维有限元法研究了钢球横向撞击弹塑性自由梁现象.国外一些学者采用连续接触碰撞力模型,对接触碰撞现象进行了研究[8, 9, 10, 11, 12].Flores等[13]建立了间隙旋转铰的接触条件,并采用连续接触碰撞力模型,对间隙条件下的平面四连杆机构动态特性进行了分析.
本文基于Winkler弹性地基模型,建立刨煤机刨头三自由度碰撞振动动力学模型,提出刨头与滑架的碰撞判别条件,并采用数值方法对动力学模型进行求解,以所得到的最大碰撞力为疲劳试验载荷,对中部槽滑架体进行疲劳试验,试验结果为提高中部槽滑架体可靠性提供了理论基础.
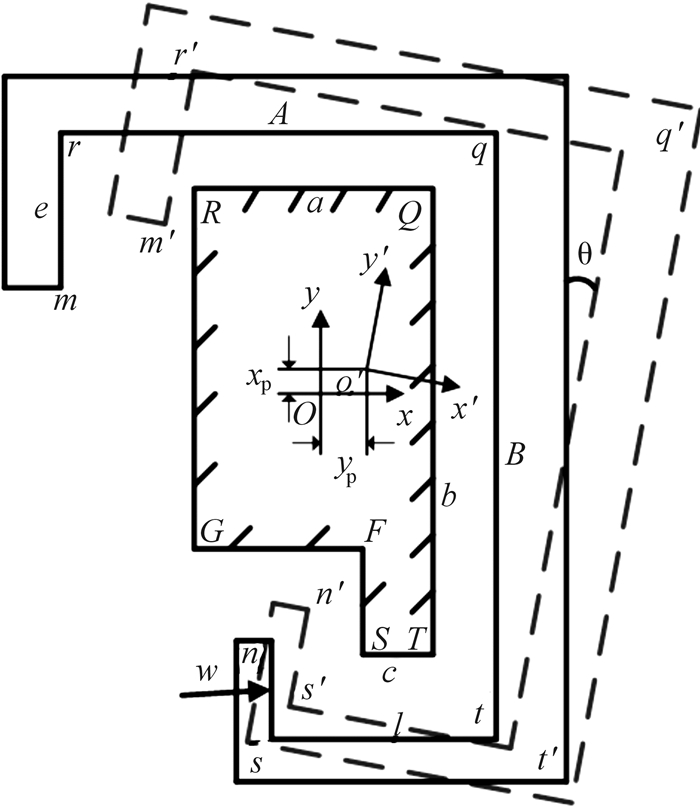
1 碰撞判别条件根据刨头与滑架体系统的相对运动特点,将模型进行简化,如图 1所示.刨头相对滑架运动过程中在外激励作用下产生摆动与移动,此时将与滑架产生弹塑性碰撞.为了描述刨头的运动特性,需要判断刨头在运动过程中与滑架碰撞的条件.
|
| 图 1 刨头间隙碰撞简化平面图 Fig. 1 Simplified planar graph of clearance impact of coal plow |
设定图 1中RQTSFG为滑架体,且固定不动.mrqtsn为刨头相对滑架运动.通过判断两者是否产生几何重叠的方法进行碰撞判别.以判断滑架体顶点Q以及刨头n点产生顺时针碰撞的条件为例,当顶点Q到边lrq的距离与顶点Q到边lst距离之和大于边lqt长时,则产生了碰撞,而当刨头上n点到直线lQT与lFS的距离之差小于滑架体边lST时,则产生了碰撞.
如图 1所示,选定滑架体中心处为坐标原点,刨头运动之前各顶点坐标为Zi=(xi,yi)(i=1,2,3,4,5,6),Q点坐标为(x0,y0).当刨头运动之后位置为图 1中图形m′r′q′t′s′n′,各点坐标Nj=(xj,yj)(j=1,2,3,4),其转化表达式为
| ${{N}_{j}}=PZ_{i}^{T}+M$ | (1) |
式中:P为旋转矩阵.
刨头逆时针转动时,
| $P=\left( \begin{align} & \cos \theta -\sin \theta \\ & \sin \theta \text{ }\cos \theta \\ \end{align} \right)$ |
顺时针转动时,
| $P=\left( \begin{align} & \text{ }\cos \theta \text{ }\sin \theta \\ & -\sin \theta \cos \theta \\ \end{align} \right)$ |
M为位移矩阵,$M=\left| \begin{align} & {{x}_{p}} \\ & {{y}_{p}} \\ \end{align} \right|$.
则
| $N_{j}^{T}=\left( {{x}_{i}}\cos \theta +{{y}_{i}}\sin \theta +{{x}_{p}},-{{x}_{i}}\sin \theta +{{y}_{i}}\cos \theta +{{y}_{p}} \right)$ |
令$\begin{align} & {{x}_{Nj}}={{x}_{i}}\cos \theta +{{y}_{i}}\sin \theta +{{x}_{p}},\\ & {{y}_{Nj}}=-{{x}_{i}}\sin \theta +{{y}_{i}}\cos \theta +{{y}_{p}},\\ \end{align}$,
由两点直线公式可得lAB以及lCD表达式为:
| $\begin{align} & {{l}_{AB}}:\left( {{y}_{N1}}-{{y}_{N2}} \right)x+\left( {{x}_{N2}}-{{x}_{N1}} \right)y+ \\ & \left( {{x}_{N1}}{{y}_{N2}}-{{x}_{N2}}{{y}_{N1}} \right)=0,\\ & {{l}_{CD}}:\left( {{y}_{N3}}-{{y}_{N4}} \right)x+\left( {{x}_{N4}}-{{x}_{N3}} \right)y+ \\ & \left( {{x}_{N3}}{{y}_{N4}}-{{x}_{N4}}{{y}_{N3}} \right)=0. \\ \end{align}$ |
令A0=yN1-yN2,B0=xN2-xN1,C0=xN1yN2-xN2yN1,A1=yN3-yN4,B1=xN4-xN3,C1=xN3yN4-xN4yN3,由点到直线距离公式,得点Q到直线lrq与lst的距离之和为
| $D=\frac{\left| {{A}_{0}}{{x}_{0}}+{{B}_{0}}{{y}_{0}}+{{C}_{1}} \right|}{\sqrt{A_{0}^{2}+B_{0}^{2}}}+\frac{\left| {{A}_{1}}{{x}_{0}}+{{B}_{1}}{{y}_{0}}+{{C}_{1}} \right|}{\sqrt{A_{1}^{2}+B_{1}^{2}}}$ | (2) |
滑架体顶点Q与刨头产生碰撞,则
| $D\text{}{{l}_{qt}}$ | (3) |
滑架体顶点Q与刨头未产生碰撞,则
| $ D={{l}_{qt}}$ | (4) |
刨头上n点与滑架体产生碰撞的条件如下:令n点坐标为(xn,yn),顺时针摆动之后的坐标为n′(x′n,y′n),其转化过程如式(1).直线lQT表达式为:$x=\frac{a}{2},{{l}_{FS}};x=\frac{a}{2}-c$.由点到直线距离公式,可得点n′到直线lQT与lFS的距离之差为
| $\begin{align} & d=\left| {{x}_{n}}\cos \theta +{{y}_{n}}\sin \theta +{{y}_{p}}-\frac{a}{2} \right|- \\ & \left| {{x}_{n}}\cos \theta +{{y}_{n}}\sin \theta +{{y}_{p}}-\frac{a}{2}+c \right|. \\ \end{align}$ | (5) |
当刨头顶点n与滑架产生碰撞时,则
| $d\text{}{{l}_{ST}}$ | (6) |
当刨头顶点n与刨头未产生碰撞,则
| $d={{l}_{ST}}$ | (7) |
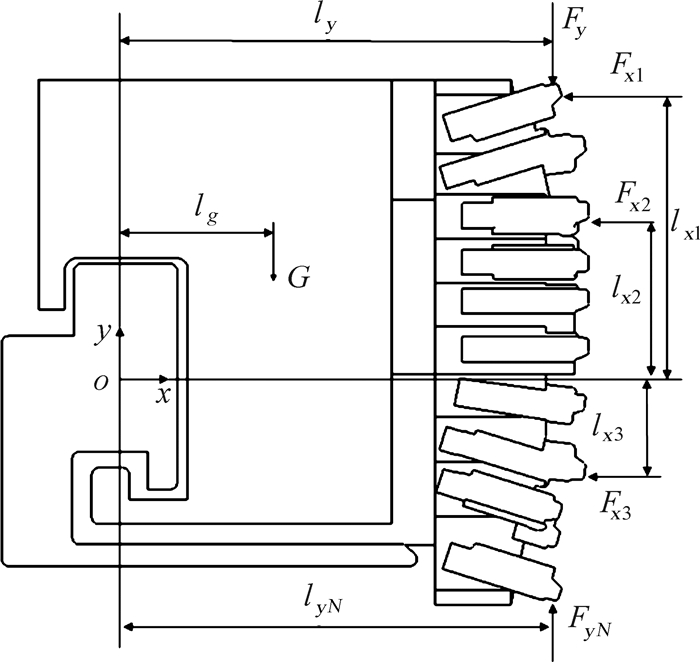
图 2为刨头受力简图,以滑架中心处为坐标原点,设坐标系为xoy,建立刨头摆动与上下、左右移动耦合的三自由度运动方程:
|
| 图 2 刨头受力模型 Fig. 2 Force model of coal plow |
| $\begin{align} & \dot{I}\dot{\theta }={{F}_{x1}}{{l}_{x1}}+{{F}_{x2}}{{l}_{x2}}+{{F}_{yN}}{{l}_{yN}}- \\ & {{F}_{x3}}{{l}_{x3}}-{{F}_{y}}{{l}_{y}}-G{{l}_{g}}+T,\\ & m\ddot{x}=-{{F}_{x1}}-{{F}_{x2}}-{{F}_{x3}}+{{Q}_{1}},\\ & m\ddot{y}=-G-{{F}_{y}}+{{F}_{yN}}+{{Q}_{2}} \\ \end{align}$ | (8) |
其中:I为刨头的转动惯量;m为刨头的质量;Fx1为顶刀进刀阻力的合力,Fx2为腰刀与掏腰刀的进刀阻力的合力,Fx3为底刀进刀阻力的合力;FyN为底刀侧向阻力的合力,Fy为顶刀侧向阻力的合力;G为刨头自身的重力;T为在竖直与水平方向碰撞力对刨头扭矩;lg为重力G的力臂;lx1,lx2,lx3为Fx1,Fx2,Fx3的力臂;ly为Fy的力臂,lyN为FyN的力臂;Q1为碰撞力在水平方向分力,Q2为碰撞力在竖直方向分力.
通过(3)、(4)式以及(6)、(7)式对各点碰撞状态进行逐一判断.式(8)中刨煤机各位置刨刀刨煤的动态载荷采用文献[14]方法进行模拟,选取BH30/2-160型刨刀,刨刀宽度b=30 mm,刀尖角β=50°,后角α=15°,刨削深度为70 mm,煤层硬度A=250 N/cm,则各位置刨刀动载荷统计值如表 1所示.
| 刨刀位置 | 统计值 | 进刀阻力/N | 侧向阻力/N |
| 腰刀 | 最大值 | 2 758.717 | 2 053.441 |
| 最小值 | 434.447 | 503.479 | |
| 平均值 | 1 446.482 | 1 353.479 | |
| 变异系数 | 0.516 7 | 0.340 0 | |
| 掏腰刀 | 最大值 | 4 291.8 | 2 347.887 |
| 最小值 | 1 008.912 | 488.614 | |
| 平均值 | 2 462.186 | 1 524.575 | |
| 变异系数 | 0.545 8 | 0.342 2 | |
| 顶刀 | 最大值 | 6 822.217 | 2 543.213 |
| 最小值 | 1 790.362 | 855.873 | |
| 平均值 | 4 366.812 | 1 723.878 | |
| 变异系数 | 0.558 3 | 0.344 2 | |
| 底刀 | 最大值 | 6 099.161 | 3 244.316 |
| 最小值 | 287.946 | 573.54 | |
| 平均值 | 3 193.553 | 1 989.092 | |
| 变异系数 | 0.562 3 | 0.350 1 |
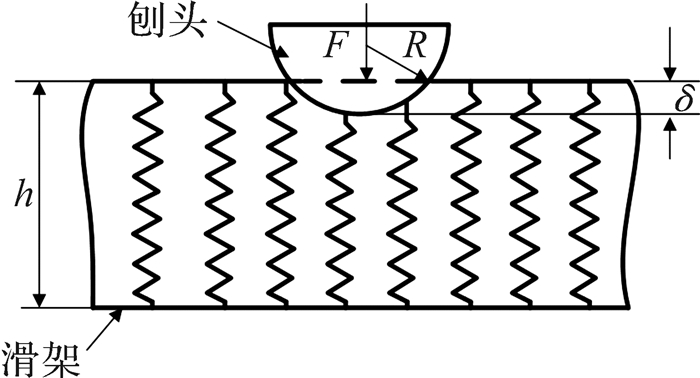
对接触碰撞力的模型描述,本文采用Winkler地基模型[15],即考虑间隙节点局部变形,将法向接触力表示为穿透量δ的函数接触点法向相对速度函数,其表达式为
| ${{Q}_{m}}=K{{\delta }^{\frac{3}{2}}}+C\dot{\delta },m=1,2$ | (9) |
|
| 图 3 弹塑性接触变形模型 Fig. 3 Elastic-plastic contact deformation model |
式中:K为等效刚度系数,$K=\frac{4}{3\pi \left( {{h}_{1}}+{{h}_{2}} \right)}{{\left( \frac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}-{{R}_{2}}} \right)}^{\frac{1}{2}}}$,${{h}_{i}}=\frac{1-v_{i}^{2}}{\pi {{E}_{i}}}\left( i=1,2 \right)$,R1和R2分别为2个质体接触点的曲率半径,vi为泊松比,Ei为杨氏模量;C为碰撞过程的阻尼系数,$C=\frac{3K\left( 1-c_{e}^{2} \right){{\delta }^{n}}}{4{{{\dot{\delta }}}^{-}}}$,ce2为恢复系数,${{{\dot{\delta }}}^{-}}$为撞击点的初始相对速度.
3 数值模拟分析本文以某种刨头的结构参数为例进行数值求解.m=2 430 kg,I=1 265 kg·m2,lRQ=0.27 m,lQT=0.33 m,lrq=0.29 m,lqr=0.36 m,lST=0.11 m,lst=0.13 m,lmr=lnsr=0.1 m,lx1=0.72 m,lx2=0.415 m,lx3=0.01 m,ly=lyN=0.615 m,lg=0.255 m.
采用数值分析方法对刨头动力学微分方程进行求解.图 4为刨头质心相对滑架质心运动的时域图.从图中可知,刨头相对滑架的运动限制在间隙带范围内.由于刨头与滑架产生了碰撞,刨头质心摆角幅值及刨头质心水平、竖直移动量出现了不同程度的振荡.而竖直振动受重力影响,其反向振动大于正向振动幅度.

|
| 图 4 刨头相对滑架运动时域图 Fig. 4 Time domain chart of relative motion of sliding framework and coal plow |
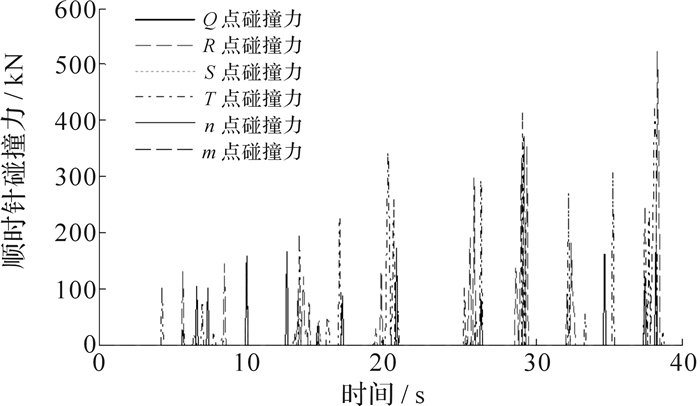
图5、图6为刨头与滑架的顺时针与逆时针碰撞力.从图中可知,刨头与滑架各点产生了不同程度的间断碰撞.当刨头逆时针摆动时,最大的碰撞力产生在Q点;当刨头顺时针摆动时,最大碰撞力为R点.表 2为刨头在不同摆动形式下与滑架产生碰撞的最大力.

|
| 图 5 刨头与滑架逆时针碰撞力 Fig. 5 Anti-clockwise collision force between plow head and sliding framework |
|
| 图 6 刨头与滑架顺时针碰撞力 Fig. 6 Clockwise collision force between plow head and sliding framework |
| 摆动形式 | 碰撞点 | 最大碰撞力/kN |
| 逆时针摆动 | Q | 880 |
| R | 150 | |
| S | 420 | |
| T | 95 | |
| m | 26 | |
| n | 0 | |
| 顺时针摆动 | Q | 182 |
| R | 524 | |
| S | 14 | |
| T | 402 | |
| m | 0 | |
| n | 25 |
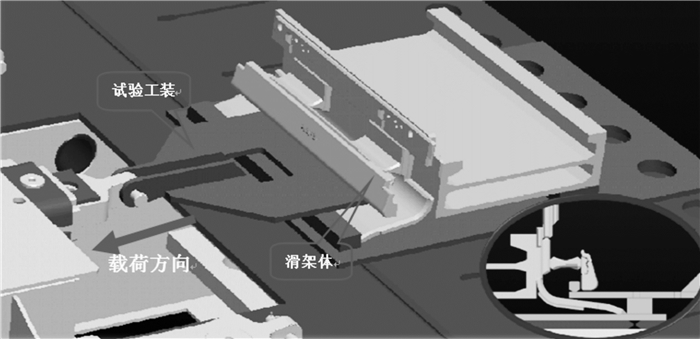
基于以上分析,对中部槽滑架体进行疲劳试验,试验方案如图 7所示.
|
| 图 7 中部槽滑架体疲劳试验方案图 Fig. 7 Fatigue test program of middle trough sliding framework |
将试验工装与中部槽进行装配,启动试验台,使工装中的拉伸组件钩住滑架体导向板.通过对刨头滑架碰撞分析可知,作用在导向板S处的最大碰撞力为420 kN,以此作为滑架体疲劳寿命试验载荷.反复加载(保压5 s),直到滑架体发生疲劳失效.中板上方有1个采集点,编号为1#,下方布置了3个应力采集点,编号分别为2#,3#,4#,进行采集,如图 8所示.

|
| 图 8 现场试验 Fig. 8 Field test |
疲劳试验第1架滑架体在420 kN(保压5 s)的脉动循环载荷下,疲劳寿命为4 425次,在3 200次时,在立板前端产生初始裂纹,并最终在此位置发生疲劳断裂,在发生疲劳断裂后的下一次载荷循环时,立板后端失效.
为验证测试结果,在疲劳试验中重新测试了4次循环载荷过程中各关注点的应力值,结果表明:1,2点的测试结果较为准确;4点接近屈服极限;但3点依然失准,3点测试结果不足为据.而从趋势来看,4点的应力值要大于其他各测试点,因此在发生静强度失效时,失效点倾向于立板后部下端.
5 结论通过数值分析方法对建立的刨煤机刨头碰撞动力学方程进行求解.同时,基于刨头与滑架的碰撞力,对中部槽滑架体进行了疲劳寿命试验.分析表明:1)当刨头相对滑架逆时针摆动时,最大的碰撞力产生在Q点;当顺时针摆动时,最大碰撞力为R点.2)滑架体在立板前端产生初始裂纹,并最终在此位置发生疲劳断裂,在发生疲劳断裂后的下一次载荷循环时,在立板后端产生断裂.
| [1] |
赵丽娟,孙中刚,李国平.刨煤机牵引块可靠性分析及疲劳寿命预测[J].煤炭学报,2012,37 (3):516-520. ZHAO LI-juan,SUN Zhong-gang,LI Guo-ping.Plow traction block reliability analysis and fatigue life prediction[J].Journal of China Coal Society,2012,37 (3):516-520. |
| Cited By in Cnki (15) | Click to display the text | |
| [2] |
赵丽娟,刘旭南,张建军,等.刨煤机刨链回转接头的可靠性[J].机械设计与研究,2013,29 (3):118-122. ZHAO Li-juan,LIU Xu-nan,ZHANG Jian-jun,et al.Reliability analysis of plow chain swivel joint based on virtual prototyping[M].Machine Design and Research,2013,29 (3):118-122. |
| Cited By in Cnki (5) | Click to display the text | |
| [3] |
赵丽娟,马联伟,刘旭南,等.难刨煤层刨刀可靠性与疲劳寿命研究[J].机械设计,2013,30 (4):85-88. ZHAO Li-juan,MA Lian-wei,LIU Xu-nan,et al.Plow bit reliability and fatigue life analysis in hard cutting seam[J].Journal of Machine Design,2013,30 (4):85-88. |
| Cited By in Cnki (5) | Click to display the text | |
| [4] |
康晓敏,李贵轩.随机动载荷作用下刨煤机刨链疲劳寿命预测[J].煤炭学报,2010,35 (3):503-507. KANG Xiao-min,LI Gui-xuan.Prediction of fatigue life of coa1 plow chain under stochastic dynamic load[J].Journal of China coal Society,2010,35 (3):503-507. |
| Cited By in Cnki (30) | Click to display the text | |
| [5] |
康晓敏,李贵轩.刨煤机刨头的稳定性分析[J].中国机械工程,2012,23 (22):2739-2742. KANG Xiao-min,LI Gui-xuan.Stability analysis of plow body of coal plow[J].China Mechanical Engineering,2012,23 (22):2739-2742. |
| Cited By in Cnki (2) | Click to display the text | |
| [6] |
卢绪祥,刘正强,黄树红,等.含间隙碰撞振动系统的非线性振动特性[J].动力工程学报,2012,32 (5):388-393. LU Xu-xiang,LIU Zheng-qiang,HUANG Shu-hong,et al.Nonlinear vibration characteristics of a vibro-impact system with clearance[J].Journal of Chinese Society of Power Engineering,2012,32 (5):388-393. |
| Cited By in Cnki (13) | Click to display the text | |
| [7] | PASHAH S,MASSENZIO M,JACQUELIN E. Prediction of structural response for low velocity impact[J].International Journal of Impact Engineering,2008,35(2):119-132. |
| Click to display the text | |
| [8] | BAPAT C N.The general motion of an inclined impact damper with friction[J].Journal of Sound Vibration,1995,184(11):417-427. |
| Click to display the text | |
| [9] | AHN Kil-young,RYU Bong-jo.A modeling of impact dynamics and its application to impact force prediction[J].Journal of Mechanical Science and Technology,2005,19(1):422-428. |
| Click to display the text | |
| [10] | FLORES P,AMBROSIO J,CLARO J C P,et al.Influence of the contact impact force model on the dynamic response of multibody systems [J].Proceedings of the Institution of Mechanical Engineers,Part K:Journal of Multi-body Dynamics,2006,220(1):21-34. |
| Click to display the text | |
| [11] | GERASIMOV S A.Vibration-impact dynamics [J].Russian Engineering Research,2013,33(3):130-132. |
| Click to display the text | |
| [12] | PAULO Flores,JORGE Ambrósio.On the contact detection for contact-impact analysis in multibody systems[J].Multibody System Dynamics,2010,24(1):103-122. |
| Click to display the text | |
| [13] | FLORES P J,AMBROSIO J C,PIMENTA Claro.Contact-impact force models for mechanical systems[J].Kinematics and Dynamics of Multibody Systems with Imperfect Joints,2008,12(34):47-66. |
| [14] |
李晓豁,付伟丽,张飞虎,等.刨头上不同位置刨刀的随机载荷模拟研究[J].微计算机信息,2011,27 (12):24-26. LI Xiao-huo,FU Wei-li,ZHANG Fei-hu,et al.Simulation and study of random loads on plow tools at different locations of plough head[J].Microcomputer Information,2011,27(12):24-26. |
| Cited By in Cnki (4) | Click to display the text | |
| [15] |
刘中华,尹晓春.钝圆头质量对简支梁的多次弹塑性撞击[J].爆炸与冲击,2010,30(2):138-144. LIU Zhong-hua,YIN Xiao-chun.Multiple elastic-plastic impacts of a simple supported beam struck by around-nosed mass[J].Explosion and Shock Waves,2010,30(2):138-144. |
| Cited By in Cnki (10) | Click to display the text |



