2. 上海量维信息科技有限公司, 上海 200233
2. Multiangle Virtual Technology Incorporation, Shanghai 200233, China
篦齿封严结构安装在高低压动静转子之间,利用独特的几何形状形成一个曲折通道,增大流体流动阻力与能量耗散,从而阻隔高低压腔间的流体泄露[1]。由于结构简单、维护方便并且封严特性好,它被广泛应用在航空发动机内流腔室间的气体封严系统中。
涡轮盘的封严篦齿在巨大的热-机械载荷交变作用下,很容易在结构强度最为薄弱的篦齿齿尖处出现疲劳裂纹[2]。在周向拉伸应力的驱动下,篦齿齿尖萌生的微观裂纹将持续扩展到篦齿根部并沿篦齿连接段向涡轮盘体方向发展,形成半穿透或穿透性裂纹。此外,短时燃烧室局部排气温度过高、燃气倒灌、封严篦齿与封严环间可能产生的碰磨,都大大增加了涡轮盘篦齿裂纹故障的危害性。据外场不完全统计,大约3%的某机I级涡轮盘由于篦齿裂纹故障在达到使用寿命之前报废[3];据某厂故检原始资料,在翻修的918台次某乙型发动机中,有154台次出现涡轮盘封严篦齿裂纹,故障率为16.78%[4]。不仅在经济上造成巨大损失,涡轮盘篦齿裂纹所引发的频繁检修与盘件更换也严重影响到了飞机的出勤率。
国内围绕着涡轮盘篦齿裂纹问题开展了很多研究,通过残余应力测量、疲劳试验、断裂力学估算以及断口分析等多种技术手段,对封严篦齿裂纹的故障起因与特征进行了归纳与分析,并为防止危害性结果的发生给出了许多指导性的建议[3, 4, 5, 6, 7]。
限于计算力学发展水平,以往对篦齿裂纹故障的研究比较缺乏精确定量的数值模拟,因而无法详细考察裂纹前沿的应力强度因子分布与裂纹扩展规律,在确定临界裂纹长度与结构剩余寿命时缺乏理论依据,并且难以制定出兼顾经济性与安全性的检修周期。
本文使用有限元软件ANSYS 13.0与三维裂纹扩展分析软件FRANC3D 6.0对涡轮盘篦齿裂纹扩展进行直接数值模拟。首先采用子模型法建立了含篦齿裂纹的涡轮盘有限元模型,使用M积分[8, 9]计算裂纹前沿的应力强度因子;在确定篦齿裂纹前沿每一节点处的局部扩展方向与扩展距离后,通过样条曲线拟合出新裂纹前沿,并依靠自适应网格划分[10]实现裂纹区有限元网格的更新;得出篦齿裂纹前沿的历史轨迹后,在应力强度因子计算结果的基础上,对扩展速率模型进行积分得到篦齿裂纹扩展寿命[11]。
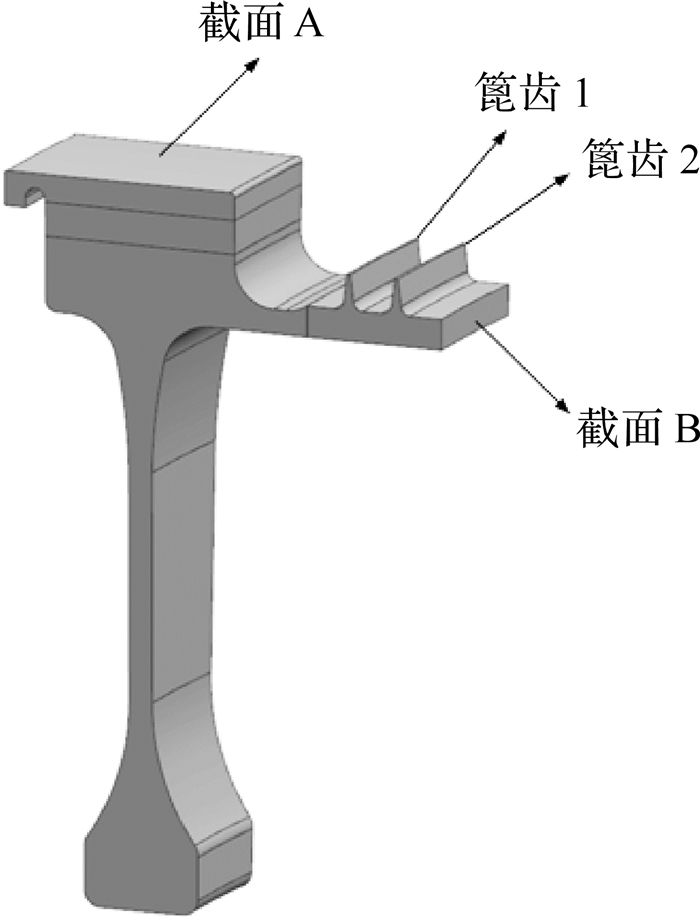
1 篦齿涡轮盘的应力分析某篦齿涡轮盘的实体模型如图 1所示,依次将其上的两个篦齿记为篦齿1与篦齿2。轮盘材料采用变形高温合金,对应的有限元模型如图 2所示,采用SOLID186单元进行离散,单元总数329954。有限元模型包含篦齿涡轮盘0°~360°的完整回转体,而没有采用只对一个扇区进行建模的周期对称方法。其原因在于,如果采用周期对称,在1/N扇区的轮盘模型上插入的一条篦齿裂纹,等效于涡轮盘上沿周向均布着N条大小、形状完全相同的篦齿裂纹,涡轮盘由此转化为包含裂纹间相互干涉作用的多裂纹结构。为从有限元数值模拟中突出涡轮盘篦齿裂纹扩展的主要特征,本文对裂纹出现的条数进行了简化,仅考虑含单一篦齿裂纹的涡轮盘结构。为了便于后续的裂纹区子模型的建立,在网格划分时对即将插入裂纹的位置进行了局部网格加密处理。
|
| 图 1 篦齿涡轮盘的实体模型 Fig. 1 Solid model of a turbine disc with labyrinth seal |

|
| 图 2 篦齿涡轮盘的有限元模型 Fig. 2 Finite element model of a turbine disc with labyrinth seal |
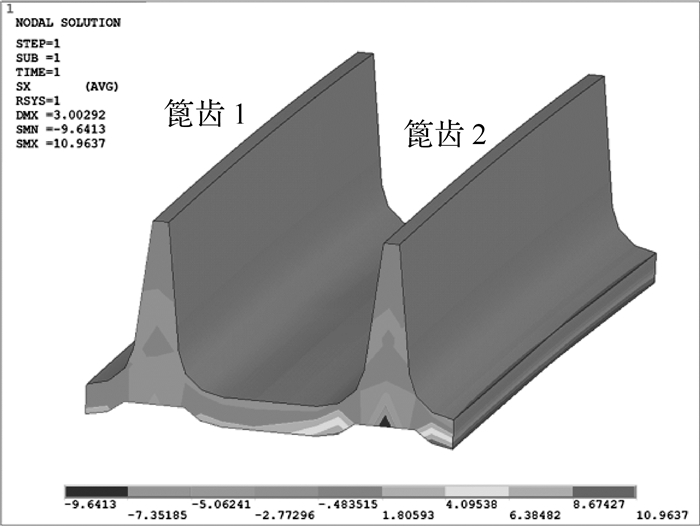
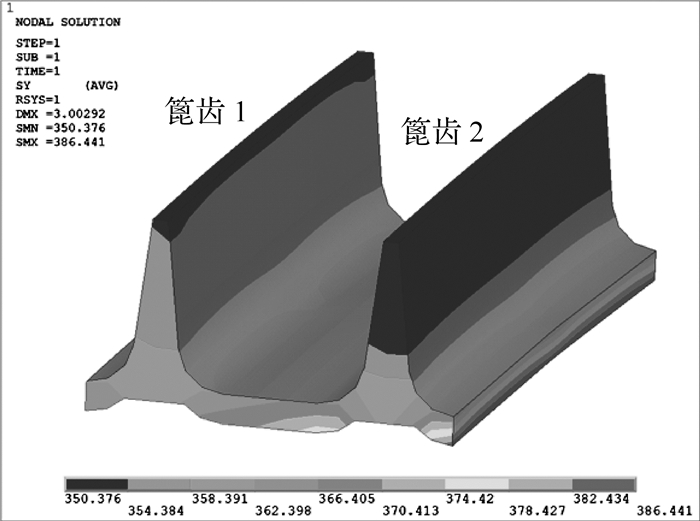
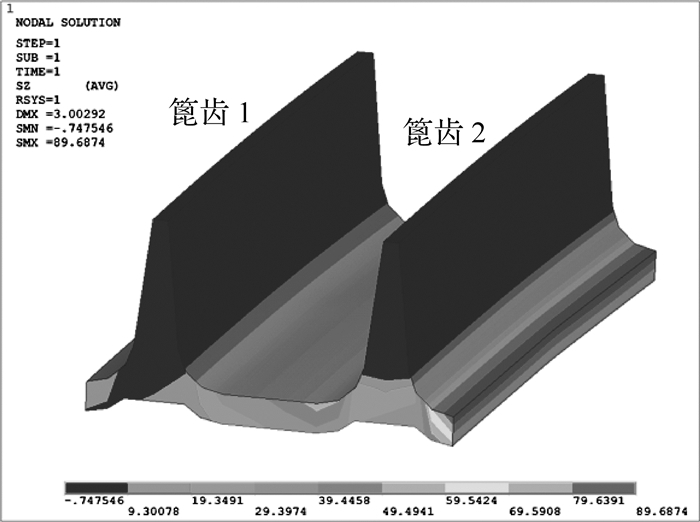
以高温起飞为计算工况,在篦齿涡轮盘有限元模型上施加对应的转速与温度场,将叶片质量产生的离心载荷转换为等效的径向面载荷施加在图 1中的截面A上,将涡轮转子轴对称分析得出的轴向位移与径向位移施加在图 1中的截面B上,取自网格加密区域的径向、周向、轴向应力云图如图 3(a)、3(b)、3(c)所示,分布范围分别为-9.6~10.9MPa,350.3~386.4MPa,-0.7~89.6MPa,可见该区域以周向拉伸应力为主导。
|
| 图 3 篦齿区域的有限元应力分析结果 Fig. 3 The stress results of finite element analysis in the vicinity of labyrinth seal |
篦齿齿尖厚度通常仅为几百微米,在周向拉伸应力与温度载荷的周期性作用下,很容易萌生微小裂纹,裂纹面往往与周向拉伸应力相垂直形成最为危险的I型裂纹,在交变载荷作用下继续向齿根方向扩展。
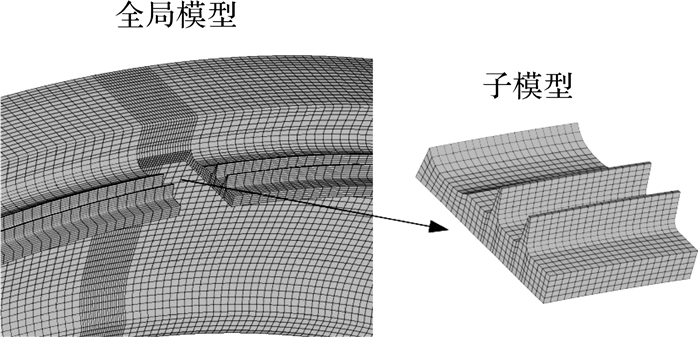
2 含篦齿裂纹有限元模型的建立为了适应裂纹区网格动态更新的需要,并同时对模型整体的计算规模加以控制,采用子模型法建立含篦齿裂纹的涡轮盘有限元模型[12]。将篦齿裂纹在扩展过程中可能影响到的轮盘体积取出作为子模型,剩余的绝大部分轮盘体积作为全局模型,如图 4所示。
|
| 图 4 篦齿涡轮盘有限元网格中的子模型与全局模型 Fig. 4 Submodel and global model for the finite element mesh of a turbine disc with labyrinth seal |
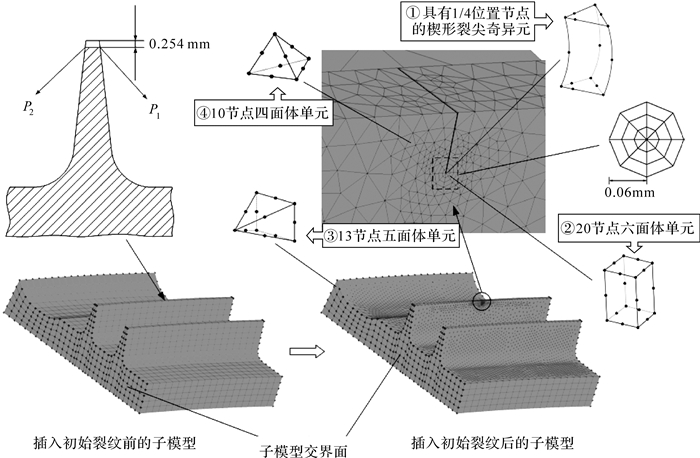
篦齿1的周向拉伸应力水平高于篦齿2,因此选择在篦齿1的齿尖插入初始裂纹。根据故障检测经验[3, 4, 5],假设初始裂纹为贯穿齿尖厚度的穿透型裂纹,初始裂纹深度为0.254mm,如图 5所示。在插入初始裂纹后,采用自适应网格划分对子模型网格进行更新:①裂纹前沿被一圈楔形奇异单元所包围,该单元在裂尖相邻两边上的中间节点被移动到1/4边长位置,以反映裂纹尖端应力的奇异性[13];②裂尖奇异元包裹在两层六面体单元围成的管道内,以保证裂纹前沿区域应力计算的精确性;③全局模型与子模型交界面上的节点保持不变,在子模型交界面内侧生成一层五面体单元,实现自由网格向映射网格的过渡;④在子模型其他区域采用四面体自由网格进行填充,以保证裂纹区网格对复杂几何形状的适应性。
|
| 图 5 初始篦齿裂纹插入前后的子模型与裂纹区的自适应网格划分 Fig. 5 Submodels with and without initial crack and self-adapting mesh generation in the vicinity of the crack |
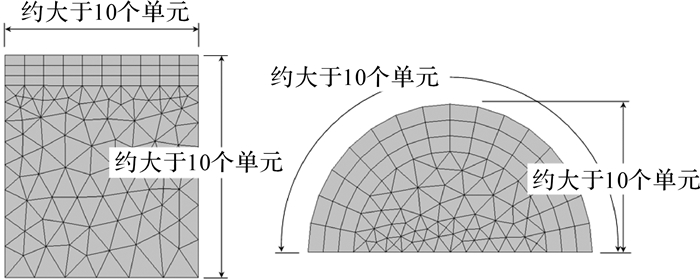
含裂纹有限元模型在建模过程中,裂纹前沿的网格尺寸及密度是一项十分重要的考量因素。经验法则认为,为确保有限元计算结果的精确性,裂纹区域的单元尺寸至少要10倍小于裂纹面的几何特征尺寸[14]:①对于穿透性裂纹,裂纹面宽度与长度均应保持10个单元以上的网格密度;②对于表面裂纹,裂纹面在半径方向及周长方向也需要保持10个单元以上的网格密度,如图 6所示。经测试发现,对于深度0.254mm的初始裂纹,裂尖奇异元与两层六面体单元围成的管道半径控制在0.06mm,围绕管道的周向布置8个单元(见图 5中的虚线框出部分) 即可满足上述经验法则。在随后每一步的扩展计算中,都需要根据当前裂纹面的几何尺寸对管道半径进行调整,在满足网格密度需求的同时对单元总数加以控制。
|
| 图 6 裂纹区域网格尺寸及密度的经验法则 Fig. 6 Experience rules for element size and density in crack region |
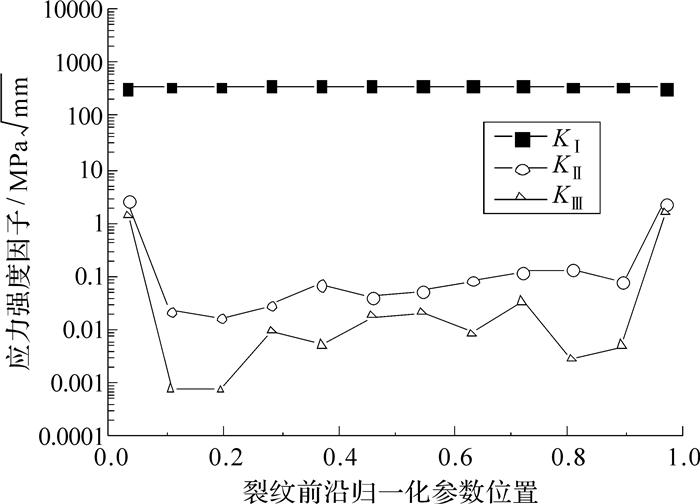
根据含篦齿裂纹有限元模型的位移计算结果,使用M积分法计算初始裂纹前沿的应力强度因子KⅠ、KⅡ、KⅢ(对应Ⅰ型、Ⅱ型、Ⅲ型裂纹) ,结果如图 7所示。沿篦齿裂纹前沿的KⅠ远大于KⅡ及KⅢ,这与周向拉伸应力占主导的应力计算结果吻合;KI沿裂纹前沿变化不大,处于中部的大部分长度上数值基本保持恒定,约375 MPa$\sqrt {mm} $;在篦齿裂纹与外部自由表面的两个交点P1、P2附近(见图 5,篦齿1齿尖靠近篦齿2的一侧交点记为P1,对应图 7中横坐标为0的位置) ,KI有一定的降低,交点P1、P2附近的裂纹扩展速率将因此低于中部区域,裂纹前沿将从初始的直线逐步过渡到一条中部下凹两端上翘的曲线。
|
| 图 7 初始情况下篦齿裂纹前沿的应力强度因子分布 Fig. 7 The distributions of the stress intensity factors along the initial crack of the labyrinth seal disc |
方案阶段选取0-Max-0三角转速谱,将初始的篦齿裂纹前沿记为C0,根据C0各节点处的应力强度因子可以通过扩展操作得出新裂纹前沿C1,过程如下:
1) 根据C0前沿KⅠ、KⅡ、KⅢ的M积分结果,使用最大环向拉伸应力准则[15]计算C0每一节点处的裂纹局部扩展方向;
2)确定扩展步长Δa(m)(Δa(m)为裂纹前沿“中位节点”处的扩展距离,该节点处的应力强度因子为裂纹前沿的中位数,本文C0前沿对应的Δa(m)取0.038 mm,后续扩展过程将逐步增大Δa(m)的数值),然后根据Δa(m)的取值,利用Paris公式推算出C0前沿其他节点处的扩展距离;
3) 根据C0前沿各节点处的扩展方向与扩展距离,得到C1前沿的离散预测结果,然后采用三次样条曲线进行拟合,得到经过光顺化处理的C1前沿;
4) 围绕C1前沿生成一圈楔形奇异元并在外部裹以2层六面体单元,在子模型交界面内侧生成1层五面体单元并在子模型其他区域填充四面体自由网格,完成裂纹区网格的更新,同时全局模型保持不变;
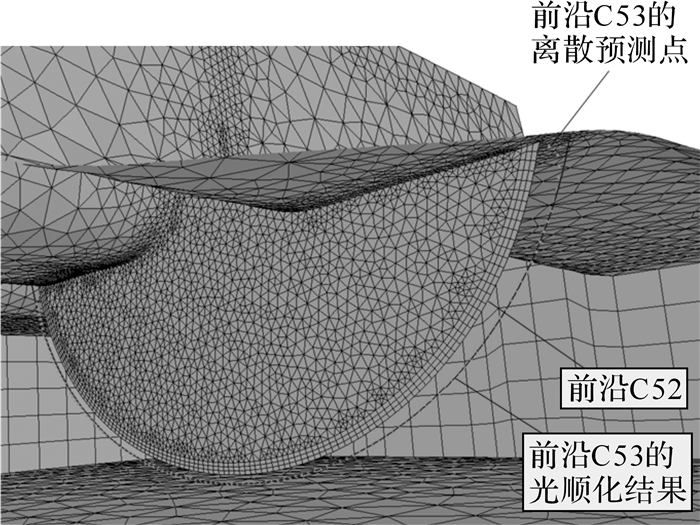
重复上述步骤依次得到C2、C3、C4、…,直至裂纹即将穿透篦齿环为止,共经历53步扩展,其中C52向C53的扩展如图 8所示。C0至C53描述了扩展过程中篦齿裂纹前沿变化的历史轨迹,如图 9所示。
|
| 图 8 篦齿裂纹前沿C52向前沿C53的扩展 Fig. 8 The extension from crack front C52 to crack front C53 for the crack of the labyrinth seal disc |
|
| 图 9 C0~C53所描述的篦齿裂纹前沿变化历史轨迹 Fig. 9 The history tracks for the variations of the crack fronts of the labyrinth seal disc represented by C0~C53 |
需要指出,上述步骤中所提到的裂纹扩展步长并非裂纹每一循环的扩展量。整个分析过程中裂纹扩展步的数量,以及其中每一步的步长值,都需要根据所研究问题的实际情况具体指定。过大的扩展步长一方面可能导致不精确的结果,另一方面也有可能使预测出的裂纹前沿出现不稳定的变化(因为未能精确捕捉到扩展过程中裂纹前沿载荷重新分布的过程) ;过小的扩展步长同样应该避免,因为它一方面会导致过多的扩展步数与过大的计算开销,另一方面还有可能导致网格划分困难。
第i步的扩展步长Δa(m),i有2种确定方法.
第1种是指定第i个扩展步内所经历的循环次数,即
| $\Delta {{a}_{(m),i}}=\Delta {{N}_{i}}\times {{\left( \frac{\text{d}a}{\text{d}N} \right)}_{(m),i}}$ | (1) |
其中:(da/dN)(m),i是中位节点的当前裂纹扩展速率;ΔNi是第i步所经历的载荷循环数,需由人工指定.由于裂纹扩展速率与裂纹尺寸间高度的非线性关系,往往需要通过“trial-and-error”的方式获得使Δa(m),i大小合适的ΔNi.
确定Δa(m),i的另一种方法是,以一个裂纹当前的几何特征尺寸为参照,以该尺寸的一定百分比作为Δa(m),i的数值.本文采用篦齿在涡轮盘半径方向上的深度作为特征尺寸,初始时取其数值的15%作为扩展步长.初始裂纹前沿C0的深度为0.254 mm,则与其对应的Δa(m)=0.254 mm×15%≈0.038 mm.根据笔者的经验,该比例取在5%~15%时,可以避免裂纹前沿出现不稳定的变化,同时将计算开销控制在合理范围内.一般来说,由于初始裂纹尺寸往往十分微小,这时宜采用相对较大的比例;随着裂纹在扩展过程中尺寸的不断增大,该比例可以视情况酌情采用较小的数值.影响扩展步长比例的并非单纯只有裂纹几何方面的因素,由于裂纹区域网格划分的复杂性,某一扩展步长比例可能会导致网格划分失败或网格高度畸形,这时也需要对比例数值作出适当调整.
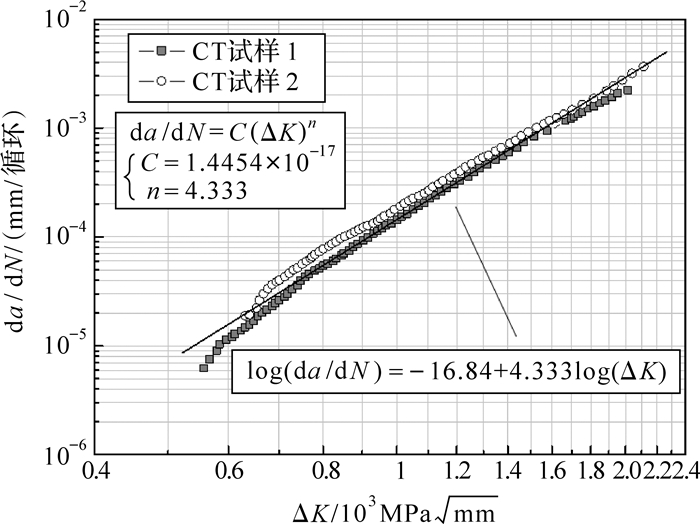
篦齿涡轮盘材料为某国产变形高温合金,根据文献[16]中基于标准CT试样的裂纹扩展速率试验结果(图 10) ,在篦齿1高温起飞时的工作温度下,其材料的裂纹扩展速率da/dN与应力强度因子变程ΔK在双对数坐标系下可以用线性关系进行近似,拟合方程见式(2),拟合优度为0.984 2,转化为Paris幂函数表达式后得出的材料常数C=1.445 4×10-17,n=4.333,采用的单位制为:长度,mm;应力强度因子,MPa$\sqrt {mm} $;裂纹扩展速率,mm/循环.
|
| 图 10 根据裂纹扩展速率试验得出的Paris模型 Fig. 10 Paris model based on the crack growth rate test |
| $\log (\text{d}a/\text{d}N)=-16.84+4.333\log (\Delta K)$ | (2) |
在裂纹扩展模拟过程中,Paris公式的意义不仅仅在于通过积分得出裂纹扩展寿命,它还影响着每一个扩展步中,裂纹前沿不同节点之间扩展距离的相对大小。设j、k是当前裂纹前沿两个不同的节点,两处的应力强度因子变程分别为ΔK(j),ΔK(k),若施加在当前裂纹扩展步的载荷循环数为ΔN,则根据Paris公式可得出该扩展步中节点j、k各自的扩展距离为
| $\Delta {{a}_{(j)}}=\Delta N\cdot C\cdot {{(\Delta {{K}_{(j)}})}^{n}}$ | (3) |
| $\Delta {{a}_{(k)}}=\Delta N\cdot C\cdot {{(\Delta {{K}_{(k)}})}^{n}}$ | (4) |
式(3)与式(4)左右两边分别相除,消去相同的因子,可得
| $\frac{\Delta {{a}_{(j)}}}{\Delta {{a}_{(k)}}}={{\left( \frac{\Delta {{K}_{(j)}}}{\Delta {{K}_{(k)}}} \right)}^{n}}或\Delta {{a}_{(k)}}=\Delta {{a}_{(j)}}\cdot {{\left( \frac{\Delta {{K}_{(k)}}}{\Delta {{K}_{(j)}}} \right)}^{n}}$ | (5) |
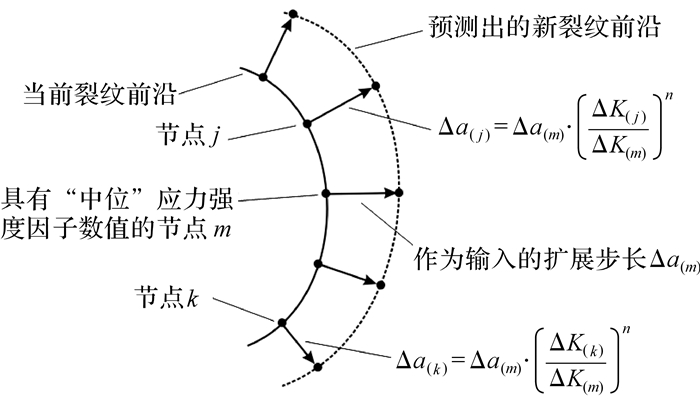
由此可见,Δa(j)与Δa(k)之比不仅取决于裂纹前沿的应力强度因子分布,还取决于Paris公式中的材料常数n.本文以当前裂纹前沿“中位节点”的扩展距离Δa(m)为输入,根据式(5)计算出其他各节点处的扩展距离,进而预测扩展步结束后的新裂纹前沿,如图 11所示。
|
| 图 11 以扩展步长为输入预测新裂纹前沿 Fig. 11 Prediction of new crack front taking as input |
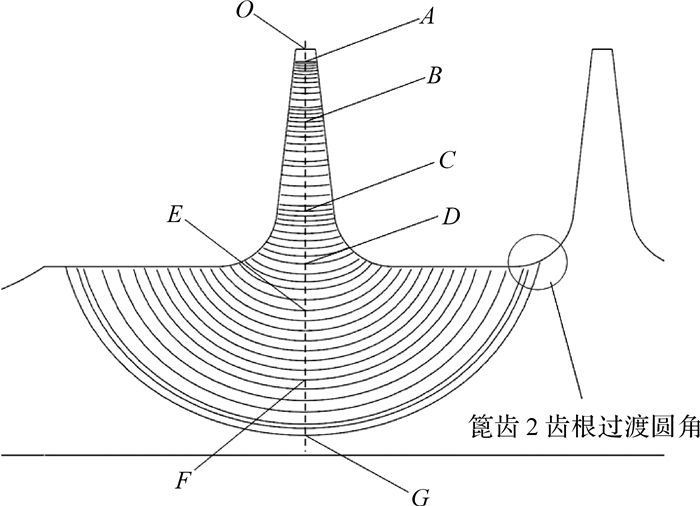
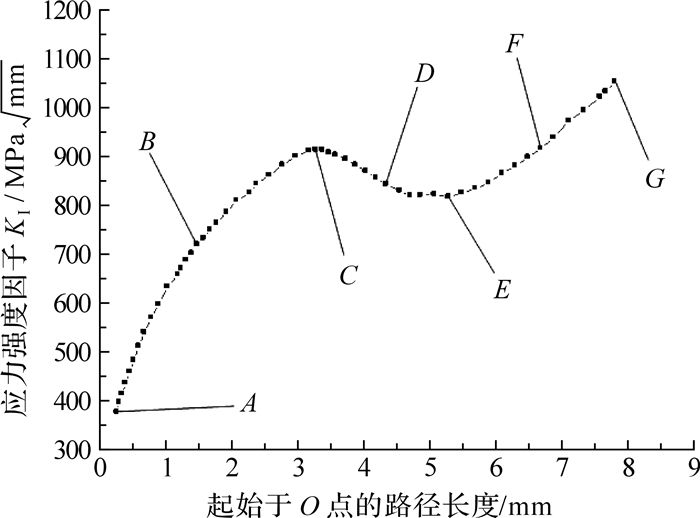
由于初始裂纹的裂纹面与占主导的周向拉伸应力相垂直,后续的裂纹扩展基本保持在一个径向平面内进行,该径向平面经过发动机的旋转轴线。将篦齿1的对称面与图 9所示径向平面的交线作为扩展寿命的计算路径(图 9中的虚线) ,该路径上的应力强度因子KⅠ随路径长度的变化曲线如图 12所示,路径长度的起点取在篦齿1齿尖上端面的O点(图 9) ,A点的路径长度等于初始裂纹深度,为0.254mm。
根据图 12中KⅠ曲线的转折变化,从中提取A、B、…、G共7个特征点,并在图 9中依次标出它们在裂纹前沿轨迹上的对应位置,可以看出:①A-B-C是篦齿裂纹从齿尖沿径向扩展直至达到齿根的过程,在该过程中,KⅠ随裂纹扩展逐步增大;②C-D-E是篦齿裂纹逐步穿透齿根过渡圆角的过程,在该过程中,篦齿裂纹由穿透型裂纹转变为表面裂纹,过渡圆角致使裂纹在扩展过程中遇到结构厚度的迅速增加,因此C-D-E阶段KⅠ随裂纹扩展有逐步减小的趋势;③E-F-G是篦齿裂纹转变为表面裂纹后的扩展过程,该阶段KⅠ随裂纹扩展逐步增大。
由图 12拟合出KⅠ与路径长度间的函数关系,然后沿计算路径对裂纹扩展速率模型(Pairs公式) 进行积分,得出路径长度随载荷循环数的变化曲线,如图 13所示,图中标出了A、B、…、G各点的对应位置以及所经历的载荷循环数,可以看出:①篦齿裂纹扩展的全过程(从A到G) 共经历20953cycles;②篦齿裂纹从齿尖沿径向扩展直至达到齿根的A-B-C阶段经历15414cycles,占总寿命的73.6%;③篦齿裂纹穿透齿根过渡圆角的C-D-E过程经历2687cycles,占总寿命的12.8%;④篦齿裂纹转变为表面裂纹后的扩展过程E-F-G经历2852 cycles,占总寿命的13.6%。
|
| 图 12 计算路径上KI随路径长度的变化曲线 Fig. 12 The variation curve of KI versus path length along the path |
|
| 图 13 路径长度随载荷循环数的变化曲线 Fig. 13 The variation of path length versus load cycle numbers |
对图 13中的曲线进行微分,可以得出路径长度增长速率随载荷循环数的变化曲线,以此衡量各阶段篦齿裂纹扩展的快慢,如图 14所示。从中可以看出:①篦齿裂纹从齿尖沿径向扩展直至达到齿根的A-B-C阶段,裂纹扩展处于不断加速的状态;②由于过渡圆角引起的结构厚度增加,C-D-E阶段的裂纹扩展速度有所减缓;③在篦齿裂纹完全转化为表面裂纹的E-F-G阶段,裂纹扩展速度首先很快地增大到最高点,然后出现一定的下降,这是因为在E-F-G的后半段,裂纹前沿的扩张开始受到来自于相邻篦齿过渡圆角的约束作用,如图 9所示。
|
| 图 14 路径长度增长速率随载荷循环数的变化曲线 Fig. 14 The variation curve of path length growth rate versus load cycle numbers |
前面的裂纹扩展计算中采用了如图 10所示的Paris公式作为裂纹扩展速率模型,图 10中150个试验点ΔK的变动范围是558.7~2 117.6 MPa$\sqrt{mm}$;而结合图 9与图 12中可以看出,篦齿裂纹扩展的全过程(从A到G)计算路径上KⅠ的变动范围是376.8~1 054.6 MPa$\sqrt{mm}$,由此可见,图 10中Paris公式的适用范围并不能保证覆盖篦齿裂纹扩展的全过程,因为初始篦齿裂纹C0之后0.3~0.4 mm的扩展是在扩展速率试验的ΔK范围之外进行的.
由于试验数据的缺乏,目前无法确定C0之后0.3~0.4 mm的扩展是否依然符合Paris公式,因此需对寿命计算结果的误差进行分析.在双对数坐标系中,裂纹扩展速率da/dN随ΔK的完整变化关系曲线近似呈反“S”形[17, 18],分为初始稳定扩展区、线性稳定扩展区(Paris区)以及快速扩展区[13];在初始稳定扩展区da/dN-ΔK曲线存在一个垂直渐近线ΔK=ΔKth,ΔKth通常称裂纹扩展门槛值.
对于所研究的篦齿盘材料,由文献[16]中的扩展速率试验数据只能估算出初始稳定扩展区与Paris区的分界点ΔK*≤558.7 MPa$\sqrt {mm} $;如果ΔK*的实际值小于等于376.8 MPa$\sqrt {mm} $,则Paris公式可以覆盖篦齿裂纹扩展的全过程,包括C0之后0.3~0.4 mm的扩展;如果ΔK*的实际值在376.8~558.7 MPa$\sqrt {mm} $之间,则ΔK < ΔK*时的裂纹扩展将不再服从Paris公式,此时da/dN-ΔK曲线位于Paris直线的下方,依然使用Paris公式等效于高估裂纹扩展速率,在这种情况下对于图 9中A-B段,基于Paris公式将得出偏于保守的寿命计算结果(也就是说ΔK*>376.8MPa$\sqrt {mm} $会致使A-B段实际经历的载荷循环数高于图 13中给出的12610循环).
5 结论根据应力强度因子以及裂纹扩展速率的变化,可以将篦齿裂纹的扩展过程分为三个阶段:穿透型裂纹扩展阶段(A-B-C) 、穿透型裂纹向表面裂纹的转化阶段(C-D-E) 、以及表面裂纹扩展阶段(E-F-G) 。A-B-C是篦齿裂纹从齿尖沿径向扩展直至达到齿根的过程,应力强度因子KⅠ随裂纹扩展逐步增大,裂纹扩展处于不断加速的状态;C-D-E是篦齿裂纹逐步穿透齿根过渡圆角的过程,KⅠ随裂纹扩展有逐步减小的趋势,裂纹扩展速度有所减缓;E-F-G是篦齿裂纹转变为表面裂纹后的扩展过程,KⅠ随裂纹扩展逐步增大,裂纹扩展速度首先增大到最高点,然后在相邻篦齿的约束作用下扩展速度出现一定下降。
A-B-C与C-D-E-F-G的路径长度比为1:1.5,扩展寿命比为3:1,所以裂纹扩展速度之比为1:4.5,这说明篦齿裂纹前沿在达到齿根过渡圆角后平均扩展速度会大大增加,所以我们建议以齿根过渡圆角顶部(图 9中的C点) 为分界,将篦齿裂纹扩展分为缓慢扩展阶段(A-B-C) 与快速扩展阶段(C-D-E-F-G) 。
缓慢扩展的A-B-C阶段,应力强度因子与裂纹扩展速度均处于较低水平,裂纹扩展局限于齿根以上区域,裂纹在发动机旋转时产生的不平衡力较小,并且能够承受相当数量的载荷循环(本例中为15414 cycles) ,所以涡轮盘即使在检修中发现了尚未扩展至齿根的篦齿裂纹,也不必立即做更换处理,但需在裂纹进入齿根以下的快速扩展阶段之前采取措施处理。
由于文献[16]中裂纹扩展速率试验的ΔK范围有限,因此对寿命计算结果可能出现的误差进行了分析:①若ΔK*≤376.8 MPa$\sqrt {mm} $,则可全程使用Paris公式进行裂纹扩展寿命计算;②若ΔK*>376.8 MPa$\sqrt {mm} $,则使用Paris公式会在篦齿裂纹扩展的起始阶段高估裂纹扩展速率,从而得出偏于保守的寿命计算结果.为了获得更精确的篦齿裂纹扩展寿命,有必要进一步补充ΔKth < ΔK < ΔK*区域内的裂纹扩展速率试验.
由本文分析结果还可以得出两条有关篦齿结构设计的参考性建议:①适当增大篦齿齿根部的过渡圆角半径有助于延缓篦齿裂纹从穿透型裂纹向表面裂纹的转化;②适当减小篦齿的排列间距,可以利用相邻篦齿齿根对裂纹后期的快速扩展起一定约束作用。
现阶段我们对于涡轮盘篦齿裂纹扩展的研究侧重于理论方法与数值模拟,随着研制工作的不断深入,后续将安排相关试验,其目的一方面是对数值模拟的结果进行验证并加以必要的修正,另一方面是结合数值模拟与试验结果建立一套行之有效的涡轮盘篦齿损伤容限设计方法。
| [1] |
黄彬彬.航空发动机篦齿封严特性数值模拟研究[D].北京:北京交通大学机械与电子控制工程学院,2014:2-9. HUANG Bin-bin.Numerical simulation of leakage character of aero-engine labyrinth seals [D].Beijing:Beijing Jiaotong University,School of Mechanical, Electronic & Control Engineering,2014:2-9. |
| Cited By in Cnki (1) | Click to display the text | |
| [2] |
陶春虎,钟培道,王仁智,等.航空发动机转动部件的失效分析与预防[M].北京:国防工业出版社,2000:138-147. TAO Chun-hu,ZHONG Pei-dao,WANG Ren-zhi,et al.Failure analysis and prevention for rotor in aero-engine [M].Beijing:National Defense Industry Press,2000:138-147. |
| [3] |
龚梦贤,王卫国,古远兴,等.某发动机I级涡轮盘篦齿裂纹故障分析[J].燃气涡轮试验与研究,1999,12(4):34-39. GONG Meng-xian,WANG Wei-guo,GU Yuan-xing,et al.Failure analysis of sealing labyrinth crack for the first stage turbine disc in an aero-engine [J].Gas Turbine Experiment and Research,1999,12(4):34-39. |
| Cited By in Cnki (3) | Click to display the text | |
| [4] |
唐光辉.某乙型发动机Ⅰ级涡轮盘封严篦齿裂纹故障分析及维修措施[J].航空发动机,1995,21(4):50-58. TANG Guang-hui.Failure analysis and maintenance measures of sealing labyrinth crack for the first stage turbine disc in a type-B areo-engine [J].Aeroengine,1995,21(4):50-58. |
| Cited By in Cnki (4) | Click to display the text | |
| [5] |
李运菊,孙智军.某发动机高压Ⅱ级涡轮盘封严篦齿裂纹分析[J].失效分析与预防,2006,1(3):27-30. LI Yun-ju,SUN Zhi-jun.Crack analysis of sealing labyrinth on high-pressure turbine disc Ⅱ in an aero-engine [J].Failure Analysis and Prevention,2006,1(3):27-30. |
| Cited By in Cnki (1) | Click to display the text | |
| [6] |
田武刚,潘孟春,罗飞路,等.某型航空发动机篦齿盘裂纹的原位涡流检测[J].测试技术学报,2008,22(3):241-244. TIAN Wu-gang,PAN Meng-chun,LUO Fei-lu,et al.In situ eddy current testing for the cracks in an aeroengine labyrinth disc [J].Journal of Test and Measurement Technology,2008,22(3):241-244. |
| Cited By in Cnki (6) | Click to display the text | |
| [7] |
卓正敏,李文闯.涡轮盘篦齿补焊工艺研究[J].金属加工(热加工),2013(2):74-75. ZHUO Zheng-ming,LI Wen-chuang.Research of repair welding technology for the sealing labyrinth in a turbine disc [J].Machinist Metal Forming,2013(2):74-75. |
| Cited By in Cnki (1) | Click to display the text | |
| [8] | YAU J F,WANG S S,CORTEN H T.A mixed-mode crack analysis of isotropic solids using conservation laws of elasticity [J].Journal of Applied Mechanics,1980,47(2):335-341. |
| Click to display the text | |
| [9] | WAWRZYNEK P A,CARTER B J,BANKS-SILLS L.The M-integral for computing stress intensity factors in generally anisotropic materials:NASA/CR-2005-214006[R].Alabama:Marshall Space Flight Center,2005. |
| [10] | HOMBAL V K,MAHADEVAN S.Surrogate modeling of 3D crack growth [J].International Journal of Fatigue,2013,47(1):90-99. |
| Click to display the text | |
| [11] | WAWRZYNEK P A,CARTER B J,INGRAFFEA A R.Advances in simulation of arbitrary 3D crack growth using FRANC3D/NG[C]// Proceedings of the 12th International Conference on Fracture.Ottawa,Jul.12-17,2009. |
| [12] | CARTER B J,SCHENCK E C,WAWRZYNEK P A,et al.Three-dimensional simulation of fretting crack nucleation and growth [J].Engineering Fracture Mechanics,2012,96(1):447-460. |
| Click to display the text | |
| [13] |
郦正能,关志东,张纪奎,等.应用断裂力学[M].北京:北京航空航天大学出版社,2012:64-73. LI Zheng-neng,GUAN Zhi-dong,ZHANG Ji-kui,et al.Application fracture mechanics [M].Beijing:Beihang University Press,2012:64-73. |
| [14] | FAC. FRANC3D reference manual[EB/OL]. (2012-05-08)[2015-07-15]. http://www.franc3d.com/wp-content/uploads/2012/05/FRANC3D_V7_Reference.pdf. |
| Click to display the text | |
| [15] | BUCZEK M B,HERAKOVICH C T.A normal stress criterion for crack extension direction in orthotropic composite materials [J].Journal of Composite Materials,1985,19(6):544-553. |
| Click to display the text | |
| [16] |
航空发动机设计用材料数据手册编委会.航空发动机设计用材料数据手册(第3册)[M].北京:航空工业出版社,2008:166-170. The Editorial Board of Material Data Handbook for Design of Aero-engines.Material data handbook for design of aero-engines (Volume 3) [M].Beijing:Aviation Industry Press,2008:166-170. |
| [17] |
赵志平,李有堂,党延祖.金属材料疲劳设计及裂纹扩展规律研究与应用[J].石油矿场机械,2010,39(9):38-41. ZHAO Zhi-ping,LI You-tang,DANG Yan-zu.Study and application on fatigue crack propagation law and design of metal material [J].Oil Field Equipment,2010,39(9):38-41. |
| Cited By in Cnki (11) | Click to display the text | |
| [18] |
倪向贵,李新亮,王秀喜.疲劳裂纹扩展规律Paris公式的一般修正及应用[J].压力容器,2006,23(12):8-15. NI Xiang-gui,LI Xin-liang,WANG Xiu-xi.General modification and application of the Paris law for fatigue crack propagation [J].Pressure Vessel Technology,2006,23(12):8-15. |
| Cited By in Cnki (58) | Click to display the text |


