2. 西南石油大学 油气藏地质及开发工程国家重点实验室, 四川 成都 610500;
3. 西北工业大学 工业设计研究所, 陕西 西安 710072
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China;
3. Institute of Industrial Design, Northwestern Polytechnical University, Xi'an 710072, China
对于布局问题的研究开始于1831年,高斯(Gauss)展开了“格(Lattice)”的研究[1].布局设计是将待布物体布置在给定的布局空间中,满足设定的约束条件,并以实现面积利用率、成本、性能等某种或多种指标最优为目标[2].布局设计问题涉及生产和生活中的许多领域,具有较广的工程应用背景,例如装箱问题(bin packing problem)、下料问题(strip packing problem)、切断问题(cutting stock problem)[3]、办公室布局设计[4]、厂房布局设计[5]和设备布局[6]等等.布局问题按照维数,分为二维布局和三维布局;按照待布物体的形状,分为规则物体布局和不规则物体布局;按照约束情况,分为无性能约束布局和带性能约束布局[7].
目前求解布局问题的思路一般是先将上述实际工程问题简化为数学模型,然后通过计算机算法求解.例如,文献[8, 9, 10]就卫星舱布局设计提出了人机合作的免疫算法、蚁群算法、遗传算法等,获得了工程满意解和较为优越的计算效率.文献[11, 12]建立了载人潜水器舱室布局优化数学模型,提出了基于Pareto的PGA进行多目标优化计算;提出了使用人工鱼群算法求解深潜舱室人员布局优化问题.文献[13]利用蚁群算法进行了主控台布局优化设计.文献[14]提出了基于模拟退火算法的核电站控制室操纵器排列优化方法.文献[15]建立了船舶舱室布局优化数学模型,利用改进的遗传算法实现了舱室内待布置物的自动布局.
可见,对于布局问题的不同应用领域,需要采用不同的方法求解.上述算法在不同应用领域所收到的效果是不同的,因此需要根据司钻控制室的特点,设计出适合的布局求解算法.司钻控制室布局设计是指将显示装置、操纵装置合理地布置在显示和控制面板上,满足布局空间的约束和人的认知特性的要求,符合人机工效设计准则.在进行操纵器布局设计时,应该从工业设计的角度出发,充分考虑人的生理和心理特性,从而使得操作姿势更为舒适.目前的布局研究多集中在提高空间利用率,这种传统的布局优化目标难以保证人体操作的舒适性.因此,本文将从认知心理学角度出发研究人的认知特性,将布局原则融合到优化目标函数中,运用遗传-蚁群算法实现司钻控制室操纵器布局的智能化.
1 布局问题描述与布局优化方法概述 1.1 布局问题描述布局设计的过程是通过数学模型描述布局问题的约束和求解目标,将形式化的描述转变为具体的数据描述.司钻控制室布局问题的基本要素包括布局空间、待布物体、约束条件和求解目标.
1)布局空间和待布物体.
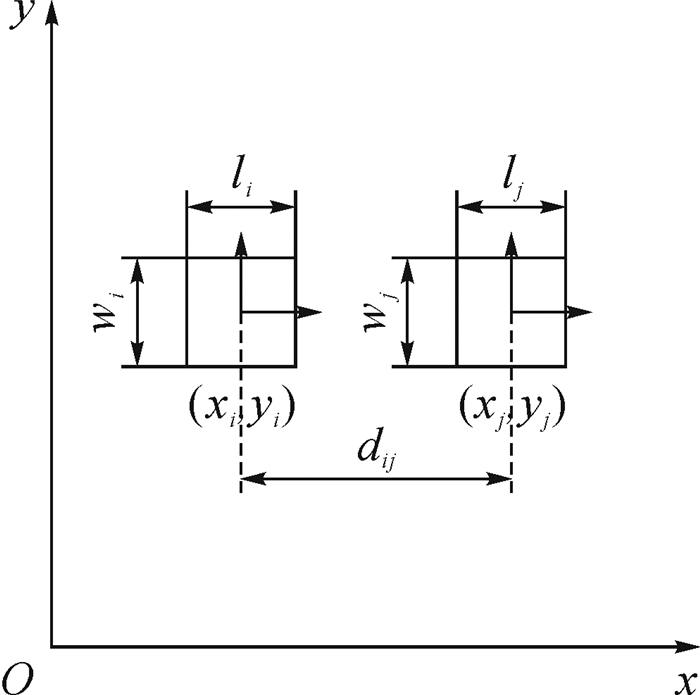
将司钻控制室布局设计简化为二维布局问题处理,在二维面板上进行显示器、操纵器的布局优化.将布局空间和待布物体简化为矩形、圆形等简单几何形体.布局示意简图如图 1所示.L代表面板总长度,W代表面板总宽度.设有n个待布物体,li和wi分别代表待布物体i的长和宽,(xi,yi)代表待布物体i在面板上的坐标值.待布物体i和待布物体j之间的距离可通过下式计算:
|
| 图 1 布局示意简图 Fig. 1 The schematic diagram of layout |
| ${{d}_{ij}}=\sqrt{{{\left( {{x}_{i}}-{{x}_{j}} \right)}^{2}}+{{\left( {{y}_{i}}-{{y}_{j}} \right)}^{2}}}$ | (1) |
2)约束条件和求解目标.
从组合优化角度来看,显示器、操纵器位置布局优化设计即是寻求待布物体的最优位置组合,在满足布局约束情况下实现多目标相对最优.本文将待布物体序列变量X作为优化设计变量,各布局位置序号所属位置布置一个待布物体,布局位置序号和待布物体序号一一对应.由待布物体序号形成一个布局方案,待布物体序列X表达为:
| $\begin{gathered} X = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}, \hfill \\ \left\{ \begin{gathered} {x_k} = \left\{ {x|x \in {N^ + },1 \leqslant x \leqslant n} \right\}, \hfill \\ {x_i} \ne {x_j}\left( {i,j = 1,2, \cdots ,n;i \ne j} \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ |
式中xk为该位置对应的待布物体序号.
将符合认知特性的布局原则用数学模型描述成Pi,i=1,2,…,m,m代表布局原则数目.在布局模型的建立过程中,以符合布局原则最大化为模型的优化设计目标,同时保证待布物体在布局过程中不发生干涉.求解目标通常是多目标的,其表达式表示如下:
| $\max f\left( x \right)=\max \sum\limits_{i=1}^{m}{{{\delta }_{i}}{{P}_{i}}}$ | (2) |
| $\begin{gathered} \left\{ \begin{gathered} \frac{{{l_i} + {l_j}}}{2} - \left| {{x_j} - {x_i}} \right| \leqslant 0, \hfill \\ \frac{{{\omega _i} + {\omega _j}}}{2} - \left| {{y_j} - {y_i}} \right| \leqslant 0. \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} {x_j} + \frac{{{l_j}}}{2} - L \leqslant 0, \hfill \\ {y_j} + \frac{{{\omega _j}}}{2} - W \leqslant 0. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ |
式中δi为各布局原则权重.
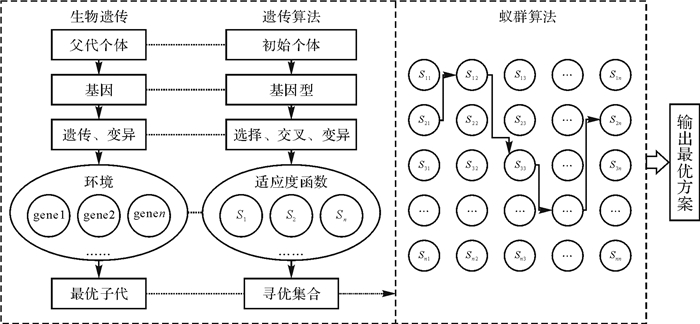
1.2 布局优化方法概述从分析人的思维过程入手,充分考虑人的生理和心理特性,根据认知工效总结布局设计原则.在此基础上,采用智能优化算法求解组合最优问题,利用遗传算法和蚁群算法的各自优势,构建基于遗传-蚁群算法的司钻控制室操纵器布局设计模型.求解思路如图 2所示:首先,利用遗传算法的随机性、快速性和全局收敛性,生成若干个司钻控制室操纵器布局方案初始解,将其转化为初始信息素轨迹强度分布;然后,采用蚁群算法对布局方案进行再次优化,利用蚁群算法的并行性、正反馈机制等特性,提高求解效率.
|
| 图 2 司钻控制室操纵器布局优化流程 Fig. 2 The layout optimization process of manipulators of driller control room |
以人的思维特性为基础,运用人的信息组织、视觉搜索和记忆特性等规律,使得司钻控制室操纵器布局符合操作者对界面信息的认知能力.总结司钻控制室操纵器布局设计涉及的一些认知规律,并将其转化为布局的指导原则.
1)认知和客观相符合(即按功能分区排列).
如果采用符合操作者习惯的处理方式,使得布局与操作者的经验和知识背景一致,可以减少学习和记忆时间,避免失误的发生.如:将具有相似功能的操纵器布置在同一区域,当需要使用该区域中的某一操纵器时,操作者会以自动的方式搜索到该熟悉区域,从而找到该操纵器.
2)任务流设计(即按操作顺序布置).
任务流设计即操作流程设计,通过设计操纵顺序流程,使操作者的工作量减小,工作效率提高.针对操作者需要完成的任务,分析其中的主要操作过程,然后根据操作者的认知习惯合并、减少以及规划操作动作,从而减轻操作者的认知负荷和认知时间.既要加快信息处理速度,又要提高操作者信息处理的质量.
3)与操作者的认知策略相匹配(即按重要性和操作频率布置).
由于人的认知具有动态特性,布局方案很难适应各类操作者的动态认知差异.应该根据操作者知识水平、认知能力和使用习惯,通过判断不同层次操作者的认知策略来进行布局设计,实现对操作者的认知过程动态适应.如:根据记忆特性,将重要的、观察与操纵频繁的显示和操纵器布置于便于观察和舒适操纵的范围之内,能够减轻操作者的短期记忆负担,有利于在直觉、模板和推理层之间合理分配认知负荷,避免造成遗忘、记忆错误等后果.
4)符合信息组织规律(即成组相关排列).
视觉的组织特性是指在视野中离散的刺激可以由于它们彼此之间的某种关系组织到一起而形成一个整体的视觉[16].可利用视觉组织的相似性原则、邻近性原则和封闭性原则指导布局设计.如:当大量操纵器需要布置时,可利用邻近性原则将相关的操纵器靠近排布或者利用相似性原则将相关的操纵器用相同颜色表示,从而形成整体感,让操作者可以快速搜索到.
2.2 布局优化目标函数司钻控制室操纵器布局设计的目标是:在给定的空间范围内,实现给定待布物体的最优排列,即搜索出最符合布局原则的布局方案.以司钻控制室操纵器布局为例,分别针对各布局原则构建布局优化数学模型和目标函数.
1)操作顺序原则.
在操作过程中,如果操纵器在操作程序上有顺序,按其顺序进行布局设计.操作顺序矩阵可以表示为
| $t=\left[{{t}_{ij}} \right]=\left| \begin{align} & {{t}_{11}}{{t}_{12}}\cdots {{t}_{1g}} \\ & {{t}_{21}}{{t}_{22}}\cdots {{t}_{2g}} \\ & \text{ }\vdots \text{ }\vdots \text{ }\vdots \\ & {{t}_{m1}}{{t}_{m2}}\cdots {{t}_{mg}} \\ \end{align} \right|$ |
式中:m为操纵器个数;g为工况数;tij为操纵器i在工况j下的操作顺序.
操作顺序原则的数学模型描述为
| $\begin{align} & {{T}_{i}}=\sum\limits_{j=1}^{g}{\left| \frac{{{t}_{ij}}}{\sum\limits_{i=1}^{m}{{{t}_{ij}}}}{{W}_{Ti}} \right|} \\ & \left( i=1,2,\cdots ,m;j=1,2,\cdots ,g \right) \\ \end{align}$ | (3) |
式中WTi为操纵器i的权重.
2)重要性和操作频率原则.
将重要的、操纵频繁的操纵器布置在操作者的最佳控制区域,如紧急制动等按钮.
不同操纵器的重要程度通过重要度矩阵表达为
| $I=\left[{{I}_{ij}} \right]=\left| \begin{align} & {{I}_{11}}{{I}_{12}}\cdots {{I}_{1r}} \\ & {{I}_{21}}{{I}_{22}}\cdots {{I}_{2r}} \\ & \text{ }\vdots \text{ }\vdots \text{ }\vdots \\ & {{I}_{m1}}{{I}_{m2}}\cdots {{I}_{mr}} \\ \end{align} \right|$ |
式中:m为操纵器个数;r为专家人数;Iij为操纵器i经专家j评估的重要度.
重要度由经验丰富的司钻员以及设计、维护司钻控制室的专家来决定.为了降低专家个体差异对评估结果的影响,需要对专家评估确定权重.专家权重矩阵可表示为
| ${W_Z} = {\left[ {{W_{Z1}}{W_{Z2}} \cdots {W_{Zr}}} \right]^T}$ |
考虑专家权重后的操纵器i的重要度可表示为
| ${{Z}_{i}}={{I}_{ij}}{{W}_{Z}}$ | (4) |
不同操纵器的操纵频繁度通过频率矩阵表达为
| $F=\left[{{f}_{ij}} \right]=\left| \begin{align} & {{f}_{11}}{{f}_{12}}\cdots {{f}_{1g}} \\ & {{f}_{21}}{{f}_{22}}\cdots {{f}_{2g}} \\ & \text{ }\vdots \text{ }\vdots \text{ }\vdots \\ & {{f}_{m1}}{{f}_{m2}}\cdots {{f}_{mg}} \\ \end{align} \right|$ |
式中:fij为操纵器i在工况j下的操纵频繁度.
每个工况的权重由其发生的概率决定,表示为
| ${{W}_{C}}={{\left[{{W}_{C1}}{{W}_{C2}}\cdots {{W}_{Cg}} \right]}^{T}}$ |
考虑工况权重后的操纵器i的操作频率可表示为
| ${C_i} = {f_{ij}}{W_C}$ | (5) |
因此,根据公式(4)和(5),重要性和操作频率原则的数学模型可以描述为
| $\left. \begin{align} & {{S}_{i}}=u{{Z}_{i}}+v{{C}_{i}},\\ & u+v=1. \\ \end{align} \right\}$ | (6) |
式中,u和v分别表示重要性与操作频率的权重.
3)相关性原则.
相关性反映了操纵器之间关系的密切程度,关系越密切的操纵器布局距离越靠近.操纵器间的距离根据公式(1)计算.
操纵器的相关性矩阵可以表示为
| $O=\left[{{o}_{ij}} \right]=\left| \begin{align} & {{o}_{11}}{{o}_{12}}\cdots {{o}_{1m}} \\ & {{o}_{21}}{{o}_{22}}\cdots {{o}_{2m}} \\ & \text{ }\vdots \text{ }\vdots \text{ }\vdots \\ & {{o}_{m1}}{{o}_{m2}}\cdots {{o}_{mm}} \\ \end{align} \right|$ |
式中:m为操纵器个数;oij为操纵器i和操纵器j的关联程度.
操纵器i和其余操纵器相关性的数学模型描述为
| ${{O}_{i}}=\sum\limits_{j=i+1}^{m}{\left( {{o}_{ij}}/{{d}_{ij}} \right)}$ | (7) |
4)目标函数.
在既定的待布空间中,便于操纵的位置有限,无法将每个操纵器都布置到最佳位置.因此,在构建目标函数时需要综合考虑上述布局原则,并添加系数进行调控.优化目标是要使得方案解的整体评价值最高,在布局约束条件下使所确定的系统目标函数得到极大值.综合考虑上述布局原则数学模型(3)、(6)、(7)以及根据公式(2),将目标函数定义为
| $\begin{align} & f{{\left( i \right)}_{best}}=\max \left[\sum\limits_{i=1}^{n}{\left( {{\delta }_{1}}\cdot {{T}_{i}}+{{\delta }_{2}}\cdot {{S}_{i}}+{{O}_{i}} \right)} \right],\\ & {{\delta }_{1}}=1-i/n,\\ & {{\delta }_{2}}=1-{{d}_{ik}}/{{d}_{k\max }},\\ \end{align}$ | (8) |
式中:n为待布操纵器;Δ1和Δ2为位置控制系数;dik为操纵器i的位置坐标和最佳布置点k间的距离;dkmax为待布区域中与最佳布置点k的最大距离.
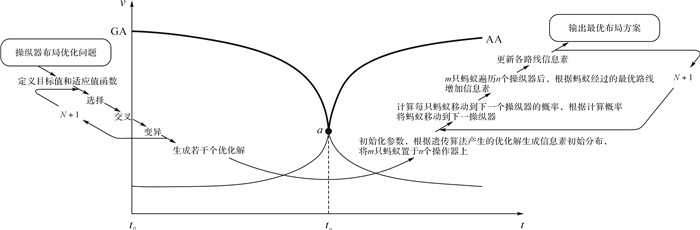
3 遗传-蚁群算法在司钻控制室操纵器布局优化中的应用 3.1 遗传-蚁群算法思想遗传算法和蚁群算法都具有全局搜索、概率随机搜索等优点.但是,遗传算法存在冗余迭代,计算量大导致求解效率低.蚁群算法由于初期信息素缺乏,从而搜索时间长,而且容易出现停滞现象[17].根据对遗传和蚁群算法的研究和实验得出如图 3所示的速度—时间曲线.遗传算法在搜索初期(t0-ta)的收敛速度较快,进化到一定程度时(ta之后),其进化速率大幅下降;相反,蚁群算法在搜索初期(t0-ta)收敛速度非常缓慢,但是当信息素的累积达到一定程度后(ta之后),蚂蚁的搜索活动会呈现一定的规律性,收敛速度迅速提高[18].因此,本文将针对上文构建的布局优化目标函数,利用遗传算法生成布局方案的次优解,并作为蚁群算法所需的初始信息分布,期望通过混合算法获得较好的优化性能和时间性能.
|
| 图 3 遗传-蚁群算法流程 Fig. 3 Genetic-ant colony algorithm process |
采用序列编码的形式对操纵器进行编码,便于进行优化计算.代码串格式如下:
| ${{C}_{m}}=\left[{{c}_{p1}},{{c}_{m2}},{{c}_{m3}},\cdots ,{{c}_{pq}},s \right]$ |
式中:p为染色体数目,即种群大小(布局方案数量);q为操纵器数量;cpq为位于染色体(布局方案)m的第p个位置上的基因(操纵器);s为每排布置操纵器数目.
3.2.2 构造适应度函数操纵器布局问题属于组合优化问题,将每一种排列组合方式作为一个个体,从操纵器的不同排列组合方案中寻求最满足布局原则的布局方案.适应度值是量化群体中个体优劣的唯一指标,决定了个体的生存机会.根据目标函数公式(8)确定适应度函数为
| $ \text{fitness}\left( i \right)=\sum\limits_{i=1}^{n}{\left( {{\delta }_{1}}\cdot {{T}_{i}}+{{\delta }_{2}}\cdot {{S}_{i}}+{{O}_{i}} \right)-\text{Con}}$ |
式中Con为特定的常数值,为目标函数的最小值.
3.2.3 确定进化机制遗传算法求解司钻控制室操纵器布局的流程如图 3左部分所示.从随机产生的初始种群出发,不断重复执行选择、交叉和变异的操作过程,按照优胜劣汰的原则,使种群一代一代地沿着既定的目标方向进化.根据个体的适应度值大小,采用赌轮法从当前种群中选择出优良的个体形成新的种群.采用顺序交叉对父代个体进行交叉操作,互相交换部分基因,从而形成新个体.采用互换变异对个体进行变异操作,保证种群的多样性,防止出现非成熟收敛现象.交叉和变异操作仅在隶属于同一布局区域的操纵器之间进行.
3.2.4 遗传算法与蚁群算法的融合在遗传算法中设置最小进化代数Genmin、最大进化代数Genmax和子代群体最小进化率Genp.然后在遗传算法运行过程中,根据下式统计子代群体的进化率.在设定的进化代数范围内,如果连续Genq代,子代群体的进化率都小于Genp,则终止遗传算法,进入蚁群算法.
| $E{{V}^{k}}=\frac{\sum\limits_{i=1}^{\text{sca}}{\left( f_{i}^{k}-f_{i}^{k-1} \right)/f_{i}^{k-1}}}{\text{sca}},k=2,3,\cdots ,n,$ |
式中:EVk为第k代群体的进化率;sca为种群规模;k为进化代数;fik为第k次迭代中个体i的适应度值.
3.3 蚁群算法求解 3.3.1 优化目标司钻控制室操纵器布局优化求解的目的是搜索出最能综合满足上述布局原则的最优方案,优化目标是得到公式(8)的最大值.而在蚁群系统模型中,每个可行解是由一只蚂蚁走过的路径表示的,也就是要找出一条从操纵器i到操纵器j的最优路径,求解的是最短路径问题.所以,将蚁群算法中的目标函数定义为遗传算法目标函数的倒数:
| $\text{Le}{{\text{n}}_{k}}=\frac{1}{f{{\left( i \right)}_{\text{best}}}}$ |
蚁群算法求解司钻控制室操纵器布局流程如图 3右部分所示.设bi(t)(i=1,2,…,n)是在t时刻操纵器i的蚂蚁数目,$m=\sum\limits_{i=1}^{n}{{{b}_{i}}\left( t \right)}$是全部蚂蚁数目,n是操纵器个数.设tabuk表示蚂蚁k的禁忌表,随着蚂蚁寻优过程作动态调整[19].初始阶段,将m只蚂蚁随机地置于n个操纵器.每一只蚂蚁的禁忌表的第1个元素设置为它所在的第1个操纵器.在每次迭代过程中,每只蚂蚁通过重复地应用状态转移规则选择下一个操纵器,经过n-1次这样的选择,最后产生一组操纵器布局排列.蚂蚁k在t时刻从操纵器i转移到操纵器j的概率为
| $\begin{gathered} \Pr {\text{o}}_{ij}^k\left( t \right) = \left\{ \begin{gathered} \frac{{{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^\alpha }{{\left[ {{\eta _{ij}}} \right]}^\beta }}}{{{\Sigma _{l \in U}}{{\left[ {{\tau _{il}}\left( t \right)} \right]}^\alpha }{{\left[ {{\eta _{il}}} \right]}^\beta }}},j \in U \hfill \\ 0,j \in U. \hfill \\ \end{gathered} \right. \hfill \\ {\eta _{ij}} = 1/{\text{c}}{{\text{w}}_{ij}}, \hfill \\ {\text{c}}{{\text{w}}_{ij}} = \left| {{T_i} - {T_j}} \right| + \left| {{S_i} - {S_j}} \right| + \left| {{O_i} - {O_j}} \right| \hfill \\ \end{gathered} $ |
式中:τij(t)为t时刻操纵器i和操纵器j之间的信息素;ηij为从操纵器i转移到操纵器j的可见度(启发信息);cwij为操纵器i和操纵器j对于布局原则的综合权值的差值;α为τ的相对重要性(α≥0);β为η的相对重要性(β≥0);U为可行点集,即t时刻蚂蚁k所能选择的操纵器的集合.
3.3.3 信息素和启发信息采用比利时学者Thomas提出的最大-最小蚂蚁系统(max-min ant system,MMAS).由于融合了遗传算法,不同于MMAS中信息素轨迹强度初始化为τmax,在初始时刻,信息素初始值设置为
| ${{\tau }_{ij}}\left( 0 \right)={{\tau }_{C}}+{{\tau }_{G}}$ |
式中:τC为信息素常量,等同于MMAS中τmin;τG为遗传算法求解的布局方案转换得到的信息素值.
蚂蚁选择下一个操纵器的依据主要是信息素τij(t)和启发信息ηij.ηij是由所要求解的布局问题给出的,受cwij的影响,但这个量在算法运行中保持不变.蚂蚁在经过的路径上释放信息素,信息素τij(t)是不断变化的.由于过多的残留信息会淹没启发信息,当蚂蚁遍历完所有的操纵器,需要对留存在环境中的信息素进行更新,更新方程为:
| $\begin{gathered} {\tau _{ij}}\left( {t + 1} \right) = \left( {1 - \rho } \right) \cdot {\tau _{ij}}\left( t \right) + \Delta {\tau _{ij}}\left( t \right), \hfill \\ \Delta {\tau _{ij}}\left( t \right) = \sum\limits_{k - 1}^m {\Delta \tau _{ij}^k\left( t \right)} , \hfill \\ \Delta \tau _{ij}^k\left( t \right) = \left\{ \begin{gathered} Q/{\text{Le}}{{\text{n}}_k},蚂蚁k经过操纵器\left( {i,j} \right), \hfill \\ 0, \hfill \\ 否则 \end{gathered} \right. \hfill \\ \end{gathered} $ |
式中:ρ为信息素挥发系数(0≤ρ≤1);Δτijk(t)为蚂蚁k在本次循环中在操纵器i和j之间释放的信息素量;Δτij(t)为本次循环后在操纵器i和j之间信息素的增量;Q代表信息素总量,为常数;Lenk为蚂蚁k在本次循环中所遍历形成的操纵器布局排列对应的目标函数值.
一次循环中只有形成本轮最优布局方案(Lenk值最小)的蚂蚁才进行信息素更新.将每条边上的信息量限制在τmin,τmax范围内[20],超出此范围则被强制设置为τmin或τmax.随着所有蚂蚁完成对操纵器的遍历,信息素不断积累与挥发,直到达到迭代次数或者现有适应度值达到某值为止,蚂蚁构建的最优路径即为最佳布局方案.
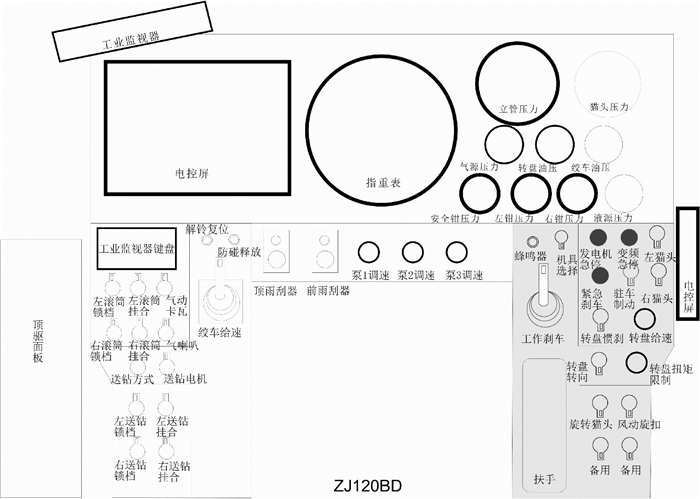
4 应用验证本文以石油钻机司钻控制室操纵器布局设计为例说明方法的实施步骤.对ZJ120/9000DB钻机控制台的16个操纵器进行排列布局,见图 4中的灰色区域.如表 1所示,首先对这16个操纵器进行编码,遵循“按功能分区排列”的布局原则,将具有相似功能的操纵器布置在同一区域,减少操作者搜索时间.
|
| 图 4 ZJ120/9000DB钻机控制台平面布局示意图(优化前) Fig. 4 Layout schematic diagram of ZJ120/9000 DB rig console (before optimizing) |
| 操纵器名称 | 紧急刹车 | 变频急停 | 发电机急停 | 驻车制动 | 转盘惯刹 | 转盘转向 | 转盘给速 | 转盘扭矩限制 | 左猫头 | 右猫头 | 旋转猫头 | 蜂鸣器 | 风动旋扣 | 机具选择 | 备用1 | 备用2 |
| 代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 分区 | 区域1 | 区域2 | 区域3 | 区域4 | ||||||||||||
其次,对布局区域(控制台)和布局物体(操纵器)进行简化处理,构建数学模型,利于设计变量的数学描述.根据人体上肢操作范围确定布局区域,简化为方形布局区域(450 mm×400 mm).操纵器有按钮、旋钮和扳钮.3种类型的操纵器尺寸略有不同,具体尺寸见表 2.操纵器等间距布局,间距是100 mm.简化之后,操纵器布局被当作排序问题处理,使用遗传-蚁群算法找出最优排序,然后根据结果建立实际的布局方案.
| 操纵器类型 | 尺寸 | 操纵器编码 |
| 按钮 | Φ/30 mm | 4,5,6,9,10,11,12,13,14,15,16 |
| 旋钮 | Φ/50 mm | 7,8 |
| 扳钮 | Φ/40 mm | 1,2,3 |
钻井过程主要分为3种工况:手动起钻、手动下钻和正常钻进.综合考虑多工况条件下的操作顺序原则,确定在多工况下各操纵器的操作顺序,并计算出各个操纵器在多工况下的操作顺序权重值Ti(见表 3).通过问卷调查等形式咨询司钻员,确定操纵器的重要性和使用频率的相对比较判断矩阵,采用层次分析法计算出各个操纵器的重要性和使用频率权重值Si.受篇幅限制,省略了权重计算过程,仅给出如表 3所示的计算结果供相关研究者参考.最后确定操纵器的相关性Oi.操纵器和自身的相关性是1,操纵器和其他操纵器之间的相关性用0~1之间的小数表示.操纵器间的关联程度越大,其相关性值越大.16个操纵器的相关性见表 4.
| 操纵器代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Ti | 0.018 | 0.018 | 0.018 | 0.055 | 0.076 | 0.113 | 0.205 | 0.163 | 0.068 | 0.068 | 0.068 | 0.016 | 0.016 | 0.098 | 0 | 0 |
| Si | 0.163 | 0.115 | 0.115 | 0.115 | 0.069 | 0.069 | 0.069 | 0.069 | 0.043 | 0.043 | 0.043 | 0.013 | 0.026 | 0.026 | 0.011 | 0.011 |
| 操纵器代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 1 | 0.7 | 0.5 | 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0.7 | 1 | 0.9 | 0.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0.5 | 0.9 | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0.9 | 0.7 | 0.5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0.9 | 0.5 | 0.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0.9 | 1 | 0.7 | 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0.5 | 0.7 | 1 | 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0.7 | 0.9 | 0.9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.9 | 0.7 | 0.5 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9 | 1 | 0.7 | 0.5 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 0.7 | 1 | 0.5 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 | 1 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.9 | 0.3 | 0.3 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9 | 1 | 0.3 | 0.3 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 1 | 0.9 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 0.9 | 1 |
完成操纵器编码、数学模型简化以及相关数据计算之后,设置遗传-蚁群算法控制参数,运用MATLAB软件进行优化求解.遗传算法控制参数设置为:种群规模sca=50,交叉率pc=0.6,变异率pm=0.2,每行排布待布物s=4个.遗传算法结束条件设置为:最小进化代数Genmin=15,最大进化代数Genmax=50,最小进化率Genp=3%,Genq=3.蚁群算法控制参数设置为:蚁群数目m=10,α=1,β=2,ρ=0.5,Q=500.选取遗传算法终止时种群中最优的10%个体作为次优解集合,将求解结果向信息素值转换.如果在遗传优化解中操纵器i和操纵器j相邻,则路径(i,j)上信息素加10,据此完成信息素初始值设置.当满足以下条件之一,蚁群算法结束:1)进化代数达到antmax=50;2)在进化过程中有连续3代,其子代优化解改进率都小于0.5%.
经过算法优化后的操纵器排列顺序是4,1,2,3,7,8,5,6,12,9,10,11,14,13,15,16.对应的布局方案如图 5所示.为了更加直观地评价布局方案,根据算法求解获得的操纵器位置排序,利用CATIA软件完成司钻控制台建模.借鉴目前国外流行的司钻椅设计和国内生产具体情况,总体设计采用显示台和控制台分开,控制台固定,通过调节座椅满足不同司钻员的操作舒适度要求.控制台前端与显示台间的空间可作为逃生通道.经详细设计后的布局方案效果图如图 6所示.
|
| 图 5 右手控制台布局方案(优化后) Fig. 5 Layout scheme of right console (after optimizing) |
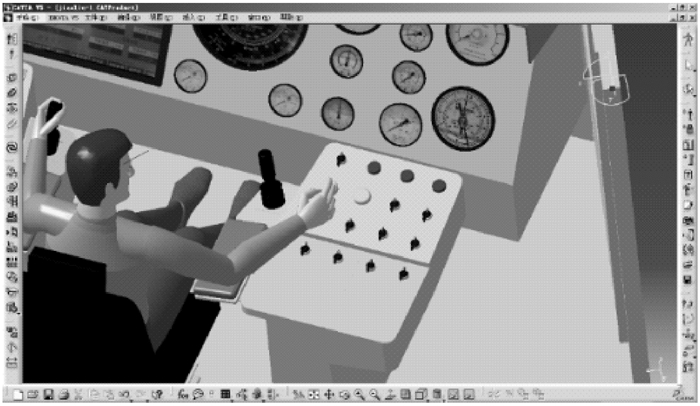
|
| 图 6 布局方案的计算机建模仿真 Fig. 6 Computer modeling and simulation of layout scheme |
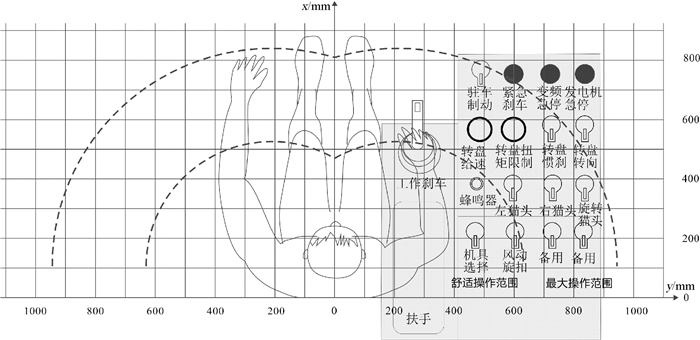
在手臂依托装置外侧的操作区域(见图 4),司钻员在操纵此区域的操纵器时,身体需要扭转一定的角度,同时上臂及肘部向后运动,操作姿态不舒适,因此应不布置或者布置不常使用的操纵器.优化后的布局方案较图 4中的控制台在横向增加了宽度.如图 7所示,利用CATIA软件的人体模型模拟司钻员的操作姿势,分析手臂在自然伸展情况下的可达操作范围.可见,增加宽度后司钻员仍然可以舒适地操作控制台上的主要操纵器,符合人体手臂运动轨迹,后方近身的区域可用于备用或作为桌子使用.
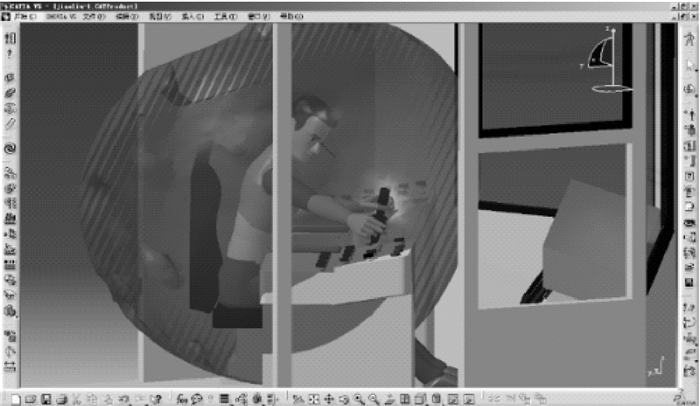
|
| 图 7 右手可达域分析 Fig. 7 The analysis of accessible area of right hand |
在分析人的认知特性规律的基础上,提出了司钻控制室操纵器布局设计原则,并将其融合到目标优化函数中,基于遗传-蚁群算法构建了司钻控制室操纵器智能布局设计模型.利用遗传算法生成次优解并转化为蚁群算法所需的初始信息素分布,将操纵器对于布局原则的综合权值的差值作为蚁群算法的启发信息,利用蚁群算法的正反馈寻优机制进一步求解.本文将司钻控制室操纵器布局方案求解问题转化为组合优化问题,该方法实现了方案求解的人工寻优过程的算法化,具有较强的可操作性,解决了以设计师经验为主进行操纵器几何位置布局时存在主观因素对布局的影响和不确定性问题,提高了设计效率.该方法可推广应用到类似舱室设备的布局优化设计中.但目前所提方法以认知特性为优化目标,仅探索了空间几何约束条件,下一步将研究工艺、结构等性能约束条件,以及三维布局计算的实现.
| [1] | DOWSLAND K A,DOWSLAND W B.Packing problems[J].European Journal of Operational Research,1992,56:2-14. |
| Click to display the text | |
| [2] |
查建中,唐晓君,陆一平.布局及布置设计问题求解自动化的理论与方法综述[J].计算机辅助设计与图形学学报,2002,14(8):705-712. ZHA Jian-zhong,TANG Xiao-jun,LU Yi-ping.Survey on packing problems[J].Journal of Computer-aided Design & Computer Graphics,2002,14(8):705-712. |
| Cited By in Cnki (130) | Click to display the text | |
| [3] | LODI A,MARTELLO S,MONACI M.Two-dimensional packing problems:a survey[J].European Journal of Operational Research,2002,141(2):241-252. |
| Click to display the text | |
| [4] | MARGARITIS S,MARMARAS N.Supporting the design of office layout meeting ergonomics requirements[J].Applied Ergonomics,2007,38(6):781-790. |
| Click to display the text | |
| [5] | SHARIATZADEH N,SIVARD G,CHEN D.Software evaluation criteria for rapid factory layout planning,design and simulation[C].45th CIRP Conference on Manufacturing Systems.Athens,Greece,May 16-18,2012:299-304. |
| [6] |
祝恒云,叶文华.模拟退火粒子群算法在动态单元布局中的应用[J].中国机械工程,2009,20(2):181-185. ZHU Heng-yun,YE Wen-hua.Application of particle swarm algorithm based on simulated annealing in variable cellular facility layout problems[J].China Mechanical Engineering,2009,20(2):181-185. |
| Cited By in Cnki (22) | Click to display the text | |
| [7] |
李广强.布局方案设计中的若干理论、方法及其应用[D].大连:大连理工大学机械工程学院,2003:7-14. LI Guang-qiang.Research on the theory and methods of layout design and their applications[D].Dalian:Dalian University of Technology,School of Mechanical Engineering,2003:7-14. |
| Cited By in Cnki (25) | Click to display the text | |
| [8] |
李广强,赵洪伦,赵凤强,等.人机合作的免疫算法及其在布局设计中的应用[J].计算机工程,2005,31(21):4-6. LI Guang-qiang,ZHAO Hong-lun,ZHAO Feng-qiang,et al.Human-computer cooperative immune algorithm and its application to layout design[J].Computer Engineering,2005,31(21):4-6. |
| Cited By in Cnki (18) | Click to display the text | |
| [9] |
钱志勤,滕弘飞,孙治国.人机交互的遗传算法及其在约束布局优化中的应用[J].计算机学报,2001,24(5):553-559. QIAN Zhi-qin,TENG Hong-fei,SUN Zhi-guo.Human-computer interactive genetic algorithm and its application to constrained layout optimization[J].Chinese Journal of Computers,2001,24(5):553-559. |
| Cited By in Cnki (183) | Click to display the text | |
| [10] |
霍军周,李广强,滕弘飞,等.人机结合蚁群/遗传算法及其在卫星舱布局设计中的应用[J].机械工程学报,2005,41(3):112-116. HUO Jun-zhou,LI Guang-qiang,TENG Hong-fei,et al.Human-computer cooperative ant colony/genetic algorithm for satellite module layout design[J].Journal of Mechanical Engineering,2005,41(3):112-116. |
| Cited By in Cnki (44) | Click to display the text | |
| [11] |
宗立成,叶聪,余隋怀,等.载人潜水器舱室设备智能布局设计方法研究[J].中国造船,2013,54(3):147-154. ZONG Li-cheng,YE Chong,YU Sui-huai,et al.Research and application of intelligent layout method in DSV cabin equipment[J].Shipbuilding of China,2013,54(3):147-154. |
| Cited By in Cnki (4) | Click to display the text | |
| [12] |
宗立成,余隋怀,孙晋博,等.基于鱼群算法的舱室布局优化问题关键技术研究[J].机械科学与技术,2014,33(2):257-262. ZONG Li-cheng,YU Sui-huai,SUN Jin-bo,et al.Study on cabin layout optimization with fish algorithm[J].Mechanical Science and Technology for Aerospace Engineering,2014,33(2):257-262. |
| Cited By in Cnki (2) | Click to display the text | |
| [13] |
范文,余隋怀,王文军,等.蚁群算法求解人机布局优化问题[J].机械科学与技术,2013,32(7):956-961. FAN Wen,YU Sui-huai,WANG Wen-Jun,et al.Ant colony algorithm for human-machine layout optimization[J].Mechanical Science and Technology for Aerospace Engineering,2013,32(7):956-961. |
| Cited By in Cnki (8) | Click to display the text | |
| [14] |
颜声远,陈玉,梁龙远.基于模拟退火算法的操纵器排列优化[J].核动力工程,2014,35(增):67-70. YAN Sheng-yuan,CHEN Yu,LIANG Long-yuan.Optimization of controls layout based on simulated annealing algorithm[J].Nuclear Power Engineering,2014,35(Supplement):67-70. |
| Cited By in Cnki (1) | Click to display the text | |
| [15] |
王运龙,王晨,纪卓尚,等.船舶居住舱室智能布局优化设计方法研究[J].中国造船,2013,54(3):139-146. WANG Yun-long,WANG Chen,JI Zhuo-shang,et al.A study on intelligent layout design of ship cabin[J].Shipbuilding of China,2013,54(3):139-146. |
| Cited By in Cnki (6) | Click to display the text | |
| [16] |
彭泉,崔德光,李晓强.基于人类认知规律的应用系统人机界面设计[J].计算机工程与应用,2001(19):148-150. PENG Quan,CUI De-guang,LI Xiao-qiang.Human-computer interface design based on human cognitive law of application system[J].Computer Engineering and Applications,2001(19):148-150. |
| Cited By in Cnki (63) | Click to display the text | |
| [17] | DORIGO M,MANIEZZO V,COLORNI A.Ant system:optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B:Cybernetics,1996,26(1):29-41. |
| Click to display the text | |
| [18] |
熊志辉,李思昆,陈吉华.遗传算法与蚂蚁算法动态融合的软硬件划分[J].软件学报,2005,16(4):503-512. XIONG Zhi-hui,LI Si-kun,CHEN Ji-hua.Hardware/software partitioning based on dynamic combination of genetic algorithm and ant algorithm[J].Journal of Software,2005,16(4):503-512. |
| Cited By in Cnki (171) | Click to display the text | |
| [19] | DORIGO M,GAMBARDELLA L.Ant colonies for the travelling salesman problem[J].Biosystems,1997,43(2):73-81. |
| Click to display the text | |
| [20] | DORIGO M,BLUMB C.Ant colony optimization theory:a survey[J].Theoretical Computer Science,2005,344(2/3):243-278. |
| Click to display the text |


