含有2个不同部件的并联系统作为一种常用结构,其可靠性模型已经被深入研究[1, 2].该类系统在舰艇中应用广泛,比如舰艇联合动力装置等,而在对该类系统的建模过程中,通常假设系统各部件的寿命和维修时间服从指数分布、威布尔分布等典型分布.曹晋华、程侃[3]利用指数分布对并联可修系统进行了研究,得出了一系列相关可靠性指标;Rakesh等[4]针对各部件维修时间分别服从指数分布和Lindley分布的包含两部件的并联系统进行了研究,系统具有两维修台,对系统可靠性进行了分析;Ram等[5]研究了维修时间服从威布尔分布的两部件并联系统,利用贝叶斯决策理论对系统可靠性特点进行了分析.在实际应用中,这些可靠性模型中的随机变量比如维修时间是不具备无后效性的,一般却假设其服从指数分布,这样显然是不够合理的.然而为了保持模型较好的求解计算特性,假设条件往往过于严格,导致这类模型的适用范围过窄.
为了保留这类典型分布所构建模型易于求解的特性,同时改善模型的适用性,Erlang[6]最早利用负指数随机变量的算术和构造了位相型的Erlang分布.此后,很多学者对混合型分布不断尝试[7],发展了超指数分布、广义Erlang分布以及广义Erlang分布的混合等.这些分布的描述能力较指数分布有很大提高,但失去了其易于求解的特性,直到Neuts[8]发展了PH分布的矩阵表示和解析方法,使得该类分布既保持了指数分布易于处理的优良特性,又具有较强的描述能力,被迅速广泛应用于系统可靠性模型研究中.Gururajan等[9]研究了具有单一维修台的两部件温贮备系统,贮备部件寿命服从PH分布,建立了可靠性模型,给出了可靠度、可用度等可靠性指标;赵丹[10]以修理工单重休假的并行可修系统为研究对象,假设修理时间服从PH分布,部件寿命服从指数分布,得出了系统可靠性模型,并给出了可靠性指标;Montoro-Cazorla等[11]研究了具有单一维修台的两部件冷贮备系统,系统工作时间和维修时间均服从PH分布,得出了更换备件时间等指标.
从PH分布的数学特性中,可得出该分布具有以下优点[12]:1)适用性强,PH分布具有很好的稠密性,可以较好地拟合可靠性模型的试验数据,达到所需的精确度,使得其能更好地替代各类复杂分布进行建模;2)运算封闭性好,易于进行矩阵建立与解析运算,且运算结果也有相应的PH分布表示;3)PH分布将数值参数转换为矩阵参数,以矩阵形式包含了大量的数据,更易于通过计算机等辅助工具进行计算.
基于上述分析,本文以并联可修系统为研究对象,考虑系统具有两不同部件和单个维修台,假设各部件寿命和维修时间服从不同的PH分布,建立了通用性更强的可靠性模型,得出了系统稳态可用度、首次故障前平均工作时间、稳态故障频度等一系列可靠性指标的解析表达式.
1 相关基础知识定义1[13]:考虑在状态空间上定义的一个时间连续、状态离散马尔科夫过程,假设状态1,2,…,m为转移状态,m+1为吸收状态,定义该马尔科夫过程的状态无穷小生成矩阵为
| $ Q=\left( \begin{matrix} T\ \ {{T}^{0}} \\ 0\ \ \ 0 \\ \end{matrix} \right), $ | (1) |
其中,m阶矩阵T=(Tij)满足Tii<0,Tij≥0,i≠j,1≤i,j≤m.Tij表示相位i至相位j的转移率,(T10,…,T0m)T是非负列向量,由各瞬态分别进入吸收态的吸收率表示为矩阵T0,满足Te+T0=0,其中e为元素均为1的m阶列向量,
定义2[13]:假设一个有限状态马尔科夫过程以概率α从转移状态i开始状态之间的转移,则该马尔科夫过程进入吸收状态的时间分布定义为PH型(Phase-type)概率分布.其概率分布函数为
| $ F\left( x \right)=1-\alpha \exp \left( Tx \right)e, $ | (2) |
[0,+∞)上的概率分布F( )称为连续PH分布,α=(α1,α2,…,αm)表示过程的初始概率向量,(α,T)称为它的m阶PH表示.
定义3[13]:一个m×n阶矩阵A和一个p×q阶矩阵B的Kronecker积被定义为
| $ A\otimes B=\left| \begin{matrix} {{\alpha }_{11}}B\ \cdots \ {{\alpha }_{1n}}B \\ \vdots \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ {{\alpha }_{m1}}B\ \cdots \ {{\alpha }_{mn}}B \\ \end{matrix} \right|. $ | (3) |
根据式(3),可得出Kronecker积有如下性质:
| $ C\left( A\otimes B \right)=\left( CA \right)\otimes B=A\otimes \left( CB \right), $ | (4) |
| $ \left( {{A}_{1}}\otimes {{B}_{1}} \right)\left( {{A}_{2}}\otimes {{B}_{2}} \right)=\left( {{A}_{1}}{{A}_{2}} \right)\otimes \left( {{B}_{1}}{{B}_{2}} \right).\ $ | (5) |
定义4[14]:一个m阶矩阵A和一个n阶矩阵B的Kronecker和被定义为
| $ A\oplus B=A\otimes {{I}_{n}}+{{I}_{m}}\otimes B. $ | (6) |
其中Im和In分别表示m和n阶的单位矩阵.
2 问题描述与假设设该并联可修系统具有单一维修台,包含两不同部件.2个不同部件分别称为部件1和部件2.下面对问题作进一步深入描述.
1) 部件1的寿命服从PH分布,该分布具有m阶不可约表示(α,T).
2) 部件2的寿命服从PH分布,该分布具有n阶不可约表示(β,S).
3) 系统是单维修台可修系统,按先到先维修的原则对故障件进行维修,且修复如新.其中,部件1的维修时间服从PH分布,该分布具有l1阶不可约表示(δ,U),部件2的维修时间也服从PH分布,该分布具有l2阶不可约表示(ξ,R).
4) 当系统中2个部件均发生故障时,系统故障;待某部件维修完毕后,系统再次投入运转.
5) 维修完毕的故障件进入系统开始工作的更换时间可以忽略,不进行考虑;
6) 部件1、部件2的寿命和维修时间均相互独立.
3 模型构建令Z(t),I(t)={i1(t),i2(t)}和J={j1(t),j2(t)}分别表示在某一时刻t系统内故障件数量、完好部件1和完好部件2各自所处的相位以及部件1和部件2的维修工作所处相位.那么,{Z(t),I(t),J(t)}是多维连续时间马尔科夫链.
由于两部件是不同的,以Z(t)为状态空间的宏状态,则状态空间可以表示为状态集Ω=H0∪H1∪H2∪H3∪H4,其中:
H0={0,(i1(t),i2(t))}表示系统完好无故障,处于工作状态,完好部件1和完好部件2分别处于相位i1(t),i2(t),其中1≤i1(t)≤m,1≤i2(t)≤n;
H1={1,i1(t),j2(t)}表示系统部件2发生故障,完好部件1处于状态i1(t),维修台维修工作处于状态j2(t),其中1≤i1(t)≤m,1≤j2(t)≤l2;
H2={1,i2(t),j1(t)}表示系统部件1发生故障,完好部件2处于状态i2(t),维修台维修工作处于状态j1(t),其中1≤i2(t)≤n,1≤j1(t)≤l1;
H3={2,j1(t)}表示系统故障停机,部件1在维修,部件2待修,维修台维修工作处于状态j1(t),其中1≤j1(t)≤l1;
H4={2,j2(t)}表示系统故障停机,部件2在维修,部件1待修,维修台维修工作处于状态j2(t),其中1≤j2(t)≤l2.
由上述划分可见,对于整个系统而言,W=H0∪H1∪H2是运行状态,E=H3∪H4是停机状态.
下面对状态转移进行分析.
1) H0内部转移:Z(t)=0时,表示系统完好,该状态转移包括部件1和部件2的各自相位转移,转移矩阵可以表示为T⊕S;
2) H1内部转移:Z(t)=1时,表示部件2故障、部件1工作.在同一时刻,完好部件1与维修工作不可能同时进行相位转移,故转移矩阵可以表示为T⊕R;
3) H2内部转移:Z(t)=1时,表示部件1故障、部件2工作.在同一时刻,完好部件2与维修工作不可能同时进行相位转移,故转移矩阵可以表示为U⊕S;
4) H3内部转移:Z(t)=2时,表示部件1正在修理、部件2等待,系统故障.这时只有部件1维修工作状态的内部转移,可以表示为U;
5) H4内部转移:Z(t)=2时,表示部件2正在修理、部件1等待,系统故障.这时只有部件2维修工作状态的内部转移,可以表示为R.
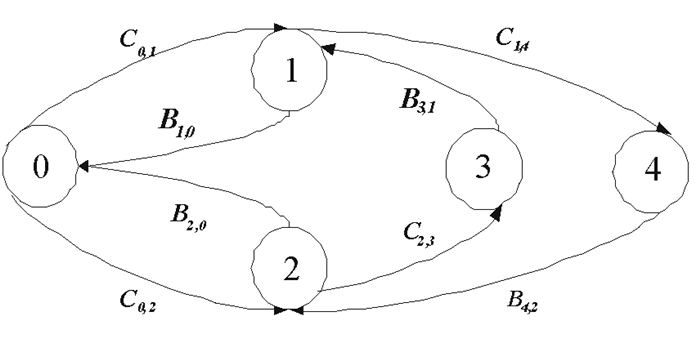
同理,可以得到宏状态k向k+1,k-1转移的表达式(k=0,1,2).系统各状态之间的转移如图 1所示.
|
| 图 1 系统状态空间转移示意图 Fig. 1 Schematic diagram of state transition of system |
根据上述分析,可以给出该马式链的无穷小生成元Q为
| $ Q=\left| \begin{matrix} {{A}_{0,0}}\ {{C}_{0,1}}\ {{C}_{0,2}}\ 0\ \ 0 \\ \begin{matrix} {{B}_{1,0}}\ {{A}_{11}}\ \ 0\ \ 0\ \ {{C}_{14}} \\ {{B}_{20}}\ \ 0\ \ {{A}_{22}}\ {{C}_{23}}\ 0 \\ 0\ \ \ {{B}_{31}}\ \ 0\ \ {{A}_{33}}\ \ 0 \\ \end{matrix} \\ 0\ \ \ 0\ \ {{B}_{42}}\ \ 0\ \ {{A}_{44}} \\ \end{matrix} \right| $ | (7) |
上述矩阵Q中,各元素分别表示为:A0,0=T⊕S,C0,1=I⊗S0ξ,C0,2=T0δ⊗I,B1,0=I⊗R0β,A1,1=T⊕R,C1,4=T0⊗I,B2,0=U0α⊗I,A2,2=U⊕S,C2,3=I⊗S0,B3,1=U0α⊗ξ,A3,3=U,B4,2=δ⊗R0β,A4,4=R.
其中:T0,S0表示部件1和部件2由工作状态中各瞬态转移至其相应吸收态的吸收率;U0,R0表示部件1和部件2由维修状态中各瞬态转移至其相应吸收态的吸收率.
4 系统稳态概率向量系统处于稳态时,其无穷小生成元矩阵中各状态所对应的概率构成稳态概率向量π,与系统状态空间Ω=H0∪H1∪H2∪H3∪H4相对应可表示为π=(π0,π1,π2,π3,π4),且满足下列条件:
| $ \left. \begin{matrix} \pi Q=0 \\ \pi e=1. \\ \end{matrix} \right\} $ | (8) |
将式(8)展开可得:
| $ {{\pi }_{0}}{{A}_{0,0}}+{{\pi }_{1}}{{B}_{1,0}}+{{\pi }_{2}}{{B}_{2,0}}=0, $ | (9) |
| $ {{\pi }_{0}}{{C}_{0,1}}+{{\pi }_{1}}{{A}_{1,1}}+{{\pi }_{3}}{{B}_{3,1}}=0, $ | (10) |
| $ {{\pi }_{0}}{{C}_{0,2}}+{{\pi }_{2}}{{A}_{2,2}}+{{\pi }_{4}}{{B}_{4,2}}=0, $ | (11) |
| $ {{\pi }_{2}}{{C}_{2,3}}+{{\pi }_{3}}{{A}_{3,3}}=0, $ | (12) |
| $ {{\pi }_{1}}{{C}_{1,4}}+{{\pi }_{4}}{{A}_{4,4}}=0, $ | (13) |
| $ {{\pi }_{0}}e+{{\pi }_{1}}e+{{\pi }_{2}}e+{{\pi }_{3}}e+{{\pi }_{4}}e=1. $ | (14) |
根据上述展开式(9)至(14)即可求出稳态概率向量π,下面介绍具体求解方法.
由式(12)、(13)可得:
| $ {{\pi }_{3}}=-{{\pi }_{2}}{{C}_{2,3}}{{\left( {{A}_{3,3}} \right)}^{-1}}, $ | (15) |
| $ {{\pi }_{4}}=-{{\pi }_{1}}{{C}_{1,4}}{{\left( {{A}_{4,4}} \right)}^{-1}}, $ | (16) |
将式(15)、(16)分别代入式(10)、(11)替换π3,π4可得:
| $ {{\pi }_{0}}{{C}_{0,1}}+{{\pi }_{1}}{{A}_{1,1}}+{{\pi }_{2}}{{C}_{2,3}}{{\left( {{A}_{3,3}} \right)}^{-1}}{{B}_{3,1}}=0, $ | (17) |
| $ {{\pi }_{0}}{{C}_{0,2}}-{{\pi }_{1}}{{C}_{1,4}}{{\left( {{A}_{4,4}} \right)}^{-1}}{{B}_{4,2}}+{{\pi }_{2}}{{A}_{2,2}}=0. $ | (18) |
根据PH分布的定义,U0=-Ue.结合式(4)、(17),可得
| $ \begin{matrix} {{\left( {{A}_{3,3}} \right)}^{-1}}{{B}_{3,1}}=\left( {{U}^{-1}}{{U}^{0}}\alpha \right)\otimes \xi = \\ -\left( {{U}^{-1}}Ue\alpha \right)\otimes \xi =-e\alpha \otimes \xi . \\ \end{matrix} $ | (19) |
同理,由式(18)可得
| $ {{\left( {{A}_{4,4}} \right)}^{-1}}{{B}_{4,2}}=-\delta \otimes {{R}^{0}}\beta . $ | (20) |
为表示方便,令D1=eα⊗ξ,D2=δ⊗R0β,则式(17)、(18)可化简为:
| $ {{\pi }_{0}}{{C}_{0,1}}+{{\pi }_{1}}{{A}_{1,1}}+{{\pi }_{2}}{{C}_{2,3}}{{D}_{1}}=0, $ | (21) |
| $ {{\pi }_{0}}{{C}_{0,2}}+{{\pi }_{1}}{{C}_{1,4}}{{D}_{2}}+{{\pi }_{2}}{{A}_{2,2}}=0. $ | (22) |
由式(5)、(9)、(21)、(22)可将π1,π2用π0表示如下:
| $ \begin{matrix} {{\pi }_{1}}={{\pi }_{0}}\left( {{C}_{0,1}}-{{A}_{0,0}}{{\left( {{B}_{2,0}} \right)}^{-1}}{{C}_{2,3}}{{D}_{1}} \right) \\ {{\left( {{B}_{1,0}}{{\left( {{B}_{2,0}} \right)}^{-1}}{{C}_{2,3}}{{D}_{1}}-{{A}_{1,1}} \right)}^{-1}}, \\ \end{matrix} $ | (23) |
| $ \begin{matrix} {{\pi }_{2}}={{\pi }_{0}}\left( {{C}_{0,2}}-{{A}_{0,0}}{{\left( {{B}_{1,0}} \right)}^{-1}}{{C}_{1,4}}{{D}_{2}} \right) \\ {{\left( {{B}_{2,0}}{{\left( {{B}_{1,0}} \right)}^{-1}}{{C}_{1,4}}{{D}_{2}}-{{A}_{2,2}} \right)}^{-1}}, \\ \end{matrix} $ | (24) |
由上述计算解析式(14)、(15)、(16)、(23)、(24)即可计算出π的各元素,即系统稳态概率向量.由于计算过程和计算式过于复杂,这里不再一一列出.
5 系统可靠性指标 5.1 系统稳态可用度已知系统稳态概率向量,则系统稳态可用度O可直接用系统处于状态空间W=H0∪H1∪H2的稳态概率之和来表示:
| $ O={{\pi }_{0}}e+{{\pi }_{1}}e+{{\pi }_{2}}e. $ | (25) |
系统t0=0时开始运行,在运行过程中首次由工作状态W=H0∪H1∪H2进入故障状态E=H3∪H4的时刻点t为系统首次故障前工作时间[15].
定理1:系统首次故障前工作时间服从PH分布,有(mn+ml2+nl1)阶的表示(γ,G),其中
| $ \gamma = \left( {1,0,0, \cdots ,0} \right),G = \left| {\begin{array}{*{20}{c}} {{A_{0,0}}\;{C_{0,1}}\;{C_{0,2}}}\\ {{B_{1,0}}\;{A_{1,1}}\;0}\\ {{B_{2,0}}\;0\;{A_{2,2}}} \end{array}} \right|. $ |
证明:根据系统首次故障前工作时间的定义,令H3,H4合并为E=H3∪H4,由于系统首次停机,系统停机状态可根据PH分布定义表示为系统首次故障前工作时间的吸收态,则此时系统状态转移矩阵可表示为
| $ {k^ * } = \left| {\begin{array}{*{20}{c}} {{A_{0,0}}\;{C_{0,1}}\;{C_{0,2}}\;\;0}\\ {{B_{1,0}}\;{A_{1,1}}\;0\;\;{C_{1,4}}}\\ {\begin{array}{*{20}{c}} {{B_{2,0}}\;0\;{A_{2,2}}\;\;{C_{2,3}}}\\ {0\;\;\;0\;\;0\;\;0} \end{array}} \end{array}} \right|. $ |
将该矩阵Q*去除第4行与第4列可得矩阵G,其中由系统首次故障前的工作状态中各瞬态转移至吸收态的吸收率G0=-Ge=(0,C1,4,C2,3)T.
由PH分布的定义和其良好的运算封闭性,可以得出系统首次故障前工作时间服从PH分布,有(mn+ml2+nl1)阶的PH表示(γ,G).
推论1:当给定系统初始状态概率向量γ,系统首次故障前平均工作时间(mean time to first failure,MTTFF)为
| $ \text{MTTFF}=-\gamma {{G}^{-1}}e. $ | (26) |
由于系统可修,则系统运行始终是系统工作状态和停机状态不断来回出现的过程.
定理2:系统稳态故障频度用以描述系统在(0,t]时间内停机的频率,可表示为
| $ \begin{matrix} k=\left( {{\pi }_{0}},{{\pi }_{1}},{{\pi }_{2}} \right)\left| \begin{matrix} 0\ \ \ 0 \\ {{C}_{1,4}}\ \ 0 \\ 0\ \ \ {{C}_{2,3}} \\ \end{matrix} \right|\left| \begin{matrix} {{e}_{1}} \\ {{e}_{2}} \\ \end{matrix} \right|= \\ {{\pi }_{1}}{{C}_{1,4}}{{e}_{1}}+{{\pi }_{2}}{{C}_{2,3}}{{e}_{2}}, \\ \end{matrix} $ | (27) |
其中e1,e2分别表示与π1C1,4,π2C2,3同阶的元素为1的列向量.
推论2:在系统进入稳态后,系统平均开工时间(mean up-time,MUT)、平均停工时间(mean down-time,MDT)和平均周期(mean cycle time,MCT)分别为:
| $ \left. \begin{matrix} \text{MUT}=O/k, \\ \text{MDT}=\left( 1-O \right)/k. \\ \end{matrix} \right\} $ | (28) |
| $ \text{MCT=MUT+MDT}=1/k $ | (29) |
本文算例由两方面的验证组成:1)假设部件1、部件2寿命和维修时间分别服从不同的指数分布,构建模型,得出相应结果,与文献[3]中的结果进行对比,验证模型的正确性;2)假设部件1、部件2寿命和维修时间分别服从不同的PH分布,验证模型对复杂分布的适用性.
6.1 模型正确性验证假设有某包含2个部件的并联可修系统,部件i的寿命分布为1-e-λit,维修时间分布为1-e-μit,其中t≥0,λi>0,μi>0,i=1,2.
根据本文中模型构建的条件,T,S,U,R可分别表示为-λ1,-λ2,-μ1,-μ2,α=β=δ=ξ=1.由式(7)可得Q表示如下:
| $ Q=\left| \begin{matrix} -{{\lambda }_{1}}-{{\lambda }_{2}}\ \ {{\lambda }_{2}}\ \ {{\lambda }_{1}}\ \ 0\ \ 0 \\ \begin{matrix} {{\mu }_{2}}\ \ -{{\lambda }_{1}}-{{\mu }_{2}}\ \ 0\ \ 0\ \ {{\lambda }_{1}} \\ {{\mu }_{1}}\ \ 0\ \ -{{\lambda }_{2}}-{{\mu }_{1}}\ \ {{\lambda }_{2}}\ \ 0 \\ 0\ \ {{\mu }_{1}}\ \ 0\ \ -{{\mu }_{1}}\ \ 0 \\ \end{matrix} \\ 0\ \ 0\ \ {{\mu }_{2}}\ \ 0\ \ \ -{{\mu }_{2}} \\ \end{matrix} \right| $ | (30) |
该式即为系统的无穷小生成元.假设运行过程中处于各状态的瞬时概率分别为P0(t),P1(t),P2(t),P3(t),P4(t),则其状态转移的微分方程组表示如下:
| $ \left. \begin{matrix} \frac{\text{d}{{P}_{0}}\left( t \right)}{\text{d}t}=-\left( {{\lambda }_{1}}+{{\lambda }_{2}} \right){{P}_{0}}\left( t \right)+{{\mu }_{2}}{{P}_{1}}\left( t \right)+{{\mu }_{1}}{{P}_{2}}\left( t \right), \\ \begin{matrix} \frac{\text{d}{{P}_{1}}\left( t \right)}{\text{d}t}={{\lambda }_{2}}{{P}_{0}}\left( t \right)-\left( {{\lambda }_{1}}+{{\mu }_{2}} \right){{P}_{1}}\left( t \right)+{{\mu }_{1}}{{P}_{3}}\left( t \right), \\ \begin{matrix} \frac{\text{d}{{P}_{2}}\left( t \right)}{\text{d}t}={{\lambda }_{1}}{{P}_{0}}\left( t \right)-\left( {{\lambda }_{2}}+{{\mu }_{1}} \right){{P}_{2}}\left( t \right)+{{\mu }_{2}}{{P}_{4}}\left( t \right), \\ \frac{\text{d}{{P}_{3}}\left( t \right)}{\text{d}t}={{\lambda }_{2}}{{P}_{2}}\left( t \right)-{{\mu }_{1}}{{P}_{3}}\left( t \right), \\ \end{matrix} \\ \frac{\text{d}{{P}_{4}}\left( t \right)}{\text{d}t}={{\lambda }_{1}}{{P}_{1}}\left( t \right)-{{\mu }_{2}}{{P}_{4}}\left( t \right), \\ \end{matrix} \\ {{P}_{0}}\left( t \right)+{{P}_{1}}\left( t \right)+{{P}_{2}}\left( t \right)+{{P}_{3}}\left( t \right)+{{P}_{4}}\left( t \right)=1. \\ \end{matrix} \right| $ | (31) |
当系统进入稳态,即方程组(31)中t→∞时,可得其稳态概率方程组如下:
| $ \left. \begin{matrix} -\left( {{\lambda }_{1}}+{{\lambda }_{2}} \right){{P}_{0}}+{{\mu }_{2}}{{P}_{1}}+{{\mu }_{1}}{{P}_{2}}=0, \\ \begin{matrix} {{\lambda }_{2}}{{P}_{0}}-\left( {{\lambda }_{1}}+{{\mu }_{2}} \right){{P}_{1}}+{{\mu }_{1}}{{P}_{3}}=0, \\ \begin{matrix} {{\lambda }_{1}}{{P}_{0}}-\left( {{\lambda }_{2}}+{{\mu }_{1}} \right){{P}_{2}}+{{\mu }_{2}}{{P}_{4}}=0, \\ {{\lambda }_{2}}{{P}_{2}}-{{\mu }_{1}}{{P}_{3}}=0, \\ \end{matrix} \\ {{\lambda }_{1}}{{P}_{1}}-{{\mu }_{2}}{{P}_{4}}=0, \\ \end{matrix} \\ {{P}_{0}}+{{P}_{1}}+{{P}_{2}}+{{P}_{3}}+{{P}_{4}}=1. \\ \end{matrix} \right| $ | (32) |
将上述状态转移矩阵(30)代入方程(8)所得结果与方程(32)相同,故本文模型计算所得的稳态概率必然与文献[3]相同,充分验证了当系统部件寿命和维修时间分别服从不同的指数分布时该模型的正确性.利用文献[3]中模型参数数值,令λ1=0.5,λ2=0.8,μ1=10,μ2=12,采用PH分布的解析方法求解,得出以下相同结果:
| $ \left\{ \begin{matrix} {{P}_{0}}={{\pi }_{0}}=0.8902, \\ \begin{matrix} {{P}_{1}}={{\pi }_{1}}=0.0598, \\ {{P}_{2}}={{\pi }_{2}}=0.0440, \\ {{P}_{3}}={{\pi }_{3}}=0.0035, \\ \end{matrix} \\ {{P}_{4}}={{\pi }_{4}}=0.0025. \\ \end{matrix} \right. $ |
O=0.994,MTTFF=16.082 6,k=0.065 1,MUT=15.268 8,MDT=0.092 2,MCT=15.361.
6.2 模型适用性验证假设有某包含2个部件的并联可修系统,则:
1) 部件1寿命分布,
| $ \alpha =\left( 0.12,0.34,0.54 \right), $ |
| $ T=\left| \begin{matrix} -2.315\ \ 0.913\ \ 0.012 \\ 3.885\ \ -4.757\ \ 0.872 \\ 0.012\ \ 1.812\ \ -1.823 \\ \end{matrix} \right|; $ |
2) 部件1维修时间分布,
| $ \delta =\left( 0,1 \right),U=\left( \begin{matrix} -10.5\ \ 0.5 \\ 1.5\ \ -9.5 \\ \end{matrix} \right); $ |
3) 部件2寿命分布,
| $ \beta =\left( 0.3,0.7 \right),S=\left( \begin{matrix} -1.2\ \ 0.6 \\ 0.8\ \ -0.8 \\ \end{matrix} \right); $ |
4) 部件2维修时间分布,
| $ \xi =\left( 0,0.32,0.68 \right), $ |
| $ R=\left| \begin{matrix} -12.015\ \ \ 1.01\ \ \ 0.005 \\ 0.006\ \ \ -9.876\ \ \ \ 0.87 \\ 0.025\ \ 0.1\ \ -10.125 \\ \end{matrix} \right|. $ |
对模型进行求解,可以得出:O=0.996 3,MTTFF=29.272 7,k=0.033 4,MUT=29.857 1,MDT=0.110 9,MCT=29.967 9.
通过对该算例结果进行分析,所得结果均符合系统可靠性模型相关指标要求,验证了模型对各种类型分布的适用性,且具有优良的解析计算性.
7 结束语本文将PH分布应用于包含2个不同部件的并联可修系统中,考虑系统具有单一维修台,建立了适用性更强的可靠性模型,得出了系统稳态可用度、首次故障前工作时间、稳态故障频度等一系列可靠性指标的解析式,较好地弥补了指数分布等典型分布所建模型的不足,可操作性更强.同时,利用算例分析验证了PH分布的正确性和较好的适用性,较传统典型分布有更高的实际应用价值.
| [1] | BAYRAMOGLU I.Reliability and mean residual life of complex systems with two dependent components per element[J].IEEE Transactions on Reliability,2013,62(1):276-285. |
| Click to display the text | |
| [2] | LIU Y,LI X Z,DU Z P.Reliability analysis of a random fuzzy repairable parallel system with two non-identical components[J].Journal of Intelligent and Fuzzy Systems,2014,27(6):2775-2784. |
| Click to display the text | |
| [3] | 曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2006:222-224. CAO Jing-hua,CHEN Kan.An introduction to mathematical of reliability[M].Beijing:Higher Education Press,2006:222-224. |
| [4] | RAKESH G,SWATI K,MADHU M.A two dissimilar unit parallel system with two phase repair by skilled and ordinary repairmen[J].International Journal of System Assurance Engineering and Management,2014,5(4):554-561. |
| Click to display the text | |
| [5] | RAM K,DIVYA J.Classical and Bayesian analysis of reliability characteristics of a two-unit parallel system with Weibull failure and repair laws[J].International Journal of System Assurance Engineering and Management,2014,5(3):252-261. |
| Click to display the text | |
| [6] | ERLANG A K.Solution of some problems in the theory of probabilities of significance in automatic telephone exchanges[J].The Post Office Electrical Engineers Journal,1917,1(10):189-197. |
| [7] | EDWARD K.An introduction to stochastic processes[M].Beijing:China Machine Press,2006:264-273. |
| [8] | NEUTS M F,MEIER K S.On the use of phase type distributions in reliability modelling of systems with two components[J].OR Spektrum,1981,2(2):227-234. |
| Click to display the text | |
| [9] | GRURUAJAN M,SRINIVASAN B.A complex two-unit system with random breakdown of repair facility[J].Microelectronics Reliability,1995,35(2):299-302. |
| Click to display the text | |
| [10] |
赵丹.寿命及修理时间服从Phase-Type分布的可修系统的可靠性分析[D].河北:燕山大学理学院,2012:23-31. ZHAO Dan.Reliability analysis of repairable system with Phase-Type life or phase type repairs[D].Hebei:The University of Yanshan,Science Faculty,2012:23-31. |
| Cited By in Cnki (2) | Click to display the text | |
| [11] | MONTORO-CAZORLA D,PEREZOCON R.A deteriorating two-system with two repair modes and sojourn times Phase-Type distributed[J].Reliability Engineering & System Safety,2006,91:1-9. |
| Click to display the text | |
| [12] | OSOGAMI T,HARCHOL M.Closed form solutions for mapping general distributions to quasi minimal PH distributions[J].Performance Evaluation,2006,63(6):524-552. |
| Click to display the text | |
| [13] | QI M H.Fundamentals of matrix-analytic methods[M].London:Springer,2013:10-22. |
| [14] | YONIT B,ESTHER F,BENNY L.Analysis of R out of N systems with several repairmen and exponential life times and phase type repair times[J].European Journal of Operational Research,2006,169:202-225. |
| Click to display the text | |
| [15] |
董兵.具有指数分布、PH分布型修理两部件系统的可靠性研究[D].四川:电子科技大学数学科学学院,2007:4-6. DONG Bing.Study of repairable system with two units based on exponential distribution and PH distribution[D].Sichuan:University of Electronic Science and Technology of China,School of Mathematical Sciences,2007:4-6. |
| Cited By in Cnki (1) | Click to display the text |



