2. 集美大学 工程训练中心, 福建 厦门 361021
2. Engineering Training Center, Jimei University, Xiamen 361021, China
平底推杆较滚子推杆在承载能力、润滑性能、使用寿命和高速性能等方面具有明显优越性,其设计问题长期以来吸引了国内外学者的浓厚兴趣和广泛关注[1, 2, 3, 4, 5, 6, 7].
机构综合中,性能评价和尺寸综合是处于机构学前沿、有挑战性的重要课题.性能评价,是机构综合的首要问题,核心是提出描述综合性能的评价指标;尺寸综合,旨在确定运动学参数,目的是揭示多种性能与尺寸型间的映射规律.
以平底直动推杆盘形凸轮机构为研究对象,阐释了形态构成、基本尺寸参数、尺寸综合问题的准确描述以及求解基本思路与步骤;提出3项性能评价指标及解析表达;构建了面向“可视化”问题求解模型,采取“遍历搜索”思想方法,先解决单一约束下边界线/解域、边界面/解空间,继之解决归并约束下边界线/解域、边界面/解空间,成功实现了二维朝三维的可视映射.据此,揭示“最优解/解区间/解集”、“非劣解区间/解域”和“谷底点”等的存在性、重要内涵和相应求解方法,为工程设计机构尺寸综合提供了一种行之有效的通用求解方法.
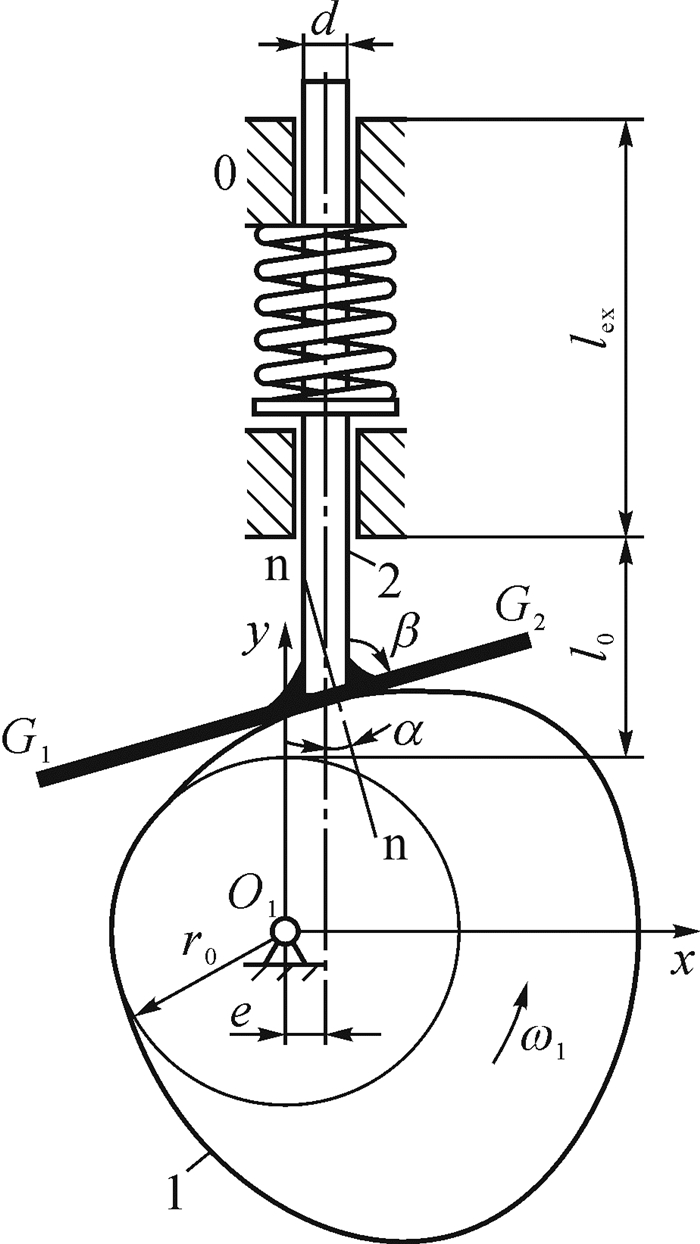
1 对象机构、尺寸综合问题和求解的基本思路与步骤 1.1 对象机构形态构成、基本尺寸和总体尺寸如图 1所示,平底直动推杆盘形凸轮机构由盘形凸轮1、平底推杆2和机架0组成.原动凸轮1等速转动,驱动平底G1G2沿导路往复移动,实现预期运动输出.
|
| 图 1 平底直动推杆盘形凸轮机构 Fig. 1 Disc cams with translating flat-faced follower |
基本尺寸:凸轮基圆半径r0、平底夹角β和偏距e.
凸轮工作轮廓基圆半径r0是首要基本尺寸.不仅决定横向和纵向尺寸,而且决定凸轮尺寸、材耗和空间需求等.
平底夹角β是重要基本参数.对机构尺寸影响较小,但决定接触应力、承载能力和运动保真等,对动力学性能亦有重要影响.
偏距e是另一重要基本尺寸.与r0不同,是相对位置参数,通过与r0,β复杂的耦合关系,影响机构横向和纵向尺寸.
须强调的是:文中β是有向角.凸轮逆时针转动,规定如下:如图 1所示,β=0,对应G1G2‖O1y,β正向为顺时针方向,β∈(0°,180°).
1.2 对象机构尺寸综合问题的准确描述对象机构的尺寸综合问题,准确描述如下:
已知:推杆行程为h,往程、返程运动角为Φg,Φr,位移规律为sg=sg(φ),sr=sr(φ),近/远休止角为Φs和Φs′,往程、返程许用压力角[α]g和[α]r,生产阻力Q=Q(φ),推杆-凸轮、推杆-机架摩擦系数为f,上、下支承面间跨距为lex,推杆宽度d,悬臂初始长度l0,凸轮弹性模量E1、泊松比μ1,平底弹性模量E1、泊松比μ2,凸轮、平底凸轮接触宽度b,往程/返程凸轮-平底许用接触应力[σH]g和[σH]r.
求解:凸轮基圆半径r0、平底夹角β和偏距e.
1.3 尺寸综合问题求解的基本思路与步骤求解基本思路与步骤,如下:
1) 构建尺寸坐标系O-r0βe、尺寸空间Ω(r0,β,e),离散-网格化处理;2) 提出约束条件Ⅰ,Ⅱ,Ⅲ,推演解析公式;3) 采取遍历方法,实现单一约束向O-r0βe,Ω(r0,β,e)映射,得到可视边界线/解域、边界面/解空间;4) 实现归并约束向O-r0βe,Ω(r0,β,e)映射,得到可视边界线/解域、边界面/解空间;5) 根据多目标规划、可视映射,揭示最优解存在性等重要结论.
2 3项重要的性能评价指标研究发现,尺寸综合须满足3项评价指标,或称约束条件[8, 9, 10, 11, 12].
2.1 约束条件Ⅰ——运动保真条件ρ>0段,即
| $ {\rho _{\rm{g}}} > 0\parallel {\rho _{\rm{r}}} > 0, $ | (1) |
| $ \rho = \rho \left( {{r_0},\beta ,e,s} \right) = {r_0} + \left( {s + s'} \right)\sin \beta , $ | (2) |
式(2)通用.式(1)等价于ρmin>0,即
| $ {\rho _{g\min }} > 0\parallel {\rho _{{\rm{rmin}}}} > 0. $ | (3) |
取定r0,β和e,ρ=ρ(r0,β,e,s)转化为φ的一元函数.通过一维搜索,可解得ρgmin和ρrmin.
2.2 约束条件Ⅱ——传动性能条件|α|≤[α],即
| $ \left| {{\alpha _{\rm{g}}}} \right| \le {[\alpha ]_{\rm{g}}}\parallel \left| {{\alpha _{\rm{r}}}} \right| \le {[\alpha ]_{\rm{r}}}, $ | (4) |
| $ \left| {{\alpha _{\max }}} \right| = \alpha = \pi - \beta . $ | (5) |
取定β,|α|max随之确定.
2.3 约束条件Ⅲ——接触强度条件σH≤[σH],即
| $ {\sigma _{{\rm{Hg}}}} \le {[{\sigma _{\rm{H}}}{\rm{]}}_{\rm{g}}}\parallel {\sigma _{{\rm{Hr}}}} \le {[{\sigma _{\rm{H}}}{\rm{]}}_{\rm{r}}}, $ | (6) |
σHmax≤[σH],即
| $ {\sigma _{{\rm{Hmaxg}}}} \le {[{\sigma _{\rm{H}}}{\rm{]}}_{\rm{g}}}\parallel {\sigma _{{\rm{Hmaxr}}}} \le [{\sigma _{\rm{H}}}{\rm{]}}, $ | (7) |
| $ \begin{array}{*{20}{c}} {{\sigma _{\rm{H}}} = \left\{ {{F_n}\left( {1/\rho } \right)} \right./\left[ {\pi b\left( {\left( {1 - \mu _1^2} \right)} \right.} \right./{E_1} + }\\ {{{\left. {\left. {\left( {1 - \mu _2^2/{E_2}} \right)} \right]} \right\}}^{1/2}}.} \end{array} $ | (8) |
Fn是与ρ,r0,β,e和s,s′(φ)等以及与凸轮、平底材料有关常量b,μ1,μ2,E1和E2等有关的复杂函数,其解析公式推导如下:
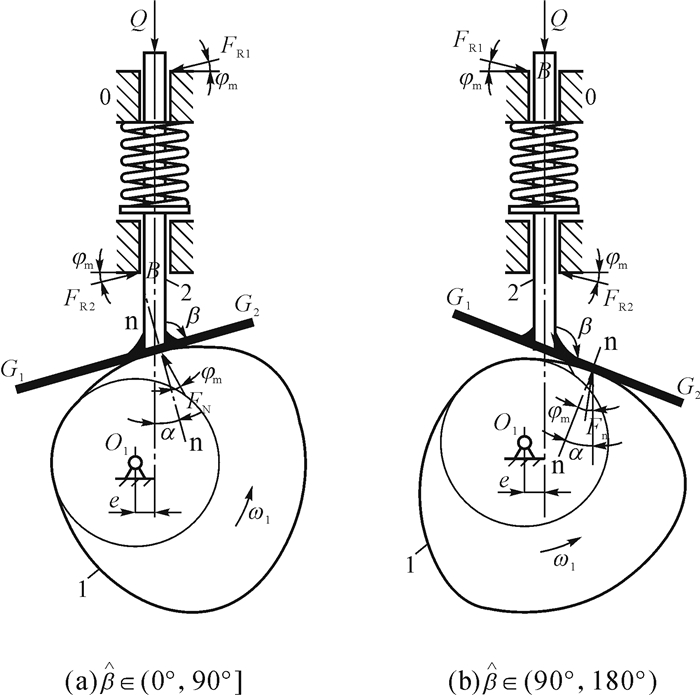
如图 2(a)所示,β∈(0°,90°]形态时,以推杆为对象,作受力分析.力平衡方程为:
|
| 图 2 平底直动推杆盘形凸轮机构受力分析 Fig. 2 Force analysis of disc cams with translating flat-faced follower |
| $ \sum {{F_x} = 0,F\cos \left( {\beta - {\varphi _{\rm{m}}}} \right) + } {F_{R1}}\cos {\varphi _{\rm{m}}} - {F_{R2}}\cos {\varphi _{\rm{m}}} = 0, $ | (9) |
| $ \sum {{F_y} = 0,F\sin \left( {\beta - {\varphi _{\rm{m}}}} \right) - \left( {{F_{R1}} + {F_{R2}}} \right)} \sin {\varphi _{\rm{m}}} - {F_{\sum {} }} = 0, $ | (10) |
| $ \begin{array}{*{20}{c}} {\sum {{M_b} = 0, - 0.5} {F_{\sum d }} + {F_{R1}}\cos {\varphi _{\rm{m}}}{l_{{\rm{ex}}}} - {F_{R1}}\sin {\varphi _{\rm{m}}}d{\rm{ + }}}\\ {F\sin \left( {\beta - {\varphi _{\rm{m}}}} \right)\left( {d/2 + L\sin \beta } \right) - F\sin \left( {\beta - {\varphi _{\rm{m}}}} \right)\left( {{l_0} - s - } \right.}\\ {L\cos \beta ) = 0,} \end{array} $ | (11) |
| $ {\varphi _{\rm{m}}} = \alpha \tan f, $ | (12) |
| $ L = s'\left( \varphi \right)\sin \beta - {r_0} + s\cot \beta /\sin \beta - e/\sin \beta , $ | (13) |
推杆受总载荷为
| $ {F_{\sum {} }} = [Q + \left( {{m_{\rm{f}}} + {m_{\rm{s}}}} \right)g + {F_{\rm{s}}} + \left( {{m_{\rm{f}}} + {m_{\rm{s}}}/2} \right)\alpha ], $ | (14) |
联立式(9)至(14),整理得法向力Fn解析式为
| $ {F_{\rm{n}}} = \left( {0.5{F_{\sum {} }}{l_{ex}}/\tan {\varphi _{\rm{m}}}/A} \right)\cos {\varphi _{\rm{m}}}, $ | (15) |
| $ \begin{array}{*{20}{c}} {A = \{ [sin\left( {\beta - {\varphi _{\rm{m}}}} \right)/sin{\varphi _{\rm{m}}} - \cos \left( {\beta - {\varphi _{\rm{m}}}} \right)/cos{\varphi _{\rm{m}}}]/2\} }\\ {\left( {\cos {\varphi _{\rm{m}}}{l_{ex}} - d\sin {\varphi _{\rm{m}}}} \right) + \sin \left( {\beta - {\varphi _{\rm{m}}}} \right)\left( {d/2 + } \right.}\\ {\left. {L\sin \beta } \right) - \cos \left( {\beta - {\varphi _{\rm{m}}}} \right)\left( {{l_0} - s - L\cos \beta } \right).} \end{array} $ | (16) |
如图 2(b)所示,β∈(90°,180°)形态时,同理,力平衡方程为:
| $ {F_{\sum x }} = 0,F\cos \left( {\beta - {\varphi _{\rm{m}}}} \right) + {F_{{\rm{R1}}}}\cos {\varphi _{\rm{m}}} - {F_{{\rm{R2}}}}\cos {\varphi _{\rm{m}}} = 0, $ | (17) |
| $ {F_y} = 0,F\sin \left( {\beta - {\varphi _{\rm{m}}}} \right) - \left( {{F_{{\rm{R1}}}} + {F_{{\rm{R2}}}}} \right)\sin {\varphi _{\rm{m}}} - {F_{\sum {} }} = 0, $ | (18) |
| $ \begin{array}{*{20}{c}} {{M_B} = 0, - 0.5{F_{\sum {} }}d + {F_{{\rm{R2}}}}\cos {\varphi _{\rm{m}}}{l_{ex}} - {F_{{\rm{R2}}}}\sin {\varphi _{\rm{m}}}d + }\\ {F\sin \left( {\beta - {\varphi _{\rm{m}}} - \pi /2} \right)\left( {d/2 + L\sin \beta } \right) + F\sin \left( {\beta - {\varphi _{\rm{m}}} - } \right.}\\ {\left. {\pi /2} \right)\left( {{l_0} - s + L\cos \beta } \right) = 0,} \end{array} $ | (19) |
联立式(12)至(14)、(17) 至(19),整理得
| $ {F_{\rm{n}}} = \left( {0.5{F_{\sum {} }}{l_{ex}}/\tan {\varphi _{\rm{m}}}/A} \right)\cos {\varphi _{\rm{m}}}, $ | (20) |
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {A = \{ [sin\left( {\beta - {\varphi _{\rm{m}}}} \right)/sin{\varphi _{\rm{m}}} - \cos \left( {\beta - {\varphi _{\rm{m}}}} \right)/cos{\varphi _{\rm{m}}}]/2\} }\\ {\left( {\cos {\varphi _{\rm{m}}}{l_{ex}} - d\sin {\varphi _{\rm{m}}}} \right) - \cos \left( {\beta - {\varphi _{\rm{m}}} - \pi /2} \right)}\\ {\left( {d/2 + L\sin \beta } \right) - \sin \left( {\beta - {\varphi _{\rm{m}}} - \pi /2} \right) - sin\left( {\beta - } \right.} \end{array}}\\ {\left. {{\varphi _{\rm{m}}} - \pi /2} \right)\left( {{l_{ex}} + {l_0} - s - L\cos \beta } \right).} \end{array} $ | (21) |
取定r0,β和e,σH=σH(r0,β,e,s)转化为φ的一元函数.一维搜索,可解得σHmax.
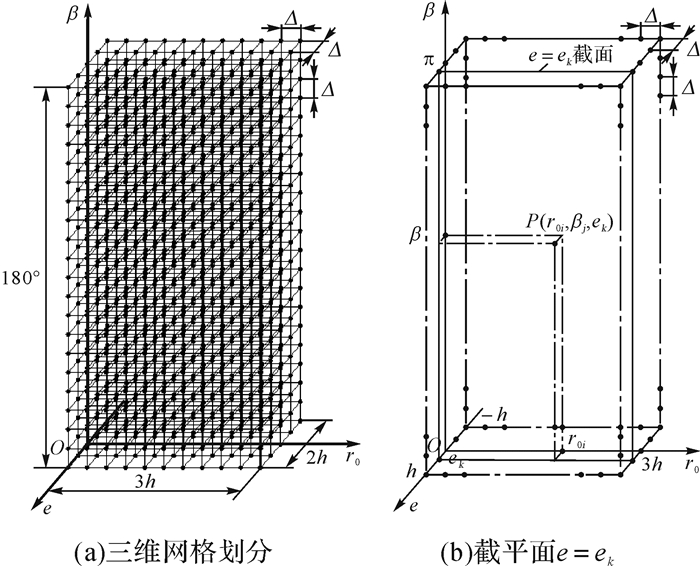
3 单一约束下:边界线(面)、解域(空间)等重要结论选取r0,β和e为三坐标轴参数,构造尺寸坐标系O-r0βe和尺寸空间Ω(r0,β,e),如图 3所示.
|
| 图 3 尺寸坐标系O-r0βe、尺寸空间Ω(r0,β,e)构建与离散-网格化 Fig. 3 Discretizing and gridding of the coordinate system O-r0βe and area Ω(r0,β,e) of dimension |
r0,β和e为基本机构尺寸参数.定义域:r0∈(0,+∞),β∈(0,180°)和e∈(-∞,+∞).故此,r0,β两轴仅有正半轴,e轴有正、负半轴.
所谓Ω(r0,β,e)坐标空间离散化,指分别沿r0,β和e轴对Ω(r0,β,e)进行离散-网格化处理[13].
为清楚呈现边界、解域形态特征,通常取r0,β和e上限:sup[r0]=(3~10)h,sup[β]=π(180°)和sup[e]=(1~3)h;e下限inf[e]=-(1~3)h,如图 3所示.
sup[r0],sup[e]和inf[e]具体取值需根据情况摸索确定.
沿r0,β和e轴,任意相邻两线皆取等间隔
| $ \vartriangle ={{r}_{0i+1}}-{{r}_{0i}}={{\beta }_{j+1}}-{{\beta }_{j}}={{e}_{k+1}}-{{e}_{k}}={{10}^{-m}}\text{mm}, $ | (22) |
| $ \begin{matrix} {{i}_{\max }}=\operatorname{int}\{sup[{{r}_{0}}]/\vartriangle \},{{j}_{\max }}=\operatorname{int}\{sup[\beta ]/\vartriangle \}, \\ {{k}_{\max }}=-{{k}_{\min }}=\operatorname{int}\{sup[e]/\vartriangle \}. \\ \end{matrix} $ | (23) |
任一网格节点(r0i,βj,ek),有:
| $ {{r}_{0i}}=i\vartriangle \ \ \ \left( i=1,2,\cdots ,{{i}_{\max }} \right),\ $ | (24) |
| $ {{\beta }_{j}}=i\vartriangle \ \ \ \left( j=1,2,\cdots ,{{j}_{\max }} \right), $ | (25) |
| $ {{e}_{k}}=k\vartriangle \ \ \ \left( k={{k}_{\min }},\cdots ,-1,0,1,\cdots ,{{k}_{\max }} \right). $ | (26) |
总共有imax·jmax·(2kmax)个网格节点.
不难理解,将约束条件Ⅰ至Ⅲ映射到O-r0βe中,对应3个边界面SⅠ至SⅢ,将空间Ω(r0,β,e)划分成:解空间ΩⅠ至ΩⅢ,非解空间ΩⅠun至ΩⅢun.
三维问题求解复杂棘手,故取截平面e=ek的“降维”方法,将三维问题简化为二维问题,如图 3(b)所示.
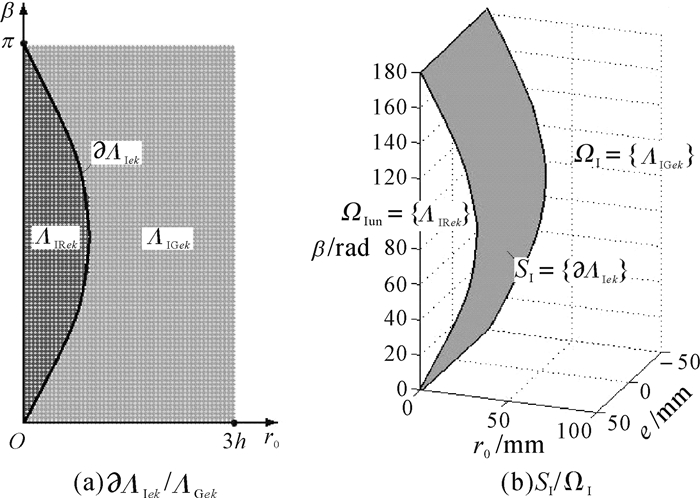
3.1 单一约束条件下的约束条件I—运动保真条件 3.1.1 边界线əΛⅠek/解域ΛⅠGek遍历网格节点(r0iek,βjek),满足式(3)的标示为浅灰色,不满足的标示为深灰色,得到约束边界əΛⅠek,如图 3(a)所示.据此,可得:
1) 边界线əΛⅠek,形态特征:正弦曲线;
2) əΛⅠek将坐标平面分为:解域ΛⅠGek,非解域ΛⅠRek,如图 4(A)所示.
|
| 图 4 运动保真约束的边界线/解域、边界面/解空间 Fig. 4 The bounding line/solution area,bounding surface/solution space based on motion fidelity conditions |
任取截平面e=ek(k=kmin,…,kmax),数“正弦曲线”堆积成“正弦曲面”——“边界面SI”,即{əΛⅠek}.
SI将尺寸空间分为:解空间ΩI={ΛⅠGek}、非解空间ΩIun={ΛⅠRek},如图 4(b).
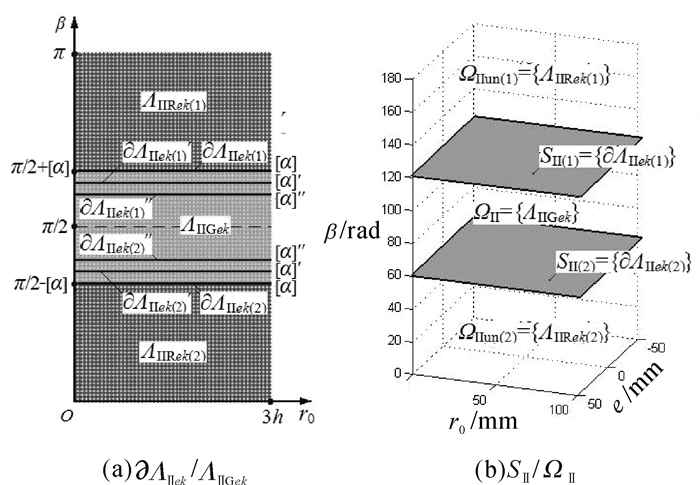
3.2 单一约束条件下的约束条件Ⅱ——传动性能条件 3.2.1 边界线əΛⅡek/解域əΛⅡGek同理,据式(4)得两约束边界əΛⅡek(1),əΛⅡek(2),如图 5(a)所示,可知
|
| 图 5 传动性能约束的边界线/解域、边界面/解空间 Fig. 5 The bounding line/solution area,bounding surface/solution space based on transmission behavior conditions |
1) 边界线əΛⅡek(1),əΛⅡek(2),形态特征:与β轴交点分别为π/2+[α],π/2-[α]的2条关于β=π/2对称的水平线;
2) əΛⅡek(1),əΛⅡek(2)将坐标平面分为:解域ΛⅠGek,非解域ΛⅡRek(1),ΛⅡRek(2).
取不同[α],əΛⅡek(1),əΛⅡek(2)分布规律:[α]″<[α]′<[α],对应边界线对称分布,逐渐向β=π/2逼近,如图 5(a)所示.
3.2.2 边界面SⅡ={əΛⅡek}/解空间ΩⅡ={ΛⅡGek}如图 5(b)所示,堆积e=ek,数平行直线堆积成平行面SⅡ(1),SⅡ(2),即{əΛⅡek}.
SⅡ(1),SⅡ(2)所夹空间是解空间ΩⅡ={ΛⅡGek},此外,非解空间ΩⅡun(1)={ΛⅡRek(1)},ΩⅡun(2)={ΛⅡRek(2)}.
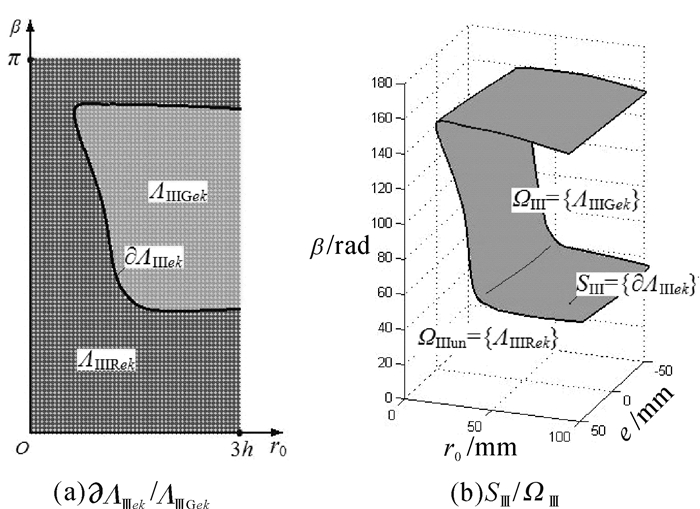
3.3 单一约束条件下的约束条件Ⅲ——接触强度条件 3.3.1 边界线əΛⅢek/解域ΛⅢGek据式(7)得到约束边界əΛⅠek,如图 6(a)所示,可知
|
| 图 6 接触强度约束的边界线/解域、边界面/解空间 Fig. 6 The bounding line/solution area,bounding surface/solution space based on tangency stress conditions |
1) 边界线əΛⅢek,形态特征:左端封闭、右端开口的“U”型曲线;
2) əΛⅢek将坐标平面分成两部分:解域ΛⅢGek,非解域ΛⅢRek.
3.3.2 边界面SⅢ={əΛⅢek}/解空间ΩⅢ={ΛⅢGek}堆积e=ek,数“U”型曲线堆积“U”型曲面——“边界面SⅢ”,即{əΛⅢek}.
SⅢ内、外:解空间ΩⅢ={ΛⅢGek}、非解空间ΩⅢun={ΛⅢRek},如图 6(b).
4 归并约束:边界线(面)、解域(空间)等重要结论 4.1 边界线/解域、边界面/解空间 4.1.1 边界线əΛ∑ek/解域Λ∑upek归并约束下的边界线(面)、解域(空间),指满足约束条件Ⅰ至Ⅲ的边界线(面)、解域(空间).
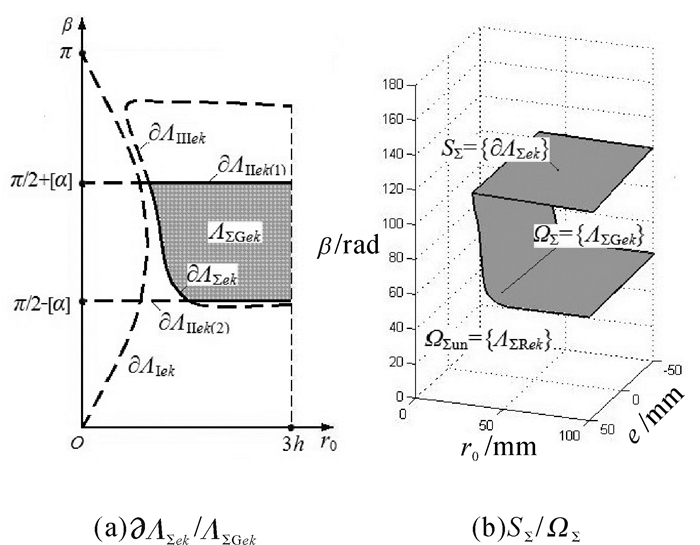
大量算例表明:多数情况下,əΛⅠek至əΛⅢek分布规律如图 7(a)所示:əΛⅠek位居əΛⅢek右侧,əΛⅡek(1),əΛⅡek(2)分别与əΛⅠek,əΛⅢek截交,Λ∑ek由əΛⅡek(1),əΛⅡek(2)和əΛⅢek截取而得.
根据3.1至3.3节,得到重要结论:
1) 边界线əΛ∑ek实际由əΛⅡek(1),əΛⅡek(2),əΛⅢek耦合而成.əΛ∑ek形态特征:“U”型弯折线,左端封闭、右端开口.
2) əΛ∑ek将坐标平面分为:解域ΛⅠ∑ek,非解域Λ∑Rek.
|
| 图 7 归并约束下的边界线/解域、边界面/解空间 Fig. 7 The bounding line/solution area,bounding surface/solution space based on merger conditions |
堆积e=ek,“U”型弯折线堆积成“边界面S∑”,即{əΛ∑ek}.S∑内、外两侧分别为:解空间Ω∑={Λ∑Gek}、非解空间Ω∑un={Λ∑Rek},如图 7(b).
4.2 “最优解区间”和“非劣解区间” 4.2.1 “最优解区间”əΛ∑ek(1)如前所述,凸轮基圆半径r0、压力角等是衡量材耗、传动和承载性能优劣的重要评价指标.
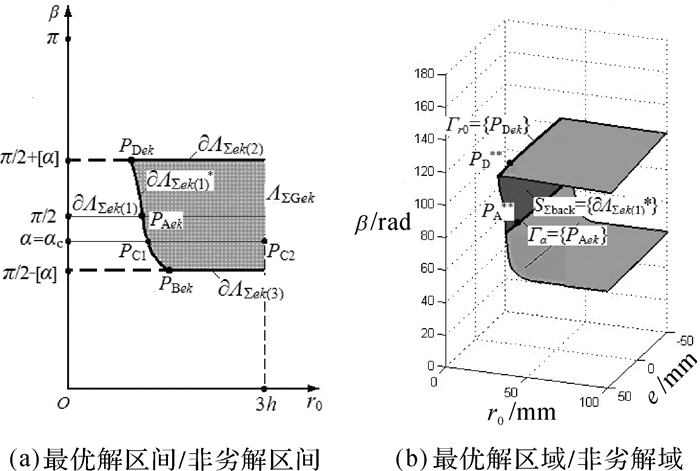
如图 8(a)所示,截平面e=ek,以PAek,PBek为节点将əΛ∑ek分为三部分əΛ∑ek(1),əΛ∑ek(2)和əΛ∑ek(3),取
| $ \alpha ={{\alpha }_{c}}\in [\pi /2-[\alpha ],\pi /2+[\alpha ]]. $ | (27) |
|
| 图 8 “最优解区间/域”和“非劣解区间/域”等 Fig. 8 “The optimal solution/ solution interval/solution” and “non-inferior solution interval/solution domain” and so on |
PC1→PC2,α相同,r0趋劣,PC1为PC1PC2上“最优解”.
故此,任取不同α值,得“最优解区间”为
| $ {{\Lambda }_{\sum{ek\left( 1 \right)}}}={{P}_{\text{D}ek}}\left( {{r}_{0i\text{D}}},{{\beta }_{j\text{D}}} \right),\cdots ,{{P}_{\text{A}ek}}\left( {{r}_{0i\text{A}}},{{\beta }_{j\text{A}}} \right),\cdots ,{{P}_{\text{B}ek}}\left( {{r}_{0i\text{B}}},{{\beta }_{j\text{B}}} \right). $ | (28) |
对于“最优解区间”əΛ∑ek(1),作进一步分析.
沿əΛ∑ek(1)自PDek至PBek:α先单调减(PDekPAek段),后单调增(PAekPBek段);r0在PDekPBek均单调增.
根据多目标优化理论[14],“最优解区间”əΛ∑ek(1)内,存在“非劣解区间”,实际综合时,仅需考虑əΛ∑ek(1)*.
əΛ∑ek(1)*的解析表达为
| $ \partial {{\Lambda }_{\sum{ek\left( 1 \right)}}}*={{P}_{\text{D}ek}}\left( {{r}_{0i\text{D}}},{{\beta }_{j\text{D}}} \right),\cdots {{P}_{\text{A}ek}}\left( {{r}_{0i\text{A}}},{{\beta }_{j\text{A}}} \right). $ | (29) |
据此,得到重要结论:
1) 满足约束条件Ⅰ至Ⅲ的“r0最优解”——PDek点;
2) 满足约束条件Ⅰ至Ⅲ的“α最优解”——PAek点;
3) 如图 1所示对象机构,“非劣解集”əΛ∑ek(1)*,恒存在于β为钝角的机构构型.
4.3 “非劣解域”、“最优解集”、“谷底点”和“影像点”等 4.3.1 “非劣解域S∑back”、“r0最优解集Гr0”和“α最优解集Гα”遍取不同e=ek,əΛ∑ek(1)*堆积得{əΛ∑ek(1)*}——“非劣解域S∑back”,如图 8(b)深灰色区域所示.
同理,遍取不同e=ek,则:
PDek堆积得{PDek}——“r0最优解集Гr0”;
PAek堆积得{PAek}——“α最优解集Гα”.
Гr0,Гα分别是S∑back的上下边界,Гr0和Гα形态:类抛物线,如图 8(b)所示.
显然,机构呈传统形态布局:β=90°(π/2),对象机构具有最佳传动性能.据上,机构呈特殊形态布局:β=120°(2π/3),对象机构具有最优尺寸.
4.3.2 “谷底点”及其“影像点”据4.3.1,引伸得重要结论:
1) “r0最优解集Гr0”类抛物线上,必存在一个“谷底点PD**”,取得最小基圆半径r0D**、对应平底夹角βD**及偏距eD**,如图 8(b)所示.其求解方法:沿əΛ∑ek搜索,通过计算、比较,筛选使满足式(8)的最小的r0Dek,以及对应βDek.
2) “α最优解集Гα”类抛物线上,必存在一个“谷底点PA**”,取得α最优解——基圆半径r0A**、平底夹角βA**及偏距eA**.其求解方法同上,不在赘述.
将“Гr0”,“Гα”向O-r0e坐标平面投影,得到2条平面曲线Гr0′,Гα′.“PD*”,“PA*”即“PD**”,“PA**”的影像点,如图 9所示.其求解方法同上,不在赘述.
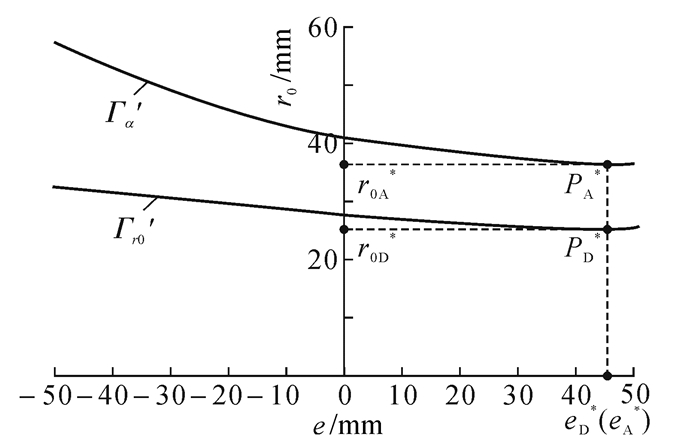
|
| 图 9 投影曲线“Гr0′”,“Гα′”和影像点“PD*”,“PA*” Fig. 9 Projective curve “Гr0′”,“Гα′” and Image points “PD*”,“PA*” |
“谷底点PD**”的特殊重要涵义:满足归并约束Ⅰ至Ⅲ下,取得最小尺寸的全局最优解.
5 尺寸综合示例已知:h=50 mm,Φg=150°,Φr=160°,Φs=30°和Φs′=20°,往程、返程分别选取3-4-5和摆线运动规律,[α]g=30°,[α]r=80°,Q=Q(φ)=8 000 N,n1=1 200 r/min,f=0.15,lex=80 mm,d=50 mm,l0=160 mm,mf=0.5 kg,ms=0.1 kg,sp=3.5 mm,k=7 N/mm,E1=2×105 MPa,E2=2×105 MPa,μ1=μ2=0.29,b=50 mm,[σH]g=350 MPa和[σH]r=20 MPa.试求解:
1) 满足聚合约束Ⅰ至Ⅲ下,“谷底点PD** (r0D**,βD**,eD**)”及“谷底点PA** (r0A**,βA**,eA**)”;
2) 已知条件同上,但其中Q,Φg,Φr等设为变量(取值见表 1),求机构尺寸最优解(r0最优).
| Φg,Φr | Q/kN | ||
| 0.8 | 8 | 80 | |
| 70°, 80° | 120, 62.83, 89.15 | 120, 150.28, 138.73 | 120, 322.17, 187.57 |
| 110°, 120° | 120, 31.21, 67.40 | 120, 52.15, 82.13 | 120, 281.53, 229.13 |
| 150°, 160° | 120, 5.73, 8.65 | 120, 24.13, 46.25 | 120, 268.83, 203.45 |
解:1) 据式(9)取m=2,即Δ=0.01 mm.取sup[r0]=150 mm,sup[β]=180°,inf[e]=-50 mm,sup[e]=50 mm,据式(12)算得imax=1.5×104,jmax=1.8×104,kmax=1×104,总共有imax·jmax·kmax=2.7×1012个网格节点.
据4.3.2,搜索求解“谷底点PD**”,解得r0D**=24.13 mm(i=2 413),βD**=120° (j=12 000),eD**=46.25 mm(k=4 625);搜索求解“谷底点PA**”,解得r0A**=37.01 mm(i=3 701),βA**=90°(j=9 000),eA**=46.25 mm(k=4 625).
同时,根据例题得到:
1) 工作载荷对机构尺寸影响,载荷越大,机构尺寸越大;
2) Φg,Φr对机构尺寸影响,且Φg,Φr越大,凸轮机构尺寸越小、越紧凑.
6 结 论1) 针对平底直动推杆盘形凸轮机构,给出形态构成、尺寸综合问题的科学准确描述和求解基本思路与步骤.
2) 系统提出“运动保真、传动性能和接触强度”等尺寸综合的3项性能评价指标,即3项约束条件.
3) 构建尺寸坐标系O-r0βe、尺寸空间Ω(r0,β,e),建立可视映射模型;揭示单一约束和归并约束下的边界线、解域和边界面、解空间,成功实现了朝二维、三维尺寸坐标系的可视映射.
4) 揭示“最优解/解区间/解集”、“非劣解区间/解域”和“谷底点”等存在性和重要意义,给出求解方法.
基于可视映射的思想和手段,构建尺寸坐标系、尺寸空间,实现复杂解析公式的可视映射,系统、全面地解决了平底直动推杆盘形凸轮机构的性能评价、尺寸综合问题,其尺寸综合思想,为解决工程设计机构尺寸综合问题提供了理论依据.
| [1] | 华大年,唐之伟.机构分析与设计[M].北京:纺织工业出版社,1985:103-162. HUA Da-nian,TANG Zhi-wei.Analysis and design of mechanisms[M].Beijing:Textile & Apparel Press,1985:103-162. |
| [2] | 伏尔默 J.凸轮机构[M].郭连声,译.北京:机械工业出版社,1983:21-78. VOLLMER J.Cam mechanisms[M].Translated by Guo Lian-sheng.Beijing:China Mechine Press,1983:21-78. |
| [3] | 常勇,徐继杨,黎庆.推导凸轮廓线外凸性判据和曲率半径的一种新方法[J].黑龙江商学院学报(自然科学版),1996,12(2):43-50. CHANG Yong,XU Ji-yang,LI Qing.A new method for deriving the external-convexity criterion and convature radius formula[J].Journal of Heilongjiang Commercial College (Natural Sciences Edition),1996,12(2):43-50. |
| Cited By in Cnki (29) | Click to display the text | |
| [4] | 魏晓鸣,常勇,李延平.最小尺寸直动平底从动杆平面凸轮机构的设计方法[J],黑龙江商学报(自然科学版),1994,10(3):30-33. WEI Xiao-ming,CHANG Yong,LI Yan-ping.A designing method of the follow planar cam mechanism with minimum size translating flat bottom[J].Journal of Heilongjiang Commercial College (Natural Sciences Edition),1994,10(3):30-33. |
| Cited By in Cnki (7) | Click to display the text | |
| [5] | 刘远伟,常勇.基于接触强度的最小尺寸凸轮机构设计[J].机械设计,1997,14(10):10-13. LIU Yuan-wei,CHANG Yong.Application innovation of cam mechanism based on tangency stress[M].Journal of Machine Design,1997,14(10):10-13. |
| Cited By in Cnki (22) | Click to display the text | |
| [6] | 石永刚,吴央芳.凸轮机构设计与应用创新[M].北京:机械工业出版社,2007:37-82. SHI Yong-gang,WU Yang-fang.The design and application innovation of cam mechanism[M].Beijing:China Machine Press,2007:37-82. |
| [7] | 牧野洋.自动机械机构学[M].胡茂松,译.北京:科学出版社,1980:176-234. HIROSHI M.Automatic mechanism and machine theory[M].Translated by HU Mao-song.Beijing:Chinese Science Press,1980:176-234. |
| [8] | 华大年.按许用压力角设计最小尺寸摆动从动杆平面凸轮的解析法[J].机械工程学报,1982,18(4):74-79. HUA Da-nian.Method for designing minimum size oscillating follower plane cam mechanisms according to alloyvable pressureAngle[J].Journal of Mechanical Engineering,1982,18(4):74-79. |
| [9] | NAVARRO O,WU C J,ANGELES J.The size-minimization of planar cam mechanisms[J].Mechanism and Machine Theory,2001,36(3):371-386. |
| Click to display the text | |
| [10] | SCHOENHERR J.Synthesis of planar cam mechanics with lowest dimensions[J].Mechanism and Machine Theory,1993,28(3),317-325. |
| Click to display the text | |
| [11] | 李延平,林荣富,常勇.浮动平底推杆凸轮机构的第Ⅱ类尺寸综合问题[J].中国机械工程,2015,26(5):611-619. LI Yan-ping,LIN Rong-fu,CHANG Yong.Class Ⅱ synthesis of cam mechanism with floating flat faced pushrod[J].Journal of Mechanical Engineering,2015,26(5):611-619. |
| Cited By in Cnki | |
| [12] | 常勇,林荣富,李延平.浮动平底推杆共轭凸轮机构的第Ⅱ类机构综合问题研究[J].农业机械学报,2014,45(3):331-338. CHANG Yong,LIN Rong-fu,LI Yan-ping.Class II synthesis of conjugate cam mechanism with floating flat faced pushrod[J].Transactiongs of the Chinese Society for Agricultural Machiney,2014,45(3):331-338. |
| Cited By in Cnki | |
| [13] | 李晓梅,黄朝晖,蔡勋,等.并行与分布式可视化技术及应用[M].北京:国防工业出版社,2001. LI Xiao-mei,HUANG Chao-hui,CAI Xun,et al.Parallel and distributed visualization:techniques and applications[M].Beijing:National Defense Industry Press,2001. |
| [14] | 刘三明.多目标规划的理论方法及其应用研究[M].上海:上海交通大学出版社,2014:16-55. LIU San-ming.Research on synthetical analysis and assessmentch of multi-objective planning[M].Shanghai:Shanghai Jiaotong University Press,2014:16-55. |



