2. 河海大学 沿海开发保护协同创新中心, 江苏 南京 210098
2. Coastal Development and Protection Synergy Innovation Center, Hohai University, Nanjing 210098, China
风能是现有能源中具有较大开发价值和大规模利用可行性的优质可再生能源,世界各国都将风能视作当下新能源开发的重要方向.据统计:2014年中国风电新增装机量为23 196 MW,同比增长44.2%;累计装机达到114.61 GW,同比增长25.4%[1],正处在高速发展的黄金时期.
塔架在风力机结构系统中的作用是支撑上部机组结构,将来自于自重、环境和运行过程等的结构载荷传递到基础,既为风轮在空间中提供了足够的工作高度,也为整个风力机组的稳定可靠工作提供保障.现代风力机向大型化发展的同时,也使整机的体型更加庞大,其中,塔架部分可达百吨以上,占总造价的20%左右,是风力机的重要组成部分,因此对设计方案的经济性与可靠性提出了更高的要求.本文围绕塔架结构形式、静动力学特性、稳定性与疲劳特性等问题,总结了现有设计方法与分析思路,并对一些研究热点的发展方向作出展望.
1 塔架选型根据实际的风场条件、功率配置以及设计要求选择合理的塔架结构形式,不仅能够提高塔架的刚度、强度、稳定性,充分发挥材料性能,而且在经济性、美观性及生产运输等方面起到积极作用.目前,风力机塔架的结构形式主要分为2类.
图 1筒型塔架在当前的风力机设计中被大量使用,其优点是外形简洁美观、构造简单、传力明确、占地面积小、用钢量少,上下塔架安全可靠.图 2格构式塔架在高度和刚度设计要求相同时,材料消耗比筒型塔架减少约40%,且格构式塔架的构件尺寸小,具有加工工艺简单、成本低、运输方便等优点.缺点是占地面积大,上塔梯子不好安排且不安全等,限制了此型塔架的应用[2].从结构的角度,两型塔架各有特点,筒型塔架的刚度条件通常是主要设计控制因素,而格构式塔架的刚度相对较好,设计过程中主要考虑经济因素,前者可通过选择塔身最佳顶底径比、宽高比、斜率控制,后者则要求综合考虑宽高比与腹板布置方式[3].综上,筒型塔架结构性能好,人工维修方便安全,外形美观,仍是目前设计制造的主流[4].同时,格构式塔架也有应用,特别在风力机大型化趋势下,其成本低、便于运输的优点表现更为突出.近年来国外的一些高度在100 m以上的风电项目中,格构式设计被重新重视,有研究则直接提出塔架高于50 m时,应采用格构式塔架,而低于40 m的塔架宜采用圆筒式塔架[5].

|
| 图 1 圆(锥)筒型塔架 Fig. 1 Round (cone) type tower |

|
| 图 2 格构(桁架)式塔架 Fig. 2 Lattice (truss) type tower |
随着风力机大型化和装备制造技术的发展,越来越多的新结构和新材料被应用到塔架设计中,补充了风电技术发展对塔架性能的要求.例如,钢管混凝土三肢柱塔架在轴向力作用下具有更加优越的力学性能,结合了钢材与混凝土的材料优点,提升结构性能的同时,降低了整体用钢量[6].这些研究,为风力机塔架设计的多样化选型提供了科学的依据,完善了体型设计的理论体系,同时,新型塔架结构普遍存在的设计论证不足、制备工艺缺失以及实验研究落后的问题,仍待后续研究进行补充和突破.
2 塔架静力与动力特性 2.1 静力分析静力设计保障了结构的强度和刚度两项主要性能指标,是其他设计分析环节的基础.塔架结构形式和材料的选用一般随项目对产品性能与适用工况的要求而定,实际的设计分析方法和工具因人而异,但是,静力分析的理论依据基本一致,即建立线弹性模型,确定危险截面,进行内力分析.当结构大变形等非线性性质带来的影响无法忽略时,则应进行相应的非线性分析[7].
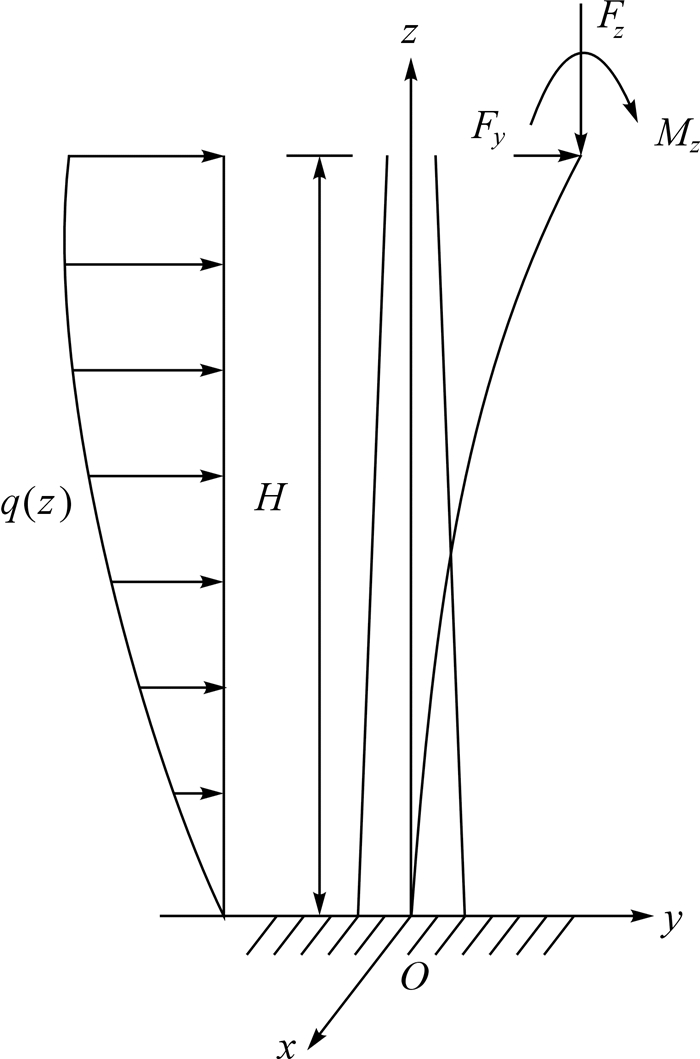
建模与加载是力学特性分析的首要步骤.风力机塔架静力分析的建模相对简单,其中,具有代表性的方案如图 3,根据锥筒型塔架的几何与受力特点将其简化成集弯曲变形、轴向压缩变形及扭转变形为一体的复杂梁柱问题,设定坐标原点后,对水平风向推力、轴向上部结构压力及侧向风压等荷载进行简化加载,模型即可被视为一端固定、一端自由的变截面悬臂梁结构[8].
|
| 图 3 锥筒型塔架静力学模型 Fig. 3 Statics model of cones type tower |
风力机塔架作为一类薄壁高耸构筑物,侧向变形较大,刚度往往是结构设计的主要控制因素.在同一载荷情况下,塔架的位移量随着高度的增加而增加,因而通过计算塔顶位移程度可以定量分析设计刚度指标.根据上述力学模型,塔架顶端的水平位移Δ可由结构位移公式计算得出[9]:
| $ \vartriangle =\sum{_{L}\frac{{{M}_{\text{k}}}{{M}_{\text{f}}}}{EI}\text{ds}}, $ | (1) |
结合材料力学[10]知识可将(1)式求解得到
| $ \vartriangle =\frac{P{{L}^{3}}}{3E{{I}_{\text{p}}}}+\frac{M{{L}^{3}}}{2E{{I}_{\text{m}}}}+\frac{P{{L}^{3}}}{8E{{I}_{\text{q}}}}, $ | (2) |
式中:Ip,Im,Iq分别表示由横向力、弯矩、均布载荷作用下结构对应的当量惯性矩.需根据不同载荷的组合情况,由刚度条件,分别建立惯性矩与当量惯性矩关系式,推导出计算阶梯型与锥型风力机塔架的当量惯性矩计算式,代入式(2)得到变截面塔架顶端水平位移的理论计算公式.在校核设计安全性时,根据经验,塔架许用挠度应控制在塔架总高度的0.5%~0.7%[11].
上述理论计算方法是一种简化计算方法,不仅过程繁琐,效率低,且计算值与实际值之间的差异较大.随着有限元分析技术的发展,国内外研究者更多地使用ANSYS等有限元分析软件进行电算研究,理论计算结果则提供了验证模型合理性与计算结果可靠性的重要参考依据.有限元静力分析发现塔架上应力分布并非是均匀的,沿风向两侧由风载引起的弯曲应力较大,若考虑塔底开门洞,会改变局部截面尺寸,影响结构整体性,计算结构中塔顶端位移及底部应力都有一定增加,因此在风力机塔架建模时应按实际情况考虑.
2.2 动力分析风力机结构设计分析的荷载条件十分复杂,而塔架的柔性特征会使结构对动荷载作用格外敏感,因此在满足结构静强度要求的前提下,需要对塔架进行动力分析.
动力分析是用来确定惯性(质量效应)和阻尼起着重要作用时结构或构件动力学特性的技术,核心是通过模态分析得到塔架的固有频率和振型,即动态特性[12].通过模态分析,掌握塔架的固有频率就可以从结构设计的角度避免与外部激励荷载频率接近而发生共振,进而获得结构动态响应等方面的数据,掌握相邻结构之间的耦合关系和系统整体的动态特性,为结构动态设计与改进提供依据.动力分析的理论基础是动力学方程:
| $ M\cdot \ddot{u}+C\cdot \dot{u}+K\cdot u=F, $ | (3) |
动态特性的分析方法一般可分为3类:
1) 由机械能守恒定律推演而来的瑞利法,将塔架模型视作顶端作用荷载的悬臂梁结构,对前3阶振动模态进行较为精确的估算.瑞利法是塔架固有频率的经典计算方法,边界条件要求简单,计算简便,可以满足一般工程计算的需要[13].
2) 模态叠加法由国外研究者提出[14],现已成为模态分析中的常用方法,它利用结构的前几阶主模态构成坐标变换矩阵Φ进行变换,建立以模态坐标为基本未知量的运动方程:
| $ m\cdot \ddot{q}+k\cdot q={{F}_{\text{m}}}, $ | (4) |
式中:m为模态质量矩阵;k为模态刚度矩阵;q为模态坐标;Fm为模态激振力.通过恰当选择Φ变换,使新坐标q具有解耦性质.
该方法可以用较少的自由度模拟塔架的动态行为,简化计算,但精度较低.
3) 有限元法是利用有限元原理及计算机技术对模态叠加法的改进,在多自由度空间中考虑了离散分布的质量产生的惯性力,并借助大型有限元软件提升了计算的精度,是动态分析领域的主流方法.
在模态分析的基础上,动力分析还包括了谐响应分析、瞬态动力学分析、响应谱分析、随机振动分析和显示动力学分析,不同的分析类型对应求解(3)式不同形态的方程.
与静力分析中的简化力学模型不同,结构在复杂荷载作用下的响应模式较难有统一的建模参考.一方面,固有频率和主振型是结构振动系统的自然属性,因此塔架结构形式的变化会影响塔架动力特性分析的计算结果.例如,转动惯量会影响扭转自振频率的计算,如果要求计算较高精度的高阶自振频率,可将机仓的转动惯量简化为作用在塔架顶端节点上的集中转动惯量[15].在塔架设计的将来,针对门洞、连接法兰、变壁厚、基础等结构变型的精细化建模分析会逐渐成为重要的研究方向.
另一方面,对激励荷载不同的加载处理,也会影响动力分析的结果.
共振分析时,多数研究者考虑了风轮叶片的转动对塔架振动的激励作用[16],由于风轮是整个结构体系中最大的运动体,而通过频率是其主要的周期荷载,因而这一方法可满足一般工程设计的需要.进一步研究风轮的复杂运动过程对塔架的动力学影响,可建立风力机叶片和塔架的耦合动力学模型来模拟整个系统的动态行为,采用模态综合法,对两部分进行耦合求解[17],耦合分析法的计算结果更加逼近现实工况,分析过程也相对繁琐.除了风轮旋转,传动系统、变桨及偏航控制机构等的运行同样会产生动荷载,针对不同的研究需求,分析结构在特定激振荷载条件动态特性,能够帮助完善塔架结构的设计.
风荷载作用由风场条件决定,与机械荷载相比,随机性明显,表现形式更复杂,因此增大了荷载模拟的难度.显然,此问题的解决,必然是多学科方法综合应用的结果,近些年来,随着与风电场关联的力学[18]、环境科学[19]等的发展,国内外研究者对完善塔架力学模型进行了许多具有创新性的探索,提出了考虑风力机空气动力学与结构弹性力学耦合的设计模型[20].在对风荷载进行数值模拟时,一些研究以随机数学模型为基础,建立风能参数随机统计模型,进行相应的频域动态分析[21],这一方法在过去被工程与研究领域大量使用,优点是简化了随机风场模型,使得计算效率大大提高,缺点是无法充分考虑随机风场的非线性特征,尤其是风力机塔架这类高耸结构,因复杂气象导致的瞬时非稳态荷载所产生的非线性响应现象不应被忽视.时域分析是解决这一问题的主要思路,方法众多,小波变换是其中适用性较好的一种代表方法,受各国研究者重视,Thai-Hoa[22]于2015年提出以降阶wavelet-Galerkin (WG)方法可将耦合、非线性微分方程分解为小波域内的随机代数方程进行求解,并通过仿真数值计算验证了其理论的可行性与实用性.目前对非稳态随机过程的数值分析方法的研究还在继续,新方法层出不穷,旧方法的适用性及计算效率都有待提高.
3 塔架屈曲特性锥筒式风力机塔架所使用的细长圆柱薄壳结构广泛应用于工业及民用的各个领域,这类结构在受压时,常发生整体或局部的失稳破坏,因此其承载力往往取决于结构的稳定性,对其屈曲强度的可靠预测一直为人们所关注[23].总结目前以风力机塔架为对象的屈曲特性研究,可将分析方法概括为理论计算、工程计算与有限元计算三种.
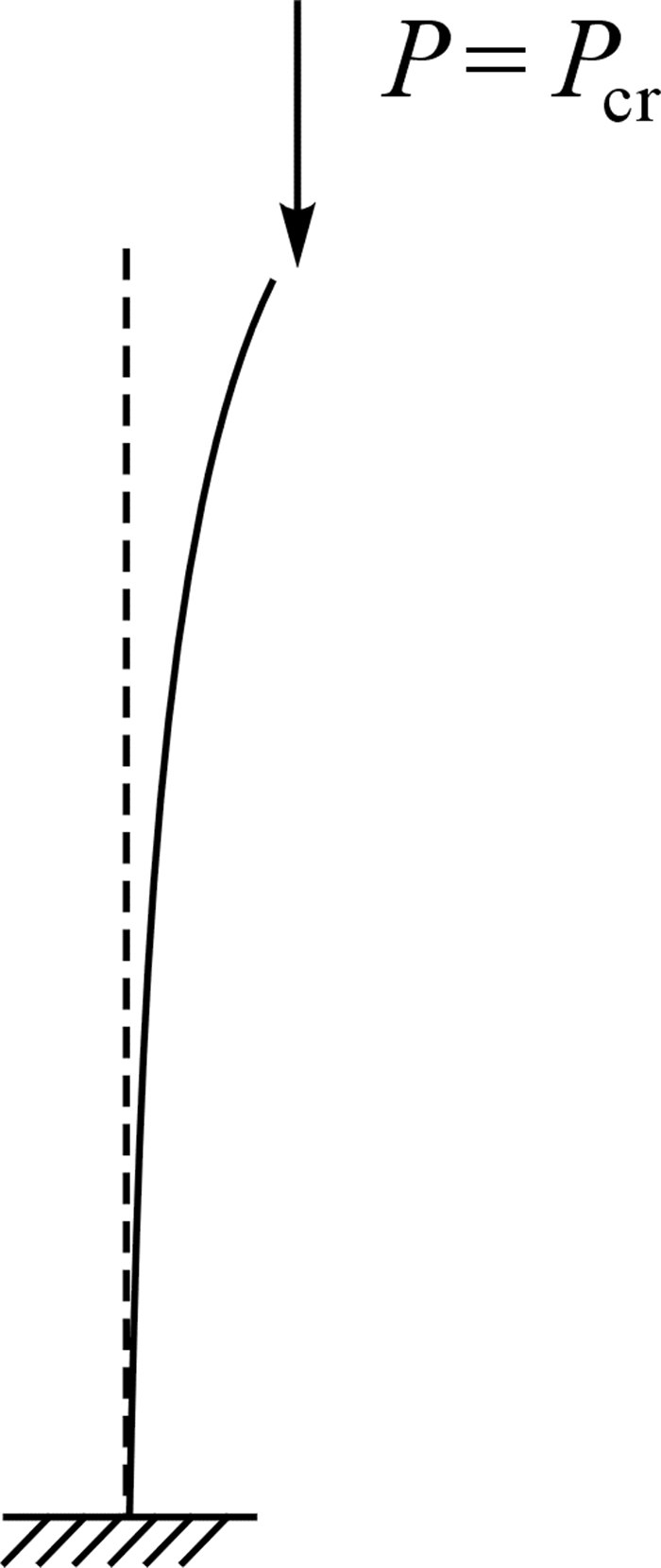
细长杆件稳定性的理论研究历史悠久,16世纪瑞士科学家欧拉(L.Euler)提出了压杆弹性稳定问题,并给出了著名的求解如图 4小挠度下线性屈曲临界荷载的欧拉公式(5)[10],至今仍是解决细长或薄壁构件屈曲稳定性问题的重要理论基础.
| $ {{P}_{\text{cr}}}=\frac{{{\pi }^{2}}EI}{{{\left( \mu l \right)}^{2}}}, $ | (5) |
|
| 图 4 压杆临界受力示意图 Fig. 4 Critical force diagram of compressive bar |
风力机塔架的体型属于长圆柱壳,适用欧拉屈曲模式进行理论计算,先由弯曲变形的微分公式导出相应约束条件的欧拉公式,并保证屈曲临界应力小于比例极限.也有如文献[23],应用弹性稳定性理论中的能量准则[24]计算临界压力,最终推导出的公式与文献[10]中一端固定、一端自由约束条件下的等截面压杆欧拉公式相同.然而,实际算例结果表明,欧拉算法得到的屈曲临界荷载远大于结构实际抗屈曲强度,这是由经典弹性稳定性理论小变形、等截面以及忽略初始缺陷等理想假设与实际工程结构存在较大差异造成的,影响了设计的安全性,无法被广泛应用.
为弥补理论算法的不足,简化计算过程,以满足工程设计的需要,各国规范给出了以大量轴压圆柱壳屈曲稳定实验结果为依据的经验公式,结合薄壁圆柱壳的线性屈曲理论构建了风力机塔架屈曲分析的工程计算方法.其中,英国Eurocode3 1-6[25]及德国DIN18800-4[26]是目前塔架稳定性分析应用较多的2份标准.两者有着相似的组织架构、理论基础、计算过程以及工程解释,主要差别在于,前者加入了制造公差质量等级概念,根据初始缺陷幅值将圆柱壳分成A,B,C三级制造质量,并与计算公式紧密结合,通过参数变化体现了质量要求对计算结果的影响[27],而后者的计算过程相对简化[28].以此为基础,2010年GL规范[29]针对塔架开门洞和分段制造、法兰连接的设计,对工程算法进行了改进.
随着风力机设计制造技术的发展,塔架门洞、门框形式渐趋于多样化,使得某些经验算法已不再适用.因此,在塔架屈曲设计分析实践中,有限元等数值分析方法应运而生[30].以ANSYS软件为例,程序提供了2种进行屈曲分析的方法:线性(特征值)屈曲分析和非线性屈曲分析.线性屈曲分析即传统的理想线弹性屈曲分析方法,其求解思路是根据内力分布的计算结果构造几何刚度矩阵,代入增量有限元平衡方程:
| $ \left( {{K}_{0}}+{{K}_{\sigma }}+{{K}_{\varepsilon }} \right)\cdot \vartriangle {{u}_{c}}=0, $ | (6) |
式中:K0为单元的弹性刚度矩阵;Kσ为单元的初应力刚度矩阵;Kε为单元的初应变刚度矩阵;Δue为节点位移增量向量.
得到线性稳定控制方程:
| $ {{K}_{0}}+{{\lambda }_{\text{cr}}}K_{\sigma }^{p}=0. $ | (7) |
然而,实际结构中不可忽视的非线性因素使得线性分析方法对屈曲极限载荷往往产生过于乐观的预计,影响了结构的安全与可靠,因此,在设计与分析过程中应该考虑几何非线性和失稳前应力状态的影响[32].非线性屈曲分析中通过不断更新刚度矩阵来考虑非线性效应,并提取线性屈曲分析结果作为几何缺陷条件,通过逐渐加载直至最大荷载的非线性静力分析方法得到失稳临界载荷,既考虑了变形对平衡方程的影响,又采用了非线性变形几何关系,可以得到更精确的屈曲载荷[33].
不论采用何种数值计算方法进行非线性屈曲分析,都需要解决大挠度非线性建模与非线性代数方程求解两个重要问题[34],前者将研究前沿从几何非线性问题引入物理非线性层面以及几何、荷载混合缺陷对结构的影响等,而后者则促进了有限元领域的发展,一些国外学者引入模糊理论、神经网络、专家系统等新兴学科提出多种新型计算方法.
4 塔架疲劳特性近年来,各地风场出现了多起风力机倒塌造成巨大经济损失的事故,分析表明,结构疲劳引起的断裂破坏是这些事故主要原因,因此,疲劳特性分析是塔架结构设计中必不可少的环节.
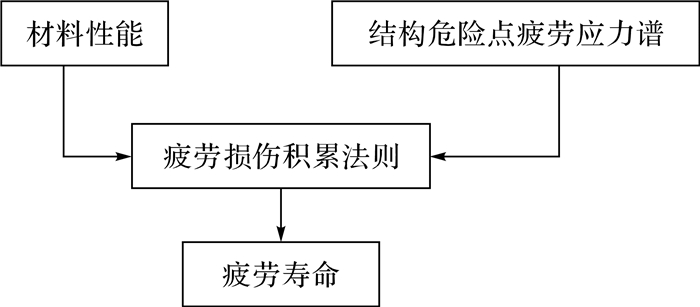
预测结构及构件的疲劳寿命是疲劳分析的核心,为设计分析提供依据.有限寿命结构的疲劳分析应根据实际的荷载情况与结构特征,选用应力疲劳(S—N)分析或应变疲劳(E—N)分析方法.风力机塔架是典型的高周疲劳构件,适用S—N曲线法,关键环节包括危险点应力谱的提取以及损伤积累模型的选取两部分.疲劳寿命分析流程图如图 5所示.
|
| 图 5 疲劳寿命分析流程图 Fig. 5 Flow chart of the fatigue life analysis |
结构危险点由静动力分析得到,结合疲劳荷载谱,可以求解相应位置的疲劳应力谱.疲劳荷载由周期荷载与随机荷载组成,前者主要由叶轮偏心、塔影效应、风力剪切等产生,而后者多为随机风荷载作用,其中,随机荷载因其在时间与空间上的无规律,给编制荷载谱造成了困难,是解决疲劳问题的关键技术环节.文献[35]在对海上风力发电机组塔架的疲劳分析中,应用线性波理论模拟非规则的海浪,分析作用在圆筒型塔架上的波浪载荷,建立了波浪力的分析模型,应用数值方法对随机风载荷和波浪载荷作用下的塔架动力响应与疲劳寿命问题进行了分析.该研究根据监测数据,结合数学模型,近似地模拟不规则荷载的作用,是目前提取随机荷载谱的重要手段,具有一定代表性,对陆上风力发电机同样具有参考价值.文献[36]基于MCMC(马尔可夫链蒙特卡洛)理论建立了风速的预测模型,并应用POT(超定量法)外推理论对载荷谱进行了有效的极值载荷推断,得到了更为符合风场实测数据的模拟结果.2015年韩国研究者[37]根据冯卡门各向同性湍流模型及威布尔分布理论构建了小型风力机复合叶片的疲劳分析模型,通过非线性回归分析得到了以威布尔分布型参数K与尺度参数C为变量的二阶回归方程,并根据对方程的敏感性分析了威布尔参数对疲劳寿命预测的影响.这类研究普遍是通过改进或革新数学模型提高了对随机荷载模拟的准确性,但是荷载谱编制过程及随机模型计算方法仍需简化推广,待进一步研究.
疲劳损伤是指结构在超过疲劳极限的应力循环作用下,从微观裂纹到宏观裂纹并最终引起破坏的发展过程.通过对疲劳荷载谱的分析,将持续作用在结构上的疲劳荷载离散为众多荷载循环步,每一次循环都会给材料造成一定的损伤,依据损伤积累理论,随着循环次数的增加,损伤量被累积,最终导致结构疲劳破坏.国内外研究者提出了多种损伤积累理论,分为线性与非线性两大类,线性理论将各个循环步视作相互独立,进行累加计算,而非线性理论则需要考虑材料上不同点之间、不同时间步之间相互的影响.疲劳损伤积累理论的发展经历了线性疲劳积累理论、修正的线性疲劳积累理论和非线性疲劳积累理论三个过程.
1999年,美国学者Herbert J.Sutherland[38]基于线性疲劳损伤累积理论和S—N曲线对风力机叶片进行了寿命预测.2012年,国内学者由实验数据拟合得到了塔架钢材的S—N曲线,并根据经验估计了塔架载荷谱,使用线性Miner理论完成了风机塔架的寿命评估[39].线性疲劳积累理论在应用与发展的过程中,其在时空概念上过于理想的独立性假设导致的寿命预测偏差问题暴露出来,一些修正的线性积累理论随之提出,其中,文献[40]认为风力机工作工况复杂,不宜直接应用Miner法则,提出了两级疲劳损伤累积法,依次进行单工况级和总工况级的损伤累积对线性计算进行修正.该研究在国内具有突破性和代表性,计算结果验证了所提出的经过修正的线性损伤模型,然而,由于缺少实测数据,通过计算得到的荷载谱,无法全面反映风力机所在工况的疲劳荷载情况,有待进一步深入研究.
国外学者的研究认为线性理论不仅不适用于金属材料,也被证明不适用于复合材料[41],这一结论得到了学术界的广泛认可,促使如非线性理论、双线性理论以及能量法等新的损伤积累模型的提出.一些学者利用风速观测数据,提出了计算风力机叶片疲劳载荷的新方法[32],这种方法在保证精度的前提下有效降低了获取叶片疲劳载荷的复杂性,研究了疲劳损伤的非线性特性.然而,大多数创新模型因计算过程的复杂和分析方法的不成熟,而长期停留在理论研究的阶段,仍待后续研究进行改良与定型.
上述线性或非线性疲劳寿命预测方法的原理及应用都是在数值计算范围内进行的,然而,科学研究尤其是工程问题的研究,实验是直接有效的手段.21世纪初,爱尔兰人将实验引入了风力机的设计分析过程,对随机采样获得的风载荷与风力机塔架的动态耦合关系进行了全面分析[43].依据实验结果对数值计算过程进行修正,完善了现有的设计理论,而实验设计的局限也影响了成果的适用性,但这一方法仍然值得思考和借鉴.同一时期,清华大学的研究者搭建了一个模拟风力机实验台,通过实验研究模拟风力机的动力响应状态,研究其疲劳损伤过程,弥补了纯理论分析在实际应用上的不足[44].近期,美国的一个研究团队结合3D打印技术制作了风力机模型,并进行了一系列风洞实验,研究了叶片不同攻角及扭转动作对临界与超界流体状态下结构动态响应的影响[45].这一研究,进一步发展了风力机动力及疲劳特性的实验研究方法,融合了不同工业门类前沿技术,对柔性结构设计与未来3D打印成型技术进行了超前研究,具有一定的开拓性,而国内相关领域未见有类似研究出现,也缺少针对性的风洞实验,值得投入更多的关注.
5 结 论1) 现阶段,风力机塔架的设计仍以锥筒型为主,但随着风电产业发展,风场条件趋于多样化,相关制造工艺与材料科学不断进步,可以预见如柔性塔架及混合型塔架等新型塔架结构形式会逐渐投入使用.
2) 静动态特性分析仍是当前研究领域的主流与前沿,尤其是动力学问题的发展,已经突破旧有理论与规范标准的限制,向随机荷载条件、材料非线性行为以及多体耦合问题发展.
3) 实践证明,Eurocode 31-6和DIN18800-4两部标准经过修订与补充后已经能够满足工程设计的需要,对塔架结构稳定性分析具有指导作用.
4) 疲劳寿命预测的2个关键技术问题是编制疲劳荷载谱与建立损伤积累模型,前者与结构选型和静动态特性分析环节发生交叉,后者则围绕非线性、模型化等关键问题成为该领域的主要研究发展方向.
5) 实验研究能够解决数值分析方法在处理复杂流体环境以及高周疲劳构件寿命理论预测结果验证的难题.国外研究证明,将大气观测数据和平台实验数据应用于理论计算与分析,能够显著提高分析效率.
| [1] |
中国可再生能源学会风能专业委员会.2014年中国风电装机容量统计[J].风能,2015(2):36-49. Chinese Wind Energy Association.China's wind power installed capacity in 2014[J].Wind Energy,2015(2):36-49. |
| Cited By in Cnki (4) | Click to display the text | |
| [2] |
芮晓明,柳亦兵,马志勇.风力发电机组设计[M].北京:机械工业出版社,2010:152-153. RUI Xiao-ming,LIU Yi-bing,MA Zhi-Yong.Wind turbine design[M].Beijing:China Machine Press,2010:152-153. |
| [3] |
孙晓颖.风力机塔架结构选型研究[EB/OL].[2013-02-07].http://www.paper.edu.cn/releasepaper/content/201302-190. SUN Xiao-ying.Structure from selections of wind turbine towers[EB/OL].[2013-02-07].http://www.paper.edu.cn/releasepaper/content/201302-190. |
| Cited By in Cnki | Click to display the text | |
| [4] |
单蕾.风力机塔架结构选型与受力性能研究[D].哈尔滨:哈尔滨工业大学土木工程学院,2009:16-23. SHAN Lei.Structural performance and design of wind turbine towers[D].Harbin:Harbin Institute of Technology,School of Civil Engineering,2009:16-23. |
| Cited By in Cnki (21) | Click to display the text | |
| [5] | TRACY L,TOM C.A new tower technology for reducing cost of energy[J].North American Wind Power,2005,48(4):48-53. |
| [6] |
姜顺先,王存堂,于浩源.格构式钢管混凝土风力发电塔架设计[J].辽宁工程技术大学学报(自然科学版),2012,31(2):202-205. JIANG Shun-xian,WANG Cun-tang,YU Hao-yuan.Design of wind turbine tower using lattice concrete-filled steel tube[J].Journal of Liaoning Technical University(Natural Science),2012,31(2):202-205. |
| Cited By in Cnki (4) | Click to display the text | |
| [7] |
中国机械工业联合会.风力发电机组设计要求:JB/T 10300-2001 [S].北京:中国机械工业出版社,2001:33-35. China Machinery Industry Federation.Wind turbine generator system:design requirements:JB/T10300-2001 [S].Beijing:China Machinery Industry Press,2001:33-35. |
| [8] |
宋曦,戴建鑫.水平轴风力机塔架的力学建模及ANSYS仿真分析[J].甘肃科学学报,2011,23(1):91-95. SONG Xi,DAI Jian-xin.Mechanical modeling and ANSYS simulation analysis of horizontally axial wind turbine tower[J].Journal of Gansu Sciences,2011,23(1):91-95. |
| Cited By in Cnki (22) | Click to display the text | |
| [9] |
蔡新,孙文俊.结构静力学[M].南京:河海大学出版社,2003:51-55. CAI Xin,SUN Wen-jun.Mechanics of structures[M].Nanjing:Hohai University Press,2003:51-55. |
| [10] |
徐道远.材料力学[M].南京:河海大学出版社,2006:107-111. XU Dao-yuan.Mechanics of materials[M].Nanjing:Hohai University Press,2006:107-111. |
| [11] |
斯建龙,涂刚,沈风亚,等.大型风力发电机组塔架顶端的水平位移的计算[J].能源工程,2009,134(2):28-30. SI Jian-long,TU Gang,SHENG Feng-ya,et al.Horizontal displacement calculation of the top of large-scale wind turbine tower[J].Energy Engineering,2009,134(2):28-30. |
| Cited By in Cnki (11) | Click to display the text | |
| [12] |
黄文怡,梁波,代洪庆,等.风力发电机塔筒的强度、稳定性及动力学分析[J].黑龙江八一农垦大学学报,2010,22(3):30-33. HUANG Wen-yi,LIANG Bo,DAI Hong-qing,et al.Analysis for wind turbine tower strength,stability and dynamics[J].Journal of Heilongjiang Bayi Agricultural University,2010,22(3):30-33. |
| Cited By in Cnki (7) | Click to display the text | |
| [13] |
李立本.风力机结构动力学[M].北京:北京航空航天大学出版社,1999:135-147. LI Li-ben.Dynamics of wind turbine structure[M].Beijing:Beijing University of Aeronautics and Astronautics Press,1999:135-147. |
| [14] | BURTON T,SHARPE D,JENKINS N,et al.Wind energy handbook[M].Chichester:John Wiley & Sons,2001:453-464. |
| [15] |
陆萍,秦惠芳,栾芝云.基于有限元法的风力机塔架结构动态分析[J].机械工程学报,2002,38(9):127-130. LU Ping,QIN Hui-fang,LUAN Zhi-yun.Dynamic analysis of tower structure for wind turbine based on finite element method[J].Journal of Mechanical Engineering,2002,38(9):127-130. |
| Cited By in Cnki (116) | Click to display the text | |
| [16] |
刘林.水平轴风力发电塔架的有限元分析及优化设计[D].南京:河海大学力学与材料学院,2013:39-52. LIU Lin.The finite element analysis and design optimization of the cone-type wind tower[D].Nanjing:Hohai University,College of Mechanics and Materials,2013:39-52. |
| [17] |
刘雄,张宪民,陈严,等.水平轴风力机结构动力响应分析[J].太阳能学报,2009,30(6):804-809. LIU Xiong,ZHANG Xian-min,CHEN Yan,et al.Structure dynamic response analysis of horizontal axis wind turbines[J].Acta Energiae Solaris Sinica,2009,30(6):804-809. |
| Cited By in Cnki (33) | Click to display the text | |
| [18] | WANG J H,QIN D T,LIM T C.Dynamic analysis of horizontal axis wind turbine by thin-walled beam theory[J].Journal of Sound and Vibration,2010,329(17):3565-3586. |
| Click to display the text | |
| [19] | LI Y,CASTRO A M,SINOKROT T,et al.Coupled multi-body dynamics and CFD for wind turbine simulation including explicit wind turbulence[J].Renewable Energy,2015,76(4):338-361. |
| Click to display the text | |
| [20] | CARRIÓN M,STEIJL R,WOODGATE M,et al.Aeroelastic analysis of wind turbines using a tightly coupled CFD-CSD method[J].Journal of Fluids and Structures,2014,50(26):392-415. |
| Click to display the text | |
| [21] | BIERBOOMS W,CHENG E W.Stochastic gust model for design calculations of wind turbines[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90(11):1237-1251. |
| Click to display the text | |
| [22] | LE T H,CARACOGLIA L.Reduced-order wavelet-Galerkin solution for the coupled nonlinear stochastic response of slender buildings in transient winds[J].Journal of Sound and Vibration,2015,344(22):179-208. |
| Click to display the text | |
| [23] |
戴建鑫.风力机塔架的有限元建模及静动态特性分析[D].兰州:兰州理工大学理学院,2011:37-45. DAI Jian-xin.Finite element modeling and analysis of static and dynamic characteristics of wind turbine tower[D].Lanzhou:Lanzhou University of Technology,College of Science,2011:37-45. |
| Cited By in Cnki (12) | Click to display the text | |
| [24] |
铁摩辛柯 S P,盖莱 J M.弹性稳定理论[M].张福范,译. 北京:科学出版社,1965:87-100. TIMOSHENKO S P,GERE J M.Theory of elastic stability[M].Translated by ZHANG Fu-fan.Beijing:Beijing Science Press,1965:87-100. |
| [25] | CEN.Strength and stability of shell structures:Eurocode3 1-6[S].Brussels:European Committee for Standardisation,2004:30-40. |
| [26] | Section 08 of the Building and Civil Engineering Standards Committee,German Committee for Structural Steelwork.Part 4:structural steelwork analysis of safety against buckling of shells:DIN18800 [S].Berlin:Building and Civil Engineering Standards Committee,1990:2-16. |
| [27] |
赵阳,滕锦光.轴压圆柱钢薄壳稳定设计综述[J].工程力学,2003,20(6):116-126. ZHAO Yang,TENG Jin-guang.Stability design of axially compressed thin steel cylindrical shell[J].Engineering Mechanics,2003,20(6):116-126. |
| Cited By in Cnki (64) | Click to display the text | |
| [28] |
王露.Eurocode3 1-6与DIN18800-4在风电机组塔架屈曲分析中的对比研究[J].风能,2013(12):108-112. WANG Lu.Contrast research of Eurocode3 1-6 and DIN18800-4 in wind turbine tower buckling analysis[J].Wind Energy,2013(12):108-112. |
| Cited By in Cnki | Click to display the text | |
| [29] | LLOYD G.Part 1:guideline for the certification of wind turbines:GL Wind 2010 Ⅳ[S].Hamburg:Gemanische Lloyd Wind Energie GmbH,2010:220-223. |
| [30] |
赵世林,李德源,黄小华.风力机塔架在偏心载荷作用下的屈曲分析[J].太阳能学报,2010,31(7):901-906. ZHAO Shi-lin,LI De-yuan,HUANG Xiao-hua.Bucking analysis of wind turbine tower under eccentric loading[J].Acta Energiae Solaris Sinica,2010,31(7):901-906. |
| Cited By in Cnki (31) | Click to display the text | |
| [31] |
王勖成.有限单元法[M].北京:清华大学出版社,2003:221-250. WANG Xu-cheng.Finite element method[M].Beijing:Tsinghua University Press,2003:221-250. |
| [32] | 梅毅,曲建俊,许明伟.垂直轴风力机塔架稳定性研究:第十届全国风能应用技术年会论文集[C/OL].[2015-09-20].]http://xueshu.baidu.com/s?wd=paperuri%3A%28abd0988a27ba66253888afec66e442dd%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.docin.com%2Fp-1345669189.html&ie=utf-8. MEI Yi,QU Jian-jun,XU Ming-wei.The study of vertical axis wind turbine tower stability:the tenth Session of National Wind Energy Application Technology Conference Proceedings[C/OL].[2015-09-20].http://xueshu.baidu.com/s?wd=paperuri%3A%28abd0988a27ba66253888afec66e442dd%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.docin.com%2Fp-1345669189.html&ie=utf-8. |
| Cited By in Cnki | Click to display the text | |
| [33] |
唐瑞宏,汤赫男,许增金,等.兆瓦级风力机塔架的有限元非线性屈曲分析[J].机械工程师,2015(1):87-89. TANG Rui-hong,TANG He-nan,XU Zeng-jin,et al.Nonlinear buckling finite element analysis on MW wind turbine tower[J].Mechanical Engineer,2015(1):87-89. |
| Cited By in Cnki (1) | Click to display the text | |
| [34] |
郭智.大型风力发电机塔架承载能力研究[D].重庆:重庆大学机械工程学院,2014:29-41. GUO Zhi.The study of load bearing capacity on the large wind turbine tower[D].Chongqing:Chongqing University,College of Mechanical Engineering,2014:29-41. |
| [35] |
刘胜祥,李德源,黄小华.风波联合作用下的风力机塔架疲劳特性分析[J].太阳能学报,2009,30(10):1430-1436. LIU Sheng-xiang,LI De-yuan,HUANG Xiao-hua.Fatigue characteristic analysis of the offshore wind turbine tower under combined wind and wave[J].Acta Energiae Solaris Sinica,2009,30(10):1430-1436. |
| Cited By in Cnki (33) | Click to display the text | |
| [36] |
张建华.风力机叶片疲劳寿命估算方法研究[D].长春:吉林大学机械科学与工程学院,2013:7-35. ZHANG Jian-hua.Fatigue life prediction of wind turbine blade[D].Changchun:Jilin University,College of Mechanical Science and Engineering,2013:7-35. |
| Cited By in Cnki (4) | Click to display the text | |
| [37] | YUN J J,CHAN W C,JANG H L,et al.Development of fatigue life prediction method and effect of 10-minute mean wind speed distribution on fatigue life of small wind turbine composite blade[J].Renewable Energy,2015,79(1):187-198. |
| Click to display the text | |
| [38] | SUTHERLAND H J.On the fatigue analysis of wind turbines[M].Albuquerque:Sandia National Laboratories,1999:5-9. |
| [39] |
王永玲.风力机塔架优化设计与疲劳分析[D].大连:大连理工大学机械工程学院,2012:53-56. WANG Yong-ling.Optimization design and fatigue analysis for wind turbine tower[D].Dalian:Dalian University of Technology,School of Mechanical Engineering,2012:53-56. |
| Cited By in Cnki (7) | Click to display the text | |
| [40] |
岳勇.风力发电机组机械零部件抗疲劳设计方法的研究[D].乌鲁木齐:新疆农业大学机械交通学院,2005:27-42. YUE Yong.The research of the design method against fatigue for the mechanical components in wind turbines[D].Urumchi:Xinjiang Agricultural University,College of Mechanical and Transportation,2005:27-42. |
| Cited By in Cnki (37) | Click to display the text | |
| [41] | MANDEL J F,SAMBORSKY D D,CAIRNS D S.Fatigue of composite materials and substructures for wind turbine blades[M].Albuquerque:Sandia National Laboratories,2002:72-93. |
| [42] | JAYANTHA A E,PHILIP D C.The development of a fatigue loading spectrum for small wind turbine blades[J].Journal of Wind Engineering and Industrial Aerodynamics,2006,94(4):207-223. |
| Click to display the text | |
| [43] | MURTAGH P J,BASU B,BRODERICK B M.Along-wind response of a wind turbine tower with blade coupling subjected to rotationally sampled wind loading[J].Engineering Structures,2005,27(8):1209-1219. |
| Click to display the text | |
| [44] |
贾要勤.风力发电实验用模拟风力机[J].太阳能学报,2004,25(6):735-739. JIA Yao-qin.A wind turbine simulator for wind generation research[J].Acta Energiae Solaris Sinica,2004,25(6):735-739. |
| Cited By in Cnki (98) | Click to display the text | |
| [45] | SHRUTI L,YAHYA M S.Supercritical and subcritical dynamic flow-induced instabilities of a small-scale wind turbine blade placed in uniform flow[J].Journal of Fluids and Structures,2015,54(2):936-946. |
| Click to display the text |



