天然气作为一种清洁、高效、安全能源越来越受到青睐.由于天然气用气量会随着时间的变化而出现大幅波动,城市管网供气易出现气压不稳甚至停气的现象,因此调峰设施的建设必不可少.液化天然气(liquefied natural gas,LNG)汽化站是一种快速灵活、高安全性的城市燃气调峰系统,对城市管道燃气调峰具有重要意义[1, 2, 3].
LNG汽化站实现调峰通常需要对LNG储罐内压力和出口压力进行控制,国内外对LNG站储罐内压力的调节主要采用Bang-Bang算法控制增压阀的开闭,使得储罐压力维持在设定的阈值范围内,同时,通过采用压缩机或低温泵进行增压[4],实现出口压力的控制.这种调峰方式将两者分离,增加了系统复杂度和故障率,增加了成本投入.
储罐系统涉及气液转换、储罐内气体动态混合和热交换以及汽化器和外界空间的传热过程,因此该系统具有大滞后、非线性、强耦合的特点.此外,储罐内压力还受液体充装率、增压气体温度等因素影响,系统模型难以建立且易变[5].传统的PID控制器对这种非线性、强耦合系统难以达到良好的控制效果,虽然结合大林算法、Smith预估算法等可提升控制效果,但此类算法都需要精确的控制模型[6].预测控制采用多步预测、滚动优化和反馈校正等控制策略,具有控制效果好、鲁棒性强等特点,适用于不易建立精确数学模型且复杂的工业过程控制[7].
本文提出一种通过LNG储罐自增压法对LNG汽化储配站出口压力进行调节的方案,将LNG储罐自增压压力调节直接应用到LNG出口压力的调节上,同时针对LNG汽化站出口压力系统具有大滞后、时变、非线性、易受随机因素干扰等特点,采用先进的预测模糊控制算法进行出口压力控制,从而保证了LNG汽化站出口压力的稳定和良好的调峰效果,降低了投入产出比.
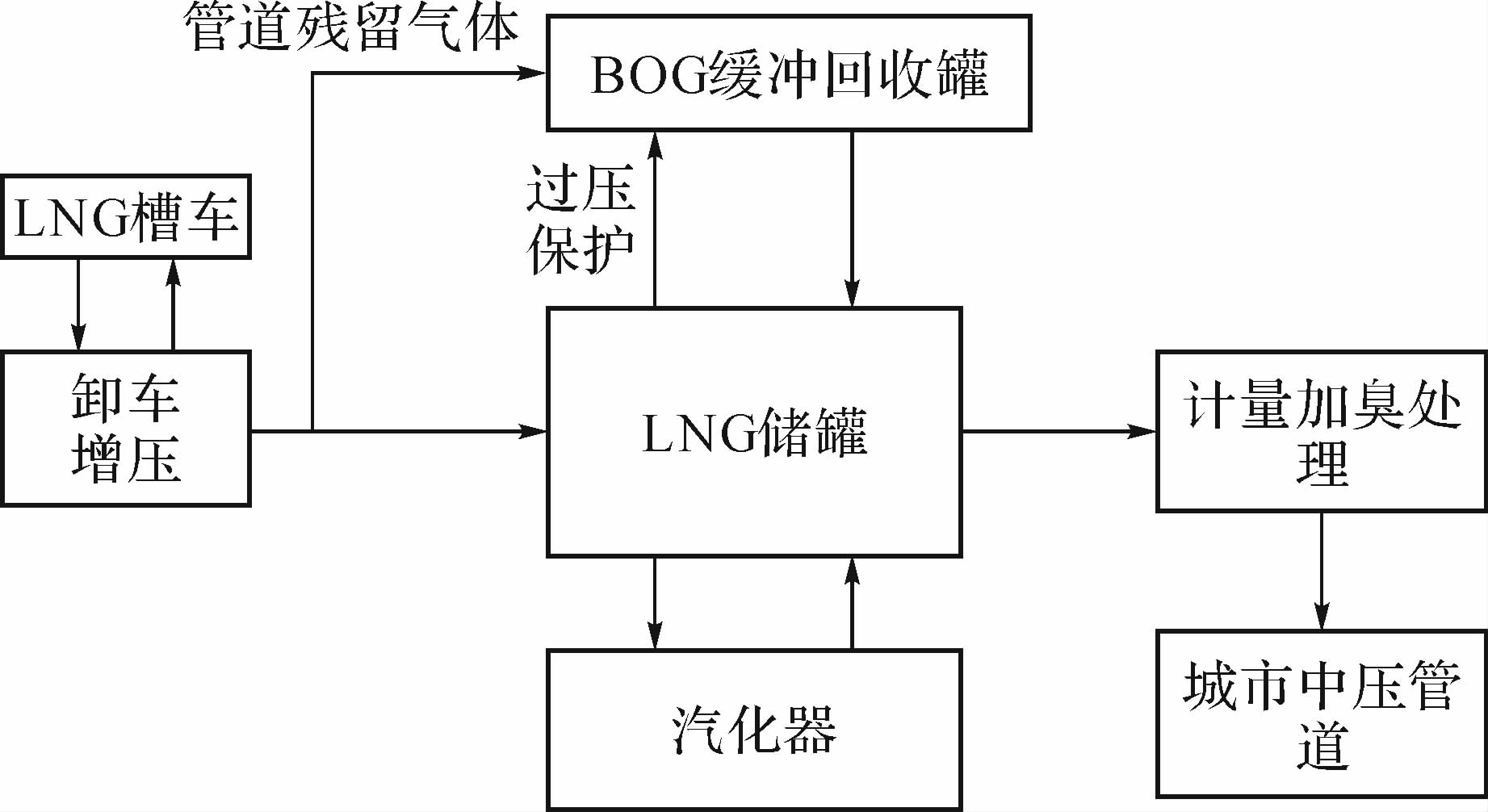
1 LNG汽化站系统目前LNG汽化站采用压缩机或低温泵对出口压力进行调节.本课题采用储罐自增压方式对出口压力进行直接控制,系统结构框图如图 1,其主要有LNG卸车增压、储罐自增压调压、BOG回收、计量加臭装置等功能.
|
| 图 1 LNG汽化站系统简化框图 Fig. 1 The simplified block diagram of LNG gasification station system |
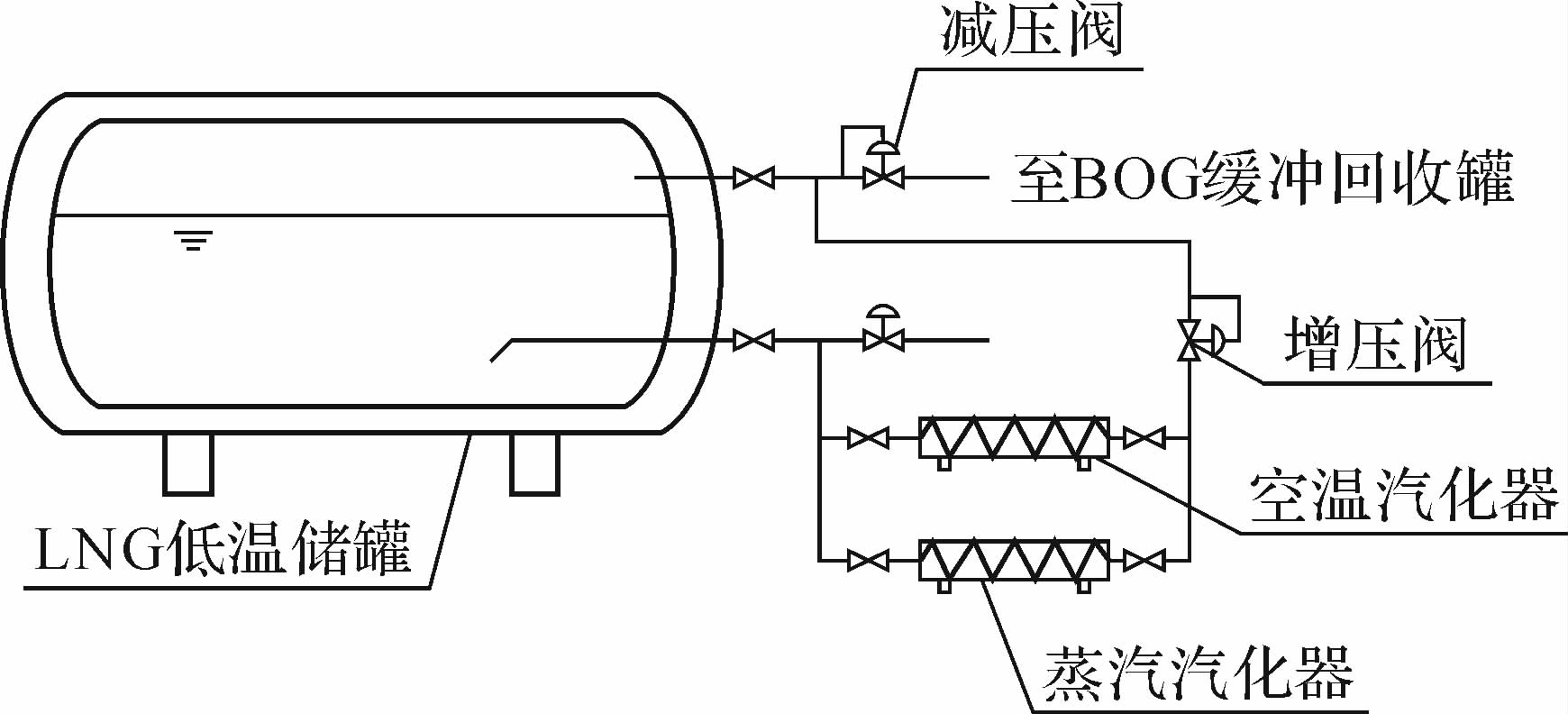
自增压原理图如图 2所示,采用2种汽化器相结合的方式对液化天然气进行汽化处理,环境温度较高时采用空温汽化方式,温度低时采用热蒸汽汽化方式.由于汽化器低于储罐最低液面,LNG可通过重力作用流入其中,LNG在汽化器中与大气/蒸汽进行热交换,实现汽化.气体通过增压阀回到LNG储罐,从而实现储罐自增压的目的.
|
| 图 2 自增压原理图 Fig. 2 The principle diagram of self-pressurization |
此外可通过减压阀来降低异常增加的压力,保证储罐安全.储罐自增压法调节LNG出口压力方式为:将储罐增压阀作为执行机构,控制器输出的控制量调节增压阀开度,从而实现对LNG出口压力的控制.
2 控制系统的设计 2.1 系统控制指标系统控制指标为:
1)汽化站输出总管压力为0.35 MPa.
2)出口压力波动小于3.5%.
3)系统响应速度大于0.05 MPa/min.
2.2 控制系统组成本课题采用基于工控机和PLC的二级控制系统方案.第1级以研祥IPC-810B工控机作为顶层硬件控制平台,采用组态软件Kingview 6.55作为上位机软件开发平台,实现数据分析、系统运行监控、人机操作、故障报警等功能.第2级以三菱公司Q系列PLC实现数据采集、底层驱动控制,通过工业以太网实现与上位机的数据传输.
2.3 控制器的设计本课题采用广义单值预测控制器调节汽化站出口压力,并根据预测误差特性进行模糊推理补偿,以弥补传统预测控制算法在系统信息处理上的不足.
2.3.1 广义单值预测控制器的设计对于物理可实现的被控对象,总可以构造出CARIMA模型[8],由于LNG汽化站出口压力系统具有大滞后的特点,故用CARIMA模型表述被控对象,为:
| $A\left( {{z}^{-1}} \right)y\left( t \right)={{z}^{-d}}B\left( {{z}^{-1}} \right)u\left( t-1 \right)+\frac{1}{\Delta }C\left( {{z}^{-1}} \right)\xi \left( t \right),$ | (1) |
| $\overline{A}\left( {{z}^{-1}} \right)=A\left( {{z}^{-1}} \right)\Delta =A\left( {{z}^{-1}} \right)\left( 1-{{z}^{-1}} \right),$ | (2) |
其中:z-1是后移算子;Δ=1-z-1是差分算子;d表示滞后时间;A(z-1),B(z-1)和C(z-1)为后移算子的多项式;ξ(t)表示随机噪声序列.为了简化算法这里假定C(z-1)=1.
引入Diophantine方程:
| $I={{E}^{\prime }}_{j}\left( {{z}^{-1}} \right)\overline{A}\left( {{z}^{-1}} \right)+{{z}^{-j}}{{F}_{j}}\left( {{z}^{-1}} \right),$ | (3) |
其中: E′j(z-1)=E0+E1z-1+…+Ej-1z-(j-1),Fj(z-1)=Ej0+Ej1z-1+…+EjnA(z-nA).
式(1)两侧均乘以E′j(z-1),并利用式(3)化简后有
| $\begin{align} & y\left( k+j \right)={{\overline{G}}_{j}}\left( {{z}^{-1}} \right)\Delta u\left( t+j-1 \right)+ \\ & {{F}_{j}}\left( {{z}^{-1}} \right)y\left( k \right)+{{E}^{\prime }}_{j}\left( {{z}^{-1}} \right)\xi \left( k+j \right), \\ \end{align}$ | (4) |
式中:Gj -(z-1)=z-dB(z-1)E′j(z-1).
上式右边第3项为噪音增量,可看成预测误差,所以j步导前最优预测输出为
| ${{y}_{p}}\left( k+j/k+d \right)={{\overline{G}}_{j}}\left( {{z}^{-1}} \right)\Delta u\left( t+j-1 \right)+{{F}_{j}}\left( {{z}^{-1}} \right)y\left( k \right).$ | (5) |
若忽略模型估计误差的影响,即可认为
| ${{\overline{G}}_{j}}\left( {{z}^{-1}} \right)=G\left( {{z}^{-1}} \right).$ |
在式(5)中,右边第1项包含未来项和已知项,对于j步导前输出预测,有
| $\begin{align} & {{y}_{p}}\left( (k+p+d)/k \right)={{G}_{1,0}}\Delta u\left( k+j-1 \right)+{{G}_{2,1}}\Delta u\left( k+j-2 \right)+\cdots + \\ & {{G}_{j,j-1}}\Delta u\left( k \right)+{{G}_{j,j}}\Delta u\left( k-1 \right)+\cdots +{{G}_{j,{{n}_{B}}+j-1}}\Delta u\left( k-{{n}_{B}} \right)+{{F}_{j}}\left( {{z}^{-1}} \right)y\left( k \right). \\ \end{align}$ | (6) |
通常预测控制器的输出是多个预测值计算出的最优控制值,需要正确选择预测步数p和控制作用计算步数m,还要确定最优指标中的加权阵,这就使得计算最优控制率效率低下,难以达到实时控制的效果[9].本文选用单值广义预测控制,即只用未来某一时刻的预测值来求解当前控制作用,其相应的控制步数只取1步,可以得到与多步预测控制相同的调节性能,因此计算量只是广义预测控制的几分之一,有利于实现实时控制.预测时域长度只取j=N一步,控制时域长度取Nu=1,即有
| $\begin{align} & {{y}_{p}}\left( (k+p+d)/k \right)={{G}_{p,p-1}}\Delta u\left( k \right)+{{G}_{p,p}}\Delta u\left( k-1 \right)+\cdots + \\ & {{G}_{p,{{n}_{B}}+p-1}}\Delta u\left( k \right)+{{F}_{j}}\left( {{z}^{-1}} \right)y\left( k \right)={{F}_{p}}\left( {{z}^{-1}} \right)\Delta u\left( k \right)+{{F}_{j}}\left( {{z}^{-1}} \right)y\left( k \right). \\ \end{align}$ | (7) |
式中:Fp(z-1)=Gp,p-1+Gp,pz-1+…+Gp,nB+p-1z-nb.
最优预测控制律可运用加权二次型性能指标求得:
| ${{J}_{p}}={{y}_{p}}\left( (k+p)/k \right)-{{y}_{r}}\left( k+p \right)\overset{2}{\mathop Q+}\,\Delta u\left( k \right)\overset{2}{\mathop{\wedge .}}\,$ | (8) |
将(7)式代入(8)式,并对u(k)求导,化简后得
| $\begin{align} & \Delta u\left( k \right)={{F}_{p}}\left( {{z}^{-1}} \right)+\wedge /Q{{G}_{p,p-1}} \\ & \left[ {{y}_{r}}\left( k+d+p \right)-{{F}_{j}}\left( {{z}^{-1}} \right)y\left( k \right) \right]. \\ \end{align}$ | (9) |
将(4)式转化为最小二乘式形式,得:
| $y\left( k+j \right)={{\varphi }^{T}}{{\theta }_{j}}+\varepsilon \left( k+j \right),$ | (10) |
| ${{\varphi }^{T}}={{\left[ {{y}^{T}}\left( k \right),\cdots {{y}^{T}}\left( k-{{n}_{a}} \right),\Delta {{u}^{T}}\left( k+j-1 \right),\cdots ,\Delta {{u}^{T}}\left( k-{{n}_{b}} \right) \right]}^{T}},$ | (11) |
| ${{\theta }_{i}}=\left[ f_{i0}^{T},\cdots f_{in}^{T},g_{i0}^{T},\cdots {{g}_{i{{n}_{b}}+j-1}}^{T} \right].$ | (12) |
因此单值预测控制过程为将测量值和给定值组成观测数据矩阵φT(k-j),再运用最小二乘法辨识得到式(4)的参数θj并根据式(10)求得y(k+j),最后通过式(9)计算出控制量u(k).
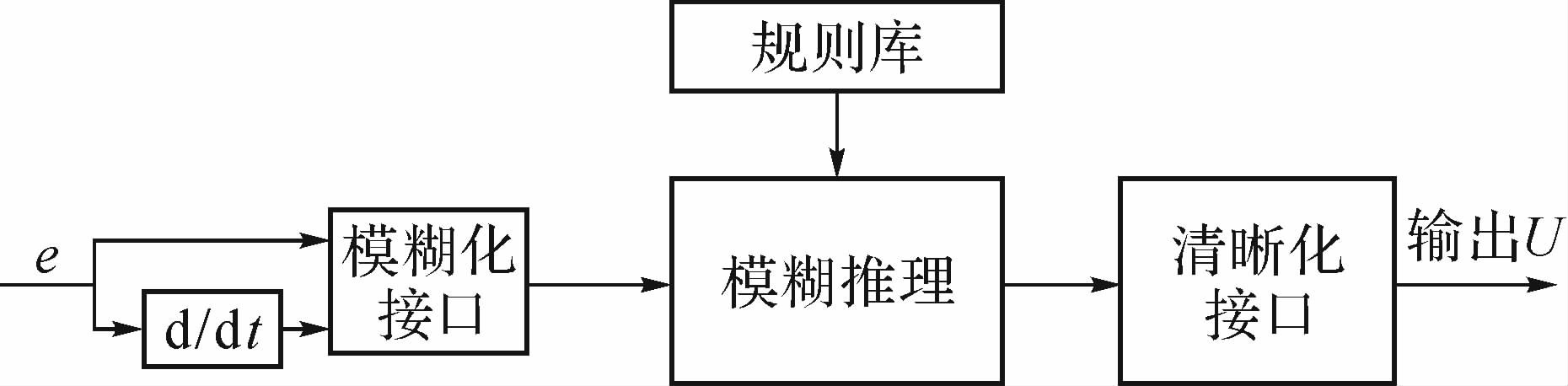
2.3.2 二维模糊控制器的设计模糊控制器主要由模糊化接口、规则库、模糊推理、清晰化接口等部分组成[10, 11],控制器结构如图 3.输入量选用受控变量和输入给定的偏差e和偏差变化ec.将偏差e和偏差变化ec以及控制量U分为5个模糊集{NB,NS,Z,PS,PB},本文采用三角形隶属度函数描述偏差e和偏差变化ec的模糊集合.
|
| 图 3 二维模糊控制器结构图 Fig. 3 The structure diagram of two-dimensional fuzzy controller |
模糊规则是基于专家知识或手动操作人员长期积累的经验,按人的直觉推理的一种语言表示形式[12, 13].根据预测误差的历史数据和储罐压力变化的特性,模糊规则需遵循如下规律:
1)当偏差e较大时,应增大控制量,以加快系统响应速度.
2)当偏差的绝对值|e|较小且偏差变化率ec负向较大时,为了减小超调量,应当减小控制量.
3)当偏差和偏差变化率的绝对值均很小时,应减小输出,削弱模糊补偿作用,减小震荡.
根据以上规律,并结合工程操作人员的经验知识,建立的模糊规则表如表 1.
| 偏差e | 偏差变化率ec | ||||
| NB | NS | Z | PS | PB | |
| NB | NB* | NB | NB | NS | NS |
| NS | NB | NB | Z | Z | Z |
| Z | NS | NS | Z | Z | Z |
| PS | Z | Z | PS | PS | PB |
| PB | PS | PB | PB | PB | PB |
根据Mamdani推理法,表 1中第*条规则的关系矩阵为 ( NB e× NB ec)T1 NB u,T1为列向量转换.
模糊控制器的模糊关系R是所有模糊规则的关系矩阵的并集,即
| $R={{R}_{1}}\bigcup {{R}_{2}}\bigcup \cdots \cdots \bigcup {{R}_{m\times n}}.$ | (13) |
模糊控制器的输出为误差向量e以及误差变化率向量 ec 和模糊关系的合成,即U=(e×ec)R.
本文采用加权平均法(式(14))对控制器输出进行反模糊化,并可根据预测误差特点调节系数Ki以提高预测精度,
| $u=\frac{\sum\limits_{i-1}^{m}{{{U}_{i}}{{K}_{i}}}}{\sum\limits_{i-1}^{m}{{{K}_{i}}}}.$ | (14) |
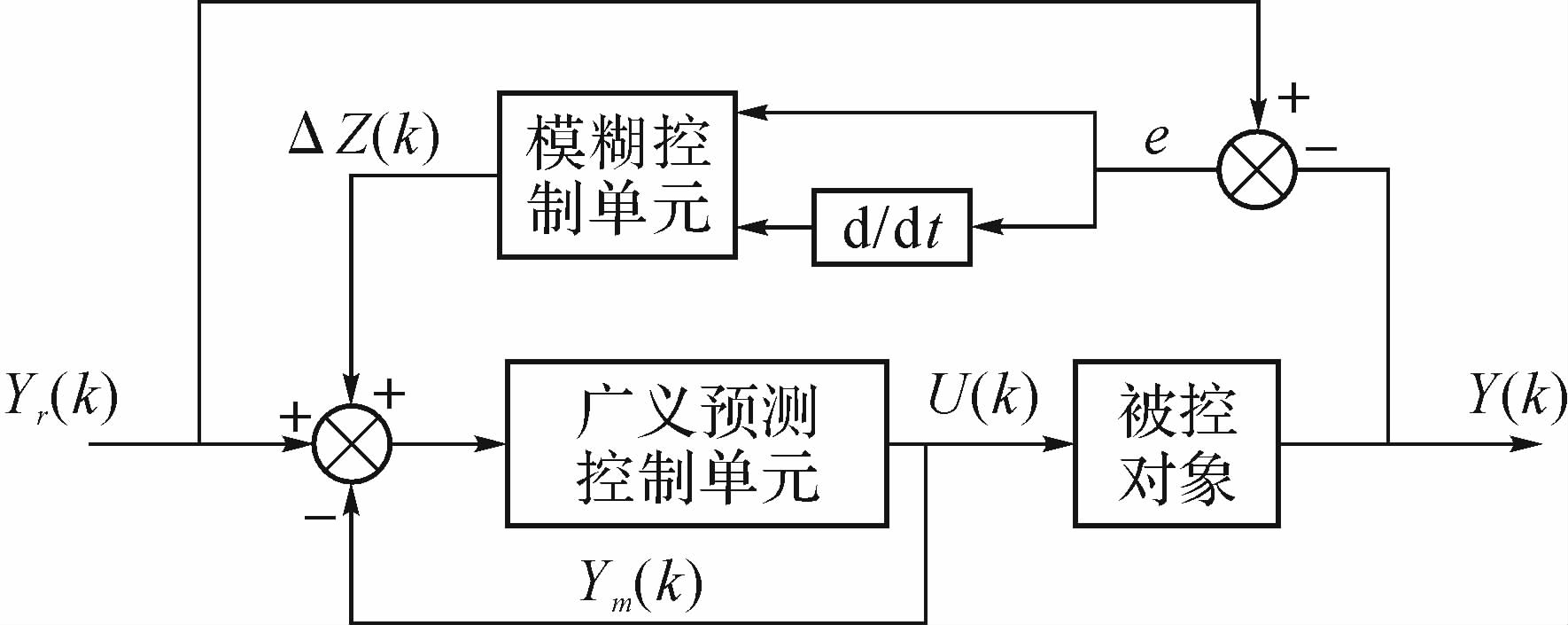
广义预测模糊控制器采用高层模糊控制单元作为辅助单元进行闭环优化补偿[14, 15, 16].预测模糊控制器的结构框图如图 4所示.
|
| 图 4 预测模糊控制器框图 Fig. 4 The block diagram of predictive fuzzy controller |
设D=Fp(z-1)+∧/QGp,p-1,则广义预测控制单元的控制输出为
| $u\left( k \right)=u\left( k-1 \right)+D\left[ {{y}_{r}}(k+d+p)-{{y}_{m}}(k+d+p) \right]+\delta u\left( k \right),$ |
其中δu(k)为一反馈补偿信号,可写成δu(k)=D▽z(k),上式可写成
| $u\left( k \right)=u\left( k-1 \right)+D\left[ {{y}_{r}}(k+d+p)+\Delta z\left( k \right)-{{y}_{m}}(k+d+p) \right].$ | (15) |
式中▽z(k)即二维模糊控制单元的输出,模糊控制器的输入即为预测误差e和误差变化率 ec .根据预测误差特性运用模糊推理弥补传统预测控制算法在系统信息处理上的不足.
2.4 控制器的实现本课题设计的控制器采用单值广义预测控制,通过减少预测量,缩短控制时域长度,大幅降低了运算量.但是单值广义预测控制器的实现仍然需要进行大规模的矩阵运算和迭代运算,系统资源占用量大,运算耗时长,这是限制其广泛应用的最主要原因.
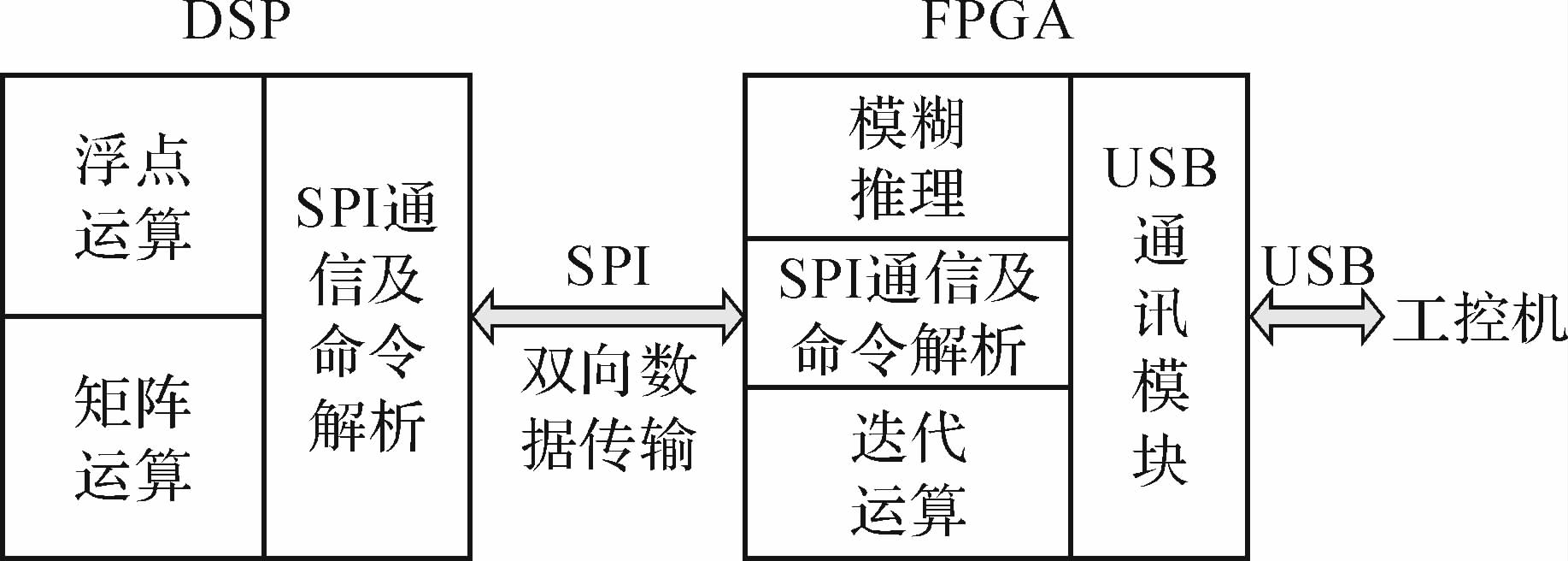
本课题采用DSP和FPGA相协作的高速数据处理板卡作为预测模糊控制器实现的硬件平台,其中,DSP芯片采用TI公司的TMS320C6678,其主要负责浮点型运算,FPGA芯片采用Xilinx公司的XC7K325T-1ffg900,其主要负责逻辑控制,两者通过高速SPI进行数据通信,任务分工如图 5.该方案充分利用了DSP和FPGA的特性,大大提高了运算速度,控制器输出周期由5.7 s降低至1.3 s,采样控制频率可提高4.3倍.
|
| 图 5 DSP和FPGA数据处理协作分工图 Fig. 5 The collaboration diagrams of DSP and FPGA in data processing |
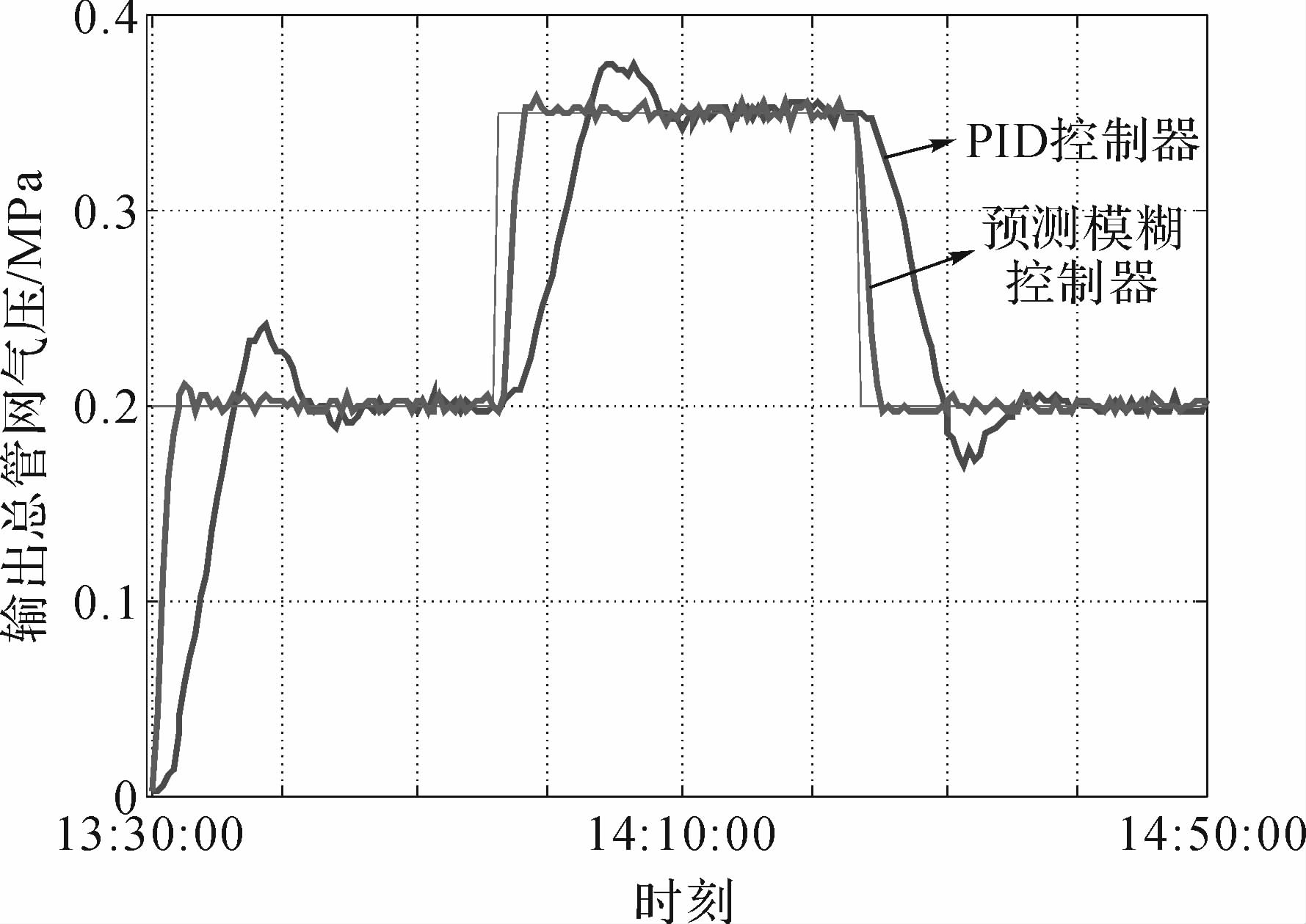
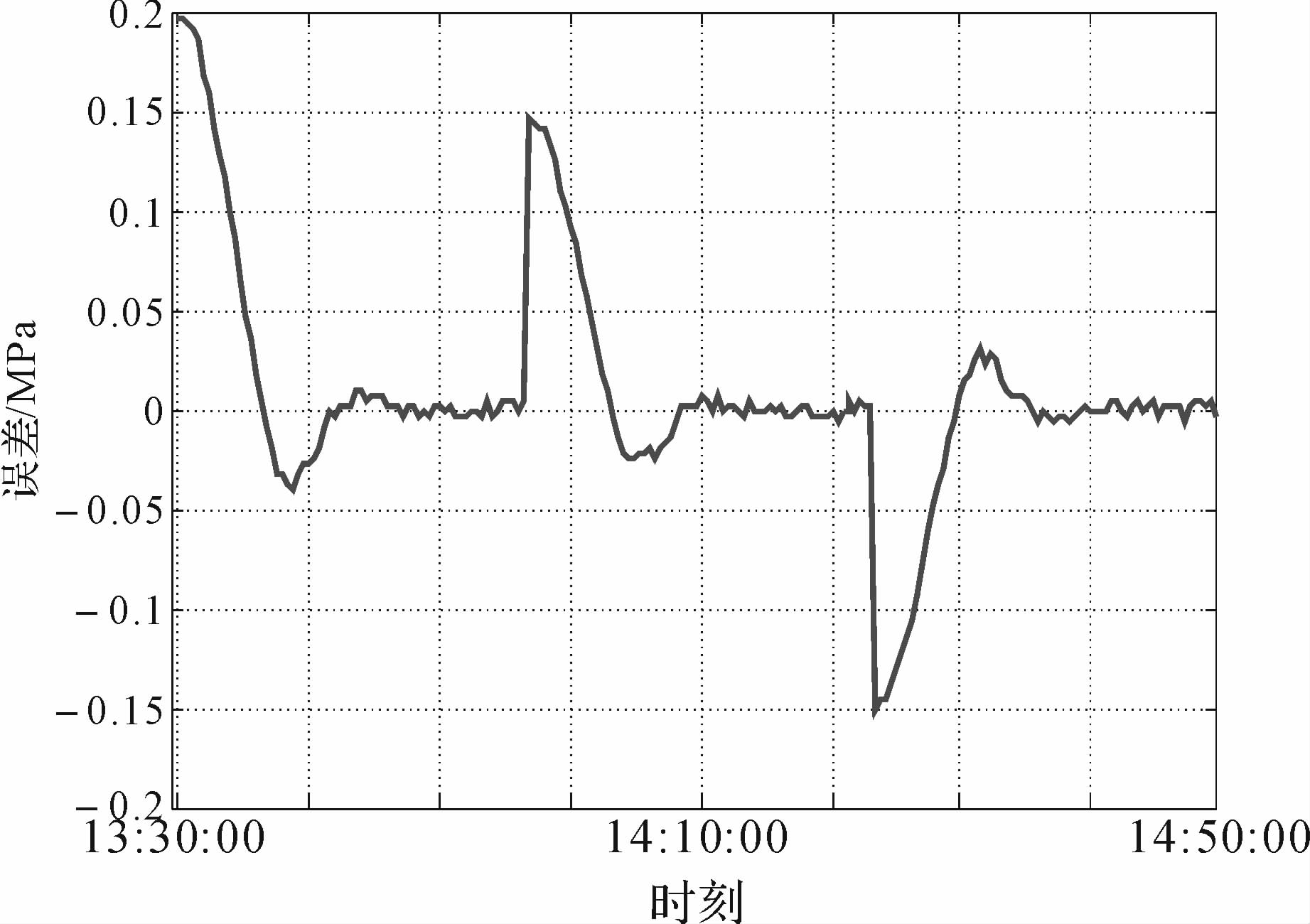
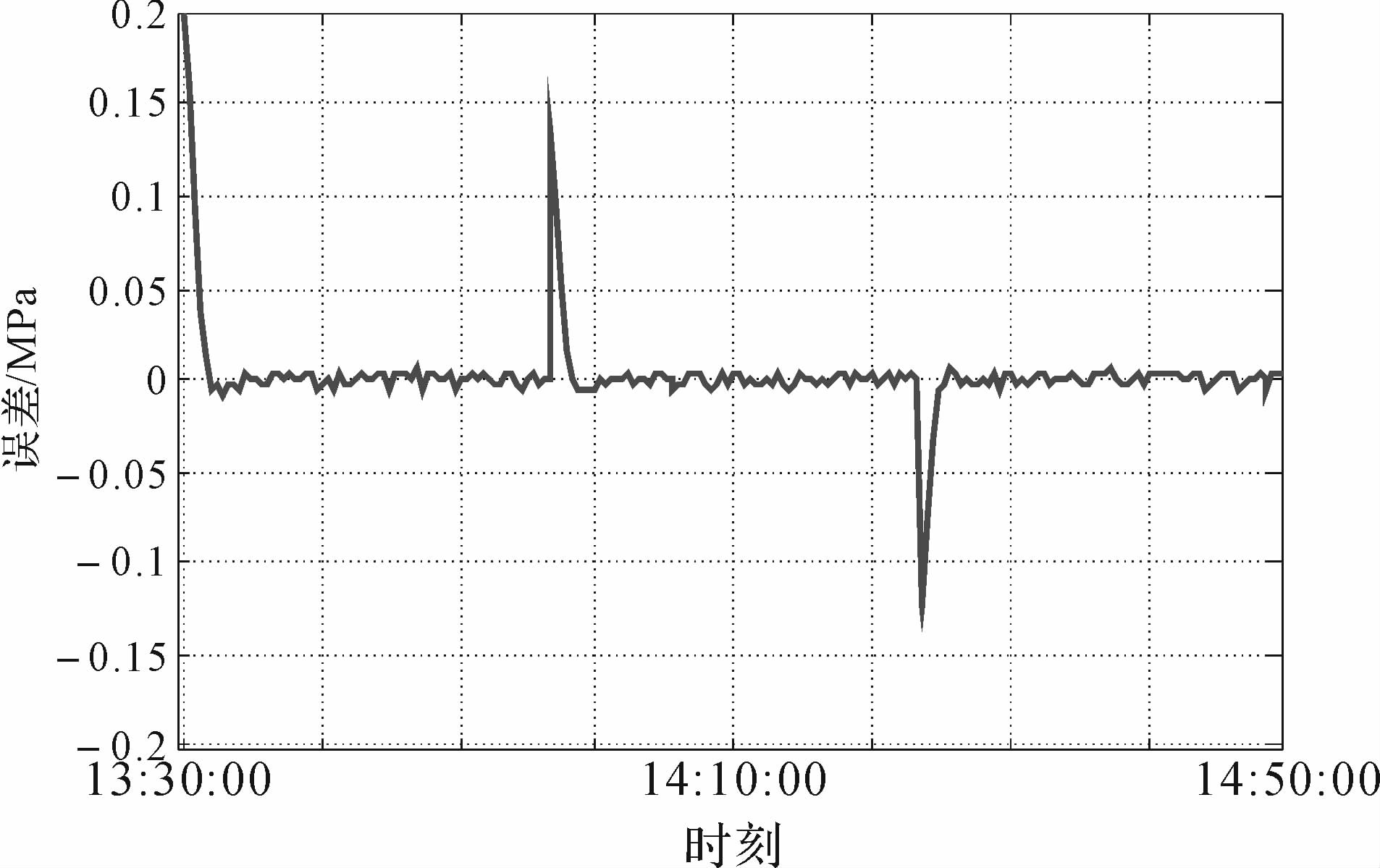
为了验证本课题设计的控制器的性能,采用传统PID控制器作为基准对象,比较两者对输入阶跃扰动的响应速度和系统超调量.控制器设定输入由0.2 MPa变成0.35 MPa再降为0.2 MPa,汽化站输出总管压力响应曲线如图 6.由图可看出,PID控制器响应速度为0.02 MPa/min,超调量为18.4%.本课题设计的预测模糊控制器超调量为2.89%,响应速度为0.075 MPa/min,完全满足控制指标响应速度大于0.05 MPa/min、超调量小于3.5%的设计要求.从图 7、图 8输出总管压力误差曲线可以更加直观地看出,预测模糊控制器动态跟随性明显好于PID控制器.
|
| 图 6 采用PID控制器输出总管压力的响应曲线 Fig. 6 The response curves of pipe output pressure applied in PID controller |
|
| 图 7 采用PID控制器输出总管压力误差曲线 Fig. 7 The error curves of pipe output pressure applied in PID controller |
|
| 图 8 采用预测模糊控制器输出总管压力误差曲线 Fig. 8 The error curves of pipe output pressure applied in predictive fuzzy controller |
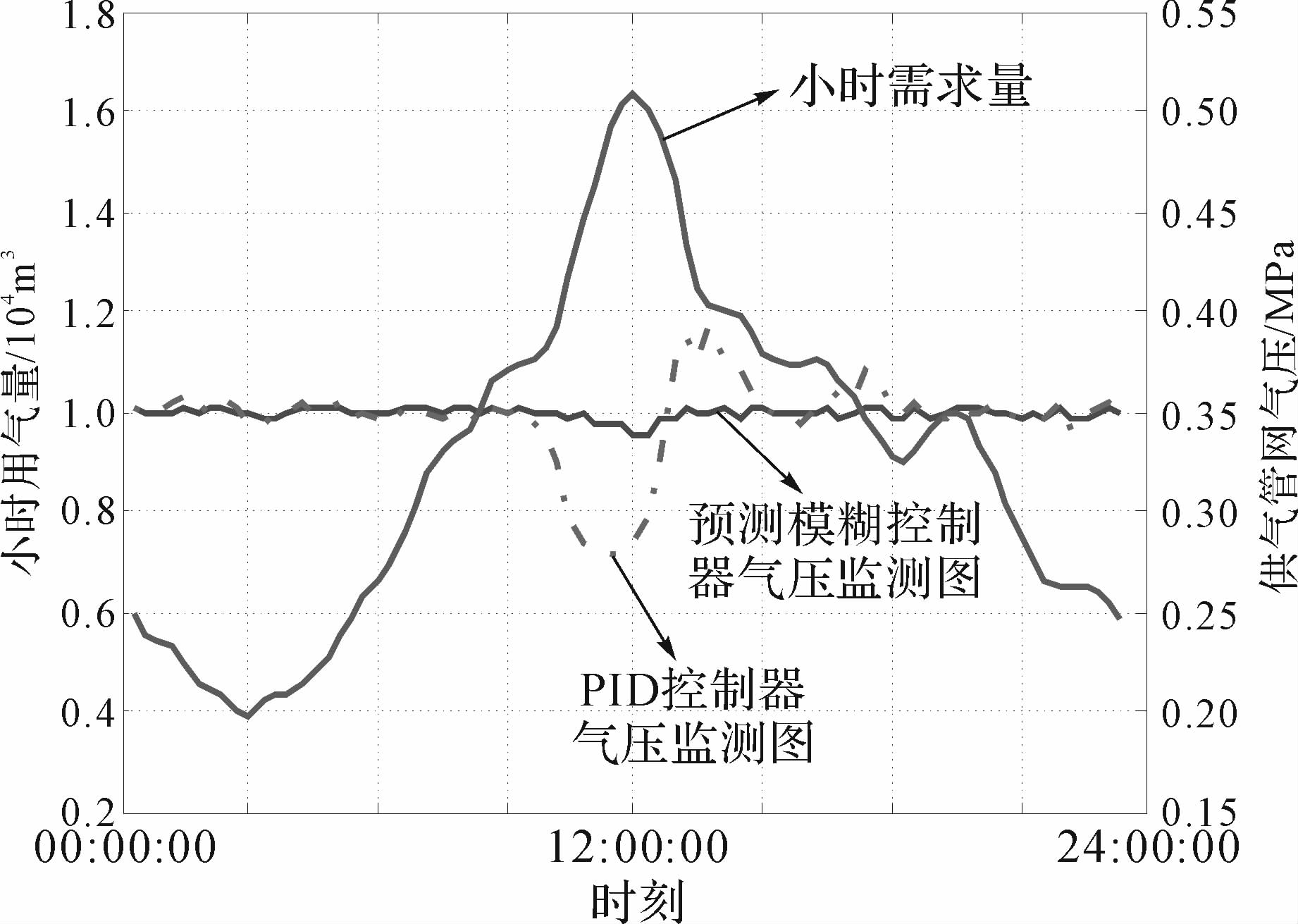
南昌市某天然气公司供气区域夏季日均用气量为20万m3,主要采用管道天然气供气,供气管道压力设计为0.35 MPa,其小时最大供气量为10 000 m3.该区域拥有1座采用本课题提出的调峰控制方案的LNG汽化站.该供气区域高峰期小时用气量可达16 200 m3,用气高峰期存在6 200 m3的用量差,将导致供气管网气压下降,故需要LNG汽化站进行调峰,平稳气压,提高供气质量.图 9为7月份某天天然气小时需求量与供气管网气压监测图.从图中可看出,在上午10:00:00到13:00:00出现用气高峰,管道天然气供气缺口最高达62%,采用PID控制器时,管网气压波动明显,气压压降超过20%.采用预测模糊控制器的管网,气压降小于3.5%,LNG汽化站及时补充了用气缺口,稳定了供气压力,保证了用气高峰期供气质量,调峰效果显著.
|
| 图 9 城市小时用气量与管网气压监测图 Fig. 9 The figures of the hourly consumption of the city and the pipe network pressure |
本文介绍了一种LNG储罐压力调节与调峰技术相结合的LNG汽化站系统,并详细介绍了汽化站出口压力控制过程.该系统采用一体化调峰技术,简化了LNG汽化站控制系统,系统搭建投入降低了17%;采用单值广义预测控制,大大降低了运算量,提高了系统控制实时性;利用二维模糊控制器,根据预测误差对预测控制器进行信息补偿,实现了双重误差预测,提高了系统的鲁棒性.目前,采用该方案改造的南昌某LNG汽化站调峰系统,在6个月的试运行中,故障率相比改造前降低了80%,供气区域管网气压稳定,未出现用户气压不稳、断气现象,调峰效果显著.
| [1] |
邢云,刘淼儿.中国液化天然气产业现状及前景分析[J].天然气工业,2009,29(1):120-123. XING Yun,LIU Miao-er.Statuesque and prospect analysis on LNG industry in China[J].Natural Gas Industry,2009,29(1):120-123. |
| Click to display the text | |
| [2] |
徐正康,张宝金,乔珩.城市天然气调峰的探讨[J].煤气与热力,2005,25(4):44-47. XU Zheng-kang,ZHANG Bao-jin,QIAO Heng.Discussion on natural gas peak shaving in cities[J].Gas & Heat,2005,25(4):44-46. |
| Click to display the text | |
| [3] |
张薇.LNG项目的储气调峰作用:兼论LNG项目建设理念的转变[J].天然气工业,2010,30(7):107-109. ZHANG Wei.Storage and peak-shaving role of LNG project:a new concept in the LNG project construction[J].Natural Gas Industry,2010,30(07):107-109. |
| Click to display the text | |
| [4] |
魏明.LNG汽化站调峰研究[D].武汉:华中科技大学环境科学与工程学院,2012:10-12. WEI Ming.Study on peak shaving by LNG gasification station[D].WuHan:Huazhong University of Science & Technology,College of Environmental Science and Engineering,2012:10-12. |
| [5] |
刘之定,刘晓东.低温储罐自增压过程仿真研究[J].节能技术,2010,28(6):508-511. LIU Zhi-ding,LIU Xiao-dong.Simulation research on self-pressurization process of cryogenic tank[J].Energy Conservation Technology,2010,28(6):508-511. |
| Click to display the text | |
| [6] |
孙建平,谭悦,李冰.单值模糊广义预测控制及其在热工对象中的应用[J].仪器仪表学报,2008,29(7):1494-1498. SUN Jian-ping,TAN Yue,LI Bing.Simplified general predictive control and its application in thermal system[J].Chinese Journal of Scientific Instrument,2008,29(8):1494-1498. |
| Click to display the text | |
| [7] |
樊兆峰,马小平,邵晓根.非线性系统RBF神经网络多步预测控制[J].控制与决策,2014,29(7):1274-1278. FAN Zao-feng,MA Xiao-ping,SHAO Xiao-gen.RBF neural network multistep predictive control for nonlinear systems[J].Control and Decision,2014,29(7):1274-1278. |
| Click to display the text | |
| [8] |
李奇安,褚健.对角CARIMA模型多变量广义预测控制改进算法[J].控制理论与应用,2007,24(3):423-426. LI Qi-an,CHU Jian.Improved algorithm for multivariable generalized predictive control of diagonal CARIMA model[J].Control Theory & Applications,2007,24(3):423-426. |
| Click to display the text | |
| [9] |
何仁初,印大伟,侯明辉,等.基于Matlab/Simulink的乙烯精馏塔多变量预测控制仿真研究[J].自动化技术与应用,2014,33(5):37-43. HE Ren-chu,YIN Da-wei,HOU Ming-hui,et al.Simulation study of multivariable predictive control for ethylene rectifier based on Matlab/Simulink[J].Techniques of Automatic and Applications,2014,33(5):37-43. |
| Click to display the text | |
| [10] |
于广鹏,谭德荣,初敏,等.基于模糊多目标决策的驾驶员反应状态辨识[J].科学技术与工程,2014,14(33):294-299. YU Guang-peng,TAN De-rong,CHU Ming,et al.Drivers' reaction state recognition based on fuzzy multi-objective decision[J].Science Technology and Engineering,2014,14(33):294-299. |
| Click to display the text | |
| [11] |
吕宽州,陈素霞,黄全振.柔性机械臂的轨迹跟踪与振动模糊控制[J].工程设计学报,2015,22(1):78-83. LÜ Kuan-zhou,CHEN Su-xia,HUANG Quan-zhen.Flexible manipulator trajectory tracking and vibration fuzzy control[J].Chinese Journal of Engineering Design,2015,22(1),78-83. |
| Click to display the text | |
| [12] |
胡启国,任龙.汽车四轮转向自适应模糊神经网络控制研究[J].工程设计学报,2013,20(5):434-440. HU Qi-guo,REN Long.Research on adaptive fuzzy neural network control of four-wheel steering system[J].Chinese Journal of Engineering Design,2013,20(5),434-440. |
| Click to display the text | |
| [13] |
罗伟.基于灰色预测的参数自校正构架电阻炉温度模糊控制系统[J].计算机测量与控制,2013,21(4):965-967. LUO Wei.Temperature fuzzy control system for frame resistance furnace based on gray prediction model's parameter self-control[J].Computer Measurement & Control,2013,12(4):965-967. |
| Click to display the text | |
| [14] |
顾星,钟鸣,姚玉峰.基于模糊自适应PID的加样臂位置控制[J].工程设计学报,2012,19(5):385-390. GU Xing,ZHONG Ming,YAO Yu-feng.Position control for sampling arm based on self-adapting fuzzy-PID[J].Chinese Journal of Engineering Design,2012,19(5),385-390. |
| Click to display the text | |
| [15] |
李如林,张根宝,李勤勇.基于预测模糊/PID控制的盘磨控制器设计[J].化工自动化及仪表,2010,37(5):26-28. LI Ru-lin,ZHANG Gen-bao,LI Qin-yong.Design of plate mill controller based on predictive fuzzy/PID[J].Control and Instruments in Chemical Industry,2010,37(5):26-28. |
| Click to display the text | |
| [16] |
王士星,孙富春,许斌.高超声速飞行器的模糊预测控制[J].东南大学学报(自然科学版),2013,43(Z1):22-27. WANG Shi-xing,SUN Fu-chun,XU Bing.Fuzzy hypersonic flight control with prediction model[J].Journal of Southeast University (Natural Science Edition),2013,43(Z1):22-27. |
| Click to display the text |



