引用本文
侯勇俊, 余乐, 方潘, 陈普春. 三激振器双质体振动系统自同步特性研究[J]. 工程设计学报, 2016, 23(1): 82-89
HOU Yong-Jun, YU Le, FANG Pan, CHENG Pu-chun. Study on self-synchronization of double mass vibrating system with tri-exciter[J]. Chinese Journal of Engineering Design, 2016, 23(1): 82-89.
三激振器双质体振动系统自同步特性研究
1. 西南石油大学 机电工程学院, 四川 成都 610500;
2. 西南石油大学 理学院, 四川 成都 610500
2. 西南石油大学 理学院, 四川 成都 610500
摘要: 提出了一种三机驱动双质体自同步振动系统,该系统具有有效筛分面积大、占地面积小和地基受动载荷小的优点.首先,依据Lagrange方程推导出双质体振动系统的运动微分方程,并求出了其稳态解.然后,由Hamilton原理推导出系统的同步性条件和稳定性条件;运用控制变量法分析了中间弹簧刚度和电机安装位置对系统同步性以及同步相位差角的影响.研究结果表明:当系统参数满足同步性和稳定性条件时系统可以实现稳定的自同步运动,同步时上质体两电机的相位差角为0°,上质体和下质体电机间的相位差角为180°.最后,用机电耦合仿真结果验证了理论分析的正确性.研究结果为该系统的设计分析提供了理论基础.
关键词:
双质体振动系统
Hamilton
控制变量
同步性
稳定性
基金项目: 国家自然科学基金资助项目(51074132);西南石油大学研究生创新基金资助项目(CX2014SY38).
Study on self-synchronization of double mass vibrating system with tri-exciter
1. School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China;
2. School of Sciences, Southwest Petroleum University, Chengdu 610500, China
2. School of Sciences, Southwest Petroleum University, Chengdu 610500, China
Abstract: A double mass vibrating system of self-synchronization with tri-exciter was put forward. The advantages of this system included that it had larger screening area, smaller share space and little loads transmitted to the foundation. Firstly, the dynamic differential equation of the system was established based on the Lagrange equation, and the stable solutions were obtained. Then using Hamilton principle, the self-synchronization qualification and stability condition were obtained. Using the method of controlling variables, the effects of stiffness of middle spring and the installation position of motors to the system self-synchronization and its phase difference were analyzed. The research results showed that the system could realize a stably synchronized motion when the parameters satisfied the synchronization and stability condition. The synchronous phase difference of two motors of upper body was 0° , and the phase difference which was between upper and lower body was 180°. Finally, the results of electromechanical-coupling simulation model verified the correctness of theoretical analysis. The study provides theoretical basis for design and analysis of this system.
Key words:
double mass vibration system
Hamilton
controlling variables
synchronization
stability
2 系统的自同步理论
2.1 系统的同步性条件
3 系统同步运动数值分析
4.2 仿真验证理论
在振动机械中,常常要求其内部2个或2个以上的部件同步运转以实现所需的运动轨迹,如多机驱动自同步振动系统.1665年荷兰物理学家Huygens[1]发现,2个并排悬挂的钟摆在震荡一段时间之后能够实现完全同步.1953年,前苏联的Blekhman博士等[2, 3]实现了机械系统两电机轴上的偏心块以相同转速0或π相位差旋转的同步运动.1982年,中国科学院院士闻邦椿等[4, 5]出版了国内该领域的第1部专著.进入21世纪,韩清凯等[6]推导出关于两偏心转子相位差角的微分方程,并针对该方程建立了同步运动的必要性条件,分析了系统平衡点的稳定性及分岔特性.文献[7, 8]提出了一种自同步四电机激振的大型振动机,并给出了其同步性条件和稳定性条件.随后,赵春雨等[9, 10, 11]用修正平均小参数法研究了多个耦合激振器的同步性和稳定性,深入阐述了振动系统的耦合动力学特性和动态对称性.李鹤等[12]对一种含有二次隔振架的(三质体)双机驱动振动机的自同步特性及其稳定性进行了分析.
上述研究的单质体以及多质体自同步振动系统中的多个激振电机均安装在同一个质体上,对于多个电机分别安装在不同质体上的振动系统的自同步特性研究尚属空缺.本文研究的双质体三机驱动自同步振动系统的3个激振电机分别安装在2个质体上.2个质体均具有筛分作用,所以该系统具有有效筛分面积大、占地面积小、处理能力强和筛分效率高的优点；下质体同时具有隔震作用,所以该系统工作噪音小、地基受动载荷小.
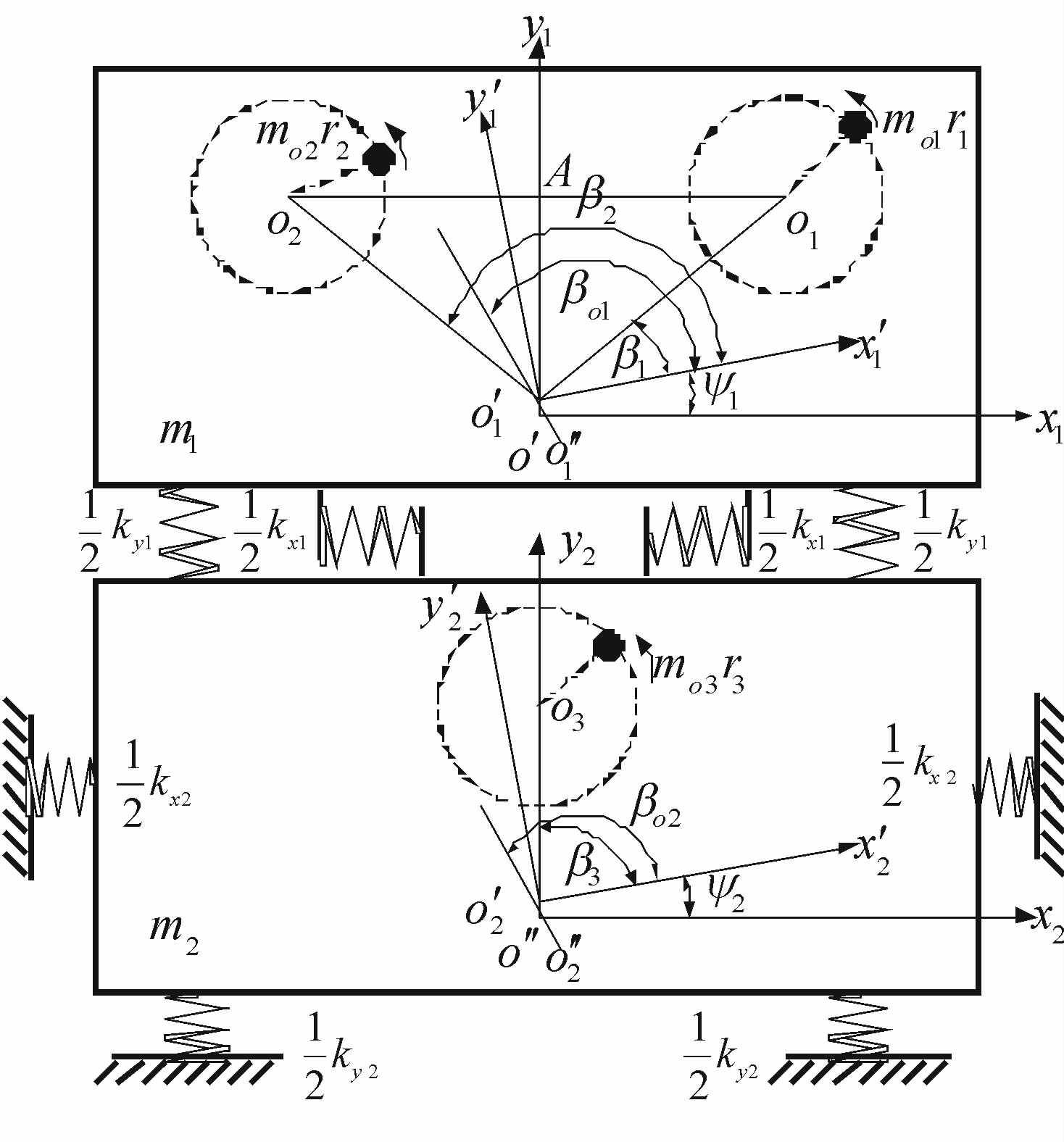
1 系统的运动微分方程双质体振动系统的动力学模型如图 1所示.该系统由上质体m1、下质体m2、激振器moi(i=1,2,3)、弹簧kxj，kyj和kψj(j=1,2)组成.系统工作时,3 个激振电机作如图 1所示的等速旋转.上质体两电机产生的激振力合力通过中间弹簧传递给下质体；下质体电机的激振力也通过中间弹簧传递给上质体.上、下质体激振力通过中间弹簧的相互作用,使上、下质体实现不同轨迹的运动.o′x1y1和o″x2y2是系统的固定坐标系，o′1x′1y′1和o′2x′2y′2是分别相对于o′x1y1和o″x2y2的动坐标系.o″1,o″2分别为上、下质体质心,o′1,o′2分别为上、下质体与激振器合成质心,该系统有6个自由度.
|
| 图 1 双质体振动系统动力学模型 Fig. 1 The dynamics model of double mass vibrating system |
由Lagrange方程得系统的运动微分方程如式(1):
| $\left. \begin{array}{*{35}{l}} {{M}_{1}}{{{\ddot{x}}}_{1}}-{{f}_{x1}}({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})-{{k}_{x1}}({{x}_{2}}-{{x}_{1}})=\sum\limits_{i=1}^{2}{{{m}_{oi}}{{r}_{i}}(}{{{\ddot{\varphi }}}_{i}}\sin {{\varphi }_{i}}+\dot{\varphi }_{i}^{2}\cos {{\varphi }_{i}}), \\ {{M}_{1}}{{{\ddot{y}}}_{1}}-{{f}_{y1}}({{{\dot{y}}}_{2}}-{{{\dot{y}}}_{1}})-{{k}_{y1}}({{y}_{2}}-{{y}_{1}})=\sum\limits_{i=1}^{2}{{{m}_{oi}}{{r}_{i}}(}-{{{\ddot{\varphi }}}_{i}}\cos {{\varphi }_{i}}+\dot{\varphi }_{i}^{2}\sin {{\varphi }_{i}}), \\ {{M}_{2}}{{{\ddot{x}}}_{2}}-{{f}_{x2}}{{{\dot{x}}}_{2}}+{{f}_{x1}}({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})+{{k}_{x2}}{{x}_{2}}+{{k}_{x1}}({{x}_{2}}-{{x}_{1}})={{m}_{o3}}{{r}_{3}}({{{\ddot{\varphi }}}_{3}}\sin {{\varphi }_{3}}+\dot{\varphi }_{3}^{2}\cos {{\varphi }_{3}}), \\ {{M}_{2}}{{{\ddot{y}}}_{2}}-{{f}_{y2}}{{{\dot{y}}}_{2}}+{{f}_{y1}}({{{\dot{y}}}_{2}}-{{{\dot{y}}}_{1}})+{{k}_{y2}}{{y}_{2}}+{{k}_{y1}}({{y}_{2}}-{{y}_{1}})={{m}_{o3}}{{r}_{3}}({{{\ddot{\varphi }}}_{3}}\cos {{\varphi }_{3}}+\dot{\varphi }_{3}^{2}\sin {{\varphi }_{3}}), \\ {{J}_{z1}}{{{\ddot{\varphi }}}_{1}}-{{f}_{\phi 1}}({{{\dot{\phi }}}_{2}}-{{{\dot{\phi }}}_{1}})-{{k}_{\phi 1}}({{\phi }_{2}}-{{\phi }_{1}})=\sum\limits_{i=1}^{2}{{{m}_{oi}}{{r}_{i}}{{l}_{i}}\left[ -{{{\ddot{\varphi }}}_{i}}\cos ({{\varphi }_{i}}-{{\beta }_{i}})+\dot{\varphi }_{i}^{2}\sin ({{\varphi }_{i}}-{{\beta }_{i}}) \right]}, \\ {{J}_{z2}}{{{\ddot{\varphi }}}_{2}}-{{f}_{\phi 2}}{{{\dot{\phi }}}_{2}}+{{f}_{\phi 1}}({{{\dot{\phi }}}_{2}}-{{{\dot{\phi }}}_{1}})-{{k}_{\phi 2}}{{\phi }_{2}}+{{k}_{\phi 1}}({{\phi }_{2}}-{{\phi }_{1}})={{m}_{o3}}{{r}_{3}}{{l}_{3}}\left[ -{{{\ddot{\varphi }}}_{3}}\cos ({{\varphi }_{i}}-{{\beta }_{i}})+\dot{\varphi }_{i}^{2}\sin ({{\varphi }_{i}}-{{\beta }_{i}}) \right], \\ ({{J}_{o1}}+{{m}_{o1}}r_{1}^{2}){{{\ddot{\varphi }}}_{1}}+{{f}_{1}}{{{\dot{\phi }}}_{1}}={{T}_{\text{e}1}}+{{m}_{o1}}{{r}_{1}}({{{\ddot{x}}}_{1}}\sin {{\varphi }_{1}}-{{{\ddot{y}}}_{1}}\cos {{\varphi }_{1}})-{{m}_{o1}}{{l}_{1}}{{r}_{1}}\left[ {{{\ddot{\varphi }}}_{1}}\cos ({{\varphi }_{1}}-{{\beta }_{1}})+\dot{\varphi }_{1}^{2}\sin ({{\varphi }_{1}}-{{\beta }_{1}}) \right], \\ ({{J}_{o2}}+{{m}_{o2}}r_{2}^{2}){{{\ddot{\varphi }}}_{2}}+{{f}_{2}}{{{\dot{\phi }}}_{2}}={{T}_{\text{e2}}}+{{m}_{o2}}{{r}_{2}}({{{\ddot{x}}}_{2}}\sin {{\varphi }_{2}}-{{{\ddot{y}}}_{1}}\cos {{\varphi }_{2}})-{{m}_{o2}}{{l}_{2}}{{r}_{2}}\left[ {{{\ddot{\varphi }}}_{1}}\cos ({{\varphi }_{2}}-{{\beta }_{2}})+\dot{\varphi }_{1}^{2}\sin ({{\varphi }_{2}}-{{\beta }_{2}}) \right], \\ ({{J}_{o3}}+{{m}_{o3}}r_{3}^{2}){{{\ddot{\varphi }}}_{3}}+{{f}_{3}}{{{\dot{\phi }}}_{3}}={{T}_{\text{e3}}}+{{m}_{o3}}{{r}_{3}}({{{\ddot{x}}}_{2}}\sin {{\varphi }_{3}}-{{{\ddot{y}}}_{2}}\cos {{\varphi }_{3}})-{{m}_{o3}}{{l}_{3}}{{r}_{3}}\left[ {{{\ddot{\varphi }}}_{2}}\cos ({{\varphi }_{3}}-{{\beta }_{3}})+\dot{\varphi }_{2}^{2}\sin ({{\varphi }_{3}}-{{\beta }_{3}}) \right], \\ \end{array} \right]$ | (1) |
式中:M1=m1+mo1+mo2为上质体(包括电机及偏心块)的总质量；M2=m2+mo3为下质体(包括电机及偏心块)的总质量；${{J}_{z1}}={{J}_{1}}+{{m}_{1}}l_{o1}^{2}+\sum\limits_{i=1}^{2}{{{m}_{oi}}l_{i}^{2}}$为上质体绕o′1点的转动惯量(包括电机及偏心块)；Jz2=J2+m2lo22+mo3l32为下质体绕o′2点的转动惯量(包括电机及偏心块)；Tei(i=1,2,3)分别为电机i的电磁转矩；${{x}_{j}},{{y}_{j}},{{\phi }_{j}},{{{\dot{x}}}_{j}},{{{\dot{y}}}_{j}},{{{\dot{\phi }}}_{j}},{{{\ddot{x}}}_{j}},{{{\ddot{y}}}_{j}},{{{\ddot{\phi }}}_{j}}(j=1,2)$为质体沿着xj,yj方向的位移、速度以及加速度和绕o′j转动的角位移、角速度以及角加速度；loj=o′jo″j为合成质心与质体质心之距；li为oi与o′j之距；ri为偏心块i的偏心半径；${{\varphi }_{i}},{{{\dot{\varphi }}}_{i}},{{{\ddot{\varphi }}}_{i}}$的角位移、角速度和角加速度；Jj,Joi分别为质体和偏心块i绕各自质心的转动惯量；fxj,fyj,fψj为x方向、y方向和ψ方向的阻尼；fi分别表示电机i转轴的阻尼.
令mo1=mo2=mo3=m,r1=r2=r3=r,l1=l2=l,l3=0.设系统稳态运行时3个转子的平均相位为φ,即φ1=φ+α1,φ2=φ-α1,φ3=φ-α1-2α2,φ=ωt.解得式(1)中前6个方程的稳态响应为
| $\left. \begin{array}{*{35}{l}} {{x}_{1}}=F\left[ {{\mu }_{x11}}\sum\limits_{i=1}^{2}{\cos ({{\varphi }_{i}}-{{\theta }_{x1}})+{{\mu }_{x12}}\cos ({{\varphi }_{3}}-{{\theta }_{x2}})} \right], \\ {{x}_{2}}=F\left[ {{\mu }_{x21}}\sum\limits_{i=1}^{2}{\cos ({{\varphi }_{i}}-{{\theta }_{x2}})+{{\mu }_{x22}}\cos ({{\varphi }_{3}}-{{\theta }_{x3}})} \right], \\ {{y}_{1}}=F\left[ {{\mu }_{y11}}\sum\limits_{i=1}^{2}{\sin ({{\varphi }_{i}}-{{\theta }_{y1}})+{{\mu }_{y12}}\sin ({{\varphi }_{3}}-{{\theta }_{y2}})} \right], \\ {{y}_{2}}=F\left[ {{\mu }_{y21}}\sum\limits_{i=1}^{2}{\sin ({{\varphi }_{i}}-{{\theta }_{y2}})+{{\mu }_{y22}}\sin ({{\varphi }_{3}}-{{\theta }_{y3}})} \right],{{\varphi }_{i}} \\ {{\varphi }_{1}}=Fl{{\mu }_{\phi 11}}\sum\limits_{i=1}^{2}{\sin ({{\varphi }_{i}}-{{\beta }_{i}}-{{\theta }_{{{\varphi }_{1}}}}),} \\ {{\varphi }_{2}}=Fl{{\mu }_{\phi 21}}\sum\limits_{i=1}^{2}{\sin ({{\varphi }_{i}}-{{\beta }_{i}}-{{\theta }_{\varphi 2}}),} \\ \end{array} \right]$ | (2) |
其中：
| $\begin{align} & F=mr{{\omega }^{2}}, \\ & {{a}_{i}}={{M}_{1}}{{M}_{2}}{{\omega }^{4}}-\left[ {{M}_{2}}{{k}_{i1}}+{{M}_{1}}({{k}_{i1}}+{{k}_{i2}})+{{f}_{i1}}{{f}_{i2}} \right]{{\omega }^{2}}+{{k}_{i1}}{{k}_{i2}}, \\ & {{b}_{i}}=-\left[ {{M}_{2}}{{f}_{i1}}+{{M}_{1}}({{f}_{i1}}+{{f}_{i2}}) \right]{{\omega }^{3}}+({{f}_{i1}}{{k}_{i2}}+{{f}_{i2}}{{k}_{i1}})\omega , \\ & {{p}_{i}}=-{{M}_{1}}{{\omega }^{2}}+{{k}_{i1}},{{c}_{i1}}=-{{M}_{2}}{{\omega }^{2}}+{{k}_{i1}}+{{k}_{i2}},{{c}_{i2}}={{k}_{i1}}, \\ & {{d}_{i1}}=({{f}_{i1}}+{{f}_{i2}})\omega ,{{d}_{i2}}={{f}_{i1\omega }} \\ & i=x,y, \\ & {{a}_{\phi }}={{J}_{z1}}{{J}_{z2{{\omega }^{4}}}}-\left[ {{J}_{z2}}{{k}_{\phi 1}}+{{J}_{z1}}({{k}_{\phi 1}}+{{k}_{\phi 2}})+{{f}_{\phi 1}}{{f}_{\phi 2}} \right]{{\omega }^{2}}+{{k}_{\phi 1}}{{k}_{\phi 2}}, \\ & {{b}_{\phi }}=-\left[ {{J}_{z2}}{{f}_{\phi 1}}+{{J}_{z1}}({{f}_{\phi 1}}+{{f}_{\phi 2}}) \right]{{\omega }^{2}}+({{f}_{\phi 1}}{{k}_{\phi 2}}+{{f}_{\phi 2}}{{k}_{\phi 1}})\omega , \\ & {{p}_{\phi }}=-{{J}_{z1}}{{\omega }^{2}}+{{k}_{\phi 1}},{{c}_{i1}}=-{{J}_{z2}}{{\omega }^{2}}+{{k}_{\phi 1}}+{{k}_{\phi 2}}, \\ & {{c}_{i2}}={{k}_{\phi 1,}} \\ & {{d}_{\phi 1}}=({{f}_{\phi 1}}+{{f}_{\phi 2}})\omega ,{{d}_{\phi 2}}={{f}_{\phi 1\omega }}, \\ & {{\mu }_{j11}}=\overline{\left){\frac{c_{j1}^{2}+d_{j1}^{2}}{a_{j}^{2}+b_{j}^{2}}}\right.},{{\theta }_{j1}}=\arctan \frac{{{b}_{j}}{{c}_{j1}}-{{a}_{j}}{{d}_{j1}}}{{{a}_{j}}{{c}_{j1}}+{{b}_{j}}{{d}_{j1}}}, \\ & {{\mu }_{j12}}={{\mu }_{j12}}=\overline{\left){\frac{c_{j2}^{2}+d_{j2}^{2}}{a_{j}^{2}+b_{j}^{2}}}\right.},{{\theta }_{j2}}=\arctan \frac{{{b}_{j}}{{c}_{j2}}-{{a}_{j}}{{d}_{j2}}}{{{a}_{j}}{{c}_{j2}}+{{b}_{j}}{{d}_{j2}}}, \\ & {{\mu }_{j22}}=\overline{\left){\frac{p_{j}^{2}+d_{j2}^{2}}{a_{j}^{2}+b_{j}^{2}}}\right.},{{\theta }_{j3}}=\arctan \frac{{{b}_{j}}{{p}_{j}}-{{a}_{j}}{{d}_{j2}}}{{{a}_{j}}{{p}_{j}}+{{b}_{j}}{{d}_{j2}}}, \\ & j=x,y,\phi . \\ \end{align}$ |
若不计阻尼力的影响,该力学系统在运动过程中,除受到重力的作用外,还受3个电动机电磁转矩Tei的作用,所以系统是一个完整的非保守系统.由系统的Hamilton原理[13],有
| $\delta H+{}_{0}^{2\pi }(\sum\limits_{i=1}^{n}{{{Q}_{i}}\delta {{q}_{i}})\text{d}\varphi =0,}$ | (3) |
式中:H为Hamiton作用量,Qi为广义力,qi为广义坐标.
系统的总动能为
| $\begin{align} & T=\frac{1}{2}{{M}_{1}}\dot{x}_{1}^{2}+\frac{1}{2}{{M}_{1}}\dot{y}_{1}^{2}+\frac{1}{2}{{J}_{z1}}\dot{\varphi }_{1}^{2}+ \\ & \frac{1}{2}{{M}_{2}}\dot{x}_{2}^{2}+\frac{1}{2}{{M}_{2}}\dot{y}_{2}^{2}+\frac{1}{2}{{J}_{z2}}\dot{\varphi }_{2}^{2}+{{T}_{z}}, \\ \end{align}$ | (4) |
式中Tz为3个激振电机的旋转动能总和.在电机稳定运转的情况下,Tz可看做常数.
系统的势能为
| $\begin{align} & V=\frac{1}{2}{{k}_{x1}}{{({{x}_{2}}-{{x}_{1}})}^{2}}+\frac{1}{2}{{k}_{y1}}{{({{y}_{2}}-{{y}_{1}})}^{2}}+ \\ & \frac{1}{2}{{k}_{\phi 1}}{{({{\phi }_{2}}-{{\phi }_{1}})}^{2}}+\frac{1}{2}{{k}_{x2}}x_{2}^{2}+\frac{1}{2}{{k}_{y2}}y_{2}^{2}+\frac{1}{2}{{k}_{\phi 2}}\phi _{2}^{2}. \\ \end{align}$ | (5) |
拉格朗日函数:
| $L=T-V.$ | (6) |
一个运动周期内系统的Hamilton作用量为
| $\begin{align} & H={}_{0}^{T}(T-V)\text{d}t={}_{0}^{2\pi }(T-V)\text{d}\varphi \text{=} \\ & {{M}_{1}}{{F}^{2}}{{\omega }^{2}}\pi \sum\limits_{i-x}^{y}{\left[ \mu _{i11}^{2}+\frac{1}{2}\mu _{i12}^{2}+\mu _{i11}^{2}\cos 2{{a}_{1}}+ \right.} \\ & {{\mu }_{i11}}{{\mu }_{i12}}\cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{i2}}+{{\theta }_{i1}})+ \\ & {{\mu }_{i11}}{{\mu }_{i12}}\left. \cos (2{{a}_{2}}+{{\theta }_{i2}}-{{\theta }_{i1}}) \right]+ \\ & {{F}^{2}}{{\omega }^{2}}{{l}^{2}}\pi \left[ 1+ \right.\cos \left. (2{{a}_{1}}+{{\beta }_{2}}-{{\beta }_{1}}) \right]({{J}_{z1}}\mu _{\varphi 11}^{2}+{{J}_{z2}}\mu _{\varphi 21}^{2})+ \\ & {{M}_{2}}{{F}^{2}}{{\omega }^{2}}\pi \sum\limits_{i-x}^{y}{\left[ \mu _{i21}^{2}+\frac{1}{2}\mu _{i22}^{2}+\mu _{i21}^{2}\cos 2{{a}_{1}}+ \right.} \\ & {{\mu }_{i21}}{{\mu }_{i22}}\cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{i3}}+{{\theta }_{i2}})+ \\ & {{\mu }_{i21}}{{\mu }_{i22}}\left. \cos (2{{a}_{2}}+{{\theta }_{i3}}-{{\theta }_{i2}}) \right]+ \\ & {{F}^{2}}\pi \sum\limits_{i-x}^{y}{{{k}_{i2}}}\left[ \mu _{i21}^{2}+\frac{1}{2}\mu _{i22}^{2}+\mu _{i21}^{2}\cos 2{{a}_{1}}+ \right. \\ & {{\mu }_{i21}}{{\mu }_{i22}}\cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{i3}}+{{\theta }_{i2}})+ \\ & {{\mu }_{i21}}{{\mu }_{i22}}\left. \cos (2{{a}_{2}}+{{\theta }_{i3}}-{{\theta }_{i2}}) \right]+ \\ & {{k}_{\phi 2}}{{F}^{2}}\mu _{\phi 21}^{2}{{l}^{2}}\pi \left[ 1+\cos (2{{a}_{1}}+{{\beta }_{2}}-{{\beta }_{1}}) \right]+ \\ & {{F}^{2}}\pi \sum\limits_{i-x}^{y}{{{k}_{i1}}}\left[ \mu _{i11}^{2}+\frac{1}{2}\mu _{i12}^{2}+\mu _{i21}^{2}+ \right.\frac{1}{2}\mu _{i22}^{2}+ \\ & \mu _{i22}^{2}\cos 2{{a}_{1}}+{{\mu }_{i21}}{{\mu }_{i22}}\cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{i3}}-{{\theta }_{i2}})- \\ & \mu _{i21}^{2}\cos ({{\theta }_{i1}}-{{\theta }_{i2}})-{{\mu }_{i21}}{{\mu }_{i11}}\cos (2{{a}_{1}}+{{\theta }_{i1}}-{{\theta }_{i2}})- \\ & {{\mu }_{i21}}{{\mu }_{i12}}\cos (2{{a}_{1}}+2{{a}_{2}})+{{\mu }_{i21}}{{\mu }_{i22}}\cos (2{{a}_{2}}+{{\theta }_{i3}}-{{\theta }_{i2}})- \\ & {{\mu }_{i21}}{{\mu }_{i11}}\cos (-2{{a}_{1}}-{{\theta }_{i2}}+{{\theta }_{i1}})-{{\mu }_{i21}}{{\mu }_{i11}}\cos ({{\theta }_{i1}}-{{\theta }_{i2}})- \\ & {{\mu }_{i21}}{{\mu }_{i12}}\cos 2{{a}_{2}}+{{\mu }_{i22}}{{\mu }_{i11}}\cos (-2{{a}_{1}}-2{{a}_{2}}+{{\theta }_{i1}}-{{\theta }_{i3}})- \\ & {{\mu }_{i22}}{{\mu }_{i11}}\cos (-2{{a}_{2}}-{{\theta }_{i3}}+{{\theta }_{i1}})-{{\mu }_{i22}}{{\mu }_{i12}}\cos ({{\theta }_{i2}}-{{\theta }_{i3}})- \\ & \mu _{i11}^{2}\cos 2{{a}_{1}}+{{\mu }_{i11}}{{\mu }_{i12}}\cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{i2}}-{{\theta }_{i1}})+ \\ & {{\mu }_{i11}}{{\mu }_{i12}}\cos \left. (2{{a}_{2}}+{{\theta }_{i2}}-{{\theta }_{i1}}) \right]+ \\ & {{k}_{\phi 1}}{{F}^{2}}{{l}^{2}}\pi \left[ \mu _{\phi 11}^{2}+\mu _{\phi 21}^{2}+\mu _{\phi 21}^{2}\cos (2{{a}_{1}}+{{\beta }_{2}}-{{\beta }_{1}}) \right.- \\ & {{\mu }_{\phi 21}}{{\mu }_{\phi 11}}\cos ({{\theta }_{\phi 1}}-{{\theta }_{\phi 2}})-{{\mu }_{\phi 21}}{{\mu }_{\phi 11}}\cos (2{{a}_{1}}+{{\beta }_{2}}-{{\beta }_{1}}+ \\ & {{\theta }_{\phi 1}}-{{\theta }_{\phi 2}})-{{\mu }_{\phi 21}}{{\mu }_{\phi 11}}\cos (-2{{a}_{1}}+{{\beta }_{1}}-{{\beta }_{2}}+{{\theta }_{\phi 1}}-{{\theta }_{\phi 2}})- \\ & {{\mu }_{\phi 21}}{{\mu }_{\phi 11}}\cos ({{\theta }_{\phi 1}}-{{\theta }_{\phi 2}})+\left. \mu _{\phi 11}^{2}\cos (2{{a}_{1}}+{{\beta }_{2}}-{{\beta }_{1}}) \right]. \\ \end{align}$ | (7) |
为了简化方程令kx1=ky1,kx2=ky2,β1=0，β2=π，则有
| $\begin{align} & \frac{\partial H}{{{\partial }_{a1}}}=4{{F}^{2}}\pi \sin 2{{a}_{1}}\left[ {{p}_{x}}\mu _{x11}^{2}+{{c}_{x1}} \right.\mu _{x21}^{2}- \\ & 2{{k}_{x1}}{{\mu }_{x21}}{{\mu }_{x11}}\left. \cos ({{\theta }_{x1}}-{{\theta }_{x2}}) \right]- \\ & 2{{F}^{2}}{{l}^{2}}\pi \sin 2{{a}_{1}}\left[ {{p}_{\phi }}\mu _{\phi 11}^{2}+{{c}_{\phi 1}} \right.\mu _{\phi 21}^{2}- \\ & 2{{k}_{\phi 1}}{{\mu }_{\phi 21}}{{\mu }_{\phi 11}}\left. \cos ({{\theta }_{\phi 1}}-{{\theta }_{\phi 2}}) \right]+ \\ & 4{{F}^{2}}\pi \sin (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x2}}-{{\theta }_{x1}}){{p}_{x}}{{\mu }_{x11}}{{\mu }_{x12}}- \\ & 4{{F}^{2}}\pi \sin (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x1}}){{k}_{x1}}{{\mu }_{x11}}{{\mu }_{x22}}+ \\ & 4{{F}^{2}}\pi \sin (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x2}}){{c}_{x1}}{{\mu }_{x21}}{{\mu }_{x22}}- \\ & 4{{F}^{2}}\pi \sin (2{{a}_{1}}+2{{a}_{2}}){{k}_{x1}}{{\mu }_{x21}}{{\mu }_{x12}}, \\ & \\ \end{align}$ | (8) |
| $\begin{align} & \frac{\partial H}{{{\partial }_{a2}}}=4{{F}^{2}}\pi \sin (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x2}}-{{\theta }_{x1}}){{p}_{x}}{{\mu }_{x11}}{{\mu }_{x12}}+ \\ & 4{{F}^{2}}\pi \sin (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x1}}){{c}_{x1}}{{\mu }_{x21}}{{\mu }_{x22}}- \\ & 4{{F}^{2}}\pi \sin (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x2}}){{k}_{x1}}{{\mu }_{x22}}{{\mu }_{x11}}+ \\ & 4{{F}^{2}}\pi \sin (-2{{a}_{2}}+{{\theta }_{x1}}-{{\theta }_{x3}}){{k}_{x1}}{{\mu }_{x22}}{{\mu }_{x11}}+ \\ & 4{{F}^{2}}\pi \sin (2{{a}_{2}}+{{\theta }_{x2}}-{{\theta }_{x1}}){{p}_{x}}{{\mu }_{x11}}{{\mu }_{x12}}+ \\ & 4{{F}^{2}}\pi \sin (2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x2}}){{c}_{x1}}{{\mu }_{x21}}{{\mu }_{x22}}- \\ & 4{{F}^{2}}\pi {{k}_{x1}}{{\mu }_{x22}}{{\mu }_{x12}}\sin (2{{a}_{1}}+2{{a}_{2}})- \\ & 4{{F}^{2}}\pi {{k}_{x1}}{{\mu }_{x22}}{{\mu }_{x12}}\sin 2{{a}_{2}}. \\ \end{align}$ | (9) |
本系统中α1,α2为广义坐标,广义力Q1,Q2为
| $\left. \begin{array}{*{35}{l}} {{Q}_{1}}={{T}_{\text{e}1}}\frac{{{\partial }_{\varphi 1}}}{{{\partial }_{a1}}}+{{T}_{\text{e2}}}\frac{{{\partial }_{\varphi 2}}}{{{\partial }_{a1}}}+{{T}_{\text{e3}}}\frac{{{\partial }_{\varphi 3}}}{{{\partial }_{a1}}}\text{=}{{T}_{\text{e}1}}-{{T}_{\text{e}2}}-{{T}_{\text{e3}}}, \\ {{Q}_{2}}={{T}_{\text{e}1}}\frac{{{\partial }_{\varphi 1}}}{{{\partial }_{a2}}}+{{T}_{\text{e2}}}\frac{{{\partial }_{\varphi 2}}}{{{\partial }_{a2}}}+{{T}_{\text{e3}}}\frac{{{\partial }_{\varphi 3}}}{{{\partial }_{a3}}}\text{=2}{{T}_{\text{e3}}}. \\ \end{array} \right]$ | (10) |
将式(8)、(9)和(10)代入式(3),得
| $\left. \begin{array}{*{35}{l}} \frac{\partial H}{{{\partial }_{a1}}}+2\pi {{T}_{\text{e}1}}-2\pi {{T}_{\text{e2}}}-2\pi {{T}_{\text{e3}}}=0. \\ \frac{\partial H}{{{\partial }_{a2}}}-4\pi {{T}_{\text{e3}}}=0. \\ \end{array} \right]$ | (11) |
系统同步时相位差角α1,α2在一个周期内保持稳定，因此,α1,α2有解是系统同步的必要条件.式(11)是关于α1,α2的二元三角函数,无法求其精确解析解,下面将用数值方法分析.
2.2 系统同步运转的稳定性条件由约束力学系统的运动稳定性[14]可知,真实运动的Hamilton作用量具有极小值.由多元函数的极值理论得系统同步运转的稳定性条件为
| $\left. \begin{array}{*{35}{l}} \frac{{{\partial }^{2}}H}{{{\partial }_{a_{1}^{2}}}}>0, \\ \frac{{{\partial }^{2}}H}{{{\partial }_{a_{1}^{2}}}}\cdot \frac{{{\partial }^{2}}H}{{{\partial }_{a_{2}^{2}}}}-{{\left( \frac{{{\partial }^{2}}H}{{{\partial }_{a1}}{{\partial }_{a2}}} \right)}^{2}}>0. \\ \end{array} \right]$ | (12) |
其中:
| $\begin{align} & \frac{{{\partial }^{2}}H}{{{\partial }_{a_{1}^{2}}}}=8{{F}^{2}}\pi \cos 2{{a}_{1}}\left[ {{p}_{x}}\mu _{x11}^{2}+{{c}_{x1}}\mu _{x21}^{2}- \right. \\ & 2{{k}_{x1}}{{\mu }_{x21}}{{\mu }_{x11}}\left. \cos ({{\theta }_{x1}}-{{\theta }_{x2}}) \right]- \\ & 4{{F}^{2}}{{l}^{2}}\pi \cos 2{{a}_{1}}\left[ {{p}_{\phi }}\mu _{\phi 11}^{2}+{{c}_{\phi 1}} \right.\mu _{\phi 21}^{2}- \\ & 2{{k}_{\phi 1}}{{\mu }_{\phi 21}}{{\mu }_{\phi 11}}\left. \cos ({{\theta }_{\phi 1}}-{{\theta }_{\phi 2}}) \right]+ \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x2}}-{{\theta }_{x1}}){{p}_{x}}{{\mu }_{x11}}{{\mu }_{x12}}- \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x1}}){{k}_{x1}}{{\mu }_{x11}}{{\mu }_{x22}}+ \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x2}}){{c}_{x1}}{{\mu }_{x21}}{{\mu }_{x22}}- \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}){{k}_{x1}}{{\mu }_{x21}}{{\mu }_{x12}}. \\ \end{align}$ | (13) |
| $\begin{align} & \frac{{{\partial }^{2}}H}{{{\partial }_{a1}}{{\partial }_{a2}}}=8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x2}}-{{\theta }_{x1}}){{p}_{x}}{{\mu }_{x11}}{{\mu }_{x12}}- \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x1}}){{k}_{x1}}{{\mu }_{x11}}{{\mu }_{x22}}+ \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x2}}){{c}_{x1}}{{\mu }_{x21}}{{\mu }_{x22}}- \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}){{k}_{x1}}{{\mu }_{x21}}{{\mu }_{x12}}, \\ \end{align}$ | (14) |
| $\begin{align} & \frac{{{\partial }^{2}}H}{{{\partial }_{a_{2}^{2}}}}=8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x2}}-{{\theta }_{x1}}){{p}_{x}}{{\mu }_{x11}}{{\mu }_{x12}}+ \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x2}}){{c}_{x1}}{{\mu }_{x21}}{{\mu }_{x22}}- \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x1}}){{k}_{x1}}{{\mu }_{x22}}{{\mu }_{x11}}- \\ & 8{{F}^{2}}\pi \cos (-2{{a}_{1}}+{{\theta }_{x1}}-{{\theta }_{x3}}){{k}_{x1}}{{\mu }_{x22}}{{\mu }_{x11}}+ \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+{{\theta }_{x2}}-{{\theta }_{x1}}){{p}_{x}}{{\mu }_{x11}}{{\mu }_{x12}}+ \\ & 8{{F}^{2}}\pi \cos (2{{a}_{2}}+{{\theta }_{x3}}-{{\theta }_{x2}}){{c}_{x1}}{{\mu }_{x21}}{{\mu }_{x22}}- \\ & 8{{F}^{2}}\pi \cos (2{{a}_{1}}+2{{a}_{2}}){{k}_{x1}}{{\mu }_{x21}}{{\mu }_{x12}}- \\ & 8{{F}^{2}}\pi \cos 2{{a}_{2}}{{k}_{x1}}{{\mu }_{x21}}{{\mu }_{x12}}. \\ \end{align}$ | (15) |
式(11)和式(12)均为包含多个系统参数的方程,很难得出单个参数对系统同步性的影响.这里采用控制变量法,通过数值计算,进一步讨论中间弹簧刚度和电机安装位置对系统同步性的影响.取激振电机为3个相同型号的电机(Te1≈Te2≈Te3),系统参数如下所示:
| $\left. \begin{array}{*{35}{l}} {{m}_{1}}=66\text{kg,}{{m}_{2}}=72\text{kg},{{m}_{o1}}={{m}_{o2}}={{m}_{o3}}=m=2\text{kg}, \\ {{J}_{z1}}=45.22\text{kg}\cdot {{\text{m}}^{2}},{{J}_{z2}}=44.16\text{kg}\cdot {{\text{m}}^{2}},{{k}_{x2}}={{k}_{y2}}= \\ 50\text{kN/m},{{J}_{o1}}={{J}_{o2}}={{J}_{o3}}=0.01\text{kg}\cdot {{\text{m}}^{2}},{{k}_{\phi 1}}={{k}_{\phi 2}}= \\ 10\text{kN/rad,}{{\beta }_{1}}=0,{{f}_{x1}}={{f}_{y1}}=1\text{kN}\cdot \text{s/m},{{f}_{x2}}={{f}_{y2}}= \\ 1\text{kN}\cdot \text{s/m},{{\beta }_{2}}=\pi ,{{f}_{\phi 1}}={{f}_{\phi 2}}=1\text{kN}\cdot \text{s/rad},{{\beta }_{3}}=0, \\ {{f}_{1}}={{f}_{2}}={{f}_{3}}=0,{{r}_{1}}={{r}_{2}}={{r}_{3}}=0.05\text{m,} \\ {{l}_{1}}={{l}_{2}}=l=0.4\text{m},{{l}_{3}}=0\text{m},\omega =157\text{rad}/\text{s}. \\ \end{array} \right]$ | (16) |
将待研究的参数作为变量,其余参数代入式(11)和(12)中，则有
| $\left. \begin{array}{*{35}{l}} {{f}_{1}}\left( {{a}_{1}},{{a}_{2}},q \right)+2\pi {{T}_{\text{e}1}}-2\pi {{T}_{\text{e2}}}-2\pi {{T}_{\text{e3}}}=0, \\ {{f}_{2}}\left( {{a}_{1}},{{a}_{2}},q \right)-4\pi {{T}_{\text{e3}}}=0. \\ \end{array} \right\}$ | (17) |
| $\left. \begin{array}{*{35}{l}} {{f}_{3}}\left( {{a}_{1}},{{a}_{2}},q \right)>0, \\ {{f}_{4}}\left( {{a}_{1}},{{a}_{2}},q \right)>0. \\ \end{array} \right\}$ | (18) |
式(17)、(18)中q(ki1,m,l,…)是自变量.随着q的变化，式(17)可以解出不同的α1,α2；再将α1,α2以及q代入式(18)中,若均满足,则说明在此参数条件下系统可以实现稳定的自同步运动.
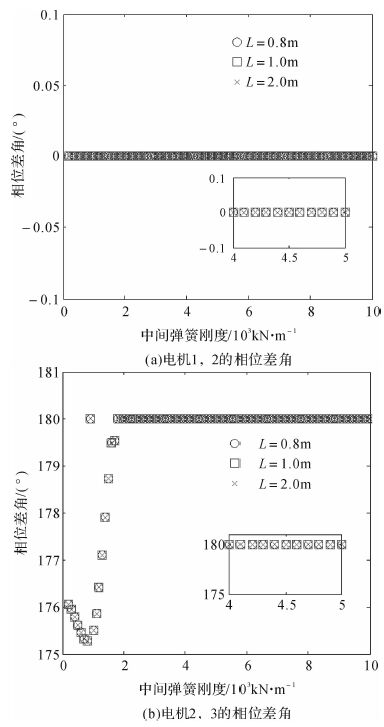
3.1 同步性条件3个激振电机没有安装在同一刚体上,所以中间弹簧刚度必然是一个影响系统同步性的重要因素；在工程设计中,激振电机的安装位置也是一个调节同步性以及同步相位差角的重要参数.在对中间弹簧刚度进行分析的时候,以中间弹簧刚度k(kx1=ky1=k)作为自变量,通过式(17)可解得k与相位差角2α1,2α2的变化曲线；对电机安装位置进行分析时采用同样的方法,上质体两电机采用如图 1所示的水平对称安装,取Ao′1=0 m,L=o1o2,β1=0,β2=π,下质体电机位于其质心上.数值分析结果如图 2所示.
|
| 图 2 中间弹簧刚度以及上质体电机安装位置对系统相位差角的影响 Fig. 2 Effects of stiffness of middle spring and the installation position of motors on phase difference |
对式(17)进行求解时：k≤200 kN/m时方程组无解,说明此时系统不能实现自同步运动；当k>200 kN/m时,α1,α2均可求解出来.由图 2(a)，(b)可知：随着k的增大，电机1，2的相位差角2α1基本不变,2α1=0°>；200
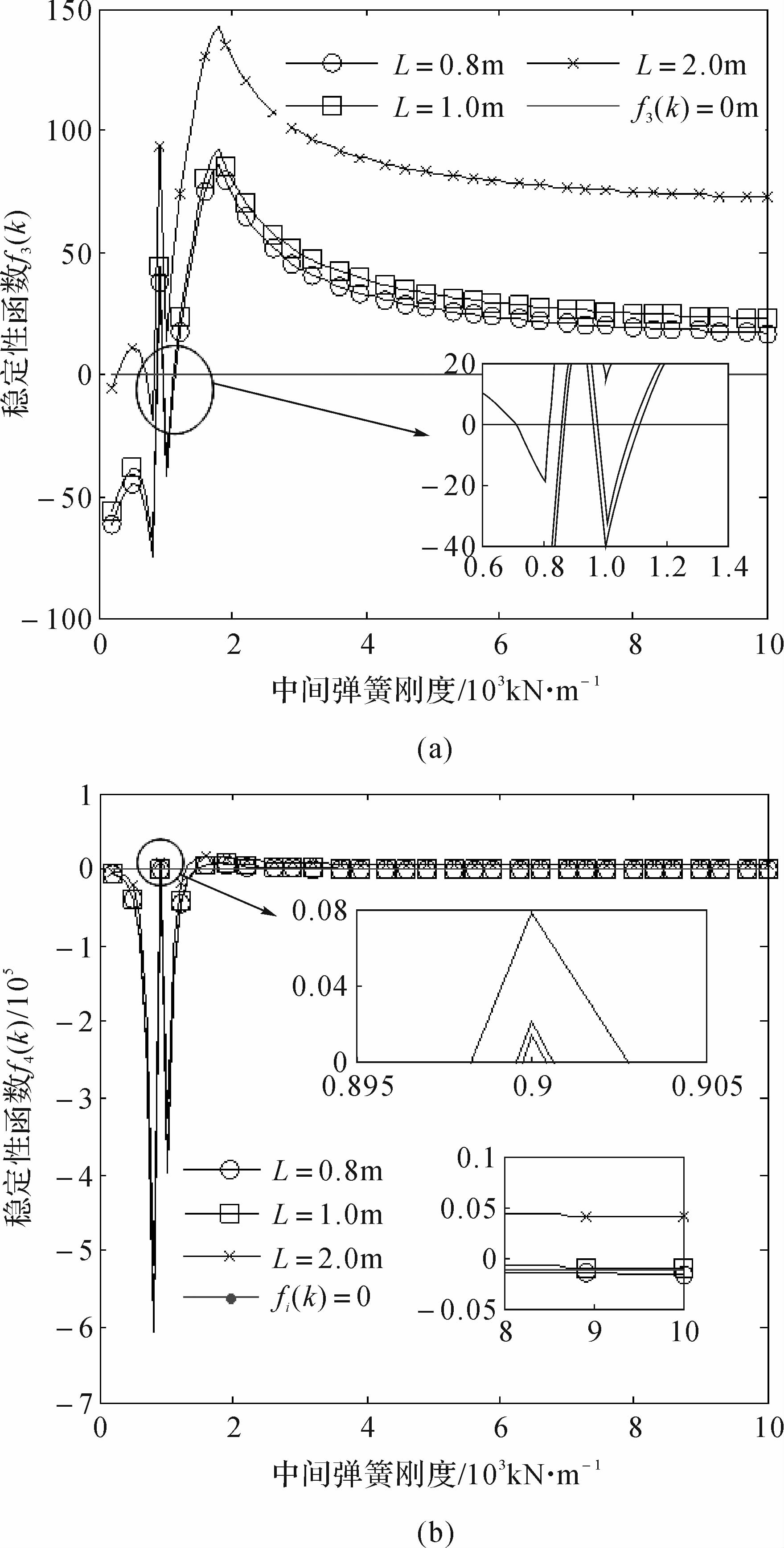
将式(17)中求解出来的相位差角2α1,2α2以及与之对应的k(L)值代入(18)式中,同样运用控制变量法分别研究中间弹簧刚度和激振电机安装位置对系统同步稳定性的影响,若f3(k)>0,f4(k)>0，则系统可以实现稳定的自同步运动,分析结果如图 3所示.
|
| 图 3 中间弹簧刚度以及上质体电机安装位置对系统同步稳定性的影响 Fig. 3 Effects of stiffness of middle spring and the installation position of motors on synchronous stability |
从图 3(a)中可以看出：L=0.8 m,870≤k≤950 kN/m或k≥1 100 kN/m时，f3(k)>0；且当k≥9 000 kN/m时f3(k)收敛于18；图 3(b)的变化规律和(a相似：当899≤k≤901 kN/m或1 300≤k≤5 000 kN/m时，f4(k)>0；且当k≥8 000 kN/m时，f4(k)收敛于-450.因此,L=0.8 m时系统实现稳定同步运转的条件为899≤k≤901 kN/m或1 300≤k≤5 000 kN/m.由式(13)可知f3(L),f4(L)均为关于L的增函数,结合图 3(a)、(b)得在L=1.0 m,899≤k≤901 kN/m或k≥1 300 kN/m时,f3(k),f4(k)恒大于0,所以L的增大有益于系统实现稳定的同步运转.
当中间弹簧刚度k足够大时，上、下质体间几乎没有相对运动,此时k的变化将不再引起α1,α2和f3(k),f4(k)的变化,这与图 3(a)和图 3(b)中的曲线最后均收敛于某一数值是一致的.
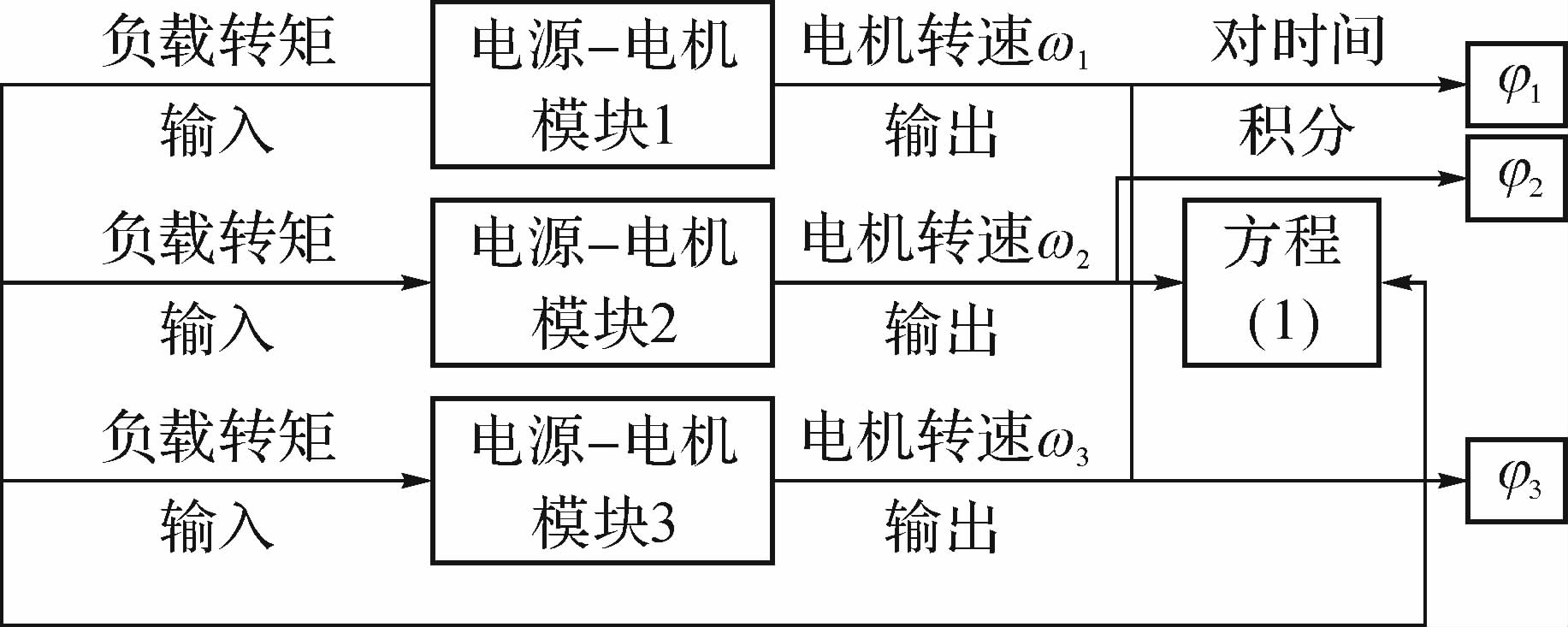
4 仿真验证 4.1 机电耦合仿真结果选取电机模块为3个相同的三相异步电动机(p=2),根据系统的运动微分方程(1)在MATLAB/Simulink中建立其机电耦合仿真模型[15, 16],如图 4所示.采用式(16)中的参数,电机1在15 s时断开电源,运用控制变量法在数值分析的基础上分别研究中间弹簧刚度和电机安装位置对系统同步相位差角的影响.
|
| 图 4 系统机电耦合仿真模型 Fig. 4 Electromechanical-coupling simulation model of system |
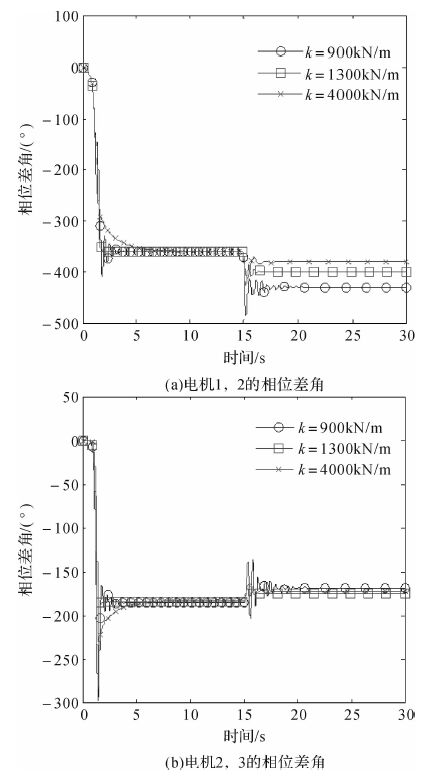
图 5(a)、(b)为L=1.0 m时,不同中间弹簧刚度k条件下,相位差角2α1,2α2随时间的变化关系,相位差角曲线收敛于某一数值表明系统处于同步状态.结合两图可知,k=900 kN/m,k=1 300 kN/m和k=4 000 kN/m时系统均可实现稳定的同步运动,且在未切断电源之前不同的弹簧刚度k对应的相位差角曲线在稳定后基本是重合的.在没有切断电机1电源之前,电机1,2的相位差角基本稳定在0°>,电机2,3的相位差角基本稳定在-180°>.15 s时切断电机1电源,一段时间后系统重新达到稳定状态.此时,不同弹簧刚度的系统相位差角有所不同,电机1,2的相位差角随着中间弹簧刚度的增大而增大,-66°>≤2α1≤-13°>,电机2,3的相位差角也随着中间弹簧刚度的变化而变化,-178°>≤2α2≤-171°>.
|
| 图 5 中间弹簧刚度对系统相位差角的影响 Fig. 5 Effect of stiffness of middle spring on phase difference |
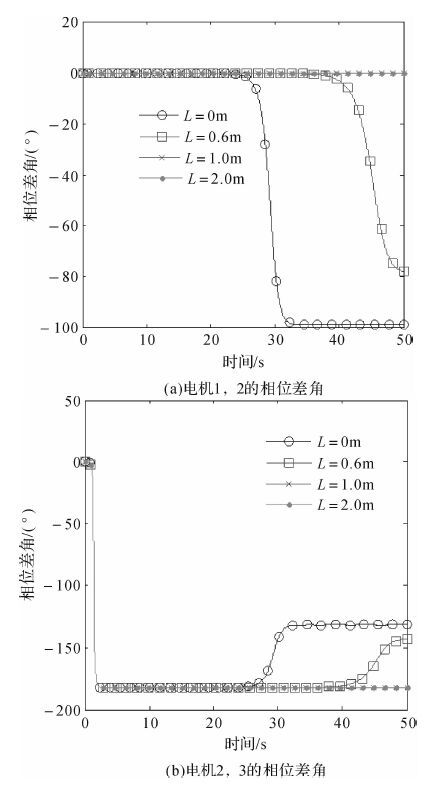
图 6(a)，(b)为k=8 000 kN/m时,将电机安装位置作为变量得出的曲线,图中L=0 m和L=0.6 m曲线均是在开始实现了同步状态,随着时间的推移又进入了一种新的同步状态,说明此时同步运动是不稳定的；L=1.0 m和L=2.0 m曲线基本重合,且不随时间的变化而变化,说明在这种参数条件下系统的同步运动是稳定的.因此,电机1，2水平安装距离的增大有益于系统的自同步运动.电机1，2的同步相位差角稳定在0°,电机2，3的同步相位差角稳定在-180°.
|
| 图 6 电机安装位置对系统相位差角的影响 Fig. 6 Effect of the installation position of motors on phase difference |
图 2、图 3为理论分析结果.图 3解出的系统的同步相位差角为：2α1=0°>,175.3°>≤2α2≤180°>.L=0.8 m时系统实现稳定的 自同步运动的区域为:899≤k≤901 kN/m或1 300≤k≤5 000 kN/m,k≥5 000 kN/m时系统的同步运动不稳定；L≥1.0 m系统实现稳定的自同步运动的区域为:899≤k≤901 kN/m或k≥1 300 kN/m.图 5、图 6为计算机仿真结果.由图 5得,L=1.0 m,899≤k≤901 kN/m或k≥1 300 kN/m时,系统可以实现稳定的自同步运动,同步相位差角2α1≈0°>,2α2≈-180°>.由图 6得k=8 000 kN/m时,L=0 m和L=0.6 m时系统的同步运动是不稳定的；L=1.0 m和L=2.0 m时系统的同步运动是稳定的,同步相位差角2α1≈0°>,2α2≈-180°>.
综上所述,理论分析的中间弹簧刚度k和上质体水平安装距离L对系统同步性以及稳定性的影响规律与仿真分析结果是一致的,两者所计算出来的具体数值有着较小的误差,这样的精度已经可以满足工程中的实际应用.产生误差的主要原因是:用理论分析法求解多元微分方程(1)时,所求结果为其近似解析解,而仿真模型则是通过循环,所求结果为其精确数值解；理论分析时,代入的电机转速ω为其平均值,而仿真模型中电机转速则是在其稳定值附近微小波动的.
5 结 论1)本文提出了一种三激振器双质体振动系统,利用Lagrange方程推导出系统运动微分方程,并求出其稳态解.运用Hamilton原理推导出系统实现自同步运动的条件为:式(11)中α1,α2有解；系统自同步运动的稳定性条件为:式(12)成立.
2)对理论分析结果进行数值分析得出:中间弹簧刚度是一个影响双质体振动系统实现自同步运动的重要因素,在式(16)参数条件下系统实现稳定自同步运动的区域为899≤k≤901 kN/m或1 300≤k≤5 000 kN/m；电机安装位置也是一个影响系统自同步运动的重要因素,上质体两电机水平安装距离的增大有益于系统的自同步运动,令式(16)参数L≥1.0 m,则系统实现稳定的自同步区域为899≤k≤901 kN/m或k≥1 300 kN/m.几种不同的参数条件下,系统的同步相位差角基本相同,电机1,2的相位差角2α1=0°,电机2,3的相位差角2α2=180°.
3)用机电耦合仿真模型在理论分析的基础上研究了中间弹簧刚度k和上质体水平安装距离L对系统同步性的影响,得出了与理论分析方法一致的结论,验证了理论分析的正确性.
参考文献
| [1] | BLEKHMAN I I,LANDA P S,ROSENBLUM M G.Synchronization and chaotization in interacting dynamical systems[J].Applied Mechanics Reviews,1995,48(11):733-752. |
| Click to display the text | |
| [2] | BLEKHMAN I I,FRADKOV A L,TOMCHINA O P,et al.Self-synchronization and controlled synchronization general definition and example design[J].Mathematics and Computers in Simulation,2002,58(4/6):367-384. |
| Click to display the text | |
| [3] | BLEKHMAN I I.Selected topics in vibrational mechanics[M].Singapore:World Scientific,2004:9-32. |
| [4] |
闻邦椿,刘凤翘.振动机械的理论及应用[M].北京:机械工业出版社,1982:40-41,294-317. WEN Bang-chun,LIU Feng-qiao.Theory of mechanical vibration and its applications[M].Beijing:China Machine Press,1982:40-41,294-317. |
| [5] |
闻邦椿,刘树英,何勍.振动机械的理论与动态设计方法[M].北京:机械工业出版社,2001:307-312. WEN Bang-chun,LIU Shu-ying,HE Qing.Theory and dynamic design method of vibration machinery[M].Beijing:China Machine Press,2001:307-312. |
| [6] |
韩清凯,秦朝烨,闻邦椿.自同步振动系统的稳定性与分岔[J].振动与冲击,2007,26(1):31-34. HAN Qing-kai,QIN Zhao-ye,WEN Bang-chun.Stability and bifurcation of self-synchronous vibration system[J].Journal Vibration and Shock,2007,26(1):31-34. |
| Click to display the text | |
| [7] |
张楠,侯晓林,闻邦椿.四电机驱动自同步振动筛同步稳定性判据[J].矿山机械,2008,19(36):99-103. ZHANG Nan,HOU Xiao-lin,WEN Bang-chun.Criterion of synchronization stability for self-synchronization shaker with four motion excitation[J].Mining & Processing Equipment,2008,19(36):99-103. |
| Click to display the text | |
| [8] |
张楠,侯晓林,闻邦椿.基于Hamilton多机振动系统同步稳定特性分析[J].东北大学学报,2008,29(5):709-713. ZHANG Nan,HOU Xiao-lin,WEN Bang-chun.Synchronization/stability characteristic analysis based on Hamilton principle for multi-machine vibration systems[J].Journal of Northeastern University,2008,29(5):709-713. |
| Click to display the text | |
| [9] |
赵春雨,王得刚,张昊,等.同向回转双机驱动振动系统的频率俘获[J].应用力学学报,2009,26(2):283-287. ZHAO Chun-yu,WANG De-gang,ZHANG Hao,et a1.Frequency capture of vibration system with two-motor drives rotating in same direction[J].Chinese Journal of Applied Mechanics,2009,26(2):283-287. |
| Click to display the text | |
| [10] | ZHANG Xue-liang,WEN Bang-chun,ZHAO Chun-yu.Experimental investigation on synchronization of three co-rotating non-identical coupled exciters driven by three motors[J].Journal of Sound and Vibration,2014,333(13):2898-2908. |
| Click to display the text | |
| [11] | ZHANG Xue-liang,WEN Bang-chun,ZHAO Chun-yu.Vibratory synchronization and coupling dynamic characteristics of mutiple unbalanced rotors on a mass-spring rigid base[J].International Journal of Non-linear Mechanics,2014,60(2):1-8. |
| Click to display the text | |
| [12] |
李鹤,刘丹,姜来,等.含二次隔振架的双机驱动振动机的自同步理论研究[J].振动与冲击,2014,33(8):134-140. LI He,LIU Dan,JIANG Lai,et al.Self-synchronization theory of a vibrating system with a two-stage vibration isolation frame driven by two motors[J].Journal Vibration and Shock,2014,33(8):134-140. |
| Click to display the text | |
| [13] |
梅凤翔,刘端,罗勇.高等分析力学[M].北京:北京理工大学出版社,1991:52-129. MEI Feng-xiang,LIU Duan,LUO Yong.Advanced analytical mechanics[M].Beijing:Press of Beijing Institute of Technology,1991:52-129. |
| [14] |
梅凤翔,史荣昌,张永发,等.约束力学系统的运动稳定性[M].北京:北京理工大学出版社,1997:33-97. MEI Feng-xiang,SHI Rong-chang,ZHANG Yong-fa,et al.Stability of constrained mechanical systems[M].Beijing:Press of Beijing Institute of Technology,1997:33-97. |
| [15] |
王锋,姜建国,颜天佑.基于Matlab的异步电动机建模方法的研究[J].系统仿真学报,2006,18(7):1733-1741. WANG Feng,JIANG Jian-guo,YAN Tian-you.Methods of asynchronous motor model simulation based on Matlab[J].Journal of System Simulation,2006,18(7):1733-1741. |
| Click to display the text | |
| [16] |
高景德,王祥珩,李发海.交流电机及其系统的分析[M].北京:清华大学出版社,2005:220-232. GAO Jing-de,WANG Xiang-heng,LI Fa-hai.Analysis of AC motor and its system[M].Beijing:Tsinghua University Press,2005:220-232. |