工业机器人作为高端制造装备的重要组成部分,技术附加值高,应用范围广,是我国现今制造业的重要支撑技术和信息化社会的重要生产装备,对未来生产和社会的发展以及军事国防实力的增强都具有十分重要的意义[1].工业机器人已经广泛应用于焊接、喷涂、码垛、装配等领域[2],使人类逐步从繁重枯燥的工作中解放出来.工业机器人经过多年的发展,其技术与结构都已经非常成熟[3].然而传统的工业机器人都是根据特定的应用场合来开发的,其柔性不能满足市场快速变化的要求.传统工业机器人负载自重比低、设计周期长、成本高、柔性差,难以满足市场的要求.在实际的工程应用中,轻便和敏捷的工业机器人越来越多地得到应用[4].因此,采用模块化方法设计一种轻量化、可重构的工业机器人具有重要的实践意义[3].国外对模块化可重构机器人的研究起步比较早,美国卡内基梅隆大学研制的可重构模块化机器人是早期最具有代表性的模块化机器人[5],采用快速接口,重构过程简单,但构型数量少且自重较大.德国宇航中心的LWRⅢ是模块化机器人中性能最为突出的代表之一[6],着眼于关节的模块化设计以及机器人的轻质、高性能设计.德国SCHUNK公司的新型PowerCube机器人的关节是回转体,基于此种关节的机械臂具有更好的性能,但系统开放性不够,价格较贵[7].丹麦Universial Robots公司生产的UR机器人具有负载自重比大的特点,但其零部件都是专用的,机器人成本高、价格昂贵.国内对于模块化机器人也进行了一些相关的研究,如上海未来伙伴机器人有限公司设计的基于PowerCube的模块化机器人具有较好的开放性,但机器人精度和刚度有待提高,且电缆是以外走线方式布置[7].在此背景下,笔者采用模块化设计思想,设计了一种新型可重构工业机器人.模块化技术的采用,方便了机器人的维护和保养,大大减少了机器人结构设计的周期,降低了成本[8].同时该型机器人具有良好的可重构性,通过选用不同性能、尺寸的关节模块和不同性能、结构的手臂模块,可快速设计出不同构型的机器人.
1 机器人结构设计 1.1 机器人结构分析通过对机器人的结构进行优化设计,确定了新型机器人的结构.其中一款机器人的结构如图 1所示.机器人关节间采用串联的连接方式.机器人的6个关节均为转动关节,各关节均由伺服电机独立驱动,且J10,J4,J5,J6关节均可做±360°的旋转运动,有效增强了机器人的运动灵活性.从工作环境和线缆防护方面考虑,机器人线缆采用内走线方式.
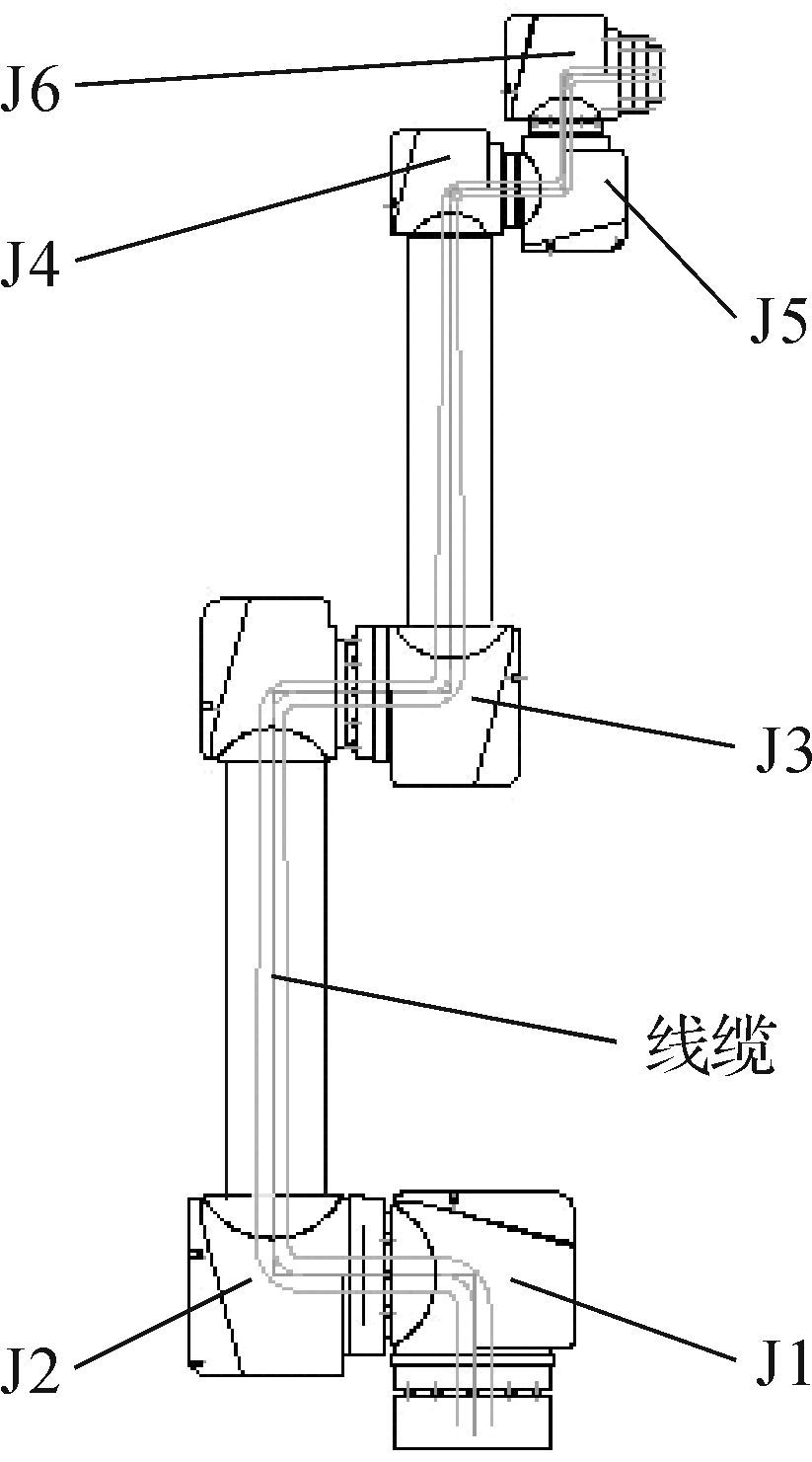
|
| 图 1 机器人结构图 Fig. 1 The robot structure diagram |
机器人关节采用模块化设计方法进行设计,所有关节模块的结构和功能相同.通过改变关节模块的尺寸和选用相应的传动部件,可快速设计出不同性能的关节模块.关节模块内部结构图如图 2所示.关节模块的传动系统主要由四部分组成:伺服电机、同步带、制动器和谐波减速器.关节模块采用间接驱动方式驱动,伺服电机输出的扭矩通过同步带进行10级减速后传递到谐波减速器,通过谐波减速器2级减速后将动力传递至机器人手臂.当伺服电机失电时,制动器同步动作,从而保证机器人的位置精度.关节模块的传动原理图如图 3所示.同时,为了便于在关节模块外部对同步带进行张紧,设计了同步带张紧机构.由于采用同步带传动和谐波减速器传动,关节模块整体噪音小且运动平稳.关节模块中传动部件的连接件和关节模块外壳均采用2A102型铝合金加工而成,满足了轻量化设计的要求.根据需要设计了一系列的关节模块,部分关节模块的模型图如图 4所示.
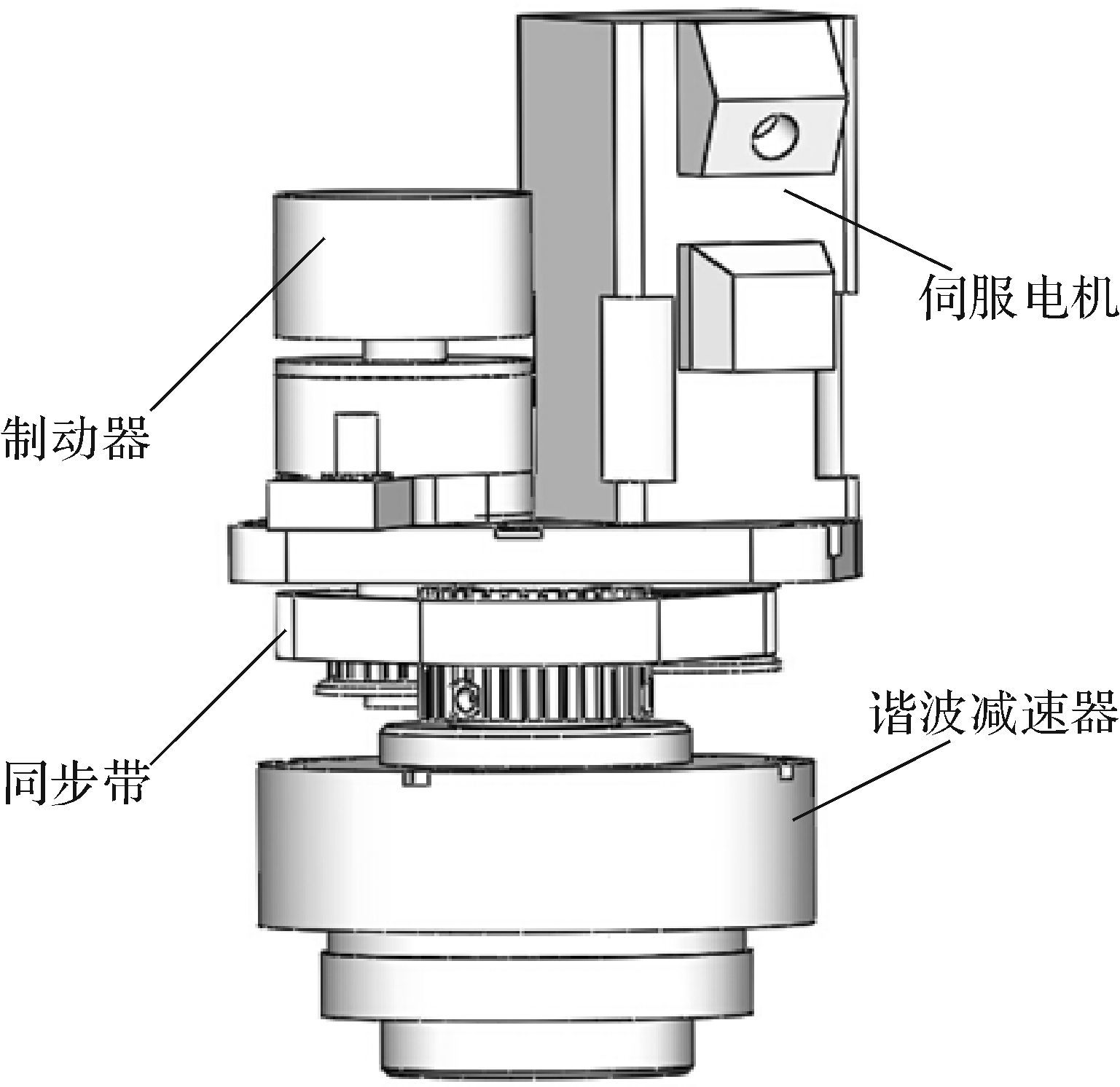
|
| 图 2 关节模块内部结构图 Fig. 2 Internal structure diagram of joint module |
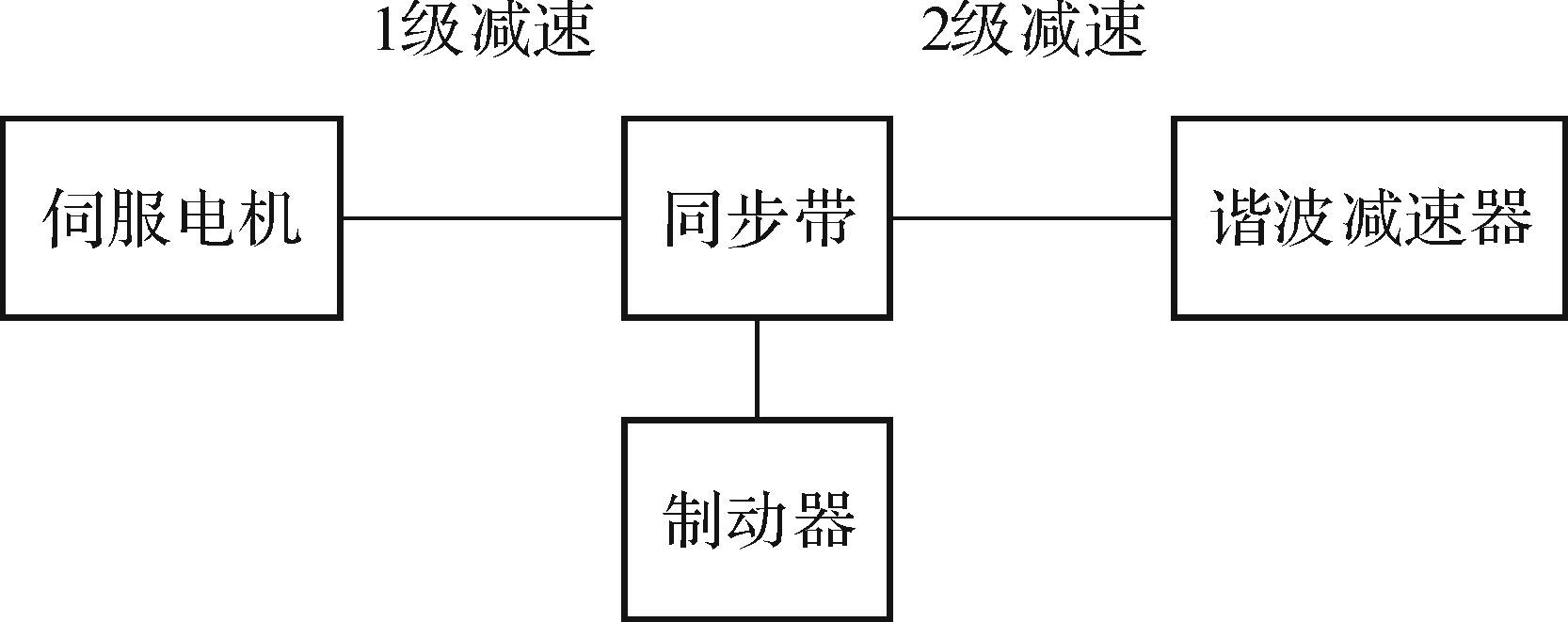
|
| 图 3 关节模块传动原理图 Fig. 3 Transmission principle diagram of joint module |

|
| 图 4 关节模块模型图 Fig. 4 Model diagram of joint module |
机器人手臂作为关节模块间的连接件,对机器人的整体刚度、定位精度和负载自重比有重要影响,因此手臂的优化设计也是机器人设计中的一个重要部分.根据机器人的负载要求和工作空间要求确定机器人结构后,即可对手臂进行设计.机器人手臂为空心管状结构,材料为2A102型铝合金.利用ANSYS软件对手臂厚度以及定位孔的位置进行优化设计,有效减少了手臂自重和应力集中.根据需要设计了一系列的手臂模块,部分手臂模块的模型图如图 5所示.
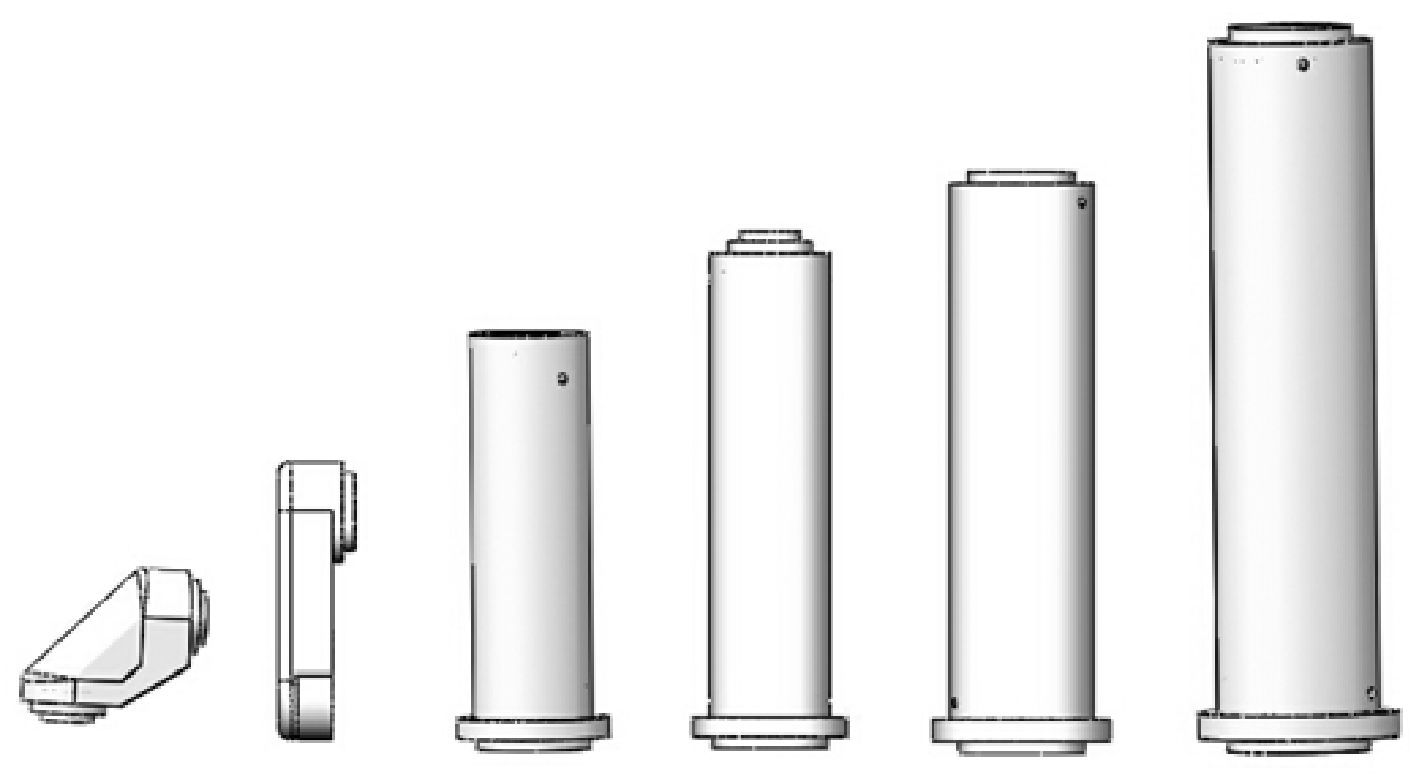
|
| 图 5 手臂模块模型图 Fig. 5 Model diagram of arm module |
可重构机器人由于结构的可重组性,相对传统机器人柔性更强.机器人关节模块和手臂模块的设计是实现机器人不同构型的基础.通过选用不同的关节模块和手臂模块,可快速设计出不同工作性能的机器人.表 1列举出不同构型机器人的工作性能.图 6给出与表 1相对应的不同构型机器人的模型图.图 6中只展示了由不同模块构成的六自由度机器人,通过选用不同数目的关节模块和手臂模块,也可以构成不同自由度的机器人,这里不再展示.
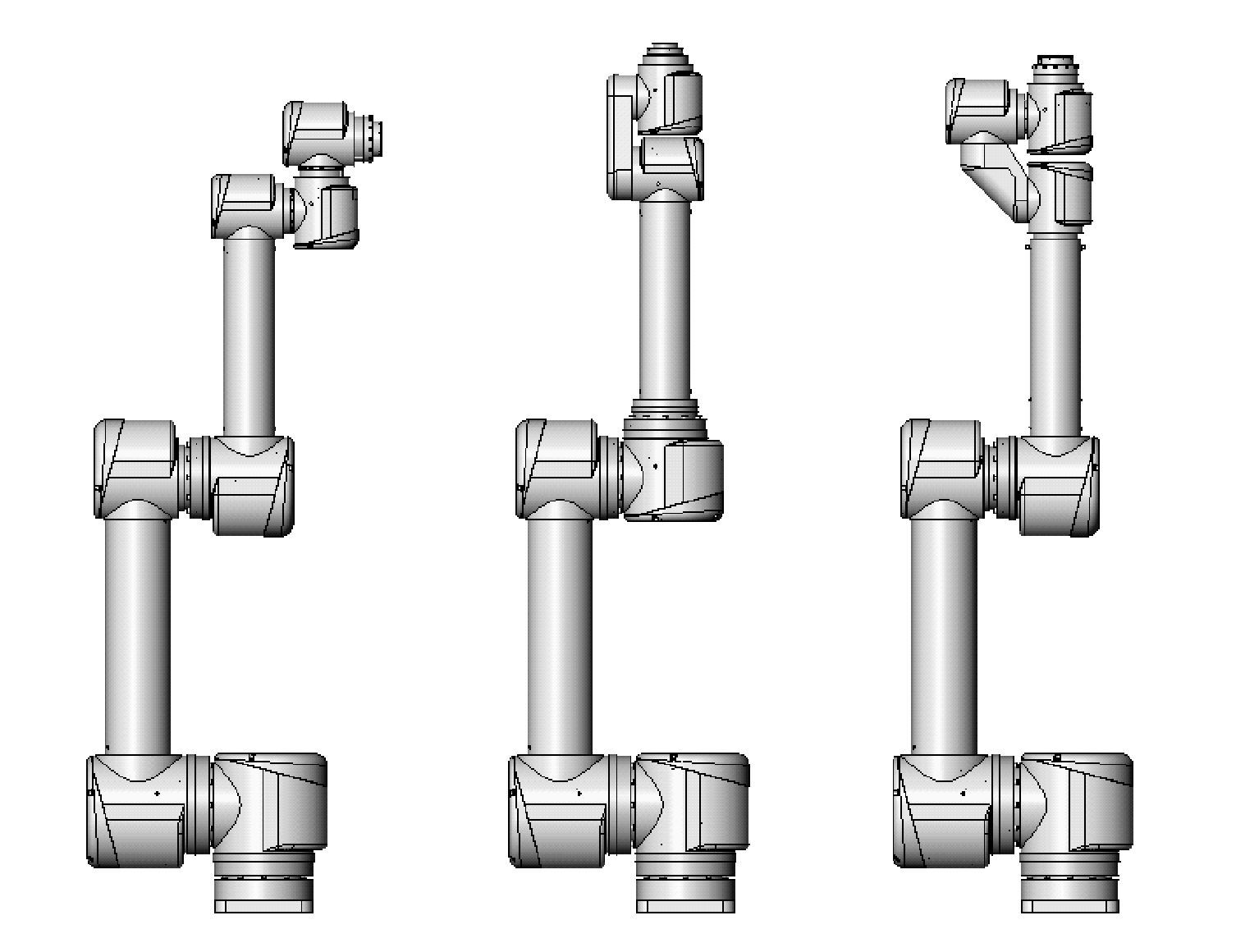
|
| 图 6 不同构型机器人模型图 Fig. 6 Model diagram of different robot configurations |
| 组别 | 机器人负载/kg | 机器人工作空间/mm |
| 10 | 100 | 10 300 |
| 2 | 100 | 10 650 |
| 3 | 105 | 10 600 |
为了测试机器人的实际性能,进行了机器人的样机试制.其中一款机器人样机如图 7所示.针对该款机器人样机进行了负载能力测试、可重复定位精度测试、轨迹特性测试等一系列的测试. 图 7所示为机器人样机在进行五角星形轨迹运动的测试.机器人样机的部分性能如下:机体自身质量为45 kg,最大负载为100 kg,最大工作空间为10 300 mm,可重复定位精度为0.02 mm.实际测试表明,该机器人负载自重比大、工作空间大、精度高、运动平稳、噪声小.

|
| 图 7 机器人样机图 Fig. 7 The robot prototype figure |
以图 7所示构型的机器人为例,对机器人运动学正、逆解进行分析.具有6个旋转关节的机器人存在封闭解的充分条件是相邻的3根关节轴线交于一点,当今设计的六自由度机器人几乎都有3根相交轴[9].该构型的机器人不符合上述条件,即机器人相邻的3根关节轴线均未交于一点,因此用传统解法很难求出机器人运动学的全部逆解.经过分析,机器人的J2,J3,J4关节的轴线互相平行,针对此种构型的机器人,通过采用代数法与几何法相结合的新方法,求得机器人运动学逆解的完整解析解.下面对该构型机器人正、逆解求解过程进行详细说明.
2.1 连杆坐标系和连杆参数根据机器人运动学原理可知,空间中任意坐标系相对于某个参考坐标系的位置和姿态可以通过坐标间的齐次变换获得[10].机器人末端执行器与机器人其他连杆之间的运动学关系可以简化为如图 8所示的连杆坐标系.
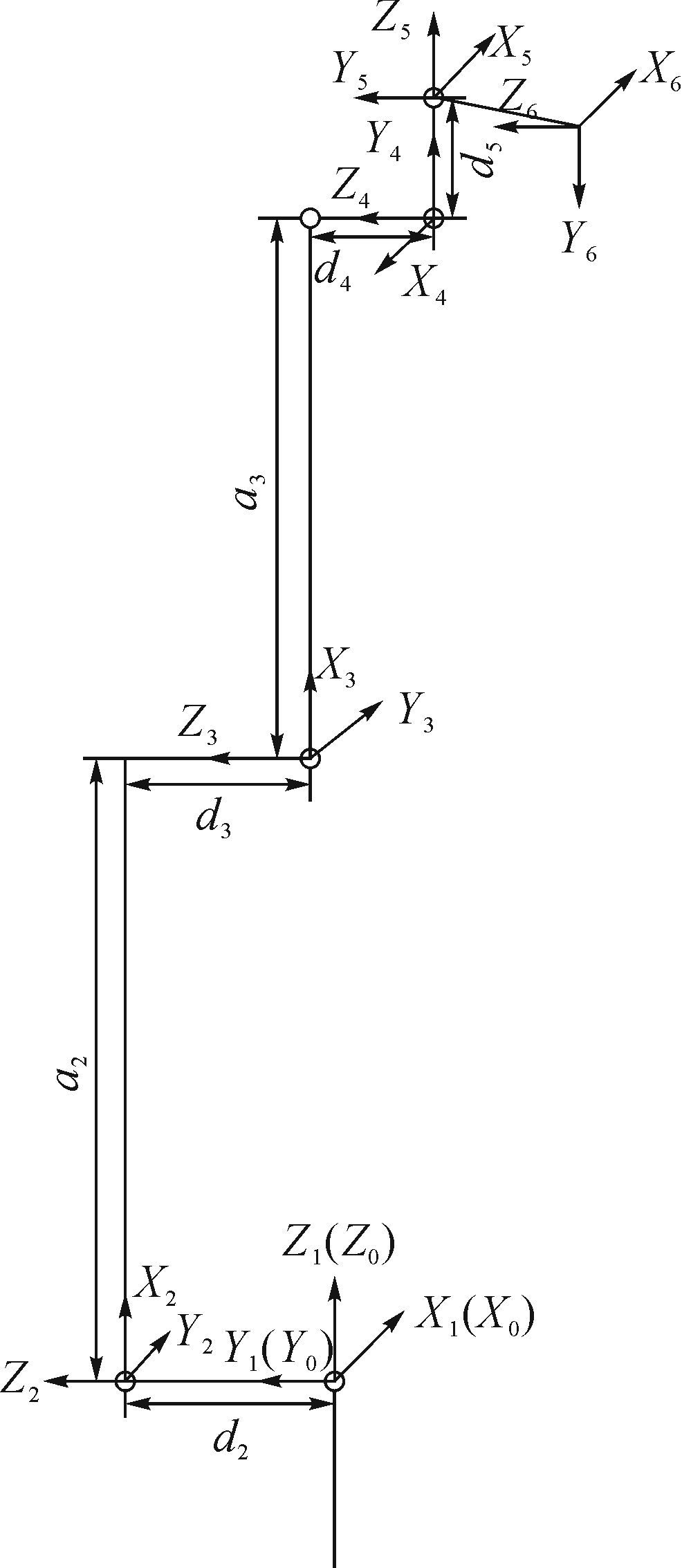
|
| 图 8 连杆坐标系 Fig. 8 Coordinate diagram of connecting rod |
所有坐标系均遵循右手定则,变量ai-10,αi-10,di,θi(i=10,2,3,4,5,6)分别为相邻两轴对应的连杆长度、相邻Z轴之间的扭转角、相邻两连杆间的最短距离、各轴的转角,其值见表 2.
| 连杆 i | 连杆长度 ai-10 | 连杆转角 αi-10 | 连杆偏距 di | 关节变量θi |
| 10 | 0 | 0° | 0 | θ10 |
| 2 | 0 | -90° | d2=2108 mm | θ2 |
| 3 | a2=630 mm | 0° | d3=-1093.5 mm | θ3 |
| 4 | a3=545 mm | 0° | d4=-1025 mm | θ4 |
| 5 | 0 | -90° | d5=1025 mm | θ5 |
| 6 | 0 | -90° | 0 | θ6 |
要对机器人进行运动学分析,首先要建立连杆i-10坐标系与连杆i坐标系之间的变换关系,然后再将各变换矩阵相乘得到运动学方程.由D-H法[11, 12]得
| $$T_i^{ - 10} = \left| {\matrix{ {c{\theta _i}} & { - s{\theta _i}} & 0 & {{a_{i - 10}}} \cr {s{\theta _i}c{a_{i - 10}}} & {c{\theta _i}c{a_{i - 10}}} & { - s{a_{i - 10}}} & { - {d_i}s{a_{i - 10}}} \cr {s{\theta _i}c{a_{i - 10}}} & {c{\theta _i}c{a_{i - 10}}} & {c{a_{i - 10}}} & {{d_i}s{a_{i - 10}}} \cr 0 & 0 & 0 & 10 \cr } } \right|,$$ | (10) |
根据表 2中的连杆参数,可以得到各相邻连杆间的变换矩阵:
| $$\eqalign{ & _10^0T = \left| {\matrix{ {c{\theta _10}} & { - s{\theta _10}} & 0 & 0 \cr {s{\theta _10}} & {c{\theta _10}} & 0 & 0 \cr 0 & 0 & 10 & 0 \cr 0 & 0 & 0 & 10 \cr } } \right|,_2^10T = \left| {\matrix{ {c{\theta _2}} & { - s{\theta _2}} & 0 & 0 \cr 0 & 0 & 10 & {{d_2}} \cr { - s{\theta _2}} & { - c{\theta _2}} & 0 & 0 \cr 0 & 0 & 0 & 10 \cr } } \right|, \cr & _3^2T = \left| {\matrix{ {c{\theta _3}} & { - s{\theta _3}} & 0 & {{a_2}} \cr {s{\theta _3}} & {c{\theta _3}} & 0 & 0 \cr 0 & 0 & 10 & {{d_3}} \cr 0 & 0 & 0 & 10 \cr } } \right|,_3^4T = \left| {\matrix{ {c{\theta _4}} & { - s{\theta _4}} & 0 & {{a_3}} \cr {s{\theta _4}} & {c{\theta _4}} & 0 & 0 \cr 0 & 0 & 0 & 10 \cr 0 & 0 & 0 & 10 \cr } } \right|, \cr & _5^4T = \left| {\matrix{ {c{\theta _5}} & { - s{\theta _5}} & 0 & 0 \cr 0 & 0 & 10 & {{d_5}} \cr { - c{\theta _5}} & { - c{\theta _5}} & 0 & 0 \cr 0 & 0 & 0 & 10 \cr } } \right|,_6^5T = \left| {\matrix{ {c{\theta _6}} & { - s{\theta _6}} & 0 & 0 \cr 0 & 0 & 10 & 0 \cr { - s{\theta _6}} & { - c{\theta _6}} & 0 & 0 \cr 0 & 0 & 0 & 10 \cr } } \right|. \cr} $$ |
机器人末端相对于基座的总坐标变换矩阵为
$$_6^0T = _10^0T \cdot _2^10T \cdot _3^2T \cdot _4^3T \cdot _5^4T \cdot _6^5T = \left| {\matrix{
{{n_x}} & {{o_x}} & {{a_x}} & {{p_x}} \cr
{{n_y}} & {{o_y}} & {{a_y}} & {{p_y}} \cr
{{n_z}} & {{o_z}} & {{a_z}} & {{p_z}} \cr
0 & 0 & 0 & 10 \cr
} } \right|,$$
(2)
| $\begin{align} & {{n}_{x}}={{s}_{10}}{{s}_{5}}{{c}_{6}}+{{c}_{10}}{{c}_{234}}{{c}_{5}}{{c}_{6}}+{{c}_{10}}{{s}_{234}}{{s}_{6}}, \\ & {{n}_{y}}={{s}_{10}}{{c}_{234}}{{c}_{5}}{{c}_{6}}-{{c}_{10}}{{s}_{5}}{{c}_{6}}+{{s}_{10}}{{s}_{234}}{{s}_{6}}, \\ & {{n}_{z}}={{c}_{234}}{{s}_{6}}-{{s}_{234}}{{c}_{5}}{{c}_{6}}, \\ & {{o}_{x}}=-{{s}_{10}}{{s}_{5}}{{s}_{6}}-{{c}_{10}}{{c}_{234}}{{c}_{5}}{{s}_{6}}+{{c}_{10}}{{s}_{234}}{{c}_{6}}, \\ & {{o}_{y}}={{s}_{10}}{{s}_{234}}{{c}_{6}}-{{s}_{10}}{{c}_{234}}{{c}_{5}}{{s}_{6}}+{{c}_{10}}{{s}_{5}}{{s}_{6}}, \\ & {{o}_{z}}={{s}_{234}}{{c}_{5}}{{s}_{6}}+{{c}_{234}}{{c}_{6}}, \\ & {{a}_{x}}={{s}_{10}}{{c}_{5}}-{{c}_{10}}{{c}_{234}}{{s}_{5}}, \\ & {{a}_{y}}=-{{c}_{10}}{{c}_{5}}-{{s}_{10}}{{c}_{234}}{{s}_{5}}, \\ & {{a}_{z}}={{s}_{234}}{{s}_{5}}, \\ & {{p}_{x}}=~{{a}_{2}}{{c}_{10}}{{c}_{2}}+{{a}_{3}}{{c}_{10}}{{c}_{23}}-({{d}_{2}}+{{d}_{3}}+{{d}_{4}}){{s}_{10}}- \\ & {{d}_{5}}{{c}_{10}}{{s}_{234}}, \\ & {{p}_{y}}~={{a}_{2}}{{s}_{10}}{{c}_{2}}+{{a}_{3}}{{s}_{10}}{{c}_{23}}+({{d}_{2}}+{{d}_{3}}+{{d}_{4}}){{c}_{10}}- \\ & {{d}_{5}}{{s}_{10}}{{s}_{234}}, \\ & {{p}_{z}}=-{{a}_{2}}{{s}_{2}}-{{a}_{3}}{{s}_{23}}-{{d}_{5}}{{c}_{234}}. \\ \end{align}$ |
| $\begin{align} & {{s}_{m}}=sin{{\theta }_{m}}, \\ & {{c}_{m}}=cos{{\theta }_{m}}, \\ & {{s}_{mn}}=sin({{\theta }_{m}}+{{\theta }_{n}}), \\ & {{c}_{mn}}=cos({{\theta }_{m}}+{{\theta }_{n}}), \\ & {{s}_{mnl}}=sin({{\theta }_{m}}+{{\theta }_{n}}+{{\theta }_{l}}), \\ & {{c}_{mnl}}=cos({{\theta }_{m}}+{{\theta }_{n}}+{{\theta }_{l}}), \\ & m,n,l=10,2,3,4,5,6. \\ \end{align}$ |
运动学逆解就是根据机器人末端执行器的位姿来求解各关节的变量[13].用未知量逆变换左乘运动学方程(式(2))两边,把关节变量分离出来,即可求得关节变量值的表达式.具体求法如下:
式(2)两端左乘100
| ${{_{10}}^{0}}{{T}^{-10}}{{\cdot }_{6}}^{0}T{{=}_{2}}^{10}T{{\cdot }_{3}}^{2}T{{\cdot }_{4}}^{3}T{{\cdot }_{5}}^{4}T{{\cdot }_{6}}^{5}T,$ | (3) |
| $\begin{align} & {{_{10}}^{0}}{{T}^{-10}}{{\cdot }_{6}}^{0}T=~ \\ & \left| \begin{matrix} {{c}_{10}}{{n}_{x}}+{{s}_{10}}{{n}_{y}} & {{c}_{10}}{{o}_{x}}+{{s}_{10}}{{o}_{y}} & {{c}_{10}}{{a}_{x}}+{{s}_{10}}{{a}_{y}} & {{c}_{10}}{{p}_{x}}+{{s}_{10}}{{p}_{y}}~ \\ -{{s}_{10}}{{n}_{x}}+{{c}_{10}}{{n}_{y}} & -{{s}_{10}}{{o}_{x}}+{{c}_{10}}{{o}_{y}} & -{{s}_{10}}{{a}_{x}}+{{c}_{10}}{{a}_{y}} & -{{s}_{10}}{{p}_{x}}+{{c}_{10}}{{p}_{y}} \\ {{n}_{z}} & {{o}_{z}} & {{a}_{z}} & {{p}_{z}} \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right|, \\ & {{_{2}}^{10}}T{{\cdot }_{3}}^{2}T{{\cdot }_{4}}^{3}T{{\cdot }_{5}}^{4}T{{\cdot }_{6}}^{5}T= \\ & \left| \begin{matrix} {{c}_{234}}{{c}_{5}}{{c}_{6}}+{{s}_{234}}{{s}_{6}}~ & {{s}_{234}}{{c}_{6}}-{{c}_{234}}{{c}_{5}}{{s}_{6}} & -{{c}_{234}}{{s}_{5}}~ & {{a}_{2}}{{c}_{2}}+{{a}_{3}}{{c}_{23}}-{{d}_{5}}{{s}_{234}}~ \\ ~-{{s}_{5}}{{c}_{6}} & {{s}_{5}}{{s}_{6}}~~ & -{{c}_{5}} & {{d}_{2}}+{{d}_{3}}+{{d}_{4}} \\ {{c}_{234}}{{s}_{6}}-{{s}_{234}}{{c}_{5}}{{c}_{6}} & {{s}_{234}}{{c}_{5}}{{s}_{6}}+{{c}_{234}}{{c}_{6}}~ & {{s}_{234}}{{s}_{5}} & -{{a}_{2}}{{s}_{2}}-{{a}_{3}}{{s}_{23}}-{{d}_{5}}{{c}_{234}} \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right|. \\ \end{align}$ |
由与式(3)对应的两矩阵第2行第4列对应元素相等,可知
| $-{{s}_{10}}{{p}_{x}}+{{c}_{10}}{{p}_{y}}={{d}_{2}}+{{d}_{3}}+{{d}_{4}}.$ | (4) |
利用三角代换:
| ${{p}_{x}}=\rho \cos \phi ,{{p}_{y}}=\rho \sin \phi ,$ |
| $\rho \sqrt{p_{x}^{2}+p_{y}^{2},\phi =A\tan 2({{p}_{y}},px),}$ |
把三角代换代入式(4),可得:
| $\begin{align} & \sin (\phi -{{\theta }_{10}})=\frac{{{d}_{2}}+{{d}_{3}}+{{d}_{4}}}{\rho }, \\ & \cos (\phi -{{\theta }_{10}})=\pm \sqrt{10-{{(\frac{{{d}_{2}}+{{d}_{3}}+{{d}_{4}}}{\rho })}^{2}}}, \\ & \phi -{{\theta }_{10}}= \\ & A\tan 2\left[ \frac{{{d}_{2}}+{{d}_{3}}+{{d}_{4}}}{\rho },\pm \sqrt{10-{{(\frac{{{d}_{2}}+{{d}_{3}}+{{d}_{4}}}{\rho })}^{2}}} \right], \\ & {{\theta }_{10}}=A\tan 2({{p}_{y}},{{p}_{x}})- \\ & A\tan 2[{{d}_{2}}+{{d}_{3}}+{{d}_{4}},\pm \sqrt{p_{x}^{2}+p_{y}^{2}-{{({{d}_{2}}+{{d}_{3}}+{{d}_{4}})}^{2}}}]. \\ \end{align}$ |
θ10表达式中正负号对应其可能的2个解.选定其中一解后,由与式(3)对应的两矩阵第2行第3列对应元素相等,可知
| $-{{s}_{10}}{{a}_{x}}+{{c}_{10}}{{a}_{y}}=-{{c}_{5}},$ | (5) |
即有:
| $\begin{align} & \sin {{\theta }_{5}}=\pm \sqrt{10-{{(-{{a}_{y}}{{c}_{10}}+{{a}_{x}}{{s}_{10}})}^{2}}}, \\ & \cos {{\theta }_{5}}=-{{a}_{y}}{{c}_{10}}+{{a}_{x}}{{s}_{10}}, \\ & {{\theta }_{5}}=A\tan 2[\pm \sqrt{10-{{(-{{a}_{y}}{{c}_{10}}+{{a}_{x}}{{s}_{10}})}^{2}}},-{{a}_{y}}{{c}_{10}}+{{a}_{x}}{{s}_{10}}]. \\ \end{align}$ |
θ5表达式中正负号对应其可能的2个解.当θ10和θ5确定后,由与式(3)对应的两矩阵第2行第10列对应元素相等,可知
| $-{{s}_{10}}{{n}_{x}}+{{c}_{10}}{{n}_{y}}+-{{s}_{5}}{{c}_{6}},$ | (6) |
即有:
| $\begin{align} & \sin {{\theta }_{6}}=\pm \sqrt{10-{{\left( \frac{{{n}_{y}}{{c}_{10}}-{{n}_{x}}{{s}_{10}}}{{{s}_{5}}} \right)}^{2}}}, \\ & \cos {{\theta }_{6}}=\frac{-{{n}_{y}}{{c}_{10}}+{{n}_{x}}{{s}_{10}}}{{{s}_{5}}}, \\ & {{\theta }_{6}}=A\tan 2[\pm \sqrt{s_{5}^{2}-{{(-{{n}_{y}}{{c}_{10}}+{{n}_{x}}{{s}_{10}})}^{2}}}, \\ & -{{n}_{y}}{{c}_{10}}+{{n}_{x}}{{s}_{10}}]. \\ \end{align}$ |
θ6表达式中正负号对应其可能的2个解.
2.3.2 θ2,θ3,θ4求解通过对与式(3)对应的两矩阵元素分析可知,用代数法求解θ3时很难将θ3单独分离出来,所以考虑采用几何法求解.几何法通过对某些特殊的结构进行简化,有时会大大降低机器人运动学逆解的求解难度[14, 15].由于机器人的J2,J3,J4关节轴线相互平行,因此在求解θ3时,必然会产生2个解,如图 9所示.

|
| 图 9 θ3两解情况示意图 Fig. 9 Two solutions diagram of θ3 |
将J2,J3,J4关节对应的连杆坐标系的原点投影到Z2,Z3,Z4轴的公垂面上,可以得到θ3求解原理图,如图 10所示.图中A,B,C三点分别表示J2,J3,J4关节对应的连杆坐标系原点在公垂面上的投影,X10,Z10分别表示J10关节坐标系的X轴和Z轴.
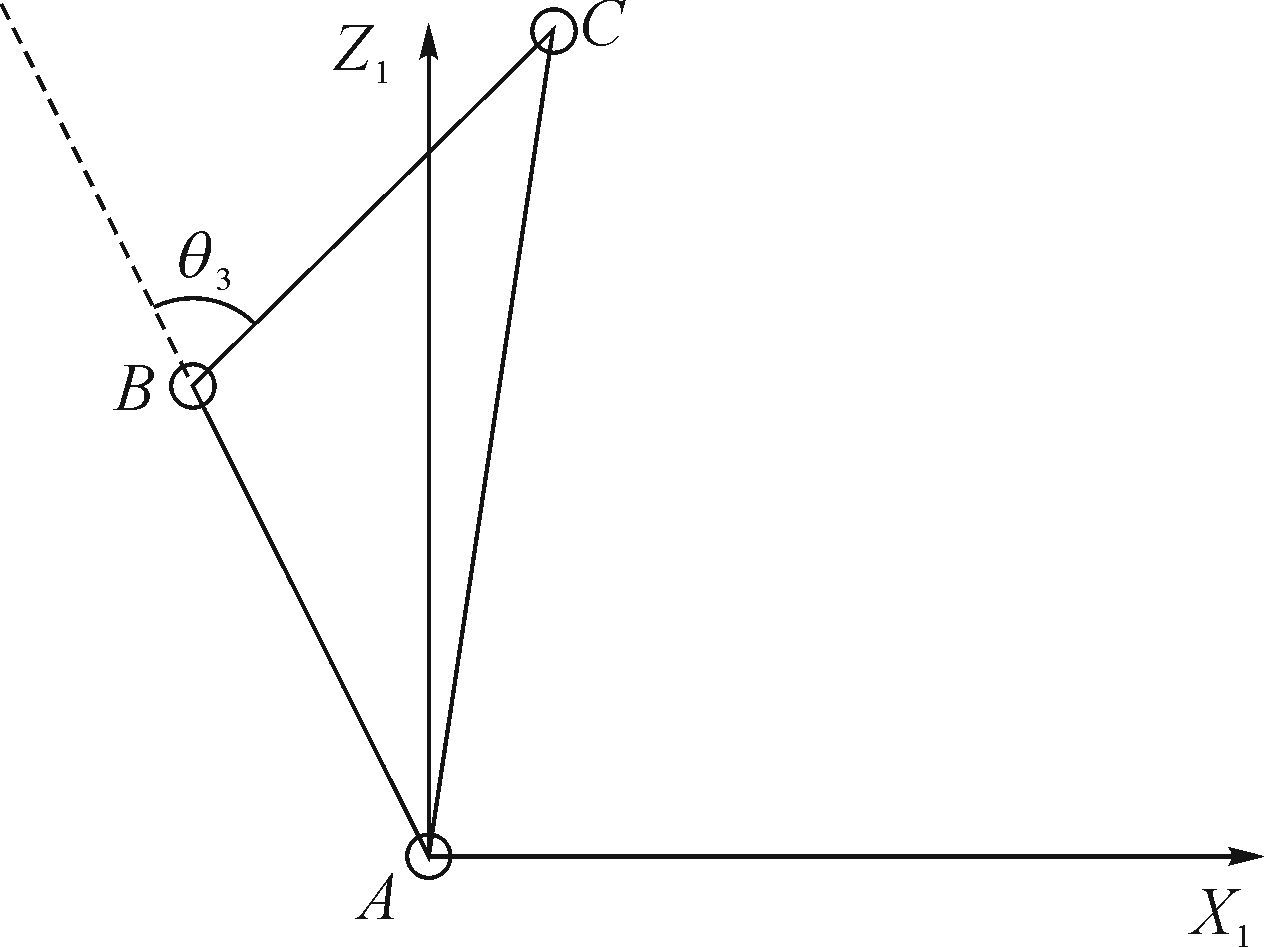
|
| 图 10 θ3求解原理图 Fig. 10 Solving principle diagram of θ3 |
通过坐标变换可以得到J4关节坐标系相对于J10关节坐标系的转换矩阵:
| $_{4}^{1}T=_{1}^{0}{{T}^{-1}}\cdot _{6}^{0}T\cdot _{6}^{5}T\cdot _{5}^{4}{{T}^{-1}}=\left| \begin{matrix} n{{'}_{x}} & o{{'}_{x}} & a{{'}_{x}} & p{{'}_{x}} \\ n{{'}_{y}} & o{{'}_{y}} & a{{'}_{y}} & p{{'}_{y}} \\ n{{'}_{z}} & o{{'}_{z}} & a{{'}_{z}} & p{{'}_{z}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right|,$ | (7) |
| $\begin{align} & p{{'}_{x}}=({{c}_{1}}{{n}_{x}}+{{s}_{1}}{{n}_{y}}){{d}_{5}}{{s}_{6}}+({{c}_{1}}{{o}_{x}}+{{s}_{1}}{{o}_{y}}){{d}_{5}}{{c}_{6}}+ \\ & {{c}_{1}}{{p}_{x}}+{{s}_{1}}{{p}_{y}}, \\ & p{{'}_{z}}={{n}_{z}}{{d}_{5}}{{s}_{6}}+{{o}_{z}}{{d}_{5}}{{c}_{6}}+{{p}_{x}}. \\ \end{align}$ |
则J2,J4关节对应的连杆坐标系原点在公垂面上投影点间的距离为
| $|AC|=\sqrt{p\text{ }\!\!'\!\!\text{ }_{x}^{2}+p\text{ }\!\!'\!\!\text{ }_{z}^{2}},$ | (8) |
| $cos(\pi -{{\theta }_{3}})=\frac{|AB{{|}^{2}}+|BC{{|}^{2}}-|AC{{|}^{2}}}{2|AB|\cdot |BC|},$ | (9) |
| $\begin{align} & \sin (\pi -{{\theta }_{3}})=\pm \sqrt{1-{{[\frac{a_{2}^{2}+a_{3}^{2}+(p\text{ }\!\!'\!\!\text{ }_{x}^{2}+p\text{ }\!\!'\!\!\text{ }_{z}^{2})}{2{{a}_{2}}{{a}_{3}}}]}^{2}}}, \\ & \cos (\pi -{{\theta }_{3}})=\frac{a_{2}^{2}+a_{3}^{2}+(p\text{ }\!\!'\!\!\text{ }_{x}^{2}+p\text{ }\!\!'\!\!\text{ }_{z}^{2})}{2{{a}_{2}}{{a}_{3}}}, \\ & {{\theta }_{3}}=\pi -A \\ & \tan 2\{\pm \sqrt{{{(2{{a}_{2}}{{a}_{3}})}^{2}}+[{{(a_{2}^{2}+a_{3}^{2}-(p\text{ }\!\!'\!\!\text{ }_{x}^{2}+p\text{ }\!\!'\!\!\text{ }_{z}^{2})]}^{2}}}, \\ & a_{2}^{2}+a_{3}^{2}-(p\text{ }\!\!'\!\!\text{ }_{x}^{2}+p\text{ }\!\!'\!\!\text{ }_{z}^{2})\}. \\ \end{align}$ |
θ3表达式中正负号对应其可能的2个解.当θ10,θ3确定后,由与式(3)对应的两矩阵第10行第3列对应元素和第3行第4列对应元素分别相等,可知:
| $-{{s}_{5}}{{c}_{234}}={{c}_{1}}{{a}_{x}}+{{s}_{1}}{{a}_{y}},$ | (10) |
| $-{{a}_{2}}{{s}_{2}}-{{a}_{3}}{{s}_{23}}-{{d}_{5}}{{c}_{234}}={{p}_{z}}.$ | (11) |
联立式(10)和式(11)消去c234整理后得
| $({{a}_{2}}+{{a}_{3}}{{c}_{3}}){{s}_{2}}+{{a}_{3}}{{s}_{3}}{{c}_{2}}=-{{p}_{z}}+{{d}_{5}}\frac{{{a}_{x}}{{c}_{1}}+{{a}_{y}}{{s}_{1}}}{{{s}_{5}}},$ |
经过三角变换,可得:
| $\begin{align} & k=-{{p}_{z}}+{{d}_{5}}\frac{{{a}_{x}}{{c}_{1}}+{{a}_{y}}{{s}_{1}}}{{{s}_{5}}}, \\ & {{\theta }_{2}}=A\tan 2[k,\pm \sqrt{{{({{a}_{2}}+{{a}_{3}}{{c}_{3}})}^{2}}+{{({{a}_{3}}{{s}_{3}})}^{2}}-{{k}^{2}}]}- \\ & A\tan 2({{a}_{3}}{{s}_{3}},{{a}_{2}}+{{a}_{3}}{{c}_{3}}). \\ \end{align}$ |
θ2表达式中正负号对应其可能的2个解.当θ2,θ3确定后,由与式(3)对应的两矩阵第3行第3列对应元素相等,可知
| ${{s}_{234}}{{s}_{5}}={{a}_{z}},$ | (12) |
| $\begin{align} & \sin ({{\theta }_{2}}+{{\theta }_{3}}+{{\theta }_{4}})=\frac{{{a}_{z}}}{{{s}_{5}}}, \\ & \cos ({{\theta }_{2}}+{{\theta }_{3}}+{{\theta }_{4}})=\pm \sqrt{1-{{\left( \frac{{{a}_{z}}}{{{s}_{5}}} \right)}^{2}},} \\ & {{\theta }_{4}}=A\tan 2({{a}_{z}},\pm \sqrt{s_{5}^{2}-a_{z}^{2}})-{{\theta }_{2}}-{{\theta }_{3}}. \\ \end{align}$ |
θ4表达式中正负号对应其可能的2个解.
2.4 数值验证当机器人处于图 10所示位姿时,机器人各关节角度值分别为(0°,-90°,0°,-90°,1080°,0°),此时由图 8可知,机器人末端在基座坐标系中的坐标为(0,-|d4|+(|d2|-|d3|),a2+a3+|d5|),即(0,-1000.5 mm,10 300 mm).将上述关节角度值代入运动学正解公式中,通过MATLAB计算得到机器人末端的位姿矩阵,从中可以得到机器人末端的位置坐标为(0,-1000.5 mm,10 300 mm),与机器人的实际位置一致.再验证几组特殊角度也得到了相同的结论,由此说明机器人运动学正解是正确的.
对于运动学逆解的验证,先对各关节变量随机赋值,求出其运动学正解,然后将正解得到的位姿矩阵代入逆解公式中,利用MATLAB求出各关节变量值后与初始给定的关节变量值进行比较.若逆解中有一组关节值与初始随机给定的关节值相同,则说明运动学逆解是正确的.具体方法如下:随机赋予一组关节角度值为(0°,100°,20°,30°,60°,30°),经过MATLAB编制的运动学正解程序运算后得到的位姿矩阵如式(13)所示,
| $_{6}^{0}T=\left| \begin{matrix} 0.5 & 0.866025 & 0 & 693.096004 \\ -0.433013 & 0.25 & -0.866025 & -100.5 \\ -0.75 & 0.433013 & 0.5 & -786.983845 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right|.$ | (13) |
以式(13)为已知条件,借助MATLAB计算机器人运动学逆解,其中4组解如表 3所示.表 3中第10组解与正解中给定的关节角度值相同,从而验证了运动学逆解的正确性.
| 组别 | θ10/(°) | θ2/(°) | θ3/(°) | θ4/(°) | θ5/(°) | θ6/(°) |
| 10 | 0 | 100.0000 | 20.0000 | 30.0000 | 60.0000 | 30.0000 |
| 2 | 0 | 106.7086 | 20.0000 | 82.9999 | -60.0000 | 30.0000 |
| 3 | 0 | 28.5384 | -20.00010 | 510.0000 | 60.0000 | 30.0000 |
| 4 | 0 | 35.2470 | -20.00010 | 1005.0000 | -60.0000 | 30.0000 |
针对目前工业机器人的负载自重比小、设计周期长、成本高、柔性差的问题,设计了一种新型模块化可重构工业机器人.机器人的各关节模块结构和性能相同,通过改变关节的尺寸和性能即可得到多种关节模块,减少了设计工作量,缩短了设计周期.在关节模块的设计中,大量使用通用件,降低了机器人的成本.同时,通过对机器人结构进行优化设计和采用高强度铝合金材料,机器人的负载自重比达到10/4.5.该机器人具有良好的可重构性,通过选用不同的关节模块和手臂模块,可快速设计出不同构型的机器人.机器人样机的实际测试结果表明,该机器人具有负载自重比大、工作空间大、精度高、运动平稳、噪声小、设计周期短、成本低、柔性好的特点.针对机器人有相邻3根关节轴线互相平行的特点,采用代数法和几何法相结合的新方法,求得机器人运动学逆解的完整解析解.该机器人的研制成功为其他机器人的设计提供了一种新的思路.
| [1] |
王田苗,陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报,2014,50(9):1-13. WANG Tian-miao,TAO Yong.Research status and in-dustrialization development strategy of Chinese indus-trial robot[J].Chinese Journal of Mechanical Engineering,2014,50(9):1-13. |
| Click to display the text | |
| [2] |
谭民,王硕.机器人技术研究进展[J].自动化学报,2013,39(7):963-972. TAN Min,WANG Shuo.Research progress on robotics[J].ACTA Automation Sinica,2013,39(7):963-972. |
| Click to display the text | |
| [3] |
刘爽,殷国富,李雪琴,等.可重构模块化工业机器人构形及其静力学分析[J].机械设计与制造,2011(11):205-207. LIU Shuang,YIN Guo-fu,LI Xue-qin,et al.Configura- tion of industrial robots based on reconfigurable modularization and its statics analysis[J].Machinery Design & Manufacture,2011(11):205-207. |
| Click to display the text | |
| [4] |
肖智勇,段建中,杜鑫强,等.Motoman 工业机器人有限元静态分析及改进设计[J].长沙理工大学学报(自然科学版),2011,8(4):71-76. XIAO Zhi-yong,DUAN Jian-zhong,DU Xin-qiang,et al.Finite element static analysis and design improvement for motorman industrial robot[J].Journal of Changsha University of Science and Technology (Natural Science),2011,8(4):71-76. |
| Click to display the text | |
| [5] | PAREDISC J J,BROWN H B,KHOSLA P K.Rapidly deployable manipulator system[J].Robotics and Auto-nomous Systems,1997,21(3):289-304. |
| Click to display the text | |
| [6] | ALBU-SCHAFFER A,EIBERGER O,GREBENSTEIN M,et al.Soft robotics[J].IEEE Robotics and Automa-tion Magazine,2008,15(3):20-30. |
| Click to display the text | |
| [7] |
潘新安,王洪光,姜勇,等.一种模块化可重构机器人系统的研制[J].智能系统学报,2013,8(4):292-298. PAN Xin-an,WANG Hong-guang,JIANG Yong,et al.Development of a modular reconfigurable robot system[J].CAAI Transaction on Intelligent System,2013,8(4):292-298. |
| Click to display the text | |
| [8] |
吴文强,管贻生,朱海飞,等.面向任务的可重构模块化机器人构型设计[J].哈尔滨工业大学学报,2014,46(3):93-98. WU Wen-qiang,GUAN Yi-sheng,ZHU Hai-fei,et al.Task-oriented configuration design of reconfigurable modular robots[J].Journal of Harbin Institute of Tech-nology,2014,46(3):93-98. |
| Click to display the text | |
| [9] |
克来格.机器人学导论(3版)[M]. 贠超,等,译.北京:机械工业出版社,2006:78-81. CRAIG J J.Introduction to robotics:mechanics and control(3th ed)[M].Translated by YUN Chao,et al.Beijing:Machinery Industry Press,2006:78-81. |
| [10] |
李爱成,唐火红,冯宝林,等.关节式码垛机器人运动学分析与动力学仿真[J].机械设计,2013,30(10):16-20. LI Ai-cheng,TANG Huo-hong,FENG Bao-lin,et al.Kinematics analysis and dynamics simulation of the joint type stacking robot[J].Journal of Machine Design,2013,30(10):16-20. |
| Click to display the text | |
| [11] |
蔡自兴.机器人学[M].北京:清华大学出版社,2000:47-52. CAI Zi-xing.Robotics[M].Beijing:Tsinghua University Press,2000:47-52. |
| [12] |
刘极峰,易际明.机器人技术基础[M].北京:高等教育出版社,2006:31-34. LIU Ji-feng,YI Ji-ming.Fundamentals of robotics[M].Beijing:Higher Education Press,2006:31-34. |
| [13] |
曹电锋,杨启志,庄佳奇,等.一种六自由度上肢康复机器人的结构设计及运动学分析[J].工程设计学报,2013,20(4):338-343. CAO Dian-feng,YANG Qi-zhi,ZHUANG Jia-qi,et al.Structure design and analysis of kinematics of a 6-DOF upper-limbed rehabilitation robot[J].Chinese Journal of Engineering Design,2013,20(4):338-343. |
| Click to display the text | |
| [14] |
李宪华,郭永存,张军,等.模块化六自由度机械臂逆运动学解算与验证[J].农业机械学报,2013,44(4):246-251. LI Xian-hua,GUO Yong-cun,ZHANG Jun,et al.Inverse kinematics solution and verification of modular 6-DOF manipulator[J].Journal of Agricultural Machinery,2013,44(4):246-251. |
| Click to display the text | |
| [15] |
姜宏超,刘士荣,张波涛.六自由度模块化机械臂的逆运动学分析[J].浙江大学学报(工学版),2010,44(7):1348-1354. JIANG Hong-chao,LIU Shi-rong,ZHANG Bo-tao.In- verse kinematics analysis for 6 degree-of-freedom modular manipulator[J].Journal of Zhejiang University (Engineering Science),2010,44(7):1348-1354. |
| Click to display the text |



