在能源和环境问题日益突出的背景下,电动汽车作为新能源汽车的代表,在节能减排、降低对化石能源的依赖方面具有传统汽车不可比拟的优势,成为各国政府和汽车生产商的关注热点[1, 2].伴随电动汽车技术和电池技术的不断发展,电动汽车在技术方面独具电动汽车-电网互动(vehicle-to-grid,V2G)优势,从而开启了一个新的收益机会:可在电价高的用电高峰期向电网输送电能,既降低电网运行费用,也为用户创造收益[3].
以可再生能源为基础的发电规模正不断增大.研究表明,在解决风能和太阳能等可再生能源出力并网后维持电力出力平衡的方法中,固定的能源存储系统和负荷调度控制是最可行的[2].据统计,汽车每天的停驶率基本都在90%以上[4],因此可对具有V2G功能的电动汽车采取有效的调度与控制策略,从而增强电力系统接纳间歇性能源的能力,提高系统运行的经济性与安全性[5].
目前,已有部分学者对含电动汽车充电负荷和可再生能源的协同调度进行相关研究[5, 6].文献[7]从电力系统的安全性和经济运行角度出发,计及电动汽车和风电机组出力不确定性,建立了以系统总发电成本最小为目标的随机经济调度模型.文献[8]研究了联合光伏与电动汽车分别在随机充电、智能充电及V2G控制策略情况下的效益和影响分析,结果表明,智能充电控制和V2G能更好地吸纳光伏能源并降低出力波动,并起到削减负荷高峰的作用.文献[9]为平滑等效负荷波动及消纳过剩风电,建立了多时间尺度的电动汽车与风电协同调度模型,但未计及电动汽车的V2G功能.文献[10]提出了一种计及风电和光伏出力不确定性的地区电网电动汽车充电调度方法,但同样忽略了电动汽车的V2G模式情况.文献[11]考虑了电动汽车的V2G功能,以可再生能源有功出力波动最小为目标,构建了随机协同优化调度模型,但只考虑了总功率波动最小,并未顾及电动汽车用户的经济效益.
本文提出了考虑V2G模式运行情况下的电动汽车、风力发电和光伏发电系统的多目标协同调度模型.该模型以同时降低系统负荷波动和电动汽车用户充电费用为目标函数,通过对目标函数的模糊处理,将需求解问题转化为单目标非线性优化问题,并应用自适应权重粒子群优化算法进行求解,得到最优调度方案.最后以某地区电网的数据为算例进行仿真,结果表明,通过调度合理安排电动汽车的充放电可显著降低地区电网负荷峰谷差,同时为电动汽车用户带来收益.这为电动汽车的优化调度提供了一条有效途径.
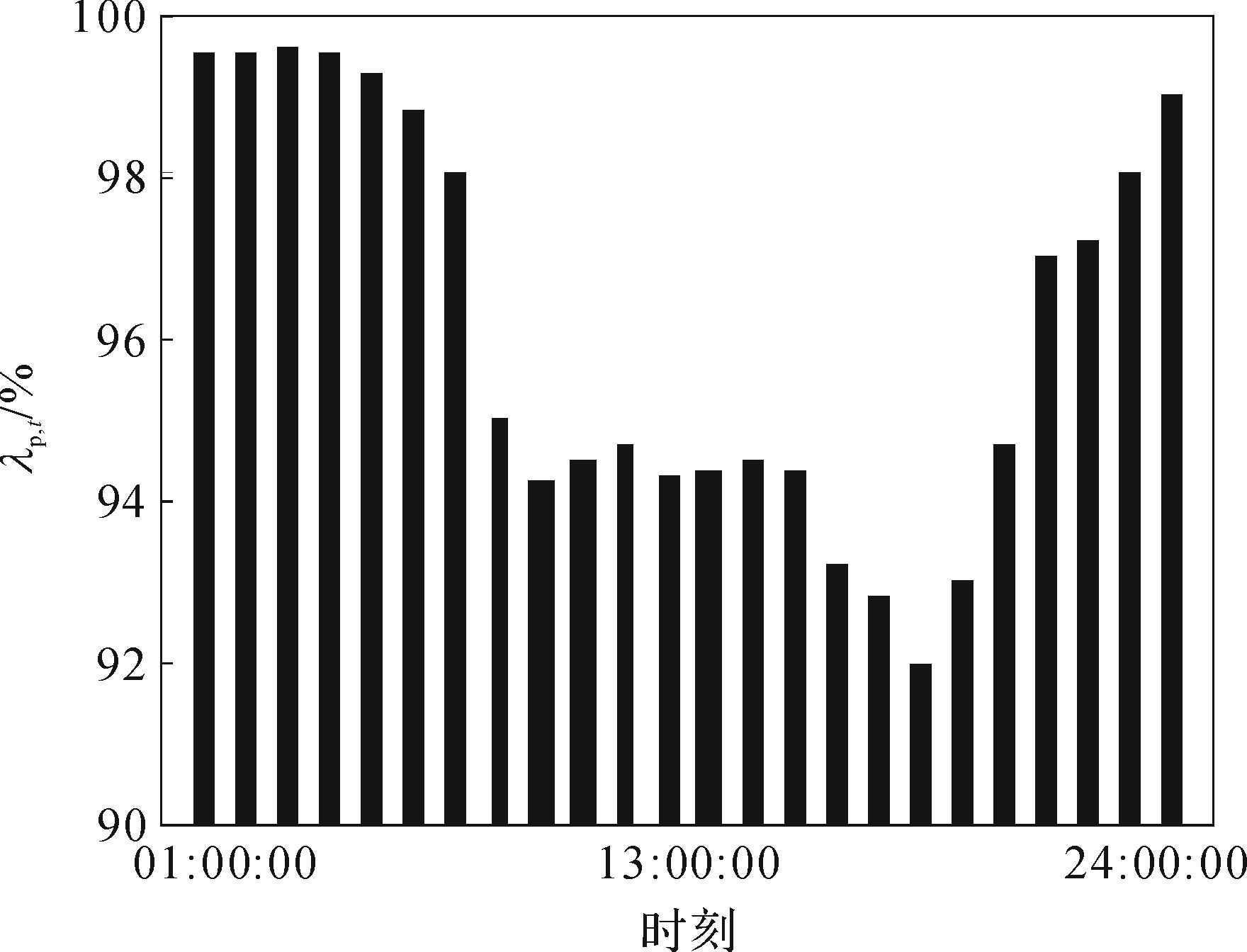
1 电动汽车与可再生能源优化调度模型前文提及汽车在一天中有90%以上时间处于停驶状态,本文研究的对象为电动私家车,其使用用途与传统汽车并无明显区别,因而假定具有相同的行驶规律.根据对居民汽车行驶规律调查统计,得到电动汽车典型的日停驶概率λp,t如图 1所示.
|
| 图 1 电动汽车停驶概率 Fig. 1 Probability of EV to be parked |
显然,每个时段处于停驶状态的电动汽车数量即为该时段可入网电动汽车数量的上限,电网可对其进行优化调度.
1.1 目标函数
为使电动汽车与可再生能源两者充分发挥低碳优势,降低可再生能源出力波动对电网的影响,同时为使电动汽车用户充分响应调度控制策略,本文以等效负荷的波动(即等效负荷的方差和)最小及电动汽车用户的充电成本最低为优化目标,1 d为一个调度周期,1 h作为一个调度时间窗口的话,则将一天分为24个时间段,优化变量为每个时间段内电动汽车的充放电功率.电动汽车与可再生能源协同调度的总目标函数可表示为
$F = \min ({F_1},{F_2}),$
(1)
1) 以等效负荷方差和最小为优化目标.具体目标函数如下:
$$\min {F_1} = \sum\limits_{t = 1}^{24} ( {P_{L,t}} - {P_{w,t}} - {P_{s,t}} + {P_{ev,t}} - {P_{avg}}{)^2},$$
(2)
$${P_{avg}} = \left[ {\sum\limits_{t = 1}^{24} ( {P_{L,t}} - {P_{w,t}} - {P_{s,t}} + {P_{ev,t}})} \right]/24,$$
(3)
2) 以电动汽车用户充电费用最优为目标函数,同时考虑到电动汽车充放电过程中的电能损失和电池寿命折损带来的成本[12, 13],通过折算制定为相应的充放电电价.则目标函数可以描述为
$$\min {F_2} = \sum\limits_{t = 1}^{24} ( {k_{t + }}{P_{ev,t}}{C_{1,t}} + {k_{t - }}{P_{ev,t}}{C_{2,t}})\Delta t,$$
(4)
| $$\eqalign{ & {k_{t + }} = \left\{ {\matrix{ {0,{P_{ev,t}}≤0,} \cr {1,{P_{ev,t}} > 0,} \cr } } \right. \cr & {k_{t - }} = \left\{ {\matrix{ {0,{P_{ev,t}} > 0,} \cr {1,{P_{ev,t}}≤0,} \cr } } \right. \cr} $$ |
由于Pev,t正值代表充电,负值代表放电,则F2为正值时表示充电费用,为负值时表示放电收益.
1.2 约束条件电动汽车参与电网互动受到的约束条件主要为可用时间、电池可用容量与充放电功率三个方面.
1) 本文假定电动汽车可用时间为24 h.
2) 电池剩余电量的约束.
设时段t开始时,系统中所有电动汽车的电池剩余电量为St,则从时段t+1开始,储存的总电量St+1满足以下约束:
$${S_{t + 1}} = {S_t} + \eta {P_{ev,t}}\Delta t - {S_{dr,t}},$$
(5)
$${S_{dr,t}} = {N_{dr,t}}{S_{dr,av}},$$
(6)
$${N_{dr,t}} = {N_{ev}}(1 - {\lambda _{p,t}}),$$
(7)
$${S_{dr,av}} = {S_{km}}{V_{ev}}\Delta t,$$
(8)
电池剩余电量的上下限约束为
$${S_{\min }}≤{S_t}≤{S_{\max }},$$
(9)
为避免电动汽车过度充放电,电池的荷电状态应保持在一定范围内,至少保有ε电量,且至多保有γ电量,则有
$\left. {\matrix{
{{S_{\min }} = \varepsilon {N_{ev}}{S_{ev,\max }},} \cr
{{S_{{\mathop{\rm mix}\nolimits} }} = \gamma {N_{ev}}{S_{ev,\max }},} \cr
} } \right\}$
(10)
3) 电动汽车充放电功率约束.
假定电动汽车以恒功率充放电,若充电为正,放电为负,则电动汽车的充放电功率不应超过电动汽车的最大充放电能力,如下式表示:
$$\left. {\matrix{
{ - {N_{p,t}}{p_{\max }}≤{P_{ev,t}}≤{N_{p,t}}{p_{\max }},} \cr
{{N_{p,t}} = {N_{ev}}{\lambda _{p,t}}.} \cr
} } \right\}$$
(11)
为使所求的解最符合决策者的要求,本文选用模糊决策方法.通过计算各目标函数的隶属度函数,将多目标优化问题模糊化,以隶属度的大小来反映决策者对于目标值的满意程度.然后用最大模糊满意度法将多目标优化问题转化为非线性的单目标优化问题来求解[14],可以较好地解决多目标优化问题中权重较难确定和量纲不一致的问题.
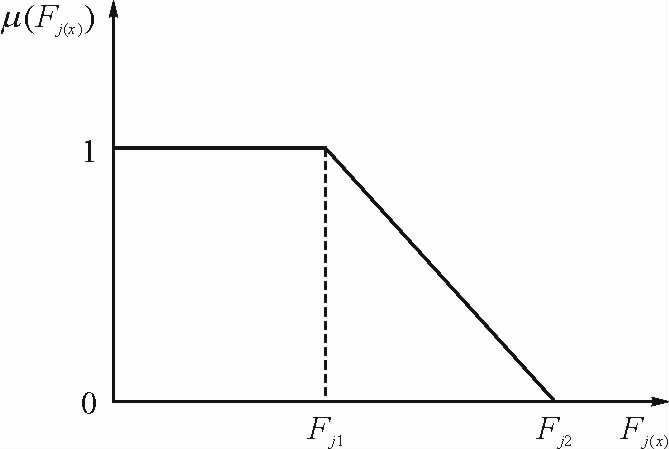
确定各目标的隶属度函数是多目标模糊优化建模的关键.对于本文所建的优化调度模型,期望其在满足所有约束的前提下,等效负荷的波动越小越好,充电费用越低越好,都为有上限而无下限的情况,因此本文选用降半直线形为2个优化目标的梯形隶属度函数,如图 2所示.隶属度函数的数学计算表达式如式(12)及式(13)所示.
|
| 图 2 降半直线梯形隶属度函数 Fig. 2 Trapezoidal membership function |
| $\mu (f(x))=\left\{ \begin{matrix} 1,f(x)aaa{{f}_{1}}, \\ \frac{{{f}_{2}}-f(x)}{{{f}_{2}}-{{f}_{1}}},{{f}_{1}}≤f(x)≤{{f}_{2}}, \\ 0,f(x)≥{{f}_{2}}. \\ \end{matrix} \right.$ | (12) |
| $\mu (h(x))=\left\{ \begin{matrix} 1h(x)aaa;{{h}_{1}}, \\ \frac{{{h}_{2}}-h(x)}{{{h}_{2}}-{{h}_{1}}},{{h}_{1}}aaah(x)aaa{{h}_{2}}, \\ 0,h(x)bbb{{h}_{2}}. \\ \end{matrix} \right.$ | (13) |
根据模糊集理论的最大最小法则[15],定义λ为μ(f(x))和μ(h(x))的满意度,是所有隶属度函数的最小值,即
| $$\lambda = \min \{ \mu (f(x)),\mu (h(x))\} ,$$ | (14) |
传统的PSO算法收敛精度不高,易陷入局部极值造成算法早熟.为克服以上缺陷,实现目标函数的快速寻优,本文采用自适应粒子群优化算法(adaptive particle swarm optimization,APSO)求解.
PSO算法的数学模型中粒子根据下列公式更新自己的速度和位置:
| $$\left. {\matrix{ {V_{id}^{k + 1} = \omega V_{id}^k + {c_1}{r_1}(P_{id}^k - X_{id}^k) + {c_2}{r_2}(P_{gd}^k - X_{id}^k),} \cr {X_{id}^{k + 1} = X_{id}^k + V_{id}^{k + 1}.} \cr } } \right\}$$ | (15) |
惯性权重因子ω使粒子保持其运动惯性,决定了微粒的局部搜索能力和全局搜索能力.较大的ω有利于提高算法的全局搜索能力,而较小的ω会增强算法的局部搜索能力.本文运用非线性的动态惯性权重策略来自适应调节ω:
| $$\omega = \left\{ {\matrix{ {{\omega _{\min }} - {{({\omega _{\max }} - {\omega _{\min }})(f - {f_{\min }})} \over {{f_{avg - }}{f_{\min }}}},faaa{f_{avg}},} \cr {{\omega _{\max }},f > {f_{avg}}.} \cr } } \right.$$ | (16) |
在式(16)的算法运行中,粒子适应度值较好趋向于局部最优时,将使ω增大,而粒子的适应度值相对分散时将使ω减小.同时对于适应度值优于平均适应度值的微粒,其对应的ω较小,从而保留了该微粒,反之适应度值差于平均适应度值的微粒,其对应的ω较大,使得该微粒以较大步长对可行域进行“全局粗略探测”向较好的搜索区域靠拢.可以看出,ω会随微粒的适应度值而自适应改变,这可以使粒子群保持多样性和良好的收敛特性,提高了APSO算法的收敛速度和精度.
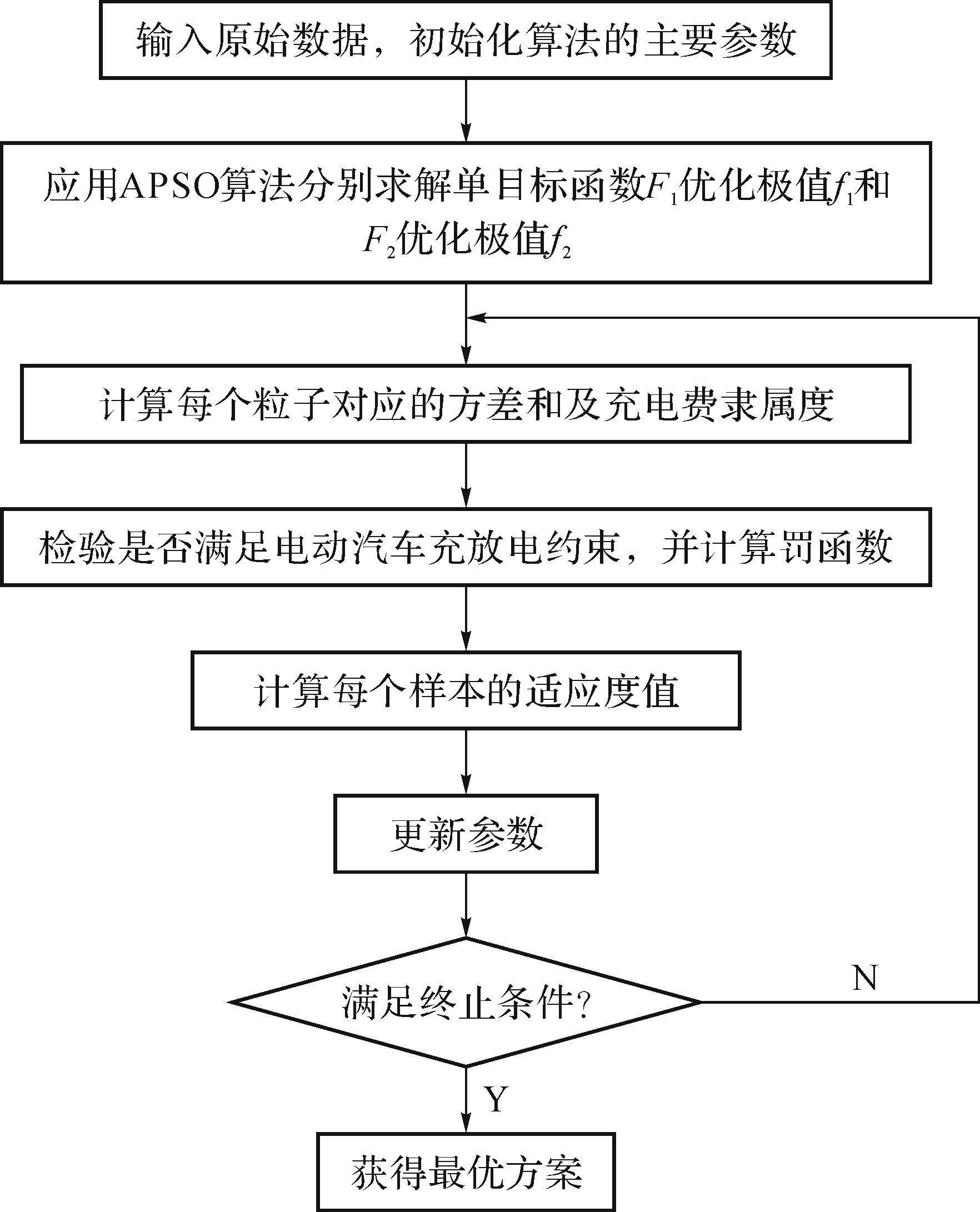
2.2 求解流程本文以所有电动汽车在各个调度时间窗口的充放电功率总和为决策变量,即设定决策变量为[Pev1,Pev2,…,Pev24].应用APSO算法求解模型时,一个粒子就是电动汽车一种调度策略.原始数据包括各时段用电负荷、各时段风电场和光伏输出功率、各时段的电价、各时段电动汽车停驶概率、电池剩余电量的上下限值和单位时段的充放电功率限制、电动汽车初始电量等.基于APSO算法求解本文多目标优化问题的具体流程如图 3所示.
|
| 图 3 基于APSO算法的求解流程 Fig. 3 Solving flow chart besed on APSO algorithm |
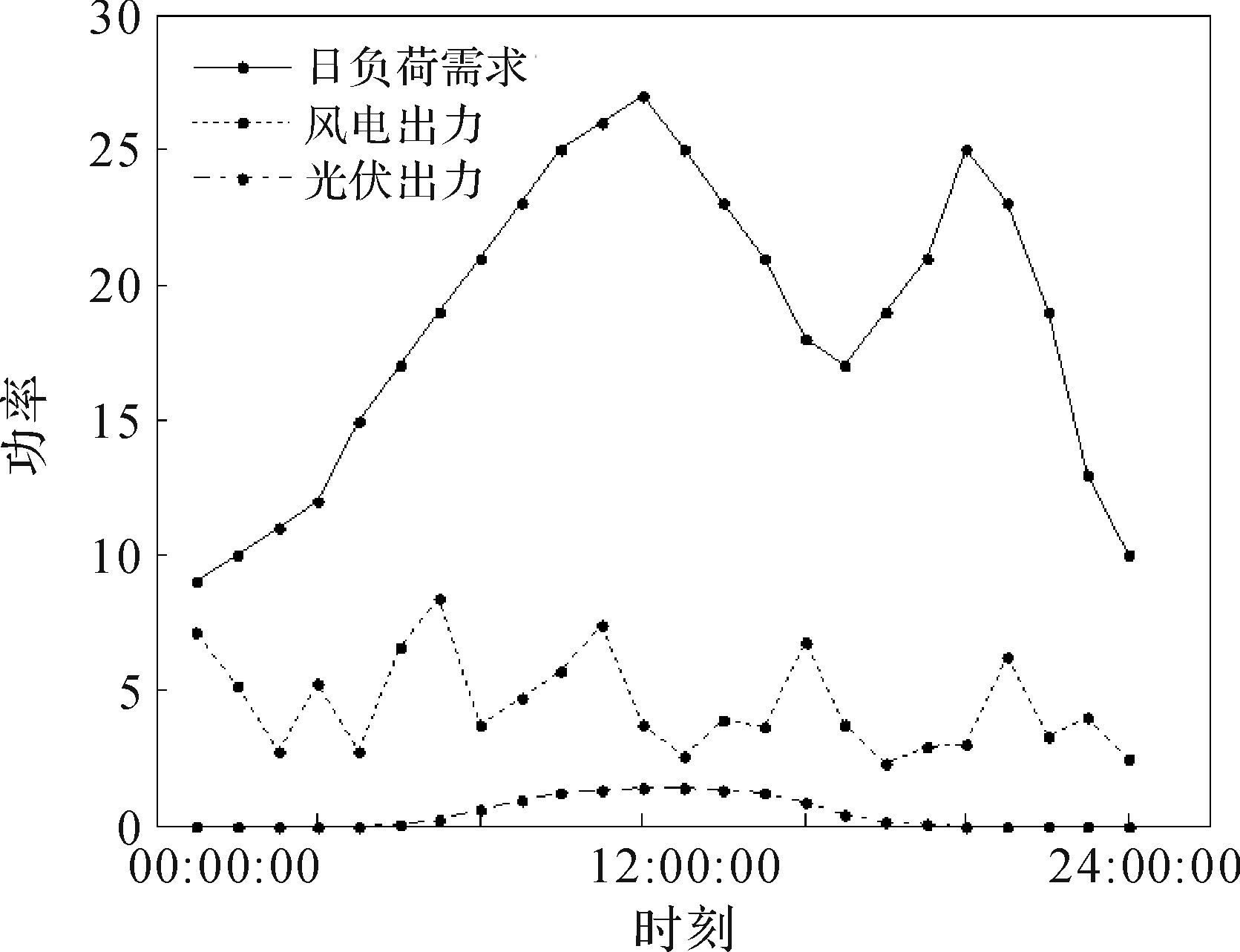
本文以某地用电负荷及当地风电场和光伏发电系统为例,可供调度的电动汽车数量为50 000辆.图 4给出了某地典型的日负荷需求以及风电和光伏各自的输出功率曲线图.为方便计算,将功率单位用标幺值(per unit)表示,基准值取100 MW.
|
| 图 4 各时段负荷值及风光发电出力 Fig. 4 Load value and wind and photovoltaic generation outputs in each time |
本算例假设电动汽车初始时刻电池均含有50%的电量,充放电功率均为3.6 kW,充放电效率均为0.75,电池的容量均为21.6 kWh,平均行驶速度取40 km/h,平均行驶耗电量为0.139 kW·h/km;取
| 时段 | 性质 | 充电电价C1,t/ (元(kW·h)-1) | 放电电价C2,t/(元(kW·h)-1) |
| 23:00:00—07:00:00 | 谷 | 0.335 | 0.168 |
| 07:00:00—10:00:00 | 平 | 0.781 | 0.468 |
| 10:00:00—15:00:00 | 峰 | 1.253 | 1.007 |
| 15:00:00—18:00:00 | 平 | 0.781 | 0.468 |
| 18:00:00—21:00:00 | 峰 | 1.253 | 1.007 |
| 21:00:00—23:00:00 | 平 | 0.781 | 0.468 |
输入电网的原始数据,求解2个目标函数的单目标模型最优值以及各个时段电动汽车的总充放电功率,具体见表 2和表 3.再根据单目标优化的结果经过适当的伸缩确定各模糊参数,其中期望的方差和f1=454.887 3,最大可接受的等效负荷方差和f2=697.236 6,期望的充电费用h1=-60.826 73万元,最大可接受的充电费用h2=-18.355 93万元.用APSO算法计算得到的多目标优化计算结果如表 3所示.为更直观地查看,表 3中将负值的充电费用等效为正值的放电收益.
| 时段1) | 单目标F1 优化2) | 单目标F2 优化 | 多目标模糊 优化 | 时段 | 单目标F1 优化 | 单目标F2 优化 | 多目标模糊 优化 |
| 1 | 1.791 0 | 1.468 2 | 1.771 5 | 13 | -1.696 9 | -1.543 9 | -1.694 5 |
| 2 | 1.790 5 | 1.251 6 | 1.765 0 | 14 | -0.893 5 | -1.297 8 | -1.093 6 |
| 3 | 0.504 5 | 1.271 1 | 1.061 8 | 15 | -0.383 4 | -1.622 4 | 0.185 4 |
| 4 | 1.744 4 | 0.702 0 | 1.033 1 | 16 | 1.677 6 | 1.314 0 | 1.677 6 |
| 5 | -0.490 0 | -0.729 1 | -0.395 8 | 17 | 1.453 7 | 1.656 1 | 1.670 3 |
| 6 | 0.441 2 | 1.194 4 | 0.413 1 | 18 | -0.493 1 | 1.227 4 | 0.638 4 |
| 7 | 0.193 3 | 0.816 9 | 0.326 3 | 19 | -1.319 9 | -0.866 9 | -1.291 7 |
| 8 | -0.841 3 | -0.159 6 | -0.079 1 | 20 | -1.704 6 | -1.460 8 | -1.690 6 |
| 9 | 0.206 0 | -0.191 0 | -0.351 0 | 21 | 0.368 1 | -1.508 1 | -1.401 2 |
| 10 | -0.812 3 | 0.804 9 | -0.856 8 | 22 | -0.164 5 | 0.184 8 | -0.297 5 |
| 11 | -0.249 2 | -1.704 3 | -0.680 8 | 23 | 1.764 0 | -0.023 5 | 0.362 2 |
| 12 | -1.697 4 | -1.697 4 | -1.697 4 | 24 | 1.782 0 | -1.778 0 | 1.488 1 |
| 注: 1) 时段1表示00:00:00—01:00:00,依此类推,时段24表示23:00:00—00:00:00;2)各优化结果单位用标幺值表示. | |||||||
| 目标 | 单目标F1 优化 | 单目标F2 优化 | 多目标 模糊优化 |
| 方差和/104MW2 | 454.887 3 | 542.992 0 | 469.815 4 |
| 收益/万元 | 22.781 92 | 60.826 73 | 41.634 26 |
从表 2可看出,电动汽车的多目标优化结果表现为在用电的高峰时段对电网输送电能,而在负荷低谷时段进行充电,与分时电价相协调,既降低了电网负荷的峰谷差,也为用户带来效益.
由表 3可得:采用多目标模糊优化模型时,等效负荷的方差和比单目标F1优化模型增大了3.28%,但比F2优化模型减少了13.48%;充电收益比单目标F2优化模型减少了31.55%,但比单目标优化模型F1增大了82.75%.
以上分析可知,采用多目标模糊优化时,对电动汽车的优化调度综合考虑了等效负荷波动和充电费用的因素,本文提出的多目标模糊优化模型能较好地兼顾对2个目标的综合要求,更符合实际情况,比单目标优化调度模型更具优势.
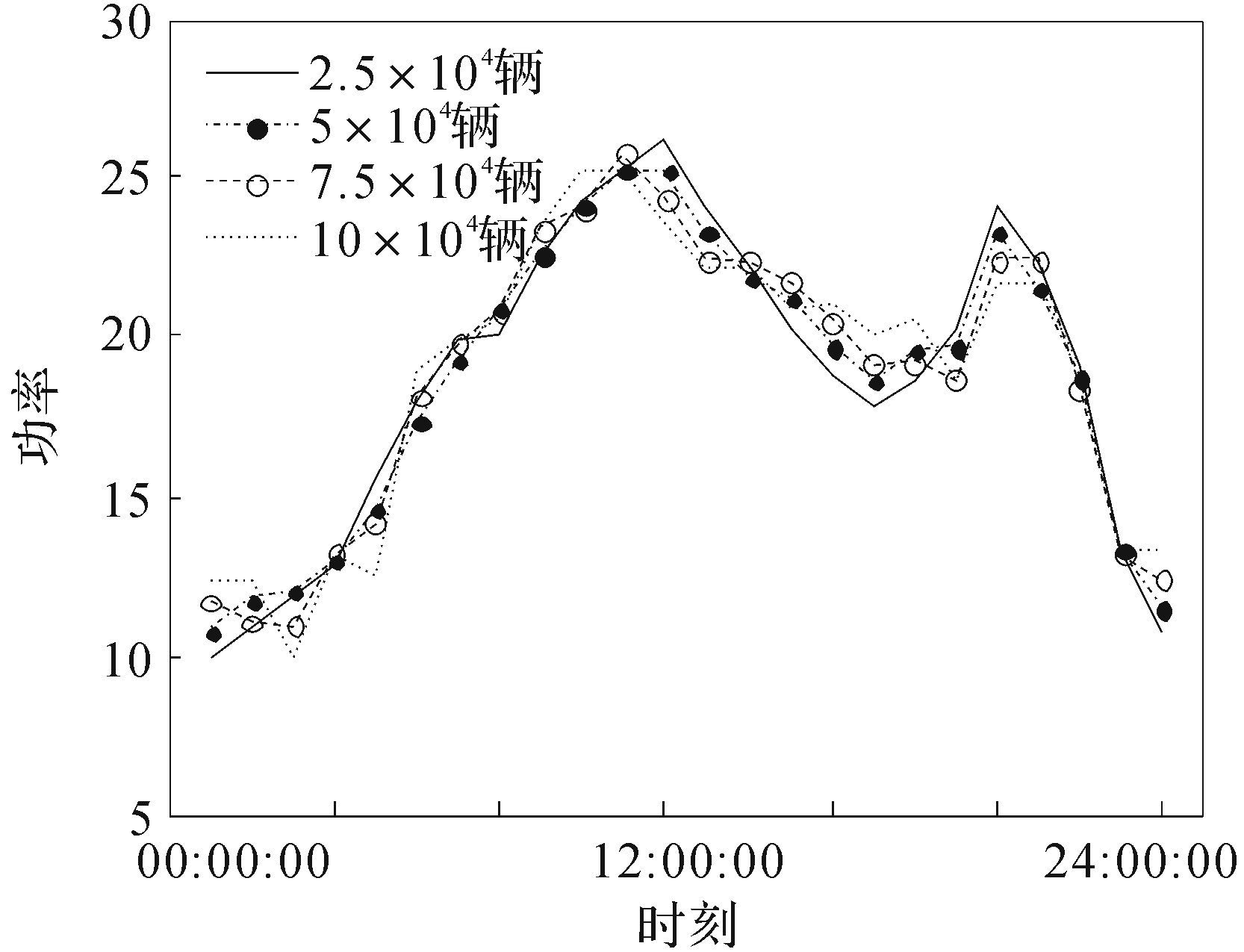
另外,为验证电动汽车并网数量对系统负荷波动的影响,分别选取2.5×104,5×104,7.5×104和10×104 辆电动汽车进行仿真分析,运用最大模糊满意度法进行求解,寻优所得结果见图 5和表 4.
|
| 图 5 需求负荷曲线对比 Fig. 5 Demand load curve comparison |
| 数量/104辆 | 2.5 | 5 | 7.5 | 10 |
| 方差和/104MW2 | 537.280 2 | 469.815 4 | 438.996 5 | 413.436 6 |
| 峰荷/MW | 2 615.13 | 2 531.92 | 2 579.66 | 2 530.56 |
| 谷荷/MW | 989.55 | 1077.15 | 1 167.89 | 1 227.6 |
由图 5可以看出,随着电动汽车并网数量的逐渐增加,负荷需求曲线的波动程度会逐渐趋于平缓,降低峰谷差的效果也愈发明显.从表 4可知,电动汽车的数量为2.5×104辆时,峰谷差为1 625.58 MW,当电动汽车数量达到10×104辆时,峰谷差减少到1 302.96 MW,峰谷差降低了20%.可见随着电动汽车渗透率的提高,降低峰谷差效果更为显著.
4 结 论电动汽车的入网给电力系统的安全与稳定运行带来新的挑战,有必要对电动汽车进行优化调度.本文在地区电网含有风电和光伏等可再生能源发电系统的条件下,建立了V2G模式情况下电动汽车充放电的多目标优化调度模型.对某地区电网的数据利用APSO算法进行仿真分析,结果表明,对电动汽车的合理优化调度可以有效降低电网等效负荷波动,同时为电动汽车用户带来一定收益,兼顾了促进可再生能源吸纳、减少弃风光和提高用户满意度等方面的需求.并且随着电动汽车渗透率的提高,优化效果更佳,有利于电动汽车的推广.
| [1] |
王锡凡,邵成成,王秀丽,等.电动汽车充电负荷与调度控制策略综述[J].中国电机工程学报,2013,33(1):1-10. WANG Xi-fan,SHAO Cheng-cheng,WANG Xiu-li,et al.Survey of electric vehicle charging load and dispatch control strategies[J].Proceedings of the CSEE,2013,33(1):1-10. |
| Click to display the text | |
| [2] | MWASILU F,JUSTO J J,KIM E,et al.Electric vehicles and smart grid interaction:a review on vehicle to grid and renewable energy sources integration[J].Renewable and Sustainable Energy Reviews,2014,34:501-516. |
| Click to display the text | |
| [3] | DRUDE L,JUNIOR L C P,RUTHER R.Photovoltaics (PV) and electric vehicle-to-grid (V2G) strategies for peak demand reduction in urban regions in Brazil in a smart grid environment[J].Renewable Energy,2014,68:443-451. |
| Click to display the text | |
| [4] |
韩海英,和敬涵,王小君,等.基于改进粒子群算法的电动车参与负荷平抑策略[J].电网技术,2011,35(10):165-169. HAN Hai-ying,HE Jing-han,WANG Xiao-jun,et al.An improved particle swarm optimization-based load response strategy with participation of vehicle to grid[J].Power System Technology,2011,35(10):165-169. |
| Click to display the text | |
| [5] |
赵俊华,文福拴,杨爱民,等.电动汽车对电力系统的影响及其调度与控制问题[J].电力系统自动化,2011,35(14):2-10. ZHAO Jun-hua,WEN Fu-shuan,YANG Ai-min,et al.Impacts of electric vehicles on power systems as well as the associated dispatching and control problem [J].Automation of Electric Power Systems,2011,35(14):2-10. |
| Click to display the text | |
| [6] |
李正烁,孙宏斌,郭庆来,等.计及碳排放的输电网侧:"风-车协调"研究[J].中国电机工程学报,2012,32(10):41-48. LI Zheng-shuo,SUN Hong-bin,GUO Qing-lai,et al.Study on wind-EV complementation on the transmission grid side considering carbon emission[J].Proceedings of the CSEE,2012,32(10):41-48. |
| Click to display the text | |
| [7] |
赵俊华,文福栓,薛禹胜,等.计及电动汽车和风电出力不确定性的随机经济调度[J].电力系统自动化,2010,34(20):22-29. ZHAO Jun-hua,WEN Fu-shuan,XUE Yu-sheng,et al.Power system stochastic dispatch considering uncertain outputs from plug-in electric vehicles and wind generators[J].Automation of Electric Power Systems,2010,34(20):22-29. |
| Click to display the text | |
| [8] | FATTORI F,ANGLANI N,MULIERE G.Combining photovoltaic energy with electric vehicles,smart charging and vehicle-to-grid[J].Solar Energy,2014,110:438-451. |
| Click to display the text | |
| [9] |
于大洋,宋曙光,张波,等.区域电网电动汽车充电与风电协同调度的分析[J].电力系统自动化,2011,35(14):24-29. YU Da-yang,SONG Shu-guang,ZHANG Bo,et al.Synergistic dispatch of PEVs charging and wind power in Chinese regional power grids [J].Automation of Electric Power Systems,2011,35(14):24-29. |
| Click to display the text | |
| [10] |
张学清,梁军,张利,等.计及风光电源的一种地区电网电动汽车充电调度方法[J].电工技术学报,2013,28(2):28-35. ZHANG Xue-qing,LIANG Jun,ZHANG Li,et al.Approach for plug-in electric vehicles charging scheduling considering wind and photovoltaic power in Chinese regional power grids [J].Transactions of China Electrotechnical Society,2013,28(2):28-35. |
| Click to display the text | |
| [11] |
王贵斌,赵俊华,文福拴,等.配电系统中电动汽车与可再生能源的随机协同调度[J].电力系统自动化,2012,36(19):22-29. WANG Gui-bin,ZHAO Jun-hua,WEN Fu-shuan,et al.Stochastic optimization dispatching of plug-in hybrid electric vehicles in coordination with renewable generation in distribution systems [J].Automation of Electric Power Systems,2012,36(19):22-29. |
| Click to display the text | |
| [12] |
项顶,宋永华,胡泽春,等.电动汽车参与V2G最优峰谷电价研究[J].中国电机工程学报,2013,33(31):15-25. XIANG Ding,SONG Yong-hua,HU Ze-chun,et al.Research on optimal time of use price for electric vehicle participating V2G [J].Proceedings of the CSEE,2013,33(31):15-25. |
| Click to display the text | |
| [13] |
于浩明,黄纯,张磊,等.基于分时电价机制的电动汽车用户侧有序充放电控制策略[J].中国电力,2014,47(12):95-98. YU Hao-ming,HUANG Chun,ZHANG Lei,et al.Coordinated charge and discharge control strategy based on time-of-use price from electric vehicle customer side [J].Electric Power,2014,47(12):95-98. |
| Click to display the text | |
| [14] |
胡国强,贺仁睦.梯级水电站多目标模糊优化调度模型及其求解方法[J].电工技术学报,2007,22(1):154-158. HU Guo-qiang,HE Ren-mu.Model and algorithm of multi-objective fuzzy optimal scheduling for cascaded hydroelectric power plant[J].Transactions of China Electrotechnical Society,2007,22(1):154-158. |
| Click to display the text | |
| [15] |
刘合香.模糊数学理论及应用[M].北京:科学出版社,2012:185-196. LIU He-xiang.Fuzzy mathematics theory and applications [M].Beijing:Science Press,2012:185-196. |
| [16] | CAO Yi-jia,TANG Sheng-wei,LI Can-bing,et al.An optimized EV charging model considering TOU price and SOC curve[J].IEEE Transactions on Smart Grid,2012,3(1):388-393. |
| Click to display the text |



