由于汽车轻量化的需要,高强度钢板和热冲压成形技术开始得到广泛应用.对于热冲压成形过程,国内外研究主要集中于高强钢板料的成形性能、板料和模具的冷却能力,对于模具的结构分析和优化设计的研究还比较少.由于板料抗拉强度的大幅提高,热冲压过程中模具受力变得更加恶劣,根据经验,模具通常设计得较为厚重,从而使生产成本和使用成本提高.通过拓扑优化技术寻求模具内部材料的最优分布,去除对模具强度贡献不大的材料,可以有效减轻模具的质量.
国内外对于冲压模具结构拓扑优化进行了一定的研究.Anna Nilsson等[1]对冷冲压模具凹模进行拓扑优化设计,最终使模具的应力分布更加合理,改善了模具结构刚度和减轻了模具质量.Sheu等[2]利用拓扑优化方法对冲压模具凹模底面的筋板分布和形状进行了优化设计,在符合安全性的同时,对模具结构进行了简化,减轻了模具质量.汤禹成等[3]基于载荷映射工具,对复杂零件的压边圈结构进行拓扑优化,在结构性能影响不大的前提下,有效减轻压边圈的质量,改善了压边圈的筋板结构.
虽然有少数学者对冲压模具进行了一定的拓扑优化研究,然而这种关注度是不够的,同时这些研究都是围绕冷冲压模具.对于热冲压成形,模具受力更加复杂,对热冲压模具进行结构分析和优化设计更加有必要.本文将热冲压数值模拟和拓扑优化技术相结合,对热冲压凹模结构进行了拓扑优化设计,在保证模具强度的前提下,对凹模进行了减重设计.
1 基于ABAQUS的有限元仿真高强度钢板热冲压成形数值模拟是一个包含应力场、温度场的多场耦合问题.热成形时板料和模具的接触让板料温度快速降低,板料温度的降低进而改变金属的塑性,使金属的流动应力发生变化.冲压过程中产生的形变能和摩擦热传递给板件,并作为一种内部热源使板件温度升高[4-5].因此,热力耦合分析主要是温度场分析和变形分析.
1) 温度场分析的计算模型为
| $\begin{align} & pc\frac{\partial T}{\partial t}=\frac{\partial T}{\partial x}\left( {{\lambda }_{x}}\frac{\partial T}{\partial x} \right)+\frac{\partial }{\partial y}\left( {{\lambda }_{y}}\frac{\partial T}{\partial y} \right)+ \\ & \frac{\partial }{\partial z}\left( {{\lambda }_{z}}\frac{\partial T}{\partial z} \right)+\dot{Q}, \\ \end{align}$ |
由于本文所用的材料为各项同性材料,即λx=λy=λz=λ,于是有
| $pc\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left( \lambda \frac{\partial T}{\partial x} \right)+\frac{\partial }{\partial y}\left( \lambda \frac{\partial T}{\partial y} \right)+\frac{\partial }{\partial z}\left( \lambda \frac{\partial T}{\partial z} \right)+\dot{Q},$ |
2)在变形场对温度场的改变中,板料的塑性变形能转化为体热源,摩擦功转化为板料和模具间的表面热流.体热源、热流密度模型为:
| $\begin{align} & \dot{Q}=\eta \bar{\sigma }\dot{\bar{\varepsilon }}, \\ & q=fu, \\ \end{align}$ |
3)温度场改变板料流动应力,流动应力是与等效应变、等效应变率、温度相关的函数,即
| $\bar{\sigma }=f(\bar{\varepsilon },\dot{\bar{\varepsilon }},T),$ |
本文以汽车工程领域普遍应用的U形件作为研究对象,板料几何尺寸为220 mm×130 mm×1.8 mm[6]. 基于模型结构几何对称性,通过施加对称边界条件,取结构的1/2进行仿真分析.板料和模具相关热物理参数参考文献[6].为了获取模具与板料之间的接触力,采用模具弹性-板料弹塑性的有限元模型.模具和板料网格类型为C3D8RT(八节点温度位移耦合减缩积分单元).为了减少沙漏问题,板料沿厚度方向使用了4层单元.数值仿真模型如图 1所示.

|
| 图 1 热冲压仿真模型 Fig. 1 Simulation model of hot stamping |
板料热冲压成形过程是一个涉及材料非线性、几何非线性、接触非线性的高度非线性和非连续性过程.由于ABAQUS/Explicit不需要同时求解联立方程组,具有计算成本低、容易收敛的特性,为此在ABAQUS/Explicit中创建2个分析步,类型为显示动态热力耦合分析.分析步1为板料冲压成形(0—3.6 s),分析步2为保压冷却淬火(3.6—13.6 s).
在热力耦合数值模拟中,变形场通过内热产生的热流矢量对温度场产生影响,温度场通过对流动应力的影响而影响变形场[7-8].在1个时间增量步▽t内耦合有限元分析流程如图 2所示.

|
| 图 2 热力耦合有限元分析流程 Fig. 2 Process of thermal-mechanical coupled finite elementanalysis |
图 3、图 4、图 5分别为淬火结束后(t=13.6 s)成形件、凸模和凹模温度分布云图(单位为℃).

|
| 图 3 淬火结束后U形件温度分布云图 Fig. 3 Distribution of temperature on U shaped part after cooling |

|
| 图 4 淬火结束后凸模温度分布云图 Fig. 4 Distribution of temperature on punch after cooling |

|
| 图 5 淬火结束后凹模温度分布云图 Fig. 5 Distribution of temperature on die after cooling |
以文献[6]中的试验结果作为参考温度,得到图 6中A,B两点在成形和淬火过程中仿真温度与实验温度的对比情况,如图 7所示.总体上,仿真的温度曲线较好地贴合试验过程的温度变化曲线,表明该仿真模型有效.

|
| 图 6 温度参考点 Fig. 6 Temperature monitors |

|
| 图 7 实验与仿真温度对比 Fig. 7 Temperature comparison between that by experiment and simulation |
拓扑优化是在特定约束条件下寻找结构中材料的最佳分布.Michell等[9]最先基于桁架理论提出结构拓扑优化设计;Dorn等[10]提出基结构法,把数值方法引入该领域;Bendsoe等[11]提出了均匀化方法,将复合材料的多孔介质理论引入拓扑优化中,在拓扑结构材料中引入带方形空洞的单胞模型,以单胞尺寸作为设计变量,将拓扑优化转换为相对简单的尺寸优化问题;Mlejnek等[12]提出了变密度法,该理论通过引入一种假想的密度可变材料,定义离散单元的相对密度为设计变量,这样结构拓扑优化问题就被转化为材料的最优分问题.
本文基于相对密度法对热冲压凹模进行拓扑优化.该方法把离散单元内部的材料性质规定为常数,设计变量规定为离散单元的相对密度,用 x e表示.如果原始设计单元密度为
| ${{\rho }_{e}}={{x}_{e}}\cdot {{\rho }_{0}},$ |
| ${{E}_{e}}={{({{x}_{e}})}^{p}}\cdot {{E}_{0}}.$ |
| ${{K}_{e}}={{({{x}_{e}})}^{p}}\cdot {{K}_{0}}.$ |
图 8、图 9分别是凹模在冲压成形和淬火结束时刻的应力云图(单位是Pa).可知距离接触面较远的区域应力值非常小,即该区域对结构强度无贡献.说明在现有加载条件下,结构比较厚重,存在减重空间.

|
| 图 8 成形结束时凹模应力云图(t=3.6 s) Fig. 8 Distribution of stress at the end of stamping for die (t=3.6 s) |

|
| 图 9 淬火结束时凹模应力云图(t=13.6 s) Fig. 9 Distribution of stress at the end of quenching for die (t=13.6 s) |
在对模具结构进行拓扑优化时,若每一时刻的受力状态都考虑,优化的时间成本非常高.因此,选取关键的受力工况是进行模具结构拓扑优化的前提.
选取图 10中5个节点作为参考点,得到图 11、图 12所示板料成形和冷却过程中凹模上参考节点位移、应力随时间的变化图,可知在冲压成形结束时刻(t=3.6 s)凹模变形和受力最恶劣.因此,选取凹模在冲压成形结束时的载荷状态进行拓扑分析.

|
| 图 10 凹模参考节点 Fig. 10 Die reference nodes |

|
| 图 11 凹模参考节点位移变化曲线 Fig. 11 Displacement changes for nodes in die |

|
| 图 12 凹模参考节点应力变化曲线 Fig. 12 Stress changes for nodes in die |
拓扑优化是一个不断逼近目标多次迭代求解的过程,如果直接利用上文的热冲压有限元模型进行拓扑优化,分析时间是巨大的.为此,本文采用将板料热冲压成形模拟和凹模拓扑优化分别进行的方案,重新建立凹模结构分析模型,将热冲压过程中的接触力转化为结构分析模型中力的边界条件.图 13为热冲压成形结束时刻凹模与板料接触应力云图,可知板料对模具作用力主要分布在1,2,3,4四个区域,其余区域接触应力接近于4 000 Pa.

|
| 图 13 热冲压成形结束时凹模与板料接触应力云图 Fig. 13 Distribution of contact stresses between blank and die at the end of stamping |
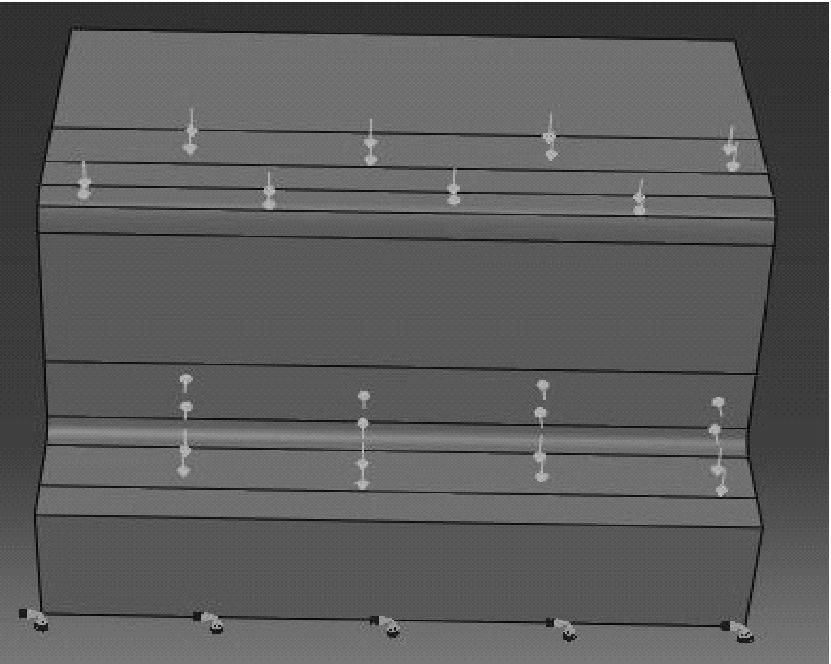
基于ABAQUS的脚本程序Python求出图 13中4个区域的平均接触力,如表 1所示.将4个平均接触力作为外在载荷施加到凹模结构分析模型对应区域上,如图 14所示,并在凹模接触表面其它区域赋予4 000 Pa的接触力.图 15为施加接触力后凹模的接触应力分布云图.为了验证该载荷赋予方法的有效性,选取图 15中a,b,c,d,e五点的应力值与热冲压成形结束时应力值(图 8)进行对比,对比结果如图 16所示,可知凹模结构分析模型与热冲压模型应力分布比较吻合,证明该结构分析模型可用于拓扑优化设计.
| 区域 | 1 | 2 | 3 | 4 |
| 接触应力/Pa | 5.59×106 | 2.78×108 | 3.08×107 | 1.48×108 |
|
| 图 14 凹模结构分析模型 Fig. 14 Structure analysis model for die |

|
| 图 15 凹模结构分析模型应力分布云图 Fig. 15 Distribution of stress of structure analysis model for die |

|
| 图 16 参考点应力对比情况 Fig. 16 Stresses comparison of reference points |
为了保证优化时不影响模具冷却管道孔,并保持凹模基本外形,划分出一定的壁厚结构作为非设计区,剩余部分为设计区,设计区与非设计区如图 17所示.

|
| 图 17 设计区与非设计区 Fig. 17 Design and non-design space |
如图 18为热冲压成形结束时刻凹模变形图(变形量×1 000),可知变形区域主要集中在凹模圆角区域(区域A)和凹模底部冷却孔上方平面区域(区域B).

|
| 图 18 热冲压结束时凹模变形云图(×1 000) Fig. 18 Deformation and stress distribution at the end of hot stamping for die (×1 000) |
为保证拓扑优化后凹模结构与初始结构的变形量相当,将受力后A,B两区域最大位移分别作为设计约束,则拓扑优化目标、设计约束、设计变量数学模型为:
优化目标:min V1,
设计约束: max(DspA1)/max(DspA0)≤λ,
max(DspB1)/max(DspB0)≤λ,
F=KU.
设计变量: x = x1,x2,…,xn T,
0≤xi≤1,i=1,2,…,n.
式中:V1是优化后设计区体积;max(DspA1)为优化后区域A最大位移,max(DspA0)为优化前区域A最大位移;max(DspB1)为优化后区域B最大位移,max(DspB0)为优化前区域B最大位移;x为设计区各单元相对密度;n为单元总量;λ为调整系数.由于凹模材料的减少会降低模具刚度,为保证拓扑优化后的结构与初始结构变形量相当,此处取λ=1.05.
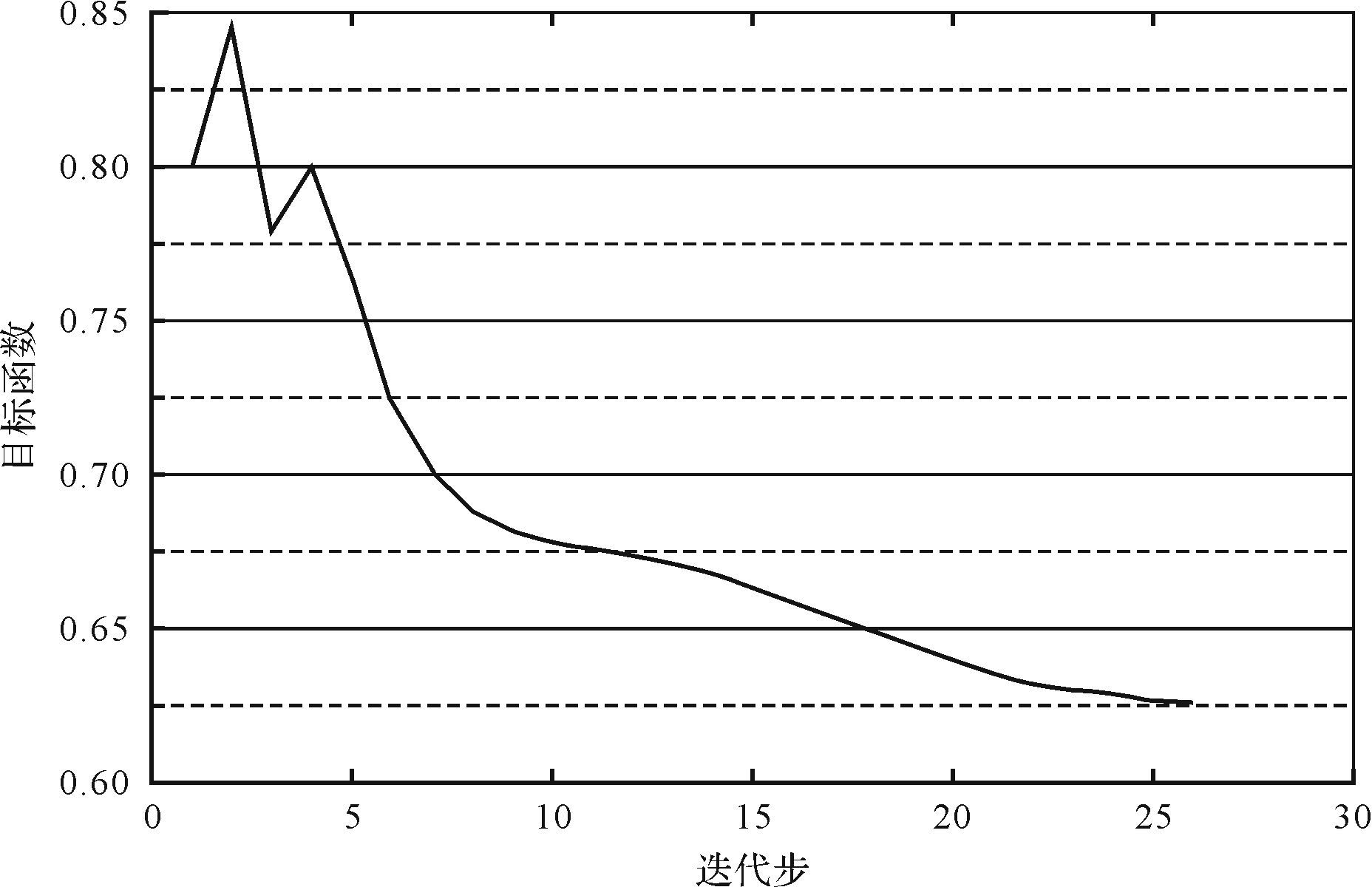
拓扑优化后模具材料分布如图 19所示,此时凹模设计区域质量减轻约37%,凹模结构总质量减轻约20%.
|
| 图 19 凹模结构拓扑优化结果 Fig. 19 Topology optimization result of die structure |
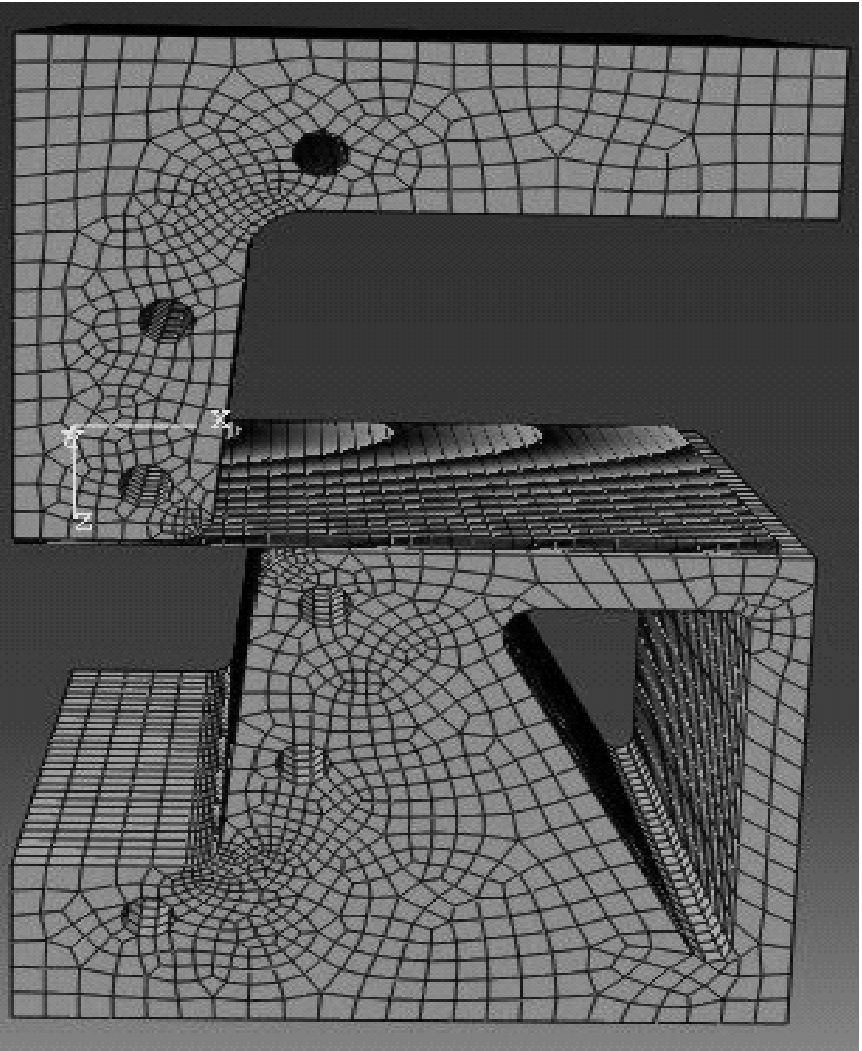
对凹模拓扑优化结果进行修整后重新建立热冲压数值模拟有限元模型,如图 20所示.对热冲压成形过程重新进行数值仿真,得到成形结束后凹模位移和应力分布云图,如图 21、图 22所示.

|
| 图 20 优化后热冲压有限元模型 Fig. 20 Finite element model of hot stamping after topology optimization |
|
| 图 21 优化后凹模位移云图 Fig. 21 Distribution of displacement of optimized die structure |

|
| 图 22 优化后凹模应力云图 Fig. 22 Distribution of stresses of optimized die structure |
与拓扑优化前仿真结果进行对比知,优化后凹模区域A最大位移值为8.108×10-6 m,区域B最大位移值为4.097×10-6 m,与原始结构最大位移值(区域A为7.997×10-6 m,区域B为4.323×10-6 m)相近,结构的最大应力为4.266×108 Pa,与原始结构的最大应力4.148×108 Pa相近.可知凹模结构在拓扑优化时,凹模受力和变形基本保持不变,结构实现减重37%.
3 结 论1) 建立了板料冲压热力耦合有限元模型,数值模拟了高强钢板U形件的热冲压成形和淬火过程.
2) 选取热冲压过程中的关键载荷工况,提取该状态下板料对模具的作用力,作为凹模结构分析模型的外在载荷.
3) 以单元相对密度作为设计变量,建立约束凹模结构关键区域节点位移的体积最小化模型,对凹模结构进行拓扑优化,最终有效减轻了凹模的设计质量.
本文研究了高强钢板热冲压数值模拟的方法,提出了一种热冲压模具结构减重的方法.
| [1] | NILSSON A,BIRATH F.Topology optimization of a stamping die[C].The 9th International Conference on Numerical Methods in Industrial Forming Processes.New York:AIP,2007:449-454. |
| Click to display the text | |
| [2] | SHEU J J,YANG C H.A simplified column model for the automatic design of the stamping die structure[J].Journal of Materials Processing Technology,177 (1/3):109-113. |
| Click to display the text | |
| [3] |
汤禹成,徐栋恺,陈军.高强度钢板复杂零件的冲压压边圈拓扑优化[J].上海交通大学学报,2010,44(1):6-10. TANG Yu-cheng,XU Dong-kai,CHEN Jun.Topology optimization of blank holder structure of stamping die for forming complicated automotive part of high-strength sheet metal[J].Journal of Shanghai Jiaotong University,2010,44(1):6-10. |
| Click to display the text | |
| [4] |
刘庄.热处理过程的数值模拟[M ].北京:科学出版社, 1996:5-11. LIU Zhuang.Numerical simulation for the process of heat treatment[M].Beijing:Science Press,1996:5-11. |
| [5] |
李烨.热成形模具冷却系统优化设计[D].大连:大连理工大学运载工程与力学学部,2013:10-15. LI Ye.The optimization design of cooling system in hot stamping dies[D].Dalian:Dalian University of Technology,Faculty of Vehicle Engineering and Mechanics,2013:10-15. |
| Click to display the text | |
| [6] |
张新悦.U形件热成型模具冷却系统实验与仿真研究 [D].长沙:湖南大学机械与运载工程学院,2013:23-41. ZHANG Xin-yue.Test and simulation study on U-shaped sheet hot stamping mould cooling system[D].Changsha:Hunan University,College of Mechanical and Vehicle Engineering,2013:23-41. |
| Click to display the text | |
| [7] |
苌群峰.镁合金板材温热冲压成形理论与实验研究[D].上海:上海交通大学机械与动力工程学院,2007:63-65. CHANG Qun-feng.Theoretical and experimental investigation of warm forming of magnesium alloy sheet [D].Shanghai:Shanghai Jiaotong University,School of Mechanical Engineering,2007:63-65. |
| Click to display the text | |
| [8] |
卫原平,阮雪榆.金属成形过程中热力耦合分析技术的研究[J].塑性工程学报,1994,1(2):3-10. WEI Yuan-ping,RUAN Xue-yu.A study on thermal-mechanical coupled analysis technigue of metal forming process[J].Journal of Plasticity Engineering,1994,1(2):3-10. |
| Click to display the text | |
| [9] | MICHELL A G M.The limits of economy of materials in frame structures[J].Philosophical Magazine,1904,47(8):589-597. |
| Click to display the text | |
| [10] | DORN W,GOMORY R,GREENBERG H.Automatic design of optical structures[J].Design Mechaniuque,1964, 3(1):25-52. |
| [11] | BENDSOE M P,KIKUCHI N.Generating optimal topologies in structural design using a homogenization method[J].Computer Methods in Applied Mechanics and Engineering,1988,71(2):197-224. |
| Click to display the text | |
| [12] | MLEJNEK H P,SCHIRRMACHER R.An engineer's approach to optimal material distribution and shape finding[J].Computer Methods in Applied Mechanics and Engineering,1993,106(1/2):1-26. |
| Click to display the text |


