随着人们消费水平的提高和汽车工业的高速发展,汽车已经成为人们日常生活中的一部分.由于存在规划不合理与汽车数量爆炸式增长等原因,停车难已经是广大车主所面临的首要问题[1].停车难问题主要出现在住宅小区、商业区、写字楼等人员密集区[2],而立体停车结构在一定程度上缓解了停车难的现状.由于机械设备和容车量要求的不同,出现了多种形式立体停车设备.目前立体车位有水平循环式、垂直循环式、升降横移式和简易升降式等形式.水平循环和垂直循环式采用所有车辆都是按照一定的次序作循环传送的方法,停取车都需转动1周,停车、取车所需时间长;升降横移式多应用在大型公共场所或停车数量多的场所,停车、取车所需时间长.毛君、谢苗等人自2010年至今研究了框架平移回转式智能立体停车位的结构、驱动系统和控制系统[3, 4, 5, 6, 7],该立体停车位属于简易升降式立体停车位,也是本文需要研究的智能立体停车位.立体停车位在我国部分城市得到了应用,并且缓解了“停车难”的问题,但是立体停车位在实际工作过程中出现了一些问题:立体停车位载车上升过程中,设备整体框架晃动量较大,使部分元部件严重受损,影响了设备的稳定性.
2003年彭斌、龚海峰对升降横移式立体车库的结构、控制系统等进行了研究[8, 9];2005年周智慧和廖庆对垂直升降式机械立体停车设备的总体结构、存取机构进行了研究并进行了最优化设计[10, 11];2008年汤伟对升降横移式立体车库结构进行了优化[12];2011年杨承超对隔层桁架式抗侧力钢构架立体停车结构进行了一系列研究[13];2012年至2013年毛君等人利用理论分析和虚拟样机技术相结合的方法对智能立体停车位进行了研究[14, 15, 16];2013年刘小华、陈婷婷对框架立体停车结构进行了静力学和动力学分析,为提高结构的强度、刚度及稳定性提供了建议[17, 18].
本文首先对智能立体停车位的结构和工作原理进行描述;然后建立了立体停车位设备框架的多自由度动力学模型,并且通过ANSYS-workbench模块,对框架进行了模态分析,得到智能立体停车位框架的固有频率和振型云图;最后利用测试系统对实验样机进行模态试验,为设计出更合理的框架提供一定的参考.
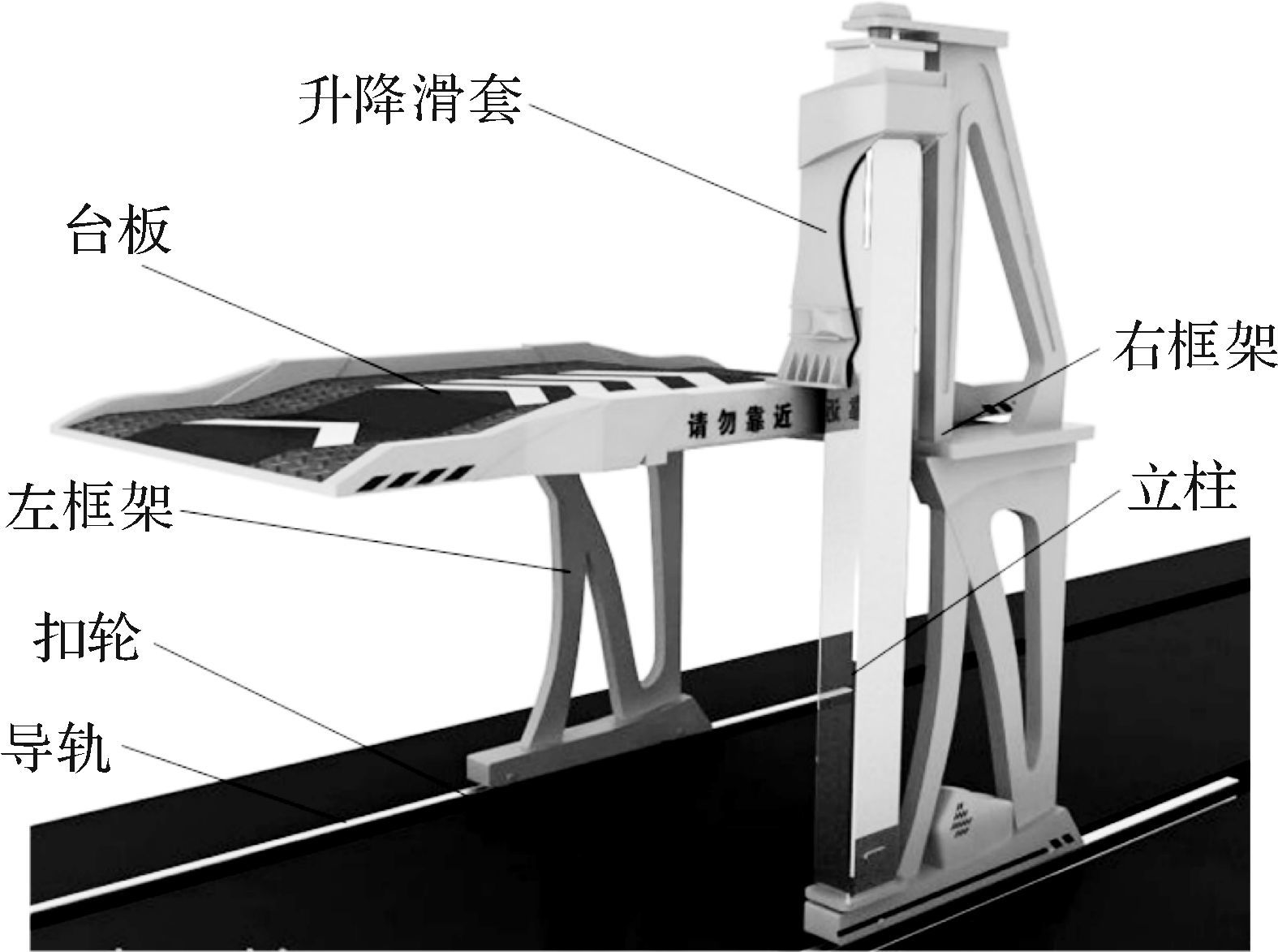
1 工作原理本文研究的智能立体停车位以单臂式立体停车位为例.设备由导轨、行走驱动、框架主体、回转升降立柱、升降滑套、台板和驱动控制系统组成.框架主体是本文研究的重点也是整个设备的主体,起到支撑作用.框架分为左、右框架以及连接两框架的部分,左框架由底梁、左前立柱、左后立柱、支撑等几大零部件组成,右框架由底梁、右前立柱、右后立柱、斜拉梁、支撑等几大零部件组成,左、右框架通过横筋、斜筋相连互相支撑.回转立柱安装在右框架上,行走装置安装在左右框架的底梁上.智能立体停车位的模型如图 1所示.
|
| 图 1 单臂式立体停车位模型 Fig. 1 Model of single arm type stereo parking space |
运动原理采用的是框架的横移、立柱的旋转、台板的升降三个动作.工作过程分为存车过程和取车过程.存车过程:第1步,行走轮带车位沿导轨移出至一层停车位的外端;第2步,回转立柱向外回转90°;第3步,升降滑套带台板沿立柱降至地面;第4步,司机将车开到台板上的指定位置并拉起停车制动;第5步,台板上升至指定高度;第6步,立柱向内回转90°;第7步,台板缓慢下降,当台板下端的耐磨垫与框架横筋接触时台板停止下降;第8步,车位沿导轨回至初始位置.取车过程和存车过程相似.
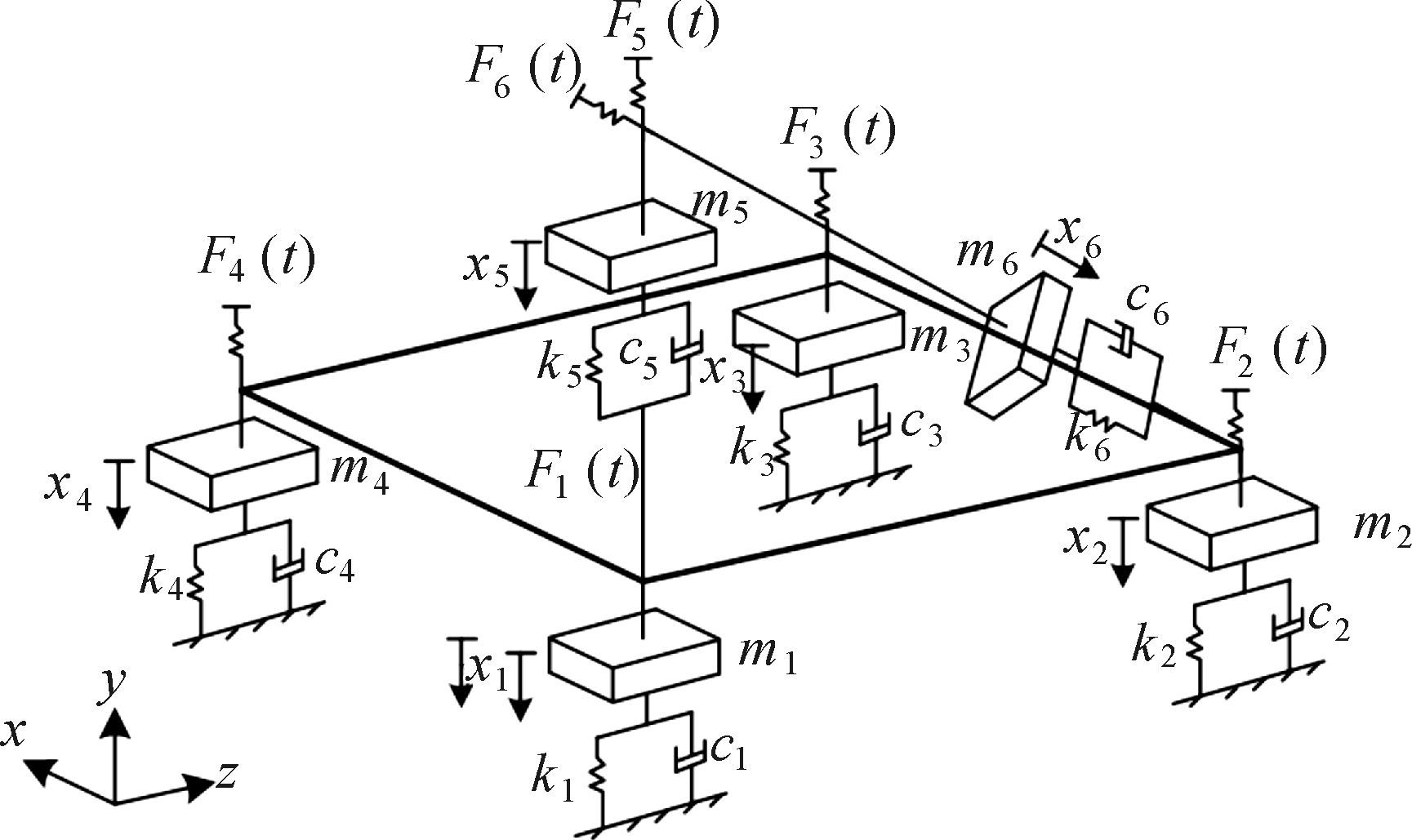
2 力学模型的建立智能立体停车位台板在上升和下降中左右框架上的立柱和梁受力变长或缩短,各立柱和梁变长或缩短变化量随台板移动而变化,所以设备在工作过程中出现了晃动现象.把智能立体停车位框架振动模型进行了简化,简化模型如图 2所示.
|
| 图 2 框架简化动力学模型 Fig. 2 Simplified dynamic model of framework |
图中:m1为右前下立柱质量,m2为右后立柱质量,m3为左后立柱质量,m4为左前立柱质量,m5为右前上立柱集中质量,m6为右斜梁质量;c1,c2,c3,c4,c5,c6为各立柱和斜梁的阻尼参数;k1,k2,k3,k4,k5,k6为各立柱和斜梁的刚度参数;F1(t),F2(t),F3(t),F4(t),F5(t),F6(t)为施加立柱和梁上的激励.
利用拉格朗日方程可以比较简单地推导出用广义坐标表示的振动系统的运动微分方程[19].假如系统的动能为T,势能为V,瑞丽损耗能为R,则智能立体停车位框架能量表达式为:
| $\begin{align} & T=\frac{1}{2}{{m}_{1}}{{{\dot{x}}}^{2}}_{1}+\frac{1}{2}~{{m}_{2}}{{{\dot{x}}}^{2}}_{2}+\frac{1}{2}~{{m}_{3}}{{{\dot{x}}}^{2}}_{3}+\frac{1}{2}{{m}_{4}}\dot{x}_{4}^{2}+ \\ & \frac{1}{2}{{m}_{5}}{{{\dot{x}}}^{2}}_{5}+\frac{1}{2}{{m}_{6}}{{{\dot{x}}}^{2}}_{6}, \\ \end{align}$ | (1) |
| $V=\frac{1}{2}{{k}_{1}}x_{1}^{2}+\text{ }\frac{1}{2}{{k}_{2}}x_{2}^{2}+\frac{1}{2}~{{k}_{3}}x_{3}^{2}+\frac{1}{2}{{k}_{4}}x_{4}^{2}+\frac{1}{2}~{{k}_{5}}x_{5}^{2}+\frac{1}{2}~{{k}_{6}}x_{6}^{2},$ | (2) |
| $R=\frac{1}{2}~{{c}_{1}}{{\dot{x}}^{2}}_{1}+\frac{1}{2}~{{c}_{2}}{{\dot{x}}^{2}}_{2}+\frac{1}{2}~{{c}_{3}}{{\dot{x}}^{2}}_{3}+\frac{1}{2}{{c}_{4}}{{\dot{x}}^{2}}_{4}+\frac{1}{2}~{{c}_{5}}{{\dot{x}}^{2}}_{5}+\frac{1}{2}~{{c}_{6}}{{\dot{x}}^{2}}_{6}.$ | (3) |
拉格朗日方程表达式为
| $\frac{dt}{d}\left( \frac{\partial T}{\partial {{{\dot{x}}}_{i}}} \right)-\frac{\partial T}{\partial {{x}_{i}}}+\frac{\partial R}{\partial {{{\dot{x}}}_{i}}}+\frac{\partial V}{\partial {{x}_{i}}}={{F}_{i}}(t).$ | (4) |
将式(1)至式(3)代入方程式(4)中,得到系统各部分振动微分方程:
| $\eqalign{ & \left. \matrix{ {m_1}{{\ddot x}_1} + {c_1}{{\dot x}_1} + {k_1}{x_1} = {F_1}(t), \hfill \cr \matrix{ {{m_2}{{\ddot x}_2} + {c_2}{{\dot x}_2} + {k_2}{x_2} = {F_2}(t),} \cr {{m_3}{{\ddot x}_3} + {c_3}{{\dot x}_3} + {k_3}{x_3} = {F_3}(t),} \cr } \hfill \cr} \right| \cr & \left. {\matrix{ {\matrix{ {{m_4}{{\ddot x}_4} + {c_4}{{\dot x}_4} + {k_4}{x_4} = {F_4}(t),} \cr {{m_5}{{\ddot x}_5} + {c_5}{{\dot x}_5} + {k_5}{x_5} = {F_5}(t),} \cr } } \cr {{m_6}{{\ddot x}_6} + {c_6}{{\dot x}_6} + {k_6}{x_6} = {F_6}(t),} \cr } } \right| \cr} $ | (5) |
动力学微分方程矩阵形式:
| $M\ddot{x}+C\dot{x}+Kx=F.$ | (6) |
框架的固有频率由框架本身的属性所确定,与外载荷无关;阻尼对框架的固有频率和振型影响不大.当忽略阻尼并无外载荷作用时,其振动微分方程(6)可简化为
| $M\ddot{x}+Kx=0.$ | (7) |
方程(7)是常系数线性其次方程组,设方程(7)通解的形式为
| $x=\delta \sin (\omega t+a),$ | (8) |
将式(8)代入(7)中可得到整个框架系统固有频率与振型的特征方程:
| $(K-{{\omega }^{2}}M)\delta \sin (\omega t+a)=0.$ | (9) |
在自由振动过程中,结构的振幅δ不全为零,所以式(9)中括号内矩阵的行列式之差为零,由此可以得出框架结构自由振动频率方程:
| $|K-{{\omega }^{2}}M|=0.$ | (10) |
对式(10)进行求解,可以得到n个特征值ωi(i=1,2…,n),即为系统的n个固有频率.将ωi代入式(9),即可求得振动频率ωi下的振动型态.
借助MATLAB计算机辅助软件,得到智能立体位框架在0~100 Hz激励频率范围内的频响.计算结果表明:超前支护的振幅在1~2 mm范围内变化,振幅波动较大的激励频率为0~30 Hz.
3 仿真分析智能立体停车位框架主要在台板载车沿立柱上升过程中发生振动和变形,因此主要对该工作状态进行分析.
3.1 有限元模型的建立由于计算机条件的限制,为减少有限元的计算工作量,进行了模型简化:
1) 省去了如轴承、垫板、螺栓、螺母等对计算结构影响不大的零件.
2) 将左右框架底座简化成与地面接触.
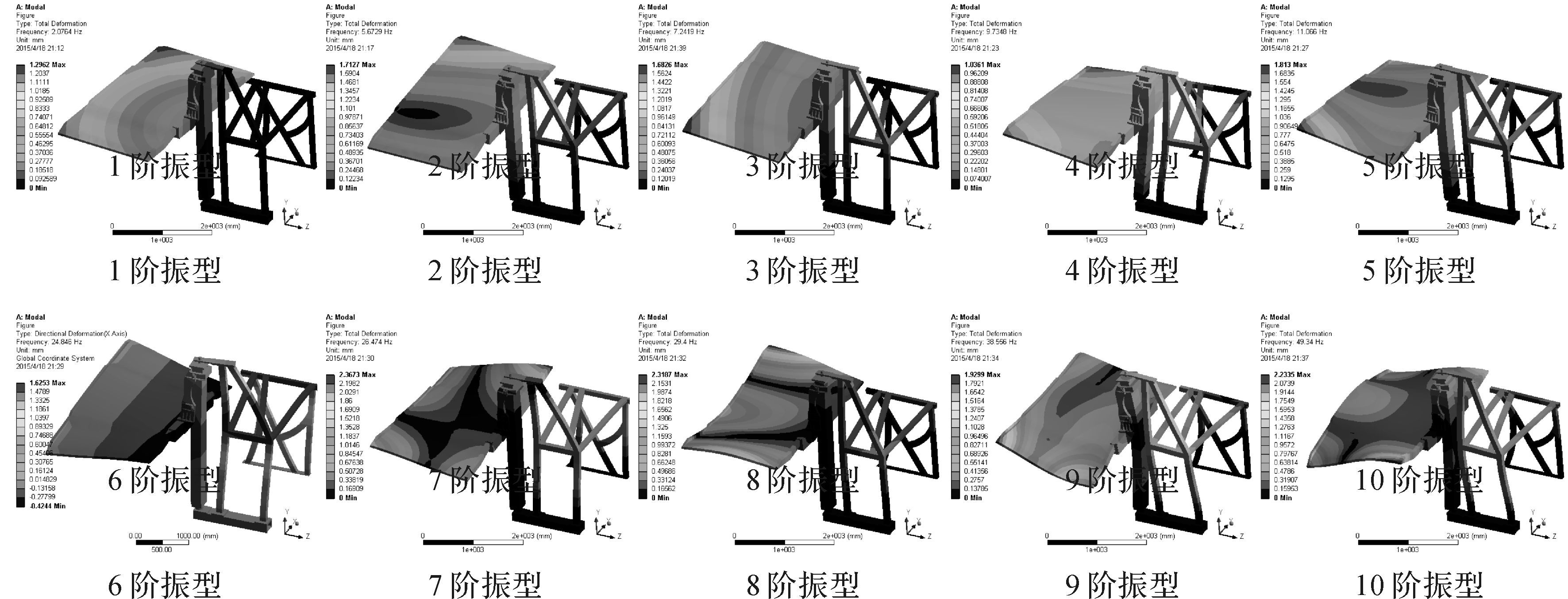
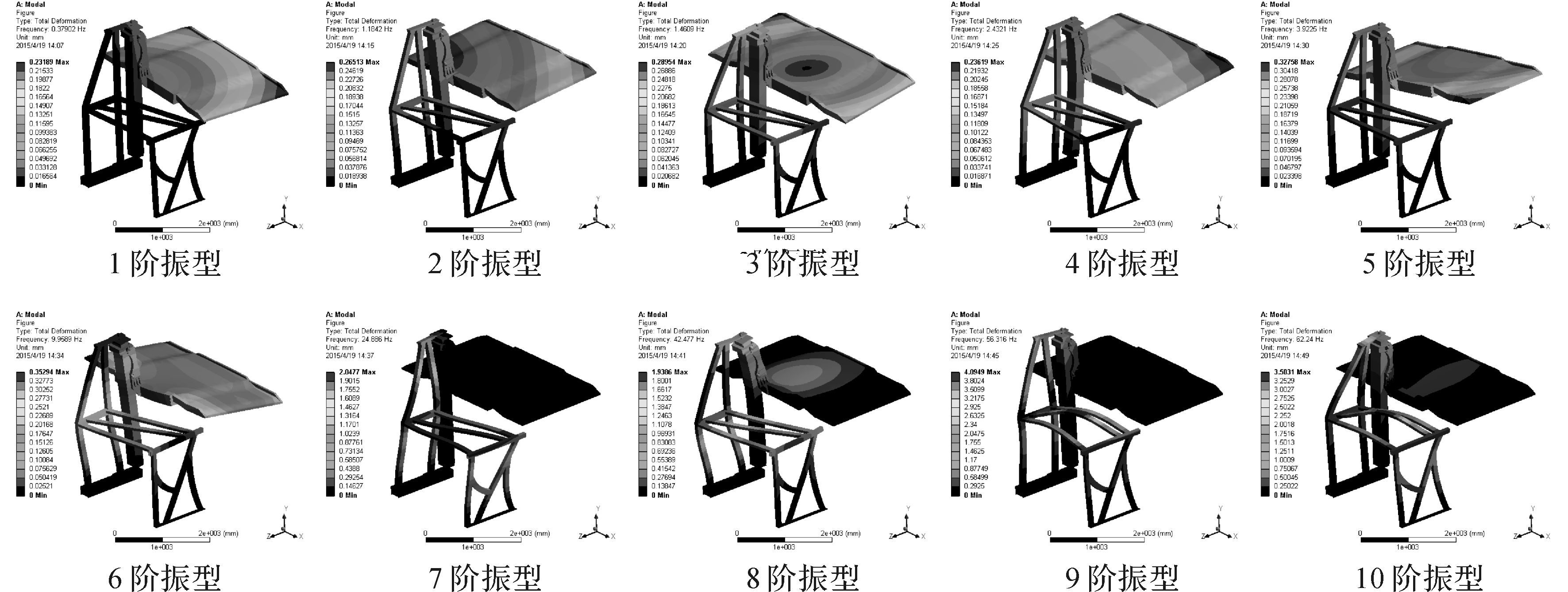
框架、立柱和台板采用45钢,材料的密度为7.86×10-6kg/mm3,材料的弹性模量E=206 GPa,剪切模量为560 MPa,泊松比μ=0.25,屈服极限为1 170 MPa.采用六面体域网格划分方式对立柱和框架进行网格划分,网格划分后对模型施加约束和边界条件.框架底座采用固定约束,台板和立柱旋转90°并且台板升至最高工作位置,然后进行求解.表 1为无载荷框架前10阶固有频率,图 3为无载荷框架前10阶振型云图.框架底座采用固定约束,在台板上施加等效的载荷后,台板和立柱旋转90°并且台板升至最高工作位置,然后进行求解.表 2为有载荷框架前10阶固有频率,图 4为有载荷框架前10阶振型云图.
| 阶数 | 固有频率/Hz | 振型描述 |
| 1 | 2.076 4 | 主要为x方向振型 |
| 2 | 5.672 9 | 主要为y方向振型 |
| 3 | 7.241 9 | 主要为y方向振型 |
| 4 | 9.734 8 | 主要为z方向振型 |
| 5 | 11.066 | 主要为y方向振型 |
| 6 | 24.846 | 主要为x方向振型 |
| 7 | 26.474 | 主要为y方向振型 |
| 8 | 29.4 | 主要为y方向振型 |
| 9 | 38.556 | 主要为y方向振型 |
| 10 | 49.34 | 主要为y方向振型 |
|
| 图 3 无载框架前10阶振型 Fig. 3 The first 10 natural mode shapes of no-load framework |
| 阶数 | 固有频率/Hz | 振型描述 |
| 1 | 0.3790 2 | 主要为z方向振型 |
| 2 | 1.184 2 | 主要为y方向振型 |
| 3 | 1.460 9 | 主要为y方向振型 |
| 4 | 2.432 1 | 主要为y方向振型 |
| 5 | 3.922 5 | 主要为x方向振型 |
| 6 | 9.958 9 | 主要为z方向振型 |
| 7 | 24.886 | 主要为x方向振型 |
| 8 | 42.477 | 主要为z方向振型 |
| 9 | 56.316 | 主要为y方向振型 |
| 10 | 62.24 | 主要为x方向振型 |
|
| 图 4 有载框架前10阶振型 Fig. 4 The first 10 natural mode shapes of on-load frame |
从表 1和图 3可以看出空载运行过程中框架系统在2~12 Hz之间可以发生共振,发生共振时主要振型方向有y方向和x方向.
从表 2和图 4可以看出重载运行过程中框架系统在0.3~10 Hz之间可发生共振,共振主要振型方向有y方向和z方向.
从表 1与表 2和图 3与图 4对比来看,有载过程比无载过程发生共振时频率降低了,并且振型方向也发生改变,在z方向的变形增大.
4 框架系统测试振动测试是在有载和无载的条件下,应用江苏东华测试仪器力锤敲打立体停车位设备样机框架,对框架系统施加瞬态脉冲激励,使框架系统产生振动,而后通过传感器采集振动信号,利用Polymax方法对动态采集分析信号进行分析,最后通过计算机显示其频响曲线.实验样机和测试系统如图 5、图 6所示,其测试结果如图 7和图 8所示.

|
| 图 5 实验平台 Fig. 5 Experimental platform |

|
| 图 6 动态信号测试系统 Fig. 6 Dynamic signal test system |
|
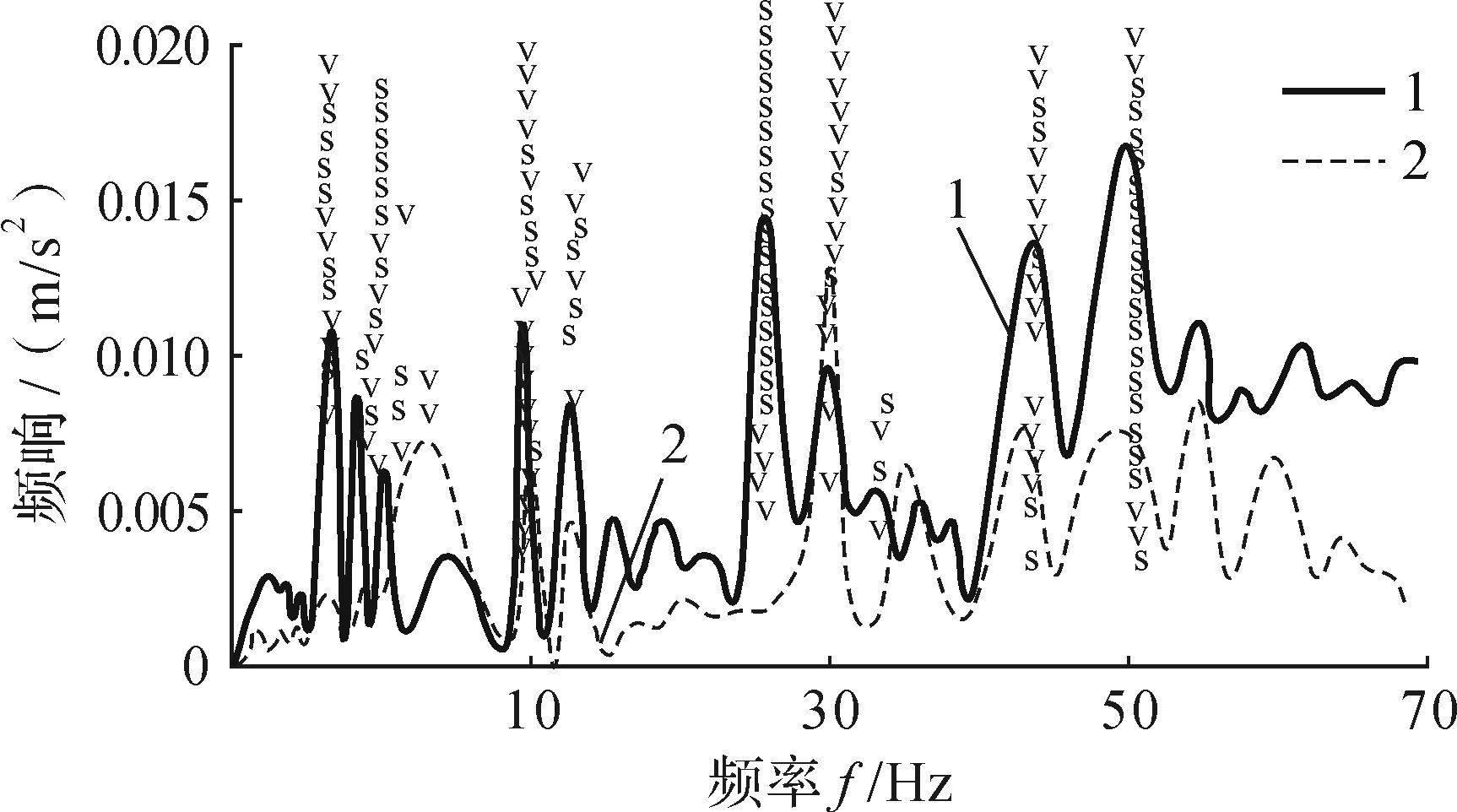
| 图 7 无载时框架模态试验稳态图 Fig. 7 Modal test steady state diagram of no-load framework |
|
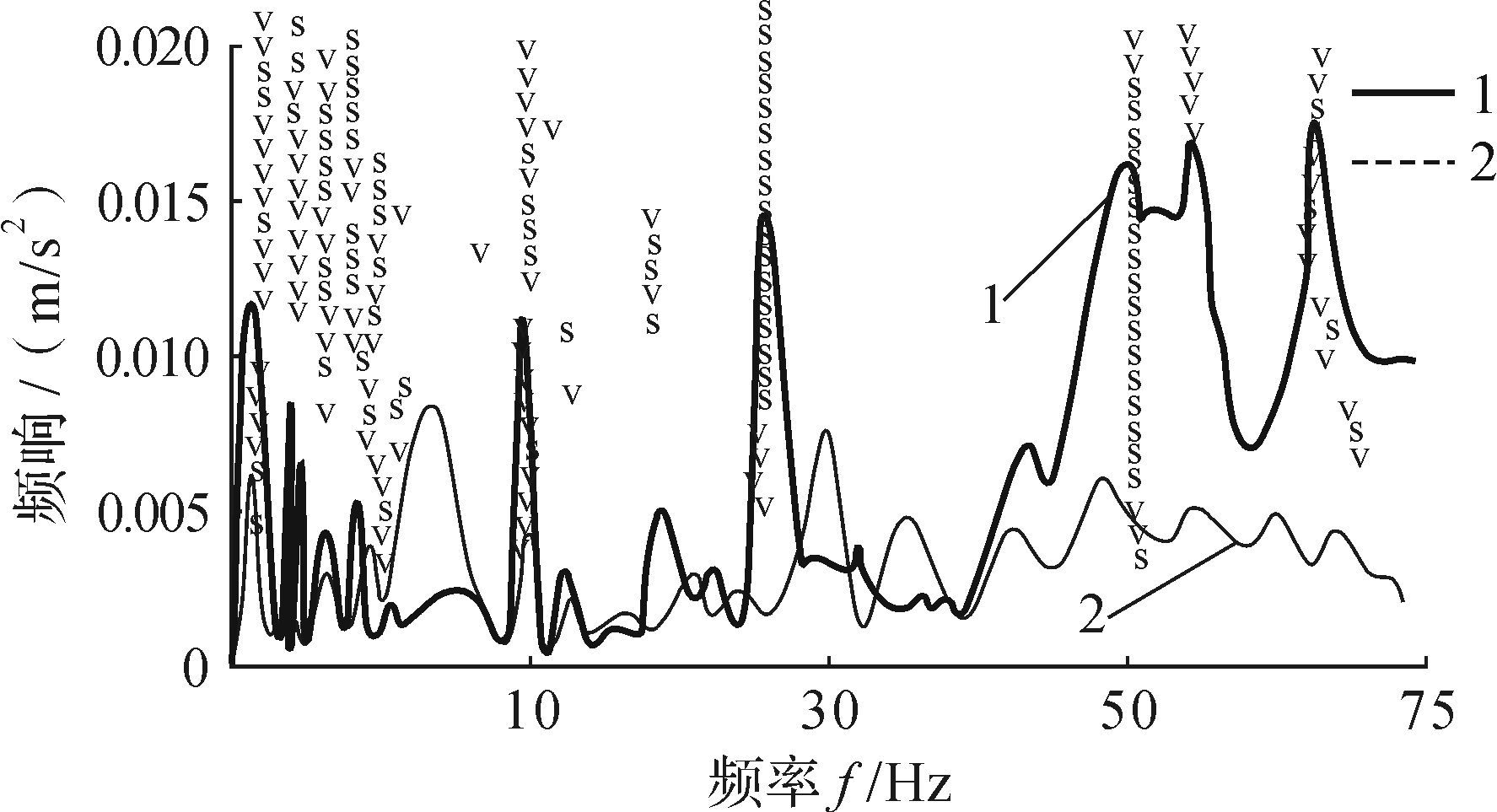
| 图 8 有载时框架模态试验稳态图 Fig. 8 Modal test steady state diagram of on-load framework |
Polymax方法在稳态图中,“o”表示未找到极点,“d”表示频率和阻尼稳定,“v”表示模态参与因子和频率稳定,“f”表示模态频率稳定,“s”表示3种参数全部稳定.可见在有模态的位置出现一列稳定的“s”标识,说明该方法分析得到的频率阻尼值稳定.
图 7是无载时智能立体停车位样机框架系统频响稳态图,图 8是有载时智能立体停车位样机框架系统频响稳态图.其中1号线是所有频率响应之和,2号线是超前支护装备的瞬时响应.提取出各阶模态参数并与仿真值进行比较,如表 3所示.
| 阶次 | 无载 | 有载 | ||
| 频率/Hz | 误差/% | 频率/Hz | 误差/% | |
| 1 | 2.253 | 7.8 | 0.412 | 8 |
| 2 | 5.525 | 2.6 | 1.306 | 9.3 |
| 3 | 6.859 | 5.5 | 1.627 | 10 |
| 4 | 9.256 | 2.2 | 2.533 | 4 |
| 5 | 12.548 | 11 | 4.505 | 12 |
| 6 | 25.745 | 3.5 | 9.807 | 2 |
| 7 | 28.579 | 7 | 27.052 | 8 |
| 8 | 33.274 | 11 | 48.116 | 11 |
| 9 | 42.859 | 9 | 54.104 | 4 |
| 10 | 50.256 | 2 | 70.356 | 11 |
由图 7、图 8和表 3知,立体停车位框架在无载时2~25 Hz可发生共振,有载时0.4~10 Hz可发生共振.共振频率与仿真分析的共振频率有偏差,这是由理论仿真分析无法精确地确定结构约束和结构参数与实际参数不同导致的,但是两者频率值相接近.
5 结 论本文以智能式立体停车位设备框架为研究对象,介绍了设备组成和工作原理,运用了振动学理论建立了框架的振动微分方程,进行数值求解,通过有限元分析软件进行了模态分析,对样机进行了模态试验,最后得到以下结论:
1) 通过对立体停车位框架系统的仿真模态分析和试验模态分析得出框架系统的固有频率,并得出框架系统在发生共振时的频率有载过程比无载过程的低,验证了力学模型的可靠性.所以在设计框架结构和选材过程中应予以重视.
2) 通过对立体停车位框架系统进行仿真和试验测试模态分析得出:立体停车位无载振幅最大的位置在右斜梁和右前立柱;有载过程中振幅最大的位置在右斜梁、右前立柱和滑套位置.为此应加强该位置的强度.
仿真模态分析和试验模态分析结果为停车位框架相应的动力学分析提供了重要的模态参数,为停车位框架的设计及其优化提供了理论依据,为研究停车位的振动、疲劳和噪声等问题奠定了基础.
| [1] |
杨杨.新型智能立体车库控制系统设计[D].太原:中北大学机械工程学院,2014:1-4. YANG Yang.The design of control system of intelligent stereo garage [D].Taiyuan:North University of China,College of Mechanical Engineering,2014:1-4. |
| Click to display the text | |
| [2] |
刘剑,王鑫,冯海涛,等.基于三菱PLC控制塔式立体车库系统设计[J].控制工程,2009,16(S4):99-102,111. LIU Jian,WANG Xin,FENG Hai-tao,et al.Tower garage control system design based on the Mitsubishi PLC[J].Control Engineering of China,2009,16(S4):99-102,111. |
| Click to display the text | |
| [3] |
毛君,谢苗,陈红月,等.框架平移回转式智能泊车装备:201110256469.8[P].2012-03-21. MAO Jun,XIE Miao,CHEN Hong-yue,et al.Intelligent parking equipment rotated and translated by frame:201110256469.8[P].2012-03-21. |
| [4] |
毛君,谢苗,陈红月,等.载车板回转立体停车位装备:201220183739.7[P].2012-11-21. MAO Jun,XIE Miao,CHEN Hong-yue,et al.Rotating stereoscopic parking equipment worked with a plate:201220183739.7[P].2012-11-21. |
| [5] |
毛君,谢苗,陈红月,等.单边液压驱动式立体框架停车位:201210553685.3[P].2013-04-24. MAO Jun,XIE Miao,CHEN Hong-yue,et al.Unilateral stereoscopic framework parking space driven by hydraulic power:201210553685.3[P].2013-04-24. |
| [6] |
毛君,谢苗,陈红月,等.单边液压驱动式立体框架停车位:201220705206.0[P].2013-06-05. MAO Jun,XIE Miao,CHEN Hong-yue,et al.Unilateral stereoscopic framework parking space driven by hydraulic power:201220705206.0[P].2013-06-05. |
| [7] |
毛君,谢苗,陈红月,等.单边电动式立体框架停车位:201220705248.4[P].2013-06-12. MAO Jun,XIE Miao,CHEN Hong-yue,et al.Unilateral stereoscopic framework parking equipment driven by electronic power:201220705248.4[P].2013-06-12. |
| [8] |
彭斌.升降横移式立体停车库的结构设计与控制[D].兰州:兰州理工大学机械工程学院,2003:1-4. PENG Bin.Structure design and control of lifting and cross sliding type stereo parking garage[D].Lanzhou:Lanzhou University of Technology,College of Mechanical Engineering,2003:1-4. |
| Click to display the text | |
| [9] |
龚海峰.升降横移式立体停车库及控制系统的研究[D].兰州:兰州理工大学石油化工学院,2003:5-28. GONG Hai-feng.Study of lifting and cross sliding type stereo parking garage and its control system[D].Lanzhou:Lanzhou University of Technology,College of Petrochemical Engineering,2003:5-28. |
| Click to display the text | |
| [10] |
周智慧.立体停车库刚架结构CAE分析及其优化设计[D].苏州:苏州大学机械工程学院,2005:1-6. ZHOU Zhi-hui.The CAE analysis and optimum design of three-dimensional car parking lot rigid-framed structure[D].Suzhou:Soochow University,College of Mechanical Engineering,2005:1-6. |
| Click to display the text | |
| [11] |
廖庆.垂直升降式机械立体停车系统的研究[D].武汉:武汉理工大学机械工程学院,2005:15-20. LIAO Qing.A study on vertical lifting mechanical parking system[D].Wuhan:Wuhan University of Technology,College of Mechanical Engineering,2005:15-20. |
| Click to display the text | |
| [12] |
汤伟.升降横移式立体车库结构优化[D].合肥:合肥工业大学机械与汽车工程学院,2008:1-4. TANG Wei.Structural optimization of up-down and translation stereo garage and analysis of its control strategies[D].Hefei: Hefei University of Technology,School of Mechanical and Automotive Engineering,2008:1-4. |
| Click to display the text | |
| [13] |
杨承超.基于立体停车的隔层桁架式抗侧力钢构架的性能研究[D].长沙:湖南大学土木工程学院,2011:1-5. YANG Cheng-chao.The research on performance of interlayer truss lateral resisting steel skeleton based on three-dimensional parking[D].Changsha:Hunan University,Civil Engineering College,2011:1-5. |
| Click to display the text | |
| [14] |
刘爽.PJSC型立体停车设备研究[D].阜新:辽宁工程技术大学机械工程学院,2012:7-21. LIU Shuang.Study on PJSC type stereo parking equinpment[D].Fuxin:Liaoning Technical University,College of Mechanical Engineering,2012:7-21. |
| Click to display the text | |
| [15] |
毛君,佟阳,谢苗,等.智能立体车位防坠落系统动力学特性仿真[J].计算机系统应用,2012,21(11):80-83. MAO Jun,TONG Yang,XIE Miao,et al.Dynamic characteristics simulation of intelligent three-dimensional parking spaces falling protection system[J]. Computer Systems & Applications,2012,21(11):80-83. |
| Click to display the text | |
| [16] |
毛君,路朝留,谢苗,等.立体车位提升系统动力学仿真及分析[J].现代制造工程,2013(10):64-66,133. MAO Jun,LU Chao-liu,XIE Miao,et al.Stereo parking lifting system dynamics simulation and analysis[J].Modern Manufacturing Engineering,2013(10):64-66,133. |
| Click to display the text | |
| [17] |
刘小华.带环箍层钢框架立体停车结构静力及动力性能研究[D].长沙:湖南大学土木工程学院,2013:1-9. LIU Xiao-hua.Research on static and dynamic performance of steel-framed tridimensional parking structures with hoop-storeys[D].Changsha:Hunan University,Civil Engineering College,2013:1-9. |
| Click to display the text | |
| [18] |
陈婷婷.机械式立体停车库的设计研究[D].兰州:兰州大学土木工程与力学学院,2013:1-11. CHEN Ting-ting.The study of design for mechanical stereo garage[D].Lanzhou:Lanzhou University,College of Civil Engineering and Mechanics,2013:1-11. |
| Click to display the text | |
| [19] |
卢进南,毛君,谢苗,等.巷道超前支架全支撑态动力学模型[J].煤炭学报,2015,40(1):50-57. LU Jin-nan,MAO Jun,XIE Miao,et al.Dynamics model of advanced powered support in heading under full support situation[J].Journal of China Coal Society,2015,40(1):50-57. |
| Click to display the text | |
| [20] |
于天彪,王学智,关鹏,等.超高速磨削机床主轴系统模态分析[J].机械工程学报,2012,48(17):183-188. YU Tian-biao,WANG Xue-zhi,GUAN Peng,et al.Modal analysis of spindle system on ultra-high speed grinder[J].Chinese Journal of Mechanical Engineering,2012,48(17):183-188. |
| Click to display the text | |
| [21] |
张春林.高等机构学[M].北京:北京理工大学出版社,2005:36-63. ZHANG Chun-lin.Advanced mechanism[M].Beijing:Beijing University of Technology Press,2005:36-63. |
| [22] |
陈艳霞,陈磊.ANSYS Workbench工程应用案例精通[M].北京:电子工业出版社,2012:30-89. CHEN Yan-xia,CHEN Lei.Proficient in ANSYS Workbench engineering application cases [M].Beijing:Publishing House of Electronics Industry,2012:30-89. |



