2. 中国工程物理研究院 总体工程研究所, 四川 绵阳 621900
2. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621900, China
离心机是惯性导航系统加速度计的标定和校准设备[1, 2],离心机转盘加速度计安装位置的半径误差是影响标定精度的主要因素.对于转盘半径为1.2 m的离心机,1 μm的半径变化引起的加速度相对误差为0.83×10-6,因此对于标定精度要求为10-6级的精密离心机,其半径误差需控制在微米级.45号钢线膨胀系数为11.59×10-6/℃,转盘半径为1 m的结构在单位温度变化下发生的线性尺寸变化达11.59 μm.因此,准确计算转盘温度及热变形对于控制精密离心机的标定精度具有重要意义.
离心机因转盘转动带动气流运动,流体与钝体的摩擦及湍流耗散产生黏性热,本文研究离心机由于转盘旋转产生能量损耗引起的热变形的计算方法.论文考虑流体和固体的共轭传热,采用流固耦合换热整场求解法计算离心机温度场,再采用顺序耦合法计算转盘位移场,形成流-热-固多物理场耦合系统.热变形计算结果可为加速度计安装位置的半径误差控制提供参考.
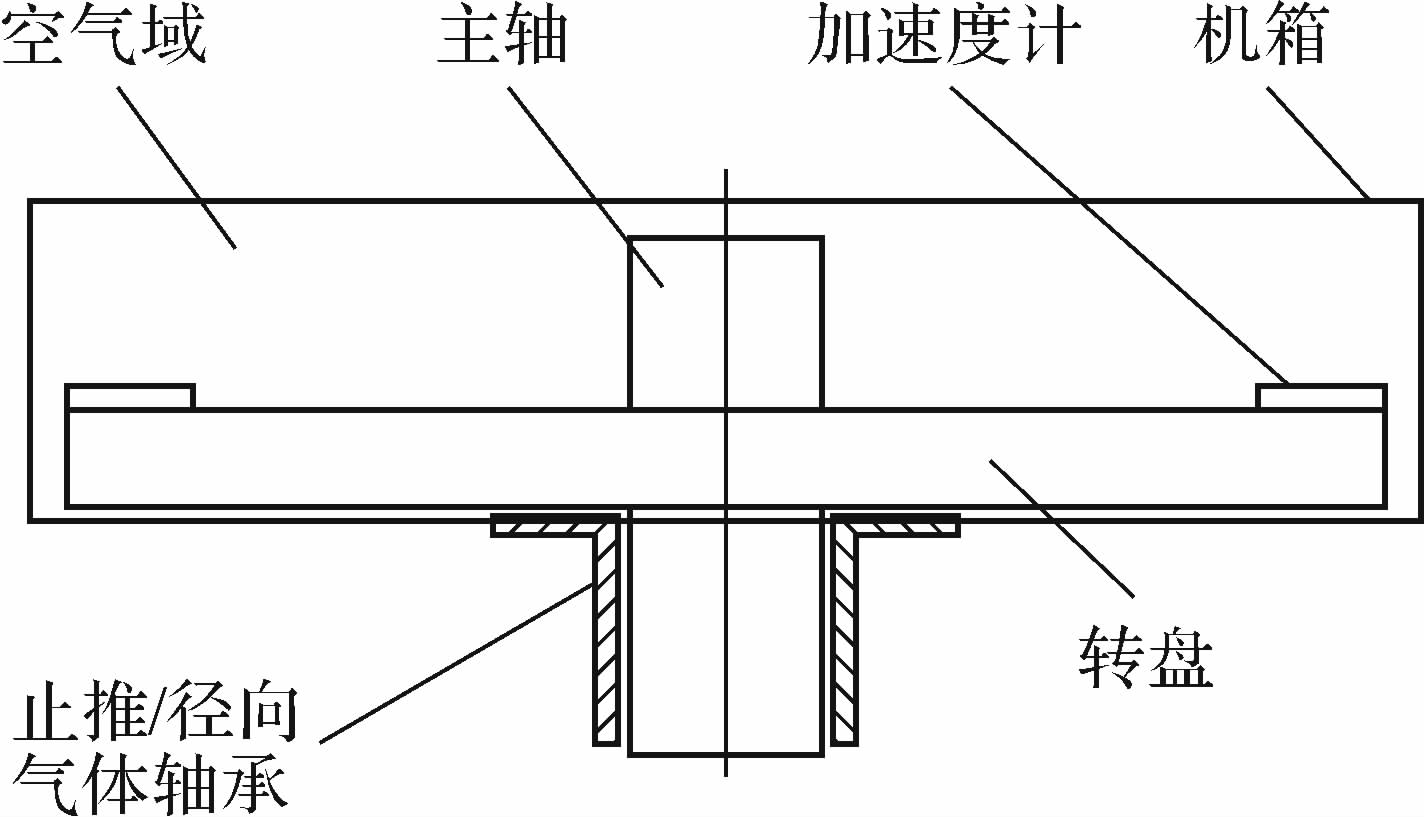
1 离心机热变形的多场耦合问题描述精密离心机由主轴、转盘、止推/径向气体轴承、机箱等组成,结构示意如图 1所示.
|
| 图 1 精密离心机结构示意图 Fig. 1 Structure diagram of precision centrifuge |
多场耦合是由多个物理场交互作用而相互影响的物理现象[5].电机驱动转盘旋转,带动周围空气气团随之运动;气团由于湍流耗散、摩擦将动能转化为内能,导致流场温度升高.流场热量一部分被机箱吸收并传递到外界,一部分通过强迫对流运动将热量传给转盘,是流-热耦合问题;转盘吸收热量后发生变形,是热-结构耦合问题.图 2为离心机多场耦合关系向图:方框代表物理场,括号内为该物理场的基本变量;箭头反映场间作用,箭头上方文字代表发生作用的物理量,单向箭头表示单向耦合.温度联系流场与温度场,热应力联系温度场与位移场,这便是离心机流-热-固多物理场耦合关系.

|
| 图 2 离心机多场耦合关系向图 Fig. 2 Multi-physics coupling relationship of centrifuge |
离心机温度场计算采用整场求解法,流、固两区域采用通用的控制方程.把离心机内空气视为不可压流体,密度为常数,建立离心机流固耦合换热统一控制方程,即
| $\frac{\partial \left( \rho \varphi \right)}{\partial t}+\text{div}\left( \rho U\varphi \right)=\text{div}\left( \Gamma \text{grad}\varphi \right)+S,$ | (1) |
式中:ρ为流体密度;t为时间项;φ为通用变量,可为速度分量u,v,w和温度T等求解变量;
质量守恒方程:
| $\text{div}\left( \rho U \right)=0.$ | (2) |
动量守恒方程:
| $\left. \begin{array}{*{35}{l}} \text{div}\left( \rho Uu \right)=\text{div}\left( \mu \text{grad}u \right)-\frac{\partial P}{\partial x}+{{S}_{u}}, \\ \text{div}\left( \rho U\upsilon \right)=\text{div}\left( \mu \text{grad}\upsilon \right)-\frac{\partial P}{\partial y}+{{S}_{\upsilon }}, \\ \text{div}\left( \rho U\omega \right)=\text{div}\left( \mu \text{grad}\omega \right)-\frac{\partial P}{\partial z}+{{S}_{\omega }}. \\ \end{array} \right]$ | (3) |
式中:μ为运动黏度;u,v,w为速度矢量
能量守恒方程:
| $\text{div}\left( \rho UT \right)=\text{div}\left( \frac{\lambda }{{{C}_{\text{p}}}}\text{grad}T \right)+{{S}_{T}},$ | (4) |
式中:T为温度;λ为导热系数;Cp为定压比热容;ST为源项,主要是由于黏性作用使机械能转化为内能.固体运动黏度为无穷大,故能量方程中对流项为零,若忽略温度对流体动力黏度的影响,则能量方程就转化为导热方程:
| $\frac{\lambda }{\rho {{C}_{\text{p}}}}\left[ \frac{\partial }{\partial x}\left( \frac{\partial T}{\partial x} \right)+\frac{\partial }{\partial y}\left( \frac{\partial T}{\partial y} \right)+\frac{\partial }{\partial z}\left( \frac{\partial T}{\partial z} \right) \right]=0.$ | (5) |
上述方程既可描述流体域的流动与传热,也可描述固体域的导热,事实上只有能量方程应用到固体域上.
离心机转盘热变形是热-结构耦合.温度场对结构的作用表现为温度差导致单元体的膨胀或缩小从而产生应力,应力大小为
| $\sigma =E\varepsilon -\alpha \left( T-{{T}_{0}} \right),$ | (6) |
式中:σ为应力张量;ε为应变张量;E为弹性系数张量;α热弹性系数;T为计算所得的转盘温度,T0为环境温度.
2.2 多物理场耦合计算方法流固耦合换热是对流和导热耦合,耦合界面上的热边界条件由热量交换过程动态地决定,不能预先给出,需要计算才能得到[8].离心机转盘热边界是耦合换热问题,从整场求解数学模型可知,流体、固体区域有通用控制方程,界面上满足以下连续性条件:
| ${{T}_{\text{w}}}{{\text{ }\!\!|\!\!\text{ }}_{\text{f}}}\text{=}{{T}_{\text{w}}}{{\text{ }\!\!|\!\!\text{ }}_{s}},$ | (7) |
| ${{\psi }_{\text{w}}}{{\text{ }\!\!|\!\!\text{ }}_{\text{f}}}\text{=}{{\psi }_{\text{w}}}{{\text{ }\!\!|\!\!\text{ }}_{\text{s}}},$ | (8) |
式中:Tw为离心机流固交界面温度;Ψw为交界面上的热流密度;下标f和s分别代表流体和固体区域.
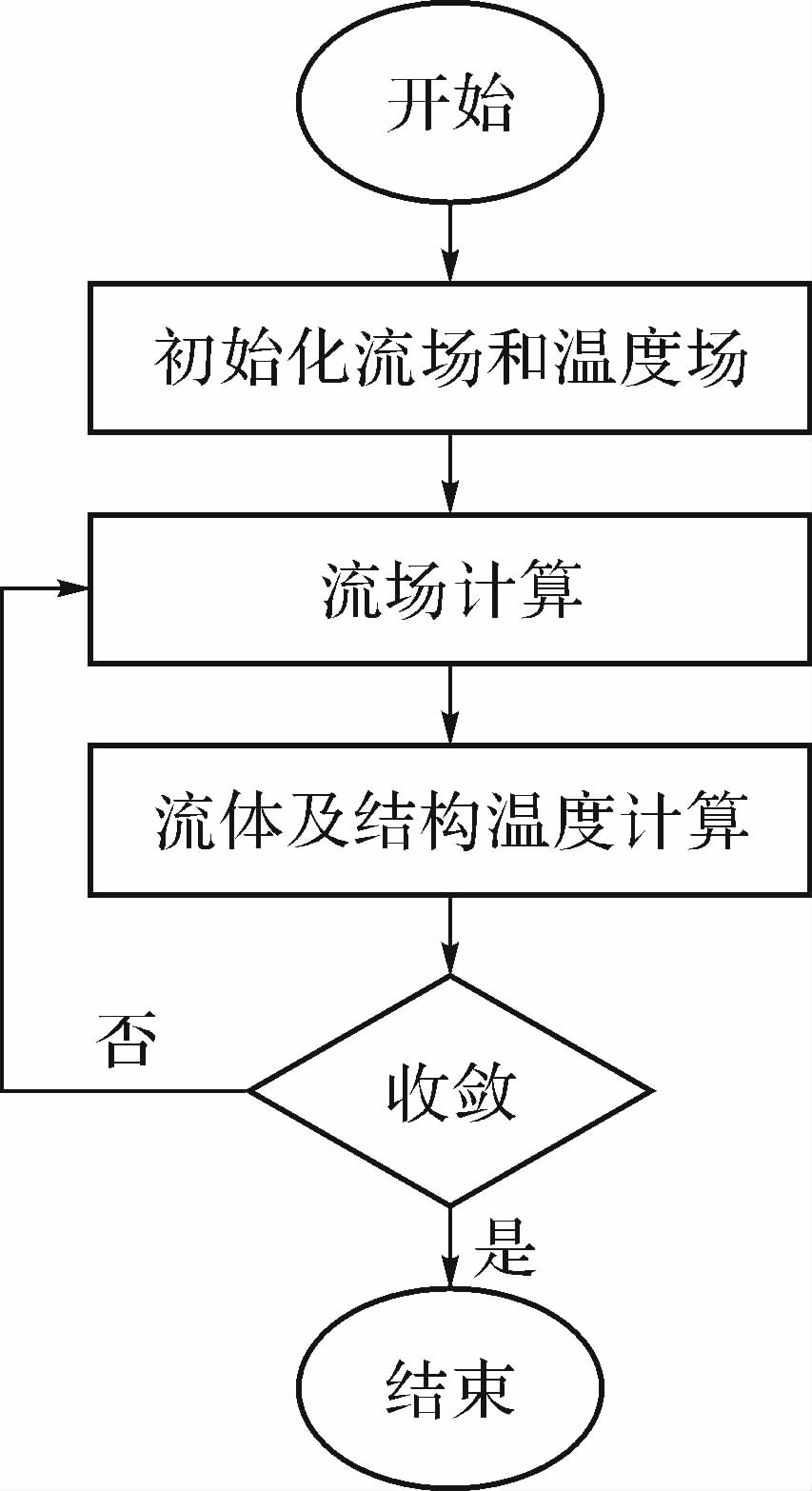
耦合分析指考虑多个物理场之间相互作用的分析,主要有直接法和间接法[6].直接法通常只包含一次分析,它将不同场的控制方程整合到一个方程矩阵中计算.离心机稳态温度场的整场求解可通过直接法实现,即将CFD求解域扩展到固体域,如式(5)所示,计算流程见图 3,即先给定流场边界条件和环境温度,然后计算流场.CFD软件采用分离求解器,故先计算动量和质量方程,然后求解能量方程,最后同时得到流场和结构温度场.由于流、固区域网格不相似,通过设置耦合界面共轭传热来实现界面温度数据传递.
|
| 图 3 整场求解流程图 Fig. 3 Whole-field solution process |
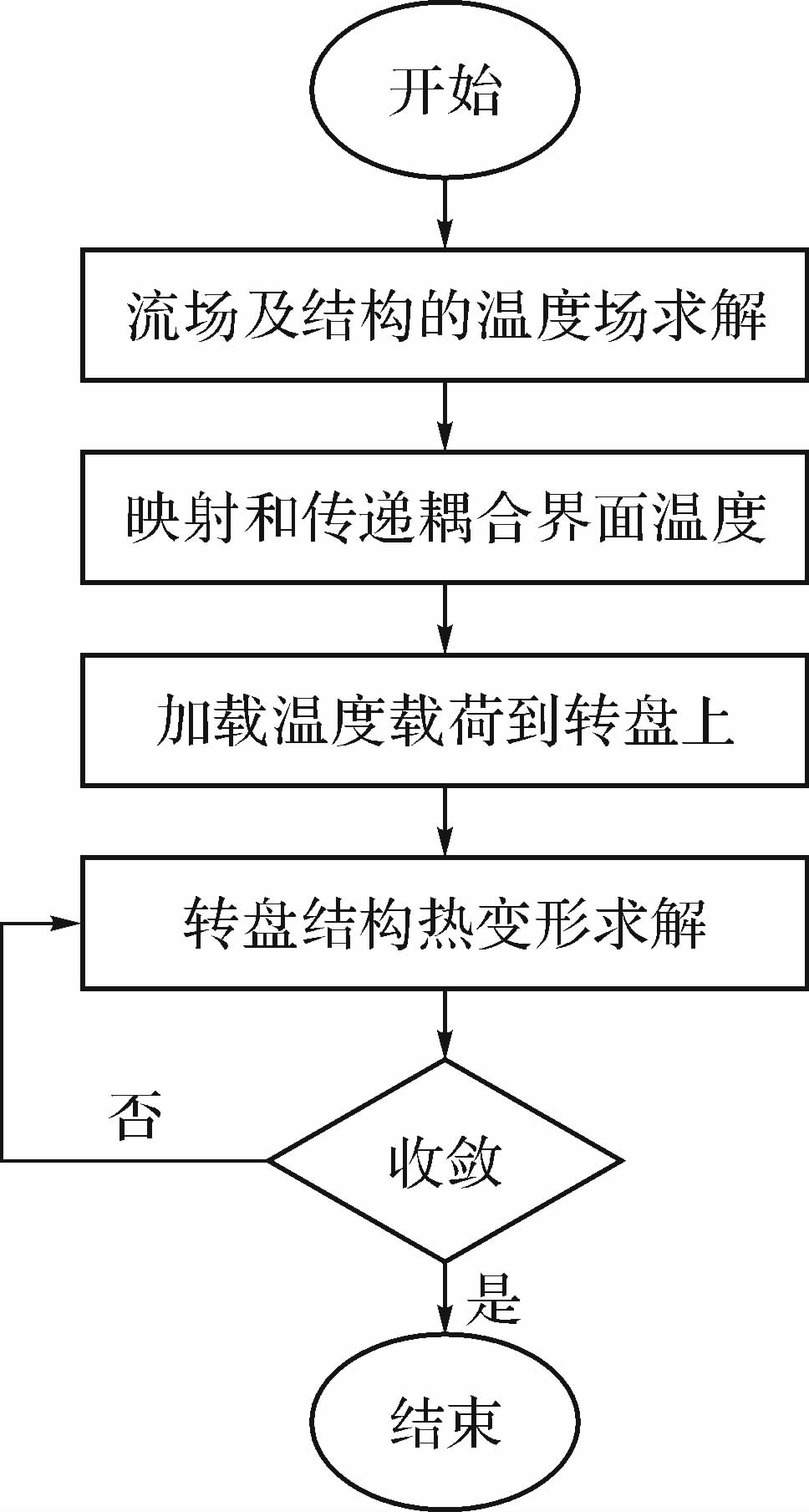
间接法包含多次分析,每一次分析属于不同的场.它首先对一个场进行分析,再将耦合区域内的物理量通过映射和插值传递给外场进行计算.间接法根据界面是否反复迭代分为顺序耦合法和迭代耦合法.顺序耦合法实质上是对单个场的一次求解,没有完整的迭代收敛过程,它把耦合简化为边界条件加载到另一场,常用于耦合效应不明显的分析.本文采用顺序耦合法计算离心机热变形,计算流程见图 4.首先求解转盘温度场,然后将温度场作为热边界条件加载到结构上,计算结构变形.
|
| 图 4 热变形顺序耦合求解流程 Fig. 4 Thermal deformation sequential coupling solution process |
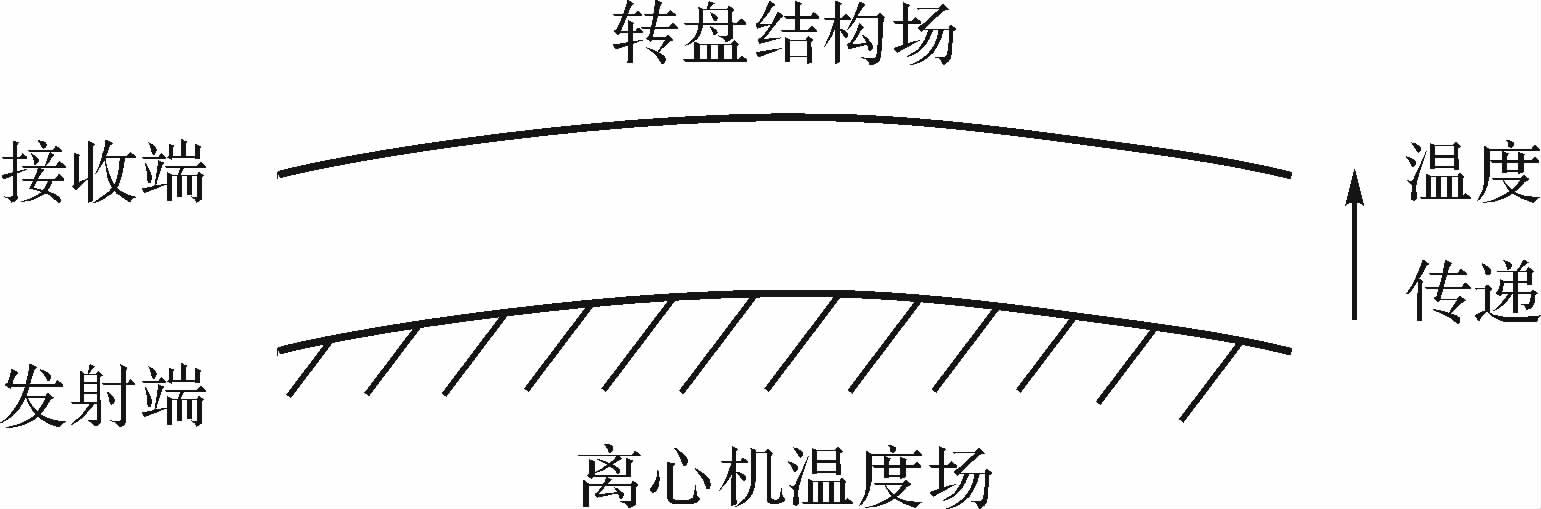
由于离心机温度场与位移场节点数量和位置不一样,使用顺序耦合法时需解决插值方向和节点匹配方式的问题[5],因此其关键技术在于网格映射和耦合界面的数据传递,数据传递的难点在于保证界面总功守恒及耦合仿真精度[6].本文采用局部数据插值,其原理如图 5所示.即结构场的数据接收端的所有节点(1,2,…,5)映射到温度场发射端的相应单元,温度在单元的映射点(α1,α2,…,α5,其中叉点为温度场单元节点温度值)完成插值后传递到结构场,数据在两场可能不守恒,但对于位移和温度,整体守恒意义不大[7],反而局部分布更需精确传递,映射算法采用快速映射法.图 6为热-结构耦合载荷传递.

|
| 图 5 场间数据传递 Fig. 5 The data transfer between physical fields |
|
| 图 6 热-结构耦合载荷传递 Fig. 6 Heat structural coupling load transfer |
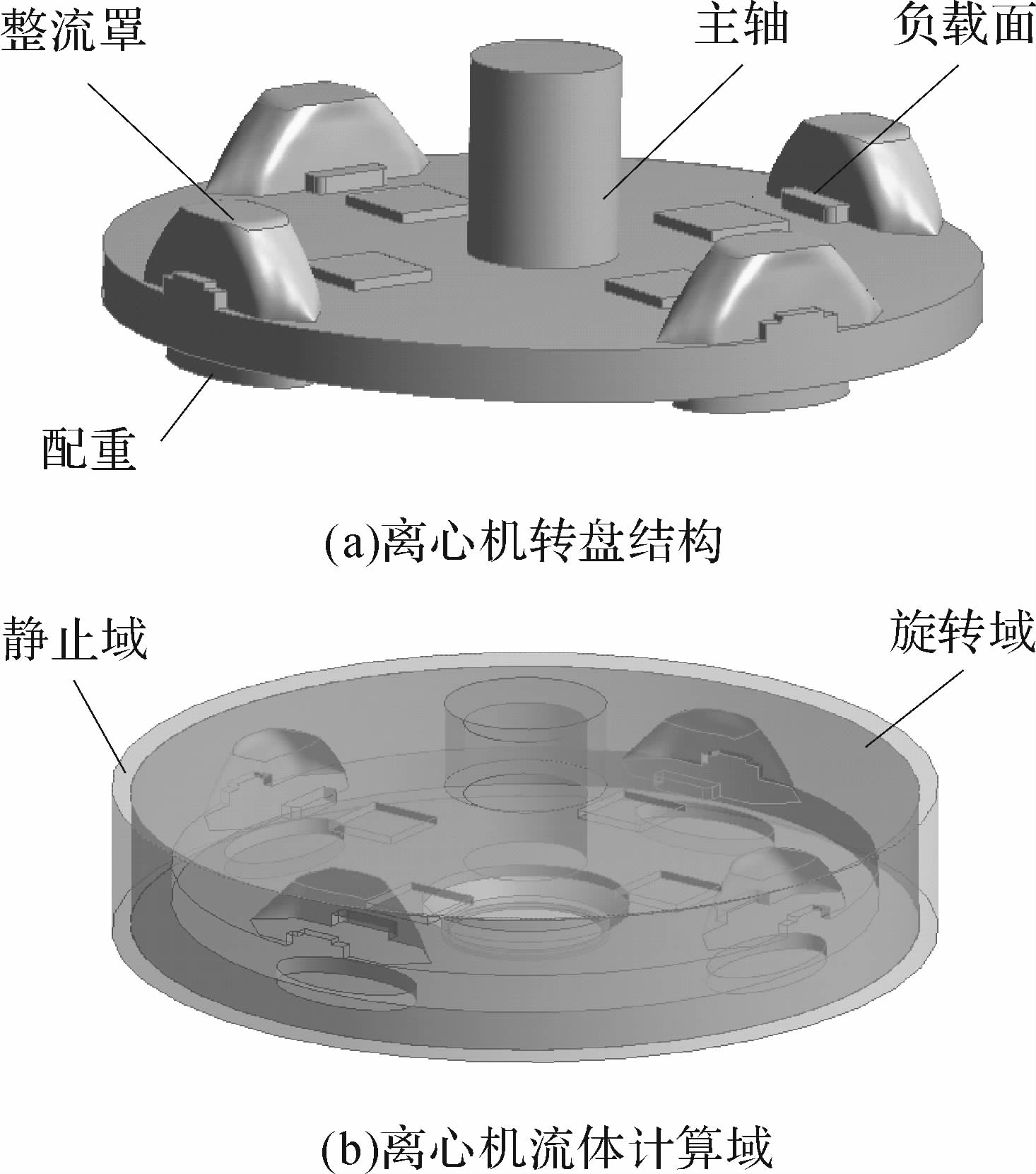
对离心机流固耦合换热问题的整场求解,需对流体域和固体域同时建模.转盘上有配重、负载、整流罩等,配重用于转盘上的动、静平衡,负载用于安装待标定加速度计,整流罩安装在负载上方,用于减小钝体风阻及其波动.离心机流场为旋转流场,本文采用多坐标系MRF方法来模拟流场及温度场,因此流体域在建模时被分为静止域和旋转域.图 7为离心机转盘结构及计算域.
|
| 图 7 离心机整体结构 Fig. 7 The whole structure of centrifuge |
在流体域和固体域耦合界面上采用双边壁面仿真技术.转盘上除了主轴圆面外,其余都为流固耦合界面,具体边界条件设置如下:
1)转盘转速为300 r/min;
2)流场旋转域和静止域的交界面为interface;
3) 对转盘旋转模拟采用多坐标系模型和MRF方法;
4)流体域上靠近转盘的壁面为移动壁面,相对流场转速为零;
5)流体域和固体域接触面为耦合界面,在界面上应用共轭传热仿真技术;
6) 机箱底部小圆面为压力出口,温度恒为20 ℃;
7) 环境温度恒为20 ℃,机箱外部与环境自然对流.
转盘直径为2.2 m,采用四面体非结构化网格,并加密流固耦合界面上的网格,网格长宽比为9.2,纵横比为0.77,网格数为4.83×106个,网格划分结果见图 8.

|
| 图 8 整场求解网格剖分结果 Fig. 8 Results of the whole solving grid |
本文选用三维稳态压力基求解器;打开能量方程及黏性热开关;压力项离散格式为PRESTO!,为了配合非结构化网格的使用,其余项的离散格式均采用二阶迎风离散格式;压力速度耦合方式为SIMPLE方式.离心机空气流场包含大曲率流动的旋转流,所以选择能够对旋转、强反向压力梯度下的边界层及分离流动模拟的基于时间平均的RNG k-ε 湍流模型;选用尺度化(Scalable)壁面函数.
3.2 转盘热变形计算将转盘温度场计算结果作为体热载荷加载到转盘上.热变形计算边界条件为:转盘轴承面为固定约束;环境温度为20 ℃;主轴圆面Z方向位移为0;转盘采用四面体二次单元离散.转盘材料为45号钢,机箱材料为5A06,流体为不可压缩空气.计算所需物性参数如表 1所示.
| 材料 | 密度/ (kg/m3) | 导热率/(W/m·K) | 热膨胀 系数/(/℃) | 比热容/ (J/kg·K) | 弹性模量/ Pa | 泊松比 | 动力黏度/ (kg/m·s) |
| 45钢 | 7 850 | 50.2 | 1.159×10-5 | 480 | 2.1×1011 | 0.31 | ∞ |
| 5A06 | 2 750 | 117 | 2.36×10-5 | 921 | — | — | ∞ |
| 空气 | 1.225 | 0.024 2 | — | 1 006.43 | — | — | 1.7894×10-5 |
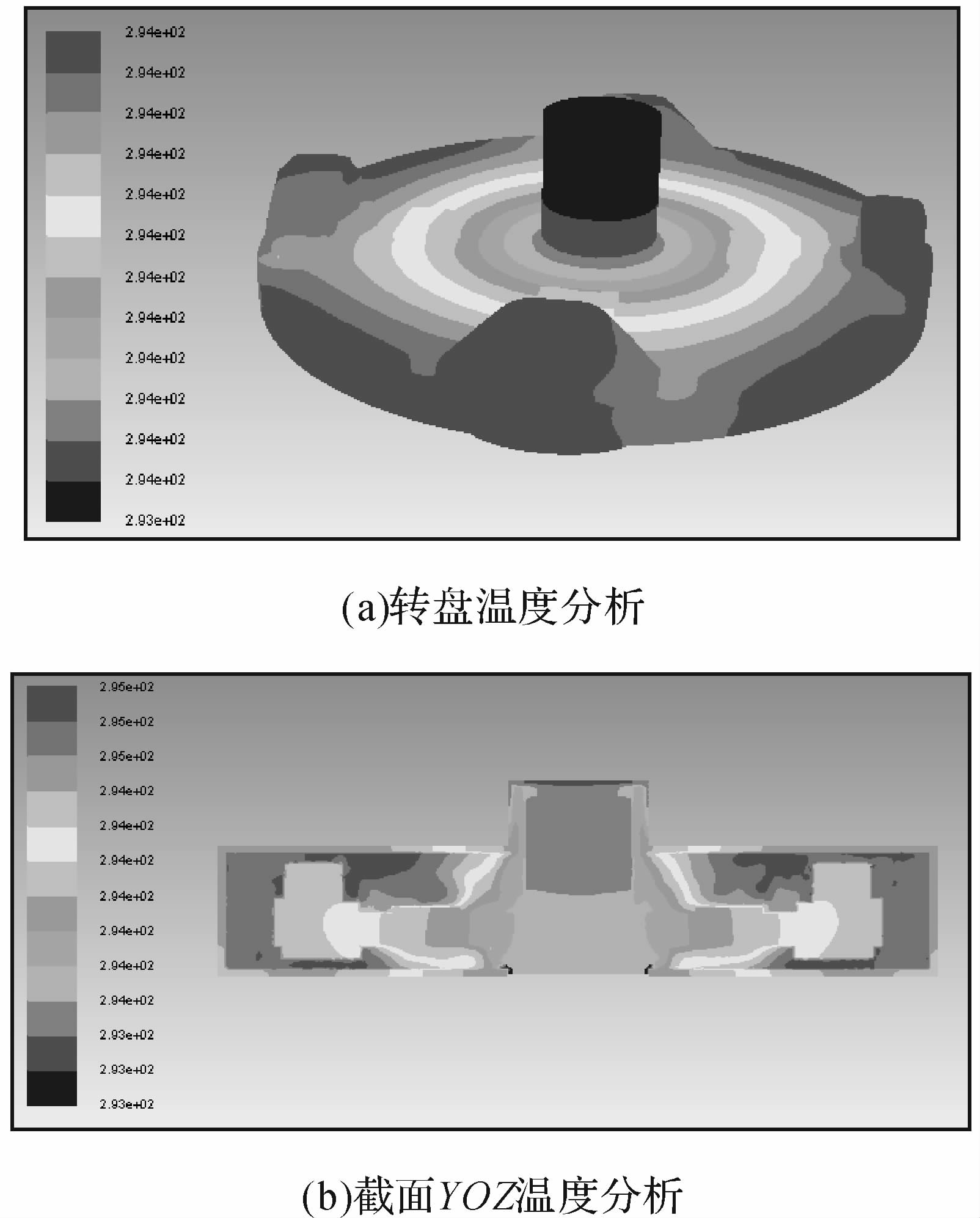
在转速为300 r/min、环境温度为20 ℃工况下,计算得到转盘和流场温度如图 9所示.越靠近转盘边缘,温升越大,最大温升1.23 ℃,整流罩上背风面(左侧)温升高于迎风面(右侧),这是因为在迎风面和空气发生撞击,流体在整流罩后方形成卡门涡列,这些涡列的消失伴随着机械能转化为内能.从图 9(b)可看到流场温度分布基于主轴对称,流体域的最大温升为1.83 ℃,位于整流罩附近.由于流体的黏性热为结构温度场的热源,流体温升高于固体温升.加速度计安装位置的温度测试值与实测值一致,温升为0.8 ℃,验证本文方法的正确性.
|
| 图 9 温度场计算结果 Fig. 9 The temperature field calculation results |
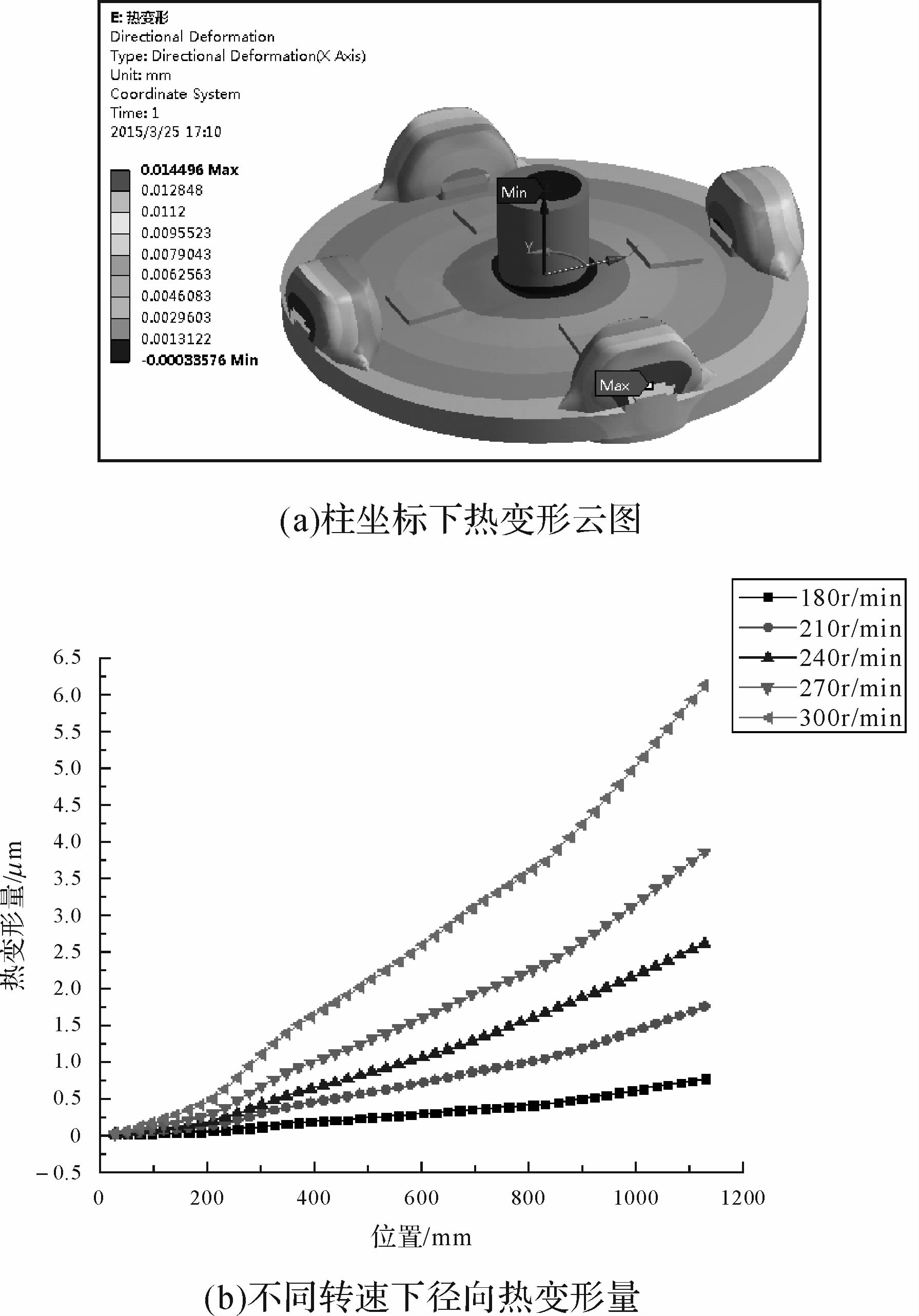
图 10(a)为柱坐标下转盘的热变形云图.其中加速度计安装位置的径向变形为7.89 μm,相对实测值误差为7.8%,原因是动态半径还受到主轴回转误差和外轮廓误差影响.转盘的热变形量越远离旋转中心越大,最大变形量出现在整流罩上,为14.5 μm,这是一个变形累积的结果.转盘主轴在Z方向有上翘也有下压趋势,盘面上整体下压,这是因为盘面上表面刚度比下表面的刚度小,由于热膨胀,上表面的尺寸增大量多,下表面尺寸增大量少,盘面的下压趋势也是变形累积的结果.图 10(b)为不同转速下转盘的热变形变化规律.随着转速的增加,转盘径向变形增大,且越远离转盘旋转中心变形量越大,不同转速下的热变形规律基本一致.
|
| 图 10 热变形计算结果 Fig. 10 Thermal deformation calculation results |
文中对精密离心机进行全三维流-热-固多物理场耦合数值计算,建立了流场、温度场及位移场的耦合计算方法,并分析了离心机热变形涉及的耦合方法机理.仿真结果表明:离心机在300 r/min工况下,转盘最大温升为1.23 ℃,实测值与仿真计算值一致,验证离心机热变形耦合方法的正确性;转盘最大热变形量在整流罩上为14.5 μm,加速度计安装位置的径向变形量为7.89 μm,热变形是一个累积过程,越远离转盘中心位置的变形越大;随着转速增加,变形量增加,不同转速下的变形规律一致.
| [1] | YAZDI N,AYAZI F,NAJAFI K.Micro-machined inertial sensors[J].Proceedings of the IEEE,1998,86(8):1640-1655. |
| Click to display the text | |
| [2] | 何铁春,周世勤.惯性导航加速度计[M].北京:国防工业出版社,1983:352-353. HE Tie-chun,ZHOU Shi-qin.Inertial navigation accelerometer [M].Beijing:National Defence Industry Press,1983:352-353. |
| [3] | YANG Y,HUO X.Measuring and balancing dynamic unbalance of precision centrifuge[J].International Symposium on Instrumentation Science and Technology,2008:11-16. |
| Click to display the text | |
| [4] | 尹小恰.精密离心机工作半径的测试方法与误差分析[D].哈尔滨:哈尔滨工业大学航天学院,2013:2-12. YIN Xiao-qia.The measurement method and error analysis for the working radius of precision centrifuge[D].Harbin:Harbin Institute of Technology,School of Astronautics,2013:2-12. |
| Click to display the text | |
| [5] | 宋少云.多场耦合问题的协同求解方法研究与应用[D].武汉:华中科技大学机械科学与工程学院,2007:2-3. SONG Shao-yun.Research and application of collaborative solution method for multiphysics problems[D].Wuhan:Huazhonhg University of Science and Technology,School of Mechanical Science and Engineering,2007:2-3. |
| Click to display the text | |
| [6] | FELIPPA C A,PARK K C,FARHAT C.Partitioned analysis of coupled mechanical systems[J].Computer Methods in Applied Mechanics and Engineering,2001,190(24/25):3247-3270. |
| Click to display the text | |
| [7] | 黄唐,毛国良,姜贵庆,等.二维流场、热、结构一体化数值模拟[J].空气动力学报,2000,18(1):115-119. HUANG Tang,MAO Guo-liang,JIANG Gui-qing,et al.Two dimensional coupled flow-thermal-structural numerical simulation[J].Acta Aerodynamica Sinica,2000,18(1):115-119. |
| Click to display the text | |
| [8] | 钱若军.流固耦合理论研究进展[J].空间结构,2008,14(1):3-14. QIAN Ruo-jun.Advances in research on fluid-structure interaction theory[J].Spatial Structures,2008,14(1):3-14. |
| Click to display the text | |
| [9] | MALATIP A,WANSOPHARK N,DECHAUMPHAI P.Fractional four-step finite element method for analysis of thermally coupled fluid-solid interaction problems[J].Applied Mathematics and Mechanics,2012,33(1):99-116. |
| Click to display the text | |
| [10] | 徐太栋.精密离心机空气流场的数值模拟[D].成都:电子科技大学机械电子工程学院,2014:22-30. XU Tai-dong.Numerical simulation of airflow field for the precision centrifuge[D].Chengdu:University of Electronic Science and Technology of China,School of Mechatronics Engineering,2014:22-30. |
| Click to display the text |



