箱体类零件通常有若干具有相互位置要求的孔,一般在坐标镗床或加工中心加工,各孔之间中心距及其公差由工作台或镗头的纵横坐标的移动精度来保证.孔系尺寸不同于线性尺寸,它既包含长度尺寸又包含角度尺寸,它们的计算要比线性尺寸复杂得多,许多国内外学者一直在作这方面的研究.1999年,王伯平等[1]应用多元函数的偏微分理论和工艺尺寸链原理,简化平面尺寸链公差的计算,并可在计算过程中修正公差值的大小.2002年,石一民[2]应用全微分和概率法进行了箱体类零件在镗床上加工时的坐标尺寸和公差计算.2003年,王世伟等[3]建立了平面尺寸链的分解方法,并讨论了公差带的分布情况.2004年,Xue等[4]在基于离散成本公差模型的基础上讨论了平面尺寸公差下包含角度的工序尺寸的公差分配法.2006年,安虎平等[5]论述了箱体平行孔系加工时将平面尺寸链换算成线性尺寸链求解坐标尺寸和公差的基本方法.2007年,Gonzalez等[6]提出了二维尺寸下尺寸公差的等量转换,建立了由二维尺寸图转换为二维尺寸链的尺寸模型,包含了尺寸、角度和定向公差.2007年,胡志敏等[7]等提出了基于尺寸链图形理论的公差计算方法,与解析法相比,尺寸链计算更直观易行,并且无需微分运算.2009年,吴如恩等[8]建立了用尺寸式来计算平面尺寸的方法,避免了尺寸链图的绘制,降低了计算误差,适合计算机辅助设计.2011年,阎艳等[9]提出了将尺寸公差的信息用图形表示的方法,开发了一个平面尺寸链的公差分析系统.
以上研究对平面尺寸链的建立和公差分析有重要的作用,但是这些方法仅仅能够表达尺寸关系,不能描述平面尺寸的加工顺序及其基准;同时尺寸链中增减环的判别及计算都比较困难,易出错.针对以上问题,本文建立孔系尺寸的工艺尺寸路径图来描述孔的加工顺序和加工基准,并建立工序尺寸的数学模型求解所有的工序尺寸和公差.
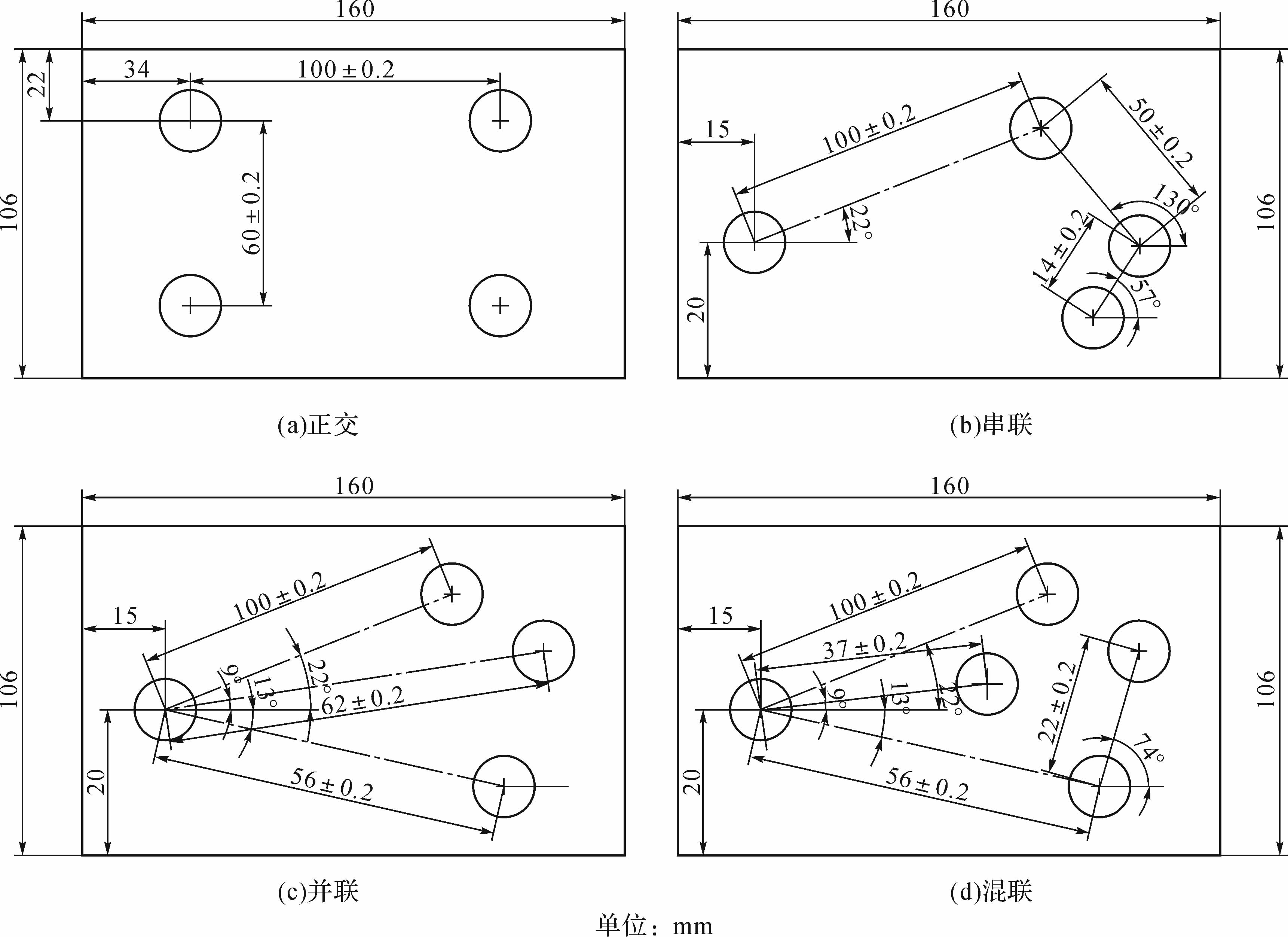
1 孔及其尺寸的表示 1.1 孔及其尺寸标注形式箱体上的孔可以分为平行孔系、同轴孔系和交叉孔系.本文只讨论平面孔系的加工.平面上的孔根据其排列方式又可分为正交孔和非正交孔.本文以图 1 所示的平面孔系为例,其中图 1(a)所示为正交孔的常见标注方式,非正交孔的标注方式主要有图 1(b)串联、图 1(c)并联、图 1(d)混联等三种形式.
|
| 图 1 平面孔系的标注类型 Fig. 1 The labeling types of planar holes |
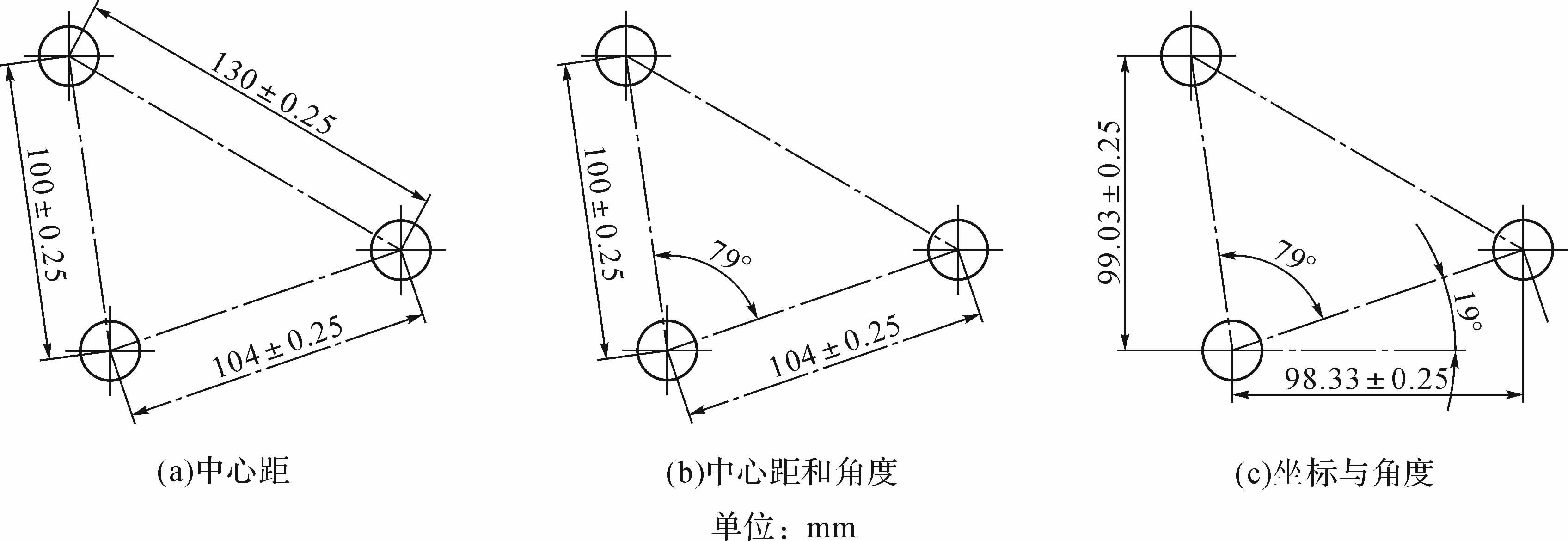
孔系零件的尺寸标注不同于线性尺寸,主要有如图 2(a)中心距、图 2(b)中心距和角度、图 2(c)坐标与角度三种形式,但不管其如何标注尺寸,它们之间总有着一定的三角函数关系.
|
| 图 2 孔的几种尺寸标注形式 Fig. 2 Several dimensioning modes of holes |
平面孔系在坐标镗床或者数控机床上加工时,主要为串联加工或者并联加工.图 1(a),(b),(c)所示的孔系,若按照其串联或者并联加工,其坐标尺寸是很容易计算出来的.而对于图 1(d)所示的混联来说,串联或者并联加工时孔的坐标尺寸很难计算,而且极易出错.
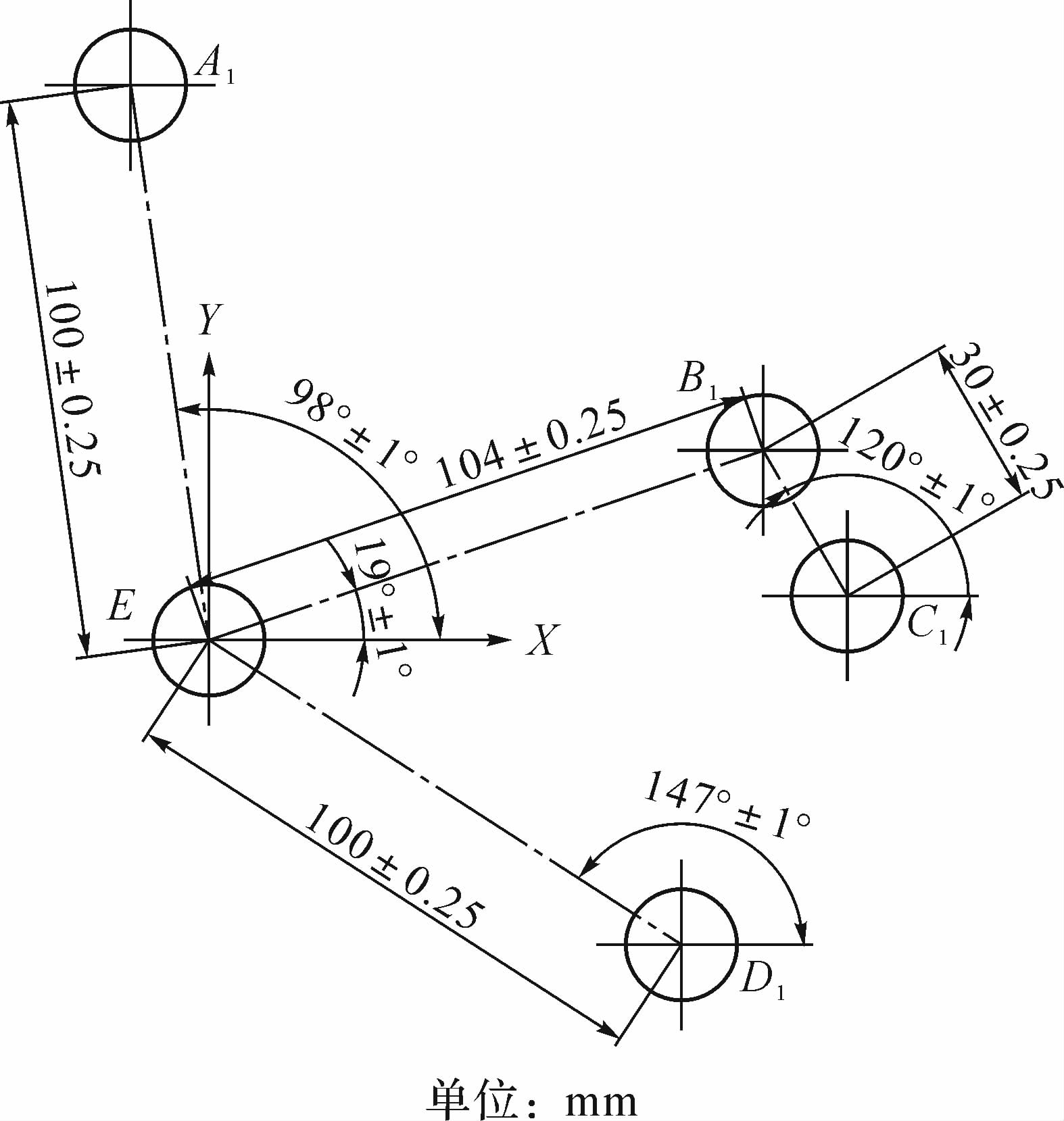
1.2 孔的表示孔系零件上孔的个数一般较多,为了避免混乱,给每个孔进行标示.本文用A,B,C,D等英文字母表示孔的中心,给字母加上数字下标来表示孔的第几次加工.图 3是一典型的平面孔系的尺寸联系图,图中孔E为粗基准,直接用E 表示;孔A需要经过1次加工,用A1表示;若孔A需要经过2次加工,则用A2表示.按照上述表示方式,图中的孔如图 3所示.
|
| 图 3 孔系零件尺寸联系图 Fig. 3 Dimension relation graph of multiple-holes |
孔系零件的尺寸通常有3种,以图 3 为例:1)长度尺寸.如孔E与孔A1之间的尺寸,直接用EA1表示,孔B1与孔C1 之间的尺寸用B1C1表示.2)角度尺寸.规定角度以逆时针方向为正方向,如角度98°±1°,应表示成αEA1,不可表示成αA1E.3)坐标尺寸.矢量 EB1 在X轴方向的坐标尺寸表示成XEB1,在Y轴方向的坐标尺寸表示成YEB1;若是表示成XB1E和YB1E,则代表的是矢量 B1E 在X轴和Y轴上的分量.
2 工艺尺寸路径图的建立 2.1 工序尺寸的表示零件在加工过程中的工序尺寸用基准要素至加工要素构成的有向线段表示.例如,以经过1次加工的B1孔为工序基准加工C孔时的工序尺寸用B1→C1 表示,矢量表示为 B1C1 .
图 3所示孔系零件的工艺路线和工序尺寸为:
工序5:粗镗,基准孔为E,加工孔为A1,工序尺寸为E→A1,矢量表示为 EA1 ;
工序10:粗镗,基准孔为A1,加工孔为B1,工序尺寸为A1→B1,矢量表示为 A1B1 ;
工序15:粗镗,基准孔为B1,加工孔为C1,工序尺寸为B1→C1,矢量表示为 B1C1 ;
工序20:粗镗,基准孔为C1,加工孔为D1,工序尺寸为C1→D1,矢量表示为 C1D1 .
2.2 工艺尺寸路径图的生成工序尺寸是由零件的基准要素与加工要素在加工过程中形成的,将各工序尺寸依次以树图的形式画出就得到了零件的工艺尺寸路径图.本例中首先将第1道工序尺寸E→A1用树图的形式画出,然后添加第2道工序尺寸A1→B1,按照工序顺序依次添加其它工序尺寸,直到所有的工序尺寸添加完.图 4为图 3所示孔系零件的工艺尺寸路径图.
|
| 图 4 工艺尺寸路径图 Fig. 4 Process dimension path graph |
工艺尺寸路径图的特点:
1)工艺尺寸路径图是一个不封闭的有向图,描述了加工中的工序基准和加工顺序,箭头左端是该道工序的工序基准,箭头右端是加工要素,如A1是工序5的加工要素,同时是工序10的工序基准,依次类推.
2)路径图的每2个顶点所组成的边表示的是一个工序尺寸,边的大小和方向不代表工序尺寸的大小和方向,只是一个拓扑结构,可以任意画出.
3 尺寸模型的建立与求解 3.1 尺寸模型的建立机械加工过程最终要保证2类目标尺寸:一类是零件蓝图上的尺寸,也叫零件的设计尺寸;另一类就是各个加工余量.零件的设计尺寸,其对应的2个要素一定是加工中最后形成的要素,如图 3 所示,设计尺寸用矢量应表示为 EA1,EB1,B1C1,ED1.
路径图中的各个目标尺寸都是通过工序尺寸来直接或者间接保证的,有着各自的形成路径,通过路径图寻找到它们之间的关系也就建立了尺寸之间的 数学模型.从图 4的路径图可以看出图 3的4个设计尺寸 EA1,EB1,B1C1,ED1 的形成路径,如设计尺寸 EB1 是通过工序尺寸 EA1,A1B1 来间接保证的,用矢量方程可以表示成 EB1=EA1+A1B1 ,等号左端为目标尺寸,等号右端为该目标尺寸相关的工序尺寸.根据图 4,建立目标尺寸的矢量方程(1),这样目标尺寸与工序尺寸的数学模型就建立了.
| $\left. \begin{array}{*{35}{l}} E{{A}_{1}}=E{{A}_{1}}, \\ E{{B}_{1}}=E{{A}_{1}}+{{A}_{1}}{{B}_{1}}, \\ {{B}_{1}}{{C}_{1}}={{B}_{1}}{{C}_{1}}, \\ E{{D}_{1}}=E{{A}_{1}}+{{A}_{1}}{{B}_{1}}+{{B}_{1}}{{C}_{1}}+{{C}_{1}}{{D}_{1}}. \\ \end{array} \right]$ | (1) |
平面孔系一般在镗床上加工,后一孔以前一孔中心为基准进行加工,因此加工时需要准确地知道各孔中心的精确坐标值,即X和Y方向的坐标值.图 3所示的零件是镗孔加工,将矢量方程组(1)投影到X和Y轴方向,写成矩阵方程则分别为式(2)和式(3).
| $\left. \begin{array}{*{35}{l}} {{X}_{E{{A}_{1}}}}={{X}_{E{{A}_{1}}}}, \\ {{X}_{E{{B}_{1}}}}={{X}_{E{{A}_{1}}}}+{{X}_{{{A}_{1}}{{B}_{1}}}}, \\ {{X}_{{{B}_{1}}{{C}_{1}}}}={{X}_{{{B}_{1}}{{C}_{1}}}}, \\ {{X}_{E{{D}_{1}}}}={{X}_{E{{A}_{1}}}}+{{X}_{{{A}_{1}}{{B}_{1}}}}+{{X}_{{{B}_{1}}{{C}_{1}}}}+{{X}_{{{C}_{1}}{{D}_{1}}}}. \\ \end{array} \right]\Rightarrow \left| \begin{array}{*{35}{l}} {{X}_{E{{A}_{1}}}} \\ {{X}_{E{{B}_{1}}}} \\ {{X}_{{{B}_{1}}{{C}_{1}}}} \\ {{X}_{E{{D}_{1}}}} \\ \end{array} \right|=\left| \begin{array}{*{35}{l}} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ \end{array} \right|\left| \begin{array}{*{35}{l}} {{X}_{E{{A}_{1}}}} \\ {{X}_{{{A}_{1}}{{B}_{1}}}} \\ {{X}_{{{B}_{1}}{{C}_{1}}}} \\ {{X}_{{{C}_{1}}{{D}_{1}}}} \\ \end{array}. \right|$ | (2) |
| $\left. \begin{array}{*{35}{l}} {{Y}_{E{{A}_{1}}}}={{Y}_{E{{A}_{1}}}}, \\ {{Y}_{E{{B}_{1}}}}={{Y}_{E{{A}_{1}}}}+{{Y}_{{{A}_{1}}{{B}_{1}}}}, \\ {{Y}_{{{B}_{1}}{{C}_{1}}}}={{Y}_{{{B}_{1}}{{C}_{1}}}}, \\ {{Y}_{E{{D}_{1}}}}={{Y}_{E{{A}_{1}}}}+{{Y}_{{{A}_{1}}{{B}_{1}}}}+{{Y}_{{{B}_{1}}{{C}_{1}}}}+{{Y}_{{{C}_{1}}{{D}_{1}}}}. \\ \end{array} \right]\Rightarrow \left| \begin{array}{*{35}{l}} {{Y}_{E{{A}_{1}}}} \\ {{Y}_{E{{B}_{1}}}} \\ {{Y}_{{{B}_{1}}{{C}_{1}}}} \\ {{Y}_{E{{D}_{1}}}} \\ \end{array} \right|=\left| \begin{array}{*{35}{l}} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ \end{array} \right|\left| \begin{array}{*{35}{l}} {{Y}_{E{{A}_{1}}}} \\ {{Y}_{{{A}_{1}}{{B}_{1}}}} \\ {{Y}_{{{B}_{1}}{{C}_{1}}}} \\ {{Y}_{{{C}_{1}}{{D}_{1}}}} \\ \end{array}. \right|$ | (3) |
需要注意的是:坐标尺寸都是相对坐标,方向与右手笛卡尔坐标系方向相同.如矢量 EB1,与X轴正方向的夹角为αEB1=19°.根据三角函数关系,可得XEB1=EB1cos αEB1=104cos 19°=98.33 mm,YEB1=EB1sin αEB1=104sin 19°=33.85 mm;如果写成矢量 B1E ,与X轴正方向的夹角将是αB1E=199°,那XB1E=B1Ecos αB1E=104cos 199°=-98.33 mm,YB1E=B1Esin αB1E=104sin 199°=-33.85 mm.
根据矢量投影和三角函数公式,求解得4个目标尺寸 EA1,EB1,B1C1,ED1 的坐标尺寸分别为:XEA1=-13.92 mm,YEA1=99.03 mm;XEB1=98.33 mm,YEB1=33.85 mm;XB1C1=15 mm,YB1C1=-25.98 mm;XED1=83.86 mm,YED1=-54.46 mm.将其值代入矩阵方程组(2)和(3),得到4个工序尺寸的坐标值,再利用三角函数得到4个角度和工序尺寸的值,如表 1所示.
| 工序尺寸 | X 坐标 | Y坐标 | 与X轴角度 | 工序尺寸值 |
| EA1 | XEA1=-13.92 mm | YEA1=99.03 mm | αEA1=98° | EA1=100 mm |
| A1B1 | XA1B1=112.25 mm | YA1B1=-65.17 mm | αA1B1=330° | A1B1=129.8 mm |
| B1C1 | XB1C1=15 mm | YB1C1=-25.98 mm | αB1C1=300° | B1C1=30 mm |
| C1D1 | XC1D1=-29.47 mm | YC1D1=-62.33 mm | αC1D1=295° | C1D1=68.96 mm |
从以上路径图所建立的尺寸模型求解坐标尺寸的过程可以看出,相比传统的尺寸链来说,除了避免绘制尺寸链图和进行增减环判断外,可以一次求解得到所有具有方向性的坐标尺寸,这将有利于孔加工的计算机编程计算.
3.3 公差的计算 3.3.1 尺寸公差的计算在方程组(1)中,目标尺寸 ED1 所包含的相关工序尺寸最多,其精度要求最不易满足,应最先分配其相关工序尺寸的公差.运用微分学原理和公差为绝对值的特点[10],有$T\left( N \right)=\sum\limits_{i=1}^{n=1}{\left| \frac{\partial f}{\partial {{A}_{1}}} \right|}\times T\left( {{A}_{i}} \right)$,其中Ai是用三角函数或者弧度表示的角度尺寸.由于 ED1=EA1+A1B1+B1C1+C1D1,则有
| $\begin{align} & T\left( E{{D}_{1}} \right)=\left| \frac{\partial E{{D}_{1}}}{\partial E{{A}_{1}}} \right|T\left( E{{A}_{1}} \right)+\left| \frac{\partial E{{D}_{1}}}{\partial {{A}_{1}}{{B}_{1}}} \right|T\left( {{A}_{1}}{{B}_{1}} \right)+ \\ & \left| \frac{\partial E{{D}_{1}}}{\partial {{B}_{1}}{{C}_{1}}} \right|T\left( {{B}_{1}}{{C}_{1}} \right)+\left| \frac{\partial E{{D}_{1}}}{\partial {{C}_{1}}{{D}_{1}}} \right|T\left( {{C}_{1}}{{D}_{1}} \right). \\ \end{align}$ |
根据等精度法补充方程:
| $\frac{T\left( E{{A}_{1}} \right)}{\sqrt[3]{E{{A}_{1}}}}=\frac{T\left( {{A}_{1}}{{B}_{1}} \right)}{\sqrt[3]{{{A}_{1}}{{B}_{1}}}}=\frac{T\left( {{B}_{1}}{{C}_{1}} \right)}{\sqrt[3]{{{B}_{1}}{{C}_{1}}}}\frac{T\left( {{C}_{1}}{{D}_{1}} \right)}{\sqrt[3]{{{C}_{1}}{{D}_{1}}}},$ |
代入已知值求解:T(EA1)= 0.136 mm,T(A1B1)=0.148 mm,T(B1C1)=0.09 mm,T(C1D1)=0.12 mm.由于EA12=XEA12+YEA12,对其全微分:2 |EA1| dEA1=2| XEA1| dXEA1+2 |YEA1 |dYEA1,各自的微分近似公差:
| $\left| E{{A}_{1}} \right|T\left( E{{A}_{1}} \right)=\left| XE{{A}_{1}} \right|T\left( XE{{A}_{1}} \right)+\left| YE{{A}_{1}} \right|T\left( YE{{A}_{1}} \right).$ |
在同一镗床加工,误差条件相似,
| $T\left( XE{{A}_{1}} \right)=T\left( YE{{A}_{1}} \right)=\frac{\left| E{{A}_{1}} \right|T\left( E{{A}_{1}} \right)}{\left| XE{{A}_{1}} \right|\left( YE{{A}_{1}} \right)},$ |
求解得:T(XEA1)=T(YEA1)=0.12 mm.同理求得: T(XA1B1)=T(YA1B1)=0.1 mm,T(XB1C1)=T(YB1C1)=0.066 mm,T(XC1D1)=T(YC1D1)= 0.09 mm. 由于各孔在同一台镗床 加工取公差最小值作为当前坐标尺寸的公差,即T(XEA1)=T(YEA1)=T(XA1B1)=T(YA1B1)=T(XB1C1)=T(YB1C1)=T(XC1D1)=T(YC1D1)=0.066 mm.
3.3.2 角度公差的计算由于目标尺寸 ED1=EA1+A1B1+B1C1+C1D1 所包含的相关尺寸最多,根据$T\left( N \right)=\sum\limits_{i=1}^{n=1}{\left| \frac{\partial f}{\partial {{A}_{1}}} \right|}\times T\left( {{A}_{i}} \right)$,其角度公差为
| $\begin{align} & T\left( {{a}_{E{{D}_{1}}}} \right)=\left| \frac{\partial {{a}_{E{{D}_{1}}}}}{\partial {{a}_{E{{A}_{1}}}}} \right|T\left( {{a}_{E{{A}_{1}}}} \right)+\left| \frac{\partial {{a}_{E{{D}_{1}}}}}{\partial {{a}_{{{A}_{1}}{{B}_{1}}}}} \right|T\left( {{a}_{{{A}_{1}}{{B}_{1}}}} \right)+ \\ & \left| \frac{\partial {{a}_{E{{D}_{1}}}}}{\partial {{a}_{{{B}_{1}}{{C}_{1}}}}} \right|T\left( {{a}_{{{B}_{1}}{{C}_{1}}}} \right)+\left| \frac{\partial {{a}_{E{{D}_{1}}}}}{\partial {{a}_{{{C}_{1}}{{D}_{1}}}}} \right|T\left( {{a}_{{{C}_{1}}{{D}_{1}}}} \right). \\ \end{align}$ |
根据等公差法补充方程:
T(aEA1)=T(aA1B1)=T(aB1C1)=T(aC1D1),代入T(aED1)=2°及相关数值,求解得:T(aEA1)=T(aA1B1)=T(aB1C1)=T(aC1D1)=0.693°=0.012 rad.角度公差分解到坐标尺寸上的公差为[10]${{T}_{LY}}=\frac{L}{\left| \cos a \right|+\left| \sin a \right|}{{T}_{a}}.$. 将以上数值代入求解得:T(XEA1)=T(YEA1)=1.07 mm,T(XA1B1)=T(YA1B1)=1.14 mm,T(XB1C1)=T(YB1C1)=0.258 mm,T(XC1D1)=T(YC1D1)=0.628 mm.同样各孔在同一镗床上加工,取最小值为当前坐标尺寸公差,T(XEA1)=T(YEA1)=T(XA1B1)=T(YA1B1)=T(XB1C1)=T(YB1C1)=T(XC1D1)=T(YC1D1)=0.258 mm.
3.3.3 小 结当设计尺寸既有尺寸公差又有角度公差时,需考虑其各自对工序尺寸公差的影响.按照公差确定原则,取计算所得值中的较小者作为当前坐标尺寸公差,因此本例中坐标尺寸的公差为T(XEA1)=T(YEA1)=T(XA1B1)=T(YA1B1)=T(XB1C1)=T(YB1C1)=T(XC1D1)=T(YC1D1)=0.066 mm.
综上,整个孔系零件的加工工艺路线及坐标尺寸和公差如表 2所示.
| 工序号 | 工序 | 基准孔 | 加工孔 | 工序尺寸 | 坐标尺寸及公差 |
| 工序5 | 粗镗 | E | A1 | EA1=100 | XEA1=-3.92±0.033,YEA1=99.03±0.033 |
| 工序10 | 粗镗 | A1 | B1 | A1B1=129.8 | XA1B1=112.25±0.033,YA1B1=-65.17±0.033 |
| 工序15 | 粗镗 | B1 | C1 | B1C1=30 | XB1C1=15±0.033,YB1C1=-25.98±0.033 |
| 工序20 | 粗镗 | C1 | D1 | C1D1=68.96 | XC1D1=-29.47±0.033,YC1D1=-62.33±0.033 |
与传统的孔系尺寸的计算相比,本文所建立的工艺尺寸路径图可描述孔的加工顺序和加工基准,可建立所有尺寸的全相关的数学模型;由尺寸模型能一次求解得到所有具有方向性的坐标尺寸,能更简便地用全微分法对尺寸模型进行公差求解,特别适合复杂孔系零件的计算机辅助编程设计与计算,应用前景广阔.
| [1] |
王伯平,朱建儒,李萍,等.简化平面尺寸链公差计算的方法[J].太原重型机械学院学报,1999,20(4):331-336. WANG Bo-ping,ZHU Jian-ru,LI Ping,et al.A computing method of simplifying tolerance in plane size chain[J].Journal of Taiyuan Heavy Machinery Institute,1999,20(4):331-336. |
| Click to display the text | |
| [2] |
石一民.平面孔系坐标尺寸精度的计算[J].浙江海洋学院学报(自然科学版),2002,21(2):191-194. SHI Yi-min.Calculation of coordinate's dimensional tolerance between the plane holes[J].Journal of Zhejiang Ocean University (Natural Science),2002,21(2):191-194. |
| Click to display the text | |
| [3] |
王世伟,谭建荣,张树有.平面尺寸链的设计和反求[J].中国机械工程,2003,14(2):97-100. WANG Shi-wei,TAN Jian-rong,ZHANG Shu-you.Design and reverse of plane dimensional chain[J].China Mechanical Engineering,2003,14(2):97-100. |
| Click to display the text | |
| [4] | XUE J,JI P.Process tolerance allocation in angular tolerance charting[J].International Journal of Production Research,2004,42(18):3929-3945. |
| Click to display the text | |
| [5] |
安虎平,孟刚.箱体平行孔系加工的坐标法原理及保证加工精度的方法[J].机械研究与应用,2006,19(3):67-69. An Hu-ping,MENG Gang.The principle of coordinate algorithm for machining parallel holes in box parts and the methods of keeping its accuracy[J].Mechanical Research & Application,2006,19(3):67-69. |
| Click to display the text | |
| [6] | GONZALEZ C F,ROSADO P.An alternative method to tolerance transfer for parts with 2D blueprint[J].International Journal of Production Research,2007,45(22):5309-5328. |
| Click to display the text | |
| [7] |
胡志敏,黄美发,钟艳如,等.基于尺寸链图形理论的公差计算方法[J].机械设计与制造,2007(12):106-108. HU Zhi-min,HUANG Mei-fa,ZHONG Yan-ru,et al.A tolerance calculation method based on the graphic of dimensional chain[J].Machinery Design & Manufacture,2007(12):106-108. |
| Click to display the text | |
| [8] |
吴如恩,王晓慧.尺寸式在平面孔系计算中的应用[J].机械工程与自动化,2009(2):181-184. WU Ru-en,WANG Xiao-hui.Application of dimensional formula in calculation of plane holes[J].Mechanical Engineering & Automation,2009(2):181-184. |
| Click to display the text | |
| [9] |
阎艳,余美琼,王国新,等.平面尺寸链公差分析算法研究[J].北京理工大学学报(自然科学版),2011,31 (7):799-802. YAN Yan,YU Mei-qiong,WANG Guo-xin,et al.Study on tolerance analysis algorithm of planar dimension chain[J].Journal of Beijing Institute of Technology (Natural Sciences Edition),2011,31 (7):799-802. |
| Click to display the text | |
| [10] |
杜官将.基于全微分法的平面尺寸链求解[J].南京工程学院学报(自然科学版),2007,5(4):23-28. DU Guan-jiang.Solution to planar dimension chains based on differentiation[J].Journal of Nanjing Institute of Technology (Natural Science Edition),2007,5(4):23-28. |
| Click to display the text |



