应力场强法[1, 2, 3]能考虑应力峰值点的应力梯度及其周围的应力应变场和多轴应力的影响,从而对金属缺口试件取得了好于局部应力应变法[4, 5, 6]与名义应力法[7, 8, 9]的疲劳寿命预测结果.其认为缺口局部损伤区域是以危险点为球心的球形区域,场径R即是球半径,对球形区域内各点应力分布情况进行某种处理得到场强计算结果,因此应力场强法对于疲劳寿命预测的准确性依赖于球形区域大小即场径R的确定.目前,对于场径的确定存在争议:文献[1]中的确定方法是通过试验获得某缺口件的疲劳极限σ-1d,并在此疲劳极限载荷下对缺口件进行应力分析,认为缺口根部应力场强应与光滑试件的疲劳极限σ-1相同,由此反推出场径大小,并且认为场径只由材料种类决定;文献[3]确定方法与文献[1]大致相同,区别在于缺口试件的疲劳极限σ-1d在不同应力集中系数下是不同的,对于不同的疲劳极限σ-1d按上述方法进行分析,结果表明场径并非为材料常数,而是与缺口应力集中系数具有很强的线性关系;文献[10]介绍的确定方法是,由缺口试件的疲劳寿命与同种材料光滑试件S—N曲线得出该寿命下的应力水平σ′,对缺口试件进行有限元分析,取不同场径计算缺口处应力场强值σfi,绘出应力场强场径曲线,取σ′=σfi时的场径即为所求.上述文献对于场径确定方法给出了具体的求取步骤,但都缺乏理论支撑,不能证明所求出的场径值是合理的场径值.同时,如文献[1]和[3] 所述方法只单独考虑了在应力比r′=-1时的疲劳极限作用,实际中缺口构件所受循环交变载荷多样,并不可能只维持在r′=-1的状态,那么按照所述方法求出的场径并不能代表在实际载荷条件下的场径.综上所述,本文对场径R确定方法的理论依据与任意载荷状态下R的确定方法进行研究,分析影响R大小的因素,并通过实例对R的确定方法进行验证.
1 应力场强法基本理论应力场强法[1]定量考虑了材料性能、缺口根部的最大应力、缺口附近的应力梯度、应力应变状态等,提出以应力场强σfi作为局部区域疲劳损伤的控制参量,有
| ${{\sigma }_{fi}}={{\frac{1}{V}}_{\Omega }}f\left( {{\sigma }_{ij}} \right)\phi \left( r \right)\text{d}\upsilon ,$ | (1) |
式中:Ω为局部损伤区域,是以应力峰值点为球心、半径(场径)为R的球形区域;r为损伤区域内任意点到应力峰值点的距离;V为Ω的体积;f(σij)为等效应力函数(对韧性材料而言);$\phi $(r)为权函数,在物理上表征损伤区域内各点对材料损伤贡献,常见表达式为
$\phi \left( r \right)=1-\left| \frac{1}{{{\sigma }_{\max }}}\cdot \frac{\text{d}\sigma }{\text{d}r} \right|r\left( 1+\sin \theta \right),$
(2)
式中: $\frac{\text{d}\sigma }{\text{d}r}$为损伤区域内各点应力梯度,θ为损伤区域内各点基于应力峰值点的方向角.
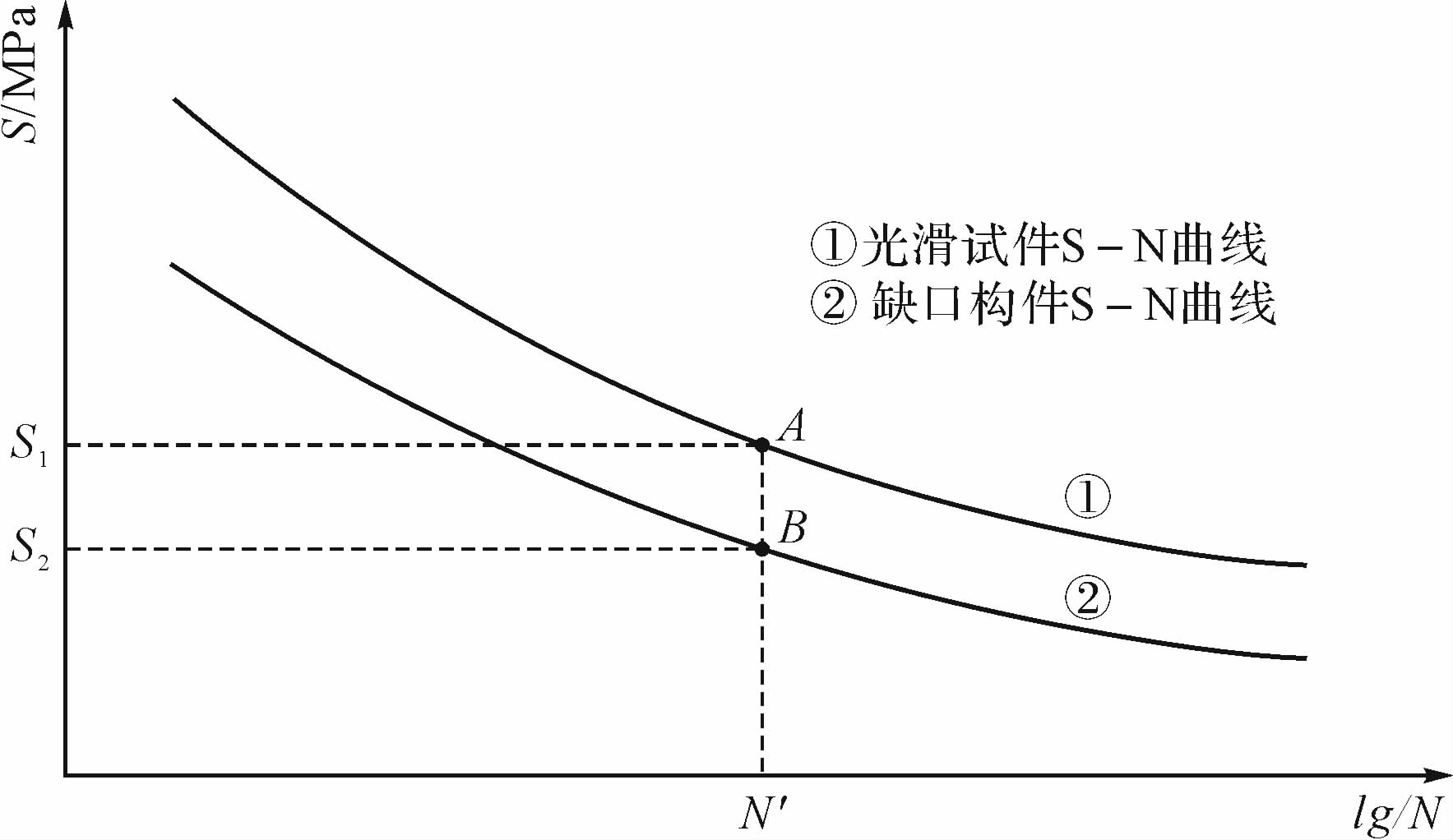
2 场径R确定方法 2.1 场径R确定的理论依据如图 1所示的光滑试件与缺口构件的S—N曲线,分别满足公式(3)、(4):
|
| 图 1 光滑试件与缺口构件S—N曲线 Fig. 1 S—N curve of smooth specimen and notch specimen |
| ${{S}^{{{a}_{1}}}}N={{C}_{1}},$ | (3) |
| ${{S}^{{{a}_{2}}}}N={{C}_{2}},$ | (4) |
取光滑试件与缺口试件为相同寿命N′,分别交于图 1中光滑试件与缺口构件S—N曲线于A,B两点,由A,B两点的纵坐标得到:光滑试件应力水平为S1,缺口构件应力水平为S2.带入S1对光滑试件进行应力场分析,带入S2对缺口构件进行应力场分析,依据应力场强法处理应力场分析结果,计算出光滑试件与缺口构件的应力场强值σfig,σfiq.根据应力场强法中“若缺口根部的应力场强度历程与光滑试件应力场强度的历程相同,则两者具有相同寿命”的假定,现光滑试件与缺口构件寿命相同为N′,反推出两者应具有相同的应力场强历程,即
| $\sigma _{fi}^{\text{g}}=\sigma _{fi}^{\text{q}},$ | (5) |
光滑试件应力集中系数kt=1,因此光滑试件应力及应力场强等于所受应力水平,即:σfig=S1.
对于缺口构件,在应力场强计算过程中,设定不同的场径R计算σfiq,直至满足等式(5),此时场径R即为所求.
2.2 场径R确定的实际方法依据描述,计算场径R需知光滑试件与缺口构件的S—N曲线,其中光滑试件的S—N曲线可从材料疲劳性能手册上获得,但缺口构件的S—N曲线是由应力集中系数、应力比、平均应力、载荷加载方式共同决定的,实际上难以花大量的人力与物力去测定某种具体缺口形式在特定载荷条件下的缺口构件S—N曲线.因此,采用文献[3]中场径的求取思路,但区别于文献[3]的是认为缺口构件在实际中载荷状态多变,应力比r′=-1仅仅是其中一个特殊的载荷状态.具体确定方法是:通过试验或理论计算求取缺口构件在其对应应力集中系数kt、应力比r′下的疲劳极限σr′d(平均应力对于疲劳极限的影响可由应力比代替),在此疲劳极限载荷σr′d作用下对缺口件进行应力分析,取不同的场径R计算缺口根部应力场强σfiq.依据上节所述的理论依据,只要某一场径R使得σfiq与光滑试件在相同应力比r′下的疲劳极限σr′相等,即
| $\sigma _{fi}^{\text{q}}={{\sigma }_{{{r}^{\prime }}}},$ | (6) |
σfiq=σr′, 此时R就是缺口构件在对应应力集中系数kt、应力比r′下的场径,即在其相应载荷状态下的场径.
3 影响场径R大小因素的分析选取6块应力集中系数不同的缺口试件,在r′=-1,r′=0.02,r′=0.278,r′=0.6四种应力比下按照2.2节中所述方法求取场径,由最后所得场径结果对影响场径R大小的因素进行分析.
研究步骤:1)求取不同缺口试件在不同应力比r′下的疲劳极限(载荷加载方式为拉伸);2)带入疲劳极限对光滑试件与缺口构件进行应力场分析;3)缺口试件场径R的计算;4)场径R大小影响因素的分析.
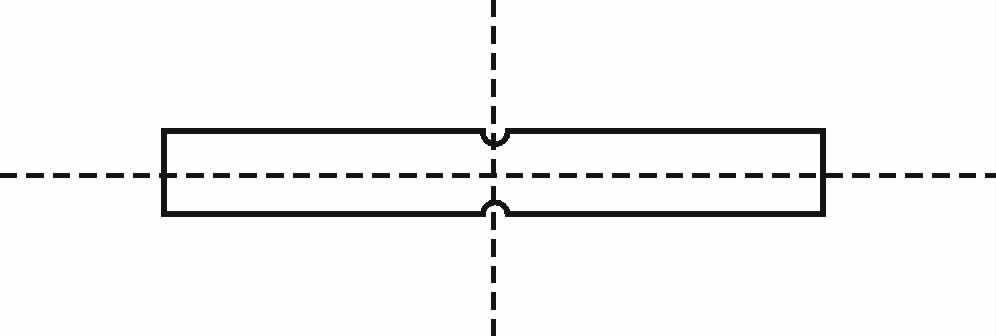
3.1 不同缺口试件在不同应力比r′下疲劳极限的求取现取材料为LY12-CZ 的6块双边U型缺口板条试件,图 2为缺口试件结构示意图,图 3为图 2的1/4示意图.表 1为缺口试件结构尺寸表.
|
| 图 2 双边缺口试件示意图 Fig. 2 Sketch map of double edge notched specimen |

|
| 图 3 缺口试件1/4示意图 Fig. 3 1/4 sketch map of notch specimen |
| 试件编号 | 板件高度 H/mm | 板件宽度 B/mm | 缺口半径 R′/mm | 缺口深度h/mm |
| 1 | 15 | 100 | 5 | 5 |
| 2 | 15 | 100 | 3 | 5 |
| 3 | 15 | 100 | 2 | 5 |
| 4 | 15 | 100 | 1.5 | 5 |
| 5 | 15 | 100 | 1 | 5 |
| 6 | 15 | 100 | 0.75 | 5 |
每块试件的应力集中系数kt不同,依照理论应力集中系数的有限元求法[11],求出6块试件各自的应力集中系数.同时通过文献[12]查出或插值得到6块试件在r′=-1的疲劳极限σ-1d,如表 2.
| 试件编号 | 理论应力集中系数kt | 疲劳极限 σ-1d/MPa |
| 1 | 2.25 | 66.24 |
| 2 | 2.75 | 60.88 |
| 3 | 3.26 | 53.86 |
| 4 | 3.67 | 47.94 |
| 5 | 4.41 | 39.01 |
| 6 | 5.02 | 35.89 |
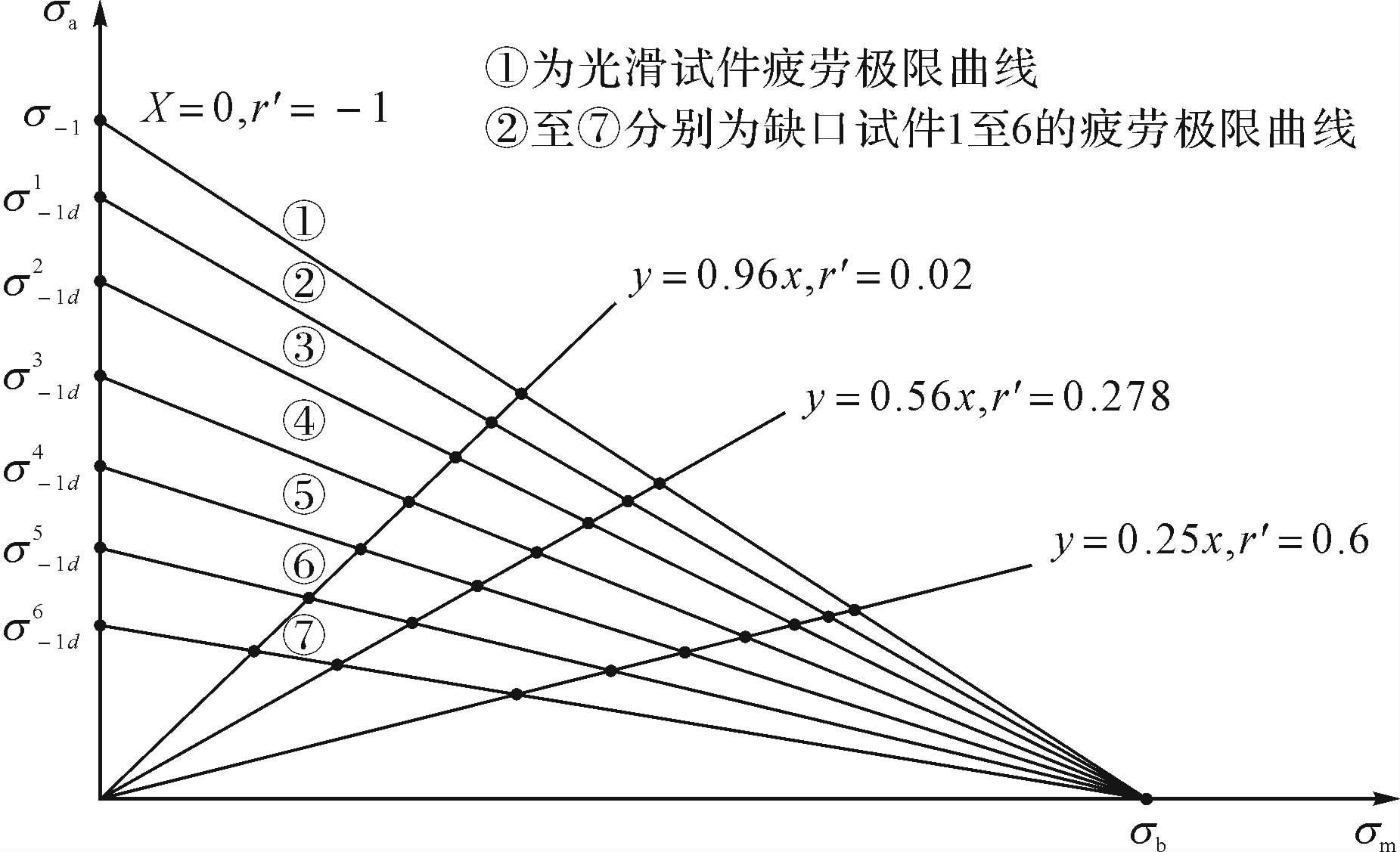
依据Goodman直线模型[13]估算不同缺口试件在不同应力比r′时的疲劳极限.由文献[14]查出光滑试件疲劳极限σ-1=137 MPa、强度极限σb=462 MPa.带入σ-1,σb与表 2中缺口试件疲劳极限σ-1d,作光滑试件与6块缺口试件各自的疲劳极限图,如图 4所示.由4种不同应力比r′,可作4条不同斜率的一次曲线,直线斜率为
| $k=\frac{{{\sigma }_{\text{a}}}}{{{\sigma }_{\text{m}}}}\text{=}\frac{{{\sigma }_{\max }}-{{\sigma }_{\min }}}{{{\sigma }_{\max }}-{{\sigma }_{\min }}}\text{=}\frac{1-{{r}^{\prime }}}{1+{{r}^{\prime }}}.$ |
|
| 图 4 光滑试件与缺口试件Goodman疲劳极限示意图 Fig. 4 Goodman fatigue limit diagram of smooth specimen and notch specimen |
每条一次曲线分别交①至⑦疲劳极限曲线于一点,这一点即表示了在当前应力集中系数、应力比r′下的应力状态(σm>,σa),进而确定疲劳极限,结果如表 3.
| MPa | ||||
| 试件编号 | 应力比r′ | |||
| -1 | 0.02 | 0.278 | 0.6 | |
| 1 | 66.24 | 117.63 | 146.36 | 210.49 |
| 2 | 60.88 | 109.25 | 136.74 | 199.31 |
| 3 | 53.86 | 98.02 | 123.67 | 183.64 |
| 4 | 47.94 | 88.26 | 112.19 | 169.37 |
| 5 | 39.01 | 73.17 | 94.01 | 145.80 |
| 6 | 35.89 | 67.75 | 87.39 | 136.88 |
| 光滑试件 | 137.0 | 213.21 | 248.53 | 313.37 |
试件为轴对称,因此选择试件的1/4进行仿真,在ANSYS仿真环境下按照图 3及表 1对试件建模,在试件缺口局部划分单元尺寸为0.03 mm的细致网格,如图 5所示.对模型左侧与下侧施加对称约束,模型右侧施加均布载荷即试件不同应力比r′下的疲劳极限σr′d,如图 6所示.试件有限元应力分析结果如图 7所示.

|
| 图 5 试件缺口处细致网格划分 Fig. 5 Detailed meshing at specimen gap |

|
| 图 6 缺口试件所受约束及载荷 Fig. 6 Constraint and load of notch specimen |

|
| 图 7 缺口试件等效应力云图 Fig. 7 Equivalent stress nephogram of notch specimen |
6块试件在4种应力比下共计得到24个应力分析结果.光滑试件kt=1,应力值是其疲劳极限值σr′.
3.3 缺口试件场径的计算结合应力场强定义式,公式(1)、(2)与APDL语言在ANSYS后处理程序中,编写程序处理所得应力场分析结果.对于缺口试件,取不同场径R计算应力场强σfiq,使得σfiq=σr′,R即为所求.例:如图 7所示为试件1在r′=0.02时带入其疲劳极限σ0.02d=117.63 MPa进行应力场分析所得结果,取R=0.59 mm使得试件1应力场强σfiq等于光滑试件在r′=0.02的疲劳极限σ0.02,即
| $\sigma _{fi}^{\text{q}}={{\sigma }_{0.02}}=213\text{MPa}.$ |
场径R具体计算结果见表 4.
| mm | ||||
| 试件编号 | 应力比r′ | |||
| -1 | 0.02 | 0.278 | 0.6 | |
| 1 | 0.28 | 0.59 | 0.72 | 0.95 |
| 2 | 0.26 | 0.55 | 0.69 | 0.87 |
| 3 | 0.24 | 0.51 | 0.60 | 0.76 |
| 4 | 0.22 | 0.45 | 0.53 | 0.68 |
| 5 | 0.20 | 0.34 | 0.42 | 0.56 |
| 6 | 0.18 | 0.31 | 0.37 | 0.51 |
1)应力集中系数kt对于场径R的影响.
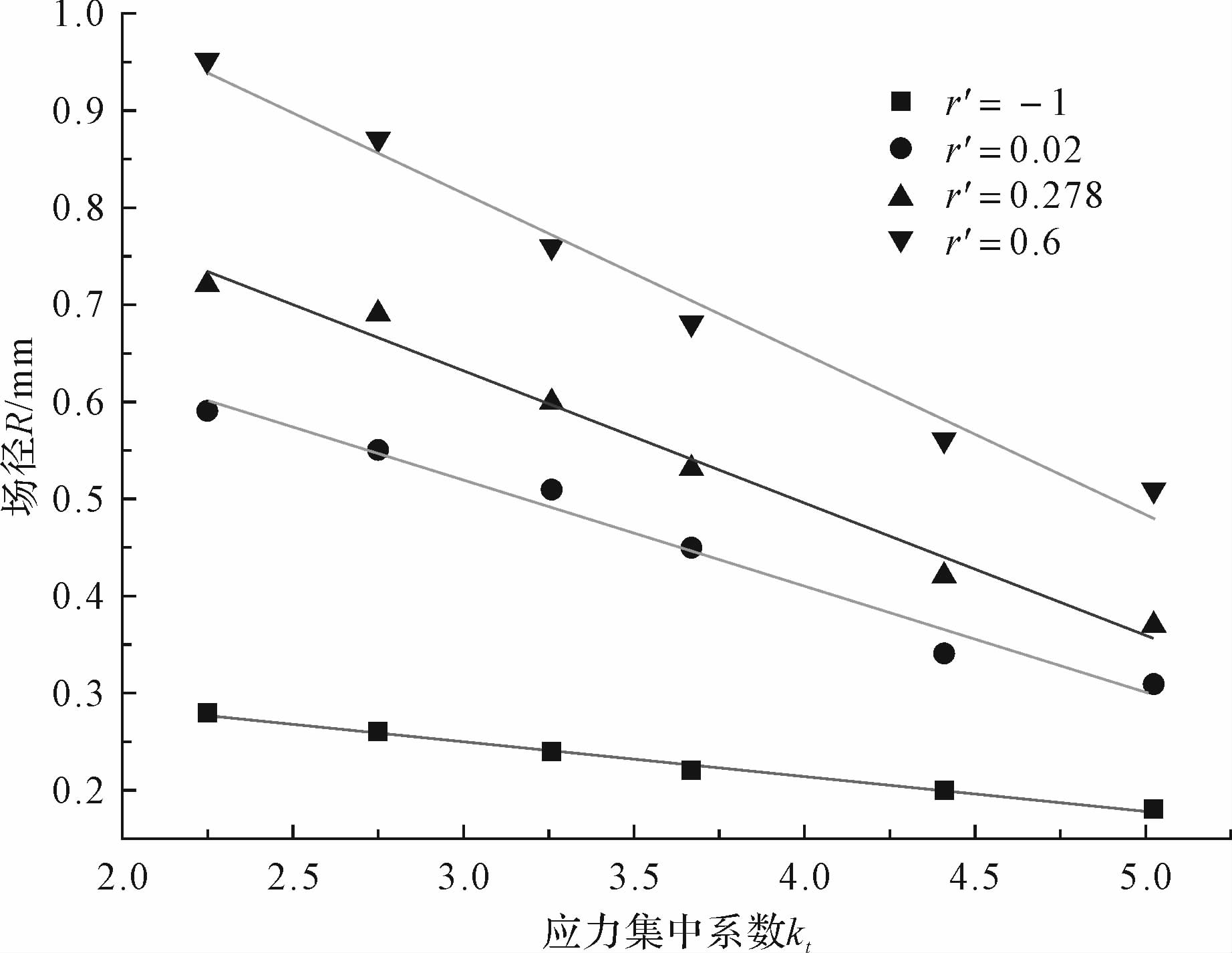
由表 4中数据,对相同应力比r′、不同应力集中系数kt下的场径进行线性拟合并作图,如图 8所示.观察图 8得出结论:在相同应力比r′下,场径值R与应力集中系数kt呈很强的线性关系且线性减小.结论与文献[2]结论是吻合的,同时与事实相符,原因是:当缺口变尖锐应力集中系数变大时,缺口根部附近的应力梯度变大,应力衰减变快,进入塑性的局部损伤场区域变小即场径R变小.
|
| 图 8 场径随应力集中系数的变化 Fig. 8 Variation of field size with stress concentration factor |
2)应力比r′对于场径R的影响.
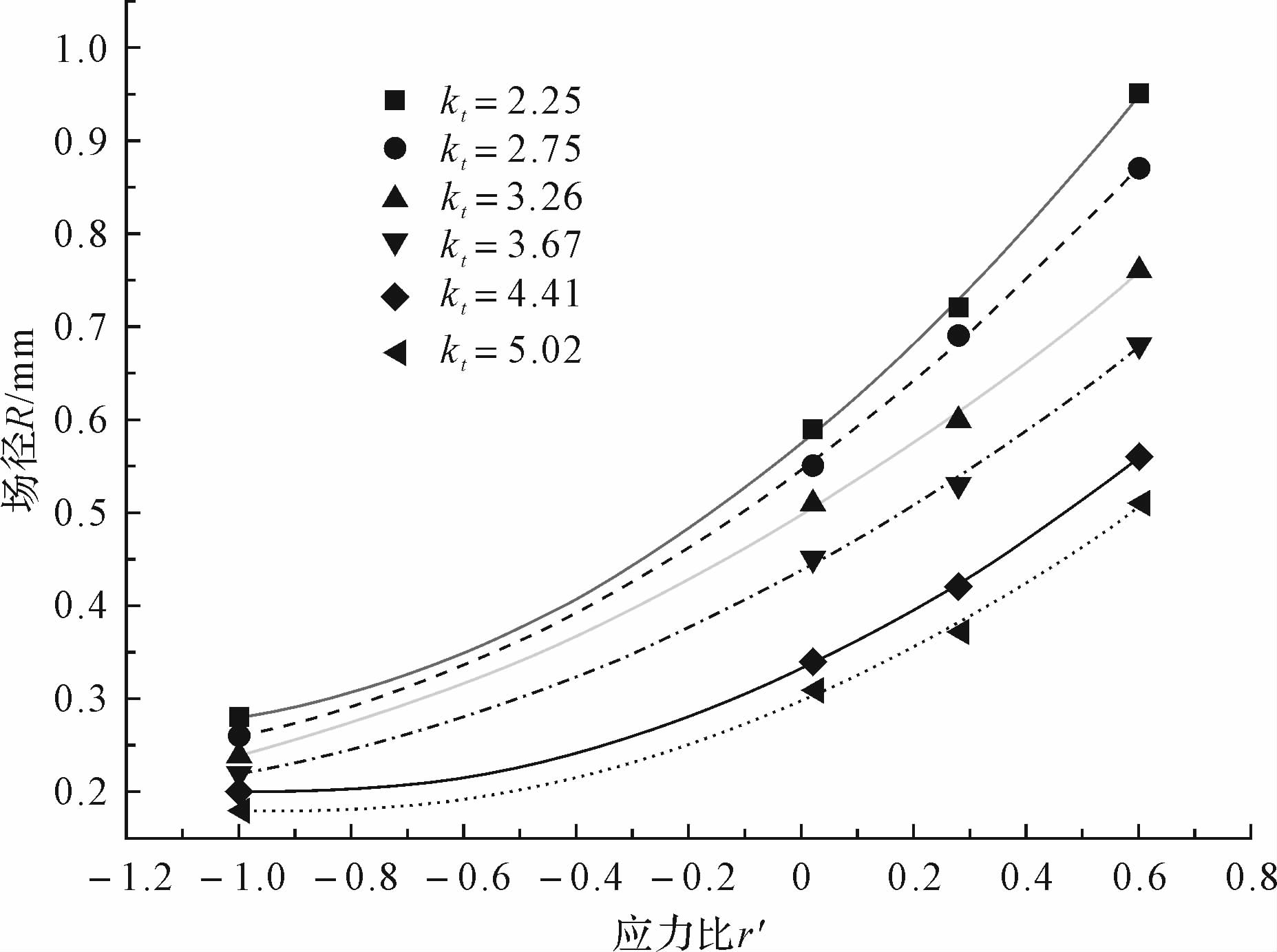
同理,对相同应力集中系数kt、不同应力比r′下的场径值进行二次多项式拟合并作图,如图 9所示.
|
| 图 9 场径随应力比的变化 Fig. 9 Variation of field size with stress ratio |
观察图 9得出结论:在相同应力集中系数kt下,场径R与应力比r′呈现很好的二次曲线关系且单调递增.当应力比逐渐增大,至最大r′=1时,构件受恒值载荷即静力加载.静力加载时,构件整个横截面共同承担载荷,应力均化,因而整个横截面都将成为损伤场,损伤半径即场径R会以较快的速度增大至整个截面的长度;当应力比逐渐减小,构件截面应力均化效果渐弱,构件截面局部区域先于截面其它位置进入塑性屈服状态,场径R同样会以较快的速度减小至塑性区的大小.因此,场径随应力比增大且呈现二次曲线式的较快速度增长是正确的.
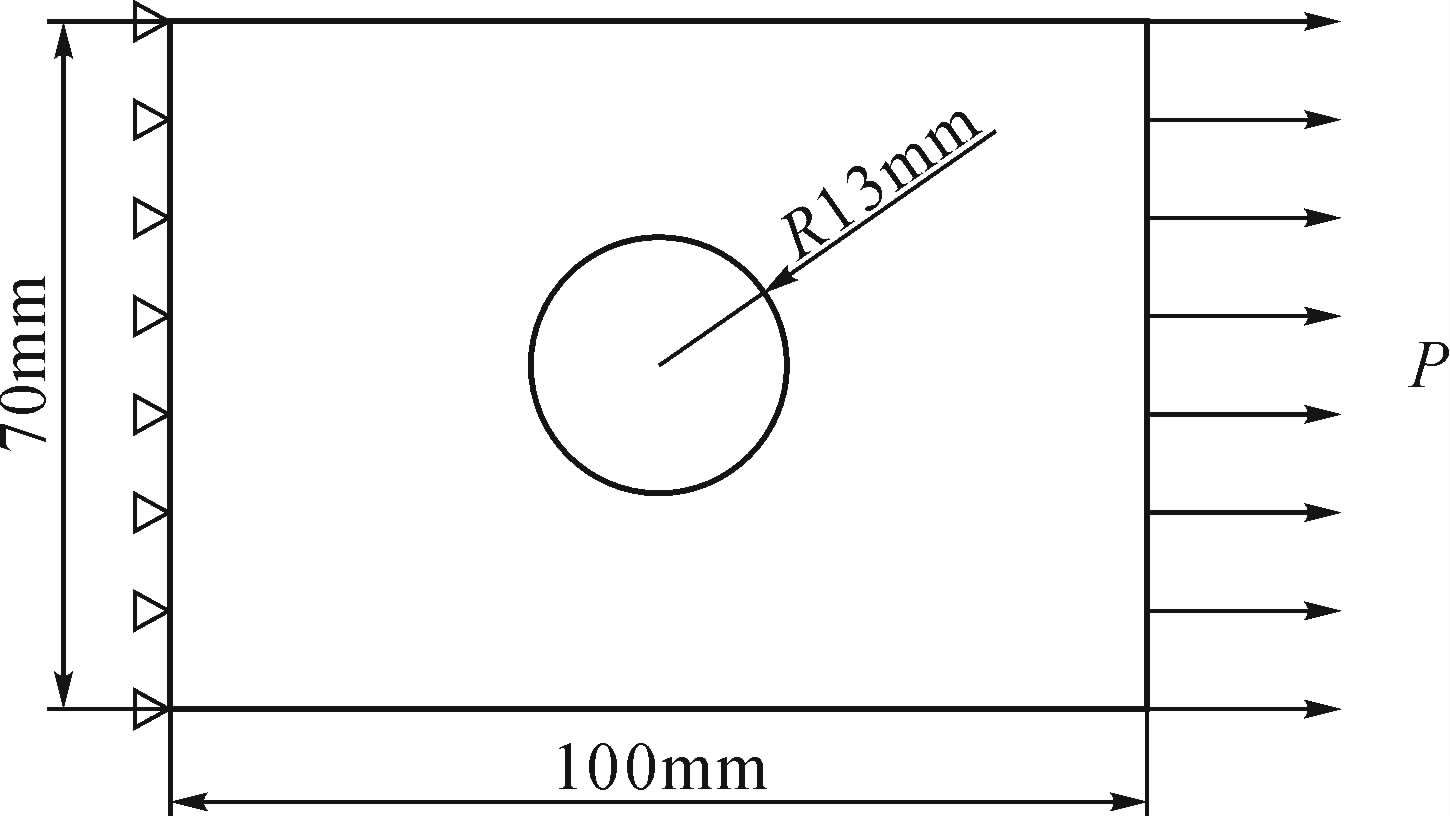
4 算 例算例参考文献[15]中带中心缺口孔平板,如图 10所示,其材料为LY12-CZ,构件模型左端固支,右端施加应力载荷80,150 MPa(即应力比r′=0),在ANSYS中进行应力场分析.采用原有场强法认为场径R=0.185 mm,文中方法计算出的场径R=0.53 mm,计算孔板原有场强、文中方法改进的场强及疲劳寿命.具体结果如表 5所示.
|
| 图 10 带中心孔平板模型 Fig. 10 Plate model with central hole |
| 载荷/ MPa | 最大 应力/ MPa | 原有 场强/ MPa | 改进 场强/ MPa | 原有 寿命/ 次 | 改进 寿命/ 次 | 试验 寿命/ 次 |
| 80 | 278.4 | 272.4 | 254.7 | 77 455 | 121 402 | 135 885 |
| 150 | 440.5 | 427.6 | 357.1 | 3 820 | 12 714 | 17 352 |
对比表中数据可见:采用文中方法计算出的场径而算出的疲劳寿命更接近于试验寿命且小于试验寿命.在保证安全的基础上提高了疲劳寿命预测的准确性.
5 结 论1)依据应力场强法假设,为场径R的确定方法提供了理论依据,并提出一种缺口试件在任意载荷状态下求取场径的方法.缺口试件在其相应应力集中系数kt、应力比r′的疲劳极限σr′d作用下进行应力场分析,取不同场径R计算缺口试件应力场强σfiq,使σfiq等于光滑试件在相同应力比下的疲劳极限σr′,R即为所求.
2)依据对场径计算结果的分析,得出结论如下:在相同应力比下,场径R的大小与应力集中系数呈很强的线性关系;在相同应力集中系数下,场径R的大小与应力比呈很强的二次曲线关系.
3)通过算例的验证,计算结果表明:由文中方法确定的场径R计算得出的疲劳寿命更贴近于试验寿命且小于试验寿命,在保证安全的基础上提高了预测的准确性.
| [1] |
姚卫星.金属材料疲劳行为的应力场强法描述[J].固体力学学报,1997,18(1):38-48. YAO Wei-xing.Metal material fatigue behavior description of the stress field intensity method[J].Acta Mechanica Solida Sinica,1997,18(1):38-48. |
| Click to display the text | |
| [2] |
郭海丁,武奇.基于场强法的平板法兰角焊缝接头的疲劳寿命估算方法[J].航空动力学报,2008,23(6):1082-1086. GUO Hai-ding,WU Qi.Way to evaluate fatigue life of fillet weld of plate with flange based on stress field intensity[J].Journal of Aerospace Power,2008,23(6):1082-1086. |
| Click to display the text | |
| [3] |
尚德广,王大康,李明,等.随机疲劳寿命预测的局部应力应变场强法[J].机械工程学报,2002,38(1):67-70. SHANG De-guang,WANG Da-kang,LI Ming,et al.Random fatigue life prediction of local stress-strain field intensity method[J].Chinese Journal of Mechanical Engineering,2002,38(1):67-70. |
| Click to display the text | |
| [4] |
熊伟红,向晓东,喻青.基于局部应力应变法的桥式起重机用钢丝绳疲劳寿命估算[J].机械科学与技术,2015,34(1):47-50. XIONG Wei-hong,XIANG Xiao-dong,YU Qing.Fatigue life prediction of bridge crane wire rope based on local stress-strain method[J].Mechanical Science and Technology for Aerospace Engineering,2015,34(1):47-50. |
| Click to display the text | |
| [5] |
周炜,周鋐,冯展辉.应用局部应力-应变法估算机械疲劳寿命[J].同济大学学报(自然科学版),2001,29(8):928-931. ZHOU Wei,ZHOU Hong,FENG Zhan-hui.Use of local stress-strain method in fatigue life prediction of grab bucket conveyer[J].Journal of Tongji University (Natural Science),2001,29( 8):928-931. |
| Click to display the text | |
| [6] |
聂宏,常龙.基于局部应力应变法估算高周疲劳寿命[J].南京航空航天大学学报,2000,32(1):75-79. NIE Hong,CHANG Long.High-cycle fatigue life prediction of local stress-strain method[J].Journal of Nanjing University of Aeronautics & Astronautics,2000,32(1):75-79. |
| Click to display the text | |
| [7] |
安刚,龚鑫茂.随机振动环境下结构的疲劳失效分析[J].机械科学与技术,2000,19(S1):40-42. AN Gang,GONG Xin-mao.The fatigue failure analysis of the structure under random vibration environment[J].Mechanical Science and Technology for Aerospace Engineering,2000,19(S1):40-42. |
| Click to display the text | |
| [8] |
李德勇,姚卫星.缺口件振动疲劳寿命分析的名义应力法[J].航空学报,2011,32(11):2036-2041. LI De-yong,YAO Wei-xing.Nominal stress approach for life prediction of notched specimens under vibration loading[J].Acta Aeronautica et Astronautica Sinica,2011,32(11):2036-2041. |
| Click to display the text | |
| [9] |
郑立春,姚卫星.疲劳裂纹形成寿命预测方法综述[J].力学与实践,1996,18(4):10-15. ZHENG Li-chun,YAO Wei-xing.Review of fatigue crack initiation life prediction methods[J].Mechanics in Engineering,1996,18(4):10-15. |
| Click to display the text | |
| [10] |
郭平,陈波华,都昌兵.基于场强法的燃烧室机匣后衬套安装座疲劳寿命预测[J].航空发动机,2011,37(6):36-39. GUO Ping,CHEN Bo-hua,DU Chang-bin.Based on the approach of field intensity combustion chamber for bushing after installation of the fatigue life prediction[J].Journal of Aircraft Engine,2011,37(6):36-39. |
| Click to display the text | |
| [11] |
董志航,廖志忠.理论应力集中系数的有限元求法[J].航空兵器,2005,2(3):15-18. DONG Zhi-hang,LIAO Zhi-zhong.Theoretical stress concentration factor of the finite element method[J].Aero Weaponry,2005,2(3):15-18. |
| Click to display the text | |
| [12] |
姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003:96-98. YAO Wei-xing.Fatigue life prediction of structures[M].Beijing:National Defense Industry Press,2003:96-98. |
| [13] |
李舜酩.机械疲劳与可靠性设计[M].北京:科学出版社,2006:62-63. LI Shun-ming.Mechanical fatigue and reliability design[M].Beijing:Science Press,2006:62-63. |
| [14] |
高镇同.航空金属材料疲劳性能手册[M].北京:北京航空材料研究所,1981:97-100. GAO Zhen-tong.Aviation metal material fatigue performance handbook[M].Beijing:National Defense Industry Press,1981:97-100. |
| [15] |
陈健,崔海涛,温卫东.基于应力场强法的缺口构件疲劳寿命预测方法研究[J].长春理工大学学报(自然科学版),2010,33(4):87-91. CHEN Jian,CUI Hai-tao,WEN Wei-dong.Study on notch specimen fatigue life prediction of stress field intensity method[J].Journal of Changchun University of Science and Technology (Natural Science Edition),2010,33(4):87-91. |
| Click to display the text |



