随着多相混合集输工艺的广泛应用,海洋立管系统中的多相流问题成为研究热点。海上油气开发中,原油介质多为油、气、水三相混合流体,当油气水三相流通过立管系统时,流体密度、压力等参数会发生变化,引起管道与流体的耦合振动。因此,在设计立管系统支承防护时,须充分考虑油气水三相流与立管系统的耦合振动效应[1]。
刘龙等[2]应用精细积分法分析了脉动流作用下黏弹性直管的动力学响应特性。柳贡民等[3]改进了输流直管与弯管的结构方程模型,研究了蒸汽参数对管路系统动力特性的影响。Omer等[4]考虑了流体和管道之间作用力的耦合作用,根据动量方程和连续性方程推导了管道输送流体横向振动的控制方程。林君哲等[5]采用牛顿法建立了管道在基础激励作用下非线性流固耦合振动数学模型。Chen等[6]提出了基于Steger-Warming矢量分解法的有限差分格式,解决了耦合水力瞬变数值计算的问题。Malekzadeh等[7]采用一维双流体模型,模拟了立管系统在恒定流入条件下,气液两相流发生严重段塞流时流体流动特性和压降变化情况。Bai等[8]将浮体惯性力和土反作用力纳入动平衡体系,建立了钢悬链立管在海洋环境下的动态响应模型,并利用Galerkin法求解了立管的动力学方程。马姗等[9]对气液固三相流在动力学环境中的流场变化情况进行了数值模拟。Binesh[10]和Liu等[11]等研究了弹性基础或弹性约束条件下构件的受力情况,并进行了数值模拟。王琳等[12-16]对段塞流或水击引起的管道耦合振动问题进行数值模拟,但是没有提出流体压强和流体作用力的计算方程,且没有分析流体压强与流体作用力之间的关系。
综上,国内外学者对液相、气液两相、气液固三相管道系统耦合振动问题的研究已取得不少可观的成果,但关于油气水三相立管系统耦合振动响应问题的研究相对较少。且当运用现有的模型进行油气水三相流立管系统耦合振动响应问题的研究时,存在计算精度不高等问题。
为此,针对文献[15]没有提出流体压强计算方程,文献[16]没有提出流体作用力计算方程, 笔者对现有的严重段塞流瞬态数学模型进行改进,建立耦合振动响应模型以模拟油气水三相流海洋立管系统在内部流体压强作用下的耦合振动响应过程。设计下倾管倾斜角度为3°的L型立管系统进行实验验证,并对改进模型与现有的严重段塞流瞬态数学模型的立管底部压强、立管底部位移计算结果进行比较。
1 油气水三相严重段塞流问题概述 1.1 油气水三相严重段塞流的产生水力输送被广泛应用于原油集输中,介质多为油气水三相流混合流体。当油气水三相流流量较小时,下倾管内气相和液相分层流动,液体在立管底部不断累积,堵塞在立管底部形成液塞,产生严重段塞流。典型段塞流在积液阶段、排液阶段、气液喷发阶段和液体回落阶段的密度分布云图如图 1所示[17]。由于立管内气体的可压缩性,使得严重段塞流产生的压力波逐渐衰减。
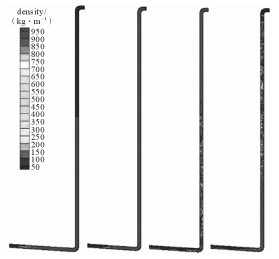
|
| 图 1 典型段塞流的密度分布云图 Fig.1 Density distribution cloud diagram of typical slug flow |
油气水三相流管道严重段塞流主要有以下3个特点:1)与纯液体管道相比,油气水三相流管道中流体介质主要为气液两相,其中液相包括油相和水相。产生严重段塞流时,油气水三相流管道中流体介质的运动状态比纯液体管道复杂,出现典型段塞流等流型变化情况;2)油气水三相流管道的严重段塞流问题的水力计算,不仅要考虑液相弹性模量的影响,还需考虑气相弹性模量的影响,且多相流体混合物的密度变化情况比纯液体复杂,需提出相应的计算方程;3)段塞流属于震荡流型,其波动幅度呈现先增大后减小的变化规律,立管弯头被液相周期性堵塞[18],造成立管底部压强的周期性波动。
1.3 油气水三相严重段塞流的影响多相流动使流体密度、压力等随时间变化,从而引发管道线密度发生改变,使得海洋立管产生振动或膨胀变形。立管的振动进一步引发立管内流体的振动,2个物理场的交互作用影响着立管、流体载荷的分布和大小,形成立管内油气水三相流体压力波动与立管结构之间的流固耦合现象。同时,受流固耦合作用的影响,管道发生膨胀变形,管道内外环断面湿周随着管道的变形发生改变,横截面也发生变化。
2 海洋立管耦合振动响应模型构建 2.1 油气水三相严重段塞流模型海洋油气工程中,原油的输送方式主要为管道水力输送,且流体介质多为油气水三相流。由于油相和水相为连续相,在立管发生水击时多相流体流型为典型段塞流,当折算气速足够大时,液塞区的含气率高,液膜区长度较长,气相对油水两相的湍流脉动力作用大于油水两相的重力作用,使油滴非常均匀地分散在连续的水相中。对于此类管输系统,可将管道内流体看作伪均质流,根据均相流理论来分析。假设油气水多相流各相间无质量传递,油气水三相均匀混合,多相流体充满管道内部而无空隙,且按多相混合均质流体构建模型。海洋立管的环形管道截面段塞流波速推导如图 2所示[15]。
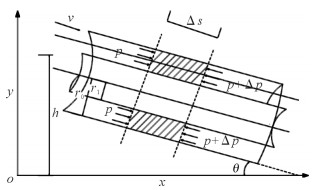
|
| 图 2 海洋立管环形管道截面段塞流波速推导示意图 Fig.2 Wave velocity deduction diagram of slug flow in the annular pipe cross section of marine riser |
1) 严重段塞流波速计算。
Δt时间内,严重段塞流压力波运动距离为:Δs= a·Δt,其中a为严重段塞流波速。在该段距离内,段塞流流速由v增至v+Δv,段塞流总压强由p增至p+Δp,段塞流密度由ρ增至ρ+Δρ。当Δt足够小时,段塞流密度为管道截面上的流体混合密度[19],计算公式为:
| $ \rho = {\rho _1} \cdot \left( {1 - \alpha } \right) + {\rho _{\rm{g}}} \cdot \alpha $ | (1) |
式中:ρ1为油水混合物密度,kg/m3;ρg为气体密度,kg/m3;α为截面含气率。
管道横截面积由A增至A+ΔA,流体质量由ρAvΔt增至(ρ+Δρ)(A+ΔA)(v+Δv)Δt,Δt时间内由压力波引起的流段内段塞流质量的增量为:
| $ \left( {\rho + \Delta \rho } \right)\left( {A + \Delta A} \right)a\Delta t - \rho Aa\Delta t = a\Delta \left( {\rho A} \right)\Delta t $ | (2) |
对式(2)进行整理, 有:
| $ \Delta \left( {\rho Av} \right) = - a\Delta \left( {\rho A} \right) $ | (3) |
由动量守恒定理得管道内动量变化量为:
| $ \begin{array}{*{20}{c}} {\left( {\rho + \Delta \rho } \right)\left( {A + \Delta A} \right)a\Delta t\left( {v + \Delta v} \right) - }\\ {\rho Aav\Delta t \approx \Delta \left( {\rho Av} \right)a\Delta t} \end{array} $ | (4) |
对Δs段上段塞流的受力情况进行分析,外力主要有:
压力差为:
| $ \rho A - \left( {p + \Delta p} \right)\left( {A + \Delta A} \right) \approx - \Delta \left( {pA} \right) $ | (5) |
重力为:
| $ G = \rho gA\Delta s\sin \theta $ | (6) |
摩擦阻力为:
| $ f = {\tau _{\rm{D}}}{x_{\rm{D}}}\Delta s + {\tau _{\rm{d}}}{x_{\rm{d}}}\Delta s $ | (7) |
式中:θ为管轴线与水平线的夹角,(°);G为段塞流流体所受重力,N;f为段塞流流体所受阻力,N; τD为外环内管壁摩擦切应力,
在Δt时间内外力的冲量为:
| $ \Delta t\left[ { - \Delta \left( {Ap} \right) + \rho gA\Delta s\sin \theta - {\tau _{\rm{D}}}{x_{\rm{D}}}\Delta s - {\tau _{\rm{d}}}{x_{\rm{d}}}\Delta s} \right] $ | (8) |
根据动量定理有:
| $ \begin{array}{*{20}{c}} { - \Delta \left( {Ap} \right) + \rho gA\Delta s\sin \theta - {\tau _{\rm{D}}}{x_{\rm{D}}}\Delta s - }\\ {{\tau _{\rm{d}}}{x_{\rm{d}}}\Delta s = \Delta \left( {\rho Av} \right)a} \end{array} $ | (9) |
对式(9)进行整理有:
| $ \begin{array}{l} \Delta p = \rho gA\Delta s\sin \theta - \frac{{{\tau _{\rm{D}}}{x_{\rm{D}}} + {\tau _{\rm{d}}}{x_{\rm{d}}}}}{A}\Delta s - \\ \;\;\;\;\;\;\;\frac{a}{A}\Delta \left( {\rho Av} \right) - \frac{{\Delta A}}{A}p \end{array} $ | (10) |
将式(4)代入式(10),有:
| $ \begin{array}{l} \Delta p = \rho gA\Delta s\sin \theta - \frac{{{\tau _{\rm{D}}}{x_{\rm{D}}} + {\tau _{\rm{d}}}{x_{\rm{d}}}}}{A}\Delta s + \\ \;\;\;\;\;\;\;\frac{{{a^2}}}{A}\Delta \left( {\rho A} \right) - \frac{{\Delta A}}{A}p \end{array} $ | (11) |
等式两边同时除以Δp,并取极限,整理得到严重段塞流波速a的计算公式为:
| $ a = \frac{{\sqrt {\frac{p}{A}\frac{{{\rm{d}}A}}{{{\rm{d}}p}} + 1 - \left( {\rho g\sin \theta - \frac{{{\tau _{\rm{D}}}{x_{\rm{D}}} + {\tau _{\rm{d}}}{x_{\rm{d}}}}}{A}} \right)/\frac{{\partial p}}{{\partial s}}} }}{{\sqrt {\rho \left( {\frac{1}{A}\frac{{{\rm{d}}A}}{{{\rm{d}}p}} + \frac{1}{\rho }\frac{{{\rm{d}}\rho }}{{{\rm{d}}p}}} \right)} }} $ | (12) |
2) 严重段塞流瞬时压强计算。
由式(12)计算得到严重段塞流波速,根据伯努利方程求严重段塞流瞬时压强,计算公式如下:
| $ {p_1} = \frac{1}{2}\rho {a^2} + \rho gh + c $ | (13) |
式中:h为段塞流铅锤高度,m;c为段塞流所得动能,J。
2.2 海洋立管结构动力学模型海洋立管悬跨在水中,受海洋环境的限制,悬跨段约束构件较少。因此,受内部流体压强的作用,极易引发立管结构动力响应。在油气水三相流立管系统中,内部的严重段塞流压强,形成对立管作用的外力。在外力作用下,立管不同质点产生位移,使立管发生振动。由于立管中流体由下往上传送,因此其压力波也由下往上传播。在内部流体压强波动影响下,与压力波传播方向平行的管道受影响更大,立管更容易发生上下振动。
发生严重段塞流问题时,立管受内部流体压强的作用发生振动,根据油气水三相严重段塞流模型得到严重段塞流压强,结合立管的受力情况,将严重段塞流压强转化为段塞流作用力进行分析。在xoy平面(见图 2)内,将立管系统简化为平面刚架,严重段塞流引起立管系统的振动采用阻尼振动微分方程进行描述[16]。
管道阻尼振动微分方程为:
| $ K\frac{{{\partial ^2}u\left( {x, t} \right)}}{{\partial {x^2}}} + \mu \frac{{\partial u\left( {x, t} \right)}}{{\partial t}} - m\frac{{{\partial ^2}u\left( {x, t} \right)}}{{\partial {t^2}}} = {F_1}\left( {x, t} \right) $ | (14) |
式中:K为立管刚度,N/m; u为立管位移, m; μ为阻尼系数; F1为立管所受外力, N。
忽略各流相间摩擦力,F1由流体和结构的重力、流体冲击力以及弹性基础的支反力组成,表达式为:
| $ {F_1}\left( {x, t} \right) = {G_{{\rm{1p}}}}\left( {x, t} \right) + {F_{{\rm{1p}}}}\left( {x, t} \right) + ku\left( {x, t} \right) $ | (15) |
| $ {F_{{\rm{1p}}}} = {P_1} \cdot {S_{\rm{p}}} $ | (16) |
式中:G1p为立管所受重力,N;F1p为流体作用力,N;k为弹性基础系数;Sp为立管单元面积,m2。
3 油气水三相流立管实验验证与结果分析 3.1 实验设备及参数设置油气水三相流立管实验设备如图 3所示。
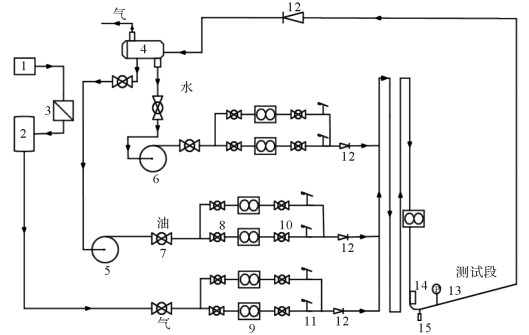
|
| 1—空气压缩机;2—稳压罐;3—过滤器;4—三相分离器;5—油泵;6—水泵;7,8,10—球阀;9—流量计;11—速开/关阀;12—止回阀;13—压力传感器;14—通径检测器;15—位移传感器 图 3 油气水三相流立管实验设备示意图 Fig.3 Sketch map of oil-gas-water three-phase flow riser experimental equipment |
实验参数取值情况见表 1。
| 参数 | 量值 |
| 管道外径 | 32 mm |
| 壁厚 | 2.5 mm |
| 管道密度 | 1 926 kg/m3 |
| 立管高度 | 3 m |
| 下倾管长度 | 5 m |
| 管道弹性模量 | 120 GPa |
| 倾斜角度 | 3° |
| 油水混合物流量 | 0.43 kg/s |
| 油水混合物密度 | 900 kg/m3 |
| 阻尼系数 | 0.012 |
| 油气水混合物弹性模量 | 2 000 MPa |
| 气体流量 | 2×10-4 kg/s |
| 气体摩尔质量 | 29 g/mol |
| 最大输送压力 | 1.5 MPa |
油气水多相流体介质为柴油、空气和自来水。实验过程中保持含油率为0.318,按气水体积比为1 :10进行实验。实验步骤为:1)按图 3所示安装布置实验设备,实验参数设置如表 1所示;2)校对测试系统,确保数据采集、传输、存储正常,实验采用TST5912动态信号测试分析系统, 避免数据的非实时同步采集影响精度,采样频率为100 HZ;3)油气水三相流分别采用油泵、空气压缩机和水泵进行泵送;4)采用开闭速开/关阀来改变管道内流体的运动状态,模拟严重段塞流现象;5)在立管系统发生耦合振动时,采集立管膨胀变形量、立管底部位移、立管底部压强等数据。为避免外部因素导致的偶然性误差对实验结果的影响,进行60~80 s的持续采样,并对数据进行周期性筛选,提取60组特征数据进行平均处理,确保数据的有效性和可靠性。
3.3 结果分析将实验测得的立管底部压强、立管底部位移等数据,与本文提出的立管耦合振动响应模型及文献[16]中基于理想气体状态方程、流体质量守恒方程和动量守恒方程建立的严重段塞流瞬态数学模型的计算值进行对比,如表 2、表 3所示。
| 序号 | 底部压强实测值/Pa | 底部压强计算值/Pa | 相对误差/% | 底部位移实测值/m | 底部位移计算值/m | 相对误差/% |
| 1 | 109 990 | 109 900 | -0.082 | -0.010 | -0.010 4 | 4.000 |
| 2 | 109 871 | 110 020 | 0.136 | -0.012 | -0.012 5 | 4.167 |
| 3 | 112 300 | 113 400 | 0.979 | -0.012 | -0.011 8 | -1.667 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 58 | 119 126 | 120 226 | 0.923 | -0.035 | -0.037 0 | 5.714 |
| 59 | 123 451 | 124 551 | 0.891 | -0.036 | -0.038 0 | 5.556 |
| 60 | 125 341 | 126 441 | 0.878 | -0.038 | -0.040 0 | 5.263 |
| 序号 | 底部压强实测值/Pa | 底部压强计算值/Pa | 相对误差/% | 底部位移实测值/m | 底部位移计算值/m | 相对误差/% |
| 1 | 109 990 | 106 910 | -2.800 | -0.010 | -0.013 | 30.000 |
| 2 | 109 871 | 120 220 | 9.419 | -0.012 | -0.015 | 25.000 |
| 3 | 112 300 | 120 400 | 7.213 | -0.012 | -0.016 | 33.333 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 58 | 119 126 | 129 326 | 8.562 | -0.035 | -0.347 | 8.571 |
| 59 | 123 451 | 135 551 | 9.801 | -0.036 | -0.041 | 13.889 |
| 60 | 125 341 | 146 541 | 16.914 | -0.038 | -0.045 | 18.421 |
表 2为立管耦合振动响应模型计算值与实测值的对比。经分析,立管底部压强计算值与实测值的平均相对误差为3.831%;立管底部位移计算值与实测值的平均相对误差为4.343%。表 3为严重段塞流瞬态数学模型计算值与实测值的对比。经分析,立管底部压强计算值与实测值的平均相对误差为19.421%;立管底部位移计算值与实测值的平均相对误差为25.153%。因此,本文提出的模型更适用于油气水三相流立管系统的耦合振动问题研究。
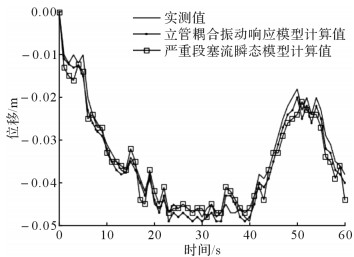
图 4为立管底部压强计算值与实测值的分布情况。由图 4可知:0—20 s,严重段塞流引起的耦合振动造成立管底部压强急剧增大,这对立管造成了巨大载荷,危害系统的安全性;20—40 s,立管底部压强增大趋势平稳,无剧烈波动;40—50 s,立管底部压强急剧减小,波动剧烈;50—60 s,立管底部压强由急剧减小到急剧增大的变化间隔时间短,易引发管道弯头处或其余管道薄弱段产生破裂,造成油气泄漏事故。图 5为立管底部位移计算值与实测值的分布情况。由图 5可知:0—5 s,立管底部位移呈现周期性波动;5—20 s,立管底部位移急剧减小,期间出现管道上下振动;20—40 s,立管降低到最低点附近,伴随有轻微振动;40—50 s,立管从最低点往上急剧升高,管道上下振动问题严重,这对管道部件可能造成极大损伤;50—55 s,立管上下往复振动;55—60 s,立管底部位移急剧减小。结合立管底部压强和立管底部位移的变化情况发现,压强和位移的变化周期基本一致。
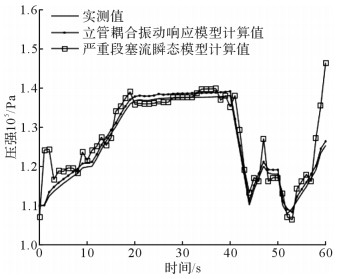
|
| 图 4 立管底部压强计算值与实测值 Fig.4 The calculated values and experimental values of pressure at the bottom of riser |
|
| 图 5 立管底部位移计算值与实测值 Fig.5 The calculated values and experimental values of displacement at the bottom of riser |
1) 立管耦合振动响应模型的底部压强计算值与实测值的平均相对误差为3.831%,底部位移计算值与实测值的平均相对误差为4.343%,相比于严重段塞流瞬态数学模型的计算结果,本文提出模型的精度更高。
2) 油气水三相严重段塞流引起海洋立管耦合振动时,立管底部压强与立管底部位移呈周期性变化。0—20 s,压强急剧增大,立管迅速降低;20—40 s,压强增大趋势平稳,立管降到最低点附近,并有轻微振动;40—50 s,压强急剧减小,立管迅速升高;50—60 s,压强急剧增大,立管迅速降低。底部压强和底部位移的变化周期基本一致。
3) 流体压强是使海洋立管系统发生耦合振动的关键因素,它通过形成对立管的流体作用力,使立管产生位移。随着流体压强的不断波动,立管的位移也不断变化。流体压强波动越剧烈,立管位移变化幅度越大;流体压强波动不剧烈,立管位移变化较平稳。
| [1] |
王琳, 李玉星, 胡其会, 等.
考虑弹性基础的气液两相流海洋立管耦合振动分析[J]. 中国石油大学学报(自然科学版), 2016, 40(1): 134–239.
WANG Lin, LI Yu-xing, HU Qi-hui, et al. Coupling vibration analysis of marine vertical pipe with gas-liquid two-phase flow considering elastic foundation[J]. Journal of China University of Petroleum (Natural Science Edition), 2016, 40(1): 134–239. DOI:10.3969/j.issn.1673-5005.2016.01.019 |
| [2] |
刘龙, 轩福贞, 董达善.
脉动流作用下粘弹性直管动力学特性分析[J]. 工程力学, 2011, 28(10): 41–45.
LIU Long, XUAN Fu-zhen, DONG Da-shan. Dynamic analysis of visco-elastic straight pipes conveying pulsating fluid in Hamiltonian system[J]. Engineering Mechanics, 2011, 28(10): 41–45. |
| [3] |
柳贡民, 陈浩, 李帅军.
蒸汽参数对管路系统动力特性的影响研究[J]. 固体力学学报, 2012, 33(2): 168–175.
LIU Gong-min, CHEN Hao, LI Shuai-jun. Research on the influence of steam parameters on dynamic characteristics of pipeline system[J]. Chinese Journal of Solid Mechanics, 2012, 33(2): 168–175. |
| [4] | OMER F, PAN L, LI B. Study of transient transverse vibration for a pipe[J]. Military Medicine, 2011, 6(2): 114–121. |
| [5] |
林君哲, 周恩涛, 杜林森, 等.
流体参数对航空发动机液压管路振动特性的影响[J]. 东北大学学报(自然科学版), 2012, 33(10): 1453–1456.
LIN Jun-zhe, ZHOU En-tao, DU Lin-sen, et al. Effect of fluid parameters on vibration characteristics of hydraulic pipe of aero-engine[J]. Journal of Northeastern University(Natural Science Edition), 2012, 33(10): 1453–1456. DOI:10.12068/j.issn.1005-3026.2012.10.021 |
| [6] | CHEN M, JIAO G W, DENG S S, et al. Flux vector splitting solutions for coupling hydraulic transient of gas-liquid-solid three-phase flow in pipelines[J]. Applied Mathematics and Mechanics (English Edition), 2013, 34(7): 811–822. DOI:10.1007/s10483-013-1709-x |
| [7] | MALEKZADEH R, RAWM H, MUDDE R F. Severe slugging in a long pipeline-riser system:experiments and predictions[J]. International Journal of Multiphase Flow, 2012, 46: 9–21. DOI:10.1016/j.ijmultiphaseflow.2012.06.004 |
| [8] | BAI X L, DUAN M L, LI Q. Dynamic response of a steel catenary riser at the touchdown point based on integrated analysis[J]. Engineering Mechanics, 2014, 31(12): 249–256. |
| [9] |
马姗, 王发展, 王博, 等.
机械搅拌自吸式浮选机气-液-固三相流场的数值研究[J]. 工程设计学报, 2014, 21(1): 62–67.
MA Shan, WANG Fa-zhan, WANG Bo, et al. Numerical study on gas-liquid-solid three-phase flow field of mechanically-stirred self-priming flotation machine[J]. Chinese Journal of Engineering Design, 2014, 21(1): 62–67. DOI:10.3785/j.issn.1006-754X.2014.01.011 |
| [10] | BINESH S M. Analysis of beam on elastic foundation using the radial point interpolation method[J]. Scientia Iranica, 2012, 19(3): 403–409. DOI:10.1016/j.scient.2012.04.003 |
| [11] | LIU G M, LI Y H. Vibration analysis of liquid-filled pipelines with elastic constraints[J]. Journal of Sound, 2011, 330(13): 3166–3181. DOI:10.1016/j.jsv.2011.01.022 |
| [12] |
王琳, 刘袒, 李玉星, 等.
基于CFD的海洋立管系统严重段塞流数值模拟[J]. 科学技术与工程, 2016, 16(16): 162–167.
WANG Lin, LIU Tan, LI Yu-xing, et al. Numerical simulation of severe slugging in offshore riser on CFD[J]. Science Technology and Engineering, 2016, 16(16): 162–167. DOI:10.3969/j.issn.1671-1815.2016.16.026 |
| [13] |
刘韩生, 樊书刚, 张丹, 等.
TVD格式在水击数值模拟中的应用[J]. 水力发电学报, 2010, 29(4): 107–112.
LIU Han-sheng, FAN Shu-gang, ZHANG Dan, et al. Numerical simulation of water hammer with TVD scheme[J]. Journal of Hydroelectric Engineering, 2010, 29(4): 107–112. |
| [14] |
杨超, 范士娟.
管材参数对输液管流固耦合振动的影响[J]. 振动与冲击, 2011, 30(7): 210–213.
YANG Chao, FAN Shi-juan. Influence of pipe parameters on fluid-structure coupled vibration of a fluid-conveying pipe[J]. Journal of Vibration and Shock, 2011, 30(7): 210–213. DOI:10.3969/j.issn.1000-3835.2011.07.040 |
| [15] |
奚斌, 韩洪升, 刘扬, 等.
环形断面管道水击波速公式推导及其摩阻损失分析[J]. 应用数学和力学, 2013, 34(9): 908–916.
XI Bin, HAN Hong-sheng, LIU Yang, et al. Deduction of formula for water hammer wave velocity in annular section and analysis of friction loss[J]. Applied Mathematics and Mechanics, 2013, 34(9): 908–916. |
| [16] |
王琳, 李玉星, 胡其会, 等.
严重段塞流引起的海洋立管振动响应[J]. 工程力学, 2017, 34(6): 236–244.
WANG Lin, LI Yu-xing, HU Qi-hui, et al. Vibration response of marine riser due to severe slugging flow[J]. Engineering Mechanics, 2017, 34(6): 236–244. |
| [17] |
李乃良, 郭烈锦, 李文升, 等.
顶部节流条件下S型柔性立管内油气水三相流流型转变实验研究[J]. 工程热物理学报, 2011, 32(4): 597–601.
LI Nai-liang, GUO Lie-jin, LI Wen-sheng, et al. Experimental study on flow pattern transition of oil-gas-water three-phase flow in S-type flexible riser with top throat condition[J]. Journal of Engineering Thermophysics, 2011, 32(4): 597–601. |
| [18] |
姚添, 郭烈锦, 刘志刚, 等.
集输立管内非稳定流压差波动特性实验研究[J]. 工程热物理学报, 2017, 38(6): 1250–1256.
YAO Tian, GUO Lie-jin, LIU Zhi-gang, et al. Experimental study on differential pressure fluctuations characteristics of unsteady flow pattern in pipeline-riser system[J]. Journal of Engineering Thermophysics, 2017, 38(6): 1250–1256. |
| [19] |
贾志海, 蔡小舒.
高含气率油气水多相流流量计算模型研究[J]. 工程热物理学报, 2010, 31(5): 789–792.
JIA Zhi-hai, CAI Xiao-shu. Study on multi-phase flow calculation model of oil-gas-water with high gas content[J]. Journal of Engineering Thermophysics, 2010, 31(5): 789–792. |



