随着石油天然气行业不断发展,硬地层、易斜地层和深部地层开采数量不断增多,提高钻井效率成为关键问题。由此研制出以液动冲击器为核心的旋转冲击钻井工具,其工作原理是将液动冲击器的单次冲击破岩和钻具旋转的连续破岩相结合,改善井底流场状况,提高破岩效率,同时通过轴向振动减少钻具和井壁的摩擦因素,有效传递钻压。常见的钻井用液动冲击器有液动射流冲击器、阀式双作用液动冲击器和射吸式液动冲击器。液动射流冲击器是利用双稳射流元件的附壁性和切换性,控制钻井液从不同流道进入活塞上腔和下腔,推动活塞冲锤上下往复运动,如YSC-178型液动射流冲击器[1];阀式双作用液动冲击器是通过流体上下作用面积差产生压力差,辅以上阀上腔产生的水击作用,使得冲锤活塞往复循环进行冲击,如YZX型双作用液动冲击器[2];射吸式液动冲击器是利用标准喷嘴对高速流体的射流卷吸作用形成压力差,结合冲锤和阀瞬间关闭时产生的水击作用,推动冲锤周期性冲击下部铁砧,如文献[3]介绍的射吸式液动冲击器。
在钻进过程中,液动冲击器以泥浆为动力介质,由于黏度较大,泥浆中的固相颗粒不易分离,导致工具冲蚀严重,据现场实测,射流冲击器的射流元件在高排量泥浆钻进过程中的寿命仅为50 h左右[4],冲蚀失效导致寿命不长是液动冲击器无法实现工业化应用的主要原因。
泥浆钻进冲蚀是一个复杂过程,在冲蚀过程中不仅伴随着腐蚀发生,泥浆还会产生绕流,影响固相粒子的运动和分布,尤其在高流速下,粒子和动力介质速度不同,影响更为明显。李伟涛[5]从微观和宏观角度考虑,建立了液动射流冲击器射流元件受泥浆冲蚀的数学模型,并结合分析结果在射流元件冲蚀严重的内表面运用离子注入和爆炸喷涂的方式进行处理,结果表明该处理方式有一定防冲蚀效果。张春艳[6]应用工程仿生研究,找出了提高液动冲击锤活塞及缸套耐冲蚀磨损性能的方法,并研究了与仿生液动冲击锤活塞相关的加工制备工艺。蔺刚等[7]设计出防空打分流结构,有效减缓冲击器在高排量下出现的磨蚀、冲蚀等问题。刘志刚[8]运用摩擦学、泥浆冲蚀等理论,结合140 h的冲蚀试验,探究了延长正作用型液动冲击器寿命的有效解决方案。彭枧明等[9]应用CFD (computational fluid dynamics,计算流体动力学)动态技术,分析不同尺寸和形状分流孔的YSC178A型液动锤的内部速度流场,探究射流元件底盖板外壁出现冲蚀坑的原因,并提出预防出现显著冲蚀坑的措施。
研究地面管汇、阀件和石油钻柱冲蚀的文献较多,如:Zhang等[10]通过电子显微成像技术和室内试验研究了水力压裂液对石油高压管道的冲蚀作用,并利用CFD软件建立管道冲蚀模型,进行求解分析;Shah等[11]利用CFD仿真和试验对压裂泥浆作用下的连续油管进行冲蚀影响因素分析;祝效华等[12]针对气体钻井岩屑造成钻柱严重冲蚀的问题,建立环空岩屑运移模型,研究了钻杆偏心率、井径等对钻柱冲蚀率的影响;王国荣等[13]运用欧拉-拉格朗日法和离散相模型,预测了节流阀内部粒子运动轨迹和分布规律,并利用半经验冲蚀模型求解了颗粒对阀芯的冲蚀率。
由上述研究可知,针对液动冲击器在泥浆钻进过程中的防冲蚀问题尚未有切实有效的解决方案,且液动冲击器本身结构设计和工作原理的复杂性也制约了其研究进展。本文从结构创新的角度提出了一种新型液动冲击器,将切换流道整合于冲锤外壁面,由上下腔室压差推动作用,完成冲击功能。本文利用商用CFD分析软件Fluent建立新型液动冲击器离散相冲蚀模型,预测液动冲击器冲蚀区域分布、颗粒冲击速度对冲击器主要零件的影响以及主要零件工作寿命,以期延长液动冲击器使用寿命,也为评估其抗冲蚀性能提供参考。
1 液动冲击器冲蚀理论基础 1.1 液动冲击器工作原理如图 1所示,笔者设计的新型液动冲击器[14]全长约为1.5 m,外径为180 mm,适用于直径为215.9 mm的井眼。该冲击器通过花键套连接在钻头上部,它主要由上接头、上套筒、冲锤、外壳、活塞套筒、花键套及钻头等构成。

|
| 图 1 新型液动冲击器结构示意图 Fig.1 Structure diagram of neo-type hydraulic impactor |
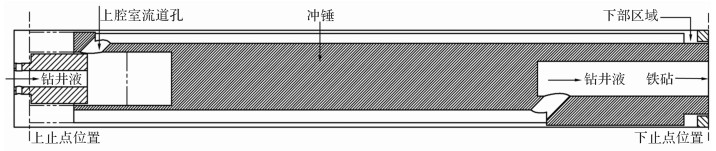
新型液动冲击器工作原理如图 2所示。假设冲锤在初始状态处于下止点,钻井液从上接头进入液动冲击器后,通过上套筒的呼吸孔和冲锤的外流道分别进入冲击器的上部和下部区域,由于下部区域存在活塞套筒的阻塞作用,冲锤上下区域产生方向向上的压力差,冲锤回程;当冲锤上腔流道孔被上套筒瞬间关闭时,发生水击作用,压力差方向反向,致使冲锤从上止点开始冲程,此过程中一部分钻井液能转化为冲锤动能,冲锤以一定速度撞击铁砧,将轴向力向下传递给钻头,同时冲锤反弹进入下一周期。
|
| 图 2 新型液动冲击器工作原理 Fig.2 Operating principle of neo-type hydraulic impactor |
采用拉格朗日粒子追踪算法研究固相颗粒冲蚀,其原理是对流域内大量固相颗粒运动轨迹的计算,且确保每一颗粒子的受力平衡。在拉格朗日坐标系下,固相颗粒在流场中的受力方程为[15]:
| $ \frac{\text{d}{{\mathit{v}}_{\text{p}}}}{\text{d}\mathit{t}}={{F}_{\text{D}}}\left( {{v}_{\text{f}}}-{{v}_{\text{p}}} \right)+g\frac{{{\rho }_{\text{p}}}-{{\rho }_{\text{f}}}}{{{\rho }_{\text{p}}}}+{{F}_{x}} $ | (1) |
其中:
| $ {{F}_{\text{D}}}=\frac{18\mu }{{{\rho }_{\text{p}}}D_{\text{p}}^{2}}\frac{{{C}_{\text{D}}}\mathit{Re}}{24} $ | (2) |
| $ \mathit{Re=}\frac{{{\rho }_{\text{f}}}\left| {{v}_{\text{f}}}-{{v}_{\text{p}}} \right|{{D}_{\text{p}}}}{\mu } $ | (3) |
| $ {{C}_{\text{D}}}={{a}_{1}}+\frac{{{a}_{2}}}{\mathit{Re}}+\frac{{{a}_{3}}}{\mathit{R}{{\mathit{e}}^{2}}} $ | (4) |
| $ \frac{\text{d}\mathit{x}}{\text{d}\mathit{t}}={{v}_{\text{p}}} $ | (5) |
式中:FD为颗粒单位质量上的曳力,N/kg;vf和vp分别为连续相和离散相颗粒的速度,m/s;g为重力加速度,m/s2;ρp和ρf分别为离散相和连续相的颗粒密度,kg/m3;Fx为颗粒单位质量上所受作用力,N/kg;μ为流体动力黏度,Pa · s;Dp为颗粒直径,m;CD为曳力系数,无量纲;a1、a2、a3为两相流系数,无量纲;Re为相对雷诺数,无量纲。
对式(1)进行积分可得粒子速度,再对粒子速度进行积分可求出粒子轨迹[16]。将式(1)化成一般形式,如式(6):
| $ \frac{\text{d}{{\mathit{v}}_{\text{p}}}}{\text{d}\mathit{t}}=\frac{{{v}_{\text{f}}}-{{v}_{\text{p}}}}{{{\tau }_{\text{p}}}}+a $ | (6) |
关联式(1)和式(6),再对这一组微分方程进行积分,可得粒子在下一位置的速度与坐标,如式(7)与式(8):
| $ v_{\text{p}}^{n+1}=v_{\text{f}}^{n}+{{\text{e}}^{\frac{\Delta t}{{{\tau }_{\text{p}}}}}}\left( v_{\text{p}}^{n}-v_{\text{f}}^{n} \right)-a{{\tau }_{\text{p}}}\left( {{\text{e}}^{\frac{\Delta t}{{{\tau }_{\text{p}}}}}}-1 \right) $ | (7) |
| $ \begin{align} & x_{\text{p}}^{n+1}=x_{\text{p}}^{n}+\Delta t\left( v_{\text{f}}^{n}+a{{\tau }_{\text{p}}} \right)+{{\tau }_{\text{p}}}\left( 1-{{\text{e}}^{\frac{\Delta t}{{{\tau }_{\text{p}}}}}} \right) \\ & \ \ \ \ \ \ \ \ \ \left( v_{\text{p}}^{n}-v_{\text{f}}^{n}-a{{\tau }_{\text{p}}} \right) \\ \end{align} $ | (8) |
式中:a为除曳力外的所有力产生的加速度;vf、τp和a均为常数。
1.3 液动冲击器冲蚀模型冲蚀与流体的物理和化学性质关系密切,流体中固相颗粒的冲击角度和冲击速度对冲击器冲蚀有很大影响[10]。本文采用CFD软件Fluent对液动冲击器进行冲蚀仿真,结合颗粒冲击角度、冲击速度等主要影响因素,建立的液动冲击器冲蚀模型如下:
| $ R=\sum\limits_{i=1}^{{{N}_{\text{p}}}}{\frac{{{m}_{\text{p}}}C\left( {{d}_{\text{p}}} \right)F\left( \alpha \right)v_{i}^{n}}{A}} $ | (9) |
式中:R为冲蚀率,kg/m2·s;Np为作用在冲击表面的固相颗粒数量;mp为钻井液质量流量,kg/s;C(dp)为固相颗粒直径函数,冲锤设置为塑性,该函数取常数1.8×10-9;F(α)为冲击角度函数,其值在0~1之间;vi为冲击速度,m/s;n为速度因子,取决于固相颗粒和冲击表面材料,通常n=2~3;A为单位冲击表面积,m2。
1.4 液动冲击器冲蚀失效计算对液动冲击器的冲蚀失效计算主要是结合泥浆冲蚀等宏观影响因素,预测冲击器理论工作时间,计算公式如下[5]:
| $ t=\frac{\frac{{{m}_{1}}}{{{m}_{2}}}}{{{d}^{0.616}}g{{v}^{n}}g{{c}_{v}}^{0.582}\left( \frac{{{H}_{1}}}{{{H}_{2}}} \right)\times 2.648\times {{10}^{-5}}} $ | (10) |
其中:
| $ {{c}_{v}}=\frac{\rho -{{\rho }_{\text{f}}}}{{{\rho }_{\text{p}}}-{{\rho }_{\text{f}}}} $ | (11) |
式中:t为工作时间,s;m1为磨损质量,kg;m2为泥浆中固相颗粒质量,kg;d为固相颗粒粒径,m;v为泥浆流速,m/s;cv为泥浆浓度系数;ρ为泥浆密度,kg/m3;H1、H2为固相颗粒与靶材的莫氏硬度,无量纲。
2 液动冲击器冲蚀数值模拟Fluent软件预测粒子冲蚀特性所采用的是离散相模型(discrete phase model,DPM),给定离散相粒子的初始位置、初始速度、尺寸、质量流量等条件,结合输入材料的物理特性,进行粒子轨迹和能量传递的计算[11]。此外,在Fluent提供的湍流模型中,标准k-ε模型是在湍流动能k方程的基础上,引入关于湍流耗散率ε的方程,该方程计算速度快以及精度较高,已经广泛应用于工业流场计算和热传递仿真分析中[17]。本文通过选用标准k-ε模型,并激活壁面函数方程处理近壁面流体流动,以提高计算精度。
2.1 液动冲击器模型建立液动冲击器的工作过程涉及水击作用和高频往复运动,因此采用动网格技术对液动冲击器工作过程进行瞬态分析。通过截取不同时刻液动冲击器内部流场分布云图,如图 3和图 4所示,分析冲击器速度和压力在整个工作过程中的变化。由图 3和图 4可知:t=0.002 5 s时冲锤上腔流体发生水击作用,在上腔底部附近区域速度最小,而压力骤然上升到最大;随着冲锤继续向上运动,到达上止点后向下运动,冲锤上腔以及冲击器下部区域的压力呈交替变大和变小,结果表明冲击器内部流场分布趋于较均匀状态。

|
| 图 3 不同时刻新型液动冲击器内部速度分布云图 Fig.3 Inner velocity distribution nephogram of neo-type hydraulic impactor at different times |

|
| 图 4 不同时刻新型液动冲击器内部压力分布云图 Fig.4 Inner pressure distribution nephogram of neo-type hydraulic impactor at different times |
由于利用CFD仿真真实工况下液动冲击器整个工作过程中的冲蚀问题时计算量较大,本文基于液动冲击器工作原理,选取压力等流场特性参数变化梯度较大的时刻,确定冲锤相对位置,合理简化计算模型,分析流场变化。用ICEM-CFD进行网格划分,新型液动冲击器流体域对称面网格划分如图 5所示。为保证流体在流道中不被完全堵塞,上套筒和冲锤上腔、冲锤和外壳内表面、冲锤和活塞套内表面均存在间隙,因冲锤设有排液通道,这些间隙的存在对流场影响不大。由流体流过液动冲击器的区域构成流体域,具体仿真参数设置见表 1。

|
| 图 5 新型液动冲击器流体域对称面网格划分 Fig.5 Symmetrical meshing of neo-type hydraulic impactor fluid domain |
| 参数 | 钻井液流速/(m/s) | 颗粒平均粒径/mm | 颗粒密度/ (kg/m3) |
| 数值 | 120 | 1 | 2 500 |
| 参数 | 流体介质黏度/Pa·s | 流体介质密度/(kg/m3) | |
| 数值 | 0.027 | 1 200 | |
边界条件设置如下:进口边界为速度入口,用于定义流动速度以及流动入口的流动属性等相关标量;出口边界为质量出口,假设除压力外所有的流动参数法向变化梯度为0,且保证流动是充分的;上套筒壁面、外壳内壁面和冲锤壁面设为非滑移壁面。
2.2 液动冲击器冲蚀数值模拟结果分析 2.2.1 流场特性分析如图 6所示,固相颗粒随着钻井液从上套筒中心流道孔进入冲锤上腔,由于壁面阻挡,流体迅速改变方向且呈发散状。由于流道环空间隙较小,一部分流体顺着环空间隙反向流动,另一部分流体在上套筒和上腔底部壁面的阻挡作用下沿圆周切线方向回到发散中心区域,形成二次流[18],与后泵入的主液体混合。另外,固相颗粒在上套筒呼吸孔周边壁面和冲锤流道孔进口壁面附近呈较大冲击角度,易发生严重冲蚀。

|
| 图 6 钻井液固相颗粒速度矢量图 Fig.6 Velocity vector diagram of solid phase particles in drilling fluid |
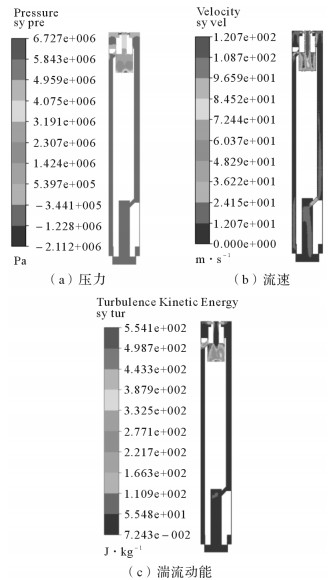
二次流对新型液动冲击器内部流场分布有显著影响,如图 7所示,冲击器内部压力、流速以及湍流动能变化明显的区域集中在上套筒和冲锤上腔,而这正是二次流发生的主要区域。在冲锤上腔底部区域出现压力峰值,特别是圆心区域和边角处有较大面积的高压分布(图 7(a));在上套筒中心孔流道出现速度较大值,由于流动方向与流道轴线平行,高速区域基本没有受到干扰(图 7(b));在冲锤上腔底部圆心区域出现湍流动能峰值,同时在上腔流道孔转角处和上套筒呼吸孔周边区域有一定湍流能量聚集(图 7(c))。
|
| 图 7 二次流影响下新型液动冲击器内部流场分布 Fig.7 Inner flow-field distribution of neo-type hydraulic impactor under the influence of secondary flow |
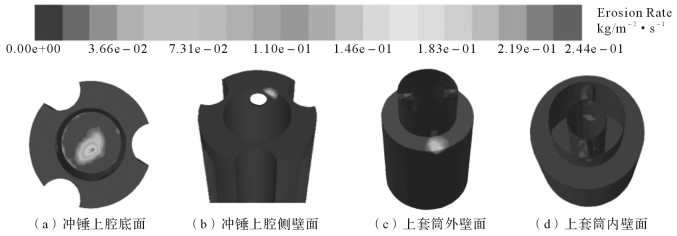
由图 8所示的冲锤和上套筒冲蚀率分布较集中,即冲蚀严重区域的截图可知,冲蚀区域基本分布在高压力、高流速和高湍流动能的区域上,主要是在冲锤上腔的底面、冲锤边角处、流道孔进口壁面、上套筒呼吸孔进口处以及上部壁面,其中冲锤上腔底面冲蚀最为严重。在实际工况下,钻井液对液动冲击器的冲蚀会在其表面产生冲蚀坑,冲蚀坑的尺寸和数量会影响冲击器内部流场分布,导致实际冲蚀区域和数值分析的有所差异,但CFD仿真对工具冲蚀区域的预测仍有很大的指导意义。
|
| 图 8 新型液动冲击器冲蚀严重区域仿真结果 Fig.8 Serious erosion area simulation results of neo-type hydraulic impactor |
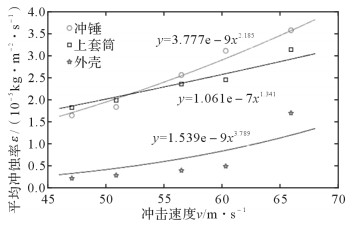
固相颗粒冲击速度不仅影响冲击器的冲蚀率,还会制约其使用寿命。固相颗粒的冲击速度存在一个临界值,低于此数值时不产生冲蚀磨损,只会发生弹性变形[19]。如图 9所示,通过Fluent软件仿真得到的冲击器主要零件冲蚀率与冲蚀速度的关系可知:钻井液从上接头进入液动冲击器时,冲击速度高于临界值,对上套筒、冲锤和外壳均有冲蚀;3个主要工作零件的平均冲蚀率和冲击速度呈幂函数关系,速度因子在1~4之间;随着钻井液中固相颗粒冲击速度的增大,冲锤、上套筒和外壳的平均冲蚀率也逐渐升高;固相颗粒冲击速度越大,撞击壁面时湍流动能越大,即冲击力越大,造成的冲蚀也越严重。当冲击速度小于51 m/s时,上套筒的冲蚀率比冲锤大,当冲击速度大于51m/s时,冲锤的冲蚀率比上套筒大,而在冲击速度变化过程中,外壳的冲蚀率始终最小。
|
| 图 9 冲锤、上套筒和外壳平均冲蚀率随冲击速度的变化曲线 Fig.9 Variation curves of average erosion rate of impact hammer, upper sleeve and shell with impact velocity |
目前可应用于深井的大尺寸液动冲击器主要有射流式和双作用式两种,但它们均处于试验阶段,尚未大规模应用[20]。液动冲击器寿命短是导致它无法实现工业化应用的重要原因。参照江苏东海科钻一井的液动射流冲击器[5],在不同颗粒粒径和泥浆流速的工况下,对比新型液动冲击器主要零件与现有液动射流冲击器射流元件的使用寿命,为评估工具抗冲蚀性能提供参考。
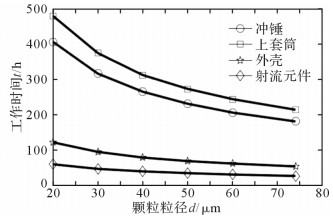
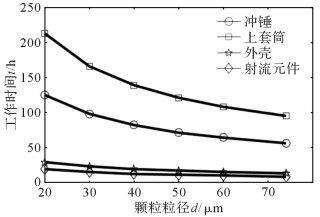
如图 10所示,当冲击器内部泥浆流速为80 m/s时,冲锤、上套筒和外壳的理论工作时间均大于射流元件,在颗粒粒径为20 μm时有最大增幅,分别为576.7%,698.3%和103.3%,在颗粒粒径为50 μm时有最小增幅,分别为560.0%,680.0%和97.1%。在液动冲击器工作过程中,理论工作寿命由长到短的工作零件分别为上套筒、冲锤、外壳。同理,如图 11所示,当冲击器内部泥浆流速为120 m/s时,冲锤、上套筒和外壳在颗粒粒径为74 μm时相对射流元件的使用寿命有最大增幅,分别为600%,1 087.5%和62.5%,在颗粒粒径为60 μm时有最小增幅,分别为540.0%, 980.0%和50.0%,依然是上套筒使用寿命最长,外壳使用寿命最短。尽管冲击器实际使用寿命除受控于冲蚀这个主要因素外,还受控于磨损甚至可能存在的腐蚀,但上文关于冲蚀的计算分析表明本文从结构改进的角度来降低冲蚀从而延长液动冲击器的工作寿命是一个较为可行的技术思路,这对推动液动锤的产业化是有积极作用的。
|
| 图 10 冲击器内部泥浆流速为80 m/s时冲锤、上套筒和外壳工作时间与射流元件对比 Fig.10 Working hours of impact hammer, upper sleeve and shell compared with that of jet at mud flow rate in impactor of 80 m/s |
|
| 图 11 冲击器内部泥浆流速为120 m/s时冲锤、上套筒和外壳工作时间与射流元件对比 Fig.11 Working hours of impact hammer, upper sleeve and shell compared with that of jet at mud flow rate in impactor of 120 m/s |
1) 新型液动冲击器冲蚀区域主要集中在内部高压力、高流速和高湍流动能区域,即冲锤上腔的底面、冲锤边角处、流道孔进口壁面、上套筒呼吸孔进口处以及上部壁面,其中冲锤上腔底面冲蚀最为严重。
2) 固相颗粒的冲击速度对冲击器的冲蚀率有显著影响,冲锤、上套筒和外壳的平均冲蚀率与冲击速度呈幂函数关系,速度因子在1~4之间。且当冲击速度小于51 m/s时,上套筒的冲蚀率比冲锤大,当冲击速度大于51 m/s时,冲锤的冲蚀率比上套筒大,外壳的冲蚀率始终最小。
3) 在泥浆流速为80 m/s和120 m/s的工况下,随着颗粒粒径从20 μm增大到74 μm,新型液动冲击器的冲锤、上套筒和外壳的理论使用寿命始终大于现有液动射流冲击器射流元件,增幅最小为50%,最大达到1 087%,尽管冲击器实际使用寿命还可能受到磨损甚至可能存在的腐蚀的影响,但分析结果表明从结构改进的角度来降低冲蚀从而延长液动冲击器的工作寿命是一个较为可行的技术思路,对评估工具抗冲蚀性能以及推动液动锤的工业化应用有积极作用。
| [1] |
沈建中, 贺庆, 韦忠良, 等.
YSC-178型液动射流冲击器在旋冲钻井中的应用[J]. 石油机械, 2011, 39(6): 52–54.
SHEN Jian-zhong, HE Qing, WEI Zhong-liang, et al. Application of YSC-178 hydraulic jet impactor in rotary percussion drilling[J]. China Petroleum Machinery, 2011, 39(6): 52–54. |
| [2] |
李博.阀式双作用液动冲击器的仿真[D].北京: 中国地质大学工程技术学院, 2013: 19-20.
LI Bo. The simulation of double-acting impactors[D]. Beijing: China University of Geosciences, School of Engineering and Technology, 2013: 19-20. |
| [3] |
刘国经, 朱乃正, 王有群.射吸式冲击器: CN1005785B[P].1989-11-15.
LIU Guo-jing, ZHU Nai-zheng, WANG You-qun. Jet-suck impactor: CN1005785B[P]. 1989-11-15. |
| [4] |
丁代坡.石油钻井冲击器关键零部件工作寿命的研究[D].长春: 吉林大学建设工程学院, 2008: 63.
DING Dai-po. Research on the working life of key accessory of oil drilling impacting machine[D]. Changchun: Jilin University, College of Construction Engineering, 2008: 63. http://cdmd.cnki.com.cn/Article/CDMD-10183-2008062673.htm |
| [5] |
李伟涛.液动锤射流元件工作寿命试验研究[D].长春: 吉林大学建设工程学院, 2004: 35-47.
LI Wei-tao. The experiment and research on the working life of the liquid jet amplifier of the hydraulic hammer[D]. Changchun: Jilin University, College of Construction Engineering, 2004: 35-47. http://cdmd.cnki.com.cn/article/cdmd-10183-2004101340.htm |
| [6] |
张春艳.液动冲击锤活塞缸套仿生耐冲蚀磨损研究[D].长春: 吉林大学生物与农业工程学院, 2013: 35-62.
ZHANG Chun-yan. Research on erosion abrasion resistance properties of hydraulic impact hammer piston-liner by bio-inspired method[D]. Changchun: Jilin University, College of Biological and Agricultural Engineering, 2013: 35-62. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013196039.htm |
| [7] |
蔺刚, 殷琨, 徐克里.
钻井用射流式液动冲击器防空打机构改型设计[J]. 石油机械, 2007, 35(5): 23–24.
LIN Gang, YIN Kun, XU Ke-li. Anti-ineffectiveness operating model change for hydraulic jet impactor in drilling[J]. China Petroleum Machinery, 2007, 35(5): 23–24. DOI:10.3969/j.issn.1001-4578.2007.05.007 |
| [8] |
刘志刚.
正作用型液动冲击器寿命的研究[J]. 地质与勘探, 1993, 29(6): 54–58.
LIU Zhi-gang. The lifetime of positive action type hydraulic percussive device[J]. Geology and Exploration, 1993, 29(6): 54–58. |
| [9] |
彭枧明, 柳鹤, 赵志强, 等.
YSC178A型液动锤射流元件底盖板外壁冲蚀机理[J]. 吉林大学学报(地球科学版), 2010, 40(5): 1140–1144.
PENG Jian-ming, LIU He, ZHAO Zhi-qiang, et al. Erosion mechanism on outer wall of bottom plate of fluidic element for YSC178A liquid-jet hammer[J]. Journal of Jilin University (Earth Science Edition), 2010, 40(5): 1140–1144. |
| [10] | ZHANG J, KANG J, FAN J, et al. Research on erosion wear of high-pressure pipes during hydraulic fracturing slurry flow[J]. Journal of Loss Prevention in the Process Industries, 2016, 43: 438–448. DOI:10.1016/j.jlp.2016.07.008 |
| [11] | SHAH S N, JAIN S. Coiled tubing erosion during hydraulic fracturing slurry flow[J]. Wear, 2004, 264(3/4): 279–290. |
| [12] |
祝效华, 刘少胡, 童华.
气体钻井钻杆冲蚀规律研究[J]. 石油学报, 2010, 31(6): 1013–1017.
ZHU Xiao-hua, LIU Shao-hu, TONG Hua. A study on the drill pipe erosion law in gas drilling[J]. Acta Petrolei Sinica, 2010, 31(6): 1013–1017. |
| [13] |
王国荣, 楚飞, 陶思宇, 等.
控压钻井节流阀液-固两相流冲蚀预测及验证[J]. 石油学报, 2015, 36(6): 754–759.
WANG Guo-rong, CHU Fei, TAO Si-yu, et al. Prediction and verification on liquid-solid two-phase flow erosion of managed pressure drilling throttle valve[J]. Acta Petrolei Sinica, 2015, 36(6): 754–759. |
| [14] |
祝效华, 刘上.一种往复冲击潜孔锤钻井工具: 2014101781319[P].2014-04-30.
ZHU Xiao-hua, LIU Shang. A reciprocating impact DTH hammer drilling tool: 2014101781319[P]. 2014-04-30. |
| [15] | BOZZINI B, RICOTTI M E, BONIARDI M, et al. Evaluation of erosion-corrosion in multiphase flow via CFD and experimental analysis[J]. Wear, 2003, 255(1/6): 237–245. |
| [16] |
巴彬.气体钻井中下部钻具冲蚀失效研究[D].成都: 西南石油大学石油与天然气工程学院, 2016: 12-13.
BA Bin. Erosion failure analysis for gas drilling bottom hole[D]. Chengdu: Southwest Petroleum University, School of Petroleum Engineering, 2016: 12-13. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016098642.htm |
| [17] | FERZIGER J H, PERIC M. Computational methods for fluid dynamics[J]. Physics Today, 1997, 50(3): 80–84. |
| [18] | ZHANG J, KANG J, FAN J, et al. Study on erosion wear of fracturing pipeline under the action of multiphase flow in oil & gas industry[J]. Journal of Natural Gas Science & Engineering, 2016, 32: 334–346. |
| [19] |
邵荷生, 曲敬信, 许小棣.
摩擦与磨损[M]. 北京: 煤炭工业出版社, 1992: 281-282.
SHAO He-sheng, QU Jing-xin, XU Xiao-di. Friction and wear[M]. Beijing: China Coal Industry Publishing House, 1992: 281-282. |
| [20] |
黄雪琴, 孟庆昆, 郑晓峰.
液动冲击器发展现状及在油气钻井应用探讨[J]. 石油矿场机械, 2016, 45(9): 62–66.
HUANG Xue-qin, MENG Qing-kun, ZHENG Xiao-feng. Development status of hydro-hammers and application of hydro-hammers in oil and gas well drilling[J]. Oil Field Equipment, 2016, 45(9): 62–66. DOI:10.3969/j.issn.1001-3482.2016.09.014 |


