2. 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122
2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment & Technology, Wuxi 214122, China
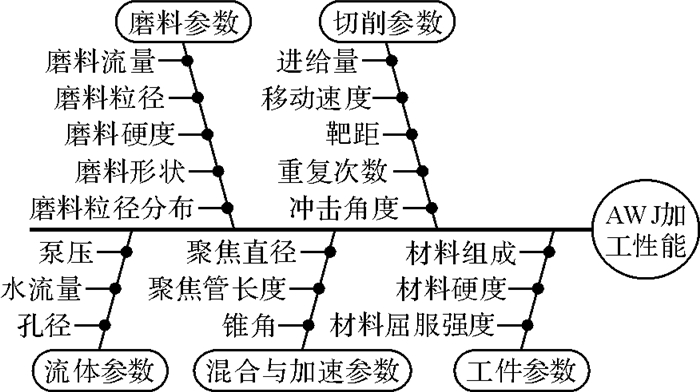
影响磨料水射流(abrasive water jet,AWJ)加工质量、加工效率及其经济性的因素很多,总的来说可以分为5类,分别为磨料参数、切削参数、流体参数、混合与加速参数以及工件参数[1-2],具体如图 1所示。但是在实际加工过程中,受到设备、工件和磨料等确定参数的限制,不会涉及这5类参数中所有因素的改变。因此,磨料水射流的加工质量取决于泵压、移动速度、靶距和磨料流量等主要参数影响下的射流冲蚀性能。
|
| 图 1 磨料水射流加工性能的影响因素 Fig.1 Influencing factors of abrasive water jet machining performance |
国内外许多学者在磨料水射流流场仿真方面进行了研究,如:Junkar、Kumar和Ahmed等[3-5]分别利用有限元法分析了磨料水射流加工中单颗粒与多颗粒冲蚀过程及颗粒的冲蚀特性;Wang、Feng等[6-7]运用SPH(smoothed particle hydrodynamics,光滑粒子流体动力学)法数值模拟了磨料水射流冲蚀过程与颗粒的加速过程;Nie等[8]对前混合喷嘴流场进行了数值模拟;孙艳斌等[9]利用神经网络建立了硬质合金的切割深度模型;刘力红等[10]数值模拟了前混合磨料水射流的运动情况;Deam等[11]建立了磨料水射流的切割模型并进行了实验,将材料加工过程可视化,模拟结果与实验结果的吻合性较好。也有学者对磨料水射流抛光喷嘴的流场进行了仿真分析,并对比了不同结构喷嘴的射流特性,如:龙新平等[12]分析了喷嘴内部流场与颗粒运动情况;左伟芹等[13]利用迭代算法对喷嘴内磨料颗粒的加速情况作了探讨;Deepak等[14]数值模拟了不同形状喷嘴对射流参数的影响。
在磨料水射流加工中,磨料与水的混合及两者之间的碰撞磨损使喷嘴内磨料的加速机制及磨料与水的混合过程变得复杂,通过实验对单颗粒与多颗粒冲蚀过程进行定性或定量分析难度大,因此应该关注喷出后射流束的冲蚀性能,即不同喷嘴距离下射流束的冲蚀性能及其中心线上的压力与速度的衰减规律。
本文基于Fluent对磨料水射流外流场的冲蚀过程进行仿真,分析射流的压力分布、速度分布及射流束中心线上压力与速度的衰减规律,并结合冲蚀实验分析工艺参数对冲蚀孔径的影响规律,最后联合仿真与实验结果综合分析磨料水射流的冲蚀性能及其衰减规律,以期为磨料水射流切割、铣削及抛光加工的参数选择提供实验依据,同时为磨料水射流加工过程的仿真提供参考。
1 磨料水射流冲蚀性能仿真分析 1.1 水和磨料的控制方程磨料水射流冲蚀过程中水与磨料的速度均为超音速,考虑到颗粒之间存在相互碰撞作用,因此选择Euler模型,连续性方程与动量方程为其控制方程[15]。冲蚀过程的数值模拟涉及水和磨料颗粒两相,因此第i相的连续方程为[16]:
| $ \frac{{\partial ({\alpha _i}{\rho _i})}}{{\partial t}} + \nabla \cdot \left( {{\alpha _i}{\rho _i}{\mathit{\boldsymbol{v}}_i}} \right) = \sum\limits_{j = 1}^2 {{m_{ji}}} \;\;\;(i = 1, 2) $ | (1) |
式中:αi为第i相的体积分数;ρi为第i相的密度;vi为第i相的速度;mji为水和磨料颗粒两相间的质量传递,满足 mij=-mij 和
第i相的动量方程为:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {{\alpha _i}{\rho _i}{\mathit{\boldsymbol{v}}_i}} \right) + \nabla \cdot \left( {{\alpha _i}{\rho _i}{\mathit{\boldsymbol{v}}_i}} \right) = - {\alpha _i}\nabla p + \nabla \cdot {\mathit{\boldsymbol{\tau }}_\mathit{i}} + F + \\ {\alpha _i}{\rho _i}\left( {{F_i} + {F_{{\rm{lift}}, i}} + {F_{{\rm{V}}m, i}}} \right) \end{array} $ | (2) |
式中:τi为第i相的压力应变张量,τi=αivi(▽vi+ viT)+ vi(λi-2/3μi)▽· viI;μi、λi为第i相的剪切黏度、体积黏度;p为两相共享的压强;F为水和磨料两相间的作用力,Fi为第i相的受力,Flift, i为第i相的升力,FVm, i为第i相的虚拟质量力。
为了使动量方程封闭,水和磨料颗粒两相间的作用力F为:
| $ F = \sum\limits_{i = 1}^2 {\left( {{F_{ij}} + \sum\limits_{i = 1}^2 {{m_{ij}}{v_{ij}}} } \right)} $ | (3) |
| $ \sum\limits_{i = 1}^2 {{F_{ij}} = } \sum\limits_{i = 1}^2 {{K_{ij}}\left( {{v_i} - {v_j}} \right)} $ | (4) |
式中:Kij=Kji,为相间动量交换系数,Fji为第j相对第i相的作用力, Fij= -Fji,Fii=0;vij是相间速度,且有:当
可实现的k-ε模型的湍流动能及其耗散率方程[17]为:
| $ \rho \frac{{{\rm{d}}k}}{{{\rm{d}}t}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} $ | (5) |
| $ \begin{array}{l} \rho \frac{{{\rm{d}}\varepsilon }}{{{\rm{d}}t}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}{S_\varepsilon } - \\ \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} + {C_1}\frac{\varepsilon }{k}{C_3}{G_{\rm{b}}} \end{array} $ | (6) |
式中:
在Fluent中,取推荐值:C3=1.44,C2=1.9,σk= 1.0,σε=1.2。
对于混合相,其连续方程为:
| $ \frac{\partial }{{\partial t}}{\rho _{\rm{m}}} + \nabla \left( {{\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}} \right) = \sum\limits_{i = 1}^2 m $ | (7) |
式中:ρm为混合相密度;
综合水相和颗粒相的动量方程可以得到混合相的动量方程:
| $ \begin{array}{l} \frac{{\partial \left( {{\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{m}}}{\mathit{\boldsymbol{v}}_{\rm{m}}}} \right) = - \nabla {p_{\rm{m}}} + \\ \nabla \left[ {{\mu _{\rm{m}}}\left( {\nabla {\mathit{\boldsymbol{v}}_{\rm{m}}} + \nabla \mathit{\boldsymbol{v}}_{\rm{m}}^{\rm{T}}} \right)} \right] + {\rho _{\rm{m}}}g + T + \nabla \left( {\sum\limits_{i = 1}^2 {{\alpha _i}{\rho _i}} {v_{{\rm{dr}}, i}}} \right) \end{array} $ | (8) |
式中:T为体积力;μm为混合相黏度;pm为混合相压强;vdr, i为第i相的飘逸速度。
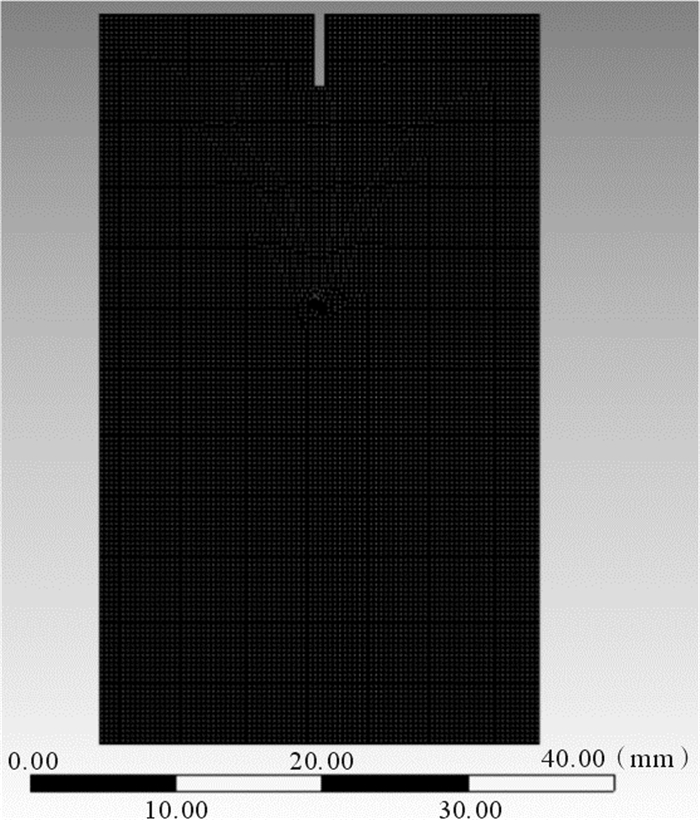
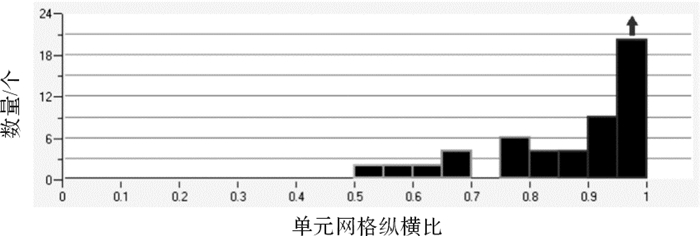
1.2 磨料水射流冲蚀模型与参数设置以射流出口处为基准,计算流体域是30 mm×50 mm的喷嘴外流场域,磨料水射流冲蚀计算域模型如图 2所示,沿射流方向设置了距射流出口分别为10,15,20,25和30 mm的横截面,以探究射流束在不同喷嘴距离下的冲蚀性能。划分网格并检查网格质量,网格质量柱形图如图 3所示,以单元网格纵横比为0.95~1的高质量网格为主,因此,模型的网格质量能够满足仿真计算要求。
|
| 图 2 磨料水射流冲蚀计算域模型 Fig.2 Model of abrasive water jet erosion computation domain |
|
| 图 3 冲蚀模型网格质量柱形图 Fig.3 Mesh quality histogram of erosion model |
仿真时,Fluent求解器选择基于压力求解器,计算模型选择Euler多相流模型,选择液相为水、固相为磨料颗粒的二相流,设置水为主相、磨料颗粒为次相。系统压力为200 MPa时喷嘴出口处水的速度为444.619 5 m/s,磨料速度为403.385 9 m/s,水的密度为998 kg/m3;喷嘴直径即为冲蚀模型的入口直径,为0.7 mm;磨料为80目的石榴石,磨料体积比为0.1,密度为2 880 kg/m3,粒径为0.18 mm;左右两边与上边的边界设置为外流场域出口,底边设置为壁面,入口处的左右两边为喷嘴的边界,设置为入口壁面,选择标准壁面函数进行计算;入口类型设置为速度入口,出口类型设置为压力出口。其他参数选择系统默认值。
1.3 冲蚀模拟结果与分析磨料水射流冲蚀过程中射流沿程上的压力分布和不同喷嘴距离横截面上的压力分布如图 4所示。由图 4(a)可知,在射流沿程上,其压力呈现出不同程度的衰减。由图 4(b)可知,中心线上的最大压力衰减较快,压力分布范围逐渐变宽;在喷嘴距离为30 mm的横截面上出现了压力反向变化的趋势,其射流压力均明显高于25 mm处,这是因为30 mm处横截面靠近工件表面,射流冲击到工件表面后反射形成的对流使该处的压力升高。

|
| 图 4 磨料水射流冲蚀过程中的压力分布 Fig.4 Pressure distribution in the erosion process of abrasive water jet |
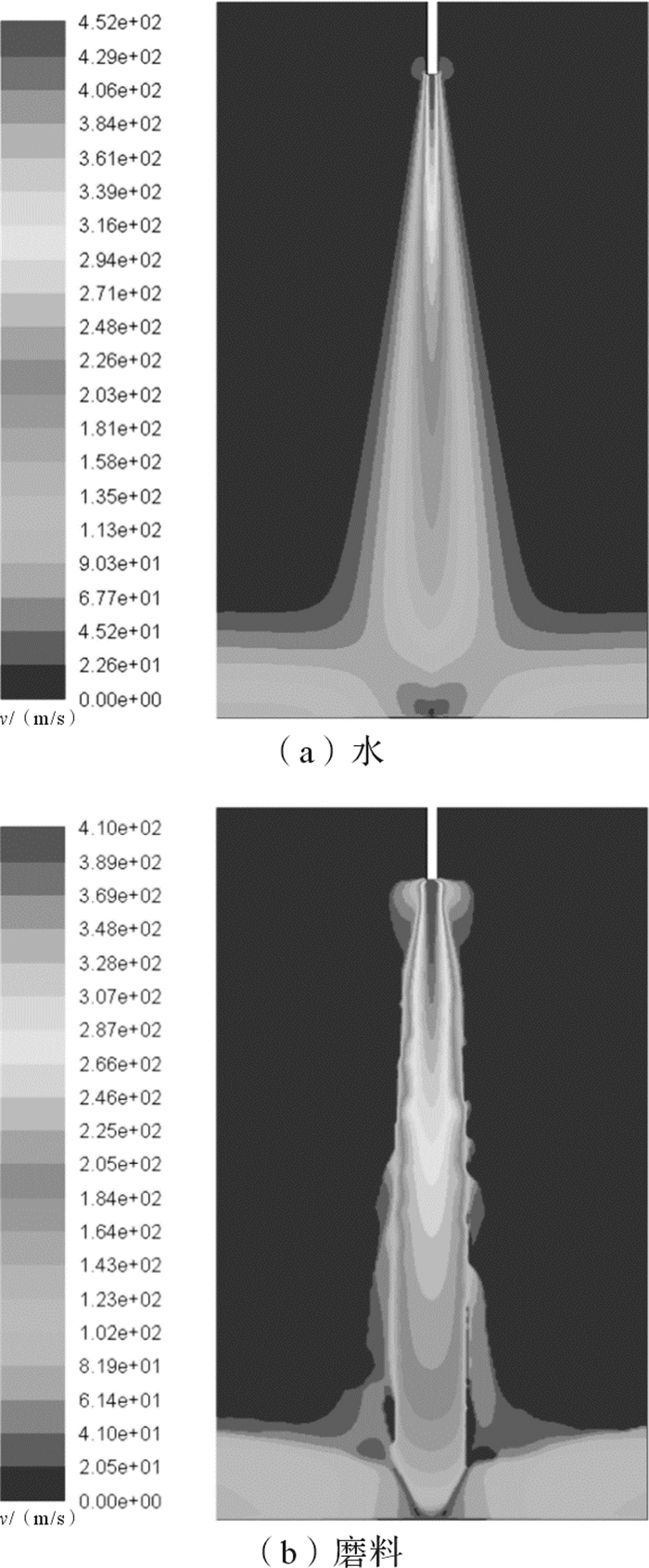
磨料水射流冲蚀过程中水与磨料的速度分布如图 5所示。在磨料水射流冲蚀过程中,水与磨料的速度变化及其分布形态不尽相同。水的速度衰减明显,形态呈三角形,射流起始段呈倒三角形且长度较短,射流基本段呈“V”形,射流基本段长度比起始段稍长。磨料颗粒速度保持性较好,以较高的速度对工件材料表面进行冲蚀,然后磨料颗粒向四周扩散与反射,磨料的速度分布形态呈“玻璃温度计”形。
|
| 图 5 磨料水射流冲蚀过程中水与磨料的速度分布 Fig.5 Velocity distribution of water and abrasive in the erosion process of abrasive water jet |
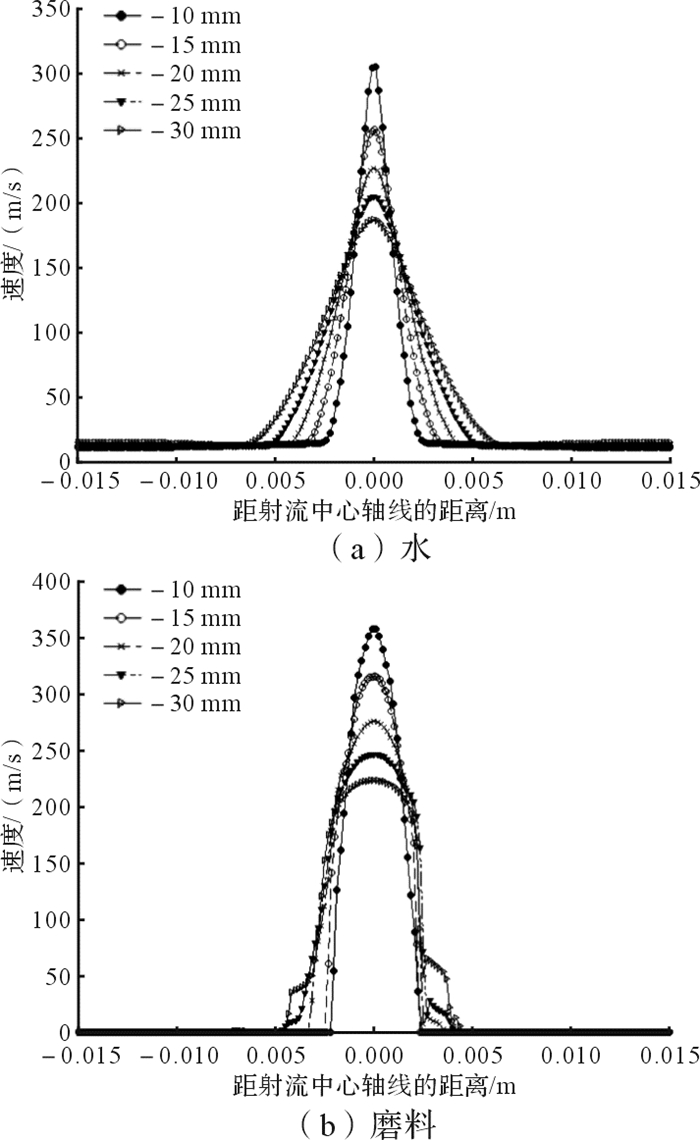
磨料水射流冲蚀过程中不同喷嘴距离横截面上水和磨料的速度分布如图 6所示。在不同喷嘴距离横截面上,水与磨料的速度衰减各异。水的速度衰减是随着喷嘴距离的增大而减缓,但分布范围增大,这致使射流中水的能量分散,削弱了水的冲蚀能力;磨料速度衰减是随着喷嘴距离的增大而减缓,速度分布范围基本不变,可见磨料对工件材料有较强的冲蚀能力。
|
| 图 6 磨料水射流冲蚀过程中不同喷嘴距离横截面上水和磨料的速度分布 Fig.6 Velocity distribution of water and abrasive on cross section with different nozzle distances in the erosion process of abrasive water jet |
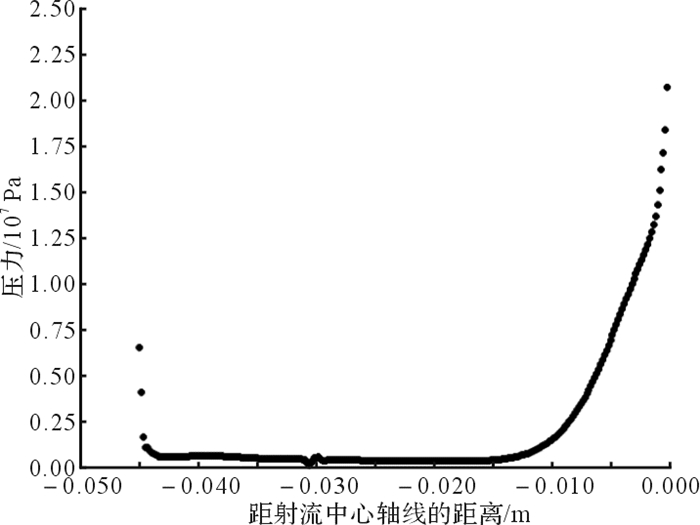
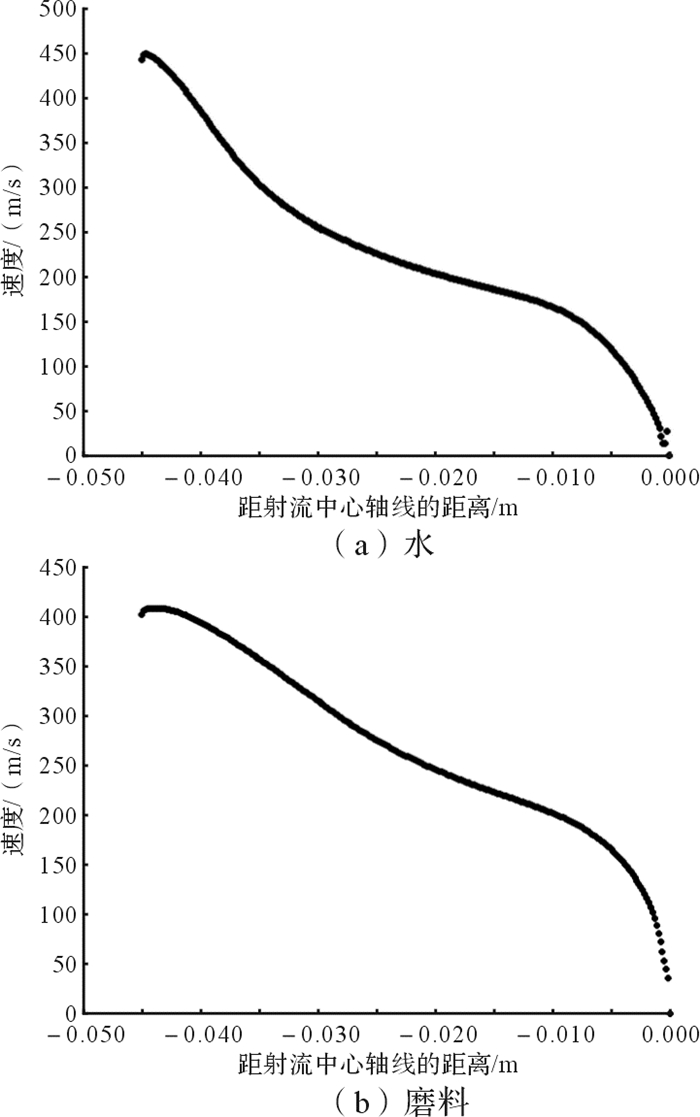
至磨料水射流稳定后,射流压力在中心轴线上呈线性衰减,且衰减速度较快,在距射流出口10 mm处衰减至常压,如图 7所示。对于混合相中的水,其速度衰减过程大致分为3个阶段:快速衰减段、缓慢衰减段和急剧衰减段, 快速衰减段长度约为13 mm、速度衰减约一半,缓慢衰减段长度约为25 mm,急剧衰减段长度约为7 mm、速度衰减至0 m/s。对于混合相中的磨料,其速度衰减过程大致可以分为3个阶段:初始衰减段、快速衰减段和急剧衰减段,在初始衰减段上磨料速度保持着射出时的高速,初始阶段长度约为3 mm,第2段为快速衰减段,呈直线式衰减,长度约为36 mm,第3段为急剧衰减段,长度约为6 mm,在壁面位置处磨料速度衰减至0 m/s。射流中心线上水和磨料的速度分布如图 8所示。
|
| 图 7 磨料水射流在射流中心线上的压力分布 Fig.7 Pressure distribution of abrasive water jet on the center line of jet |
|
| 图 8 射流中心线上水和磨料的速度分布 Fig.8 Velocity distribution of water and abrasive on the center line of jet |
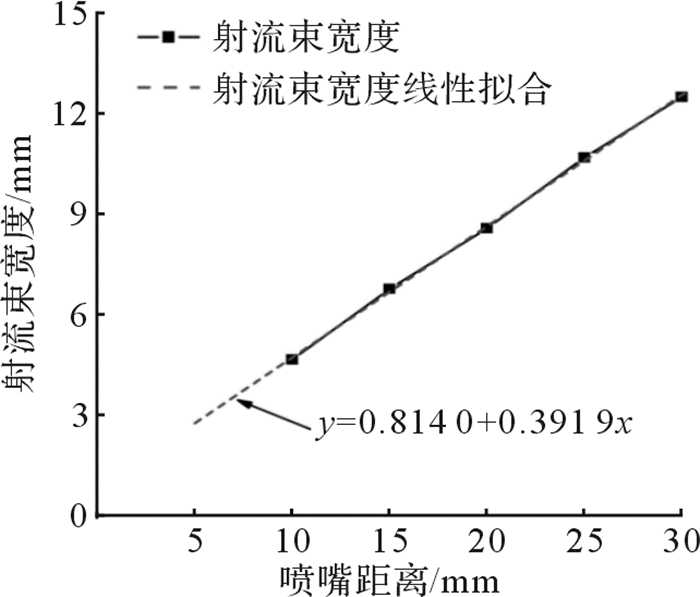
分析仿真结果可知, 在射流压力为200 MPa的冲蚀条件下,射流束在不同喷嘴距离处的宽度呈线性变化,如图 9所示,回归方程为y=0.814 0+0.391 9x(x为喷嘴距离,y为射流束宽度),拟合度为0.999 6,当喷嘴距离为0 mm时,射流宽度为0.814 0 mm,实验使用的喷嘴直径为0.7 mm,表明模型分析结果具有参考意义。
|
| 图 9 射流压力为200MPa时射流束宽度变化曲线 Fig.9 Change curve of jet beam width with jet pressure of 200 MPa |
采用型号为DWJ3020-BB-X5的五轴数控水射流加工机床进行冲蚀实验,如图 10所示,其中:高压系统为从美国KMT公司全套原装进口的STREAMLINETM SL-V 50 PLUS超高压系统,工作压力为5~420 MPa;供砂系统由美国KMT公司设计制造,可自动控制砂的供应,保障磨料水射流加工过程的稳定性。

|
| 图 10 DWJ3020-BB-X5五轴数控水射流加工机床 Fig.10 Five-axis numerical control water jet machining machine of DWJ3020-BB-X5 |
磨料颗粒对磨料水射流的加工质量和加工效率等都有非常大的影响,因此,用于水射流加工的磨料需要有非常优良的特性。石榴石磨料具有硬度大、熔点高、耐酸碱、不吸水、环保无害以及性价比较高等特点,在国内外被广泛使用[18]。因此,本文实验选择80目石榴石为磨料,氧化铝陶瓷材料(板状)为冲蚀目标工件,其主要性能参数如表 1至表 3所示。
| 参数 | 密度/(g/cm3) | 莫氏硬度 | 弹性模量/GPa | 泊松比 |
| 数值 | 3.96~4.10 | 7.49~9.00 | 248 | 0.27 |
| 成分 | Al2O3 | Fe2O3 | SiO2 | Na2O | K2O | 其他 |
| 质量分数/% | 99.7 | 0.028 | 0.03 | 0.035 | 0.002 | 0.205 |
| 参数 | 密度/ (g/cm3) |
维氏硬 度/GPa |
弹性模 量/GPa |
泊松比 | 弯曲强 度/MPa |
抗压强 度/MPa |
| 数值 | 3.85 | 12 | 350 | 0.22 | 400 | 2 500 |
实验中冲蚀倾角为0°,即工件水平放置时,射流束与工件平面法向量平行;考虑到氧化铝陶瓷板的硬度较高,冲蚀实验的工艺参数设置如表 4所示。对于各项的单因素冲蚀实验,选取各因素的中间工艺参数水平值为基准,即射流压力为200 MPa、靶距为20 mm和磨料流量为120 g/min为实验基准。
| 工艺参数 | 参数水平 |
| 冲蚀倾角θ/(°) | 0 |
| 射流压力p/MPa | 100,150,200,250,300 |
| 靶距S/mm | 10,15,20,25,30 |
| 磨料流量M/(g/min) | 40,80,120,160,200 |
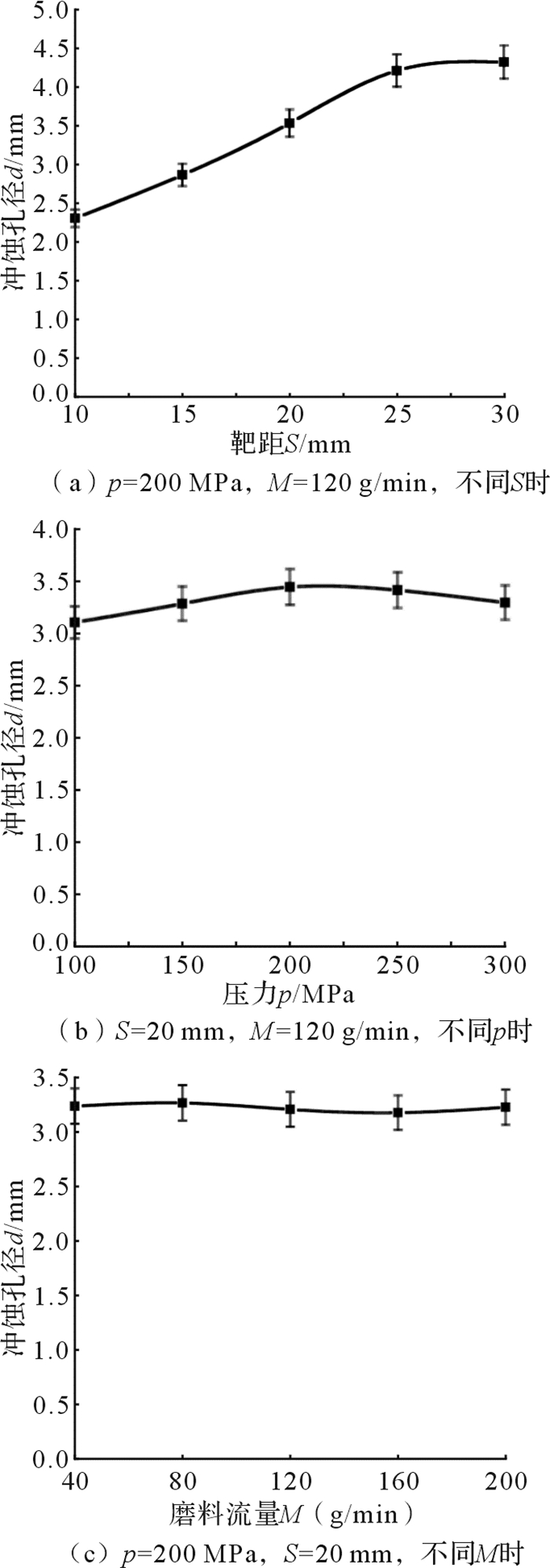
图 11为不同冲蚀工艺参数下磨料水射流的冲蚀孔径变化曲线。由图可知,冲蚀孔径随着靶距的增大呈现先近似线性增大后稳定的趋势,以靶距S=25 mm为分界点,小于25 mm时冲蚀孔径呈线性增大,大于25 mm后呈稳定趋势,即磨料水射流束冲蚀工件时,其能量半径随着靶距的增大而增大,当靶距达到分界点时,射流束的能量半径趋于稳定。射流压力的变化对冲蚀孔径影响不大,不同射流压力下冲蚀孔径基本保持在3.25 mm,这表明此时磨料水射流束的能量比较集中,在较大范围内能够保持冲蚀能力。磨料流量的变化对磨料水射流冲蚀孔径的影响也不显著,不同磨料流量下冲蚀孔径也基本保持在3.25 mm。
|
| 图 11 不同工艺参数下磨料水射流的冲蚀性能 Fig.11 Erosion performance of abrasive water jet under different process parameters |
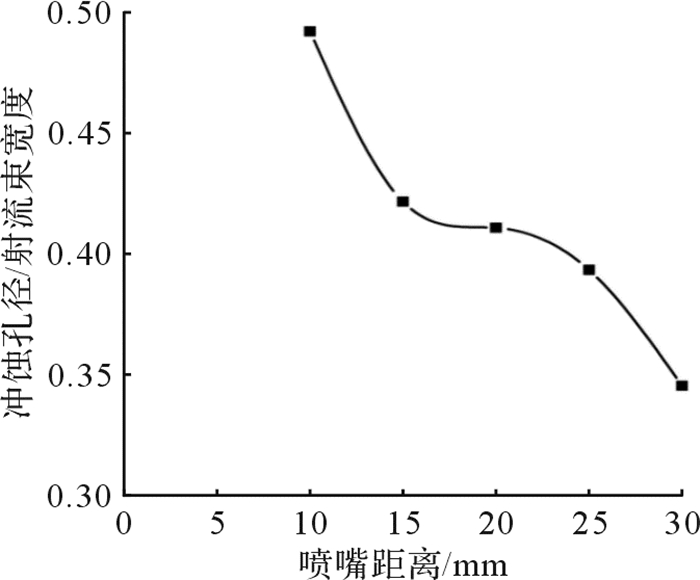
图 12为射流压力p=200 MPa、磨料流量M=120 g/min时磨料水射流冲蚀孔径与射流束宽度的比值随喷嘴距离的变化曲线。由图 11(a)可知:该冲蚀条件下,冲蚀孔径先增大后趋于稳定,这是因为喷出后的射流呈锥形,喷嘴距离越远,射流能量保持性越差,能量衰减越多,导致射流束的冲蚀能力越弱。但由图 12的冲蚀孔径与射流束宽度的比值的变化规律发现,该比值在喷嘴距离为10 mm时较大,说明此处射流束能量的有效利用部分较高,为50%;在喷嘴距离为30 mm时较小,说明此处射流束能量的有效利用部分较低,为30%;在喷嘴距离为15~25 mm时,其比值基本保持不变,说明该范围内射流束能量的有效利用部分较稳定,为40%。研究结果为磨料水射流的切割、铣削及抛光等加工提供了参考。
|
| 图 12 磨料水射流冲蚀孔径与射流束宽度的比值(p=200 MPa,M=120 g/min) Fig.12 Ratio of abrasive water jet erosion diameter to jet beam width (p=200 MPa, M=120 g/min) |
为了探究磨料水射流对脆性材料的冲蚀效果,以氧化铝陶瓷材料为目标工件,进行了磨料水射流外流场冲蚀仿真与磨料水射流冲蚀氧化铝陶瓷实验,得到的结论如下:
1) 由冲蚀过程仿真结果可知射流束中水与磨料的速度分布规律不同,水的速度随着喷嘴距离的增大而减小且分布范围变宽,射流宽度呈线性增大,磨料速度随喷嘴距离的增大而减小且分布范围基本不变。
2) 射流中心线上,射流压力在距喷嘴10 mm处衰减至常压,水和磨料的速度均呈三段式衰减,水的第1段速度衰减段长度比磨料的长,水的第2段速度衰减段长度比磨料的短。
3) 冲蚀孔径随喷嘴距离的增大呈线性增大;射流束能量的有效利用部分随着喷嘴距离的增大而逐渐减小,在喷嘴距离为15~25 mm范围内其有效利用部分较稳定,为40%。
| [1] | PARIKH P J, LAM S S. Parameter estimation for abrasive water jet machining process using neural networks[J]. The International Journal of Advanced Manufacturing Technology, 2009, 40(5): 497–502. |
| [2] | KECHAGIAS J, PETROPOULOS G, VAXEVANIDIS N. Application of Taguchi design for quality characterization of abrasive water jet machining of TRIP sheet steels[J]. The International Journal of Advanced Manufacturing Technology, 2012, 62(5/8): 635–643. |
| [3] | JUNKAR M, JURISEVIC B, FAJDIGA M, et al. Finite element analysis of single-particle impact in abrasive water jet machining[J]. International Journal of Impact Engineering, 2006, 32(7): 1095–1112. DOI:10.1016/j.ijimpeng.2004.09.006 |
| [4] | KUMAR N, SHUKLA M. Finite element analysis of multi-particle impact on erosion in abrasive water jet machining of titanium alloy[J]. Journal of Computational and Applied Mathematics, 2012, 236(18): 4600–4610. DOI:10.1016/j.cam.2012.04.022 |
| [5] | AHMED D H, NASER J, DEAM R T. Particles impact characteristics on cutting surface during the abrasive water jet machining:numerical study[J]. Journal of Materials Processing Technology, 2016, 232(1): 116–130. |
| [6] | WANG J, NA G, GONG W. Abrasive waterjet machining simulation by SPH method[J]. International Journal of Advanced Manufacturing Technology, 2010, 50(1/4): 227–234. |
| [7] | FENG Y, WANG J, LIU F. Numerical simulation of single particle acceleration process by SPH coupled FEM for abrasive waterjet cutting[J]. Journal of Shandong University, 2012, 59(1/4): 193–200. |
| [8] | NIE B, MENG J, JI Z. Numerical simulation on flow field of pre-mixed abrasive water jet nozzle[C]//2008 Asia Simulation Conference-7th International Conference on System Simulation and Scientific Computing, Beijing, Oct. 10-12, 2008. |
| [9] |
孙艳斌, 关砚聪, 宋金来, 等.
磨料水射流切割YW1硬质合金深度预测模型[J]. 硬质合金, 2016, 33(4): 223–229.
SUN Yan-bin, GUAN Yan-cong, SONG Jin-lai, et al. Research on depth prediction model of AWJ cutting hard alloy YW1[J]. Cemented Carbide, 2016, 33(4): 223–229. |
| [10] |
刘力红, 曹寒冰.
基于Fluent的前混合磨料水射流高压管道流场的数值模拟[J]. 长春理工大学学报(自然科学版), 2014, 37(5): 77–80.
LIU Li-hong, CAO Han-bing. Numerical simulation of high pressure pipeline flow field in pre-mixed abrasive water jet with fluent[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2014, 37(5): 77–80. DOI:10.3969/j.issn.1672-9870.2014.05.021 |
| [11] | DEAM R T, LEMMA E, AHMED D H. Modelling of the abrasive water jet cutting process[J]. Wear, 2004, 257(9): 877–891. |
| [12] |
龙新平, 刘琦, 阮晓峰, 等.
后混式磨料射流喷嘴内部流场模拟及分析[J]. 排灌机械工程学报, 2016, 34(8): 686–692.
LONG Xin-ping, LIU Qi, RUAN Xiao-feng, et al. Numerical analysis of the internal flow of abrasive entrained waterjet nozzle[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34(8): 686–692. |
| [13] |
左伟芹, 王晓川, 郝富昌, 等.
基于迭代算法的磨料颗粒加速机制研究[J]. 中国石油大学学报(自然科学版), 2016, 40(4): 104–109.
ZUO Wei-qin, WANG Xiao-chuan, HAO Fu-chang, et al. Research on acceleration mechanism of abrasive in pre-mixed abrasive water-jet based on iterative algorithm[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016, 40(4): 104–109. DOI:10.3969/j.issn.1673-5005.2016.04.013 |
| [14] | DEEPAK D, CORNELIO J A Q, ABRAHAM M M, et al. Numerical analysis of the effect of nozzle geometry on flow parameters in abrasive water jet machines[J]. Pertanika Journal of Science & Technology, 2017, 25(2): 497–506. |
| [15] |
王志阳, 王凯.
基于FLUENT的磨料水射流抛光喷嘴的流场仿真[J]. 中国设备工程, 2017(9): 101–103.
WANG Zhi-yang, WANG Kai. Abrasive water jet flow field simulation of polishing nozzles based on FLUENT[J]. China Plant Engineering, 2017(9): 101–103. DOI:10.3969/j.issn.1671-0711.2017.09.053 |
| [16] |
王福军.
计算流体动力学[M]. 北京: 清华大学出版社, 2004: 54-57.
WANG Fu-jun. Computational fluid dynamics[M]. Beijing: Tsinghua University Press, 2004: 54-57. |
| [17] |
唐家鹏.
FLUENT14.0超级学习手册[M]. 北京: 人民邮电出版社, 2013: 30-39.
TANG Jia-peng. FLUENT14.0 super study manua[M]. Beijing: People Post Press, 2013: 30-39. |
| [18] | PRISCO U, D'ONOFRIO M C. Three-dimensional CFD simulation of two-phase flow inside the abrasive water jet cutting head[J]. International Journal for Computational Methods in Engineering Science and Mechanics, 2008, 9(5): 300–319. DOI:10.1080/15502280802225598 |



