2. 哈尔滨工业大学 机器人技术与系统国家重点实验室, 黑龙江 哈尔滨 150001
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China
月面钻取采样及样品返回对于深空探测具有十分重要的意义,相对于遥感探测等非接触式探测手段而言,通过钻取采样获得的信息更加全面、真实,且具有更高的可靠性[1]。钻具热特性的研究对于钻具构型的设计、钻进规程的设置具有指导性作用,有助于采样探测工程的成功实施[2-3]。NASA(National Aeronautics and Space Administration)对Apollo任务返回样品中的晶质火成岩、角砾岩样本进行对比研究,发现在143~423 K的温度条件下,月壤的热扩散性较差[4]。特别地,月壤的组成与结构会对月壤颗粒间的热传递特性产生影响[5-6]。苏联的Luna 16为了削弱过高钻具温度给钻采作业带来的不良因素,选择在月夜开展采样作业。同时为确保钻进的热安全性,对不同密度的钻进对象采用不同的钻进速度。而我国探月三期工程采用回转冲击钻对月表土壤进行预计深度为2米的采样作业。采样过程中钻具的热特性对采样作业至关重要, 为了采样探测工程的顺利实施,必须研究作业全过程中钻采机具与钻采对象的温升与散热情况[7]。
本研究主要从两方面来开展。一方面,基于仿真手段,研究钻进过程中月壤的热特性。特别地,引入离散元仿真软件,建立月壤颗粒模型,逼近月壤颗粒的真实接触状态,以模拟钻探作业过程中月壤颗粒间的热传递特性[8]。另一方面,通过实验手段,利用光纤光栅传感器获取钻头多点的温度,进行钻进过程中钻具的热特性研究。
1 钻进过程月壤热特性仿真研究 1.1 月壤颗粒仿真模型的构建月壤颗粒仿真模型的构建是开展月壤热特性仿真研究的首要且必要工作。月壤颗粒的形态及其粒度的分布情况影响着月壤的颗粒组成,所以月壤颗粒仿真模型应尽量反映微元颗粒所具有的不同大小和形状,并能够反映月壤颗粒的组成[9]。
月壤颗粒的研究主要是基于Apollo和Luna所采集到的月壤样本[9-10]。根据后期在实验室的样本分析可知,月壤的粒径基本上为30 μm~1 mm,平均粒径为70 μm,其颗粒的不均匀度通常在2~3.5之间,所以月壤的分选性比较差[11-12]。
本研究针对单一颗粒微元,建立如图 1所示的4种不同构型的月壤颗粒微元模型,用以等效月壤颗粒。

|
| 图 1 月壤颗粒微元模型 Fig.1 Microelement model of lunar soil particle |
另外,针对同一构型月壤微粒,设定差异化的粒径等级。以上述月壤颗粒微元模型为基础,生成系列放大倍数的颗粒组,以模拟月壤的不均一性与不同的颗粒粒径。最终形成的月壤颗粒仿真模型的粒径分布如表 1所示。
| 颗粒微元模型类型 | 放大倍数 | 颗粒数量/个 |
| 球形月壤 | 1 | 400 |
| 1.5 | 400 | |
| 1 | 400 | |
| 长条形月壤 | 1.5 | 400 |
| 4 | 3 | |
| 1 | 400 | |
| 次棱角形月壤 | 1.5 | 400 |
| 4 | 3 | |
| 1 | 400 | |
| 棱角形月壤 | 1.5 | 400 |
| 4 | 3 |
根据现有的月壤仿真模型及月壤材料特性,设置如表 2所示的月壤颗粒物理参数[13-16]。
| 物理参数 | 数值 |
| 泊松比 | 0.43 |
| 密度/(kg/m3) | 3.1×103 |
| 回复系数 | 0.12 |
| 静摩擦系数 | 1.032 |
| 滚动摩擦系数 | 0.27 |
高温小颗粒群法是把热源设定为位于钻头下方的一族高温小颗粒群,模拟钻具在回转钻进时切削刃的切削热[17-18]。该颗粒群将粘合在同一个平面上,且始终离钻头一定距离。在回转钻进过程中,该粘合面只会对高温小颗粒起粘贴作用,而不会与模拟月壤颗粒发生作用。当模拟月壤颗粒经过该平面时,二者相互热传导,从而实现热量的传递。该方法由于热源位于钻具末端且可控,理论上能很好地反映模拟月壤颗粒受热后的温升现象。
基于该分析方法,结合实际钻进过程中的钻进参数,本研究采用EDEM软件进行月壤钻进仿真分析。表 3所示为月壤钻进仿真分析的参数设置情况[19],图 2为仿真结果。在钻进过程中,高温小颗粒群高速回转,表层月壤颗粒与实际钻进状况相似,产生飞溅运动。在仿真过程中,若月壤颗粒长时间与热颗粒接触,会导致月壤颗粒温升过高。这与实际钻进状况不符,但是这对高温颗粒的散热求解几乎没有影响。根据图 2的离散元仿真结果可知,处于钻具外侧的颗粒温度较低,无法通过仿真手段体现钻具侧壁与月壤颗粒切削、摩擦产生的热量,这是由高温颗粒集中在钻头下方的粘合面附近所造成的。
| 参数 | 数值 |
| 冷颗粒初始温度/K | 350 |
| 热颗粒初始温度/K | 1 250 |
| 热颗粒数量/个 | 140 |
| 冷颗粒数量/个 | 2 400 |
| 进尺速率/(mm/s) | 5 |
| 回转速度/(r/min) | 200 |
| 颗粒比热容/(J/(kg·K)) | 800 |
| 颗粒导热系数/(W/(m·K)) | 1 450 |

|
| 图 2 基于EDEM软件的月壤钻进离散元仿真结果 Fig.2 Simulation results of lunar soil drilling by discrete element method based on EDEM software |
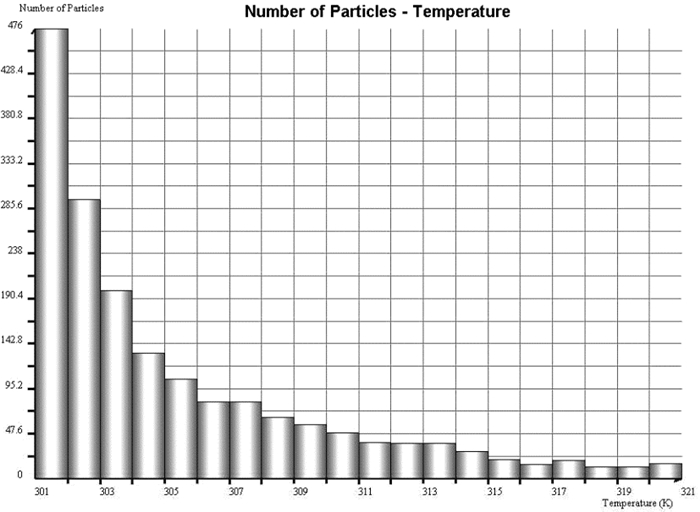
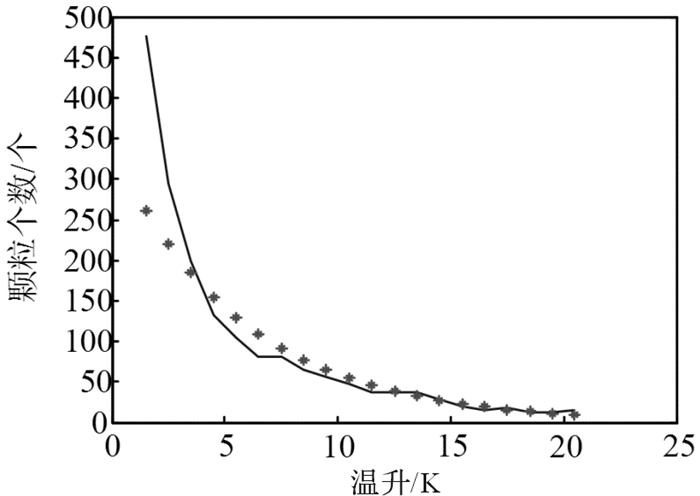
基于仿真结果,对模拟月壤颗粒温升分布进行统计,得到图 3所示温升为1~21 K的颗粒分布信息。各温升下颗粒的数量随着温度的升高呈指数分布,颗粒数量与温升之间的关系可以近似用式(1)表示,拟合曲线如图 4所示。
| $ N = 339.3{{\rm{e}}^{ - 0.1743\Delta t}} $ | (1) |
|
| 图 3 基于高温小颗粒群法得到的温升为1~21 K的颗粒分布图 Fig.3 Particle distribution diagram with temperature rise of 1~21 K based on high temperature small particle cluster method |
|
| 图 4 月壤颗粒数量与温升之间的拟合曲线 Fig.4 Fitting curve of lunar soil particles number and temperature rise |
式中:N为颗粒数量,个;Δt为颗粒温升,K。
在仿真过程中,按仿真时间长短选取2个时间步长,可以拟合得到:
| $ N = 122.8{{\rm{e}}^{ - 0.1656\Delta t}} $ | (2) |
| $ N = 210.0{{\rm{e}}^{ - 0.1632\Delta t}} $ | (3) |
月壤颗粒之间的热传递形式表现为式中的幂指数。基于式(1)至式(3),仿真时间步长越大,拟合公式的系数越大,意味着同一温升状态下,随着传热时间的增加,颗粒数量会增加。当仿真时间较短时,月壤的散热量和温升都比较小。
上述统计规律与实际钻进状况并不完全相符,但对钻具热特性研究具有一定的指导意义。位于高温小颗粒群附近的模拟月壤颗粒,由于长时间与高温颗粒接触,温升较大,这种现象与实际钻进过程不符。钻具下方的月壤颗粒在取心机构或外螺旋钻杆的作用下,会被收集到取芯软袋中或者被转移到钻杆螺旋槽内,不会被持续加热。仿真中一些颗粒存在较大的温升现象,这与某些恶劣钻进工况下的切削热现象接近。仿真分析结果及温升颗粒数量模型为后续的钻具热特性实验提供了一定的基础。
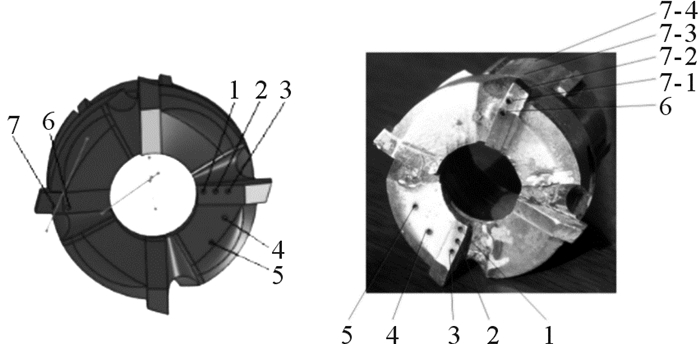
2 模拟月壤钻进过程钻具热特性实验与常规的钻取采样实验不同,钻具热特性实验需要采集钻具的温度信息。基于常规取芯钻具构型,在钻头不同部位选择温度测量点,最终选取了钻头端面的7个测量点,并在测量点7处补充了若干测点,如图 5所示。
|
| 图 5 钻头端面温度测量点分布 Fig.5 Distribution of temperature measuring points of drill bit end surface |
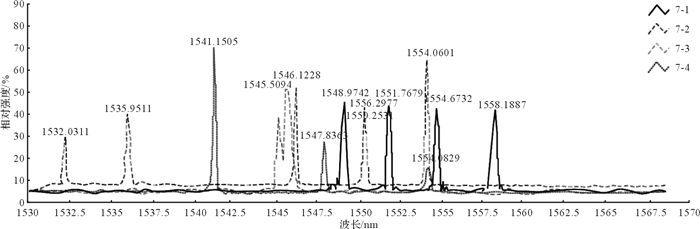
随后,在分布式测量点处布置光纤光栅温度传感器。首先在选点处开孔,从图 5可以看出测量点7沿钻杆的外壁均布,同时将均匀周期的光纤光栅封装为管状。在测量点1,2,…,6中,依次插入封装好的温度传感器,并采用耐高温胶进行固定。针对温度测量点7,将封装在毛细管中的4根串接光栅插入其中并用耐高温胶固定,用于检测钻头侧面沿轴向的温度分布情况,测试结果如图 6所示。
|
| 图 6 测量点7的传感器测试结果 Fig.6 The sensor measurement results of measuring point 7 |
图 7所示为钻取采样实验台,可实现的最大钻深为2 m,钻具的最大转速为300 r/min, 最大进尺速率为1 000 mm/min。

|
| 图 7 钻取采样实验台 Fig.7 Drilling sampling test bench |
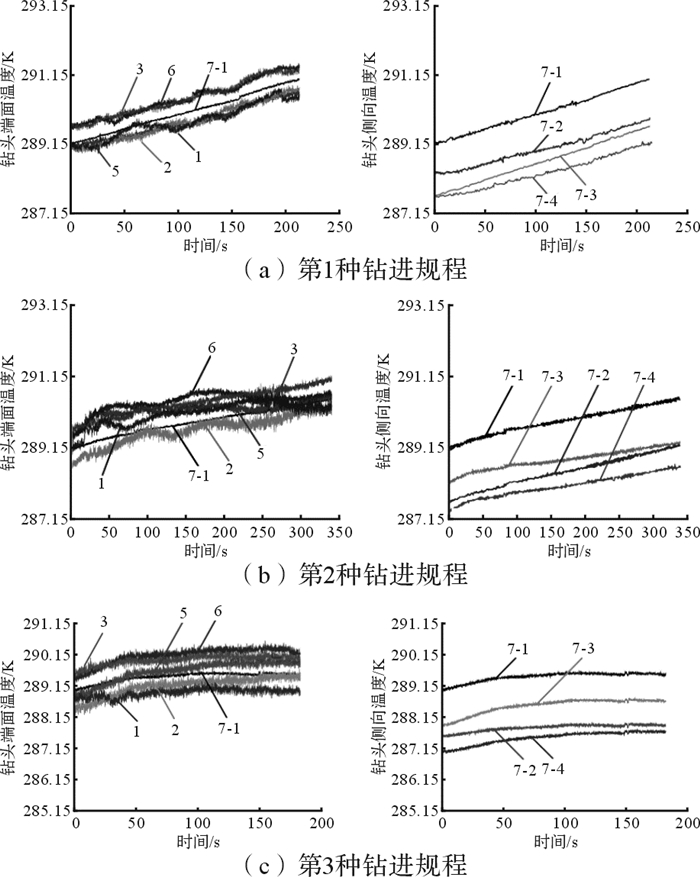
钻具热特性实验的钻进规程设置如表 4所示。该实验在地面环境下进行,暂不考虑月面的高低温、超真空环境,初步研究钻进规程对钻进温升的影响。通过改变钻具的回转转速和进尺速率,获得钻具测温点在不同钻进参数下的温度信息,以研究钻具的温升规律及钻进参数对钻具温升的影响,图 8所示为本实验的大致流程,图 9为具体的实验结果。
| 钻进规程 | 回转转速/ (r/min) |
进尺速度/ (mm/min) |
时间/s | 室温/K |
| 1 | 80 | 30 | 213 | 287.65 |
| 2 | 80 | 20 | 341 | 287.65 |
| 3 | 60 | 30 | 183 | 287.65 |
|
| 图 8 钻具热特性实验流程 Fig.8 Flow chart of drilling tool thermal characteristic experiment |
|
| 图 9 不同钻进规程下钻具热特性实验结果 Fig.9 Thermal characteristic experimental results of drilling tool under different drilling procedures |
基于上述实验结果,可以发现:
1) 相同实验时间内,回转转速和进尺速率中单一因素的变化都会引起钻头各测点温度的变化;
2) 钻头同一侧向上,靠近端面测量点的温度更高,温升也相对更明显,同时测量点间的温差趋于上升;
3) 在不考虑月面初始温度条件以及月面真空环境的情况下,本文实验所得的钻具热特性不会影响钻具正常工作。
3 结论本文基于月面钻取采样探测工程任务,主要开展了以下两方面的研究工作:
1) 利用离散元方法对模拟月壤钻进过程进行了仿真研究。建立了月壤颗粒的微元模型,提出温升颗粒数量随温度升高的近似分布函数,即温升颗粒数量模型,该指数模型可以用于预测实际钻进过程中的散热量。
2) 在对常规钻取采样实验测温点进行一定改造的基础上开展了模拟月壤钻进过程钻具热特性研究,得出钻具温升与钻进参数之间的关系,初步验证了钻具的热安全性,为后续开展低温热真空钻进试验提供依据。
| [1] |
欧阳自远, 张熇.
从人造卫星到月球探测器[M]. 上海: 上海科技教育出版社, 2007: 155-160.
OUYANG Zi-yuan, ZHANG He. From satellites to lunar probes[M]. Shanghai: Shanghai Science and Technology Education Press, 2007: 155-160. |
| [2] |
侯佑松.月面钻取采样过程钻具热特性测试系统研制与试验研究[D].哈尔滨: 哈尔滨工业大学机电工程学院, 2013: 11-25.
HOU You-song. Drill thermal characteristics test system development and experiment research of the lunar surface drilling sampling process[D]. Harbin: Harbin Institute of Technology, School of Mechanical and Electric Engineering, 2013: 11-25. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014001859.htm |
| [3] |
王长江.深井钻具失效的理论研究[D].大庆: 东北石油学院石油工程学院, 2006: 5-9.
WANG Chang-jiang. Academic research of drillstem failure in deep well[D]. Northeast Petroleum University, School of Petroleum Engineering, 2006: 5-9. http://cdmd.cnki.com.cn/article/cdmd-10220-2006058564.htm |
| [4] | HORAI K, SIMMONS G, KANAMORI H, et al. Thermal diffusivity, conductivity and thermal inertia of Apollo 11 lunar material[R]. Geochimica et Cosmochimica Acta Supplement, 1970, 1: 2243. |
| [5] | ALLTON J H. Catalog of Apollo lunar surface geological sampling tools and containers[R]. Washington: Johnson Space Center, NASA, 1989. |
| [6] |
孙灵芝, 凌宗成, 刘建忠.
美国阿波罗月球样品的处理与保存[J]. 地学前缘, 2012, 19(6): 128–136.
SUN Ling-zhi, LING Zong-cheng, LIU Jian-zhong. An introduction to the curation of Apollo lunar samples[J]. Earth Science Frontiers, 2012, 19(6): 128–136. |
| [7] | LANGSETH Jr M G, CLARK Jr S P, CHUTE Jr J L, et al. The Apollo 15 lunar heat-flow measurement[J]. The Moon, 1972, 4(3/4): 390–410. |
| [8] |
周强.基于离散元方法的颗粒材料热传导研究[D].大连: 大连理工大学工程力学系, 2011: 44-65.
ZHOU Qiang. A numerical study on thermal conduction within granular materials based on discrete element method[D]. Dalian: Dalian University of Technology, Department of Engineering Mechanics, 2011: 44-65. http://cdmd.cnki.com.cn/Article/CDMD-10141-1011109369.htm |
| [9] |
郑永春, 欧阳自远, 王世杰, 等.
月壤的物理和机械性质[J]. 矿物岩石, 2004, 24(4): 14–19.
ZHENG Yong-chun, OUYANG Zi-yuan, WANG Shi-jie, et al. Physical and mechanical properties of lunar regolith[J]. Journal of Mineralogy & Petrology, 2004, 24(4): 14–19. DOI:10.3969/j.issn.1001-6872.2004.04.003 |
| [10] | TIEN C L, NAYAK A L. Analytical models for lunar soil thermal conductivity[C]//AIAA 10th Thermophysics Conference, Denver, May 27-29, 1975. |
| [11] | GREEN D H, RINGWOOD A E. Significance of a primitive lunar basaltic composition present in Apollo 15 soils and breccias[J]. Earth and Planetary Science Letters, 1973, 19(1): 1–8. DOI:10.1016/0012-821X(73)90172-6 |
| [12] | AFSHAR M N, WU C Y, SORLOAICA H N. Efficiency determination of an electrostatic lunar dust collector by discrete element method[J]. Journal of Applied Physics, 2012, 112(2): 023305-1–023305-9. |
| [13] |
尹忠旺, 丁希仑, 郑岳山.
基于ABAQUS的月壤有限元建模及仿真分析[J]. 军民两用技术与产品, 2008(11): 46–48.
YIN Zhong-wang, DING Xi-lun, ZHENG Yue-shan. Finite element modeling and simulative analysis for lunar regolith based on ABAQUS[J]. Dual Use Technologies & Products, 2008(11): 46–48. DOI:10.3969/j.issn.1009-8119.2008.11.017 |
| [14] |
朱立平, 袁竹林, 闫亚明, 等.
基于离散单元法的丝状颗粒传热数学模型[J]. 化工学报, 2012, 63(7): 2051–2058.
ZHU Li-ping, YUAN Zhu-lin, YAN Ya-ming, et al. Model of heat transfer in filamentous granular materials based on discrete element method[J]. CIESC Journal, 2012, 63(7): 2051–2058. DOI:10.3969/j.issn.0438-1157.2012.07.008 |
| [15] | IORDANOFF I, ILIESCU D, CHARLES J L, et al. Discrete element method, a tool to investigate complex material behaviour in material forming[C]//NUMIFORM 2010: Proceedings of the 10th International Conference on Numerical Methods in Industrial Forming Processes Dedicated to Professor O. C. Zienkiewicz (1921-2009), Pohang, Jun. 13-17, 2010. |
| [16] | AMINZADEH A, HOSSEININIA E S. A study on the effect of particle shape and fragmentation on the mechanical behavior of granular materials using discrete element method[C]//Powders and Grains 2013: Proceedings of the 7th International Conference on Micromechanics of Granular Media. American Institute of Physics, Sydney, Jul. 8-12, 2013. |
| [17] | BURKHART G H, RICE R R. Determination of the thermal conductivity of barium sodium niobate[J]. Journal of Applied Physics, 2008, 48(11): 4817–4818. |
| [18] | ANDERSSON P, BÄCKSTRÖM G. Pressure dependence of the thermal conductivity of an epoxy resin[J]. Journal of Applied Physics, 2003, 44(2): 705–707. |
| [19] | BAHRAMI M, YOVANOVICH M M, CULHAM J R. A compact model for spherical rough contacts[J]. Journal of Tribology, 2005, 127(4): 884–889. DOI:10.1115/1.2000982 |


